Определение метрологических характеристик и экспериментальное исследование осциллографа приставки
Выпускная квалификационная работа. Часть 5.
5.1 Основные определения
5.2 Погрешности АЦП
5.3 Экспериментальные исследования
5.4 Выводы
Измерение – это операция, в результате которой мы узнаем, во сколько раз измеряемая величина больше или меньше соответствующей величины, принятой за эталон.
Интегральная нелинейность — представляет собой максимальное отклонение любого кода от прямой линии, проведенной через крайние точки передаточной функции АЦП. Крайними точками являются: нулевая, находящаяся на 0.5LSB ниже точки появления первого кода, и последняя — на 0.5LSB выше граничного кода шкалы.
Дифференциальная нелинейность DNL (differential non-linearity) — представляет собой разницу между измеренной и идеальной шириной 1 кванта (1 LSB) АЦП.
Ошибка смещения — представляет собой отклонение момента первичной смены кода с (000Н) на (001Н) от идеального значения, то есть +0.5LSB.
Ошибка усиления — представляет отклонение реального коэффициента усиления тот идеального.
LSB (least significant bit) или МЗБ (младший значащий бит) – это наименьшее значение напряжения, которое может быть измерено АЦП. Находиться по формуле:
где Uоп – значения источника опорного напряжения (ИОН), N разрядность АЦП. В данном случае:
Uоп = 2,5 В — значение напряжения внутреннего ИОН.
Систематические ошибки – ошибки, величина которых одинакова во всех измерениях, приводящих одним и тем же методом с помощью одних и тех же измерительных приборов. Ошибка смещения и ошибка усиления относятся к случайным ошибкам.
Случайные ошибки – ошибки, величина которых различна даже дл измерений, выполненных одинаковым образом.
Интегральная и дифференциальная нелинейности относятся к систематические ошибкам.
В АЦП и ЦАП различают четыре типа погрешностей по постоянному току: погрешность смещения, погрешность усиления и два типа погрешностей, связанных с линейностью: интегральная и дифференциальная нелинейность. Погрешности смещения и усиления АЦП и ЦАП аналогичны погрешностям смещения и усиления в усилителях.
Погрешность смещения равна погрешности нуля во всем диапазоне входного напряжения и постоянна.
Погрешность усиления вызывает погрешность смещения. Причем погрешность смещения не постоянна и не равна погрешность смещения нуля.
Интегральная нелинейность ЦАП и АЦП аналогична нелинейности усилителя и определяется как максимальное отклонение фактической характеристики передачи преобразователя от прямой линии.
В общем случае, она выражается в процентах от полной шкалы (но может представляться в значениях младших разрядов). Существует два общих метода аппроксимации характеристики передачи: метод конечных точек и метод наилучшей прямой.
При использовании метода конечных точек измеряется отклонение произвольной точки характеристики от прямой, проведенной из начала координат. Таким образом, измеряют значения интегральной нелинейности преобразователей, используемых в задачах измерения и управления.
Метод наилучшей прямой дает более адекватный прогноз искажений в приложениях, имеющих дело с сигналами переменного тока. Он менее чувствителен к нелинейностям технических характеристик. По методу наилучшего приближения через характеристику передачи устройства проводят прямую линию, используя стандартные методы интерполяции кривой. После этого максимальное отклонение измеряется от построенной прямой.
Другой тип нелинейности преобразователей – дифференциальная нелинейность. Она связана с нелинейностью кодовых переходов преобразователя. В идеальном случае изменение на единицу младшего разряда цифрового кода точно соответствует изменению аналогового сигнала на величину единицы младшего разряда. В АЦП, при переходе с одного цифрового уровня на следующий, значение сигнала на аналоговом входе должно измениться точно на величину, соответствующую младшему разряду цифровой шкалы. Наиболее распространенным проявлением
Переходы АЦП (идеальные) имеют место, начиная с 1/2 LSB выше нуля, и далее через каждый LSB, до 11/2 LSB ниже полной аналоговой шкалы. Так как входной аналоговый сигнал АЦП может иметь любое значение, а выходной цифровой сигнал квантуется, может существовать различие до 1
Этот эффект известен как ошибка или неопределенность квантования. В приложениях, использующих сигналы переменного тока, эта ошибка квантования вызывает явление, называемое шумом квантования.Среднеквадратичное значение шума. приблизительно равно весу наименьшего значащего разряда (LSB) Δ, деленному на √12. При этом предполагается, что амплитуда сигнала составляет, по крайней мере, несколько младших разрядов, так что выход АЦП изменяет свое состояние почти при каждом отсчете. Сигнал ошибки квантования от входного линейного пилообразного сигнала аппроксимируется сигналом пилообразной формы с максимальным размахом Δ , и его среднеквадратичное значение равно
Отношение среднеквадратичного значения синусоидального сигнала, соответствующего полной шкале, к среднеквадратичному значению шума квантования (выраженное в дБ) равно:
где SNR (signal to noise ratio) – отношение сигнал-шум, N — число разрядов в идеальном АЦП.
Таким образом, для АЦП микроконвертора ADUC842, используемого в лабораторном стенде LESO1, справедливо:
Для оценки погрешностей АЦП приведем характеристику АЦП, где указаны погрешности в значениях LSB и в напряжениях.
Таблица 5.1 – Характеристики АЦП ADuc842
| Параметры | Значение в LSB | Значение в мкВ | Примечание | |
| Точность по постоянному току | Разрядность | 12 битный | От внутреннего ИОН Uоп = 2,5 В | |
| Интегральная нелинейность | ±1 макс. ±0,3 сред. | ±610 макс. ±183 сред.  | ||
| Дифференциальная нелинейность | ±1 макс. ±0,3 сред. | ±610 макс. ±183 макс. | ||
| Калибровочные ошибки конечных точек шкалы | Ошибка смещения | ±3 макс | ±1830 макс. | |
| Ошибка усиления | ±3 макс. | ±1830 макс. | ||
| Аналоговый вход | Диапазон входных напряжений | 0 ÷ Uоп В. | ||
| Входной ток | ±1 мкА макс. | |||
| Входная емкость | 32 пФ сред. | |||
Так как интегральная и дифференциальная нелинейности относятся к случайным ошибкам и являются независимыми друг от друга ошибками их необходимо сложить по «закону сложения независимых случайных ошибок»:
где X1,…,Xn – номинальные значения независимых случайных величин, ΔX1,…,ΔXn – ошибки случайных величин, Y — номинальное значение конечной измеряемой величины, ΔY – абсолютная ошибка конечной измеряемой величины.
Случайная ошибка АЦП будет состоять из интегральной и дифференциальной нелинейности, а также из ошибки квантования, которая составляет Δ/2 = 610мкВ/2 = 305мкВ = 0,305·10-3 В. Номинальное значения этих величин есть опорное напряжение АЦП, которое равно 2,5В.
Итак, относительная ошибка измерения АЦП:
Из относительной ошибки измерения АЦП найдем абсолютное значение ошибки измерения:
Систематическую ошибку составляют ошибка смещения нуля и ошибка усиления. Так как основную часть ошибки смещения и ошибки усиления вносит тракт передачи сигнала (инструментальный усилитель и масштабирующее звено), поправки вносятся программной калибровкой в LabVIEW.
5.3 Экспериментальные исследования
В задачу каждого измерения входит оценка точности полученного результата. Но в результате измерении мы всегда получаем нужную величину с некоторой погрешностью.Смысл экспериментальных исследований состоит в том, чтобы проверить на опыте теоретические выкладки и дать оценку характеристикам прибора.
Результат экспериментального исследования АЧХ устройства без цифрового фильтра или аналогового фильтра Бесселя записан в таблице 5.2. Экспериментальные данные были сняты с помощью низкочастотного генератора сигналов Г3-112.
Таблица 5.2 – Измеренное АЧХ устройства без цифрового фильтра
| 0 | 5,00 | 0,00 |
| 10 | 5,00 | 0,00 |
| 20 | 4,88 | -0,21 |
| 30 | 4,68 | -0,58 |
| 40 | 4,31 | -1,28 |
| 50 | 3,95 | -2,04 |
| 60 | 3,43 | -3,28 |
| 70 | 2,90 | -4,72 |
| 80 | 2,34 | -6,60 |
| 90 | 1,77 | -8,99 |
| 100 | 1,24 | -12,10 |
| 110 | 0,94 | -14,56 |
| 120 | 0,64 | -17,90 |
| 130 | 0,43 | -21,36 |
| 140 | 0,26 | -25,75 |
| 150 | 0,18 | -29,00 |
| 160 | 0,13 | -31,77 |
Проверим, действие цифрового фильтра на сигнал.
Результаты измерения АЧХ после цифрового фильтра приведены в таблице 5.3.
Таблица 5.2 – Измеренное АЧХ устройства без цифрового фильтра
| 0 | 5,00 | 0,00 |
| 10 | 5,00 | 0,00 |
| 20 | 5,00 | 0,00 |
| 30 | 5,00 | 0,00 |
| 40 | 5,00 | 0,00 |
| 50 | 5,00 | 0,00 |
| 60 | 4,80 | -0,36 |
| 70 | 4,23 | -1,45 |
| 80 | 3,67 | -2,69 |
| 90 | 2,94 | -4,62 |
| 100 | 2,26 | -6,91 |
| 110 | 1,61 | -9,83 |
| 120 | 0,73 | -16,67 |
| 130 | 0,23 | -26,60 |
| 140 | 0,08 | -35,85 |
| 150 | 0,00 | -60,32 |
| 160 | 0,00 | -71,66 |
Для сравнения действия цифрового фильтра, приведем графики АЧХ устройства без и с цифровым фильтром.
Как видно из рисунка 6.6, цифровой фильтр выравнивает амплитудную неравномерность. Полоса пропускания цифрового осциллографа-приставки на уровне -3 дБ, равна от 0 до 80 кГц.
Нелинейные искажения измерительного тракта можно оценить по первой гармонике. Уровень первой гармоники при номинальном входном напряжении Uвх = 5В на частоте 10 кГц равен -65дБ.
На цифровой осциллограф-приставку подавались тестовые испытательные сигналы трех видов: синусоидального, треугольного и прямоугольного частотой 10 кГц. Результаты измерений приведены на рисунках 5.8, 5.9 и 5.10 соответственно синусоидального, треугольного и прямоугольного сигналов.
9 — Измерение треугольного сигнала цифровым осциллографом-приставкой
5.4 Выводы
Проанализированы основные источники погрешности измерений, определено из чего состоит ошибка измерения цифровым осциллографом-приставкой. Она состоит в из случайной и систематической ошибок. Случайная ошибка АЦП менее 0,1 %, а систематическая корректируется программной калибровкой в LabVIEW.
На рисунке 5.6 показано, насколько цифровой фильтр корректирует АЧХ аналогового фильтра.
Экспериментальные исследования тестовыми сигналами показывают, что уровень первой гармоники при номинальном входном напряжении Uвх = 5В на частоте 10 кГц равен -65дБ, что очень хорошо.
стоячих волн на струне
стоячих волн на струне Основная мода колебаний натянутой струны такова, что длина волны в два раза превышает длину струны. Применение основного волнового соотношения дает выражение для основной частоты:
можно представить в виде: Струна также будет вибрировать на всех гармониках основного тона. Каждая из этих гармоник образует на струне стоячую волну. Здесь показана резонансная стоячая волна на струне. Он приводится в действие вибратором с частотой 120 Гц. Для струн конечной жесткости частоты гармоник будут постепенно отклоняться от математических гармоник. Чтобы получить необходимую массу для струн электрического баса, как показано выше, проволока наматывается на сплошной сердечник. Это позволяет добавлять массу, не создавая чрезмерной жесткости.
| Индекс Концепции периодического движения Концепции резонанса | ||||||||||
| Назад |
Скорость бегущей волны в натянутой струне определяется натяжением и массой на единицу длины струны.
Когда волновое соотношение применяется к натянутой струне, видно, что возникают резонансные моды стоячих волн. Самая низкая частота моды для натянутой струны называется основной, и ее частота определяется как Из скорость = м/с Любое из выделенных количеств можно рассчитать, нажав на них. Если числовые значения не введены для какого-либо количества, по умолчанию будет строка длиной 100 см, настроенная на 440 Гц. Значения по умолчанию будут введены для любой величины, имеющей нулевое значение. Любые количества могут быть изменены, но затем вы должны нажать на количество, которое вы хотите рассчитать, чтобы согласовать изменения.
| Index Концепции периодического движения Концепции резонанса | ||||||||||||||||||||||||||||||||||||||||||||||||||
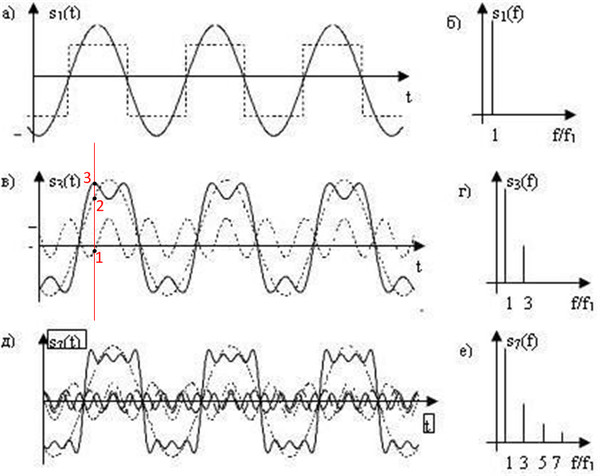
Ряд Фурье и гармоническое приближениеВ этой статье мы рассмотрим происхождение преобразования Фурье: ряд Фурье . Ряд Фурье берет периодический сигнал $x(t)$ и описывает его как сумму синусоиды и косинуса. Заметив, что синус и косинус сами по себе являются периодическими функциями, становится ясно, что $x(t)$ также является периодической функцией. 9Tx(t)\sin(2\pi \frac{nt}{T})dt\end{align}.$$ Обратите внимание, что для функции с периодом $T$ частоты синусов и косинусов равны $ \frac{1}{T}, \frac{2}{T}, \frac{3}{T}, \dots$, т.е. кратны основной частоте $\frac{1}{T}$, что является обратной длительностью периода функции. Проверим вычисление коэффициентов Фурье и восстановление функции численно. Во-первых, мы определяем некоторые функции с периодом $T=1$, которые мы хотим разложить в ряд Фурье: Теперь давайте напишем функцию И используем ее для вычисления коэффициентов до 20-го порядка для первой функции: Здесь мы делаем два замечания: Во-первых, мы видим, что $a_n=0$. Из графика для функции 1 видно, что это нечетная функция, т.е. $x(t)=-x(-t)$. В этом случае ряд Фурье содержит только нечетные функции, которые представляют собой исключительно члены, включающие синусы (поскольку $\sin(x)=-\sin(-x)$). Во-вторых, коэффициенты Фурье $b_n$ медленно убывают со скоростью $1/n$ и каждое второе $b_n$ равно нулю. Теперь рассмотрим реконструкцию сигнала, т.е. вычислим $x(t)$ по его коэффициентам ряда Фурье до заданного порядка. Для этого напишем функцию Давайте посмотрим на реконструированный сигнал для нашей прямоугольной функции до 20-й гармоники: Как мы видим, восстановленный сигнал примерно соответствует исходному, а чем больше гармоник используется, тем лучше. Однако мы также видим, что особенно в области скачка при $t=0,5$ восстановленный сигнал не является точным. Вместо этого реконструированный сигнал значительно колеблется в этом положении. Теперь посмотрим на ряды Фурье некоторых функций и на то, как выглядит их аппроксимация рядами Фурье для разного числа гармоник: Сначала мы снова видим прямоугольную функцию. С увеличением числа гармоник мы видим, что прямая аппроксимируется лучше. Однако мы также видим, что величина выброса на разрыве скачка остается постоянной, независимо от числа гармоник. Далее идет функция периодического линейного изменения. Опять же, мы видим, что величина выброса на разрыве не зависит от количества гармоник. Однако продолжительность колебаний становится короче, и в целом аппроксимация становится лучше при большем количестве гармоник. Третья функция выглядит более сложной, так как имеет больше переходов и в целом более нерегулярна, чем предыдущие функции. На самом деле в нижней части графика имеется значительный выброс, который очень медленно уменьшается с увеличением количества гармоник. Это происходит из-за большого количества разрывов функции. Функция является четной функцией, т. е. $x(t)=x(-t)$. Следовательно, все $b_n=0$, что соответствует вкладу синусоиды. Вместо этого только волны косинуса, которые являются четными функциями, составляют полный ряд Фурье. Наконец, мы рассмотрим функцию периодической параболы. Во-первых, мы признаем, что функция хорошо аппроксимируется только очень небольшим количеством гармоник. Это можно объяснить общей гладкостью функции без разрывов. Кроме того, мы снова определяем, что $b_n=0$, поскольку $x(t)$ — четная функция, т.  |
Высота тона изменяется по-разному в зависимости от этих различных параметров, как показано в примерах ниже:
Поэтому частота $\frac{n}{T}$ называется $n$-й гармоникой . Название гармоники связано с тем фактом, что для человеческого уха частоты с целочисленными отношениями звучат «хорошо», и все частоты являются целыми кратными основной частоты.
Мы можем объяснить это, связав это со знанием преобразования Фурье: функция представляет собой сумму двух прямоугольных функций ширины $\frac{1}{2}s$. Мы знаем, что преобразование Фурье такого прямоугольника является sinc-функцией, имеющей нули на расстоянии $2Hz$. Кроме того, величина sinc-функции затухает с $1/f$. Это очень согласуется с полученными коэффициентами: они затухают с $1/n$, и каждое второе значение равно нулю.
Это явление называется феноменом Гиббса и описывает тот факт, что ряд Фурье имеет большие колебания вокруг скачкообразных разрывов. В частности, высота перерегулирования или недорегулирования не зависит от числа гармоник и составляет примерно 9% высоты прыжка. Однако длительность колебаний уменьшается с увеличением числа гармоник, что в итоге приводит к правильной аппроксимации в пределе для бесконечного числа гармоник.
Также, кроме постоянной составляющей $a_0$, все коэффициенты $a_n=0$. Это опять-таки связано с тем, что функция нечетная, т.е. имеем $x(t)=1-x(-t)$. Следовательно, только компоненты синусоиды отличны от нуля.