Для чего нужна шестнадцатеричная система счисления
Содержание
- Понятие шестнадцатеричной системы счисления
- Применение
Благодаря стремительному внедрению информатизации в повседневную жизнь человека, хотя бы малейшее представление об основах информатики и систем счисления имеет каждый школьник. Но для многих надписи в компьютере вроде «1FEE» остаются загадочным шифром. Мало кто представляет, что такое шестнадцатеричная система счисления, и для чего она нужна.
Понятие шестнадцатеричной системы счисления
Привычная для человека система счисления – десятичная. В ее основу входят десять цифр от 0 до 9. Шестнадцатеричную систему отличает наличие в ней первых шести букв латинского алфавита для записи чисел помимо основных цифр. То есть после цифры 9 следует символ «A», который соответствует числу 10 для десятичной системы. Соответственно, F в шестнадцатеричной системе – это 16 в десятичной.
Использование шестнадцати символов в системе – неслучайный выбор.
Единица информации – бит. Восемь бит образуют байт. Существует такое понятие, как машинное слово – это единица данных, представляющая собой два байта, то есть шестнадцать бит. Таким образом, используя шестнадцать различных символов, можно описывать любую информацию, которая при обмене данных будет наименьшей частицей. С ними можно производить любые арифметические действия, результат, соответственно, получится тоже в шестнадцатеричной системе.
Для того чтобы отличать, что число записано в шестнадцатеричной системе, после него записываютбукву «h» или нижний индекс «16».
Применение
Наиболее широкое применение шестнадцатеричной системы счисления – это коды ошибок программных продуктов, например, операционной системы. Числа, заложенные в этих кодах, стандартизированы. Имея специальную таблицу, всегда можно определить, что именно означает та или иная ошибка.
В языках низкого уровня, максимально приближенным к машинным кодам шестнадцатеричная система применяется для написания программ.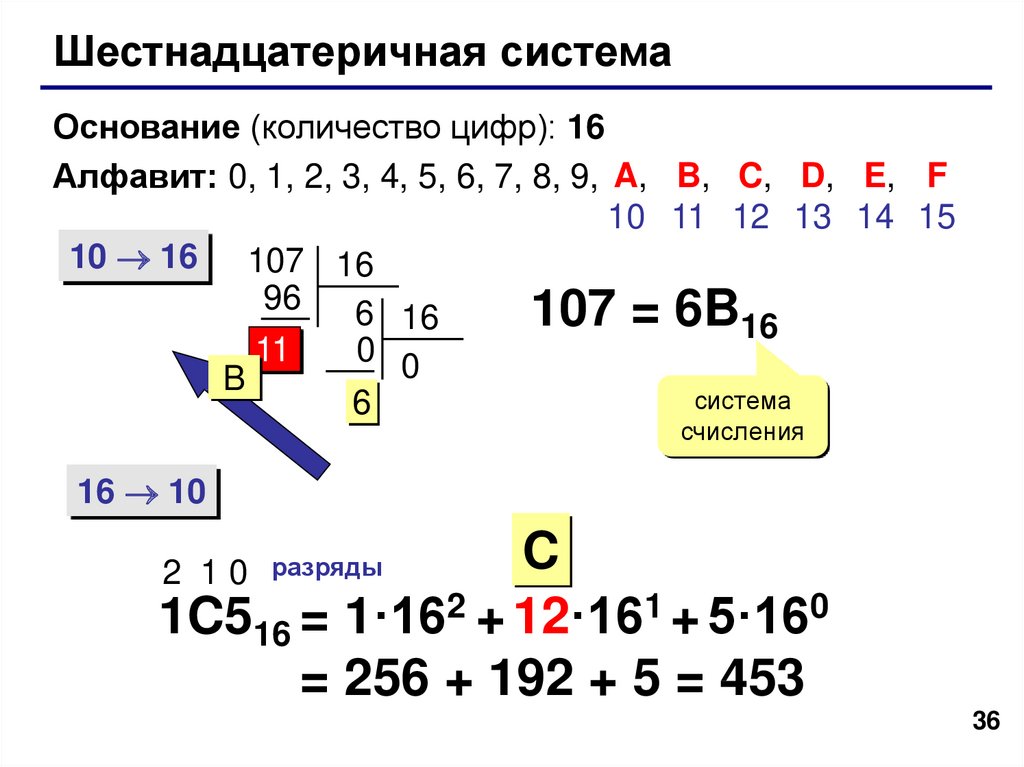
Многие программисты используют ее и при работе с языками высокого уровня, потому что числа в этой системе при помощи специальной таблицы соответствия легко переводятся в двоичную систему, на которой основана работа всей цифровой техники. Любая информация в компьютере, будь то музыкальный файл или текстовый документ, после трансляции представлена последовательностью исходного двоичного кода, а его удобнее просматривать представленным символами шестнадцатеричной системы.
Также одно из применений шестнадцатеричных символов – описание цветовых схем, то есть три компонента R, G, B описываются соответствующим данной системе способом. Данный подход к записи получил название шестнадцатеричный цвет
Возможность просмотреть программу в шестнадцатеричном коде позволяет отладить ее, внести изменения, а злоумышленниками данный подход используется для взлома программ.
Как построить прямую | Как перевести ме в мл | Как определить предел функции |
В чем измеряется сопротивление | Как начертить семиугольник | Почему нельзя вскипятить ведро воды на спиртовке |
Зачем нужна шестнадцатиричная система счисления
Всем, кто общается с компьютером или другой цифровой техникой, приходилось встречать загадочные записи типа 10FEF, которые кажутся непосвященным каким-то шифром.
Что скрывается за этими символами? Оказывается, это просто цифры. Те, которые использует шестнадцатиричная система счисления.
Системы счисления
Каждый школьник знает или хотя бы где-то слышал, что все цифры, которые мы обычно используем, образуют десятичную систему счисления. Это название она носит просто потому, что различных символов в ней всего десять (от 0 до 9). Любое число в нашей привычной системе может быть записано с их помощью. Однако, оказывается, использовать ее удобно бывает далеко не всегда. Например, при обмене информацией между цифровыми устройствами проще всего применять систему счисления, в которой есть только две цифры: «0» — нет сигнала — или «1» — есть сигнал (напряжение или что-то еще). Она называется двоичной. Однако, чтобы описать процессы внутри таких устройств с ее помощью, придется выполнять слишком длинные и трудные для понимания записи. Поэтому была придумана шестнадцатиричная система счисления.
Понятие шестнадцатеричной системы
Почему же для цифровых устройств используется именно система, которая содержит шестнадцать разных символов? Как известно, информация в компьютерах передается в виде байтов, которые обычно содержат 8 бит.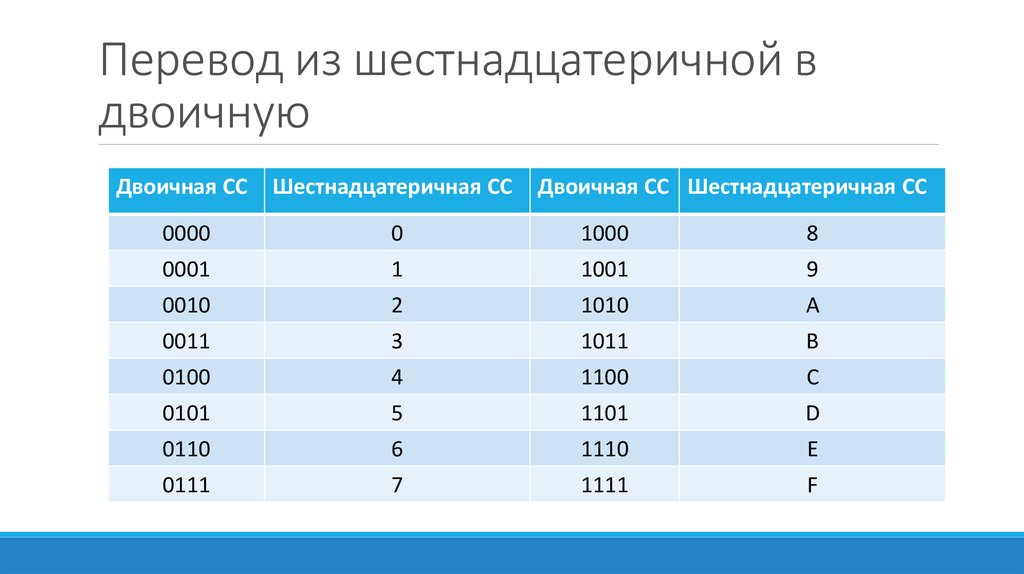
А единица данных – машинное слово – включает в себя 2 байта, то есть 16 бит. Таким образом, с помощью шестнадцати разных символов можно описать ту информацию, которая является мельчайшей частицей при обмене. Шестнадцатиричная система счисления включает наши привычные цифры (естественно, от 0 до 9), а также первые буковки латинского алфавита (A, B, C, D, E, F). Именно с помощью этих символов принято записывать любую единицу информации. С ними можно производить любые арифметические действия. То есть сложение, вычитание, умножение, деление. Результатом также будет шестнадцатеричное число.
История чисел и система счисления, позиционные системы…
Эта тема не относится сугубо к области математики, ведь способ записи, да и само понимание чисел…
Где применяется
Шестнадцатиричная система используется для записи кодов ошибок. Они могут возникать при работе различных программных продуктов. Например, так кодируются ошибки операционной системы. Каждое число при этом стандартное.
Можно выяснить, какая именно ошибка произошла в процессе работы, расшифровав его с помощью инструкции. Также применяются такие символы при написании программ на языках низкого уровня, например ассемблере. Шестнадцатиричная система счисления любима программистами еще и потому, что ее составляющие очень легко могут быть переведены в двоичные, которые являются «родными» для всей цифровой техники. С помощью таких символов описывают также цветовые схемы. Кроме того, абсолютно все файлы в компьютере (и текстовые, и графические, и даже музыкальные или видео) представляются после трансляции в виде последовательности двоичных кодов. Просматривать исходный удобнее всего как раз в виде шестнадцатеричных символов.
Конечно, любое число можно записать в различных системах счисления. Это и десятичная, и двоичная, и шестнадцатеричная. Чтобы перевести слово из одной из них в другую, следует воспользоваться таким сервисом, как переводчик систем счисления, или сделать это самостоятельно с помощью определенного алгоритма.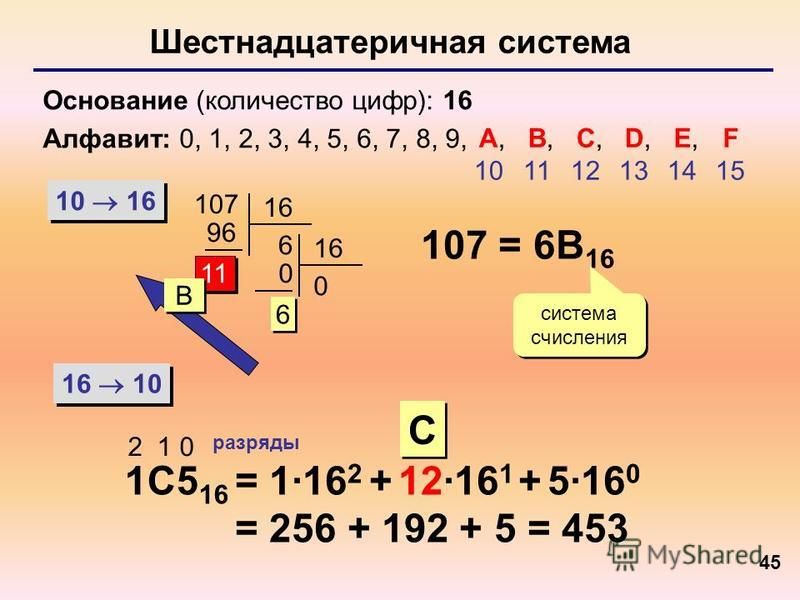
Шестнадцатеричный | IGCSE Computer Science
Введение
Почему мы используем шестнадцатеричный формат?
Двоичный код очень трудно читать людям (особенно большие числа), но компьютеры работают в двоичном формате, поэтому любое использование, в котором вам нужно иметь возможность проверять и редактировать двоичный файл напрямую (например, в машинном коде/языке ассемблера), тогда людям нужно чтобы иметь возможность читать двоичный файл легко и точно. Здесь на помощь приходит шестнадцатеричный код:
- Шестнадцатеричный позволяет людям взаимодействовать с двоичным кодом в удобочитаемой форме.
- Шестнадцатеричный код компактен и удобен для чтения
- Большие числа могут быть представлены меньшим количеством цифр, что делает их более легкими и более точными для чтения людьми.
- Шестнадцатеричное число может быть легко преобразовано в двоичное и наоборот.
Как работает шестнадцатеричный формат?
В обычной человеческой системе счета мы используем систему счисления с основанием 10, что означает, что каждая дополнительная цифра каждый раз увеличивается на 10:
Шестнадцатеричная система счисления с основанием 16, что означает увеличение в степени 16, где каждая цифра является одной из 16 различных комбинаций.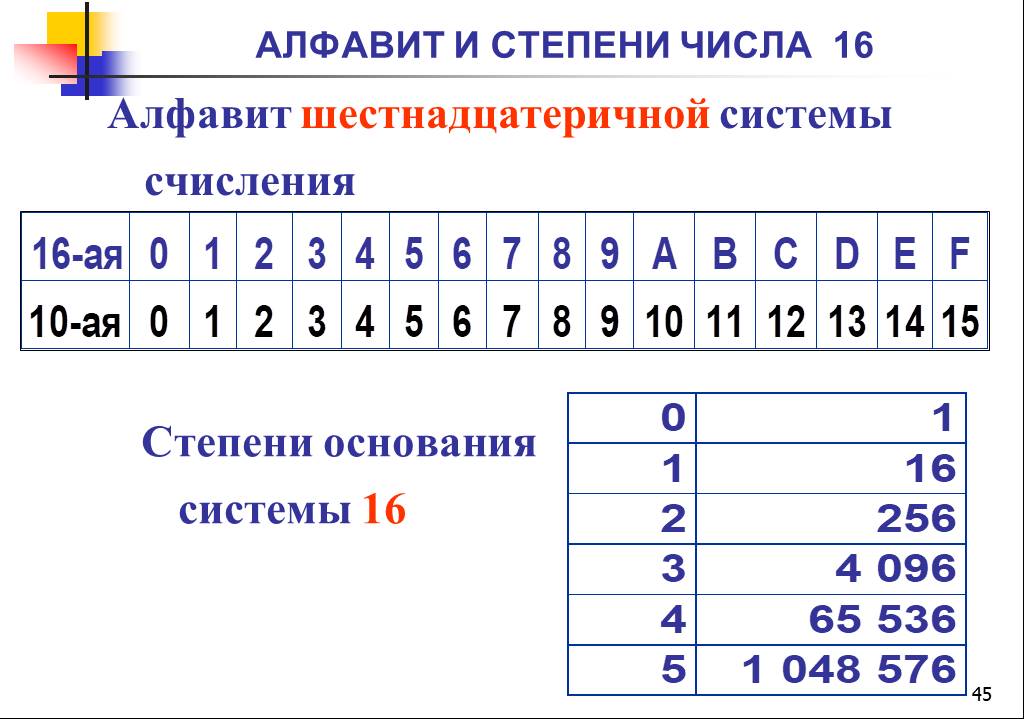
Шестнадцатеричное число состоит из:
- 0 = 0
- 1 = 1
- 2 =2
- 3 = 3
- 4 = 4
- 5 = 5
- 6 = 6
- 7 =7
- 8 = 8
- 9 = 9
- А = 10
- Б = 11
- С = 12
- Д = 13
- Е = 14
- Ф = 15
Почему мы используем от a до f вместо 11 до 15?
Мы не можем использовать числа от 11 до 15, потому что мы не знаем, какое число оно представляет. Цифры 13 могут быть 13 или 19 (1 * 16 + 3), потому что в десятичных числах больше 9 используются 2 цифры вместо одной цифры.
HTML/CSS
Шестнадцатеричный код в HTML и CSS
Шестнадцатеричный формат используется для представления цветов RGB в HTML и CSS. На видео ниже показано, как это работает.
https://www.youtube.com/watch?v=c56x1aj2CPAВидео не может быть загружено, потому что JavaScript отключен: как работают цветовые коды HEX? (через 60 секунд) (https://www.
youtube.com/watch?v=c56x1aj2CPA)
MAC
Адреса управления доступом к среде
MAC-адреса – это уникальные коды идентификаторов, присваиваемые каждой части сети. аппаратное обеспечение создано. Они выдаются производителем оборудования при создании устройства, и первая часть MAC-адреса указывает производителя.
MAC-адреса состоят из 6 пар шестнадцатеричных цифр, разделенных двоеточием.
Пример: dd:f2:c2:a1:2b:cd
Каждая пара может иметь одно из 256 возможных значений (0-255), поэтому общее количество возможных MAC-адресов равно 256 в степени 6 = 281 474 976 710 656 возможных MAC-адресов.
Почему MAC-адреса отображаются в шестнадцатеричном формате?
MAC-адреса отображаются в шестнадцатеричном формате a, потому что коды слишком длинные, чтобы люди могли точно прочитать их в двоичном формате.
Приведенный выше MAC-адрес в двоичном формате будет 110111011111001011000010101000010010101111001101
Человеку невероятно сложно прочитать/запомнить.
https://www.youtube.com/watch?v=UrG7RTWIJakВидео не может быть загружено, потому что JavaScript отключен: что такое MAC-адрес? (https://www.youtube.com/watch?v=UrG7RTWIJak)
Assembly/MC
Язык ассемблера и машинный код
Шестнадцатеричный код используется, когда люди читают/редактируют машинный код или язык ассемблера. Компьютеры могут интерпретировать только инструкции, записанные в двоичном формате, поэтому все инструкции должны быть записаны в двоичном формате. Людям это покажется невероятно медленным и трудным, поэтому мы отображаем шестнадцатеричный эквивалент для чтения людьми. Это означает, что люди могут редактировать машинный код.
Источник: Wikipedia. Этот шестнадцатеричный код содержит шестнадцатеричное представление адреса памяти, где произошла ошибка.
Позволяет инженерам быстро отлаживать код.
Обратите внимание на ячейку памяти в шестнадцатеричном формате, где произошла ошибка?
Ресурсы
Рабочий лист с пояснениями
Тестовый лист
Генератор рабочих листов
Gex Invaders Game
Прошние бумажные экзамены.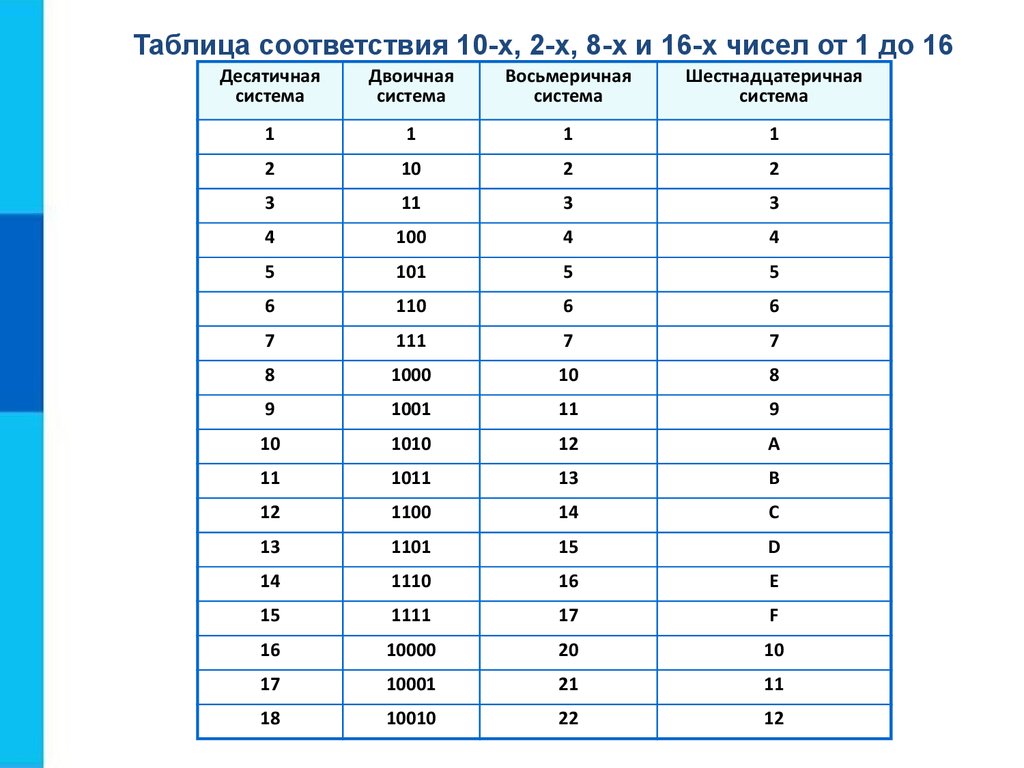
0478/12 — Документ 1 Теория мая/июнь 2016 г. QN3
0478/11 — Документ 1 Октябрь/ноябрь. /b
0478/11 – Доклад 1 Теория Май/июнь 2017 г. – Квартал 1
0478/13 – Доклад 1 Теория Май/июнь 2017 г. 1 кв. 12 – Документ 1 Теория Октябрь/ноябрь 2017 г. Qn1 – шестигранная робототехника
тестовое задание
шестнадцатеричная система счисления в компьютере
Когда мы печатаем слова на компьютере, он переводит их в числа. Фактически, для компьютера вся информация записывается в виде последовательности единиц и нулей, т. е. в компьютерных системах счисления именно так мы представляем числа в архитектуре компьютерной системы.
Системы счисления — одна из самых фундаментальных концепций, которую должны изучить специалисты по информатике. Это важный шаг для всех, кто хочет стать компьютерщиком или программистом.
В этой статье мы познакомим вас с системами счисления, которые важны для ученого-компьютерщика, а также рассмотрим двоичную и шестнадцатеричную системы счисления в компьютере.
Что такое компьютерная система счисления?
Люди давно умеют считать. Для этого мы используем системы, которые связывают уникальные символы с конкретными значениями. Это называется системой счисления, и это метод, который мы используем для представления чисел и манипулирования ими.
Вероятно, вы больше всего знакомы с десятичной системой, которая лежит в основе того, как люди считают. Десятичная система имеет основание 10, потому что она предоставляет 10 символов для представления всех чисел — 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9..
Люди используют десятичную систему, потому что у нас есть 10 пальцев, чтобы считать, но у машин нет такой роскоши. Итак, мы создали другие системы счисления, выполняющие те же функции. Компьютеры представляют информацию не так, как люди, поэтому нам нужны разные системы для представления чисел.
Обычно используемые системы счисления в компьютерах:
- Двоичная
- Шестнадцатеричная
Двоичная система счисления в компьютере
Компьютер использует биты для представления информации.
Бит — это самая основная единица хранения данных в компьютере. Важный компонент компьютеров называется транзистором. Подобно выключателю света, транзистор либо позволяет, либо предотвращает протекание тока. Таким образом, у него всего два состояния — ВКЛ и ВЫКЛ.
Каждое число в компьютере представляет собой электрический сигнал. На заре компьютеров электрические сигналы представлялись в состоянии «ВКЛ» (отрицательный заряд) и в состоянии «ВЫКЛ» (положительный заряд). Это формирует своего рода двоичный переключатель.
Эти два состояния можно представить с помощью одного из двух символов – 1 и 0. Это означает, что двоичная система счисления имеет основание 2. Только эти два символа необходимы для представления каждого числа.
Это называется двоичной системой счисления. Каждая двоичная цифра называется битом. Когда дело доходит до двоичного кода для размещения значений и цифр в этой системе, мы размещаем значения, соответствующие возрастающим степеням числа 2, слева направо.
Вы можете манипулировать битами слева и справа с помощью побитовых операторов, чтобы эффективно изменять значение числа на уровне машинного кода.
Шестнадцатеричная система счисления в компьютере
Другой распространенной системой счисления в компьютере является шестнадцатеричная система счисления. Двоичные числа просты для компьютеров, но не так просты для понимания людьми. А когда вы работаете с большими числами, становится трудно читать и писать без ошибок. Итак, чтобы решить эту проблему, двоичные числа объединяются в группы по четыре бита, образуя шестнадцатеричную систему счисления.
Шестнадцатеричная система счисления в компьютере (часто называемая «шестнадцатеричной») состоит из 16 символов, поэтому ее основание равно 16. Шестнадцатеричная использует 10 чисел десятичной системы счисления и шесть дополнительных символов A, B, C, D , E и F.
Шестнадцатеричный: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Десятичный: 0, 1, 2 , 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
Преобразование чисел между двоичной и шестнадцатеричной системами счисления в компьютере
Так как имеется 16 цифр (от 0 до 9и от A до F) в шестнадцатеричной системе счисления, поэтому мы можем представить любую цифру шестнадцатеричной системы счисления, используя только 4 бита, как показано ниже:
| Hexa | 0 | 1
|
Это будет шестнадцатеричное число заданного числа.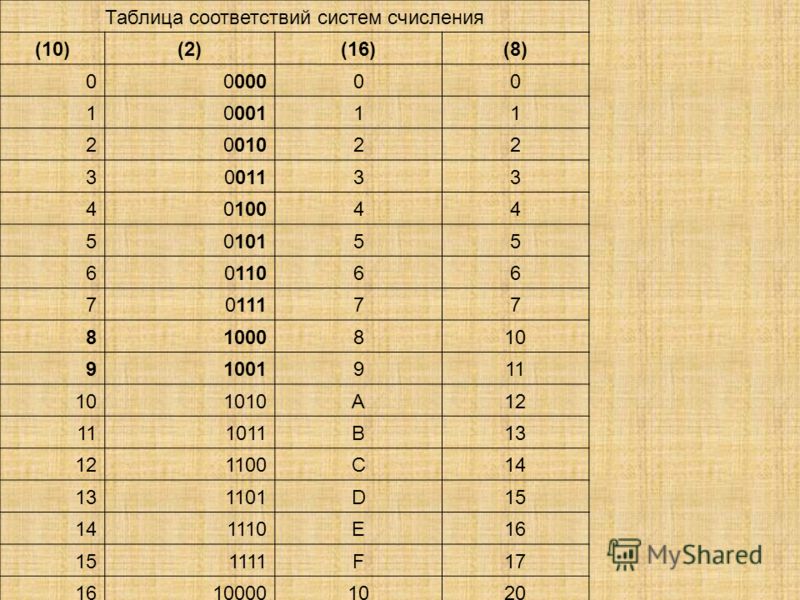
Кроме того, можно быстро и легко преобразовать шестнадцатеричные числа в двоичные.
