Методическая разработка заняия по теме «Электрическая емкость. Конденсаторы» | Методическая разработка по физике (10 класс):

Тема: Электрическая емкость. Конденсаторы.

Ход учебного занятия:

1. Организационный момент

Здравствуйте, садитесь! Давайте проверим присутствующих. Староста, пожалуйста.

Тема сегодняшнего занятия: «Электрическая емкость. Конденсаторы». Запишите в тетрадях число и тему занятия. Сегодня нам необходимо изучить  одно из  важных понятий  в электротехнике  – электрическая емкость. А также познакомиться с техническим устройством, главной ценностью которого является накопление электрического заряда и энергии электрического поля.

Цель занятия: изучить, систематизировать и закрепить полученные знания об электрической емкости и конденсаторах (их значение в природе и технике, исследовать закономерности).

2. Фронтальный опрос

Для повторения пройденного материала, предлагаю вам разделиться на группы по 5 человек. Каждая группа получит задание, а потом вы проверите друг друга.

Групповые карточки-задания:

Карточка №1: продолжите предложения, чтобы получились верные утверждения:

1. Передача телу электрического заряда называется …(электризация)
2. Вещество, не имеющее свободных носителей заряда, называется …(диэлектрик)
3. Физическая величина, определяющая способность частиц или тел вступать в электромагнитные силовые взаимодействия, – это …(электрический заряд)
4. Явление перераспределения электрических зарядов в проводнике во внешнем электрическом поле – это …(электростатическая индукция)
5. Поверхности, в каждой точке которых потенциал электрического поля, имеет одно и то же значение, называются ….(эквипотенциальными)

Карточка №2: продолжите предложения, чтобы получились верные утверждения:

1. Наэлектризовать тело можно следующими способами: …(трением, соприкосновением, через влияние)
2. Вещество, имеющее свободные носители заряда, способные перемещаться под действием электрического поля, называется …(проводником)
3. Физическая величина, определяемая отношением работы,совершаемой электрическим полем при перемещении единичного положительного заряда из данной точки в бесконечность, – это …(электрический потенциал)
4. Смещение зарядов или преимущественная ориентация диполей под действием внешнего электрического поля – это …(поляризация)
5. Физическая величина, определяемая как сила, действующая на единичный положительный заряд, помещенный в данную точку поля, называется …. (напряженность)

Теперь проверим выполненные задания друг друга. За каждый правильный ответ – 1 балл. Молодцы. Хорошо потрудились.

3. Изучение нового материала

3.1. Введение понятия «электрическая емкость»

Что нужно сделать, чтобы наэлектризовать тело? Правильно, сообщить ему электрический заряд. Уединенный проводник – это проводник, размеры которого много меньше расстояния до окружающих тел.

Возьмем электроскоп и будем передавать ему электрический заряд. Мы видим, что с ростом заряда, растет потенциал этого проводника:

Q = C·φ

Электроемкость –  скалярная физическая величина, численно равная отношению заряда, сообщенного проводнику,  к потенциалу, который этот заряд создает на поверхности проводника.

C = 

[С] = 1 Ф (фарада)

Электрическая ёмкость характеризует способность проводника накапливать электрические заряды.

Емкостью 1Ф обладает такой проводник, у которого потенциал возрастает на 1 В при сообщении ему заряда в 1 Кл.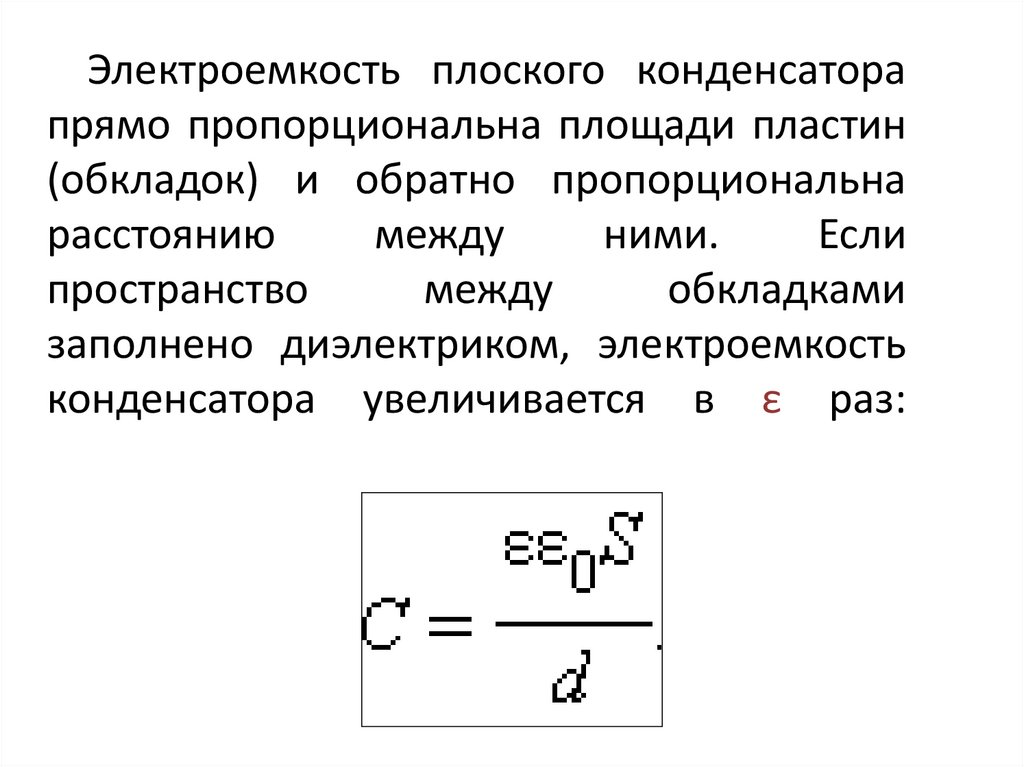

Нам нужно вспомнить, от чего же зависит электроемкость. Самое главное – емкость не нужно сравнивать с вместимостью! Емкость не зависит от заряда проводника, его потенциала, материала из которого он изготовлен. Емкость показывает зависимость между зарядом и потенциалом! Электроемкость проводника зависит от его размеров, формы и среды.

А теперь попробуем свои силы. Давайте посостязаемся. Работаем командами, решаем задачи.

1 команда: Определить потенциал металлического шарика емкостью 4,54 пФ, получившего заряд 1,8·10-7 Кл.	2 команда: При электризации емкость проводника стала равна 150 мкФ, а потенциал 200 В. Какой заряд был сообщен проводнику?
3 команда: Определить емкость металлического шарика, если при сообщении ему  заряда 3·10-8 Кл его потенциал стал равным 6000 В.	4 команда: Какой заряд был сообщен проводнику, если его емкость стала равна 9 пФ, а потенциал 800 В?

Электризация при соприкосновении или электростатическая индукция позволяют получить на поверхности тел лишь сравнительно небольшой электрический заряд. Способность уединенных проводников накапливать электрические заряды ограничена. Чтобы проводник обладал большой емкостью, он должен иметь очень большие размеры. Емкость шара: С = 4πεε0R

3.2. Электрическая емкость системы проводников

Выясним важные для практики вопросы:

• при каком условии можно накопить на проводнике большой электрический заряд?
• Влияет ли на распределение зарядов в проводнике наличие рядом другого проводника?

На практике требуются устройства, способные накапливать значительные заряды. В основы конструкции таких устройств положен тот факт, что электроемкость проводника в окружении других тел возрастает.

Объясняется это тем, что под действием электрического поля заряженного проводника, на поднесенных к нему телах, если это проводники, возникают индуцированные заряды, а если диэлектрики – поляризационные.

Эти заряды будут ослаблять поле проводника. Они понижают его потенциал и повышают его электрическую емкость. Проводники с равными по модулю зарядами будут иметь большую емкость.

Электрическая емкость системы из двух проводников определяется как отношение заряда одного из них к разности потенциалов между ними:

Из формулы видно, что по сравнению с емкостью уединенного проводника, знаменатель дроби уменьшился, а значит емкость увеличилась.

3.3 Введение понятия конденсатор

Конденсатор – это система из двух разноименно заряженных проводников (обкладок), разделенных слоем диэлектрика.

        Электроемкость конденсатора равна отношению заряда одной из пластин Q к напряжению между ними U:

C =

Конденсатор служит для накопления и сохранения  заряда и энергии электрического поля.

Емкость конденсатора зависит от:

•  размеров обкладок,
•  формы обкладок,
•  расположения обкладок,
• диэлектрической проницаемости диэлектрика.

Примерами естественных природных конденсаторов являются облака и земля, линии электропередач, две жилы кабеля. К тому же вы должны помнить, что емкостью обладают не только конденсаторы, но и другие элементы электрических цепей, на которых может накапливаться электрический заряд (провода электрических линий, электроды электронных ламп и пр. ). Чаще мы этой емкостью пренебрегаем.

ЗАДАНИЕ: Изобразите электрическое поле внутри и вне двух параллельных пластин. Пожалуйста, изобразите на доске полученный результат. Обсудим:

Вне пластин векторы Е+ и Е- направлены в разные стороны, и поэтому E = 0. Внутри конденсатора векторы Е+ и Е- сонаправлены; поэтому модуль напряженности суммарного поля равен

Электростатическое поле будет сосредоточено внутри конденсатора между обкладками!

Линии напряженности электрического поля начинаются на положительной обкладке, заканчиваются на отрицательной. Поле практически не рассеивается в окружающем пространстве. На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют:

1) две плоские пластины;

2) два коаксиальных цилиндра;

3) две концентрические сферы.

Поэтому в зависимости от формы обкладок конденсаторы делятся наплоские, цилиндрические и сферические. По типу диэлектрика, помещенного между обкладками, конденсаторы бывают: электролитические (на постоянном токе), бумажные, слюдяные, воздушные.

Сообщение конденсатору заряда называют зарядкой. Под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок. Чтобы зарядить конденсатор, достаточно сообщить заряд одной из его обкладок, а другую заземлить: при этом на другой обкладке появится заряд, равный по величине и противоположный по знаку заряду первой обкладки из-за явления электростатической индукции. Эффективнее зарядка конденсатора происходит при подключении его обкладок к разноименным клеммам источника постоянного тока.

А теперь нам предстоит определить, от чего зависит емкость конденсатора. Будем первооткрывателями. Исследуем зависимость электроемкости от расстояния между пластинами (1 студент) и от диэлектрической проницаемости диэлектрика (2 студент).

Вывод: При увеличении расстояния между пластинами, напряжение увеличивается, а электроемкость конденсатора уменьшается.

Если между обкладками конденсатора поместить диэлектрик с большей диэлектрической проницаемостью, то напряжение уменьшится, а электроемкость — увеличится.

Физкультминутка: сядьте прямо, руки отведите за спину и сомкните. Представьте, что вы едете в автобусе. Вдруг автобус резко тормозит, что с вами произойдет? А теперь разгоняемся, резко поворачиваем влево, едем прямо, опять поворот направо, стоп. Приехали. Продолжим.

3.4 Энергия заряженного конденсатора

Если обкладки заряженного конденсатора замкнуть металлическим проводником, то по цепи пойдет электрический ток (можно проверить с помощью лампочки),  и ток в цепи будет, пока конденсатор не разрядится. Значит, заряженный конденсатор содержит запас энергии.

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Источник напряжения, поставляя заряды на обкладки конденсатора, производит работу

A = F·d = Eq·d = Wp

Для одной обкладки:

Wp= =

Используя известные вам соотношения, получим формулы для расчета  энергии заряженного конденсатора:

Как сказал английский физик, один из создателей квантовой физики, лауреат Нобелевской премии (1933) Поль Андриен Морис Дирак: «Всякая физическая теория должна быть математически красивой». Формулы получились замечательные! А в каких единицах измеряется энергия?

Электрическую энергию Wр следует рассматривать именно как потенциальную энергию, запасенную в заряженном конденсаторе. По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля.

Давайте немного порассуждаем, чтобы закрепить полученные знания. Опять поработаем в командах.

Задание 1,3 команде: Как изменятся емкость, заряд, напряженность и энергия поля при удалении диэлектрика с ε? Если конденсатор не отключен от источника напряжения, то U = const!

Емкость		уменьшилась
Заряд		уменьшился
Напряженность		Не изменилась
Энергия электрического поля		уменьшилась

Задание 2,4 команде: Если расстояние между пластинами уменьшили в 2 раза, как изменились емкость, напряжение, напряженность, энергия поля?Если конденсатор отключен от источника напряжения, то q = const!

Емкость		Увеличилась
Напряжение		уменьшилось
Напряженность		Не изменилась
Энергия электрического поля		Уменьшилась

И опять любимые задачи. Работаем в командах.

1 команда: Определить емкость и заряд плоского конденсатора, обкладки которого имеют площадь 10 см2, толщина миканита между ними (ε = 5,2) равна 0,52 мм, а напряжение равно 100 В.	2 команда: Определить емкость и заряд плоского конденсатора, обкладки которого имеют площадь 5 см2, толщина миканита между ними (ε = 5,2) равна 0,885 мм, а напряжение равно 100 В.
3 команда: Определить емкость и заряд плоского конденсатора, обкладки которого имеют площадь 10 см2, толщина миканита между ними (ε = 5,2) равна 0,26 мм, а напряжение равно 100 В.	4 команда: Определить емкость и заряд плоского конденсатора, обкладки которого имеют площадь 10 см2, толщина миканита между ними (ε = 5,2) равна 0,885 мм, а напряжение равно 100 В.

Конденсатор –важное электротехническое устройство. Благодаря своим замечательным свойствам, конденсаторы нашли широкое применение в технике. Конденсаторы применяются, когда нужно:

• Накапливать на короткое время заряд или энергию для быстрого изменения потенциала. Конденсатор способен хранить электрические заряды тем больше, чем больше его емкость. Если необходимо получить электрический ток большой мощности, то выгодно иметь большую силу тока. Конденсатор большой емкости при разрядке дает большую мощность. Пример: фотовспышка
• В клавиатуре компьютера.
• конденсатор как измеритель времени: при зарядке и разрядке конденсатора время этих процессов зависит от емкости конденсатора. Это свойство можно использовать для отсчета времени. Например: часы, реле времени.
• Конденсатор в цепях переменного тока периодически перезаряжается, поэтому по подводящим к нему проводникам постоянно проходит ток, а в цепи постоянного тока конденсатор, зарядившись, ток не пропускает. Поэтому конденсатор можно использовать как фильтр. Пример: выпрямители.
• В зависимости от частоты переменного тока конденсатор быстро или медленно перезаряжается, при этом оказывая разное сопротивление переменному току. Это используют в частотных фильтрах переменного тока. Например: приемный контур радиоприемника, телевизора, генераторы переменных сигналов.

3.5 Соединение конденсаторов в батареи

Во многих случаях для получения нужной емкости конденсаторы приходится соединять в группу, которая называется батареей. Различают два основных типа соединения: последовательное и параллельное. Мы с вами сейчас рассмотрим особенности этих двух видов соединений. Для рациональной работы я попрошу вас подготовить таблицу, которую мы будем заполнять по ходу объяснения материала. Эта таблица поможет вам в подготовке к практической работе, которая будет на следующем занятии:

	Последовательное	Параллельное
схема
Электрический заряд	q = q1 = q2 = q3	q = q1 + q2 + q3
Эквивалентная емкость	=  +  +	С = С1 + С2 + С3

1) При параллельном соединении конденсаторов соединяются их одноименно заряженные обкладки:

Напряжения на конденсаторах одинаковы     U1 = U2 = U (т. к. они подключены к одним и тем же точкам цепи),  заряды равны:

q1 = С1U и    q2 = С2U.

Такую систему можно рассматривать как единый конденсатор электроемкости C, заряженный зарядом q = q1 + q2 при напряжении между обкладками равном U. Отсюда следует:

или С = С1 + С2

Таким образом, при параллельном соединении электроемкости складываются (увеличивается площадь обкладок – растет общая емкость). Такое соединение применяется для увеличения емкости батареи.

 2) При последовательном соединении конденсаторов соединяют разноименно заряженные обкладки:

Заряды обоих конденсаторов одинаковы    q1 = q2 = q (т.к. непосредственно от источника заряжаются только крайние обкладки, а соседние – через влияние),  напряжения на них равны  и 

Такую систему можно рассматривать как единый конденсатор, заряженный зарядом q при напряжении между обкладками U = U1 + U2.

Следовательно,   или  

При последовательном соединении конденсаторов складываются обратные величины емкостей. Последовательное соединение конденсаторов применяется тогда, когда во избежание пробоя большую разность потенциалов требуется распределить между несколькими конденсаторами.

Формулы для параллельного и последовательного соединения остаются справедливыми при любом числе конденсаторов, соединенных в батарею.

Т.е. в случае n конденсаторов одинаковой емкости С емкость батареи

при параллельном соединении Собщ = nС

при последовательном соединении Собщ = С/n

3) методика расчета эквивалентной емкости при смешанном соединении конденсаторов (метод свертывания):

— найти участки с простым соединением конденсаторов;

— по соответствующим формулам, вычислить эквивалентные емкости этих участков;

— перечертить схему, заменив соединения конденсаторов их эквивалентными емкостями;

— повторить алгоритм с начала, пока не останется цепь с одним конденсатором.

Рассмотрим на примере: дан участок цепи со смешанным соединением конденсаторов:

1. Определяют эквивалентную емкость участка с параллельным соединением конденсаторов:

2. Рассчитывают эквивалентную емкость двух последовательно соединенных конденсаторов с емкостями С1 и С2-3:

4 Подведение итогов  и рефлексия

Сегодня мы с вами хорошо поработали. Результаты следующие (выставить и прокомментировать оценки). А еще ответьте на вопросы:

1. Что нового узнали? Чему научились?

2. Пригодятся ли эти знания в вашей профессиональной деятельности?

5 Домашнее задание

1. Приготовить  сообщение (презентацию) по одной из предложенных тем:

— виды конденсаторов;

— применение конденсаторов;

— конденсаторы в электромеханическом оборудовании.

2. Решить задачу: При сообщении конденсатору заряда 5·10-6 Кл его энергия оказалась равной 0,01 Дж. Определить напряжение на обкладках конденсатора.

Хочу закончить это занятие следующим высказыванием: «Хитрые люди презирают знание, простаки удивляются ему, мудрые пользуются им» (Т. Маколей). Всем спасибо. До свидания.

Под новизной понимается отличие полученных (ожидаемых) результатов, рассматриваемых в методической разработке инновационного опыта, от имеющихся и отраженных в научной литературе.

Различают три степени новизны:

1. Методическая разработка уточняет и конкретизирует какие-либо теоретические положения или практические рекомендации.

2.Методическая разработка дополняет, развивает, вносит новые элементы в какие-либо теоретические положения или практические рекомендации.

3.Методическая разработка отражает принципиально новые идеи, концепции, подходы, рекомендации и отличается наиболее высокой степенью новизны.

Рекомендуемый объем — до 2 страниц машинописного текста.

что это, формула, единицы измерения / Справочник :: Бингоскул

Электрическая ёмкость конденсатора: что это, формула, единицы измерения добавить в закладки удалить из закладок

Содержание:

Ёмкостью называют свойство вещества вмещать в себя определённое количество энергии (электрической) либо материальных объектов, например, жидкости. Рассмотрим, что такое электроёмкость, что она характеризует, от чего зависит. Разберёмся, в каких единицах измеряется.

Электроёмкость в физике: что это такое

Эксперименты с распределением электрического заряда по поверхности токопроводящего материала показали, что его равномерность зависит от формы поверхности. Идеальная – шаровидная – в каждой её точке концентрируется одинаковый заряд. Наибольшая плотность заряда наблюдается на поверхности с наибольшей кривизной, на остриях проводников.  

Двухполюсный электрический компонент, способный накапливать и временно хранить электричество, называется конденсатором. Он представлен парой токопроводящих пластин – обкладок, которые расположены на малом расстоянии и разделены слоем диэлектрика. Металлические пластины накапливают одинаковый по значению заряд с противоположными знаками. 

Электрическая ёмкость (электроёмкость) конденсатора – это величина, показывающая отношение накопленного на любой обкладке электричества к разности потенциалов между ними.  В отличие от источников питания (батарей) элемент быстро накапливает и отдаёт заряд. После отключения питания – прекращения прохождения по нему электрического тока, накопитель долгое время сохраняет заряд, хоть он понемногу и истекает. На корпусах конденсаторов указывается их номинальная ёмкость, реальная зависит от ряда параметров.  

Применяется электрический накопитель, например, при подключении трёхфазных электродвигателей в однофазную сеть, для питания вспышки фотоаппарата от батареи, которая не способна в доли секунды передать ей нужное количество энергии. Обычно конденсатор блокирует прохождение постоянного тока – работает в сети с таким электротоком непродолжительное время. Переменный ток пропускает.

Применяемые на практике накопители электрической энергии имеют сложную конструкцию: множество проводящих и изолирующих слоёв либо ленты с ними. Часто сматываются в цилиндр, сворачиваются в виде параллелепипеда.

Электроёмкость конденсатора: формула, единица измерения

Электрическая ёмкость накопителя электричества вычисляется по формуле:

С = q/U, где:

• q – накопленный заряд;
• U – разница напряжения между проводниками.

Измеряется в Фарадах (Ф). 1 Ф – огромная ёмкость, которой способен обладать металлический шар размером с 12 Солнц; конденсатор размером с нашу планету способен накопить до 710 мкФ. Типичная ёмкость электрических накопителей измеряется в единицах от микро- до пикофарад. Существуют суперконденсаторы и ионисторы с ёмкостью до десятков фарад.

Для управления ёмкостью (увеличения) устройства уменьшают толщину диэлектрика, расстояние между обложками либо повышают площадь поверхности металлических пластин.

Поделитесь в социальных сетях:

27 июля 2022, 10:51

Физика

Could not load xLike class!

19.5 Конденсаторы и диэлектрики – Колледж физики главы 1-17

19 Электрический потенциал и электрическое поле

Резюме

• Опишите действие конденсатора и определите емкость.
• Расскажите о конденсаторах с плоскими пластинами и их емкостях.
• Обсудите процесс увеличения емкости диэлектрика.
• Определить емкость при данных заряде и напряжении.

Конденсатор — это устройство, используемое для накопления электрического заряда. Применение конденсаторов варьируется от фильтрации статического электричества в радиоприеме до накопления энергии в сердечных дефибрилляторах. Как правило, коммерческие конденсаторы имеют две проводящие части, расположенные близко друг к другу, но не соприкасающиеся, как показано на рис. 1. (Большую часть времени между двумя пластинами используется изолятор для обеспечения разделения — см. обсуждение диэлектриков ниже.) Когда клеммы батареи подключены к изначально незаряженному конденсатору, равные количества положительного и отрицательного заряда, [латекс]\boldsymbol{+Q}[/латекс] и [латекс]\boldsymbol{-Q}[/латекс], разделены на его две тарелки. Конденсатор в целом остается нейтральным, но в этом случае мы называем его хранящим заряд [латекс]\boldsymbol{Q}[/латекс].

Конденсатор

Конденсатор — это устройство, используемое для накопления электрического заряда.

Рисунок 1. Оба показанных здесь конденсатора были изначально разряжены перед подключением к батарее. Теперь у них есть отдельные заряды

+ Q и – Q на две половины. а) Конденсатор с плоскими пластинами. (b) Свернутый конденсатор с изоляционным материалом между двумя его проводящими листами.

Сумма заряда [латекс]\boldsymbol{Q}[/латекс] a , который может хранить конденсатор , зависит от двух основных факторов: приложенного напряжения и физических характеристик конденсатора, таких как его размер.

Количество заряда

Q  Конденсатор может хранить

Количество заряда [латекс]\boldsymbol{Q}[/latex] конденсатора зависит от двух основных факторов: приложенного напряжения и емкости конденсатора. физические характеристики, например размер.

Система, состоящая из двух одинаковых параллельных проводящих пластин, разделенных расстоянием, как показано на рисунке 2, называется конденсатором с параллельными пластинами. Легко увидеть взаимосвязь между напряжением и накопленным зарядом для плоского конденсатора, как показано на рисунке 2.

Каждая линия электрического поля начинается с отдельного положительного заряда и заканчивается отрицательным, так что поле будет больше. линии, если есть больше заряда. (Рисовать одну силовую линию для каждого заряда — это только для удобства. Мы можем нарисовать много силовых линий для каждого заряда, но их общее число пропорционально количеству зарядов.) Таким образом, напряженность электрического поля прямо пропорциональна [латексной ]\boldsymbol{Q}[/латекс]

Рисунок 2. Линии электрического поля в этом плоском конденсаторе, как всегда, начинаются с положительных зарядов и заканчиваются с отрицательными зарядами. Поскольку напряженность электрического поля пропорциональна плотности силовых линий, она также пропорциональна количеству заряда на конденсаторе.

Поле пропорционально заряду:

[латекс]\boldsymbol{E \propto Q},[/латекс]

, где символ [латекс]\жирныйсимвол{\пропто}[/латекс] означает «пропорционально». Из обсуждения в главе 19.2 Электрический потенциал в однородном электрическом поле, мы знаем, что напряжение на параллельных пластинах равно [латекс]\boldsymbol{V = Ed}[/латекс].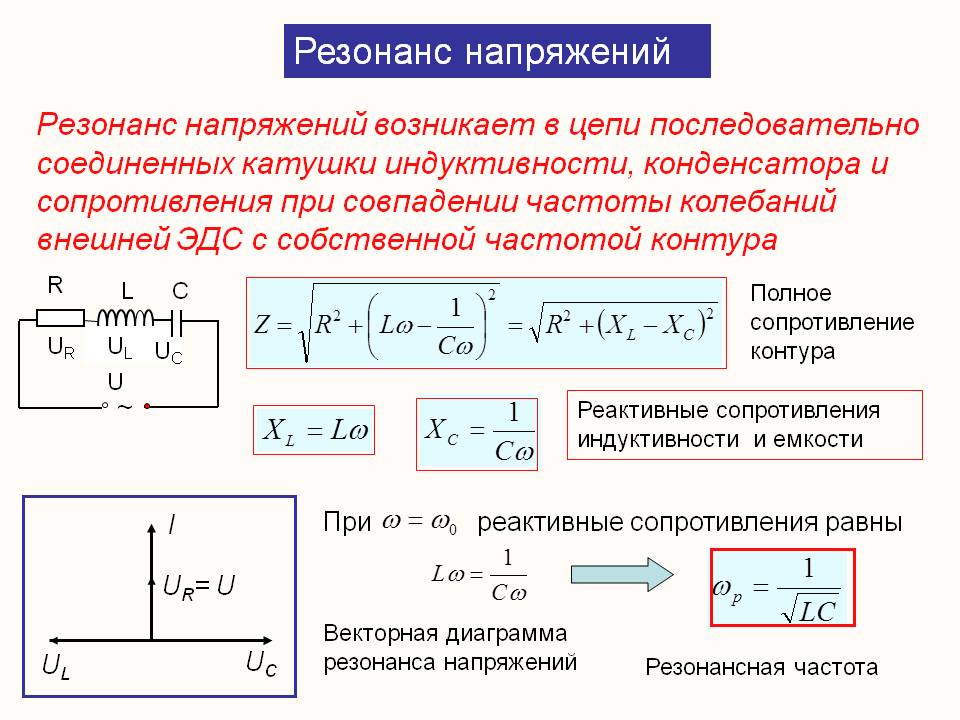

Таким образом,

[латекс]\boldsymbol{V \propto E}.[/латекс]

Отсюда следует, что [латекс]\boldsymbol{V \propto Q}[/латекс], и наоборот,

[латекс]\boldsymbol{Q \propto V}.[/латекс]

В общем случае это верно: чем больше напряжение, приложенное к любому конденсатору, тем больший заряд в нем хранится.

Различные конденсаторы сохраняют различное количество заряда при одном и том же приложенном напряжении в зависимости от их физических характеристик. Мы определяем их емкость [латекс]\boldsymbol{C}[/latex] так, чтобы заряд [латекс]\boldsymbol{Q}[/латекс], хранящийся в конденсаторе, был пропорционален [латекс]\boldsymbol{C}[ /латекс]. Заряд, хранящийся в конденсаторе, равен 9.0005

[латекс]\boldsymbol{Q = CV}.[/латекс]

Это уравнение выражает два основных фактора, влияющих на количество накопленного заряда. Этими факторами являются физические характеристики конденсатора, [латекс]\boldsymbol{C}[/латекс], и напряжение, ВВ . Преобразовав уравнение, мы видим, что емкость [латекс]\boldsymbol{C}[/латекс]  – это количество накопленного заряда на вольт, или

.

[латекс]\boldsymbol{C =}[/латекс] [латекс]\boldsymbol{\frac{Q}{V}}.[/латекс]

Емкость

Емкость [латекс]\boldsymbol{C}[/латекс] — это количество заряда, хранящегося на вольт, или

[латекс]\жирный символ{С =}[/латекс] [латекс]\жирныйсимвол{\фракция {Q}{V}}.[/латекс]

Единицей измерения емкости является фарад (Ф), названный в честь Майкла Фарадея (1791–1867), английского ученого, внесшего вклад в области электромагнетизма и электрохимии. Поскольку емкость — это заряд на единицу напряжения, мы видим, что фарад — это кулон на вольт, или

.

[латекс]\boldsymbol{1 \;\textbf{F} =}[/latex] [латекс]\boldsymbol{\frac{1 \;\textbf{C}}{1 \;\textbf{V}}} .[/латекс] 9{-3} \;\textbf{F})}[/latex].

На рис. 3 показаны некоторые распространенные конденсаторы. Конденсаторы в основном изготавливаются из керамики, стекла или пластика, в зависимости от назначения и размера. Как обсуждается ниже, в их конструкции обычно используются изоляционные материалы, называемые диэлектриками.

Рисунок 3. Некоторые типовые конденсаторы. Размер и значение емкости не обязательно связаны. (кредит: Уинделл Оскей)

Конденсатор с параллельными пластинами, показанный на рисунке 4, имеет две одинаковые проводящие пластины, каждая из которых имеет площадь поверхности [латекс]\boldsymbol{A}[/латекс], разделенную расстоянием [латекс]\boldsymbol{d}[/латекс] ( без материала между пластинами). Когда к конденсатору прикладывается напряжение [latex]\boldsymbol{V}[/latex], он накапливает заряд [latex]\boldsymbol{Q}[/latex], как показано на рисунке. Мы можем увидеть, как его емкость зависит от [латекс]\boldsymbol{A}[/латекс] и [латекс]\boldsymbol{d}[/латекс], рассматривая характеристики кулоновской силы. Мы знаем, что одинаковые заряды отталкиваются, разноименные притягиваются, а сила между зарядами уменьшается с расстоянием. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут распространяться дальше.

Таким образом, [латекс]\boldsymbol{C}[/latex] должен быть больше для больших [латекс]\boldsymbol{A}[/латекс]. Точно так же, чем ближе пластины друг к другу, тем сильнее притяжение к ним противоположных зарядов. Так что [латекс]\boldsymbol{C}[/латекс] должен быть больше для меньшего [латекс]\жирныйсимвол{d}[/латекс].

Рисунок 4. Конденсатор с параллельными пластинами с пластинами, разделенными расстоянием d . Каждая пластина имеет площадь A .

Можно показать, что для конденсатора с плоскими пластинами есть только два фактора ([латекс]\boldsymbol{A}[/латекс] и [латекс]\boldsymbol{d}[/латекс]), которые влияют на его емкость [латекс] \boldsymbol{C}[/латекс]. Емкость конденсатора с плоскими пластинами в виде уравнения равна

.

[латекс]\boldsymbol{C = {\varepsilon}_0}[/latex] [латекс]\boldsymbol{\frac{A}{d}}.[/latex]

Емкость плоскопараллельного конденсатора

[латекс]\boldsymbol{C = {\varepsilon}_0}[/latex] [латекс]\boldsymbol{\frac{A}{d}}. 2}[/latex]. Небольшое числовое значение [латекс]\boldsymbol{{\varepsilon}_0}[/латекс] связано с большим размером фарады. Плоский конденсатор должен иметь большую площадь, чтобы иметь емкость, приближающуюся к фарадам. (Обратите внимание, что приведенное выше уравнение справедливо, когда параллельные пластины разделены воздухом или свободным пространством. Когда между пластинами помещается другой материал, уравнение модифицируется, как описано ниже.) 93 \;\textbf{V}}[/latex] применяется к нему?

Стратегия

Нахождение емкости [латекс]\boldsymbol{C}[/latex] является прямым применением уравнения [латекс]\boldsymbol{C = {\varepsilon}_0 A/d}[/latex] . Как только [латекс]\boldsymbol{C}[/латекс] найден, накопленный заряд можно найти с помощью уравнения [латекс]\жирныйсимвол{Q = CV}[/латекс].

Решение для (a)

Ввод данных значений в уравнение для емкости плоского конденсатора дает 9{-9} \;\textbf{F} = 8,85 \;\textbf{nF}}. \end{array}[/latex]

Обсуждение для (a)

Это маленькое значение емкости показывает, насколько сложно сделать устройство с большой емкостью. Помогают специальные методы, такие как использование тонкой фольги очень большой площади, расположенной близко друг к другу.

Решение для (b)

Заряд, хранящийся в любом конденсаторе, определяется уравнением [латекс]\boldsymbol{Q = CV}[/латекс]. Ввод известных значений в это уравнение дает 96 \;\textbf{V} / \textbf{m}}[/latex], на этом конденсаторе нельзя накопить больше заряда за счет увеличения напряжения.

Еще один интересный биологический пример, связанный с электрическим потенциалом, обнаружен в плазматической мембране клетки. Мембрана отделяет клетку от окружающей среды, а также позволяет ионам избирательно входить и выходить из клетки. На мембране существует разность потенциалов около -70 мВ. Это связано с наличием в клетке в основном отрицательно заряженных ионов и преобладанием положительно заряженного натрия (Na 96 \;\textbf{V} / \textbf{m}}.[/latex]

Этого электрического поля достаточно, чтобы вызвать пробой воздуха.

Предыдущий пример подчеркивает сложность сохранения большого количества заряда в конденсаторах. Если [латекс]\boldsymbol{d}[/латекс] уменьшить для получения большей емкости, то максимальное напряжение должно быть уменьшено пропорционально, чтобы избежать пробоя (поскольку [латекс]\жирный символ{E = V/d}[/латекс ]). Важное решение этой проблемы состоит в том, чтобы поместить изолирующий материал, называемый диэлектриком, между пластинами конденсатора и позволить [латексу]\boldsymbol{d}[/латексу] быть как можно меньше. Мало того, что меньший [латекс]\boldsymbol{d}[/латекс] увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, прежде чем разрушиться.

Использование диэлектрика в конденсаторе имеет еще одно преимущество. В зависимости от используемого материала емкость больше, чем указанная уравнением [латекс]\boldsymbol{C = {\varepsilon}_0 \frac{A}{d}}[/latex], на коэффициент [латекс]\boldsymbol {\kappa}[/latex] , называемая диэлектрической проницаемостью . Емкость плоского конденсатора с диэлектриком между пластинами равна

.

[латекс]\boldsymbol{C = \kappa {\varepsilon}_0}[/latex] [латекс]\boldsymbol{\frac{A}{d}}[/latex] [латекс]\boldsymbol{(\textbf{ плоскопараллельный конденсатор с диэлектриком})}.[/latex]

Значения диэлектрической проницаемости [латекс]\boldsymbol{\kappa}[/латекс] для различных материалов приведены в таблице 1. Обратите внимание, что [латекс]\жирныйсимвол{\каппа}[/латекс] для вакуума ровно 1, а поэтому приведенное выше уравнение справедливо и в этом случае. Если используется диэлектрик, например, путем помещения тефлона между пластинами конденсатора в примере 1, то емкость увеличивается в [латекс]\жирныйсимвол{\каппа}[/латекс], что для тефлона составляет 2,1.

Самостоятельный эксперимент: изготовление конденсатора

Насколько большой конденсатор можно сделать из обертки от жевательной резинки? Пластины будут алюминиевой фольгой, а перегородка (диэлектрик) между ними будет бумагой.

Материал	Диэлектрическая проницаемость [латекс]\boldsymbol{\kappa}[/латекс]	Диэлектрическая прочность (В/м)
Вакуум	1. 6}[/латекс] 96}[/латекс]
Вода	80	—
Таблица 1. Диэлектрическая проницаемость и диэлектрическая прочность для различных материалов при 20ºC

Также обратите внимание, что диэлектрическая проницаемость воздуха очень близка к 1, так что конденсаторы, заполненные воздухом, действуют так же, как конденсаторы с вакуумом между пластинами , за исключением , что воздух может стать проводящим, если напряженность электрического поля становится слишком большой . (Напомним, что [латекс]\boldsymbol{E = V/d}[/латекс] для конденсатора с плоскими пластинами.) В таблице 1 также показаны максимальные значения напряженности электрического поля в В/м, называемые диэлектрической прочностью, для нескольких материалов. Это поля, выше которых материал начинает разрушаться и проводить. Диэлектрическая прочность накладывает ограничение на напряжение, которое может быть приложено для данного разделения пластин. 4 \;\textbf{V})} \\[1em] & \boldsymbol{ 1.1 \;\textbf{mC}.} \end{массив}[/latex]

Это в 42 раза больше заряда того же воздушного конденсатора.

Диэлектрическая прочность

Максимальная напряженность электрического поля, выше которой изоляционный материал начинает разрушаться и проводить ток, называется диэлектрической прочностью.

Каким образом диэлектрик увеличивает емкость под микроскопом? В этом виновата поляризация изолятора. Чем легче он поляризуется, тем больше его диэлектрическая проницаемость [латекс]\boldsymbol{\kappa}[/латекс]. Вода, например, является полярной молекулой, потому что один конец молекулы имеет небольшой положительный заряд, а другой конец имеет небольшой отрицательный заряд. Полярность воды приводит к тому, что она имеет относительно большую диэлектрическую проницаемость, равную 80. Эффект поляризации можно лучше всего объяснить с точки зрения характеристик кулоновской силы. На рис. 5 схематично показано разделение заряда в молекулах диэлектрического материала, помещенного между заряженными пластинами конденсатора. Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень велика, так как они очень близко друг к другу. Это притягивает к пластинам больше заряда, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии [латекс]\boldsymbol{d}[/латекс].

Рис. 5. (а) Молекулы изоляционного материала между пластинами конденсатора поляризуются заряженными пластинами. Это создает слой противоположного заряда на поверхности диэлектрика, который притягивает больше заряда к пластине, увеличивая ее емкость. (b) Диэлектрик снижает напряженность электрического поля внутри конденсатора, что приводит к меньшему напряжению между пластинами при том же заряде. Конденсатор сохраняет тот же заряд при меньшем напряжении, что означает, что он имеет большую емкость из-за диэлектрика.

Другой способ понять, как диэлектрик увеличивает емкость, — рассмотреть его влияние на электрическое поле внутри конденсатора. На рис. 5(b) показаны силовые линии электрического поля с установленным диэлектриком. Поскольку силовые линии заканчиваются на зарядах в диэлектрике, их меньшее количество проходит от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, хотя на пластинах находится тот же заряд. Напряжение между пластинами равно [латекс]\boldsymbol{V = Ed}[/латекс], так что диэлектрик тоже снижает его. Таким образом, существует меньшее напряжение [латекс]\boldsymbol{V}[/латекс] для того же заряда [латекс]\boldsymbol{Q}[/латекс]; поскольку [латекс]\boldsymbol{C = Q/V}[/латекс], емкость [латекс]\boldsymbol{C}[/латекс] больше.

Диэлектрическая проницаемость обычно определяется как [латекс]\boldsymbol{\kappa = E_0/E}[/латекс] или отношение электрического поля в вакууме к электрическому полю в диэлектрическом материале и тесно связано с поляризуемость материала.

Вещи большие и малые

Субмикроскопическое происхождение поляризации

Поляризация — это разделение зарядов внутри атома или молекулы. Как уже отмечалось, планетарная модель атома изображает его как имеющее положительное ядро, вращающееся вокруг отрицательно заряженных электронов, подобно планетам, вращающимся вокруг Солнца. Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет уточнена в другом месте, например, в главе 30 «Атомная физика». Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рис. 6.9.0005 Рис. 6. Представление художника о поляризованном атоме. Орбиты электронов вокруг ядра немного смещены внешними зарядами (показаны преувеличенно). Возникающее в результате разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что противоположный заряд теперь ближе к внешним зарядам, вызывая поляризацию.

В главе 30 «Атомная физика» мы найдем, что орбиты электронов правильнее рассматривать как электронные облака с плотностью облака, связанной с вероятностью нахождения электрона в этом месте (в отличие от определенных местоположений и путей планет в их орбиты вокруг Солнца). Это облако смещается кулоновской силой так, что атом в среднем имеет разделение заряда. Хотя атом остается нейтральным, теперь он может быть источником кулоновской силы, поскольку заряд, поднесенный к атому, будет ближе к одному типу заряда, чем к другому.

Некоторым молекулам, например молекулам воды, присуще разделение зарядов, поэтому их называют полярными молекулами. На рис. 7 показано разделение заряда в молекуле воды, имеющей два атома водорода и один атом кислорода [латекс]\boldsymbol{\textbf{H}_2 \textbf{O}}[/latex]. Молекула воды несимметрична — атомы водорода отталкиваются в одну сторону, придавая молекуле форму бумеранга. Электроны в молекуле воды более сконцентрированы вокруг более сильно заряженного ядра кислорода, чем вокруг ядер водорода. Это делает кислородный конец молекулы слегка отрицательным, а водородный конец оставляет слегка положительным. Присущее полярным молекулам разделение зарядов облегчает их согласование с внешними полями и зарядами. Поэтому полярные молекулы проявляют больший поляризационный эффект и имеют большую диэлектрическую проницаемость. Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды намного эффективнее собирают ионы, потому что они имеют электрическое поле и разделение зарядов для притяжения зарядов обоих знаков. Кроме того, как показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.

Рисунок 7. Представление художника о молекуле воды. Существует неотъемлемое разделение зарядов, поэтому вода является полярной молекулой. Электроны в молекуле притягиваются к ядру кислорода и оставляют избыток положительного заряда вблизи двух ядер водорода. (Обратите внимание, что схема справа представляет собой грубую иллюстрацию распределения электронов в молекуле воды. На ней не показано фактическое количество протонов и электронов, участвующих в структуре.)

PhET Explorations: Capacitor Lab

Узнайте, как работает конденсатор! Измените размер пластин и добавьте диэлектрик, чтобы увидеть влияние на емкость. Измените напряжение и увидите заряды на пластинах. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.

Рис. 8. Конденсаторная лаборатория

• Конденсатор — это устройство, используемое для накопления заряда.
• Количество заряда [латекс]\boldsymbol{Q}[/латекс], которое может хранить конденсатор, зависит от двух основных факторов: приложенного напряжения и физических характеристик конденсатора, таких как его размер.
• Емкость [латекс]\boldsymbol{C}[/латекс] представляет собой количество накопленного заряда на вольт , или

  [латекс]\boldsymbol{C} =[/латекс] [латекс]\boldsymbol{\frac{Q}{V}}. [\латекс]

• Емкость конденсатора с параллельными пластинами равна [латекс]\boldsymbol{C = {\varepsilon}_0 \;\frac{A}{d}}}[/латекс], когда пластины разделены воздухом или свободным пространством. [латекс]\boldsymbol{{\varepsilon}_0}[/латекс] называется диэлектрической проницаемостью свободного пространства.
• Емкость плоского конденсатора с диэлектриком между пластинами определяется выражением

  [латекс]\boldsymbol{C = \kappa {\varepsilon}_0}[/latex] [латекс]\boldsymbol{\frac{A}{d}},[/latex]

  , где [латекс]\boldsymbol{\kappa}[/латекс] — диэлектрическая проницаемость материала.

• Максимальная напряженность электрического поля, выше которой изоляционный материал начинает разрушаться и проводить ток, называется диэлектрической прочностью.

 

 

конденсатор

устройство, накапливающее электрический заряд

емкость

количество накопленного заряда на единицу вольта

диэлектрик

изоляционный материал

диэлектрическая прочность

максимальное электрическое поле, при превышении которого изоляционный материал начинает разрушаться и становится проводящим

плоский конденсатор

две одинаковые проводящие пластины, разделенные расстоянием

полярная молекула

молекула с присущим разделением зарядов

 

Ответ: От каких параметров зависит емкость…

Задача 9. 1CYU: проверьте свое понимание В карманных калькуляторах часто используются небольшие солнечные элементы для подачи энергии… Задача 9.2CYU: проверьте свое понимание Автоматические выключатели в доме обычно измеряются в амперах в диапазоне от…Задача 9.3CYU: проверьте правильность понимания В примере 9.4 скорость дрейфа была рассчитана для диаметра 2,053 мм…Задача 9.4CYU: проверьте правильность понимания Плотность тока пропорциональна току и обратно. ..Проблема 9.5CYU: проверьте свое понимание Медные провода обычно используются для удлинителей и домашней электропроводки для… Задача 9.6CYU: проверьте свое понимание Тензодатчик — это электрическое устройство для измерения деформации, как показано ниже…. Задача 9.7CYU: Проверьте свое понимание Сопротивление между двумя проводниками коаксиального кабеля зависит от… Задача 9.8CYU: Проверьте свое понимание Напряжение, подаваемое в ваш дом, изменяется как V( t )= V max sin( 2ft ) Если… Задача 9.9CYU: проверьте свое понимание Электродвигатели имеют достаточно высокий КПД. Мотор мощностью 100 л.с. может иметь… Проблема 9.10CYU: Проверьте свое понимание. Является ли КПД различных лампочек единственным соображением, когда… Задача 1CQ: Может ли провод пропускать ток и оставаться нейтральным, то есть иметь полный заряд, равный нулю? Объясните. Проблема 2CQ: Автомобильные аккумуляторы измеряются в ампер-часах (Ач). Какой физической величине соответствуют ампер-часы… Задача 3CQ: При работе с мощными электрическими цепями рекомендуется по возможности работать… Проблема 4CQ: Лампы накаливания заменяются более эффективными светодиодными и Лампочки КЛЛ. Есть ли… Проблема 5CQ: Было заявлено, что движение электрона кажется почти случайным, когда электрическое поле… Проблема 6CQ: Электрические цепи иногда объясняются с помощью концептуальной модели воды, протекающей по трубе…. Проблема 7CQ: Лампа накаливания частично разряжена. Почему вы полагаете, что это так? Задача 8CQ: Падение [R на резисторе означает, что есть изменение потенциала или напряжения на. .. Задача 9CQ: Примеси в полупроводниковых материалах, перечисленных в таблице 9.1, обеспечивают бесплатную оплату? (Подсказка. Изучите… Задачу 10CQ: Зависит ли сопротивление объекта от пути прохождения тока через него? Рассмотрим, например,… Задачу 11CQ: Если алюминиевый и медный провода одинаковой длины имеют одинаковое сопротивление, у которого больше… Задача 12CQ: В определении поля по потенциалу сопротивление было определено как R=VI В этом разделе мы… Задача 13CQ: Ниже показаны результаты эксперимента, в котором четыре устройства были подключены через переменная… Задача 14CQ: Ток I измеряется через образец омического материала при приложении напряжения V, (a) Что… Задача 15CQ: Обычные бытовые приборы рассчитаны на 110 В, но энергетические компании поставляют напряжение в киловольтах… Задача 16CQ: В счете за электроэнергию указано потребление в киловатт-часах (кВт·ч) Эта единица измерения… Задача 17CQ: Резисторы обычно имеют номинал 18 Вт, 14 Вт, 12 Вт, 1 Вт и 2 W для использования в электрических цепях Если a. .. Задача 18CQ: Погружной нагреватель Ail — это небольшой прибор, используемый для нагревания чашки воды для чая с помощью пропускания тока… Задача 19CQ: Какое требование к сверхпроводимости7 делает современные сверхпроводящие устройства дорогими в эксплуатации? Задача 20CQ: Назовите два приложения сверхпроводимости, перечисленные в этом разделе, и объясните, как сверхпроводимость… Задача 21P: Генератор Ван де Граафа является одним из первых ускорителей частиц и может использовать для ускорения… Задача 22P: Электронно-лучевая трубка (ЭЛТ) — это устройство, создающее сфокусированный пучок электронов в вакууме. Задача 23P: Сколько электронов проходит через точку провода за 3,00 с, если есть постоянный ток I = 4,00… Задача 24P: По проводнику течет ток, который экспоненциально уменьшается со временем. Ток моделируется как… Задача 25P: Количество заряда в проводнике моделируется как Q=4.00Cs4t41.00Cst+6.00mc. Что такое… Задача 26P: Ток в проводнике моделируется как I(t )=Imsin(2[60Hz]t) . Напишите уравнение для… Задача 27P: Заряд конденсатора в цепи моделируется как Q(t)=Qmaxcos(+) . Какова сила тока через… Задача 28P: По алюминиевому проводу диаметром 1,628 мм (калибр 14) течет ток силой 3,00 ампер. (a) Что такое… Задача 29P: Ток избирательного луча имеет измеренный ток I=50,00 А с радиусом 1,00 мм2. Что такое… Задача 30P: Ускоритель протонов высокой энергии производит пучок протонов с радиусом r — 0,90 мм. Балка… Задача 31P: Рассмотрим провод круглого сечения с радиусом R = 3,00 мм. Величина… Задача 32P: Ток электронного луча имеет измеренный ток I=50.00A с радиусом 1,00 мм2. Что… Проблема 33P: Ток, подаваемый на блок кондиционера, составляет 4,00 ампера. Кондиционер подключен с помощью … Задача 34P: Какой ток протекает через лампу фонарика на 3,00 В, когда его сопротивление в горячем состоянии равно 3,60? Задача 35P: Рассчитать эффективное сопротивление карманного калькулятора с батареей на 1,35 В. и через … Задача 36P: Сколько вольт подается для работы индикатора на DVD-плеере, который имеет сопротивление . .. Задача 37P: Каково сопротивление куска меди 12 калибра длиной 20,0 м. провод диаметром 2,053 мм? Задача 38P: Диаметр медного провода нулевого калибра равен 8,252 мм. Найти сопротивление отрезка длиной 1,00 км такого… Задача 39.P: Если вольфрамовая нить диаметром 0,10,0 мм в лампочке должна иметь сопротивление 0,200 атм… Задача 40P: Свинцовый стержень имеет длину 30,00 см и сопротивление 5,00. Каков радиус стержня? Задача 41P: Найти отношение диаметра алюминиевого провода к медному, если они имеют одинаковое сопротивление pet-… Задача 42P: Какой ток протекает через стержень Pure диаметром 2,54 см кремний длиной 20,0 см, когда 1,00103… Задача 43P: (a) До какой температуры нужно нагреть медный провод, первоначально при 20,0°C, чтобы удвоить его сопротивление,… Задача 44P: Резистор из нихромовой проволоки используется в приложениях, где его сопротивление не может измениться больше… Задача 45P: Из какого материала сделан резистор, если его сопротивление на 40,0% больше при 100,0 ° C, чем при 20,0 ° C? Задача 46P: Электронное устройство, предназначенное для работы при любой температура в диапазоне от 10,0°С до 55,0°С.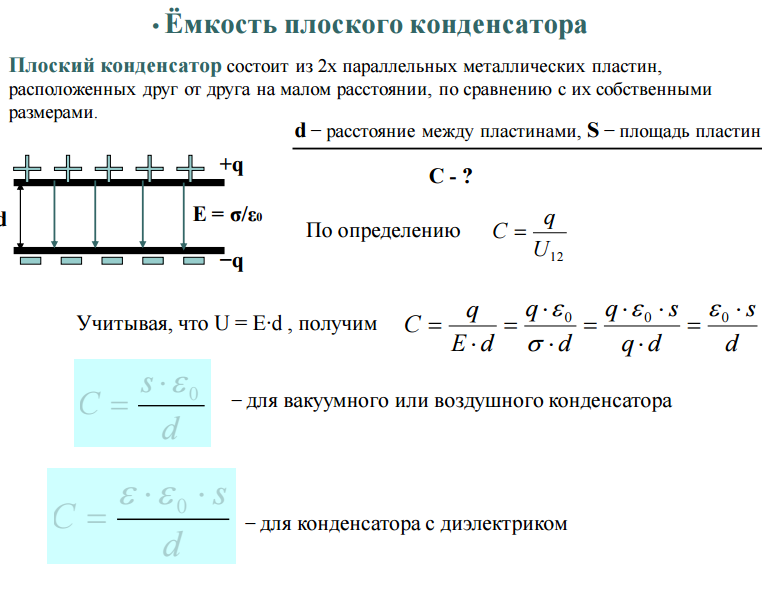 .. Задача 47П: а) Из какого материала сделана проволока, если она имеет длину 25,0 м, диаметр 0,100 мм и имеет… Задача 48П. при постоянном температурном коэффициенте удельного сопротивления чему равен максимальный процент уменьшения… Задача 49P: Медный провод имеет сопротивление 0,500 при 20,0°C, а железный провод имеет сопротивление 0,525 при… Задача 50P: Резистор 2,2 кОм подсоединен к батарейке типа D (1,5 В). Каков ток через… Задача 51P: Резистор номиналом 250 кОм подключен к двум батареям D-элементов (каждая 1,50 В) последовательно с… Задача 52P: Резистор подключен последовательно к источнику питания. питание 20,00 В. Измерение тока 0,50 А…. Задача 53P: Резистор включен в цепь с регулируемым источником напряжения. Напряжение на и… Задача 54P: В следующей таблице показаны измерения тока и напряжения на образце… Задача 55P: Батарея на 20,00 В используется для подачи тока на резистор 10 кОм. . Предположим, падение напряжения на любом… Задача 56P: Какое максимальное напряжение может быть приложено к резистору 10 кОм, номинальной мощностью 14 Вт? Задача 57P: Разрабатывается нагреватель, который использует катушку из нихромовой проволоки 14-го калибра для генерации 300 W с использованием. .. Проблема 58P: Альтернативой люминесцентным люминесцентным лампам и лампам накаливания являются светодиодные (LED) лампы. А 100-Вт… Задача 59P: Мощность, рассеиваемая резистором с сопротивлением R=100, составляет P = 2,0 Вт. Каковы текущие… Задача 60P: Опоздав, чтобы успеть на самолет, водитель случайно оставил фары включенными после парковки автомобиля… Задача 61P: SI. У студента-физика в общежитии есть одноместный ткацкий станок. У студента есть небольшой холодильник, который… Задача 62P: Резистор мощностью 0,50 Вт, 220 Ом пропускает максимально возможный ток, не повреждая резистор. Если… Задача 63P: Предположим, что электростанция расположена в 60 км от жилого района и использует провод Q-калибра (A=42,40 мм2)… Задача 64P: Провод протягивается через матрицу, растягивая его до четырех раз превышает его первоначальную длину. По какому коэффициенту… Задача 65P: Цифровые медицинские термометры определяют температуру путем измерения сопротивления полупроводника… Задача 66P: Генераторы электроэнергии иногда «испытывают под нагрузкой», пропуская ток через большой чан с. .. Задача 67P : Золотая проволока 12-го калибра имеет длину 1 м. (a) Какой должна быть длина серебряной проволоки 12-го калибра… Задача 68P: Какое изменение температуры требуется для уменьшения сопротивления угольного резистора? на 10%?Задача 69AP: Коаксиальный кабель состоит из внутреннего проводника с радиусом r1 = 0,25 см и внешним радиусом r0 = 0,5 см… Задача 70AP: медный кабель длиной 10,00 м имеет сопротивление 0,051 Ом, (a) Что такое… Задача 71AP: Нихромовый стержень длиной 3,00 мм с площадью поперечного сечения 1,00 мм2 используется для цифрового… Задача 72AP: Температура в Филадельфии, штат Пенсильвания, может варьироваться в пределах 68,00F. и 100.00F за один летний день. По какому… Задача 73AP: Когда 100,0 В приложено к проводу 5-го калибра (диаметр 4,621 мм) длиной 10 м, величина… Задача 74AP: Провод с сопротивлением 5,0 протянут через умереть так, чтобы его новая длина была в два раза больше… Задача 75AP: Каково удельное сопротивление провода 5-го калибра (A=16,8106 м2), длиной 5,00 м и 5,10 м . .. Задача 76AP: Катушки часто используются в электрических и электронных схемах. Рассмотрим катушку, образованную… Проблема 77AP: Токи силой приблизительно 0,06 А могут быть потенциально смертельными. Токи в этом диапазоне могут сделать сердце… Задача 78AP: 20,00 Ом; Резистор 5,00 Вт включен последовательно с источником питания, а) Чему равна максима… Задача 79AP: Батарея с ЭДС 24,00 В подает на устройство постоянный ток 2,00 мА. Как много… Задача 80AP: Батарея на 12,00 В имеет внутреннее сопротивление в одну десятую ома. (a) Какова сила тока, если… Задача 81CP: Медный провод 10-го калибра имеет площадь поперечного сечения A=5,26 мм2 и по нему протекает ток I=5,00A. Задача 82CP: Ток в проводе 12-го калибра определяется как I(t)=(5,00A)sin(260Hzt)). Каков ток… Задача 83CP: Ускоритель частиц производит луч радиусом 1,25 мм с током 2,00 мА. Каждая… Задача 84CP: В этой главе большинство примеров и задач связаны с постоянным током (DC). Цепи постоянного тока имеют… Задача 85CP: Ток I = 25 А поступает от 100-вольтовой батареи в течение 30 секунд.