Теоретическая механика. 20 лекций. Ч. 2. Динамика
Теоретическая механика. 20 лекций. Ч. 2. Динамика
ОглавлениеПредисловиеДинамика точки Две основные задачи динамики точки Дифференциальные уравнения движения материальной точки Способы решения основных задач динамики точки Лекция 12.  Способы интегрирования дифференциального уравнения прямолинейного движения материальной точки Способы интегрирования дифференциального уравнения прямолинейного движения материальной точкиДифференциальное уравнение и начальные условия прямолинейного движения Определение закона движения точки под действием силы, зависящей только от времени Определение закона движения точки под действием силы, зависящей только от положения О нахождении закона движения при постоянной силе и силе, зависящей только от скорости Лекция 13. Колебательные движения материальной точки Свободные колебания Явление резонанса Влияние сопротивления на свободные и вынужденные колебания Динамика системы Механическая система Масса и центр масс системы Момент инерции относительно оси Моменты инерции относительно координатных осей Моменты инерции твердого тела Осевые моменты инердии некоторых твердых тел Радиус инерции Главные оси инерции Классификация сил, действующих на точки системы Свойства внутренних сил Дифференциальные уравнения движения механической системы Теорема о движении центра масс Законы сохранения движения дентра масс Общие теоремы динамики Основные динамические величины механической системы Теорема об изменении количества движения О вычислении количества движения Интегральная форма теоремы об изменении количества движения Лекция 16.  Теорема об изменении кинетического момента Теорема об изменении кинетического моментаКинетический момент Теорема об изменении кинетического момента Законы сохранения кинетического момента Кинетический момент твердого тела (общий случай) Дифференциальные уравнения движения твердого тела Физический маятник и его малые колебания Лекция 17. Теорема об изменении кинетической энергии Работа силы тяжести Работа упругой силы пружины Работа силы трения скольжения Работа пары сил трения качения Потенциальные силы Вычисление потенциальной энергии Теорема об изменении кинетической энергии Вычисление кинетической энергии твердого тела О решении задач при помощи теоремы об изменении кинетической энергии Общие принципы механики Принцип Даламбера для материальной точки Принцип Даламбера для механической системы Определение главного вектора и главного момента сил инерции твердого тела Тело движется поступательно с ускорением Тело совершает вращательное движение Тело совершает плоскопараллельное движение Лекция 19.  Возможные перемещения Уравнения связей. Классификация связей по виду их уравнений Связи идеальные и неидеальные Принцип возможных перемещений Применение принципа возможных перемещений Лекция 20. Принцип Даламбера-Лагранжа и общее уравнение динамики. Уравнения движения механической системы в обобщенных координатах Принцип Даламбера-Лагранжа Общее уравнение динамики Обобщенные координаты и обобщенные силы Уравнения движения механической системы в обобщенных координатах |
Моменты инерции сечения. Расчет в Excel.
Опубликовано 22 Ноя 2013
Рубрика: Механика | 5 комментариев
Моменты инерции сечения балки (бруса, стержня) относятся, как и площадь сечения, к одним из основных геометрических характеристик элемента, участвующих в расчетах на прочность. Напомню, что балкой в сопромате называется элемент, у которого один из размеров — длина.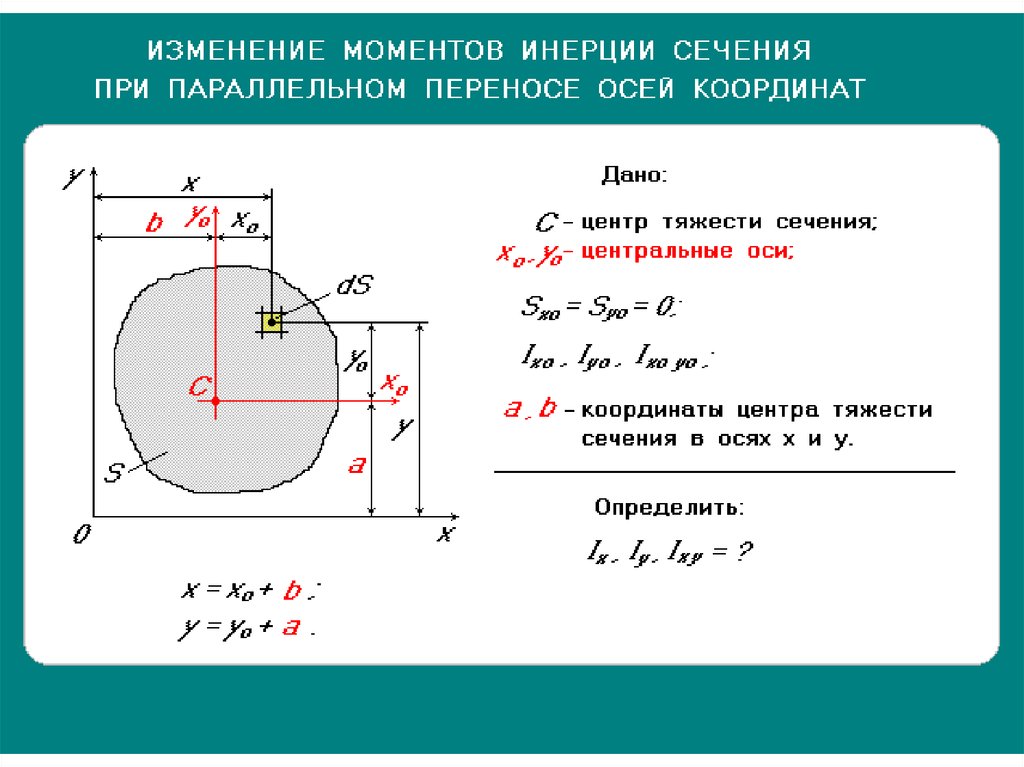 ..
..
…существенно больше двух других – ширины и высоты. Именно два последних габаритных размера плюс форма и влияют наряду со свойствами материала на прочностные характеристики балки.
Геометрические моменты инерции сечения нельзя путать с моментами инерции тел, хотя их смысл весьма схож. Момент инерции тела вокруг некоторой оси – это сумма произведений масс элементарных «объемных» точек тела на квадраты расстояний от оси до этих точек. Момент инерции сечения (плоской фигуры) — это сумма произведений площадей элементарных «плоских» точек этого сечения на квадраты расстояний от них до рассматриваемой оси.
Принято считать, что понятие и термин «момент инерции поперечного сечения» ввел в 1834-ом году француз Перси, хотя и до него многие ученые использовали в своих работах понятия, имеющие этот же смысл.
Формулы для вычисления осевых моментов инерции, а также радиусов инерции и моментов сопротивления почти тридцати элементарных фигур, из которых можно составить любое сечение бруса, можно взять в разделе «Элементы сопротивления материалов» главы №1 «Общетехнические сведения» тома №1 «Справочника конструктора-машиностроителя» В. И. Анурьева. Этот трехтомный справочник, являющийся главной настольной книгой нескольких поколений инженеров-механиков и претерпевший около десяти переизданий, и сегодня продолжает являться востребованным и актуальным. Я думаю, он должен обязательно быть у каждого инженера, тем более что найти его в Сети – не проблема. Конечно, интересующие нас формулы можно найти и в другой справочной литературе.
И. Анурьева. Этот трехтомный справочник, являющийся главной настольной книгой нескольких поколений инженеров-механиков и претерпевший около десяти переизданий, и сегодня продолжает являться востребованным и актуальным. Я думаю, он должен обязательно быть у каждого инженера, тем более что найти его в Сети – не проблема. Конечно, интересующие нас формулы можно найти и в другой справочной литературе.
Для двутавров, швеллеров, уголков, труб и прочих прокатных и гнутых профилей, широко применяемых в машиностроении и строительстве, геометрические характеристики сечений, включая моменты инерции, можно найти в таблицах ГОСТов, ОСТов и прочих нормативных документов, которые регламентируют их изготовление.
Балки и стержни, составленные из двух или более элементарных профилей, применяют для повышения прочности и жесткости элементов при отсутствии адекватной с точки зрения массы и габаритов замены одиночным профилем. На практике – это спаренные уголки, двухветвевые колонны, балки с усиленным листовой полосой поясом и другие случаи.
В статье «Как найти центр тяжести?» мы рассматривали в качестве примера составную фигуру, состоящую из треугольника и прямоугольника с вырезом в виде полукруга. Продолжим работу с этим примером. Хотя балку, имеющую столь причудливое сечение, на практике нигде и никогда, наверное, не встретишь, для не очень сложного и наглядного примера она нам подойдет!
Запускаем программу MS Excel или программу OOo Calc, и начинаем работу!
С общими правилами форматирования электронных таблиц, применяемыми в статьях блога, можно ознакомиться здесь.
Из вышеупомянутой статьи мы уже знаем координаты центров тяжести, площади элементов сечения и площадь всего составного сечения. В этой статье продолжим начатую работу, и выполним расчет других геометрических характеристик.
Исходные данные:
Пункты 1, 2, 3 копируем из файла raschet-tsentra-tyazhesti и заполняем диапазон ячеек D3:F6.
4. 0,5
0,5
Задача выполнена – вычислены моменты инерции и радиусы инерции составного сечения из трех простых элементов! Получены все необходимые данные для построения эллипса инерции.
Файл Excel с расчетной программой позволяет легко выполнить полный расчет геометрических характеристик поперечного сечения балки, состоящего из двух или трех простых элементов. При необходимости несложно расширить возможности расчетного модуля до большего количества элементов.
Ссылка на скачивание файла: geometricheskie-kharakteristiki-secheniia (xls 21,0KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
Момент инерции
Момент инерции Вот
рецепт от корки
для вычисления момента инерции еще раз:
| ||||||||||||||||||||||||||||||||||
| Критическое упрощение обведено красным. Однако, поскольку это научный модуль, мы дадим неупрощенной версии быстрый взгляд, прежде чем мы снова расслабимся и сделаем жизнь очень легкой. | ||||||||||||||||||||||||||||||||||
Ну, я уже говорил, говорю
еще раз: момент инерции на самом деле тензор второго ранга. Определяющим свойством является
угловой момент л ,
двоюродный брат линейного импульса p=mv ( m = масса, v = скорость), который оказывается (осевым) вектором
так же, как линейный импульс. Вам нужно три числа, чтобы определить его. Определяющим свойством является
угловой момент л ,
двоюродный брат линейного импульса p=mv ( m = масса, v = скорость), который оказывается (осевым) вектором
так же, как линейный импульс. Вам нужно три числа, чтобы определить его. Угловой момент L определяется следующим уравнением: | ||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||
I ij являются компонентами
тензор момента инерции,  Это означает, что угловой момент составляет , а не должны указывать в том же направлении, что и
угловая скорость, в отличие от линейного количества движения, которое всегда указывает в
направление скорости. Это означает, что угловой момент составляет , а не должны указывать в том же направлении, что и
угловая скорость, в отличие от линейного количества движения, которое всегда указывает в
направление скорости. | ||||||||||||||||||||||||||||||||||
| Как всегда с тензорами, жизнь становится
намного проще, если выбрать умную систему координат. Это очень легко в
нормальной жизни, потому что большинство вращающихся тел, представляющих интерес, обладают некоторой симметрией
и напрашиваются «естественные» оси системы координат
легко. Я рассмотрел эти « | ||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||
| Расчет трех компонентов простым (в принципе), если вы знаете распределение массы (или, другими словами, слов, плотность r ( x , y , z ) в каждой точке плюс форма предмета (спрятанного в этом невинном» В «для объем под знаками интеграла, которые означают «интегрировать по объем») | ||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||
Ну, в принципе просто, может быть,
но на самом деле довольно утомительно и практически невозможно сделать для таких форм, как
меч с карандашом на листе бумаги.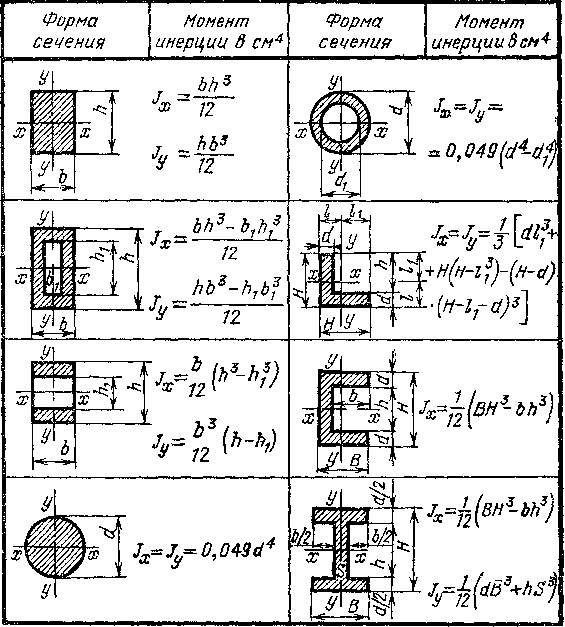 Однако есть один бонус. Когда ты
на самом деле выйти, чтобы сделать математику для некоторых общих форм, вы обнаружите, что
math содержит элементы, которые выглядят довольно знакомыми (мы надеемся). Уравнения
(математически) идентичные тем, которые уже были обнаружены (и, возможно, уже
готово) для Площадь Момент Инерции. Ведь именно поэтому
Момент области получил свое странное (и глупое) название. Отмечая, что может спасти много
работа. Однако есть один бонус. Когда ты
на самом деле выйти, чтобы сделать математику для некоторых общих форм, вы обнаружите, что
math содержит элементы, которые выглядят довольно знакомыми (мы надеемся). Уравнения
(математически) идентичные тем, которые уже были обнаружены (и, возможно, уже
готово) для Площадь Момент Инерции. Ведь именно поэтому
Момент области получил свое странное (и глупое) название. Отмечая, что может спасти много
работа. | ||||||||||||||||||||||||||||||||||
| Отлично, но кого это волнует? Выполнение этих интегралов сегодня с компьютером детская игра. Единственная проблема — получить данные о форму и плотность в систему.. | ||||||||||||||||||||||||||||||||||
Однако в старые времена люди
не было компьютеров, а у многих даже не было
выпускник
студенты, которые обожают нудную работу. Поэтому люди придумали некоторые
творческие концепции, чтобы избежать расчетов, а некоторые еще очень
поучительный и важный для рассмотрения «обращения» с мечами.
Здесь мы рассмотрим только несколько простых примеров Поэтому люди придумали некоторые
творческие концепции, чтобы избежать расчетов, а некоторые еще очень
поучительный и важный для рассмотрения «обращения» с мечами.
Здесь мы рассмотрим только несколько простых примеров | ||||||||||||||||||||||||||||||||||
| Примеры | ||||||||||||||||
| Рассмотрим простой цилиндр из какого-либо материала с
масса м , длина l и радиус р . Мы рассматриваем «естественную ось вращения как швон, которая
является, конечно, главной осью системы. Находим момент инерции как
показано. Вы можете удивиться, что уравнение не содержит длины l цилиндр.  В этом нет необходимости, так как l уже содержится в
масса м . Удвойте длину, и вы удвоите массу и, таким образом,
также момент инерции. В этом нет необходимости, так как l уже содержится в
масса м . Удвойте длину, и вы удвоите массу и, таким образом,
также момент инерции. | ||||||||||||||||
| ||||||||||||||||
Далее то же самое еще раз, но теперь на
вращение вокруг одной из двух других главных осей. | ||||||||||||||||
| ||||||||||||||||
Теперь нам явно нужна длина
в определяющем уравнении. Интересно посмотреть на ту же ситуацию сейчас для полых цилиндров с толщиной стенок во много раз больше. меньше радиуса r . Получаем приближенные уравнения, которые довольно хорошо: | ||||||||||||||||
| ||||||||||||||||
Так что моменты инерции для полнотелого
и полый цилиндр совпадают, так как уравнения не таковы. другой? Совершенно неправильно. Учтите, что для того, чтобы иметь одинаковую массу в обоих
случаях радиус полого цилиндра должен быть намного больше. другой? Совершенно неправильно. Учтите, что для того, чтобы иметь одинаковую массу в обоих
случаях радиус полого цилиндра должен быть намного больше. | ||||||||||||||||
| Мы видим очень просто, что момент инерции одной и той же массы намного больше, если масса «растекаться». Для некоторых имеет значение, как именно распределяется масса. степени и затрудняет вычисления, но общая тенденция ясна: большие разбросы в пространстве вызывают большие моменты инерции. | ||||||||||||||||
| Это дает нам представление. Для любого данного тела мы можем определяют своего рода характеристику «длина распространения массы k «, приравняв его действительный момент инерции (относительно некоторая главная ось) на | ||||||||||||||||
| ||||||||||||||||
Для компактных корпусов k будет
маленькое, у разложенных оно становится большим. Люди называют эту характеристику
длина k длина вращения тела. Это один номер (с
единица метр м ), характеризующая тело (относительно
выбранная ось). Это не очень важно в контексте динамики меча, и я
введите его только для того, чтобы подчеркнуть один важный момент: Люди называют эту характеристику
длина k длина вращения тела. Это один номер (с
единица метр м ), характеризующая тело (относительно
выбранная ось). Это не очень важно в контексте динамики меча, и я
введите его только для того, чтобы подчеркнуть один важный момент: | ||||||||||||||||
| ||||||||||||||||
Длина удара — это расстояние
между выбранной точкой разворота и ударная точка .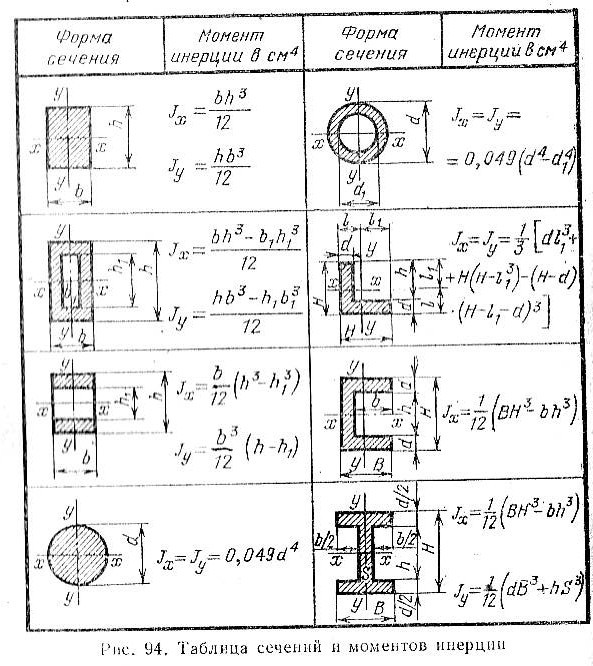 я имею дело с
ударная точка (и другие важные точки на вашем мече) в
позвоночник и
здесь. В этот момент позвольте мне просто сказать
что то, что вы найдете в литературе обо всех этих точках или длинах, не
неправильно, но обычно не легко следовать. Легко запутаться, смешивая
длину вращения с длиной перкуссии, длину перкуссии с
расстояние между узлами вибрации и так далее. я имею дело с
ударная точка (и другие важные точки на вашем мече) в
позвоночник и
здесь. В этот момент позвольте мне просто сказать
что то, что вы найдете в литературе обо всех этих точках или длинах, не
неправильно, но обычно не легко следовать. Легко запутаться, смешивая
длину вращения с длиной перкуссии, длину перкуссии с
расстояние между узлами вибрации и так далее. | ||||||||||||||||
| Возможно Моменты инерции на 1 кг железа | |||||||||||||||||||||||
Типичный меч имеет
масса м около 1000 г=1 кг . Посмотрим, что мы можем сделать
с этой массой, распределяя ее по-разному. Плотность железа р железо =7,78
г/см 3 , и для этого требуется объем V= 128,5 см 3 .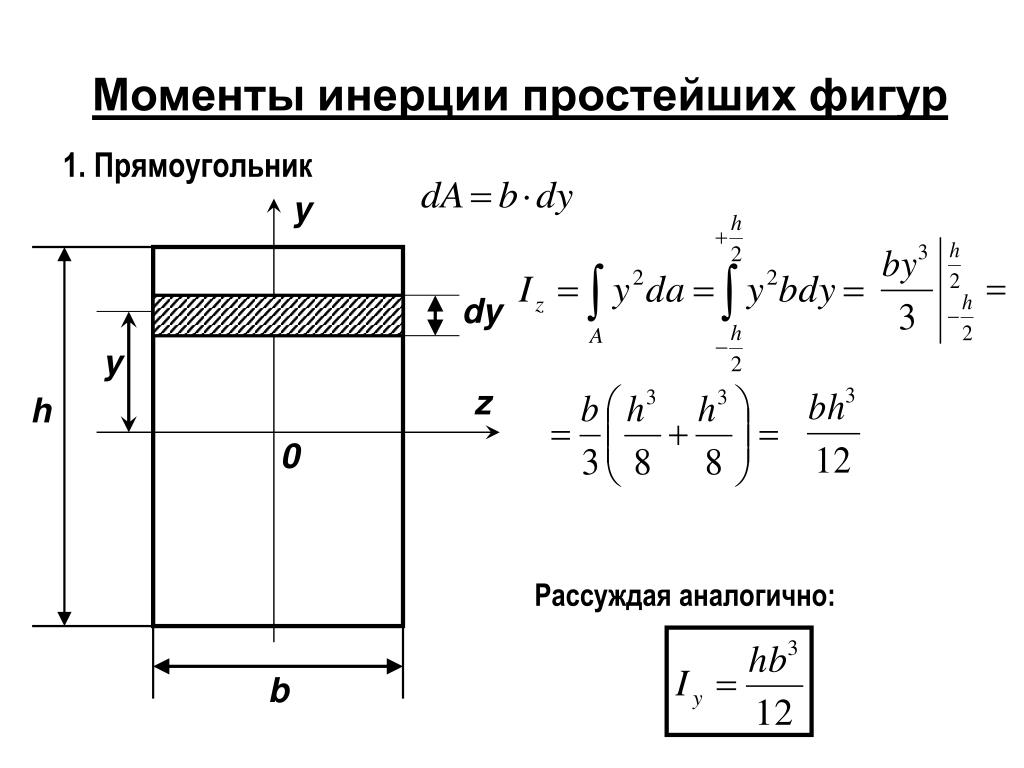 | |||||||||||||||||||||||
| Сначала давайте посмотрим на сферу весом 1
кг. Его радиус тогда составляет 3,12 см; примерно размером с большое яйцо. Сфера
не то, что вы имели бы в виду для меча, но он служит для придания абсолютного
минимум момента инерции, который можно было бы иметь (вокруг любой оси, проходящей через
Центр, конечно). Ниже показано, как вы получаете числа. | |||||||||||||||||||||||
| |||||||||||||||||||||||
Далее мы берем очень простой меч.
Просто прямоугольное лезвие, 100 см длина, 4 см ширина, а затем по
необходимо 0,32 см толщиной. Сначала рассмотрим вращение через центр
массы, которая, конечно, прямо посередине.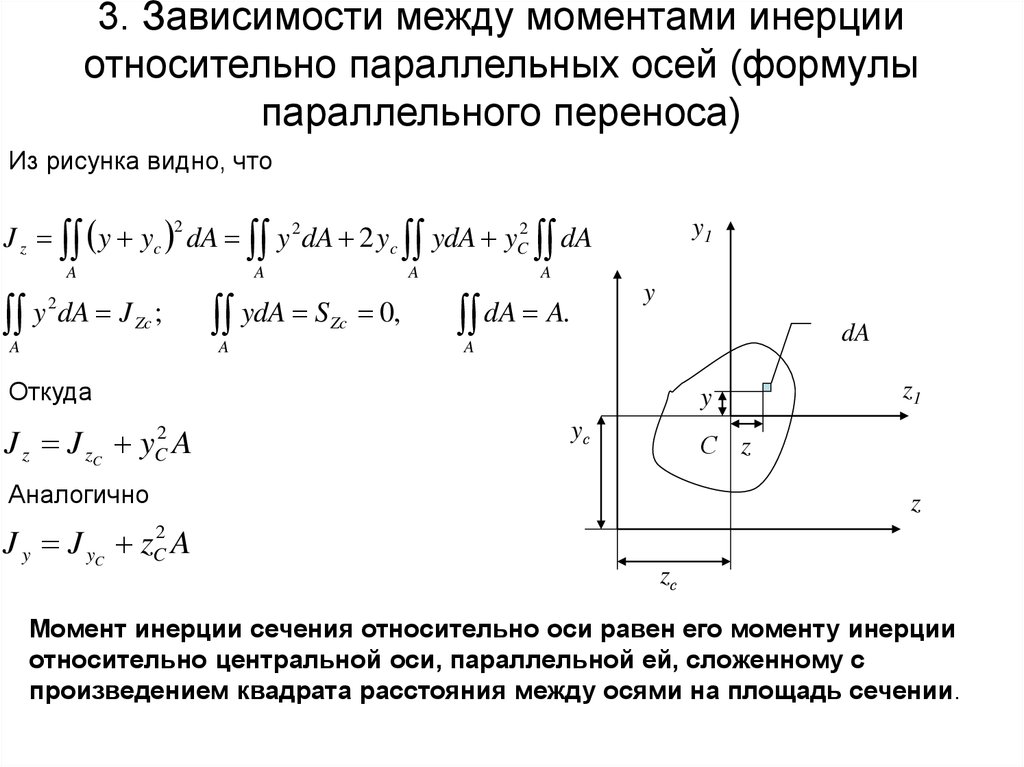 | |||||||||||||||||||||||
| |||||||||||||||||||||||
Если нам нужен момент инерции для оси
сидя на конце лезвия (красная ось), используем
теорема о параллельных осях.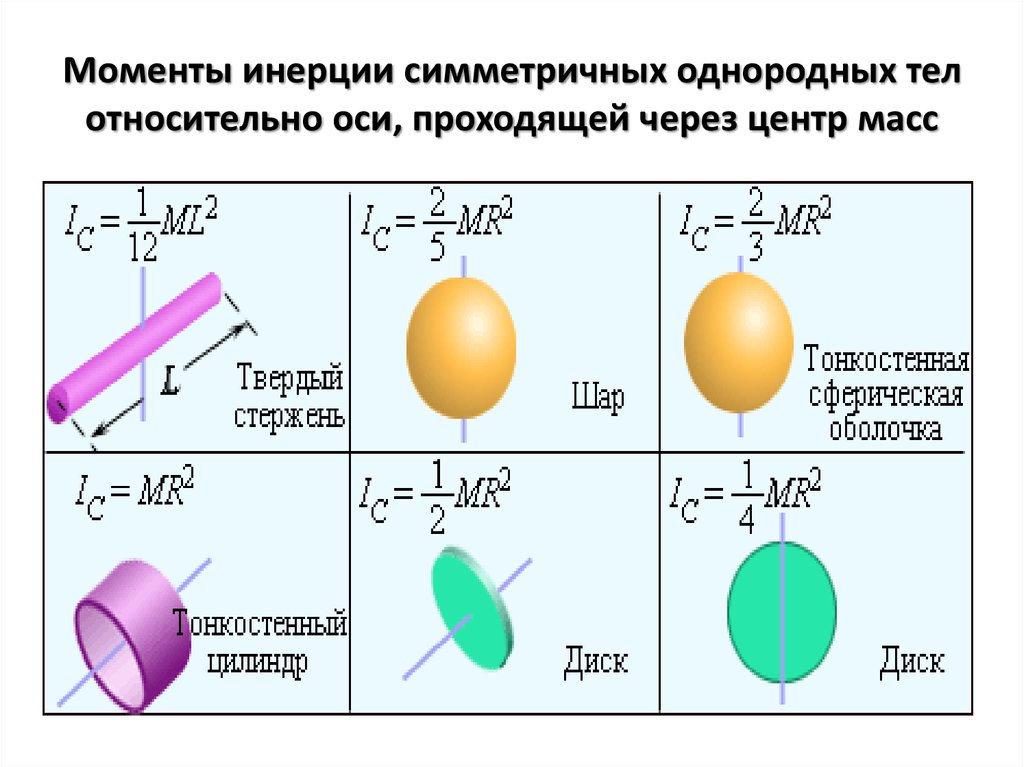 Это означает, что мы должны добавить массу, умноженную на расстояние между осями в квадрате, и получить я красный =84,7 кгсм 2 + 1кг · (50
см) 2 =2 585 кгсм 2 . Это означает, что мы должны добавить массу, умноженную на расстояние между осями в квадрате, и получить я красный =84,7 кгсм 2 + 1кг · (50
см) 2 =2 585 кгсм 2 . | |||||||||||||||||||||||
| Наконец, давайте рассмотрим топор или дубину, где сфера установлена на «безмассовом» стержне длиной 1 м с точка поворота на конце этого стержня. Еще раз воспользуемся теоремой о параллельных осях. и добавьте массу, умноженную на квадрат расстояния, к результату для сферы. Мы получаем я Клуб =4 кгсм 2 + (100 2 см 2 · 1 кг)=10 004 кг · см 2 . | |||||||||||||||||||||||
| |||||||||||||||||||||||
Имеем вариацию момента
инерция примерно от 4 кгсм 2 до 10 000
кгсм 2 ; легкий коэффициент 2 500 ! Больше не нужно говорить. | |||||||||||||||||||||||
С рамкой
Количественная оценка свойств вашего меча
Наука об одноосной деформации
Площадь Момент инерции
Наука деформации
Ударная точка
12.3.7 Ударная точка
12.3.5 Момент инерции
Столкновения
Эффективная масса
© H. Föll (скрипт Iron, Steel and Swords)
Статика: теорема о параллельных осях
Теорема о параллельной оси связывает момент инерции формы относительно произвольной оси с ее моментом инерции относительно параллельной центральной оси.
Эта теорема особенно полезна, потому что, если мы знаем центральный момент инерции формы, мы можем вычислить ее момент инерции относительно любой параллельной оси, добавив соответствующий поправочный коэффициент. С другой стороны, если мы знаем момент инерции относительно оси, мы можем найти соответствующий центральный момент инерции, вычитая тот же коэффициент.
С другой стороны, если мы знаем момент инерции относительно оси, мы можем найти соответствующий центральный момент инерции, вычитая тот же коэффициент.
Центроидальный момент инерции обычных форм хорошо известен и легко доступен в таблицах свойств форм, таких как Подраздел 10.3.2.
Подраздел 10.3.1 Вывод
Мы будем использовать определяющее уравнение для момента инерции (10.1.3), чтобы вывести теорему о параллельности осей.
На диаграмме показана произвольная форма и две параллельные оси: ось \(x’\), нарисованная красным цветом, проходит через центроид фигуры в точке \(C\text{,}\), а \(x \) ось, параллельная и разделенная расстоянием, \(d\text{.}\) Фигура имеет площадь \(A\text{,}\), которая разделена на квадратные дифференциальные элементы \(dA\text{ .}\) Расстояние от оси \(x\) до элемента \(dA\) равно \(y\text{,}\), а расстояние от оси \(x’\) равно \(y’ \текст{.}\) 92\) термин «поправочный коэффициент» для учета расстояния оси от центра тяжести. Этот член всегда положительный, поэтому центральный момент инерции всегда является минимальным моментом инерции для определенного направления оси.
В следующем примере показано, как теорема о параллельных осях обычно используется для нахождения момента инерции фигуры относительно оси с использованием формул для центроидального момента инерции, приведенных в подразделе 10.3.2.
Пример 10.3.2. Круговое кольцо.
4 \end{equation*}Решение.
Чтобы применить теорему о параллельных осях, нам нужны три элемента информации
Центроидальный момент инерции кольца, \(I_y\text{,}\)
площадь кольца, \(A\text{,}\)
расстояние между параллельными осями, \(d\text{.}\)
Площадь кольца находится путем вычитания площади внутреннего круга из площади внешнего круга. Центроидальный момент инерции рассчитывается аналогично по (10.2.10). Расстояние между осями \(y\) и \(y’\) доступно на диаграмме. Вставка этих значений в теорему о параллельной оси дает 94 \end{align*}
Интересно, что «поправочный коэффициент» более чем в 20 раз превышает центральный момент инерции кольца. 2\text{.}
\end{выравнивание*} 92\text{.}\) Обратите внимание, что центроидальный момент инерции меньше, чем момент инерции относительно любой соответствующей параллельной оси.
2\text{.}
\end{выравнивание*} 92\text{.}\) Обратите внимание, что центроидальный момент инерции меньше, чем момент инерции относительно любой соответствующей параллельной оси.
Переместите красные точки, чтобы изменить размер и положение прямоугольника.
Рисунок 10.3.6. Момент инерции прямоугольникаПример 10.3.7. Интерактив: полукруг.
Используйте этот интерактив, чтобы попрактиковаться в вычислении моментов инерции площади полукруга относительно центральной оси \(x’\), нижнего края \(x»\text{,}\) и системы \(x \) ось. Вы можете изменить положение и размер полукруга, перемещая красные точки. 92\text{.}\) Расстояние \(d\) представляет собой расстояние между интересующей осью и параллельной осью, проходящей через центр тяжести фигуры.
Перемещайте красные точки, чтобы изменить размер и положение полукруга.
Рисунок 10.3.8. Момент инерции полукругаПодраздел 10.3.2 Таблица моментов инерции
В этой таблице приведены свойства распространенных фигур, которые обсуждались ранее.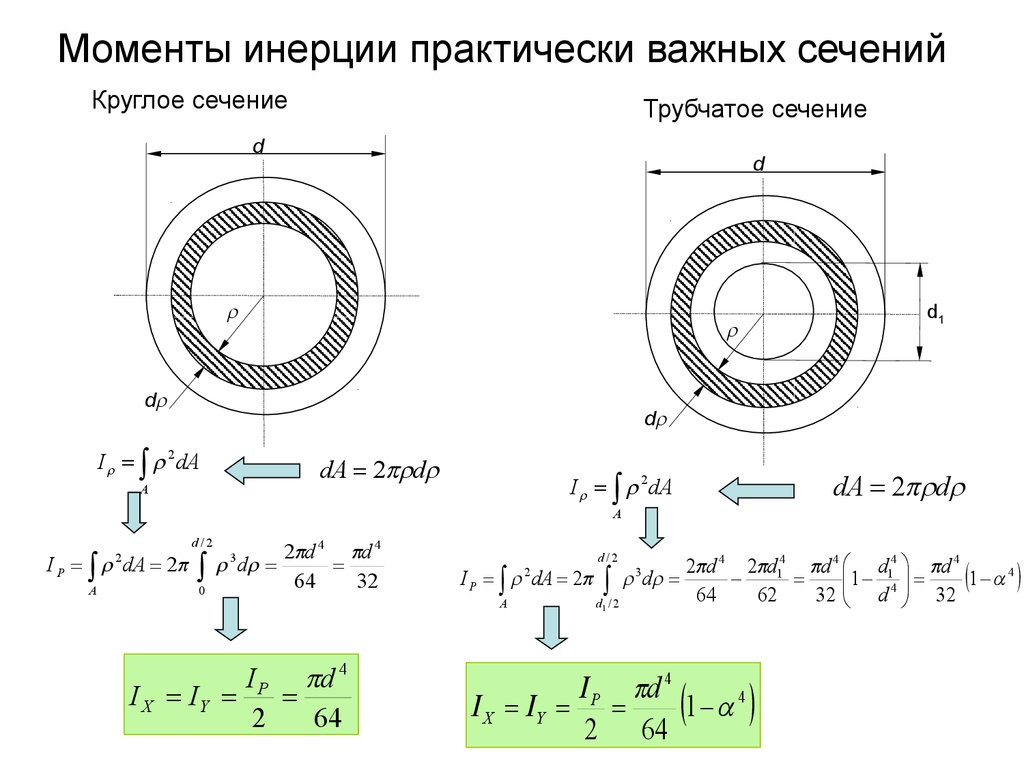



 · р 3
· р 3