Силы всемирного тяготения. Закон всемирного тяготения. Движение планет. Искусственные спутники
Силы всемирного тяготения. Закон всемирного тяготенияПлан урока
- Гравитационные силы. Закон всемирного тяготения
- Ускорение свободного падения
Цели урока
- знать понятие «гравитационные силы»; формулировку закона всемирного тяготения; формулу ускорения свободного падения
- уметь объяснять, от каких величин зависит величина силы притяжения; описывать опыт по измерению гравитационной постоянной; объяснять причины, по которым ускорение свободного падения имеет различные значения в разных точках земного шара
Разминка
- Действие какой силы обуславливает движение Земли вокруг Солнца?
- Дайте определение силы тяжести.
- Что такое ускорение свободного падения?
Гравитационные силы. Закон Всемирного тяготения
Известно, что Земля притягивает к себе все тела, находящиеся на её поверхности с силой тяжести Fт=m·g. Согласно третьему закону Ньютона, тело, в свою очередь, тоже будет притягивать к себе Землю с силой, равной по модулю силе тяжести F=Fт. Исаак Ньютон предположил, что силы притяжения существуют между всеми телами во Вселенной.
Согласно третьему закону Ньютона, тело, в свою очередь, тоже будет притягивать к себе Землю с силой, равной по модулю силе тяжести F=Fт. Исаак Ньютон предположил, что силы притяжения существуют между всеми телами во Вселенной.
Все тела во Вселенной притягиваются друг к другу с силами, которые называются силами всемирного тяготения или гравитационными силами .
Из известной нам формулы силы тяжести очевидно, что модуль силы тяжести Fт, действующей на некоторое тело, всегда пропорционален массе тела m. С другой стороны, тело тоже притягивает Землю с силой, равной по модулю силе тяжести, тогда модуль этой силы F должен быть пропорционален массе Земли MЗ. Получается, что сила гравитационного взаимодействия двух тел прямо пропорциональна величине F~m·MЗ.
Чтобы определить зависимость силы тяготения от расстояния между телами, Ньютон исследовал движение Луны. Учёный предположил, что Луна движется вокруг Земли под действием гравитационной силы Земли. Результатом действия гравитационной силы как для подброшенного в воздух камня, так и для Луны, является возникновение ускорения. Но камень падает на Землю, а Луна вращается вокруг Земли по своей орбите, следовательно, ускорения, приобретённые телами в результате действия гравитационной силы, различны. Логично предположить, что эти различия объясняются совершенно разными расстояниями между Землёй и камнем, между Землёй и Луной.
Результатом действия гравитационной силы как для подброшенного в воздух камня, так и для Луны, является возникновение ускорения. Но камень падает на Землю, а Луна вращается вокруг Земли по своей орбите, следовательно, ускорения, приобретённые телами в результате действия гравитационной силы, различны. Логично предположить, что эти различия объясняются совершенно разными расстояниями между Землёй и камнем, между Землёй и Луной.
Камень, подброшенный вверх, будет падать с ускорением свободного падения, равным по модулю g = 9,8 м/с2.
Ускорение Луны было рассчитано Ньютоном, благодаря хорошо изученной на тот момент траектории её движения. Ускорение Луны составляет примерно aцс = 0,0027 м/с2, что меньше значения g примерно в 3 600 раз.
Расстояние от центра Земли до её поверхности примерно в 60 раз меньше расстояния между центром Земли и Луной.
Таким образом, увеличение расстояния между взаимодействующими телами в 60 раз приводит к уменьшению сообщаемого ускорения в 3 600 раз.
Таким образом, сила тяготения между Землёй и некоторым телом на её поверхности прямо пропорциональна произведению массы тела и массы планеты и обратно пропорциональна квадрату расстояния между телом и центром Земли:
F~m·MЗR2.
Исследование характера движения планет вокруг Солнца позволило Ньютону выявить аналогичную зависимость для силы притяжения между Солнцем и движущимися вокруг него планетами: сила тяготения между Солнцем и планетой прямо пропорциональна произведению массы Солнца и массы планеты и обратно пропорциональна квадрату расстояния между ними:
F~mп·MСR2.
Полученная закономерность подтвердила предположение учёного, что силы тяготения испытывают на себе все тела во Вселенной.
На основании приведённых расчётов в 1687 г. Ньютон сформулировал закон всемирного тяготения:
F=G·m1·m2R2, где
F Н — сила тяготения между двумя телами;
G=6,67·10-11 Н·м2кг2 — гравитационная постоянная;
m1 и m2 кг — массы первого и второго тела соответственно;
R м — расстояние между телами.
Закон всемирного тяготения : две материальные точки массами m1 и m2 притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними: F=G·m1·m2R2.
Гравитационная постоянная G — это коэффициент, одинаковый для любой пары взаимодействующих тел.
Закон всемирного тяготения применим только к телам, расстояние между которыми во много раз больше размеров самих тел.
Для тел, имеющих форму шара, величина R соответствует расстоянию между центрами данных шаров. Для тел иной формы закон всемирного тяготения также применим, но требует более сложных математических расчётов.
Более чем через сто лет после открытия Ньютоном закона всемирного тяготения английский физик Генри Кавендиш смог экспериментально измерить значение гравитационной постоянной G. Для этого учёный использовал крутильные весы, знакомые нам по экспериментам Кулона (рис. 1).
Рис. 1. Опыт Кавендиша по определению гравитационной постоянной
1. Опыт Кавендиша по определению гравитационной постояннойНа лёгком стержне (коромысле) были закреплены два маленьких свинцовых шарика массами m. Вблизи были закреплены два тяжёлых шара массами M. В результате взаимного притяжения стержень двигался на нити, на которой было закреплено небольшое зеркальце. Отражённый от зеркальца луч попадал на шкалу, которая позволяла определить угол поворота.
Ускорение свободного падения
Если применить закон всемирного тяготения к Земле и телу массой m, формула будет иметь следующий вид:
F=G·m·MЗRЗ2,
где m кг — масса тела у поверхности Земли;
MЗ кг — масса Земли;
RЗ м — средний радиус Земли.
Сравним полученное выражение с формулой силы тяжести:
Fт=m·g.
Глядя на формулы нетрудно заметить, что ускорение свободного падения представляет собой множитель в законе всемирного тяготения, находящийся возле массы тела:
g=G·MЗRЗ2.
Таким образом, ускорение свободного падения на поверхности любой планеты можно найти как произведение гравитационной постоянной и массы:
g=G·MR2.
Ускорение свободного падения на поверхности планеты рассчитывается по следующей формуле: g=G·MR2.
Формула выше позволяет объяснить, почему в разных точках планеты ускорение свободного падения имеет разное значение. Так, ускорение свободного падения на экваторе Земли меньше, чем на полюсах, потому что наша планета имеет форму немного сплюснутого у полюсов шара.
Ещё одна причина меньшего значения ускорения у полюсов — вращение Земли вокруг своей оси. Все тела, находящиеся на поверхности Земли, вследствие этого вращения движутся по окружностям разного радиуса.
Пусть на земном экваторе тело движется по окружности радиуса R. Тогда тело, расположенное на широте φ, движется по окружности радиуса R1=R·cos(φ) (рис. 2).
Тогда тело, расположенное на широте φ, обладает центростремительным ускорением. Следовательно, ускорение данного тела складывается из ускорения свободного падения на экваторе и центростремительного ускорения.
Итоги
- Все тела во Вселенной притягиваются друг к другу с силами, которые называются силами всемирного тяготения или гравитационными силами.
- Закон всемирного тяготения : две материальные точки массами m1 и m2 притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними: F=G·m1·m2R2.
- G=6,67·10-11 Н·м2кг2 — гравитационная постоянная.
- Ускорение свободного падения на поверхности планеты рассчитывается по следующей формуле: g=G·MпRп2.
Контрольные вопросы
1. Сформулируйте закон всемирного тяготения.
2. Используя рисунок 1, опишите опыт Кавендиша по определению значения гравитационной постоянной.
3. По какой формуле рассчитывается ускорение свободного падения?
Закон всемирного тяготения.
 Движение тел под действием силы тяжести
Движение тел под действием силы тяжестиИсходя из трактовки второго закона Ньютона, можно сделать вывод, что изменение движения происходит посредствам силы. Механика рассматривает силы различной физической природы. Многие из них определяются с помощью действия сил тяготения.
Закон всемирного тяготения. Формулы
В 1862 году был открыт закон всемирного тяготения И. Ньютоном. Он предположил, что силы, удерживающие Луну, той же природы, что и силы, заставляющие яблоко падать на Землю. Смысл гипотезы состоит в наличии действия сил притяжения, направленных по линии и соединяющих центры масс, как изображено на рисунке 1.10.1. Шаровидное тело имеет центр массы, совпадающий с центром шара.
Рисунок 1.10.1. Гравитационные силы притяжения между телами. F1→=-F2→.
Далее, Ньютон искал физическое объяснение законам движения планет, которые открыл И. Кеплер в начале XVII века, и давал количественное выражение для гравитационных сил.
Определение 1При известных направлениях движений планет Ньютон пытался выяснить, какие силы действуют на них. Этот процесс получил название обратной задачи механики.
Этот процесс получил название обратной задачи механики.
Основная задача механики – определение координат тела известной массы с его скоростью в любой момент времени при помощи известных сил, действующих на тело, и заданным условием (прямая задача). Обратная же выполняется с определением действующих сил на тело с известным его направлением. Такие задачи привели ученого к открытию определения закона всемирного тяготения.
Ускорение свободного падения
Определение 2Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.
F=Gm1m2r2.
Значение G определяет коэффициент пропорциональности всех тел в природе, называемое гравитационной постоянной и обозначаемое по формуле G=6,67·10-11 Н·м2/кг2 (СИ).
Большинство явлений в природе объясняются наличием действия силы всемирного тяготения. Движение планет, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все объясняется законом тяготения и динамики.
Проявлении силы тяготения характеризуется наличием силы тяжести. Так называется сила притяжения тел к Земле и вблизи ее поверхности.
Когда М обозначается как масса Земли, RЗ– радиус, m – масса тела, то формула силы тяжести принимает вид:
F=GMRЗ2m=mg.
Где g – ускорение свободного падения, равняющееся g=GMRЗ2.
Сила тяжести направлена к центру Земли, как показано в примере Луна-Земля. При отсутствии действия других сил тело движется с ускорением свободного падения. Его среднее значение равняется 9,81 м/с2. При известном G и радиусе R3=6,38·106 м производятся вычисления массы Земли М по формуле:
M=gR32G=5,98·1024 кг.
Если тело удаляется от поверхности Земли, тогда действие силы тяготения и ускорения свободного падения меняются обратно пропорционально квадрату расстояния r к центру. Рисунок 1.10.2 показывает, как изменяется сила тяготения, действующая на космонавта корабля, при удалении от Земли. Очевидно, что F притягивания его к Земле равняется 700 Н.
Рисунок 1.10.2. Изменение силы тяготения, действующей на космонавта при удалении от Земли.
Пример 1Земля-Луна подходит в качестве примера взаимодействия системы двух тел.
Расстояние до Луны – rЛ=3,84·106 м. Оно в 60 раз больше радиуса Земли RЗ. Значит, при наличии земного притяжения, ускорение свободного падения αЛ орбиты Луны составит αЛ=gRЗrЛ2=9,81 м/с2602=0,0027 м/с2.
Оно направлено к центру Земли и получило название центростремительного. Расчет производится по формуле aЛ=υ2rЛ=4π2rЛT2=0,0027 м/с2, где Т =27,3 суток – период обращения Луны вокруг Земли. Результаты и расчеты, выполненные разными способами, говорят о том, что Ньютон был прав в своем предположении единой природы силы, удерживающей Луну на орбите, и силы тяжести.
Луна имеет собственное гравитационное поле, которое определяет ускорение свободного падения gЛ на поверхности. Масса Луны в 81 раз меньше массы Земли, а радиус в 3,7 раза. Отсюда видно, что ускорение gЛ следует определять из выражения:
gЛ=GMЛRЛ2=GMЗ3,72T32=0,17 g=1,66 м/с2.
Такая слабая гравитация характерна для космонавтов, находящихся на Луне. Поэтому можно совершать огромные прыжки и шаги. Прыжок вверх на метр на Земле соответствует семиметровому на Луне.
Искусственные спутники Земли
Движение искусственных спутников зафиксировано за пределами земной атмосферы, поэтому на них оказывают действие силы тяготения Земли. Траектория космического тела может изменяться в зависимости от начальной скорости. Движение искусственного спутника по околоземной орбите приближенно принимается в качестве расстояния до центра Земли, равняющемуся радиусу RЗ. Они летают на высотах 200-300 км.
Определение 4Отсюда следует, что центростремительное ускорение спутника, которое сообщается силами тяготения, равняется ускорению свободного падения g. Скорость спутника примет обозначение υ1. Ее называют первой космической скоростью.
Применив кинематическую формулу для центростремительного ускорения, получаем
an=υ12RЗ=g, υ1=gRЗ=7, 91·103 м/с.
При такой скорости спутник смог облететь Землю за время, равное T1=2πRЗυ1=84 мин 12 с.
Но период обращения спутника по круговой орбите вблизи Земли намного больше, чем указано выше, так как существует различие между радиусом реальной орбиты и радиусом Земли.
Спутник движется по принципу свободного падения, отдаленно похожее на траекторию снаряда или баллистической ракеты. Разница заключается в большой скорости спутника, причем радиус кривизны его траектории достигает длины радиуса Земли.
Спутники, которые движутся по круговым траекториям на больших расстояниях, имеют ослабленное земное притяжение, обратно пропорциональное квадрату радиуса r траектории. Тогда нахождение скорости спутника следует по условию:
υ2к=gR32r2, υ=gR3RЗr=υ1R3r.
Поэтому, наличие спутников на высоких орбитах говорит о меньшей скорости их движения, чем с околоземной орбиты. Формула периода обращения равняется:
T=2πrυ=2πrυ1rRЗ=2πRзυ1rR33/2=T12πRЗ.
T1 принимает значение периода обращения спутника по околоземной орбите.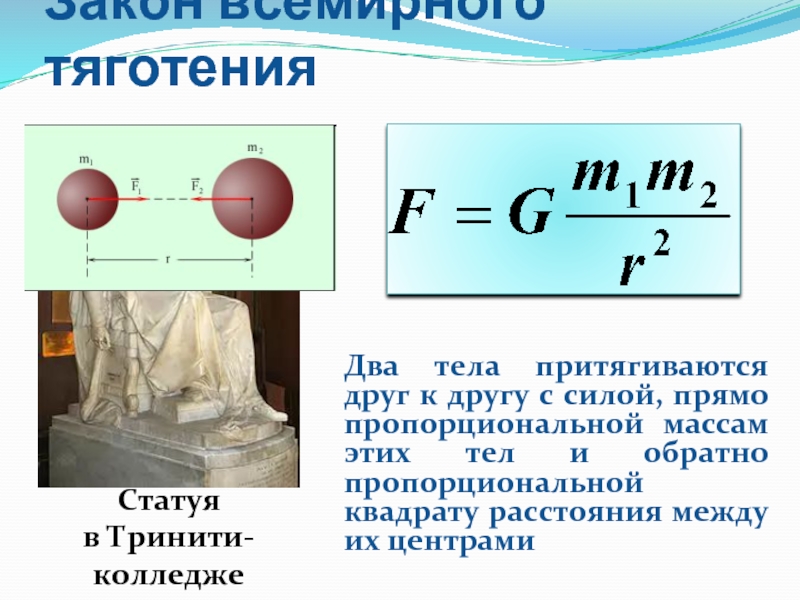 Т возрастает с размерами радиуса орбиты. Если r имеет значение 6,6 R3 то Т спутника равняется 24 часам. При его запуске в плоскости экватора, будет наблюдаться, как висит над некоторой точкой земной поверхности. Применение таких спутников известно в системе космической радиосвязи. Орбиту, имеющую радиус r=6,6 RЗ, называют геостационарной.
Т возрастает с размерами радиуса орбиты. Если r имеет значение 6,6 R3 то Т спутника равняется 24 часам. При его запуске в плоскости экватора, будет наблюдаться, как висит над некоторой точкой земной поверхности. Применение таких спутников известно в системе космической радиосвязи. Орбиту, имеющую радиус r=6,6 RЗ, называют геостационарной.
Рисунок 1.10.3.Модель движения спутников.
определение законов+гравитации по The Free Dictionary
Законы+гравитации — определение законов+тяготения по The Free Dictionary Законы+тяготения — определение законов+тяготения в The Free DictionaryСлово, не найденное в Словаре и Энциклопедии.
Пожалуйста, попробуйте слова отдельно:
законы из сила тяжести
Некоторые статьи, соответствующие вашему запросу:
Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.
Полный браузер ?
- ▲
- Наследственное право
- Законы о наследовании
- Законы о наследовании
- Законы развития технических систем
- Законы 13-го Конгресса Филиппин
- Законы игры
- Законы игры
- Законы ганзейских городов
- Законы Индии
- законы страны
- Законы ночи
- Законы двенадцати таблиц
- Законы термодинамики
- Законы термодинамики
- Законы термодинамики
- Законы термодинамики
- Законы термодинамики
- Законы термодинамики
- Законы вибрационной энергии
- Законы войны
- Законы войны
- Законы войны
- Законы wisbuy
- Законы об арбалетах
- Законы об изнасиловании
- Законы об иммиграции и гражданстве
- Законы, касающиеся военно-морского флота, аннотированные
- Юридические магазины
- законы без зубов
- законы без зубов
- законы+тяготения
- Законы, Калифорния
- Законы, Г.
 Малкольм
Малкольм - Законы, постановления, положения и стандарты
- Законы, правила и политика
- Законы, постановления и общегосударственная политика
- Лоусон
- Лоусон
- Лоусон
- Лоусон (магазин)
- Лоусон Арена
- Армейский аэродром Лоусон
- Лоусон Баронетс
- Стрела Лоусона
- Бизнес-аналитика Лоусона
- Конференция Лоусона и обмен пользователями
- Критерий Лоусона
- Критерий Лоусона
- Кипарисовик Лавсона
- Лоусон Дункан
- Лоусон Фусао Инада
- Глобальная группа пользователей Lawson
- Научно-исследовательский институт здоровья Лоусона
- Лоусон Хайтс
- Пригородный центр Лоусон-Хайтс, Саскатун
- Пригородный центр Лоусон-Хайтс, Саскатун, Саскачеван
- Лоусон Хайтс, Пенсильвания
- Лоусон Хайтс, Саскатун
- Лоусон Хайтс, Саскатун, Саскачеван
- Лоусон Инсайт
- Лоусон Инсайт
- ▼
Закон всемирного тяготения — Columbia Journal of Transnational Law
Гравитация часто упоминается в договорах, судебных решениях международных и региональных органов, докладах о правах человека, а также в резолюциях и заявлениях различных органов Организации Объединенных Наций. В этих документах определенные нарушения международного права называются «грубыми», «серьезными» и «серьезными». Эти термины часто используются взаимозаменяемо, но редко определяются, и часто неясно, что делает нарушение особенно серьезным. Является ли это крайним вредом для жертвы, типом вовлеченных прав, совершившим нарушение, или, скорее, намерением правонарушителя?
В этих документах определенные нарушения международного права называются «грубыми», «серьезными» и «серьезными». Эти термины часто используются взаимозаменяемо, но редко определяются, и часто неясно, что делает нарушение особенно серьезным. Является ли это крайним вредом для жертвы, типом вовлеченных прав, совершившим нарушение, или, скорее, намерением правонарушителя?
Несмотря на отсутствие ясности в отношении концепции, квалификация нарушения как серьезного имеет серьезные правовые последствия в соответствии с международным правом. Тяжесть может определить, обладает ли международный суд юрисдикцией для судебного преследования преступления или когда орган по наблюдению за соблюдением договоров может заняться вопросом. Государствам запрещается продавать оружие другим государствам, если они совершают серьезные нарушения прав человека или гуманитарного права. Гравитация также использовалась для оправдания военного вмешательства или более сурового наказания государства за его противоправные действия.
Эта статья дает больше оснований для гравитации, исследуя концепцию во всех ее формах, и предлагает первую научную трактовку гравитации в международном публичном праве в целом. Как показывает история права, сила тяжести является, если не главной, объединяющей силой международного уголовного права, права прав человека и гуманитарного права. Несмотря на отсутствие формального определения серьезных нарушений, внимательное изучение судебной практики в области тяжести нарушений выявляет общий набор соображений, которые обычно учитываются международными судами и другими организациями при определении того, что нарушение является серьезным. Более строгое соблюдение этих определяющих факторов приведет к более единообразной и последовательной ответственности за те нарушения, которые вызывают наибольшую озабоченность у человечества.
Читать здесь
* Адъюнкт-профессор юридического факультета Томаса Р. Клайна Дрексельского университета. Я благодарен Dila Torlak и Lindsay Steussy за их помощь в исследованиях. Я также хотел бы поблагодарить участников «Новых голосов в области прав человека и международного права» на Ежегодном собрании AALS 2020 года; Круглый стол по постконфликтному правосудию на юридическом факультете Университета Вашингтона и Ли; семинар «Женщины в международном праве» на юридическом факультете Университета Дьюка; Форум полугодовых исследований ASIL; Международная конференция врачей-правозащитников на юридическом факультете Пенсильванского университета; семинары преподавателей юридического факультета Университета Сетон Холл и юридического колледжа Аризонского университета; и Конференцию младших ученых-международников в Бруклинской школе права за поясняющие комментарии и полезные отзывы. В частности, я хотел бы поблагодарить Марка Драмбла, Маргарет де Гусман, Дженнифер Ли, Джин Гэлбрейт, Ханну Блох-Вехба, Лорен Кац Смит, Милену Стерио, Джеймса Гэтии, Кристин Хаски, Бенджамина Н. Лоуренса, Эндрю Кина Вудса, Джастина Пидо, Джим Силк, Кристиана Очоа, Табата Абу Эль-Хадж, Джеффри Стейк, Ребекка Гамильтон, Джейн Хакерби, Маргарет Дрю, Алекс Гейзингер, Анил Калхан, Рэйчел Брюстер, Джулиан Арато, Мэгги Гарднер, Нино Гурули, Форрест Райт, Роджер Кларк и другие фантастические редакторы Колумбийского журнала транснационального права.
Я также хотел бы поблагодарить участников «Новых голосов в области прав человека и международного права» на Ежегодном собрании AALS 2020 года; Круглый стол по постконфликтному правосудию на юридическом факультете Университета Вашингтона и Ли; семинар «Женщины в международном праве» на юридическом факультете Университета Дьюка; Форум полугодовых исследований ASIL; Международная конференция врачей-правозащитников на юридическом факультете Пенсильванского университета; семинары преподавателей юридического факультета Университета Сетон Холл и юридического колледжа Аризонского университета; и Конференцию младших ученых-международников в Бруклинской школе права за поясняющие комментарии и полезные отзывы. В частности, я хотел бы поблагодарить Марка Драмбла, Маргарет де Гусман, Дженнифер Ли, Джин Гэлбрейт, Ханну Блох-Вехба, Лорен Кац Смит, Милену Стерио, Джеймса Гэтии, Кристин Хаски, Бенджамина Н. Лоуренса, Эндрю Кина Вудса, Джастина Пидо, Джим Силк, Кристиана Очоа, Табата Абу Эль-Хадж, Джеффри Стейк, Ребекка Гамильтон, Джейн Хакерби, Маргарет Дрю, Алекс Гейзингер, Анил Калхан, Рэйчел Брюстер, Джулиан Арато, Мэгги Гарднер, Нино Гурули, Форрест Райт, Роджер Кларк и другие фантастические редакторы Колумбийского журнала транснационального права.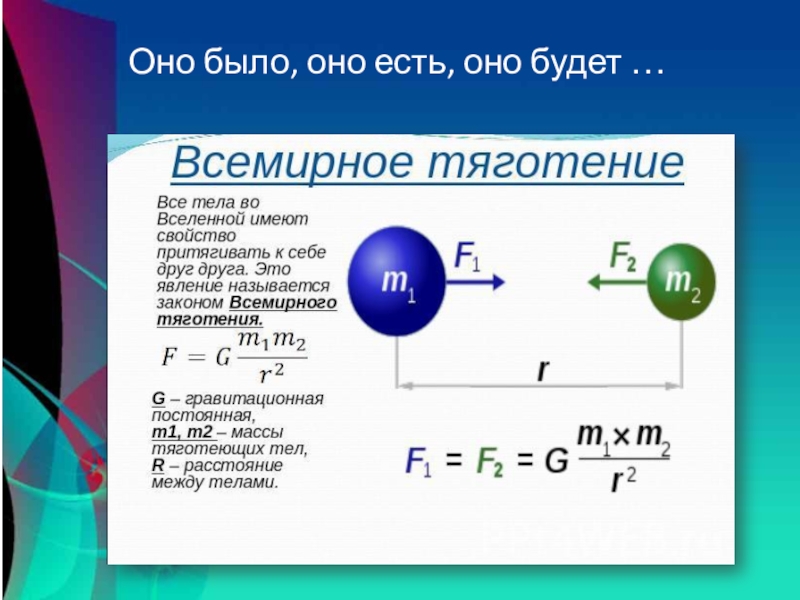


 Малкольм
Малкольм