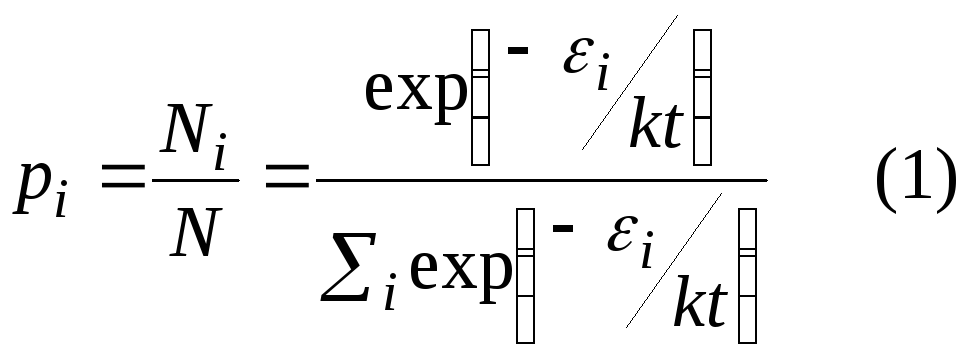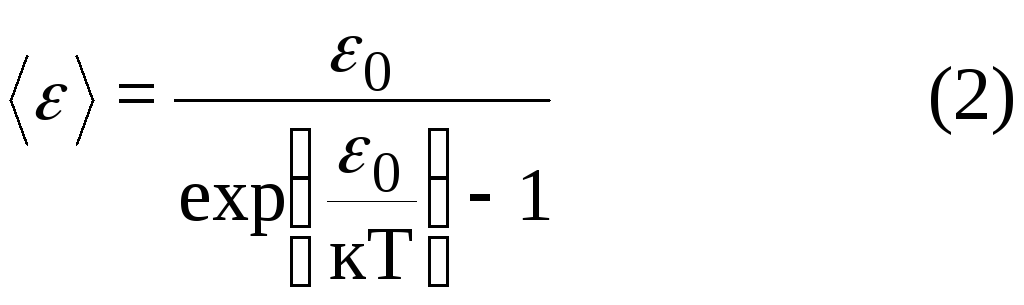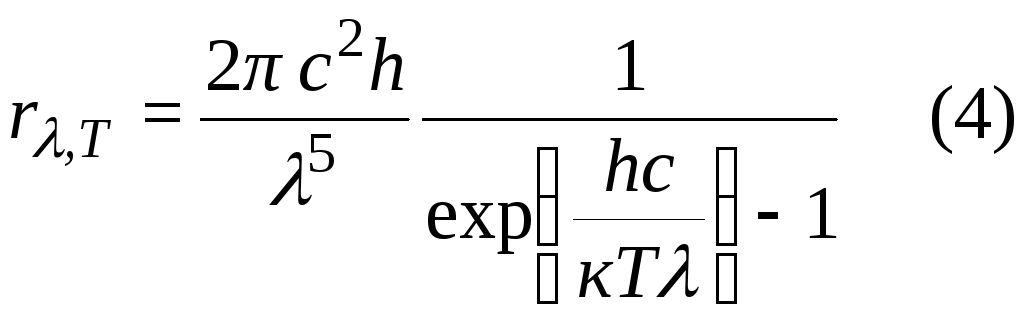Каждый закон Кирхгофа прост и понятен :: SYL.ru
Густав-Роберт Киргоф, выдающийся немецкий физик и математик позапрошлого века, открыл и сформулировал два электротехнических закона, названных в его честь.

Открытия Кирхгоффа
При всей видимой простоте и понятности, законы Кирхгофа стали фундаментальными основами современной науки и базой для методов схематических расчетов. Их практическое значение трудно переоценить. Базой для научных изысканий профессора Кирхгофа стали законы сохранения заряда и энергии, открытые ранее. Некоторые специалисты считают, что правильнее называть описанные Кирхгоффом закономерности правилами, чтобы не путать их с другими замечательными открытиями этого физика, касающимися способностей тел излучать и поглощать энергию, а также зависимости скорости протекания химических реакций от температуры. Однако в научной и технической литературе принято все же пользоваться термином «закон Кирхгофа», тем самым подчеркивая заслуги этого великого ученого в области электротехники. Итак, их два.
1. Закон Кирхгофа о токах в узлах
Узлами в электротехнике называют точки соединения проводников в количестве не менее трех. Для того чтобы понять действие Первого закона Киргофа, достаточно представить себе обычный водопроводный тройник. Если в одну из труб подается вода, то в две остальные она вытекает. Возможен и другой вариант, когда отводная труба одна, а приточных две, но в любом случае, сколько воды в тройник затечет, столько же и вытечет. Теперь задачу можно усложнить, допустив, что количество входов и выходов в узле сколь угодно большое. Однако результат будет тот же, количество поступающей и уходящей жидкости будет равным, то есть, говоря языком математики, алгебраическая сумма расходов равна нулю. Первый закон Кирхгофа рассматривает электрические токи в узлах, которые ведут себя так же, как и вода в тройнике. Если есть входящие и выходящие токи, то их сумма с учетом знака будет нулевой. При этом величина входящих токов обозначается положительным знаком «плюс», а выходящих – отрицательным «минус». Математическая формула выглядит примерно так:
∑(I вх., … I вых.) = 0
где I вх. — величины входящих токов со знаком «+»;
I вых. — величины выходящих токов со знаком «-».
2. Закон Кирхгофа о сумме падений напряжений
Второй закон Кирхгофа понять несколько сложнее, у него нет столь прямых и наглядных ассоциаций как у первого, тем не менее, он тоже несложен. Для начала следует представить себе замкнутую простейшую электрическую цепь, состоящую из источника питания и активной нагрузки в виде сопротивления. При замыкании клемм выключателя через резистор пойдет ток, и все подаваемое напряжение на нем же упадет. Задача вновь усложняется, и количество сопротивлений изменяется. Теперь их много, и у всех разная величина. При прохождении через них электрического тока он будет в цепи одинаковым и, согласно закону Ома, равен напряжению источника, поделенному на сумму всех сопротивлений. На каждом из них будет падать его часть. Так вот, Второй закон Кирхгофа гласит, что общая сумма падений напряжений на каждом из участков цепи равна величине напряжения питания. Говоря иными словами, общая алгебраическая сумма вместе с источником равна нулю.
Простейшая математическая формула описывает Второй закон Кирхгофа следующим образом:
∑U ц = 0
где U ц – падения напряжений на разных участках замкнутой электрической цепи (контура).
Закон Кирхгофа
Немецкий ученый Густав Кирхгоф наряду с другими исследованиями сформулировал основной закон, помогающий рассчитывать токи и напряжения в различных видах электрических цепей, который известен, как закон Кирхгофа.
История создания закона Кирхгофа
В середине 19-го века свойства различных электрических цепей активно исследовались с целью их дальнейшего применения на практике. К тому времени уже был совершен переход от простых цепей к более сложным и одним законом Ома было уже не обойтись. Возникла необходимость в расчетах очень сложных и разветвленных цепей.

Именно Кирхгоф сформулировал основные правила, с помощью которых стало возможным рассчитывать цепи практически любой сложности.
Первый закон Кирхгофа
В первом законе рассматривается узел цепи, представляющий собой точку схождения или разветвления трех проводов и более. В этом случае количество поступающего и исходящего электрического тока в общей сумме каждого вида будет одинаково. Таким образом, соблюдается закон сохранения электрического заряда.
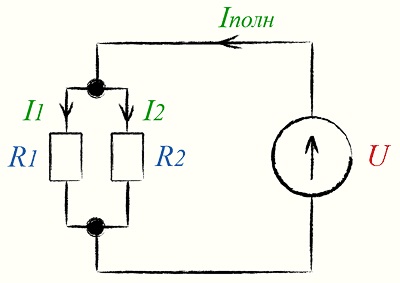
Например, при Т-образном узле сумма токов, поступающих по двум проводам, равна току, выходящему по третьему проводу. В противном случае, в узле постоянно происходило бы накопление электрических зарядов, чего, практически, никогда не случается.
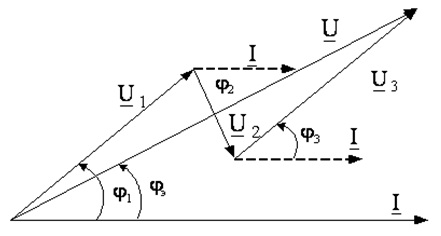
Второй закон Кирхгофа
При сложной и разветвленной цепи, она мысленно разбивается на несколько обыкновенных замкнутых контуров. Распределение тока по этим контурам происходит различными путями. В этом случае, достаточно сложно определить маршрут протекания того или иного тока. В каждом контуре у электронов происходит либо приобретение дополнительной энергии, либо ее потеря из-за возникшего сопротивления. Таким образом, общая энергия электронов в каждом замкнутом контуре имеет нулевое значение. В противном случае, с физической точки зрения, происходило бы постоянное возрастание или убывание электрического тока.
Применение законов Кирхгофа
Законы Кирхгофа широко применяются в различных видах цепей, которые могут быть последовательными либо параллельными. Наиболее типичным примером последовательной цепи служит елочная гирлянда, где все лампочки соединяются в последовательную цепь. В такой цепи в соответствии с законом Ома напряжение постепенно падает. В параллельных цепях напряжение остается одинаковым, а сила тока каждого элемента напрямую зависит от его сопротивления. Определение токов, проходящих по каждому узлу таких цепей, производится в соответствии с первым законом Кирхгофа.
Расчет цепи по законам Кирхгофа
3-й закон Кирхгофа — dmagin — LiveJournal
Продвижение по теме потоков в почти симметричных графах продолжается.Было (кратко, ес-но) изучено состояние дел в теории электрических сетей (по работам «Random Walks and Electrical Networks», «Inverse Problems for Electrical Networks»). Обнаружено, что люди почему-то не используют мой прием — задание разности потенциалов в сети через введение асимметричного ребра. А мучаются со стандартной задачей Дирихле — то есть через задание краевых условий на потенциалы. Зря. Теряется общность и простота «графического» подхода. (Правда меня немного смущает, что такую асимметрию можно задать, просто воткнув в землю диод, без всяких источников тока).
Что еще понято. Наконец-то постиг, как доказывается пресловутый инвариант для графа любой размерности. Для этого пришлось, правда, ввести 3-й закон Кирхгофа )). Ну и наиболее интересная часть — продвинулся в решении обратной задачи для электрических сетей — вычисление проводимостей графа на основе известных разностей потенциала. Поскольку материала много, то разобью на несколько постов.
Начнем с Кирхгофа.
Как известно, Кирхгофу приписывают два правила, которые полезны для расчета электрических цепей:
1) Сумма токов в каждом узле равна нулю — мы это называем балансом потоков.
2) Сумма разностей потенциалов по замкнутому контуру равна нулю (про всякие ЭДС и пр. мы здесь намеренно опускаем,- они нам без надобности).- Это тоже очевидность, на которой не останавливаемся.
А вот про 3-й закон (скорее, правило), похоже никто не знает. Включая самого Кирхгофа. А он, оказывается, тоже полезен. И важен для всех, кто занимается электроразведкой, кто подает ток/напряжение в одном месте, а снимает в другом.
В электротехнике известен принцип эквивалентности — если мы меняем местами питающие электроды (по которым подаем ток) и съемные (снимаем напряжение), то результат остается тот же самым. Вроде бы очевиден,- связан с линейностью уравнений. Для графов я особо не вникал — почему так происходит. Проверил — действительно так.
Как проверяется. Берем симметричный граф (аналог электрической сети). И вводим асимметрию, например, ребра ij,- то есть вводим разность между проводимостями: dC = Cij — Сji. Смотрим — чему равна разность потенциалов между любыми произвольными узлами графа (m и n, например). Потом восстанавливаем симметричность ребра ij и вводим асимметрию между узлами m и n. А разность меряем между i и j (как много приходится писать) — полученные разности Umn (в 1-м случае) и Uij (во 2-м) — равны. Это и есть принцип эквивалентности.
Теперь допустим, что мы снимаем разность потенциалов Umn с одних и тех же узлов (измерительные электроды фиксированы), но при этом последовательно меням расположение питающих электродов. Например, сначала задали ток через узлы 12 (измерили Umn), потом через 23 (снова измерили Umn), потом — через 34 и т.д. Теперь мы можем сформулировать 3-е правило:
Если путь, по которому меняются питающие электроды,- замкнут (12-23-34-41), то сумма измеренных разностей потенциалов Umn будет равна нулю.
Фактически, 3-е правило — это использование 2-го закона совместно с принципом эквивалентности.
Почему данное правило не пользуется популярностью (неизвестно)? Скорее всего потому, что в традиционной электротехнике (и электроразведке тоже) редко меняют положение питающих электродов.
Где мы можем применить данное правило?
Ну, доказать, наконец-то наш инвариант (след. пост).
Но более интересно — понять — какие же измерения нам нужно провести (а какие, наборот — уже будут лишними), чтобы решить обратную задачу (для электрических сетей, например). Результаты данного исследования планируется изложить через пост.
Законы Кирхгофа для расчета линейной электрической цепи постоянного тока. Первый и второй закон Кирхгофа
Общие сведения о законах Кирхгофа
Законы Кирхгофа применяют для анализа и расчета разветвленных сложных электрических цепей постоянного и переменного тока. Они позволяют рассчитать электрические токи во всех ветвях. По найденным токам можно рассчитать падение напряжения, мощность и т.д.
Существует мнение, что «Законы Кирхгофа» нужно называть «Правилами Кирхгофа», т.к. они могут быть выведены из других положений и предположений. Данные правила не являются обобщением большого количества опытных данных. Они являются одной из форм закона сохранения энергии и потому относятся к фундаментальным законам природы.
В некоторых книгах пишут фамилию ученого Густава с буквой Х — Кирхгоф. В некоторых изданиях пишут без буквы х — Киргоф.
Сколько всего законов Кирхгофа?
В отличии от Ньютона, который «придумал» три закона, Кирхгоф придумал только два закона. Они названы в его честь: 1 и 2 закон Кирхгофа. 3-ий закон Кирхгофа не существует.
Как применять правила Кирхгофа
Законы Кирхгофа необязательно использовать в виде систем уравнений. Они могут быть использованы для любого узла или для любого замкнутого контура в электрической цепи.
Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, метод контурных токов, метод узловых напряжений, принцип суперпозиции (метод наложения)) решать задачи электротехники.
Плюсы правил Кирхгофа
- Правила Кирхгофа нашли широкое применение благодаря простой формулировке уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).
- Простой и понятный алгоритм составления уравнений
Минусы законов Кирхгофа
- Большое количество уравнений по сравнению с другими методами.
Основы электротехники и электроники: Курс лекций, страница 3
При свертке параллельных ветвей эквивалентное сопротивление всегда меньше наименьшего из сворачиваемых.
Если параллельно соединены n одинаковых сопротивлений (Рис. 3.3), эквивалентное сопротивление в n раз меньше сопротивления любой из ветвей.

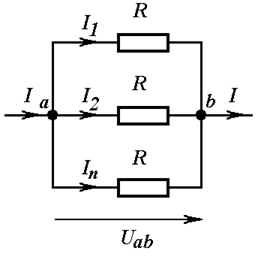
Рис. 3.3
Если на участке цепи параллельно соединены лишь два элемента (Рис. 3.4), выражение (3.2) упрощается. В этом случае эквивалентное сопротивление можно определить как отношение произведения двух сопротивлений к их сумме:


Рис. 3.4
4. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
К основным законам электрических цепей относятся закон Ома и законы Кирхгофа.
Закон Ома
Если в ветви не содержится ЭДС, к ней применим уже известный закон Ома для пассивного участка цепи (1.1). Его можно сформулировать и следующим образом. Ток в ветви, не содержащей ЭДС, равен падению напряжения в ветви, деленному на сопротивление ветви (

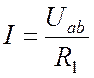
Рис. 4.1
Закон Ома для ветви, содержащей ЭДС, позволяет найти ток этой ветви по известной разности потенциалов на концах ветви. Ток в ветви, содержащей ЭДС, равен дроби, знаменатель которой – это сопротивление ветви. В числителе дроби – напряжение на концах ветви плюс алгебраическая сумма ЭДС, заключенных между концами ветви. С плюсом берутся напряжения и ЭДС, направление которых совпадает с направлением тока, с минусом – противоположные.
В частности, ток в ветви, изображенной на Рис. 4.2, равен:
 .
.
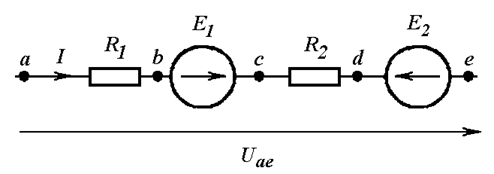
Рис. 4.2
Первый закон Кирхгофа
В любом узле цепи алгебраическая сумма токов равна нулю. При этом, токи, направленные к узлу, принято считать положительными, токи, направленные от узла, принято считать отрицательными (Рис. 4.3
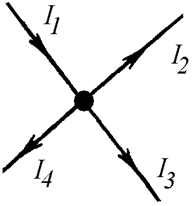
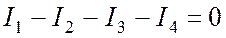
Рис. 4.3
По первому
закону Кирхгофа можно написать столько уравнений, сколько узлов содержит схема.
Но не все они будут независимыми. Если схема содержит  узлов,
независимыми будут
узлов,
независимыми будут 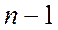 уравнений. Оставшееся
уравнение будет являться следствием всех предыдущих.
уравнений. Оставшееся
уравнение будет являться следствием всех предыдущих.
Второй закон Кирхгофа
В любом замкнутом контуре цепи алгебраическая сумма напряжений равна алгебраической сумме ЭДС, включенных в контур.
При этом, положительными считаются те напряжения и ЭДС, которые совпадают с направлением обхода контура, отрицательными считаются напряжения и ЭДС, которые противоположны направлению обхода контура. Направление обхода контура можно выбирать произвольно.
Алгоритм составления уравнения по второму закону Кирхгофа для замкнутого контура цепи
Для заданного контура (Рис. 4.4 а) уравнение по второму закону Кирхгофа составляется в следующем порядке:
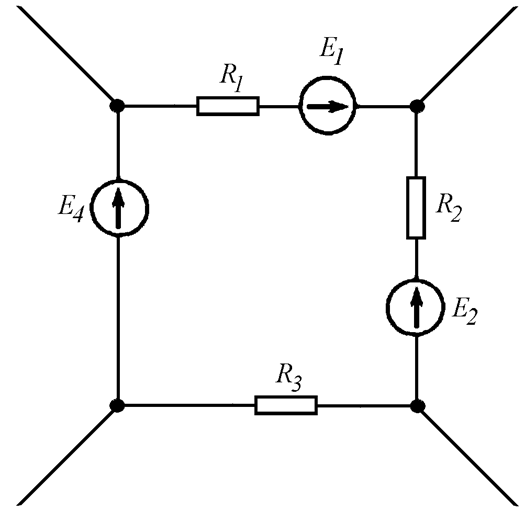
Рис. 4.4 а
- Задается направление токов в ветвях (Рис. 4.4 б).

Рис. 4.4 б
- Выбирается направление обхода контура (Рис. 4.4 в).

Рис. 4.4 в
- Записывается уравнение, в левой части которого – сумма падений напряжений на сопротивлениях ветвей. В правой части – сумма ЭДС контура.

Примечание: Падение напряжения на сопротивлении ветви записывается в соответствии с известным уже законом Ома (1.1):

Применение второго закона Кирхгофа для незамкнутого участка цепи
Второй закон Кирхгофа справедлив только для замкнутого контура. При этом, любой незамкнутый участок цепи можно дополнить до замкнутого контура с помощью напряжения в разрыве незамкнутого участка.
Пример 4.1:
Незамкнутый участок цепи abcd изображен на Рис. 4.5 а.
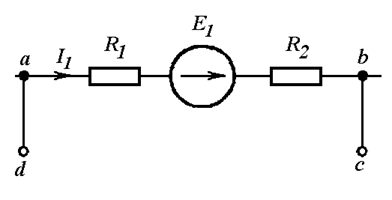
а)

б)
Рис. 4.5
Дополняем участок до замкнутого контура, добавляя напряжение между незамкнутыми точками c и d (Рис. 4.5 б). Теперь для контура abcd можно записать второй закон Корхгофа:

Применение законов Кирхгофа при наличии в цепи источника тока
Источник тока имеет бесконечно большое сопротивление, поэтому не образует замкнутого контура и не может входить в уравнения второго закона Кирхгофа. Однако, в уравнениях первого закона Кирхгофа источник тока должен содержаться обязательно.
При необходимости записать уравнение по второму закону Кирхгофа для контура, содержащего источник тока, его заменяют напряжением на выводах источника тока.
Пример 4.2:
Написать уравнение по первому закону Кирхгофа для узла a и уравнение по второму закону Кирхгофа для контура abcd (Рис. 4.6 а).
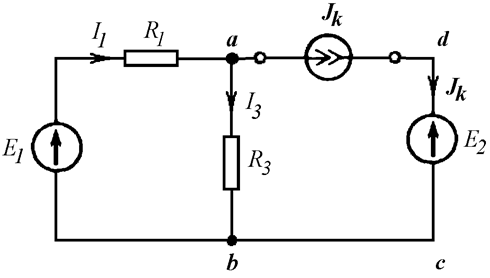
а)
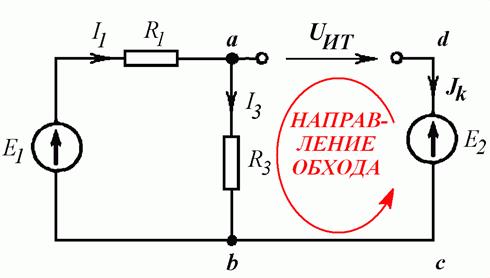
б)
Рис. 4.6
Уравнение по первому закону Кирхгофа для узла a содержит источник тока и имеет вид:

Для того чтобы написать уравнение по второму закону Кирхгофа для контура abcd, заменяем источник тока напряжением на его выводах (Рис. 4.6 б), задаем направление обхода контура против часовой стрелки и получаем:
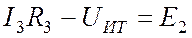
Для упрощения расчетов источник тока с параллельным сопротивлением можно заменить на эквивалентный источник ЭДС (Рис. 4.7). После расчета необходимо обязательно вернуться к исходной схеме.

Рис. 4.7
Независимый контур цепи
В принципе, по второму закону Кирхгофа можно составить столько уравнений, сколько контуров содержит цепь. Но не все эти уравнения будут независимыми. Для определения независимости уравнений по второму закону Кирхгофа вводится такое понятие как независимый контур цепи.
Независимый контур цепи – это такой контур, который содержит хотя бы одну новую ветвь, не вошедшую в другие контуры цепи.
Независимые контуры в общем случае выбираются произвольно, но проще всего выбирать их так, чтобы они совпадали с ячейками цепи (Рис. 4.8 б).

а)

б)
Рис. 4.8
Если схема
содержит  ветвей и
ветвей и  узлов,
число независимых контуров равно
узлов,
число независимых контуров равно
 .
.
Схема на Рис. 4.8 б содержит три независимых контура.
5. СИСТЕМА УРАВНЕНИЙ ПО ЗАКОНАМ КИРХГОФА ДЛЯ РАСЧЕТА ТОКОВ ЦЕПИ
Законы Кирхгофа можно использовать для расчета токов в ветвях цепи. Главное требование при этом – получение системы независимых уравнений, в которой число неизвестных равно количеству токов, подлежащих определению.
Алгоритм составления системы уравнений по законам Кирхгофа
Ответы@Mail.Ru: третий закон киргоффа срочно!
Всем известны правила Кирхгофа для электрических цепей (спасибо Nadejda Shakarova за их подробное описание) . Однако Кирхгоф занимался не только электродинамикой. Он ввел термин «абсолютно черное тело» и открыл закон излучения для данного тела, который и назван в его честь. Но этот закон нельзя назвать «третьим законом Кирхгофа» в данном контексте, поскольку он не относится к электродинамике. Но тем не менее, он тоже открыт данным ученым и носит его имя. Подробнее о законе излучения Кирхгофа см. здесь: <a rel=»nofollow» href=»http://www.astronet.ru/db/msg/1188370″ target=»_blank»>http://www.astronet.ru/db/msg/1188370</a>
их два всего<br>:)
что самое интересное, гугл о нем не знает. он вообще существует? такое ощущение, что нет: <a rel=»nofollow» href=»http://www.google.com/search?hl=en&rls=en&q=3-й+закон+киргоффа&btnG=Search» target=»_blank»>http://www.google.com/search?hl=en&rls=en&q=3-й+закон+киргоффа&btnG=Search</a>
нет их три но третий я не помню.
Оба закона Кирхгофа формулируются достаточно просто и имеют понятную физическую интерпретацию. Первый закон гласит, что если рассмотреть любой узел цепи (то есть точку разветвления, где сходятся три или более проводов) , то сумма поступающих в цепь электрических токов будет равна сумме исходящих, что, вообще говоря, является следствием закона сохранения электрического заряда. Например, если вы имеете Т-образный узел электрической цепи и по двум проводам к нему поступают электрические токи, то по третьему проводу ток потечет в направлении от этого узла, и равен он будет сумме двух поступающих токов. Физический смысл этого закона прост: если бы он не выполнялся, в узле непрерывно накапливался бы электрический заряд, а этого никогда не происходит. Второй закон не менее прост. Если мы имеем сложную, разветвленную цепь, ее можно мысленно разбить на ряд простых замкнутых контуров. Ток в цепи может различным образом распределяться по этим контурам, и сложнее всего определить, по какому именно маршруту потекут токи в сложной цепи. В каждом из контуров электроны могут либо приобретать дополнительную энергию (например, от батареи) , либо терять ее (например, на сопротивлении или ином элементе) . Второй закон Кирхгофа гласит, что чистое приращение энергии электронов в любом замкнутом контуре цепи равно нулю. Этот закон также имеет простую физическую интерпретацию. Если бы это было не так, всякий раз, проходя через замкнутый контур, электроны приобретали или теряли бы энергию, и ток бы непрерывно возрастал или убывал. В первом случае можно было бы получить вечный двигатель, а это запрещено первым началом термодинамики; во втором — любые токи в электрических цепях неизбежно затухали бы, а этого мы не наблюдаем. Самое распространенное применение законов Кирхгофа мы наблюдаем в так называемых последовательных и параллельных цепях. В последовательной цепи (яркий пример такой цепи — елочная гирлянда, состоящая из последовательно соединенных между собой лампочек) электроны от источника питания по серии проводов последовательно проходят через все лампочки, и на сопротивлении каждой из них напряжение падает согласно закону Ома. В параллельной цепи провода, напротив, соединены таким образом, что на каждый элемент цепи подается равное напряжение от источника питания, а это означает, что в каждом элементе цепи сила тока своя, в зависимости от его сопротивления. Пример параллельной цепи является — ламп «лесенкой» : напряжение подается на шины, а лампы смонтированы на поперечинах. Токи, проходящие через каждый узел такой цепи, определяются по второму закону Кирхгофа.
Конечно их ТРИ! Закон 1-й: Сумма токов в узле электрической цепи ровна нулю; 2-й: Разность потенциалов в двух точках электрической цепи равна нулю; 3-й: Это симбиоз первых двух — сопротивление в двух точках электрической цепи тоже равно нулю!
Третий? Мэн на занятия приходить надо и записывать!
Смешно, его не существует))) Хотя, третий закон Киргофа- не кому не говорить о третьем законе Киргофа.
39. Закон Кирхгофа.
Закон Кирхгофа определяет соотношение между испускательной и поглощательной способностями тел.
Отношение испускательной и поглощательной способностей тела не зависит от природы тела и является универсальной для всех тел функцией частоты и температуры rv,T | |
Для
черного тела  , поэтому универсальная
функция Кирхгофа rv,T есть
спектральная плотность энергетической
светимости (испускательная
способность) черного тела. Нахождение явной
зависимости rv,T от частоты
и температуры является важной задачей теории теплового
излучения.
, поэтому универсальная
функция Кирхгофа rv,T есть
спектральная плотность энергетической
светимости (испускательная
способность) черного тела. Нахождение явной
зависимости rv,T от частоты
и температуры является важной задачей теории теплового
излучения.
40. Закон Стефана-Больцмана.
Энергетическая светимость серого тела (интегральная по v):
 —
—
энергетическая светимость черного тела, которая зависит только от температуры. Эту зависимость описывает экспериментальный закон Стефана-Больцмана: энергетическая светимость черного тела пропорциональна четвертой степени термодинамической температуры:
Re = σ T4 (следовательно  ),
),
где σ = 5,67·10-8Вт/(м2К4) — постоянная Стефана-Больцмана.
41 .Закон смещения Вина.
 Закон
Стефана-Больцмана ничего не говорит о
спектральном составе излучения
черного тела. Положение
максимума в спектре его излучения описывается
экспериментальным законом смещения
Вина:
Закон
Стефана-Больцмана ничего не говорит о
спектральном составе излучения
черного тела. Положение
максимума в спектре его излучения описывается
экспериментальным законом смещения
Вина:
Длина волны λmах, при которой излучательная способностьrλ,Т черного тела максимальна, обратно пропорциональна его термодинамической температуре:
,
где b = 2,9·10-3м·К — постоянная Вина.
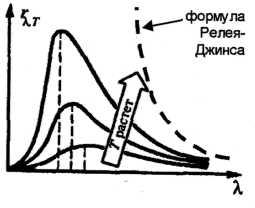
42. Формулы Рзлея-Джинса и Вина.
Применяя к тепловому излучению классический закон равнораспределения энергии по степеням свободы Рэлей и Джине получили выражение для зависимости испускательной способности черного тела rv,T от частоты света:
где 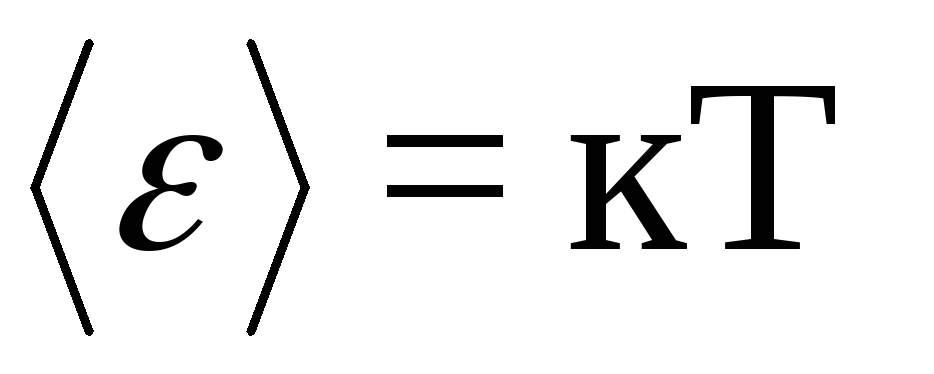 —
средняя энергия осциллятора с собственной
частотой v.
—
средняя энергия осциллятора с собственной
частотой v.
Однако попытка получить закон Стефана-Больцмана из этой формулы приводит к абсурдному результату — Re неограниченно растет, достигая чрезвычайно больших значений в ультрафиолете, — который получил название «ультрафиолетовая катастрофа»:
Формула Рэлея-Джинса согласуется с экспериментом только в области малых частот и больших температур. В области больших частот хорошо описывает эксперимент формула Вина (закон излучения Вина):
Rv,T= C1v3 exp(-C2v/T), где С1 и С2 — константы.
43. Квантовая гипотеза Планка.
Макс Планк предположил, что теория классического гармонического осциллятора неприменима к атомным осцилляторам; атомные осцилляторы излучают энергию не непрерывно, а определенными порциями — квантами.
Энергия
кванта: 
где h = 2πħ= 6,626 · 10-34 Дж·с — постоянная Планка.
В механике есть имеющая размерность «энергия×время» величина, которая называется действием. Поэтому постоянную Планка иногда называют квантом действия. Размерность h совпадает с размерностью момента импульса.
Поскольку энергия излучается порциями, то энергия осциллятора может принимать лишь определенные дискретные значения, кратные целому числу квантов: ε = nhv (n = 1,2,…)
Среднюю
энергию осцилляторов  нельзя
принимать равной kT. Планк
использовал
распределение Больцмана частиц по
энергиям. Тогда вероятность рi,
того, что энергия колебания осциллятора
частоты v имеет
значение εi,
определяется выражением (1), где Ni —
нельзя
принимать равной kT. Планк
использовал
распределение Больцмана частиц по
энергиям. Тогда вероятность рi,
того, что энергия колебания осциллятора
частоты v имеет
значение εi,
определяется выражением (1), где Ni —
число осцилляторов с энергией εi, N — полное число осцилляторов. Отсюда можно получить выражение для средней энергии осцилляторов (2). Тогда универсальная функция Кирхгофа rv,T будет иметь вид (3) — формула Планка. Или в виде (4) rλ,T — функции длины волны (учитывая с = λv, rλ,T = rv,T с/λ2). В
области малых частот hv <<kT | |

При
этом постоянная Стефана-Больцмана
равна: 
Закон смешения Вина получается при анализе формулы Планка на экстремум: Tλmax=hc/(4,965k) = b
Таким образом формула Планка обобщает все законы теплового излучения и является полным решением основной задачи теории теплового излучения.



 и
формула Планка
переходит
в формулу
Рэлея-Джинса.
и
формула Планка
переходит
в формулу
Рэлея-Джинса.