Магнитное поле соленоида и тороида
Магнитное поле соленоида и тороида.
Соленоид – цилиндрическая катушка, состоящая из большого числа витков, равномерно намотанных на сердечник. Тороид можно рассматривать как длинный соленоид, свернутый в кольцо (рис. 4.1).
Рис. 4.1. Магнитное поле соленоида
Длина соленоида l содержит N витков и по нему протекает ток I. Считаем соленоид бесконечно длинным. Эксперимент показал, что внутри соленоида поле однородно, а вне соленоида не однородно и очень слабое (можно считать, равным нулю).
Циркуляция вектора В по замкнутому контуру, совпадающему с одной из линий магнитной индукции, охватывающему все N витков, согласно (4.12) равна:
. (4.14)
Интеграл можно представить в виде суммы двух интегралов: по внутренней части контура: и по внешней: , тогда из (4.14) получим:
, (4.15)
или , (4.16)
где В – индукция магнитного поля внутри соленоида; – число витков на единицу длины соленоида.
Магнитное поле внутри тороида, так же, как в соленоиде, однородно, сосредоточено внутри; вне тороида магнитное поле, создаваемое круговыми токами тороида, равно нулю. Величина магнитного поля в тороиде определяется выражением (4.16), причем длина тороида
Отметим любопытный факт. Во всех учебниках по физике остался не отмеченным факт существования у соленоида и тороида второго магнитного поля, которое появляется из-за того, что, например, в соленоиде по отношению к средней линии соленоида витки направлены не точно перпендикулярно, а под углом меньше 90°. Это приводит к появлению тока (эффективного, но равного току I, протекающему через соленоид), вдоль соленоида (рис. 4.2).
Рис. 4.2. Второе магнитное поле соленоида
То есть соленоид создает дополнительное магнитное поле, такое же, как и прямолинейный бесконечно длинный проводник с током. Точно так же и для тороида: вдоль средней линии протекает эффективный ток I. У тороида второе магнитное поле эквивалентно магнитному полю витка с током (рис.4.3). Диаметр этого витка равен диаметру тороида (его средней линии), а магнитное поле тороида (R – радиус тороида).
Рис. 4.3. Второе магнитное поле тороида
§ 3. Поток вектора магнитной индукции
Магнитным потоком Ф через площадку S называется скалярная величина
Ф = В ∙ S (4.17)
или
(4.18)
где – проекция вектора В на направление нормали n к площадке S; – угол между векторамиВ и n.
Поток
вектора В может
быть как положительным, так и отрицательным
в зависимости от знака cos.
Если рассматривать магнитный поток
через контур с током, то положительное
направление нормали уже определено
правилом правого винта (правило
буравчика). Таким образом, магнитный
поток, создаваемый контуром через
поверхность, ограниченную этим контуром,
всегда положителен. Единица измерения
магнитного потока: 1 Вб (Вебер) = 1 Тл 1
м
Теорема Гаусса для магнитного поля: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
, (4.19)
где dS – элемент замкнутой поверхности S, Вn – проекция В на нормаль к этой поверхности.
Эта теорема говорит о том, что в природе отсутствуют магнитные заряды, а линии магнитной индукции замкнуты, то есть магнитное поле является вихревым (соленоидальным).
Магнитный поток через соленоид:
(4.20)
где . Отметим, что ВS умножено на N, т. е. каждый виток соленоида создает магнитный поток ВS, а витков N, т. е. магнитный поток увеличивается в N раз.
1.6. Магнитное поле тороида и соленоида.
Получим теорему о циркуляции магнитной индукции в вакууме в дифференциальной форме. Если контур L находится в сплошной проводящей среде, то значение полного тока, пронизывающего поверхность контура, можно определить, как поток вектора плотности тока через поверхность S, ограниченную этим контуром
|
|
| k | ∫ jndS. |
|
|
|
|
|
| ∑Ii = |
|
| (1.5.11) | |
|
|
| i=1 | S |
|
| |
Подставим выражение (1.5.11) в формулу (1.5.9) и применим тео- | |||||||
| H |
| G |
|
|
|
|
рему Стокса ( v∫ Adl | = ∫(rotA)ndS ). |
|
|
|
| ||
G G | L | S | G |
| G | G | (1.5.12) |
v∫ Bdl | = μ0 ∫ jndS ∫(rotB)ndS = μ0 | ∫ jndS rotB = μ0 | j. | ||||
L | S |
| S |
| S |
|
|
Результат подстановки – теорема о циркуляции вектора магнит- | |||||||
ной индукции в вакууме в дифференциальной форме |
|
| |||||
|
|
| rotB = μ0 j. |
|
| (1.5.13) | |
Теорема о циркуляции вектора напряженности магнитного поля в | |||||||
дифференциальной форме будет иметь вид: |
|
| |||||
|
|
| rotH = j. |
|
| (1.5.14) | |
Уравнение (1.5.14) математически выражает тот факт, что магнитное поле имеет вихревой характер и его источниками являются электрические токи.
Закон полного тока (1.5.10) часто используют для расчета индукции магнитного поля постоянного электрического тока. Для примера рассмотрим применение закона полного тока для расчета индукции магнитного поля соленоида и тороида.
Соленоид – это катушка индуктивности в виде намотанного на цилиндрическую поверхность изолированного проводника, по которому течет электрический ток. Рассмотрим соленоид длиной l, имеющей N витков. Длину соленоида считаем во много раз больше, чем диаметр его витков, то есть рассматриваемый соленоид бесконечно длинный. Внутри соленоида поле является однородным, вне соленоида – неоднородным и очень слабым, и чем длиннее соленоид, тем меньше магнитная индукция вне его. Поэтому будем считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него.

Для нахождения магнитной индукции выберем замкнутый прямоугольный контур ABCDA (рис. 1.6.1) Согласно теореме о цирку-
ляции вектора H:
ABCDA
D  A
A
C B
Рис. 1.6.1
Интеграл по ABCDA можно представить в виде интегралов по AB; BC; CD; DA. На участках AB и CD контур перпендикулярен линиям магнитной индукции и Hl = 0. На участке CB вне соленоида Н = 0, а на участке DA контурG совпадает с линией магнитной индукции и циркуляция вектора H равна
v∫ Hl dl = Hl = NI. | (1.6.2) |
DA |
|
Из последнего уравнения получаем, что напряженность магнитного поля соленоида:
| NI | (1.6.3) | |
H = | l = nI , | ||
|
где n – число витков соленоида, приходящихся на единицу длины. Используя формулу (1.1.1), выражаем индукцию магнитного поля
соленоида:
B = μμ0 | N | I = μμ0nI. | (1.6.4) | |
l | ||||
|
|
|
Тороид – это кольцевая катушка с витками, намотанными на сердечник, имеющий форму тора, по которому течет электрический ток.
Пусть R1 и R2 соответственно внешний и внутренний радиусы сечения тороида. Общее число витков тороида с током I равно N.

Если r < R2, то контур не охватывает проводники | с током, |
N |
|
∑Ik = 0, и по закону полного тока |
|
i=1 |
|
v∫ Hdl cos α= 2πrH = 0 H = 0. | (1.6.5) |
L |
|
Если r > R1, то контур охватывает 2N проводников с током I. Половина из них идет в одном направлении, а половина – в обратном направлении (рис. 1.6.2). Поэтому алгебраическая сумма токов во всех проводниках равна нулю, и поэтому
r
R2 
R1 
Рис. 1.6.2
Из полученного результата следует, что вне тороида магнитное поле отсутствует. Магнитное поле сосредоточено внутри объема (R2 ≤ r ≤ R1) тороида. Линии магнитной индукции в данном случае есть окружности, центры которых расположены на оси тороида. В этом случае контур радиуса r охватывает N проводников, токи в которых равны I и одинаково направлены. Поэтому по теореме о циркуляции
v∫ Hl dl = Hl = 2πrH = NI. | (1.6.7) |
L |
|
|
| |
Отсюда напряженность магнитного поля внутри тороида: |
| |||
| NI |
| (1.6.8) | |
H = | 2πr = nI, | |||
| ||||
где n – число витков тороида, приходящихся на единицу длины. Напряженность магнитного поля на осевой линии тороида равна:
Hср = | NI | . | (1.6.9) |
| |||
| 2πr |
| |
| ср |
| |
dΦm = BdS = BndS,
Используя формулу (1.1.1), находим индукцию магнитного поля внутри тороида:
B = μμ0 | NI | = μμ0nI. | (1.6.10) | |
2πr | ||||
|
|
|
Индукция магнитного поля на осевой линии тороида равна:
B = μμ |
| NI | = μμ | nI. | (1.6.11) | |
0 2πr | ||||||
cp | 0 |
|
| |||
|
| cp |
|
|
| |
1.7. Магнитный поток. Теорема Гаусса для магнитного поля в интегральной и дифференциальной формах.
Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется величина, равная:
(1.7.1)
где Bn = Bcosα – проекция вектора B на направление нормали nG к площадке dS, α − угол между векторами n и B (рис. 1.7.1). Магнитный поток равен числу линий магнитной индукции, пронизывающих замкнутую поверхность в направлении внешней нормали.
Bn
α B
n
dS
S
Рис. 1.7.1
Поток вектора магнитной индукции через произвольную поверхность S равен
Φm = ∫BdS = ∫BndS . | (1.7.2) | |
S | S |
|
Если магнитное поле однородно (B =const), а поверхность S плоская, то магнитный поток равен
За единицу магнитного потока принимается магнитный поток сквозь плоскую поверхность единичной площади, расположенную перпендикулярно к однородному магнитному полю, индукция которого равна единице. В системе СИ единица магнитного потока называется
вебером [Вб].
Магнитный поток через поверхность, ограниченную замкнутым контуром, называется потокосцеплением ψ этого контура (потоком, сцепленным с контуром). Если контур имеет N витков, то потокосцепление этого контура:
где Фт − поток, пронизывающий один виток контура.
В природе отсутствуют элементарные «магнитные заряды», аналогичные электрическим зарядам, поэтому линии индукции В магнитного поля не имеют ни начала, ни конца, т. е. магнитные силовые линии замкнуты. Следовательно, поток Фт через любую замкнутую поверхность будет всегда равен нулю, так как число входящих линий
равно числу выходящих силовых линий: |
| |
v∫ | G |
|
BdS =0 или v∫ BndS = 0. | (1.7.5) | |
S | S |
|
Теорема Гаусса для магнитного поля в интегральной форме:
поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю.
Так как BG =μμ0HG, | то поток вектора H через любую замкнутую | |
поверхность также равенGнулю: |
| |
v∫HdS =0 или v∫ HndS = 0. | (1.7.6) | |
S | S |
|
Для записи теоремы Гаусса для магнитного поля в дифференциальной формеG воспользуемся теоремой Остроградского − Гаусса v∫ AndS = ∫divAdV .
v∫ | G G | G | G | (1.7.7) |
BdS | = 0 ∫divBdV = 0 | divB = 0. |
S V
Для напряженности магнитного поля получится аналогичное выражение:
Выражения (1.7.7) и (1.7.8) являются дифференциальной формой теоремы Гаусса.
9.1. Циркуляция вектора магнитной индукции. Поле соленоида и тороида
В
третьей лекции было показано, что для
электростатического поля 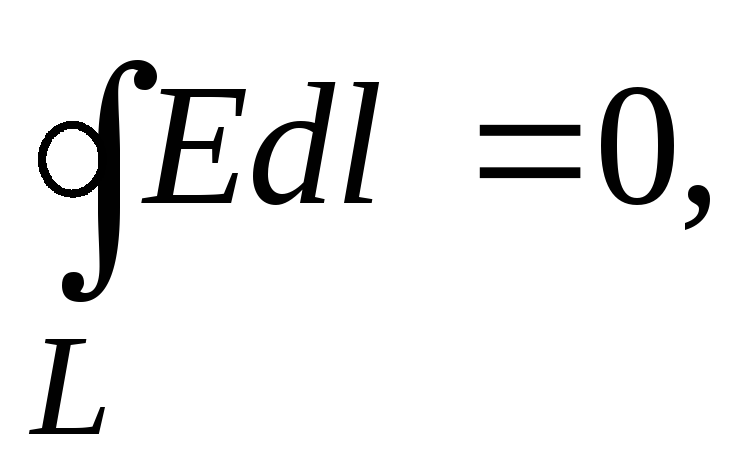
т
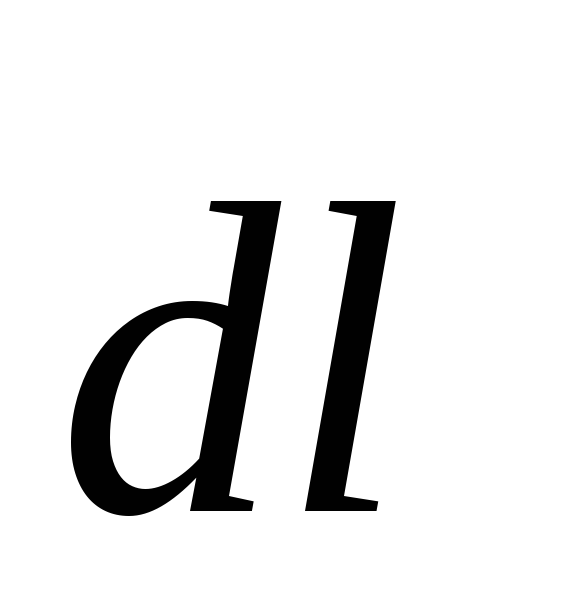
 вдоль замкнутого контура L равна
нулю. Можно показать, что циркуляция
вектора
вдоль замкнутого контура L равна
нулю. Можно показать, что циркуляция
вектора  вдоль замкнутого контура L равна алгебраической сумме токов,
охватываемых контуром, умноженной на
вдоль замкнутого контура L равна алгебраической сумме токов,
охватываемых контуром, умноженной на 
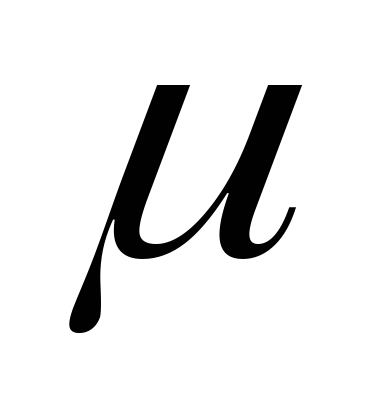 0 , т. е.
0 , т. е. 
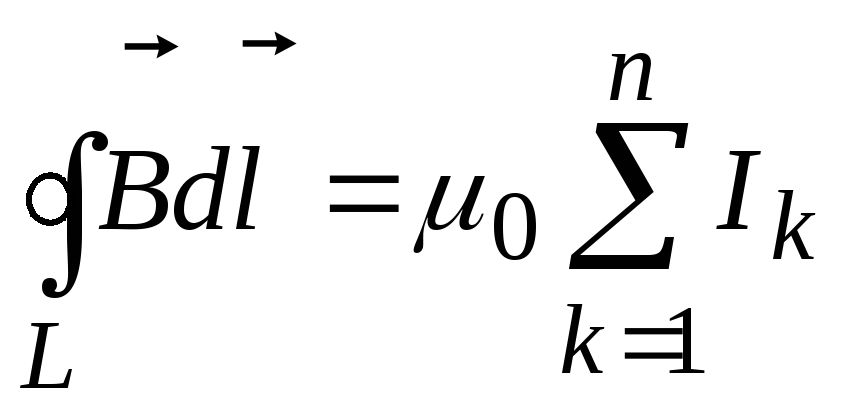 (1)
(1)
П
L


 ри
этом токи будем считать положительными,
если они совпадают с поступательным
движением правого буравчика, рукоятка
которого вращается по направлению
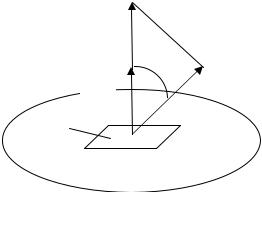
обхода контура. Для нашего случая, (см.
рис. 1).
это будут токи, текущие от нас и
обозначенные
ри
этом токи будем считать положительными,
если они совпадают с поступательным
движением правого буравчика, рукоятка
которого вращается по направлению
обхода контура. Для нашего случая, (см.
рис. 1).
это будут токи, текущие от нас и
обозначенные  .
Токи, текущие в обратном
.
Токи, текущие в обратномнаправлении, будут считаться отрицательными. Для рис. 1, это будут токи, текущие на нас и обозначенные кружком с точкой в центре.
Поскольку 
 ,
то магнитное поле не является
потенциальным, оно называется
,
то магнитное поле не является
потенциальным, оно называется
вихревым или соленоидальным.
Применим теорему о циркуляции (1)для вычисления индукции магнитного поля соленоида и тороида.
9.1.1. Поле соленоида
С

l
оленоидом, (см. рис. 2), называется цилиндрическая катушка, на которую вплотную намотано большое число витков провода. Пусть N — число витков вдоль длины соленоида l, тогда ,
где L – контур
12341
,
где L – контур
12341 
 или
или  .
.
Интегралы
на участках 1-2, 3- 4 равны нулю, т.к. 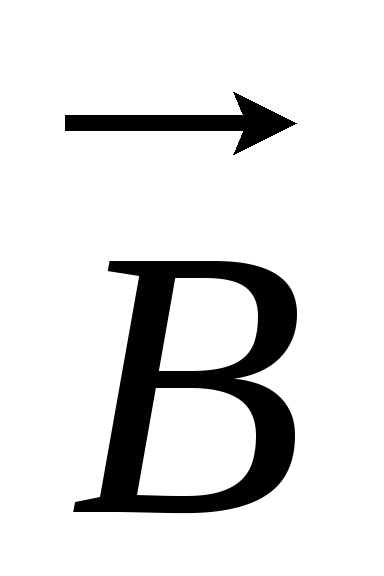
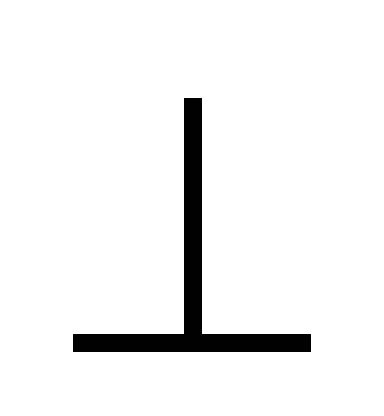 d
d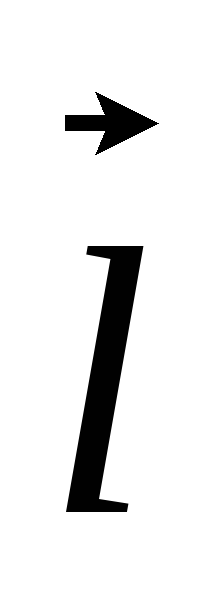 и
и  d
d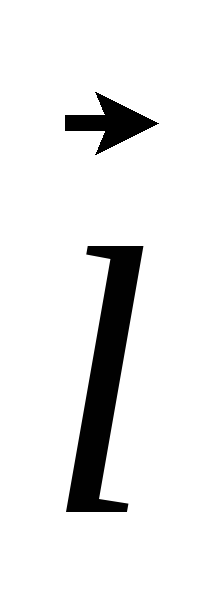 =Bdlcosπ/2
=0;
=Bdlcosπ/2
=0;
интеграл
на участке 4-1 равен нулю, т.к. вне
соленоида индукция  равна нулю.
Поэтому
равна нулю.
Поэтому  ,
отсюда B=
,
отсюда B= , (2)
, (2)
где n=N / l — число витков, приходящееся на единицу длины соленоида. Поле соленоида однородно.
9.1.2. Поле тороида
Тороид
(см.рис.3),
представляет тонкий провод, плотно
навитый на каркас, имеющий форму тора.
Для него 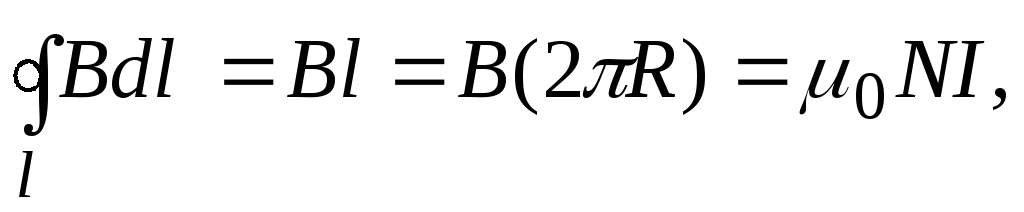
где R — радиус средней линии тора, отсюда B = 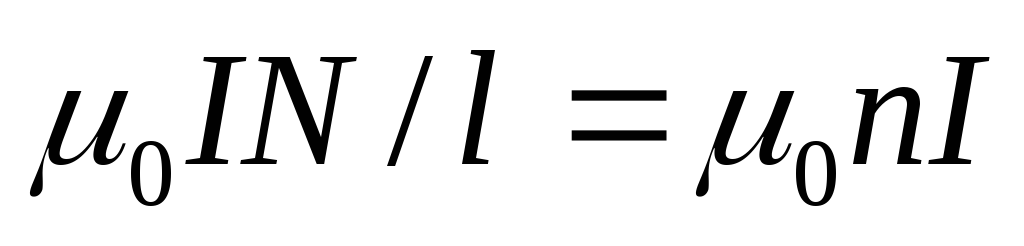 (3)
(3)
 Поле
тороида неоднородно: оно уменьшается
с увеличением r. Поле вне тороида равно нулю.
Поле
тороида неоднородно: оно уменьшается
с увеличением r. Поле вне тороида равно нулю.
9.2. Магнитный поток. Теорема Гаусса
Для однородного магнитного поля, пронизывающего плоскую поверхность площади S, ( см. рис. 4 ). магнитный поток
Ф= = BScos
= BScos =Bn S (4)
=Bn S (4)
где  = S
= S ,
,  —
нормаль к поверхности.
—
нормаль к поверхности.
В
S


dФ =  d
d =
BdS cos
=
BdS cos = B
= B dS. (5)
dS. (5)
Магнитный
поток сквозь произвольную поверхность Ф= =
=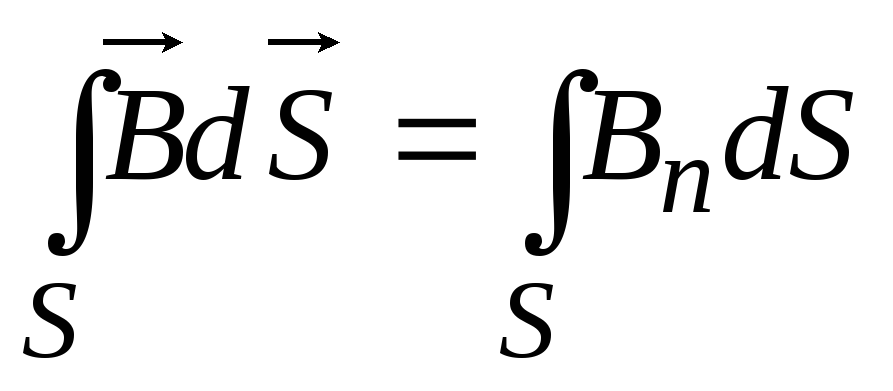 .
.
В
природе нет магнитных зарядов и поэтому
теорема Гаусса для магнитного потока
имеет вид Ф =  ,
(6)
,
(6)
т.е. магнитный поток сквозь произвольную замкнутую поверхность равен нулю.
Пусть
в формуле
(4)  = 0 , т.е.
= 0 , т.е.  (см. рис.5), тогда Ф=BS .
Магнитный поток в СИ измеряется в
веберах
—
(Вб): 1Вб = 1 Тл1
м2. Поток магнитной индукции в 1Вб —
это поток, пронизывающий площадку в 1 м2, расположенную перпендикулярно
силовым линиям однородного магнитного
поля, индукция которого равна 1Тл.
(см. рис.5), тогда Ф=BS .
Магнитный поток в СИ измеряется в
веберах
—
(Вб): 1Вб = 1 Тл1
м2. Поток магнитной индукции в 1Вб —
это поток, пронизывающий площадку в 1 м2, расположенную перпендикулярно
силовым линиям однородного магнитного
поля, индукция которого равна 1Тл.
Магнитное поле в соленоиде и тороиде
Соленоидом называется катушка с
большим числом витков. Рассмотрим
соленоид длиной  ,
имеющей N витков. По
соленоиду течет ток .
Предположим, что у соленоида:
,
имеющей N витков. По
соленоиду течет ток .
Предположим, что у соленоида:  d,
где d — диаметр витков
(бесконечно длинный соленоид).
d,
где d — диаметр витков
(бесконечно длинный соленоид).
В
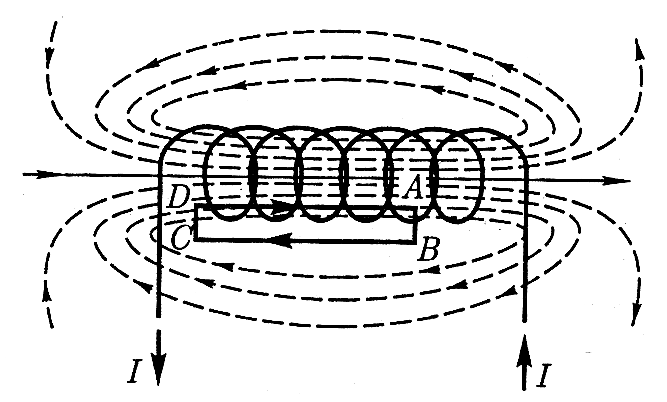
Рисунок 15. Магнитное поле соленоида
Выберем замкнутый прямоугольный контур
АВСДА, охватывающий N
витков. Тогда циркуляция: .
.
Н
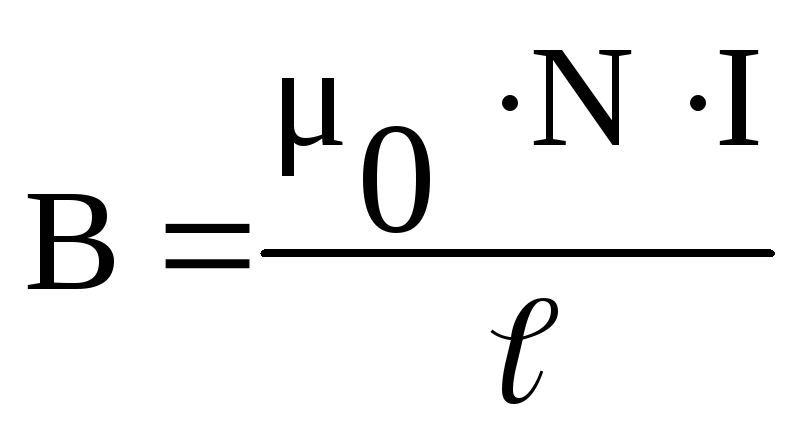
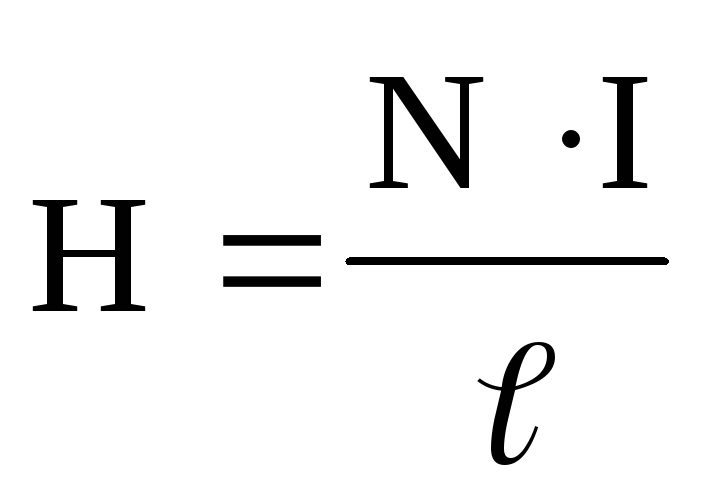
 = 0; На участке ДА циркуляция индукции
= 0; На участке ДА циркуляция индукции  равна
равна 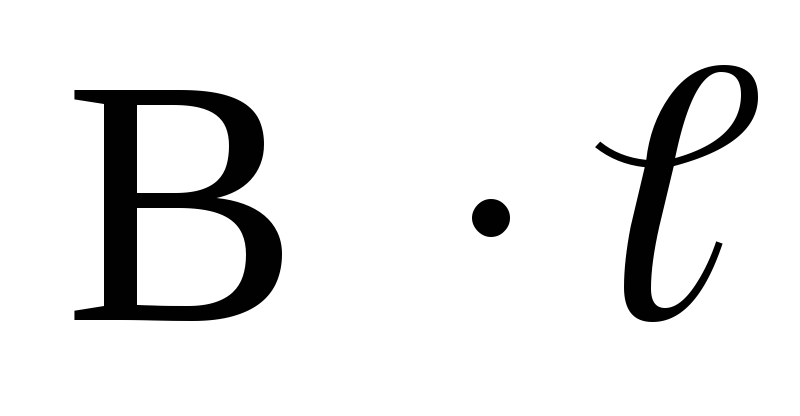 (контур совпадает с линией магнитной
индукцией):
(контур совпадает с линией магнитной
индукцией): 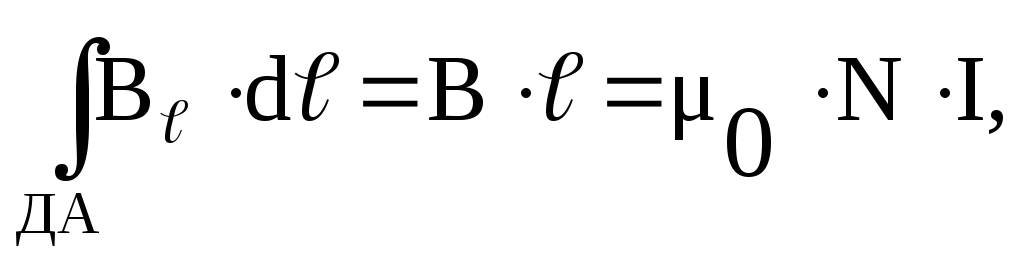 отсюда магнитная индукция и напряженность
поля внутри соленоида:
отсюда магнитная индукция и напряженность
поля внутри соленоида:Тороид – кольцевая катушка.
М

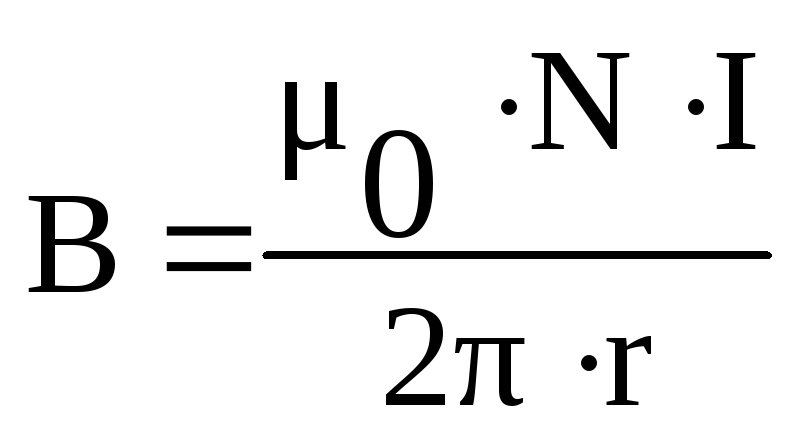 ,
где
,
где  —
число витков. Магнитное поле вне тороида
отсутствует.
—
число витков. Магнитное поле вне тороида
отсутствует.
Рисунок 16. Тороид
r
Контрольные вопросы
Изложите закон Ампера. Как определить направление силы Ампера?
Приведите формулу для определения силы взаимодействия двух параллельных токов.
Чему равна магнитная индукция, создаваемая движущимся электрическим зарядом?
Дайте определение силы Лоренца. Как определить модуль и направление силы Лоренца?
Как вычисляется циркуляция вектора
 по произвольному замкнутому контуру
и что она показывает?
по произвольному замкнутому контуру
и что она показывает?Что такое соленоид и чему равна магнитная индукция внутри соленоида?
Что такое тороид и чему равна магнитная индукция внутри тороида?
Поток вектора магнитной индукции. Теорема Гаусса для вектора .
П
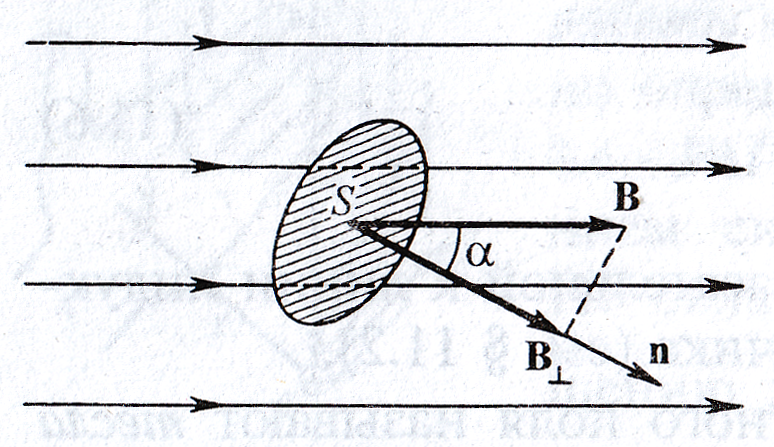
 называется скалярная физическая
величина, равная:
называется скалярная физическая
величина, равная: 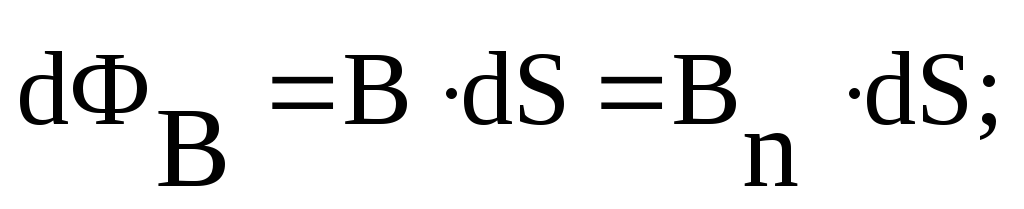
 — проекция вектора
— проекция вектора  на направление нормали к площадке
на направление нормали к площадке  (рисунок 17), — угол
между векторами
(рисунок 17), — угол
между векторами  и
и  .
. 
Поток вектора  через произвольную поверхность
через произвольную поверхность  :
:
 .
.
Размерность потока:
Рисунок 17. Проекция вектора  на нормаль
на нормаль
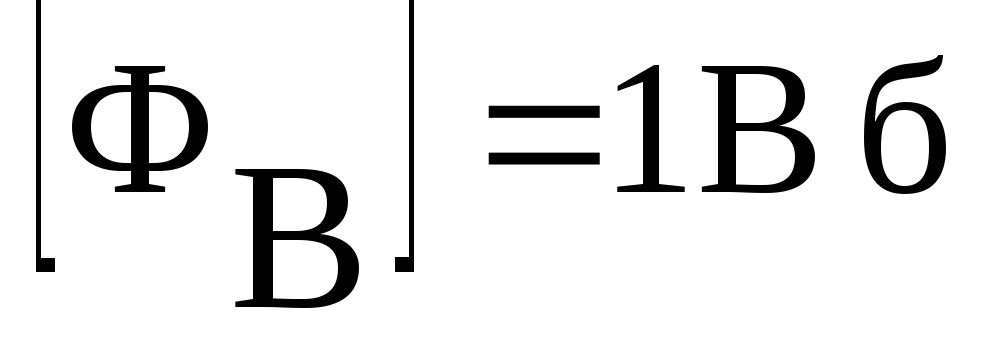 (вебер)=
1 Тл×м2
(вебер)=
1 Тл×м2Д
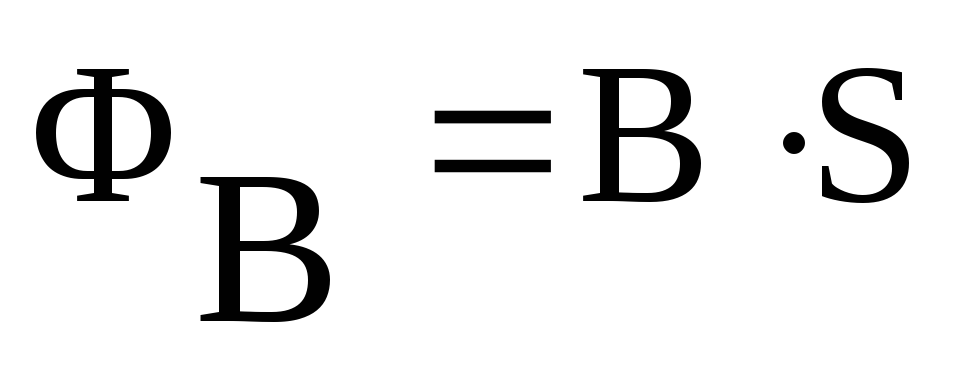
 :
: 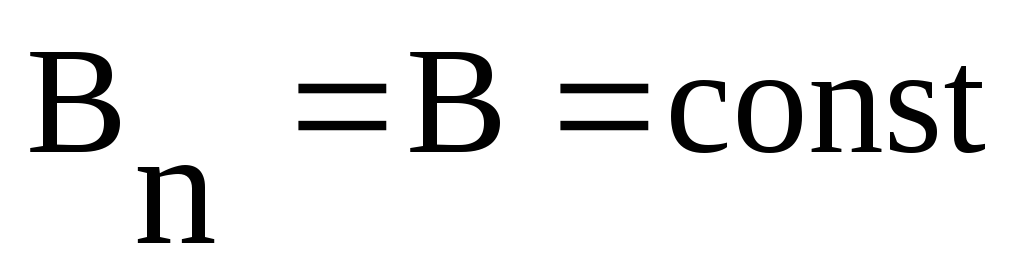 и
и Теорема Гаусса: поток вектора магнитной
индукции  через любую замкнутую поверхность равен
0.
через любую замкнутую поверхность равен
0.

Отсюда следует, что магнитных зарядов не существует, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и всегда замкнуты.
Для одного витка соленоида: 
Полный поток, сцепленный со всеми витками соленоида, называется потокосцеплением:

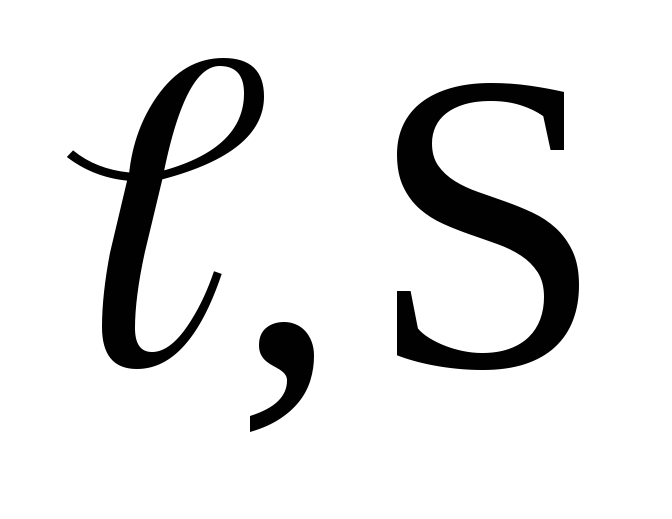 и
и  —
длина,
—
длина,площадь сечения и
число витков соленоида соответственно.
Работа по перемещению проводника и контура с током в магнитном поле
По закону Ампера  .
Элементарная работа (рисунок 18):
.
Элементарная работа (рисунок 18): 

Рисунок 18. Работа по перемещению проводника с током в магнитном поле
Работа по перемещению проводника с постоянным током  в магнитном поле равна произведению
силы тока на величину магнитного потока, пересеченного движущимся проводником.
в магнитном поле равна произведению
силы тока на величину магнитного потока, пересеченного движущимся проводником.

Работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром. Формула справедлива для контура любой формы в произвольном магнитном поле.
28.Поле тороида и соленоида. Магнитное поле соленоида.
Соленоид — катушка провода, намотанного на цилиндрическую поверхность.
Образование
магнитного потока в соленоиде.
Выбирается произвольная
точка на оси соленоида и рассчитывается
значение магнитной индукции в ней.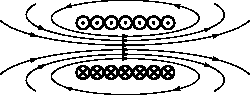


Точка в центре соленоида.
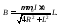




Точка на торце соленоида.


Магнитное поле тороида
Тороид представляет собой тонкий провод, плотно (виток к витку) намотанный на каркас в форме тора .
Возьмём
контур L в виде окружности радиуса r,
центр которого совпадает с центром
тора радиуса R.

В
силу симметрии, вектор  в каждом токе направлен по касательной
к контуру.
в каждом токе направлен по касательной
к контуру.
Следовательно, 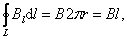 где
где  – длина контура.
– длина контура.
Если
контур проходит внутри тороида, он
охватывает ток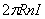 (n – число витков на единицу длины).
(n – число витков на единицу длины).
Тогда,
в соответствии с теоремой о циркуляции
вектора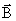 , можно записать:
, можно записать: Отсюда
следует:
Отсюда
следует: 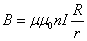 Контур вне тороида токов не охватывает,
поэтому
Контур вне тороида токов не охватывает,
поэтому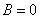 .
.
Для
тороида, где радиус тора намного больше
радиуса витка, отношение
,
тогда магнитное поле В можно рассчитать
по формуле (2.7.1): В
тороиде магнитное поле однородно только
величине, т.е. по модулю, но направление
его в каждой точке различно.
В
тороиде магнитное поле однородно только
величине, т.е. по модулю, но направление
его в каждой точке различно.
29.Работа при перемещении проводника с током в магнитном поле.
Рассмотрим
контур с током, образованный неподвижными
проводами и скользящей по ним подвижной
перемычкой длиной l (рис. 2.17). Этот контур
находится во внешнем однородном
магнитном поле 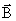 , перпендикулярном к плоскости контура.
При показанном на рисунке направлении
тока I, вектор
, перпендикулярном к плоскости контура.
При показанном на рисунке направлении
тока I, вектор сонаправлен с
сонаправлен с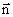 .
.
На
элемент тока I (подвижный провод) длиной
l действует сила Ампера, направленная
вправо:  Пусть проводник l переместится параллельно
самому себе на расстояние dx. При этом
совершится работа:
Пусть проводник l переместится параллельно
самому себе на расстояние dx. При этом
совершится работа: Итак,
Итак, (2.9.1) Работа, совершаемая проводником
с током при перемещении, численно равна
произведению тока на магнитный поток,
пересечённый этим проводником.
(2.9.1) Работа, совершаемая проводником
с током при перемещении, численно равна
произведению тока на магнитный поток,
пересечённый этим проводником.
Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции.
Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле.
Рассмотрим
прямоугольный контур с током 1-2-3-4-1
(рис. 2.18). Магнитное поле направлено от
нас перпендикулярно плоскости контура.
Магнитный поток 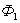 , пронизывающий контур, направлен по
нормали
, пронизывающий контур, направлен по
нормали к
контуру, поэтому
к
контуру, поэтому Переместим этот контур параллельно
самому себе в новое положение
1′-2′-3′-4′-1′. Магнитное поле в общем случае
может быть неоднородным и новый контур
будет пронизан магнитным потоком
Переместим этот контур параллельно
самому себе в новое положение
1′-2′-3′-4′-1′. Магнитное поле в общем случае
может быть неоднородным и новый контур
будет пронизан магнитным потоком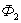 .
Площадка
4-3-2′-1′-4, расположенная между старым и
новым контуром, пронизывается потоком
.
Площадка
4-3-2′-1′-4, расположенная между старым и
новым контуром, пронизывается потоком 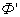 .
Полная
работа по перемещению контура в магнитном
поле равна алгебраической сумме работ,
совершаемых при перемещении каждой из
четырех сторон контура:
.
Полная
работа по перемещению контура в магнитном
поле равна алгебраической сумме работ,
совершаемых при перемещении каждой из
четырех сторон контура: 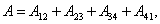 где
где  ,
,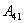 равны нулю, т.к. эти стороны не пересекают
магнитного потока, при своём перемещение
(очерчивают нулевую площадку).
равны нулю, т.к. эти стороны не пересекают
магнитного потока, при своём перемещение
(очерчивают нулевую площадку). .
Провод
1–2 перерезает поток (
.
Провод
1–2 перерезает поток (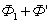 ),
но движется против сил действия
магнитного поля.
),
но движется против сил действия
магнитного поля. Тогда
общая работа по перемещению контура
Тогда
общая работа по перемещению контура 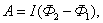 или
или здесь
здесь  – это изменение магнитного потока,
сцепленного с контуром. Работа,
совершаемая при перемещении замкнутого
контура с током в магнитном поле, равна
произведению величины тока на изменение
магнитного потока, сцепленного с этим контуром.
Элементарную
работу по бесконечно малому перемещению
контура в магнитном поле можно найти
по формуле
– это изменение магнитного потока,
сцепленного с контуром. Работа,
совершаемая при перемещении замкнутого
контура с током в магнитном поле, равна
произведению величины тока на изменение
магнитного потока, сцепленного с этим контуром.
Элементарную
работу по бесконечно малому перемещению
контура в магнитном поле можно найти
по формуле 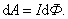 (2.9.5)
Выражения
(2.9.1) и (2.9.5) внешне тождественны, но
физический смысл величины dФ различен.
Соотношение
(2.9.5), выведенное нами для простейшего
случая, остаётся справедливым для
контура любой формы в произвольном
магнитном поле. Более того, если контур
неподвижен, а меняется
(2.9.5)
Выражения
(2.9.1) и (2.9.5) внешне тождественны, но
физический смысл величины dФ различен.
Соотношение
(2.9.5), выведенное нами для простейшего
случая, остаётся справедливым для
контура любой формы в произвольном
магнитном поле. Более того, если контур
неподвижен, а меняется  ,
то при изменении магнитного потока в
контуре на величину dФ, магнитное поле
совершает ту же работу
,
то при изменении магнитного потока в
контуре на величину dФ, магнитное поле
совершает ту же работу
27. Магнитное поле Тороида и длинного соленоида
Применим теорему о циркуляции вектора магнитной индукции. Для вычисления Тороида и длинного соленоида.
Тороид – каркас с формой бублика с навитым на него витками проводника по которому течет ток I.
Соленоид – цилиндрическая катушка из большого числа намотанного в плотную проводника с током I.
Тороид: За контур L возьмем окружность радиуса r так, что контур внутри тороида.
Тороид можно рассмотреть как систему последовательно соединенных круговых токов одинакового радиуса и нанизанных на общую o -R круговую ось радиуса R.
По
теореме циркуляции имеем  μ0
μ0 k
k
т.к.
контур L
проходит внутри тороида, то он охватывает
ток равный 2πRnI,
где n
– число витков на единицу длины –
плотность витков. Из симметрии вектор В в каждой точке направлен по касательной
к L,
тогда  B2πr.
Окончательно имеем: В2πr=μ02πRnI
=> B=μ0
B2πr.
Окончательно имеем: В2πr=μ02πRnI
=> B=μ0  nI.
Если внутри тороида среда с магнитной
проницаемостью μ, тогда Втор=μ0μ
nI.
Если внутри тороида среда с магнитной
проницаемостью μ, тогда Втор=μ0μ nI
nI
Соленоид:
есть тороид бесконечно большого радиуса,
т.е R→∞
N 
Bсол=μ0μnI – магнитное поле соленоида
n= , гдеN
– число витков; l
– длина соленоида
, гдеN
– число витков; l
– длина соленоида
29. Эффект Холла. Мгд генератор (магнитогидродинамический)
Эффект Холла(1880г) есть возникновение поперечной разности потенциалов в металле или полупроводнике по которым проходит электрический ток и при помещении их в магнитное поле перпендикулярное к направлению тока. Эффект Холла объясняется действием силы Лоренца на носителе тока в проводнике или полупроводнике и позволяет судить о знаке заряда – носителе тока.
На верхнем срезе проводника появляются отрицательные заряды, на нижнем положительные. Если носители тока – положительные заряды, то срезы проводника зарядятся обратным образом. Найдем при этом разность потенциалов ∆φ. Т.к. В⃗ перпендикулярен υ⃗ и В перп. I,
то сила Лоренца Fл=qυB. С другой стороны заряды скопившиеся на верхнем и нижнем слое проводника создадут электрическое поле с напряжением Е и сила со стороны этого поля Fэ=qE. Стационарное распределение Fл=Fэ => qυB=qE => υB=E.
С другой стороны скорость υ: j=qn0υ => υ=j/qn0 E=∆φ/d, тогда
jB/qn0=∆φ/d, тогда ∆φ=jBd/qn0, где 1/qn0 – постоянная Холла = R => ∆φ=RjBd
Изменяя разность потенциалов ∆φ можно определить постоянную Холла R и таким образом определить знак зарядов. В металлах носителем тока являются свободные электроны, но есть исключение: в цинке и кадмии носители заряда(тока) имеют положительный заряд(q>0).
Действие МГД — генератора основано так же на использовании силы Лоренца.
28. Сила Лоренца
Сила
Ампера действует на проводник с током,
но токи направленное упорядоченное
движение зарядов. Тогда сила Ампера
должна действовать и на отдельные
движущиеся заряды. Найдем исходя из
силы Ампера выражение для силы действующей
на заряд q
движущейся со скоростью  со стороны магнитного поля с индукцией
со стороны магнитного поля с индукцией — сила Лоренца.
— сила Лоренца.
Рассмотрим
проводник длиной dl
и площадью поперечного сечения S
в магнитном поле с индукцией  .
Пусть ток в проводнике –I.
Заряд q
со скоростью υ, а n0 – концентрация зарядов. На проводник
с током действует сила А. dF⃗=I[dl⃗;B⃗]
Покажем теперь, что элемент тока … Idl⃗
по своим свойствам эквивалентен
выражениям: qdnυ⃗
Idl⃗=qdnυ⃗
где q
– заряд; dn
– число зарядов; υ – скорость их
движения. Действительно сила постоянного
тока I=jS,
где S
– площадь поперечного сечения; j
– плотность тока. Умножим на dl⃗,
тогда
.
Пусть ток в проводнике –I.
Заряд q
со скоростью υ, а n0 – концентрация зарядов. На проводник
с током действует сила А. dF⃗=I[dl⃗;B⃗]
Покажем теперь, что элемент тока … Idl⃗
по своим свойствам эквивалентен
выражениям: qdnυ⃗
Idl⃗=qdnυ⃗
где q
– заряд; dn
– число зарядов; υ – скорость их
движения. Действительно сила постоянного
тока I=jS,
где S
– площадь поперечного сечения; j
– плотность тока. Умножим на dl⃗,
тогда
Idl⃗=jSdl⃗=j⃗Sdl
=> Idl⃗=j⃗dV,
а j⃗=qn0υ⃗dV,
где n0dV=dn
– число зарядов, тогда Idl⃗=qdnυ⃗ подставим
это выражение в формулу для силы Ампера,
тогда получим dF⃗=qdn[υ⃗;B⃗]
– сила действующая на рассмотриваемый
проводник в котором число зарядов dn,
тогда сила действующая на один заряд.
F⃗л=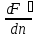 ,
,
Fл=q[υ⃗;B⃗] – сила Лоренца, знак q учитывается.
F⃗л Направление силы Лоренца определяется согласно правилу векторного произведения:
сила
Fл перпендикулярна площади, в которой
лежит υ и В. Направление определяется
правилом правого винта. Если вращать
рукоятку правого винта от первого
вектора υ ко второму вектору В на
кратчайший угол α, то поступательное
движение винта укажет направление силы
Лоренца при положительном заряде
Fл=qυBsinα=qυBsin(υ⃗,^B⃗)
Выражение для силы Лоренца зависит от
выбора системы отсчета: если заряд
движется со скоростью 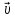 в электрическом поле с индукцией
в электрическом поле с индукцией ,
то на заряд будет действовать силаF⃗=qE⃗+q[υ⃗,B⃗].
,
то на заряд будет действовать силаF⃗=qE⃗+q[υ⃗,B⃗].
Т.к.
сила Лоренца Fл перпендикулярна к скорости заряда, то
она не меняет модуль |υ| и потому сила
Лоренца работы не совершает и кинетическую
энергию заряда не меняет. Действие силы
Лоренца лежит в основе работы ускорителей
элементарных частиц. Покажем теперь,
что магнетизм есть чисто релятивистский
эффект, т.е. для этого покажем, что 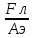 →0
при
→0
при →0;Fэ=qE.
Для этого рассмотрим два точечных
заряда q1 и q2 движущихся параллельно друг к другу с
одинаковой скоростью
→0;Fэ=qE.
Для этого рассмотрим два точечных
заряда q1 и q2 движущихся параллельно друг к другу с
одинаковой скоростью  в вакууме.
в вакууме.
Fэ=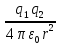 ε=μ=1
ε=μ=1
Сила
Лоренца действующая на заряд q1 в магнитном поле, создаваемом зарядом
q2 равна F⃗л=q1[υ⃗,B⃗2].
Магнитное поле, создаваемое совокупность
зарядов dn
будет очевидно равно: dB= .
Т.к. по закону Савара- Лапласа:dB⃗=
.
Т.к. по закону Савара- Лапласа:dB⃗= ,
тогда магнитное поле создаваемое одним
зарядом:B⃗2=
,
тогда магнитное поле создаваемое одним
зарядом:B⃗2= =
= подставим теперь В⃗2 в F⃗л,
тогда Fл=
подставим теперь В⃗2 в F⃗л,
тогда Fл=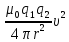 ,
тогда
,
тогда
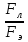 =μ0ε0υ2=
=μ0ε0υ2= ,
где с=
,
где с=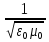 =3*108м/с
– электродинамическая постоянная =>
=3*108м/с
– электродинамическая постоянная => 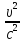 →0,
когда
→0,
когда →0
→0
Вывод:
магнетизм есть чисто релятивистский
эффект. В системе Гаусса F⃗=qE⃗+q[ ,B⃗]
,B⃗]
3.12. Магнитное поле соленоида и тороида.
Применим полученные результаты для нахождения напряженности магнитного поля на оси прямого длинного соленоида и тороида.
1) Магнитное поле на оси прямого длинного соленоида.
Соленоид представляет собой катушку, намотанную на цилиндрический каркас. Если длина соленоида много больше его диаметра, то такой соленоид называют длинным (в отличие от короткой катушки с противоположным соотношением размеров). Магнитное поле максимально внутри соленоида и направлено вдоль его оси. Вблизи оси соленоида магнитное поле можно считать однородным.
Для нахождения напряженности магнитного поля на оси прямого длинного соленоида с помощью теоремы о циркуляции магнитного поля, выберем контур интегрирования, как показано на рис.10.5.
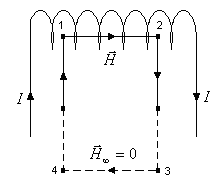
Рис.10.5. К расчету напряженности магнитного поля на оси соленоида.
На участке 1-2 направление магнитного поля совпадает с направлением обхода контура, а его напряженность постоянна в силу однородности поля. На участках 2-3 и 4-1 вне соленоида проекция магнитного поля на направление обхода равна нулю. Наконец, на участке 3-4, удаленном достаточно далеко от соленоида, можно считать, что магнитное поле отсутствует.
С учетом сказанного имеем:
 ,
,
где
 ,
,  ,
,  ,
, 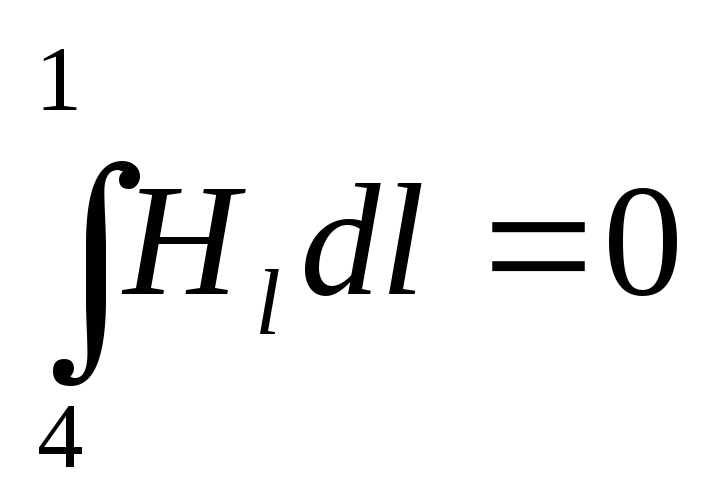 .
.
Но
согласно теореме о магнитном напряжении
этот интеграл равен 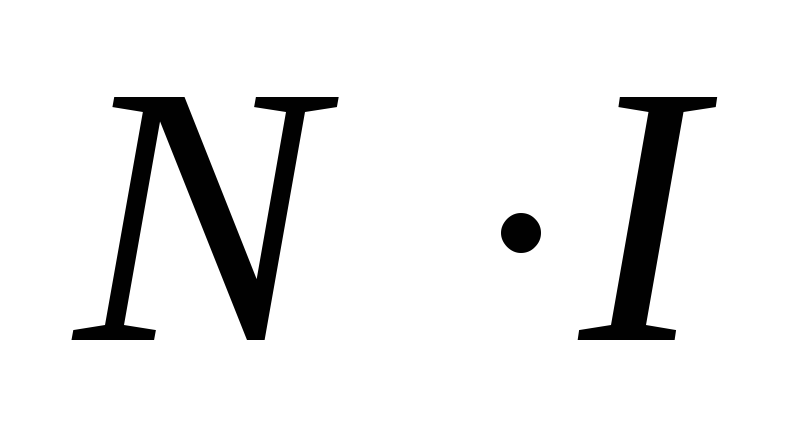 ,
где N – число витков соленоида, сцепленных
с контуром интегрирования. Следовательно
,
где N – число витков соленоида, сцепленных
с контуром интегрирования. Следовательно
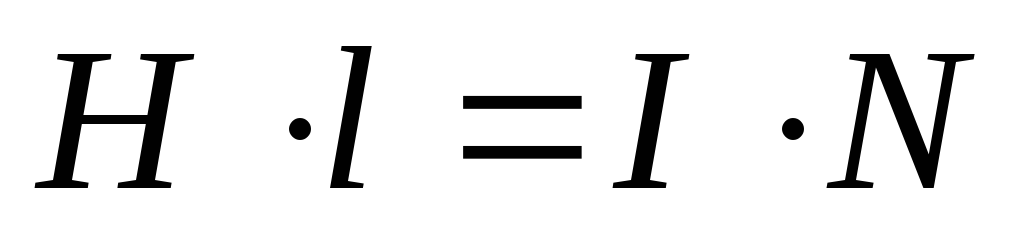 ,
,
откуда
находим: 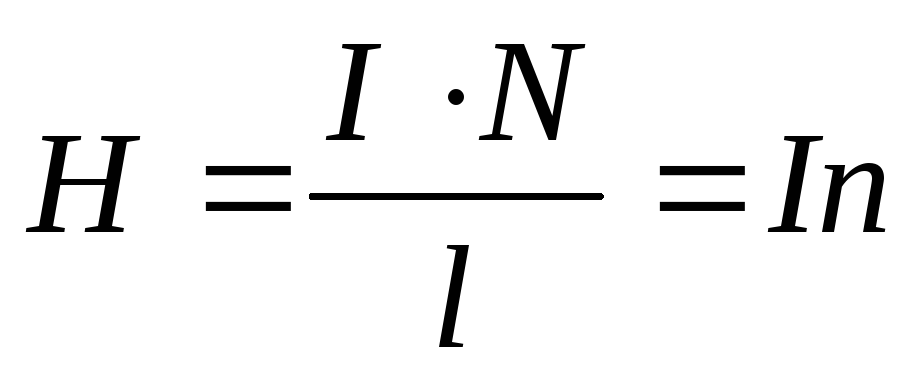 ,
,
где
через  обозначено число витков на единицу
длины соленоида.
обозначено число витков на единицу
длины соленоида.
2) Магнитное поле на оси тороида.
Тороид представляет собой катушку, намотанную на каркас, имеющий форму тора. Магнитное поле тороида целиком сосредоточено внутри него и является неоднородным. Максимальное значение напряженность магнитного поля имеет на оси тороида.
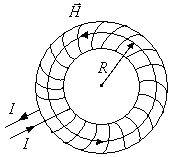
Рис.10.6. К расчету напряженности магнитного поля на оси тороида.
Для нахождения напряженности магнитного поля вблизи оси тороида применим теорему о циркуляции магнитного поля, выбрав контур интегрирования, как показано на рис.10.6.
Имеем:
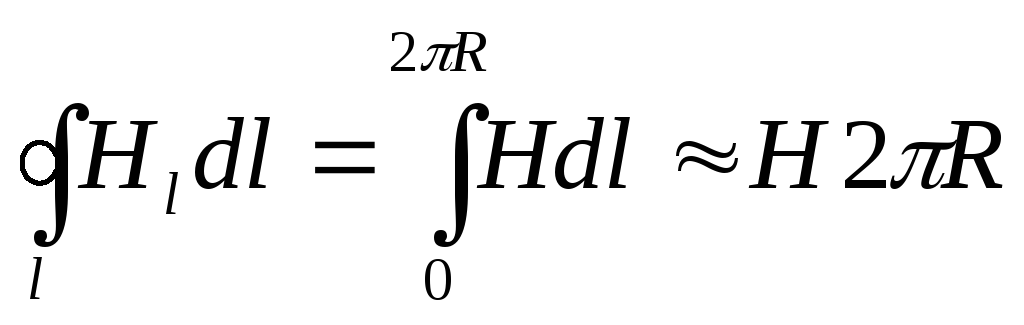 .
.
С
другой стороны, этот интеграл равен 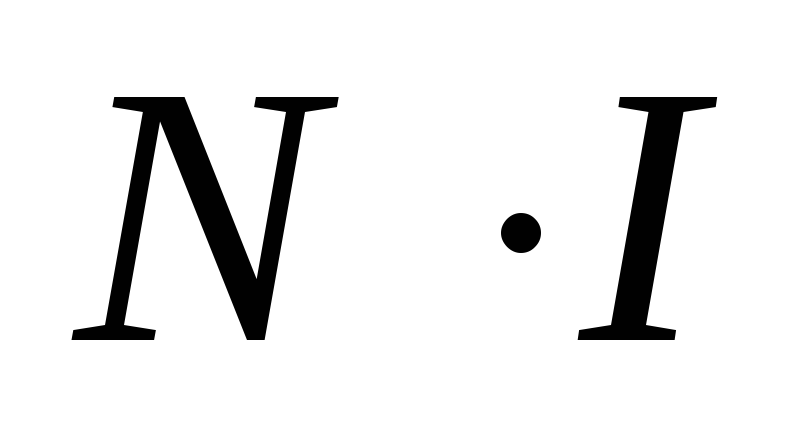 ,
откуда следует, что
,
откуда следует, что
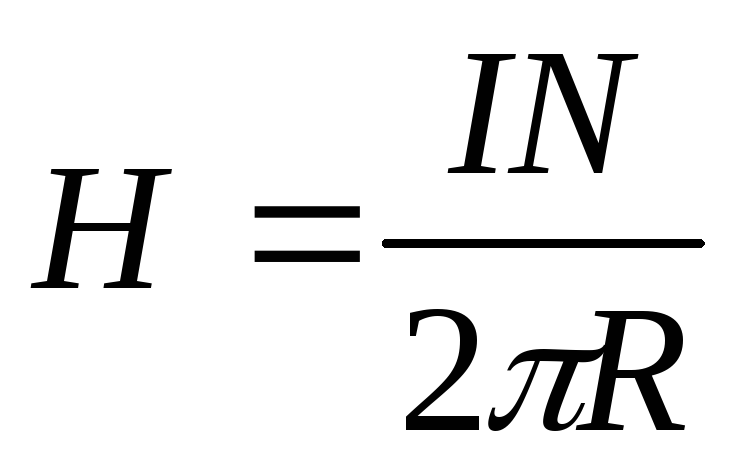 .
.
1) Система называется электрически изолированной, если через ограничивающую ее поверхность невозможен перенос зарядов, т.е. протекание электрического тока.


 по произвольному замкнутому контуру
и что она показывает?
по произвольному замкнутому контуру
и что она показывает?