РГР 2
Вопросы к защите РГР №2 по математике за 1 семестр.
Вектор — это направленный отрезок, который имеет начало и конец.
Длиной
ненулевого вектора 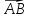 называется
длина отрезка AB.
называется
длина отрезка AB.
Нулевой вектор — вектор, начало которого совпадает с его концом.
Орты – единичный вектор.
Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Векторы называются компланарными, если существует плоскость, которой они параллельны.
Чтобы
сложить два вектора, нужно от конца
одного из них отложить второй вектор;
тогда сумма – это вектор с началом в
начале первого вектора и концом в конце
второго вектора: 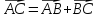
Разностью
двух векторов 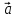 и
и 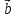 называется
такой третий вектор
называется
такой третий вектор 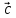 ,
который равен сумме векторов
,
который равен сумме векторов 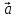 и
и 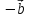
Проекцией вектора 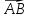 на
ось
l называется
длина его составляющей
на
ось
l называется
длина его составляющей 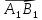 по
этой оси, взятая со знаком «+», если
по
этой оси, взятая со знаком «+», если  сонаправлен с l,
и со знаком «-»,если
сонаправлен с l,
и со знаком «-»,если 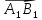 не
сонаправлен с l.
не
сонаправлен с l.
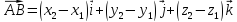


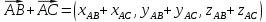
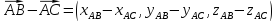
Два вектора называются равными, если они сонаправленные и имеют равные модули.
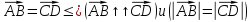
a={ax; ay; az} и b={bx; by; bz} коллинеарны если
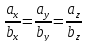
Радиус-вектор точки — называется вектор, начало которого совпадает с началом системы координат, а конец — с данной точкой.
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
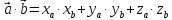
Для
перпендикулярности двух ненулевых
векторов 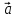 и
и 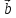 необходимо и достаточно, чтобы их
скалярное произведение равнялось нулю,
то есть, чтобы выполнялось равенство
необходимо и достаточно, чтобы их
скалярное произведение равнялось нулю,
то есть, чтобы выполнялось равенство 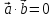 .
.
Необходимое
и достаточное условие перпендикулярности
двух векторов в координатах имеет вид  .
.
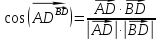
Векторным
произведением вектора  на
вектор
на
вектор  называется
третий вектор
называется
третий вектор 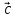 который
обладает следующими свойствами:
который
обладает следующими свойствами:
Его длина равна
 =
=
Вектор
 перпендикулярен
к плоскости, в которой лежат вектора
перпендикулярен
к плоскости, в которой лежат вектора  и
и 
Вектор
 направлен
так, что поворот от вектора
направлен
так, что поворот от вектора  к
вектору
к
вектору 
 (в
этом случае, говорят, что тройка
векторов
(в
этом случае, говорят, что тройка
векторов  и
и  –
правая).
–
правая).
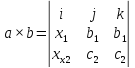
Геометрический смысл векторного произведения: модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах.
Смешанное произведение векторов a, b, c — скалярное произведение вектора a на векторное произведение векторов b и c.
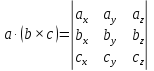
Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами a, b, c.
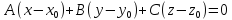
Ax + By + Cz + D = 0
Геометрическое значение коэффициентов A, B и C в общем уравнении плоскости Ax + By + Cz + D = 0 состоит в том, что они являются проекциями на координатные оси Ox, Oy, Oz вектора, перпендикулярного этой плоскости.
1) By + Cz + D = 0 — параллельна оси Ox;
2) Ax + Cz + D = 0 — параллельна оси Oy;
3) Ax + By + D = 0 — параллельна оси Oz;
4) Cz + D = 0 — параллельна оси Oxy;
5) By + D = 0 — параллельна оси Oxz;
6) Ax + D = 0 — параллельна оси Oyz;
7) Ax + By + Cz = 0 — проходит через начало координат;
8) By + Cz = 0 — проходит через ось Ox;
9) Ax + Cz = 0 — проходит через ось Oy;
10) Ax + By = 0 — проходит через ось Oz;
11) z = 0 — плоскость Oxy;
12) y = 0 — плоскость Oxz;
13) x = 0 — плоскость Oyz.
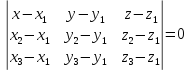
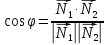
Две
плоскости параллельны тогда и только
тогда, когда их нормальные векторы
параллельны, а значит 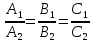 .
.
Две
плоскости перпендикулярны тогда и
только тогда, когда их нормальные векторы
перпендикулярны, а значит 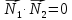
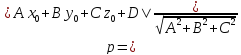
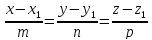
m, n, p – направляющий вектор прямой
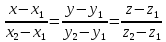
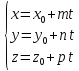
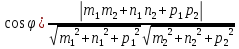
Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.
Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю (скалярное произведение).
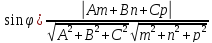
Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.
Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарные. Это условие выполняется, если векторное произведение этих векторов было равно нулю.
Привести уравнение прямой к параметрическому виду:
 ;
;
 ;
;

Подставить эти выражения в уравнение плоскости.
Из полученного найти t, а потом x,y и z.
Сумма и разность векторов
Для векторов a и b определим:
1). Сумму a+b как вектор c с координатами {ax+bx ; ay+by}.
2). Разность a –b как d вектор с координатами {ax – bx ; ay– by}.
3). Умножение вектора a на число k вектор с координатами {k · ax ; k · ay} и обозначаемый как k · a.
Сумма векторов
Сумму a+b векторов a и b можно вычислить по правилу параллелограммов.
Сперва сделаем чертеж этих векторов:
Для вычисления суммы a+b разместим начало вектора a на начало вектора b :
Теперь дополним эту схему до параллелограмма:
Сумма a+b будет вектор начало которого совпадает с началом вектора a а конец с концом вектора b:
По последней схеме сумма a+b равна диагонали параллелограмма поэтому это правило называется правилом параллелограмм.
Разность векторов
Разность a –b векторов a и b вычисляется по правилу треугольника:
Для этого сначала начертим эти векторы:
Объединим концы векторов a и b:
Разность a– b будет вектор у которого конец совпадает с началом вектора a а начало с началом вектора b:
math-public:vektory-slozhenie-vychitanie [Президентский ФМЛ №239]
$\newcommand{\updownarrows}{\uparrow\!\downarrow}$
Правило треугольника
Чтобы получить сумму векторов $\vec{a}$ и $\vec{b}$, нужно от какой-либо точки $A$ отложить вектор $\overrightarrow{AB}=\vec{a}$, затем от точки $B$ отложить вектор $\overrightarrow{BC}=\vec{b}$.
Вектор $\overrightarrow{AC}$ называется суммой векторов $\vec{a}$ и $\vec{b}$.
$\vec{a}+\vec{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$
Определение
Суммой двух векторов называется вектор, полученный по правилу треугольника.
Теорема
Определение суммы векторов корректно, то есть сумма векторов не зависит от выбора точки $A$.
Доказательство
Докажем, что если отложить вектор $a$ от точки $A_1$, то есть $\overrightarrow{A_1B_1}=\vec{a}$, а затем от точки $B_1$ отложить вектор $\overrightarrow{B_1C_1}=\vec{b}$, то сумма векторов $\overrightarrow{A_1B_1}+\overrightarrow{B_1C_1}=\overrightarrow{A_1C_1}$ будет равна вектору $\overrightarrow{AC}$, то есть $\overrightarrow{A_1C_1}=\overrightarrow{AC}$ (рис. \ref{pic133}).
Так как $\overrightarrow{AB}=\overrightarrow{A_1B_1}$, то по теореме \ref{133} имеем $\overrightarrow{AA_1}=\overrightarrow{BB_1}$.
Аналогично из равенства $\overrightarrow{B_1C_1}=\overrightarrow{BC}$ следует, что $\overrightarrow{BB_1}=\overrightarrow{CC_1}$.
Поэтому $\overrightarrow{AA_1}=\overrightarrow{CC_1}$.
Но из этого равенства по той же теореме \ref{133} следует, что $\overrightarrow{A_1C_1}=\overrightarrow{AC}$.
Правило параллелограмма
Если $ABCD$ – параллелограмм, то $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$
Доказательство
Так как $ABCD$ – параллелограмм, то $\overrightarrow{AD}=\overrightarrow{BC}$. Следовательно, $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.
Свойства сложения векторов
Для любых векторов $\vec{a}, \vec{b}$ и $\vec{c}$
$\vec{a}+\vec{0}=\vec{a}$.
$\vec{a}+\vec{b}=\vec{b}+\vec{a}$.
$(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$.
Доказательство
Первой свойство очевидно.
Докажем второе свойство.
Возможны два случая: $1)$ векторы $\vec{a}$ и $\vec{b}$ неколлинеарны, 2) вектора $\vec{a}$ и $\vec{b}$ коллинеарны.
Рассмотрим первый случай.
Пусть вектора $\vec{a}$ и $\vec{b}$ неколлинеарны.
Отложим их от точки $A$: $\overrightarrow{AB}=a$ и $\overrightarrow{AD}=b$ – и построим на этих векторах параллелограмм $ABCD$ (рис. \ref{pic136} a).
Поскольку $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}, \overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{AC}, \overrightarrow{AB}=\overrightarrow{DC}=\vec{a}$ и $\overrightarrow{BC}=\overrightarrow{AD}=\vec{b}$, то $\vec{a}+\vec{b}=\vec{b}+\vec{a}$.
Рассмотрим второй случай.
Пусть вектора $\vec{a}$ и $\vec{b}$ коллинеарны.
Если вектора $\vec{a}$ и $\vec{b}$ сонаправлены, то можно их последовательно отложить от точки $A$ двумя способами, то есть $\vec{a}+\vec{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, или $\vec{b}+\vec{a}=\overrightarrow{AB_1}+\overrightarrow{B_1C_1}=\overrightarrow{AC_1}$ (рис. \ref{pic136} b).
Докажем, что $\overrightarrow{AC}=\overrightarrow{AC_1}$.
Вектора $\overrightarrow{AC}$ и $\overrightarrow{AC_1}$ очевидно сонаправлены, кроме того их модули равны $|\vec{a}|+|\vec{b}|$.
Следовательно, эти вектора равны.
Рассмотрим случай, когда вектора $\vec{a}$ и $\vec{b}$ противоположно направлены (рис. \ref{pic136} c).
Пусть кроме того $|\vec{a}|>|\vec{b}|$.
Тогда $\vec{a}+\vec{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, при этом $|\overrightarrow{AC}|=|\vec{a}|-|\vec{b}|$.
C другой стороны $\vec{b}+\vec{a}=\overrightarrow{AB_1}+\overrightarrow{B_1C_1}=\overrightarrow{AC_1}$, при этом $|\overrightarrow{AC_1}|=|\vec{a}|-|\vec{b}|$.
Таким образом модули векторов $\overrightarrow{AC}$ и $\overrightarrow{AC_1}$ равны, кроме того они сонаправлены, следовательно, $\overrightarrow{AC}=\overrightarrow{AC_1}$.
Докажем третий пункт теоремы.
Отложим от точки $A$ вектор $\overrightarrow{AB}=\vec{a}$, затем от точки $B$ вектор $\overrightarrow{BC}=\vec{b}$, а потом от точки $C$ вектор $\overrightarrow{CD}=\vec{c}$ (рис. \ref{pic136} d).
Тогда $(\vec{a}+\vec{b})+\vec{c}=(\overrightarrow{AB}+\overrightarrow{BC})+\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}$.
C другой стороны, $\vec{a}+(\vec{b}+\vec{c})=\overrightarrow{AB}+(\overrightarrow{BC}+\overrightarrow{CD})=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AD}$. Итак $(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$.
Правило цепочки
При любом расположении точек $A_1, A_2, A_3, \ldots, A_n$ верно равенство $\overrightarrow{A_1A_2}+\overrightarrow{A_2A_3}+\ldots+\overrightarrow{A_{n-1}A_n}=\overrightarrow{A_1A_n}$
Определение
Два ненулевых вектора называются противоположными, если их длины равны и они противоположны по направлению. Ноль-вектор считается противоположным самому себе (рис. \ref{pic137}).
Теорема
$\vec{a}+(-\vec{a})=\vec{0}$.
Если $\vec{a}+\vec{b}=\vec{0}$, то $\vec{a}=-\vec{b}$.
Доказательство
Докажем первый пункт.
Пусть $\vec{a}=\overrightarrow{AB}$.
Тогда $-\vec{a}=\overrightarrow{BA}$.
Следовательно, $\vec{a}+(-\vec{a})=\overrightarrow{AB}+\overrightarrow{BA}=\overrightarrow{AA}=\vec{0}$.
Докажем второй пункт.
Пусть $\vec{a}+\vec{b}=\vec{0}$.
Тогда, если $\vec{a}=\overrightarrow{AB}$, то поскольку $\vec{0}=\overrightarrow{AA}$, то $\vec{b}=\overrightarrow{BA}$.
Таким образом, вектора $\vec{a}$ и $\vec{b}$ равны по модулю и противоположны по направлению, то есть векторы $\vec{a}$ и $\vec{b}$ противоположны.
Разность векторов
Разностью векторов $\vec{a}$ и $\vec{b}$ называется такой вектор $\vec{c}$, что $\vec{c}+\vec{b}=\vec{a}$. Принято обозначать $\vec{c}=\vec{a}-\vec{b}$.
Следствие
$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$.
Теорема
Для любых двух векторов $\vec{a}$ и $\vec{b}$ справедливо равенство $\vec{a}-\vec{b}=\vec{a}+(-\vec{b})$.
Доказательство
Пусть $\vec{c}=\overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}=\vec{a}-\vec{b}$.
По правилу треугольника $\overrightarrow{BA}=\overrightarrow{BO}+\overrightarrow{OA}$.
Кроме того $\overrightarrow{BO}=-\overrightarrow{OB}=-\vec{b}$.
Поэтому $\vec{a}- \vec{b}=\overrightarrow{BA}=\overrightarrow{BO}+\overrightarrow{OA}=\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{OA}+(-\overrightarrow{OB})=\vec{a}+(-\vec{b})$.
math-public/vektory-slozhenie-vychitanie.txt · Последние изменения: 2016/10/26 13:28 — labreslav
Какой вектор называется суммой двух векторов

 Для правильного отображения законов природы в физике требуется соответствующий математический инструментарий.
Для правильного отображения законов природы в физике требуется соответствующий математический инструментарий.
В геометрии и физике есть величины, характеризующиеся и числовым значением, и направлением.
Их целесообразно изображать направленными отрезками или векторами.
…
Вконтакте
Google+
Мой мир
У таких величин есть начало (отображается точкой) и конец, обозначаемый стрелкой. Длина отрезка называется модулем (длиной).
Примеры:
- скорость;
- ускорение;
- импульс;
- сила;
- момент;
- силы;
- перемещение;
- напряженность поля и др.
Это интересно: как переводить градусы в радианы?
Координаты на плоскости
Зададим на плоскости отрезок, направленный из точки, А (x1,y1) в точку В (x2,y2). Его координатами a (a1, a2) являются числа а1=x2-x1, а2=y2-y1.
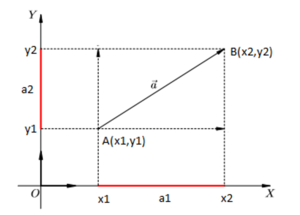

Модуль рассчитывается по теореме Пифагора: 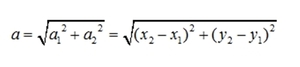
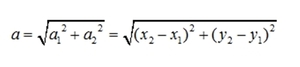
У нулевого вектора начало совпадает с концом. Координаты и длина равны 0.
Сумма векторов
Существуют несколько правил для расчета суммы
- правило треугольника;
- правило многоугольника ;
- правило параллелограмма.
Правило сложения векторов можно объяснить на задачах из динамики и механики. Рассмотрим сложение векторов по правилу треугольника на примере сил, воздействующих на точечное тело и последовательных перемещений тела в пространстве.
Допустим, тело переместилось сначала из точки A в точку B, а затем из точки B в точку C. Итоговое перемещение есть отрезок, направленный от начальной точки A к конечной точке C.
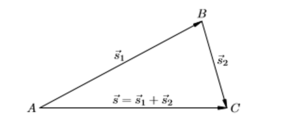

Результат двух перемещений или их сумма s = s1+ s2. Такой способ называется правилом треугольника.
Стрелки выстраивают в цепочку одну за другой, при необходимости осуществляя параллельный перенос. Суммарный отрезок замыкает последовательность. Его начало совпадает с началом первого, конец — с концом последнего. В иностранных учебниках данный метод называется «хвост к голове».
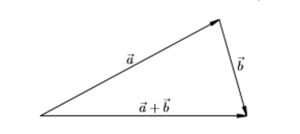

Координаты результата c = a + b равны сумме соответствующих координат слагаемых c (a1+ b1, a2+ b2).
Сумма параллельных (коллинеарных) векторов также определяется по правилу треугольника.
Если два исходных отрезка перпендикулярны друг другу, то результат их сложения представляет собой гипотенузу построенного на них прямоугольного треугольника. Длина суммы вычисляется по теореме Пифагора.
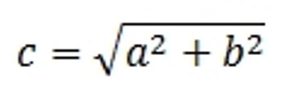
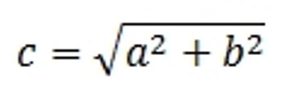
Примеры:
- Скорость тела, брошенного горизонтально, перпендикулярна ускорению свободного падения.
- При равномерном вращательном движении линейная скорость тела перпендикулярна центростремительному ускорению.
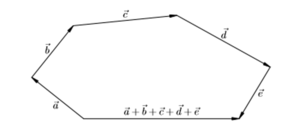
Сложение трех и более векторов производят по правилу многоугольника, «хвост к голове»

Предположим, что к точечному телу приложены силы F1 и F2.
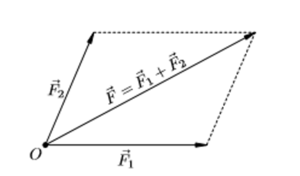

Опыт доказывает, что совокупное воздействие этих сил равнозначно действию одной силы, направленной по диагонали построенного на них параллелограмма. Эта равнодействующая сила равна их сумме F = F1 + F 2. Приведенный способ сложения называется правилом параллелограмма.
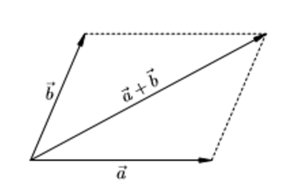

Длина в этом случае вычисляется по формуле
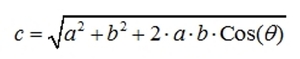
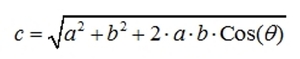
, где θ — угол между сторонами.
Правила треугольника и параллелограмма взаимозаменяемы. В физике чаще применяют правило параллелограмма, так как направленные величины сил, скоростей, ускорений обычно приложены к одному точечному телу. В трехмерной системе координат применяется правило параллелепипеда.
Обратите внимание: что такое луч в геометрии.
Элементы алгебры
- Сложение является двоичной операцией: за один раз можно сложить только пару.
- Коммутативность: сумма от перестановки слагаемых не изменяется a + b = b + a. Это ясно из правила параллелограмма: диагональ всегда одна и та же.
- Ассоциативность: сумма произвольного числа векторов не зависит от порядка их сложения (a + b)+ c = a +(b + c).
- Суммирование с нулевым вектором не меняет ни направление, ни длину: a +0= a .
- Для каждого вектора есть противоположный. Их сумма равна нулю a +(-a)=0, а длины совпадают.
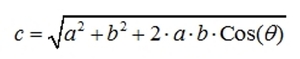
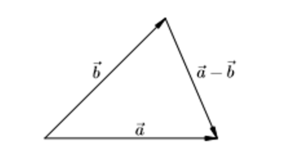
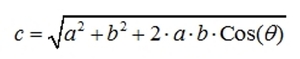 Вычитание направленного отрезка равносильно прибавлению противоположного. Координаты равны разности соответствующих координат. Длина равна:
Вычитание направленного отрезка равносильно прибавлению противоположного. Координаты равны разности соответствующих координат. Длина равна:
Для вычитания можно использовать видоизмененное правило треугольника.

Умножение на скаляр
Результатом умножения на скаляр будет вектор.
Координаты произведения получаются перемножением на скаляр соответствующих координат исходного.
Скаляр — числовая величина со знаком плюс или минус, больше или меньше единицы.
Примеры скалярных величин в физике:
- масса;
- время;
- заряд ;
- длина;
- площадь;
- объем;
- плотность;
- температура;
- энергия.
Примеры:
- Перемещение равномерно движущегося тела равно произведению времени и скорости s = vt .
- Импульс тела — масса, умноженная на скорость p = mv .
- Второй закон Ньютона. Произведение массы тела на ускорение равно приложенной равнодействующей силе ma=F.
- Сила, действующая на заряженную частицу в электрическом поле, пропорциональна заряду F = qE.
Скалярное произведение направленных отрезков a и b равно произведению модулей на косинус угла между ними. Скалярное произведение взаимно перпендикулярных отрезков равно нулю.
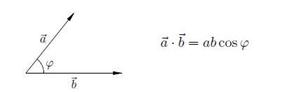
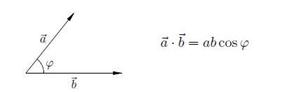
Пример:
Работа является скалярным произведением силы и перемещения A = Fs .


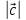 =
=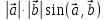
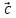 перпендикулярен
к плоскости, в которой лежат вектора
перпендикулярен
к плоскости, в которой лежат вектора 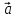 и
и 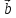
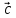 направлен
так, что поворот от вектора
направлен
так, что поворот от вектора 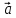 к
вектору
к
вектору 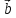
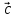 (в
этом случае, говорят, что тройка
векторов
(в
этом случае, говорят, что тройка
векторов 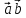 и
и 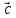 –
правая).
–
правая).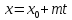 ;
;
 ;
;