§ 5. Скалярное произведение и его свойства
1. Определение скалярного произведения
Определение. Скалярным
произведением 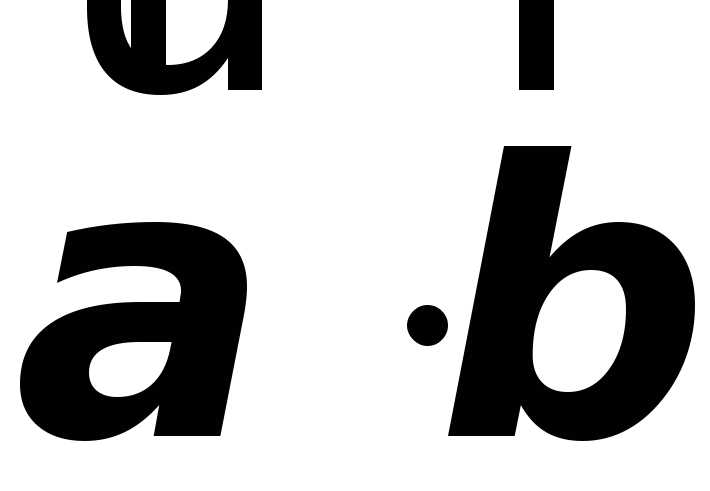 двух ненулевых векторов
двух ненулевых векторов и
и называется
число, равное произведению длин этих
векторов на косинус угла между ними,
т.е.
называется
число, равное произведению длин этих
векторов на косинус угла между ними,
т.е.
 .
.
Если хотя бы один из векторов равен нулю, то скалярное произведение этих векторов равно нулю (по определению).
Если 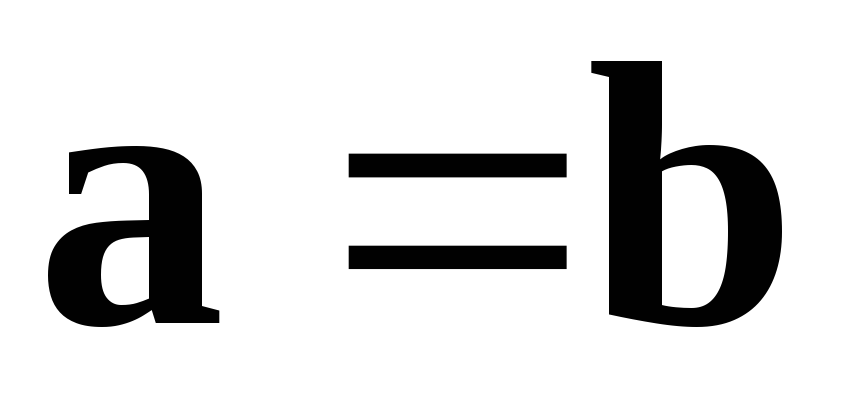 ,
то
,
то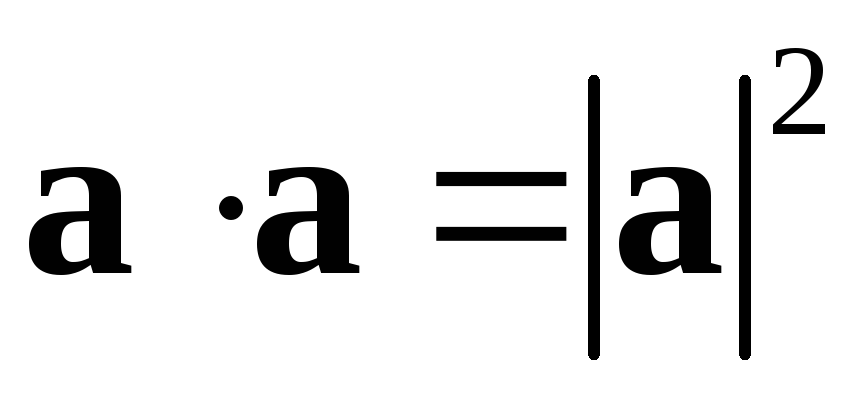
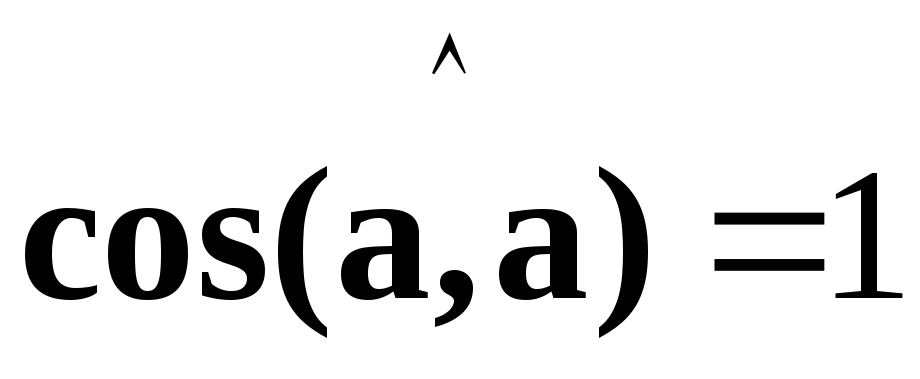 .
.Отсюда
следует, что 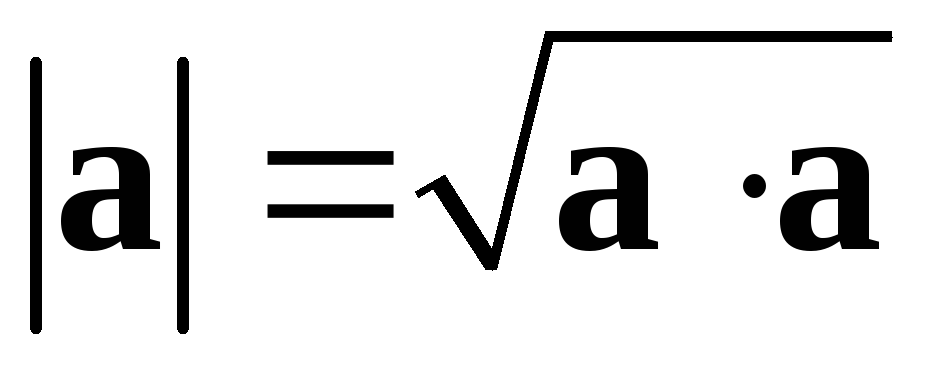 .
.
Заметим,
что скалярное произведение 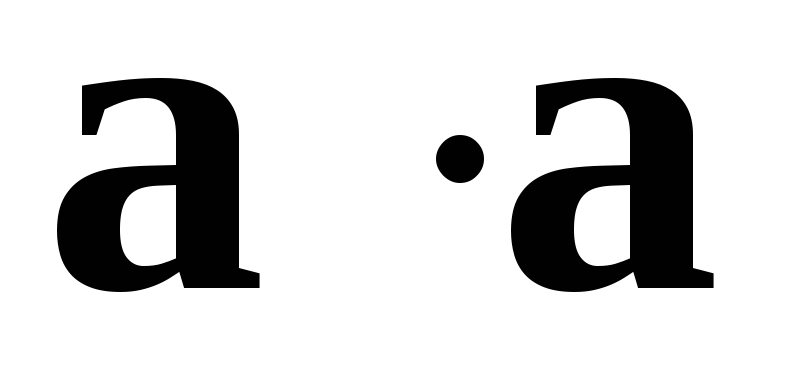 называется скалярным квадратом и
обозначается
называется скалярным квадратом и
обозначается .
Следовательно,
.
Следовательно,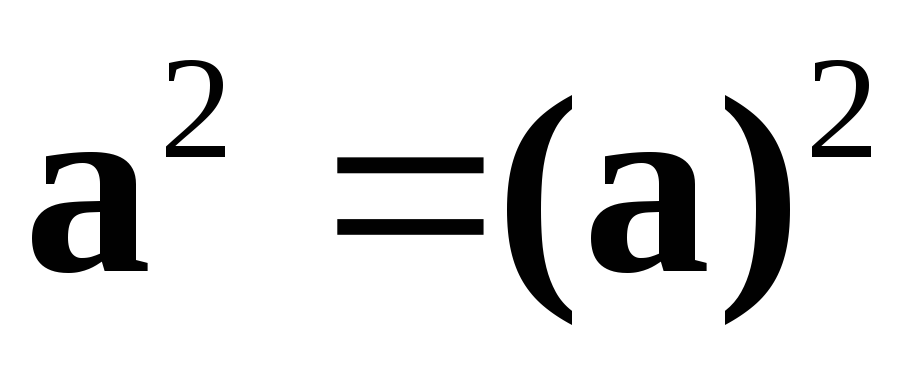 =>
=> 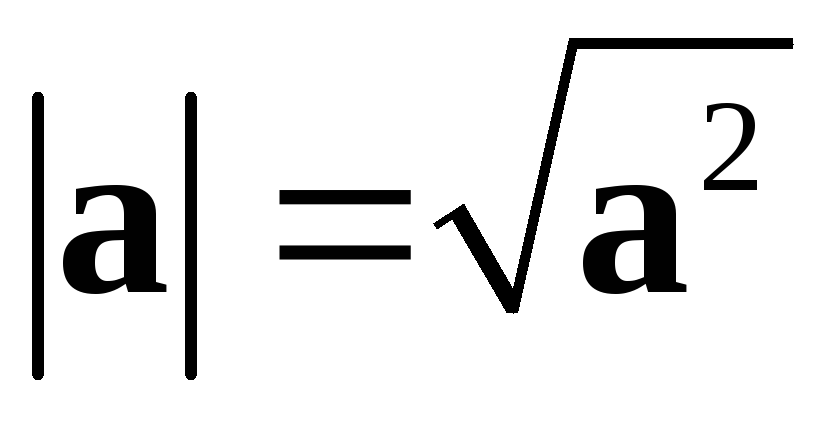
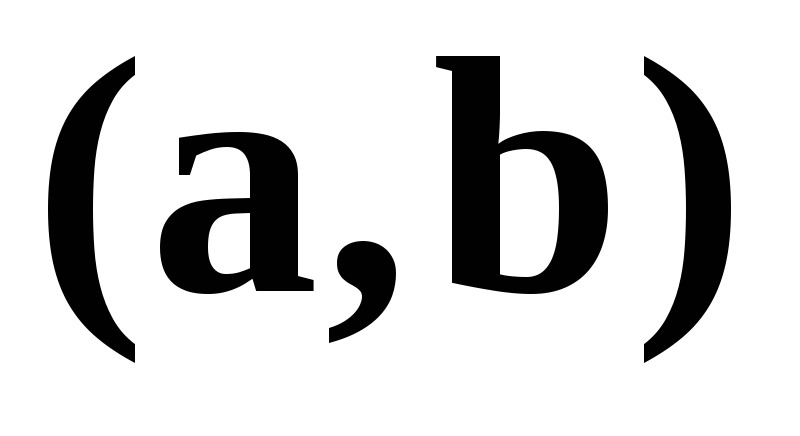 .
.Свойства скалярного произведения
 пр
пр пр
пр
Действительно, пр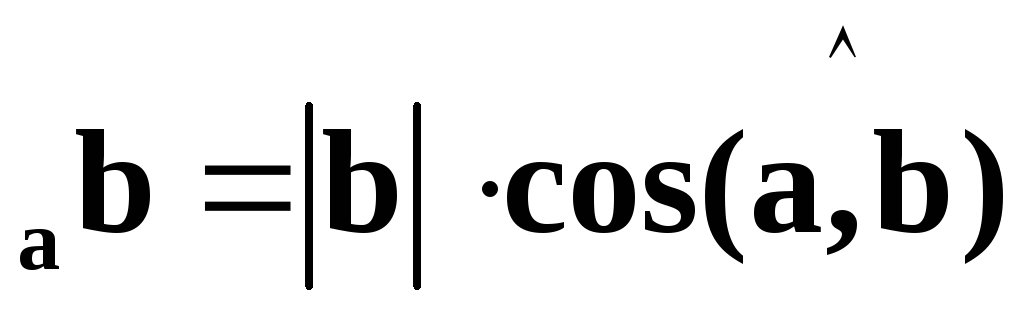
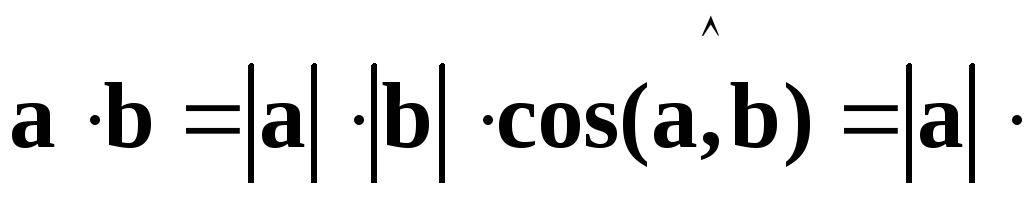 пр
пр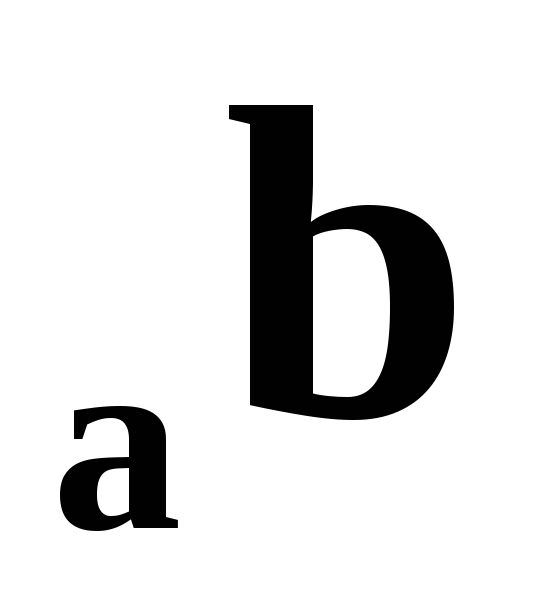 ,отсюда следует, что пр
,отсюда следует, что пр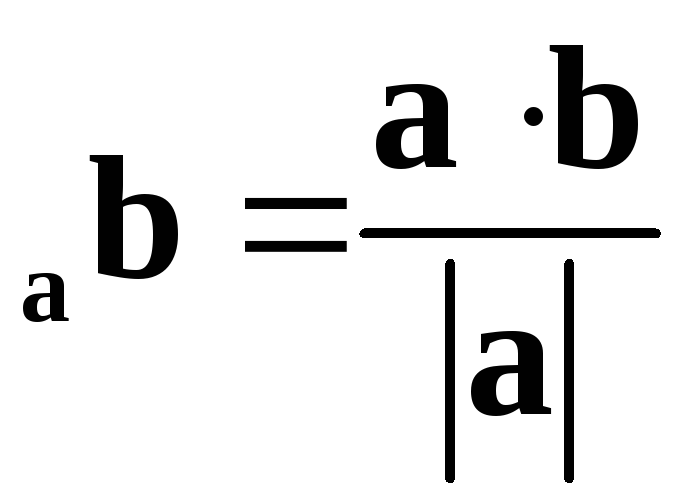 .
.Переместительноеиликоммутативноесвойство:
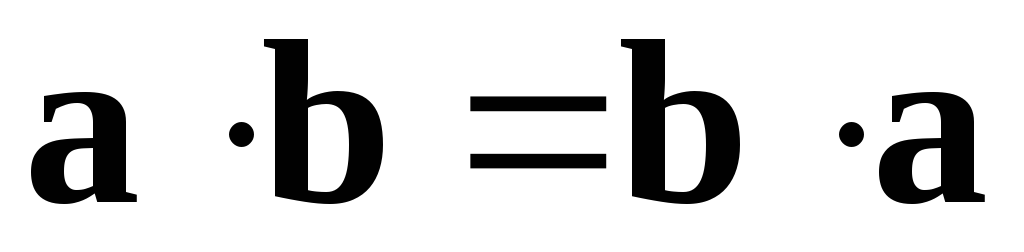 .
.
Это свойство
очевидно, так как 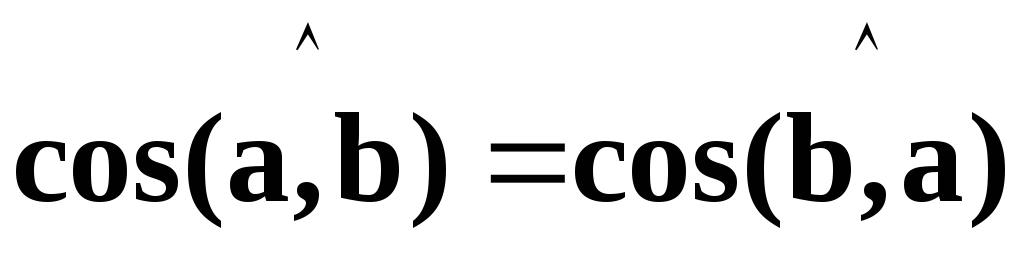
Сочетательноеилиассоциативноесвойство относительно числового множителя
 :
:
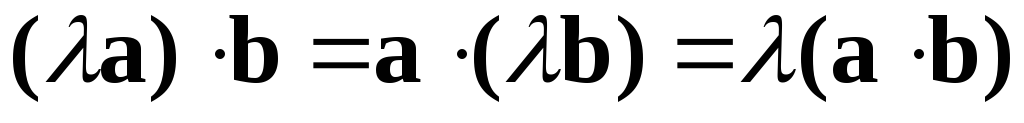
Распределительноеилидистрибутивноесвойство относительного сложения векторов:
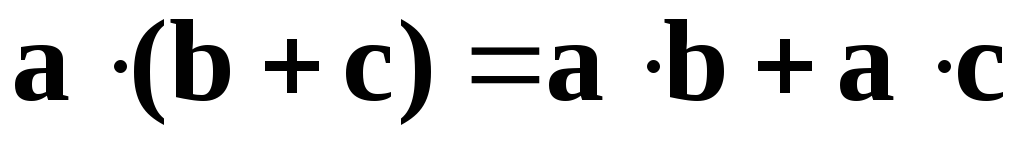 .
.
Доказательство
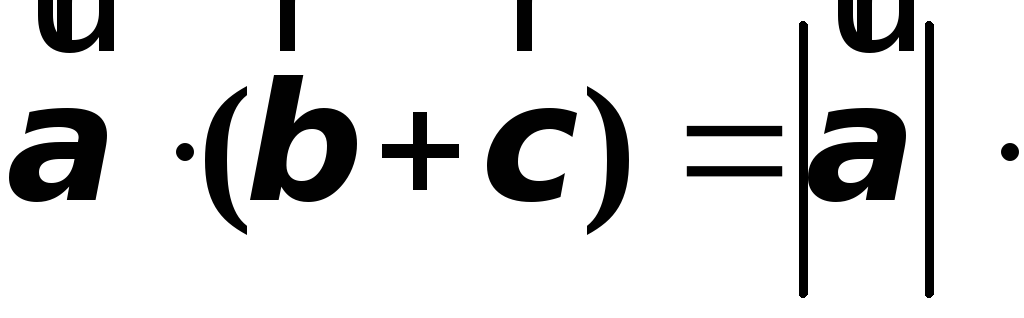 пр
пр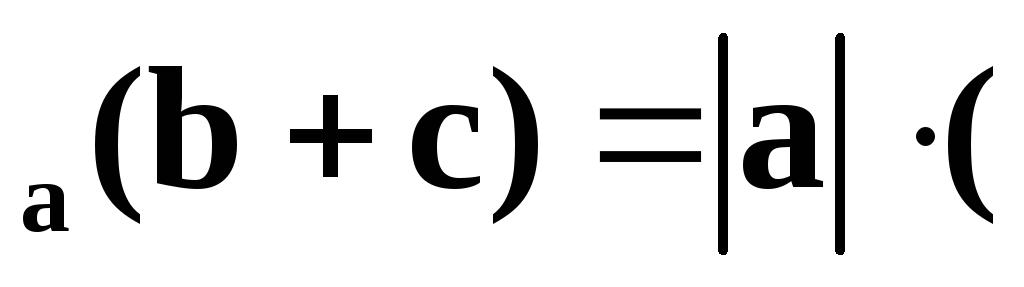 пр
пр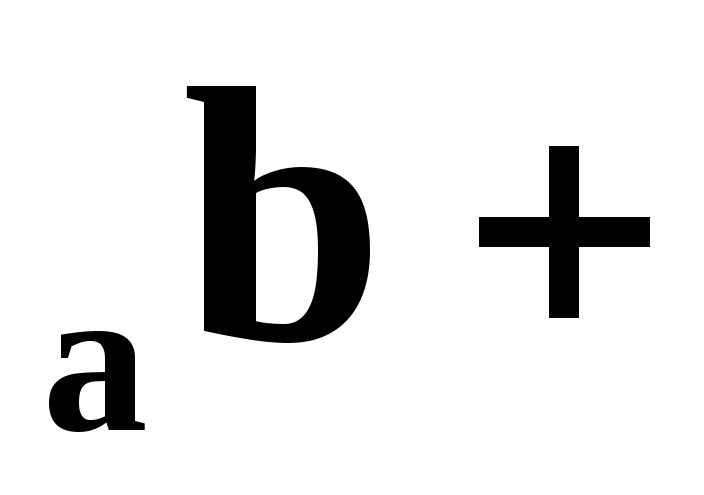 пр
пр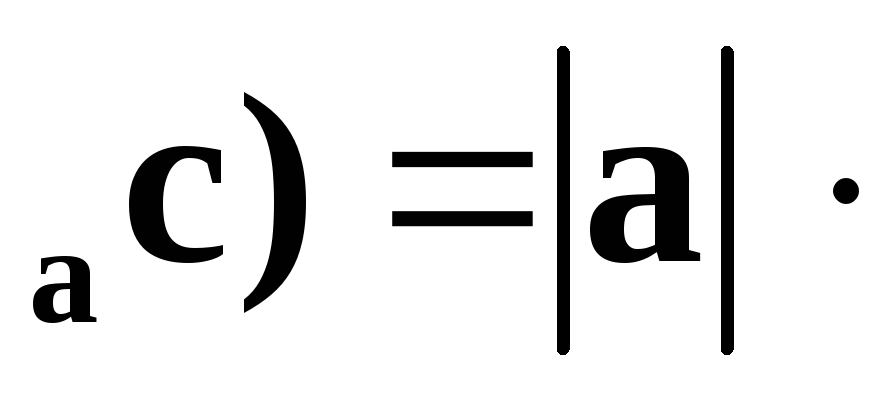 пр
пр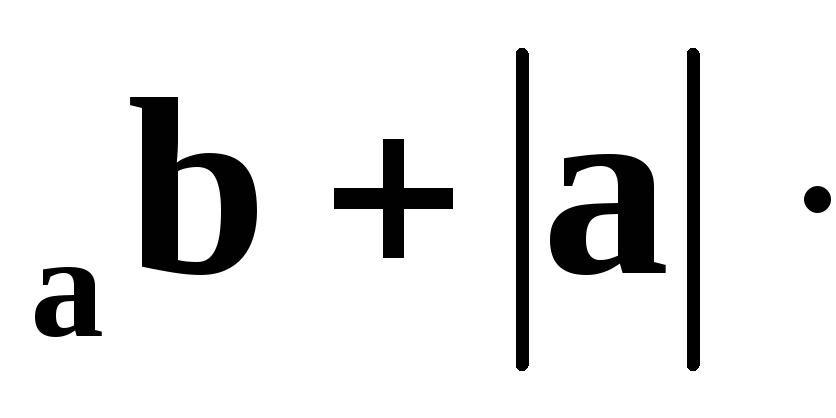 пр
пр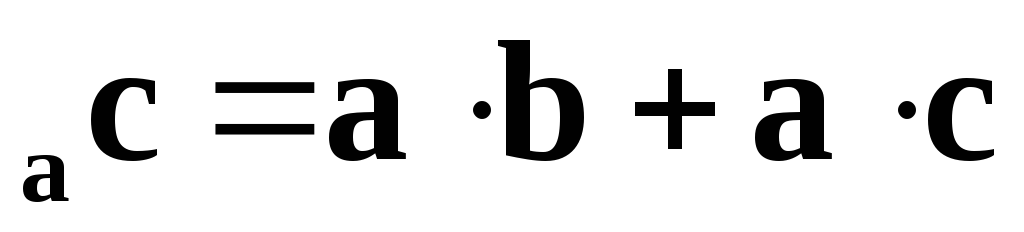
Следствие. 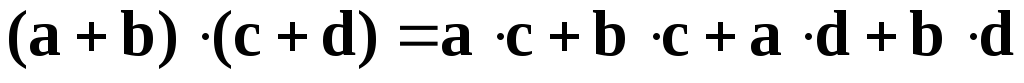
2. Необходимое и достаточное условие ортогональности двух векторов
Напомним,
что два ненулевых вектора  и
и называются ортогональными, если они
образуют прямой угол, т.е.
называются ортогональными, если они
образуют прямой угол, т.е.
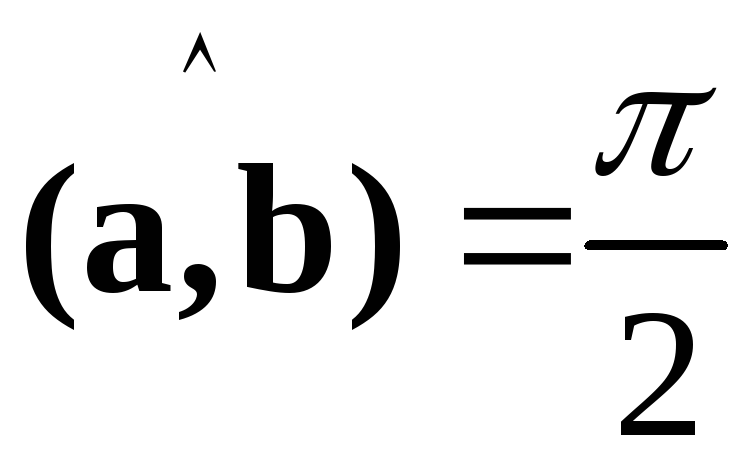 .
.
Теорема.Для того, чтобы два ненулевых вектора были ортогональны, необходимо и достаточно, чтобы их скалярное произведение обращалось в нуль.
Доказательство. Необходимость. Пусть
векторы
 ортогональны,
тогда
ортогональны,
тогда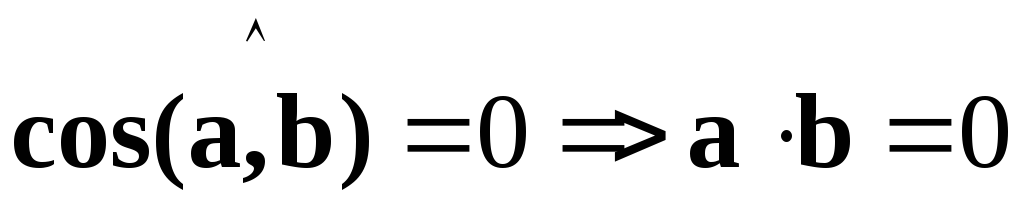 .
.Достаточность.
Пусть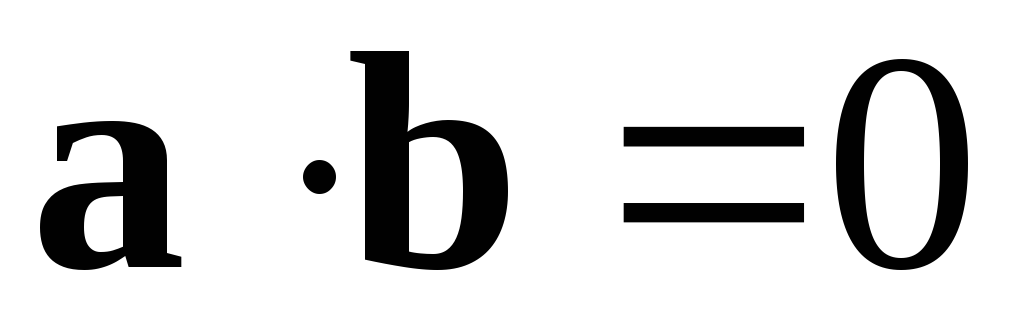 .
Так как векторы ненулевые, то отсюда
следует, что
.
Так как векторы ненулевые, то отсюда
следует, что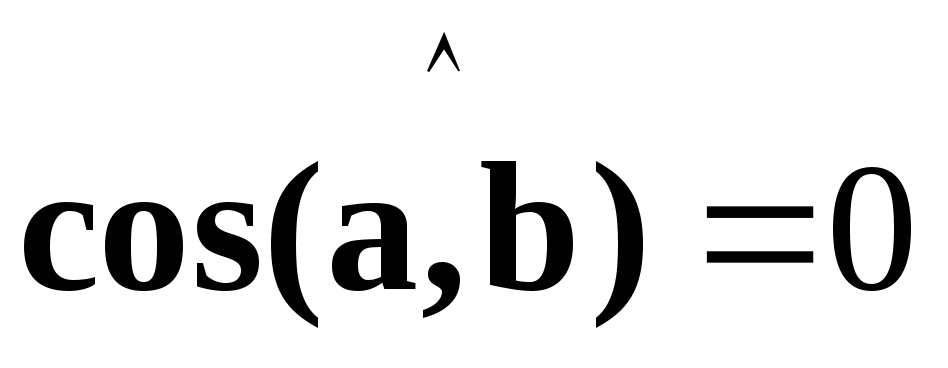 ,
а это и означает, что векторы
,
а это и означает, что векторы и
и
3. Скалярное произведение векторов, заданных своими координатами
Пусть 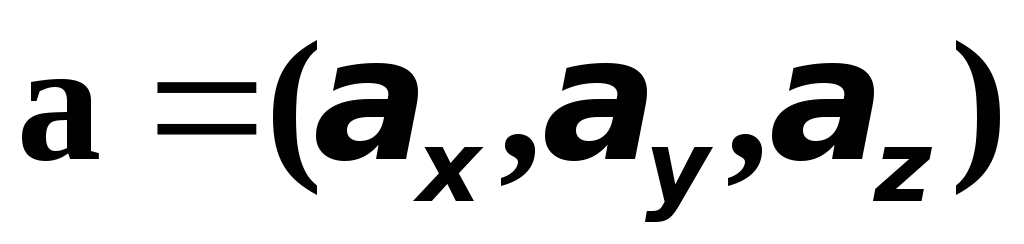 ,
,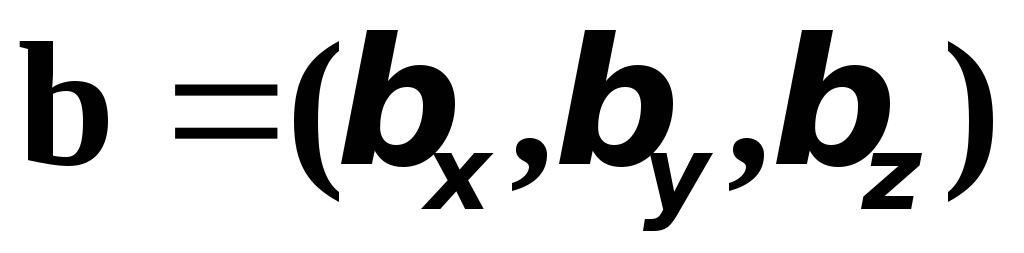 .
Очевидно, что
.
Очевидно, что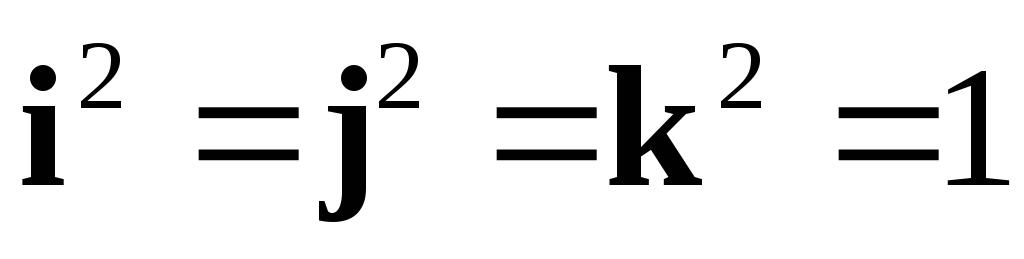 ;
; ;
;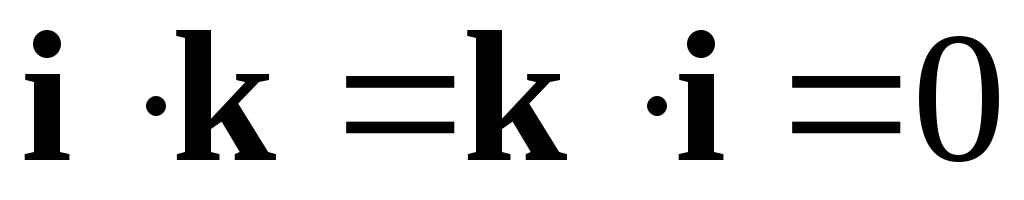 ;
;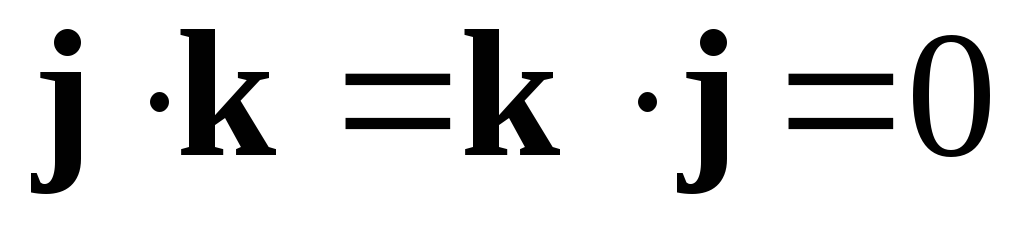
В силу свойства 4 получим
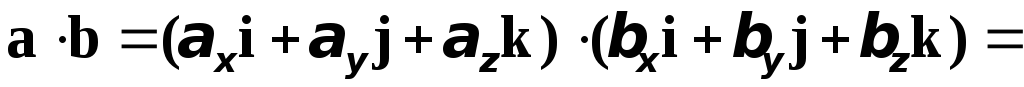
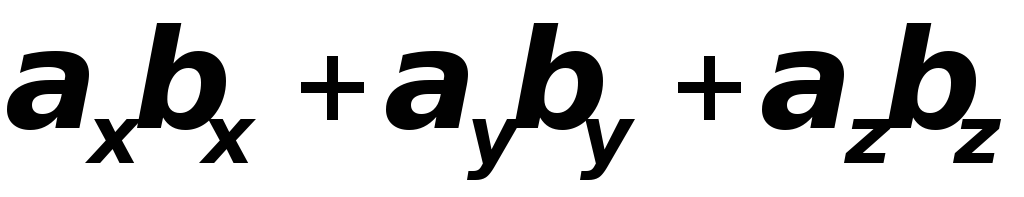 .
.
В частности,
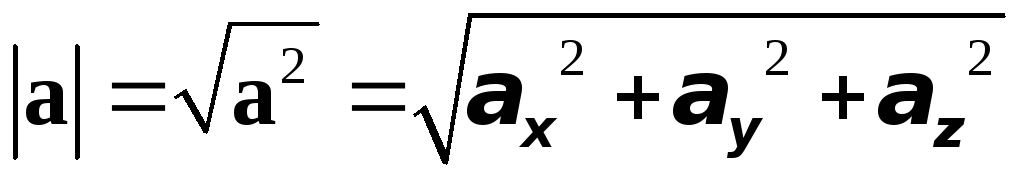 .
.
4. Угол между двумя векторами
Если  и
и — ненулевые векторы, то, принимая во
внимание определение вектора и п.4,
получим такое выражение для угла
— ненулевые векторы, то, принимая во
внимание определение вектора и п.4,
получим такое выражение для угла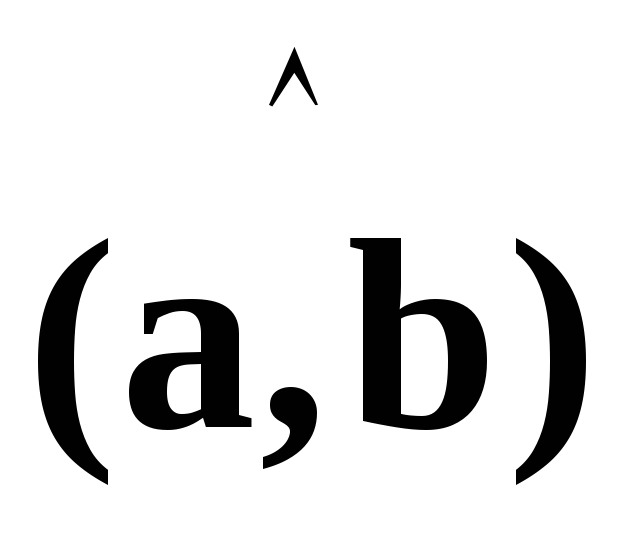 между векторамиaиb:
между векторамиaиb:
 .
.
Отсюда нетрудно получить условие
ортогональности (перпендикулярности)
двух векторов в координатной форме: 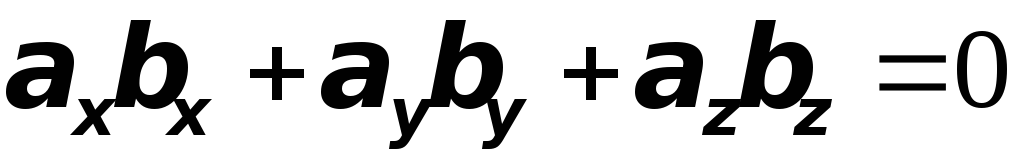
Механический смысл скалярного произведения
Если  — сила, действующая на перемещенииS,
то работаAэтой силы
на указанном перемещении, как известно,
равна
— сила, действующая на перемещенииS,
то работаAэтой силы
на указанном перемещении, как известно,
равна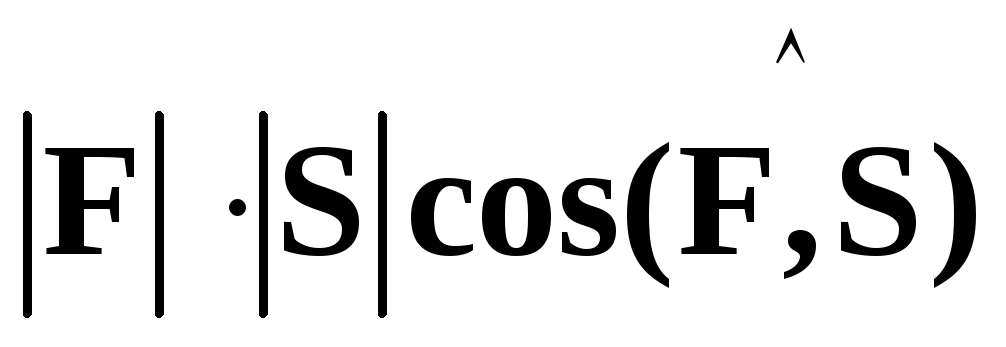 ,
т.е.
,
т.е.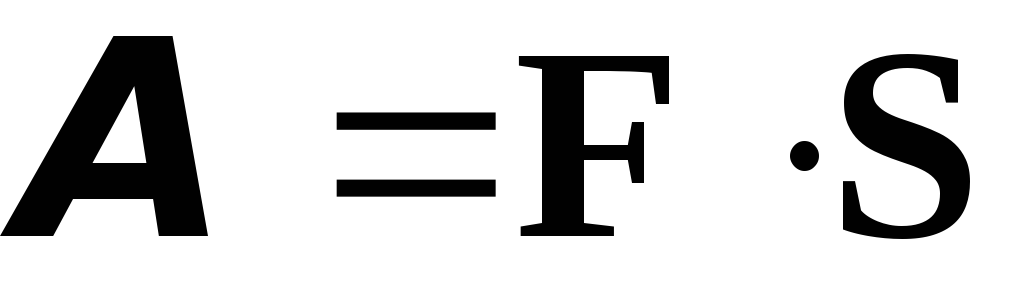 (рис. 3.5.1).
(рис. 3.5.1).


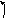



Рис. 3.5.1
Пример
1. Даны
три точки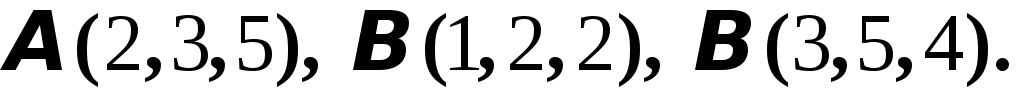
Найти 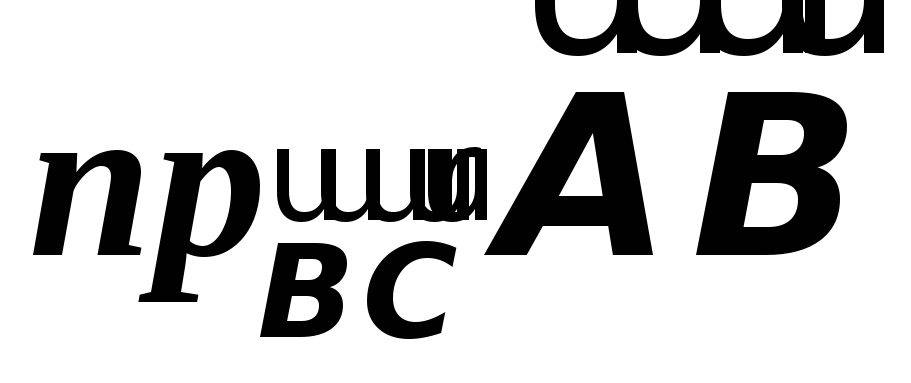
 .
.Решение.а)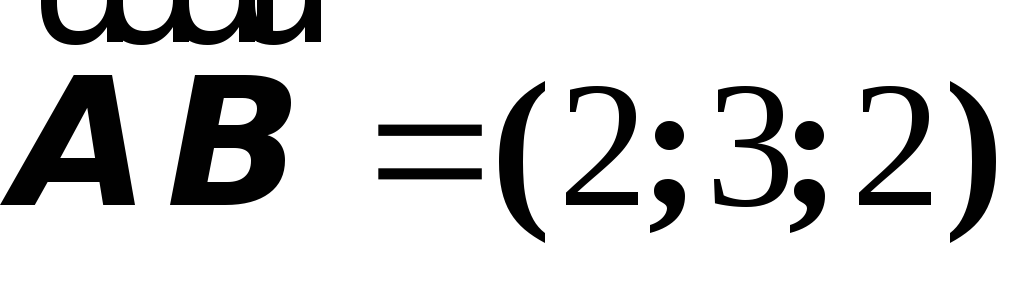 ;
; 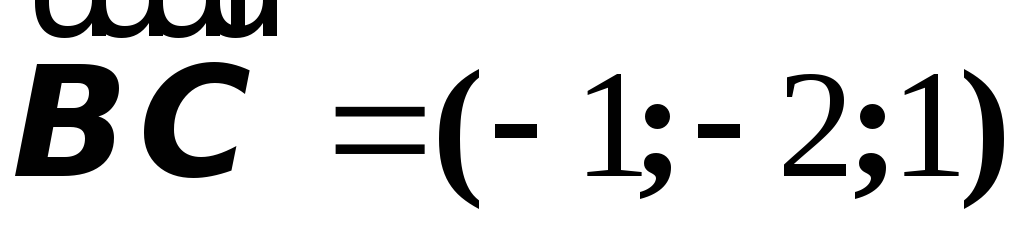
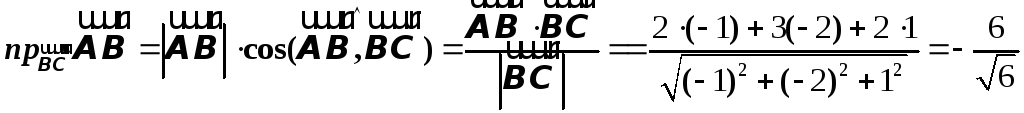
б)  ;
;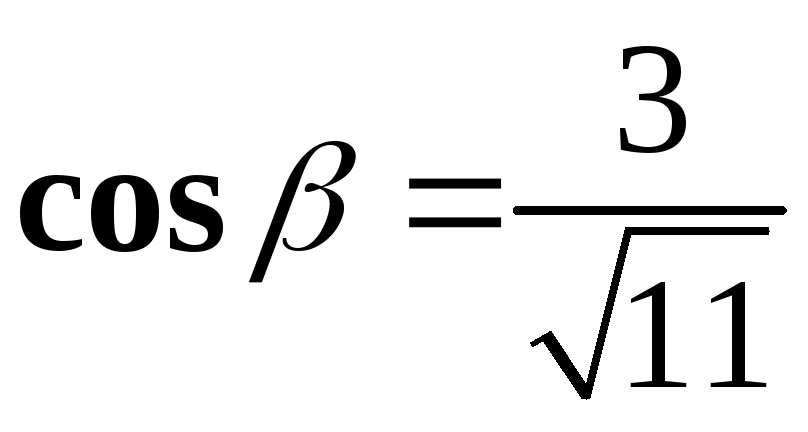
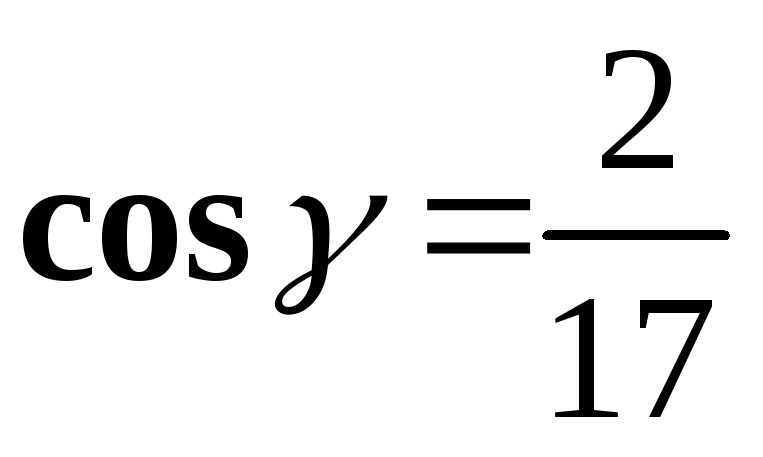
Пример
2. Дан
вектор ,
,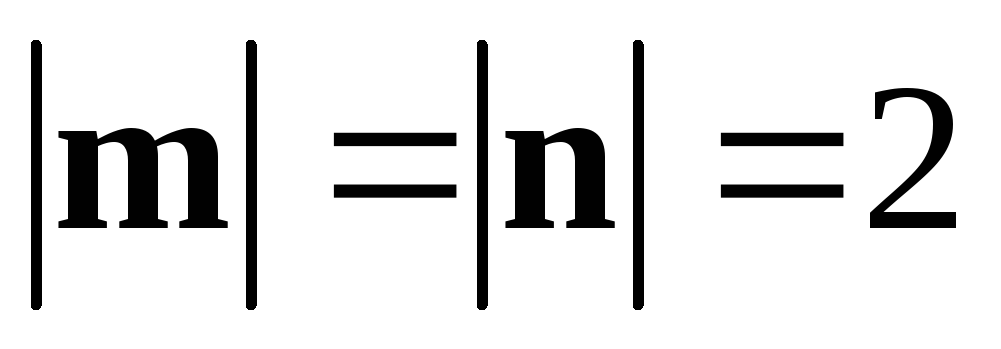 ,
,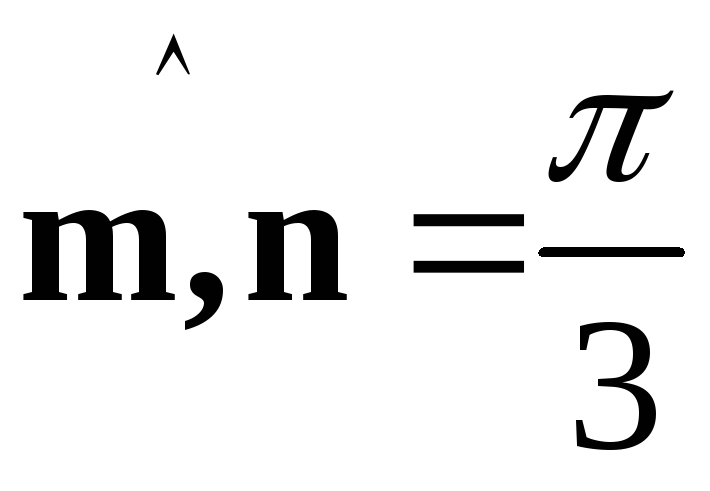 .
.
Найти
длину вектора  .
.
Решение.Найдём скалярный квадрат вектора :
: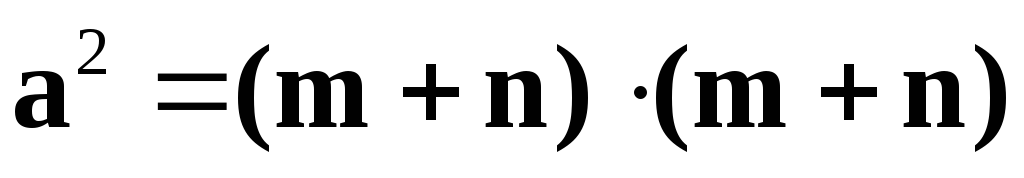 .
Раскроем скобки, пользуясь свойствами
скалярного произведения:
.
Раскроем скобки, пользуясь свойствами
скалярного произведения:
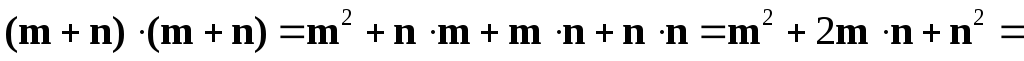
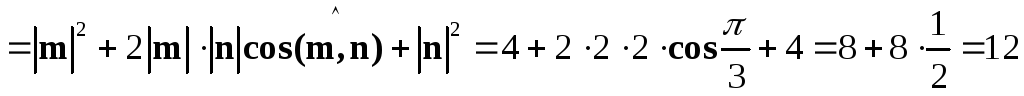 .
. 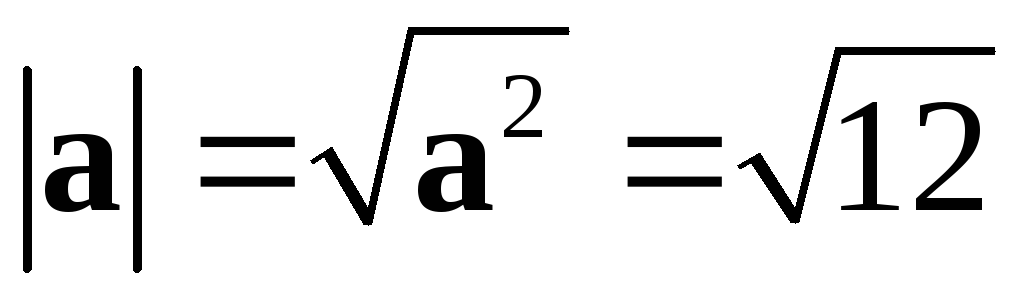
Пример
3. При каком значении вектора
вектора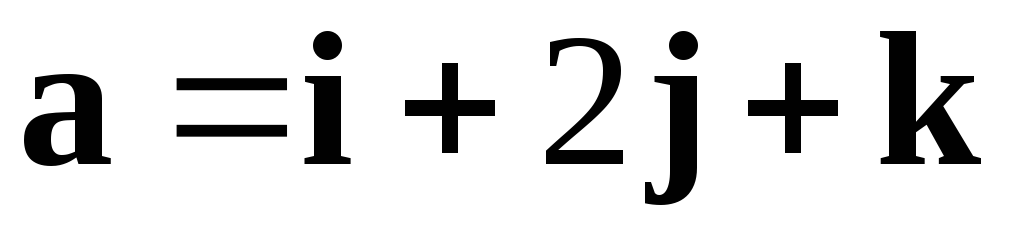 и
и ортогональны.
ортогональны.
Решение. Принимая во внимание условие
ортогональности двух векторов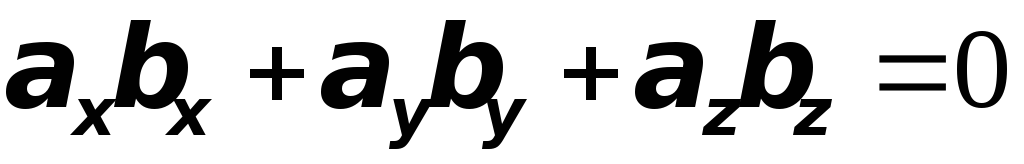 ,
получим
,
получим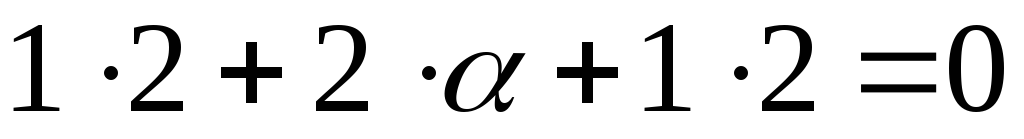 .
Следовательно
.
Следовательно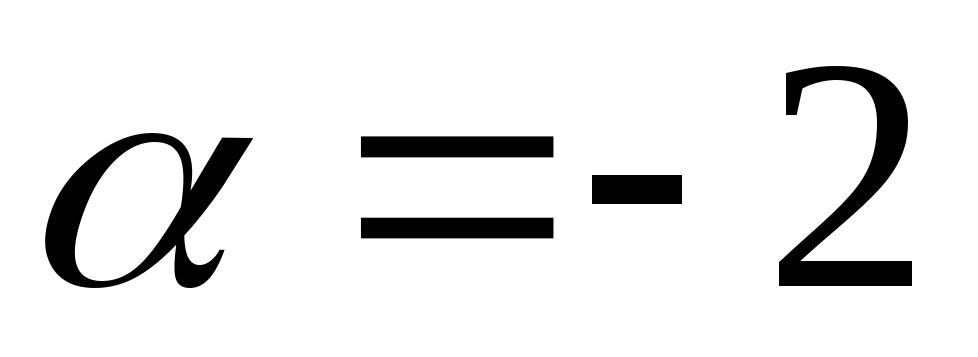 .
.
§ 6. Векторное произведение и его свойства
1. Определение векторного произведения
Определение. Векторным
произведением 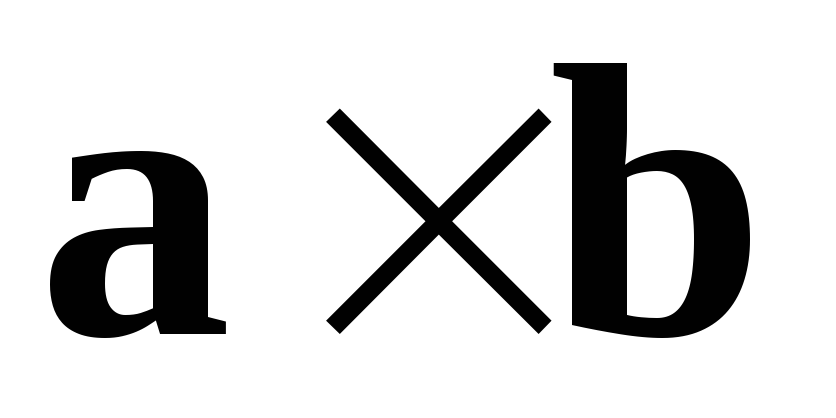 ненулевых векторов
ненулевых векторов  и
и  называется такой вектор
называется такой вектор ,
который удовлетворяет трём условиям:
,
который удовлетворяет трём условиям:
1. 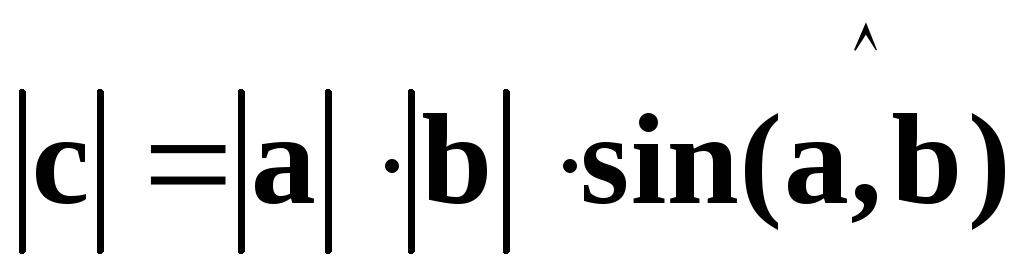 ,
т.е. длина вектора
,
т.е. длина вектора 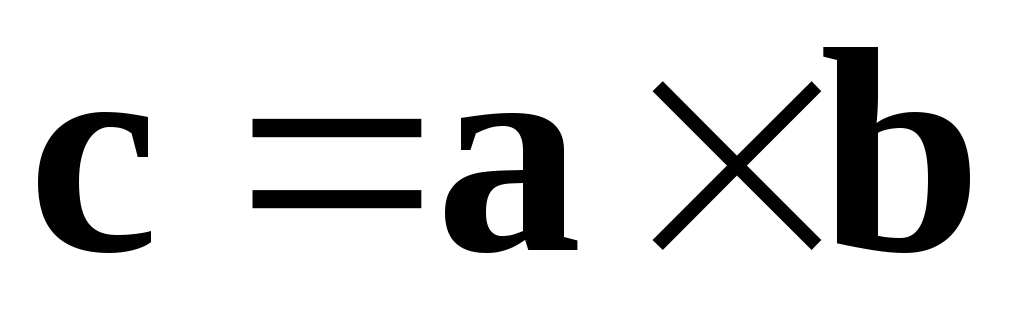 численно равна площади параллелограмма,
построенного на этих векторах.
численно равна площади параллелограмма,
построенного на этих векторах.
2.
Вектор  перпендикулярен плоскости, в которой
лежат векторы
перпендикулярен плоскости, в которой
лежат векторы  и
и  .
.
3.
Тройка  ,
, ,
, — правая(рис.
2.6.1)
— правая(рис.
2.6.1)
Если хотя бы один из векторов  и
и  нулевой, то по определению
нулевой, то по определению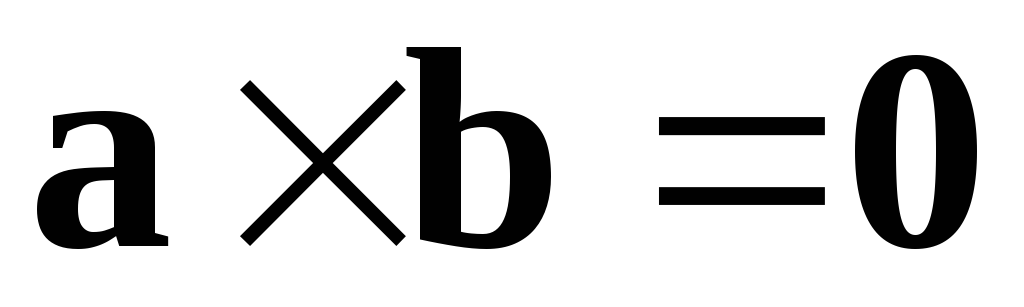 .
Заметим, что иногда векторное произведение
двух векторови
.
Заметим, что иногда векторное произведение
двух векторови обозначается символом
обозначается символом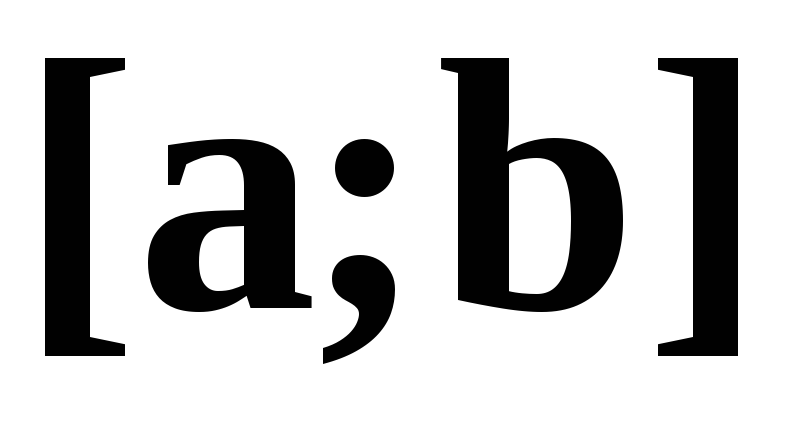 .
.






Рис. 2.6.1
Свойства векторного произведения
1. 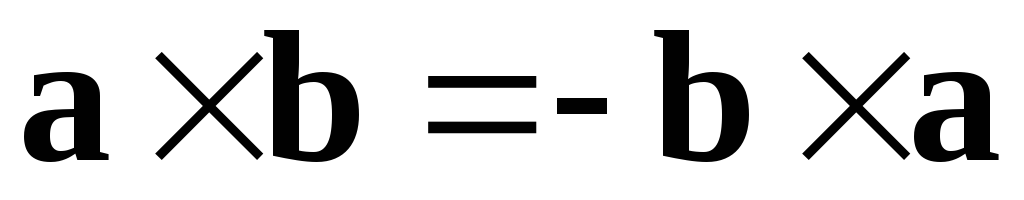 .
.
Это очевидно, так как при перестановке векторов изменится ориентация тройки.
2. Свойство сочетательности относительно скалярного множителя:
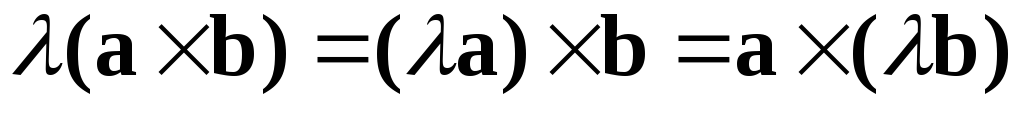 .
.
(без доказательства)
3. Распределительное свойство относительно сложения векторов :
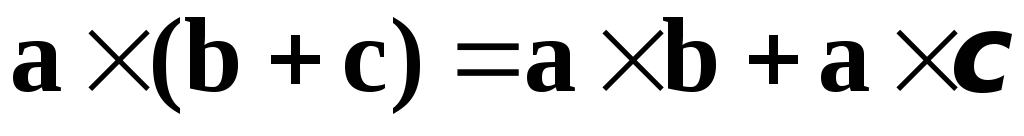 .
.
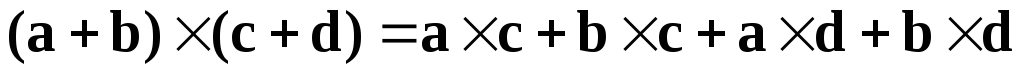 .
.
Следствие. 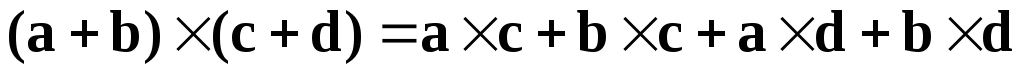 .
.
То есть скобки можно раскрывать, как при обыкновенном умножении, не переставляя местами множители (без доказательства).
Скалярное произведение Википедия
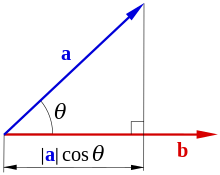 Скалярное произведение векторов (a,b){\displaystyle (\mathbf {a} ,\mathbf {b} )} равно произведению |a||b|cos(θ){\displaystyle |\mathbf {a} ||\mathbf {b} |\cos(\theta )}
Скалярное произведение векторов (a,b){\displaystyle (\mathbf {a} ,\mathbf {b} )} равно произведению |a||b|cos(θ){\displaystyle |\mathbf {a} ||\mathbf {b} |\cos(\theta )}Скаля́рное произведе́ние (иногда называемое внутренним произведением) — операция над двумя векторами, результатом которой является скаляр, то есть число, не зависящее от выбора системы координат.
Обычно для скалярного произведения векторов a{\displaystyle \mathbf {a} } и b{\displaystyle \mathbf {b} } используется одно из следующих обозначений.
- (a,b){\displaystyle (\mathbf {a} ,\mathbf {b} )}
- a⋅b, a→⋅b→{\displaystyle \mathbf {a} \cdot \mathbf {b} ,\ {\vec {a}}\cdot {\vec {b}}} или просто ab{\displaystyle \mathbf {a} \mathbf {b} }
- ⟨a,b⟩{\displaystyle \langle \mathbf {a} ,\mathbf {b} \rangle } или (обозначение Дирака, применяемое в квантовой механике для векторов состояния[1]): ⟨a|b⟩{\displaystyle \langle a|b\rangle }
В простейшем случае обычного пространства скалярное произведение ненулевых векторов a{\displaystyle \mathbf {a} } и b{\displaystyle \mathbf {b} } определяется как произведение длин этих векторов на косинус угла между ними[2]:
- (a,b)=|
2. Скалярное произведение векторов в координатной форме
Пусть
даны векторы 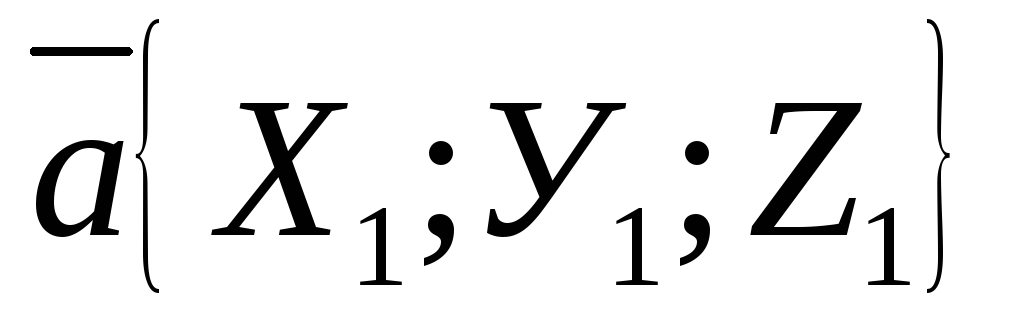 и
и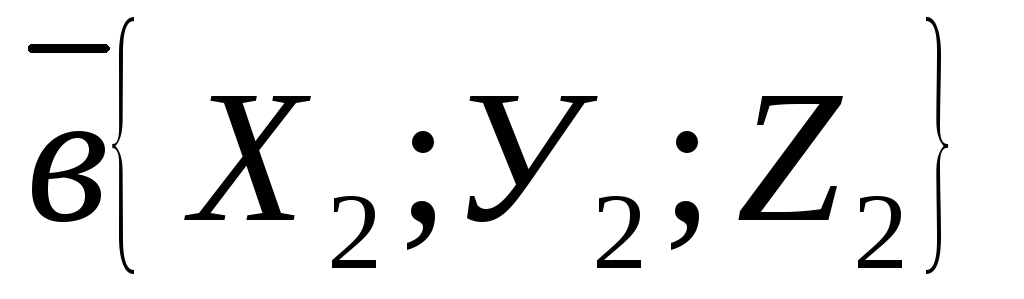 .
Тогда скалярное произведение векторов
.
Тогда скалярное произведение векторов и
и :
:
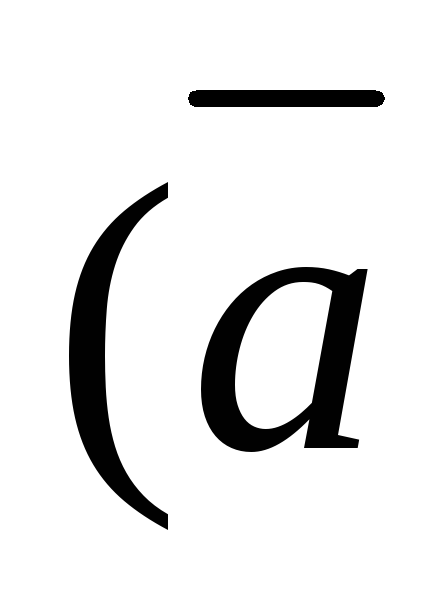
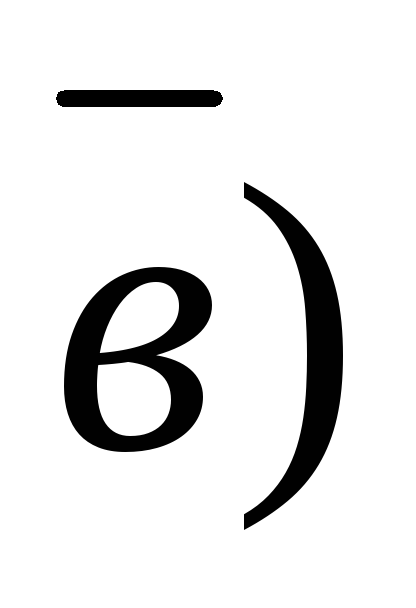 =
= 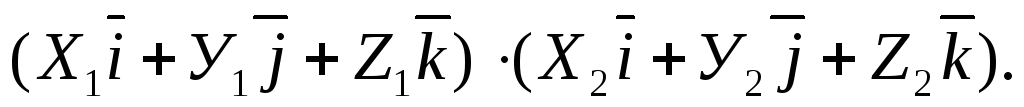 вычисляется по формуле:
вычисляется по формуле:
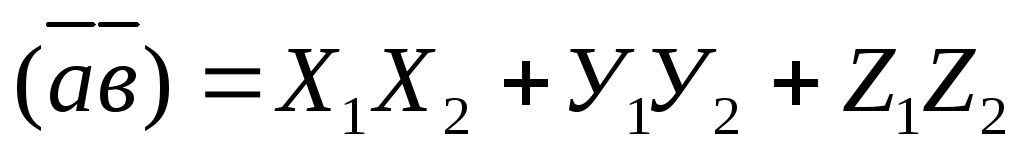 (3.18)
(3.18)
Скалярное произведение векторов равно сумме произведения одноименных координат. Из (3.18) следует, что необходимым и достаточным условием перпендикулярности векторов а и в является равенство:
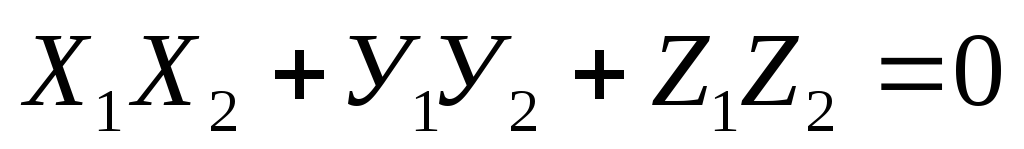 (3.19)
(3.19)
Из
определения скалярного квадрата (3.18) и
из формулы (3.19) найдём: (
( или
или  =
=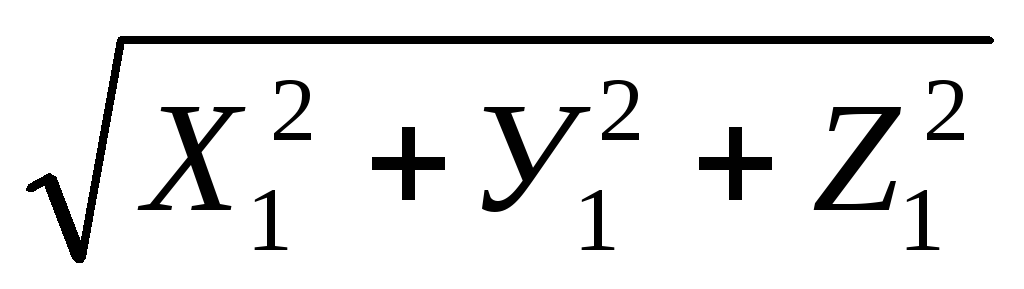 (3.20)
(3.20)
Теперь
найдём угол между двумя векторами  и
и .
На основании определения скалярного
произведения имеем:cos
.
На основании определения скалярного
произведения имеем:cos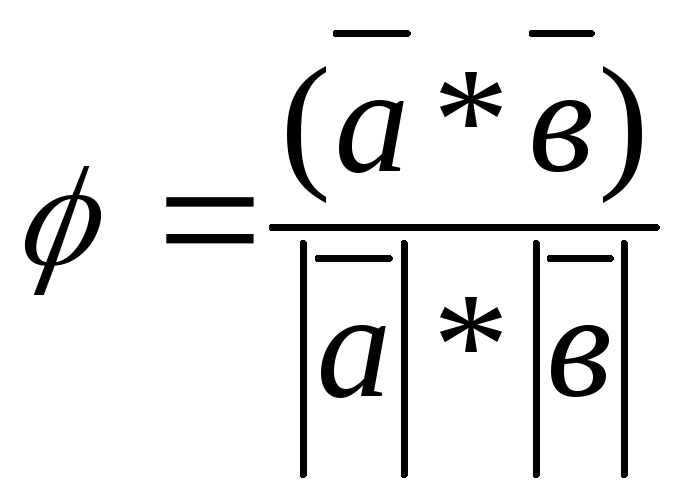
Тогда
cos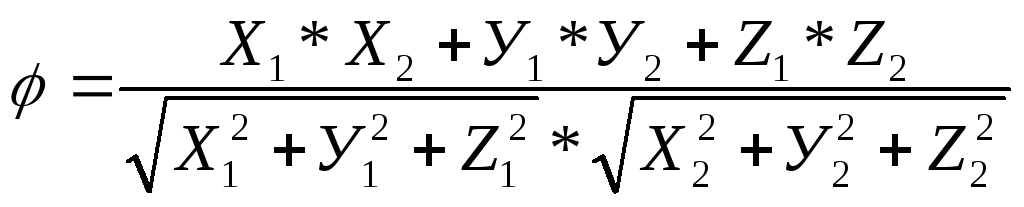 (3.21)
(3.21)
3.Проекция вектора на ось
Пусть
дана некоторая ось х, которая составляет
с осями координат углы 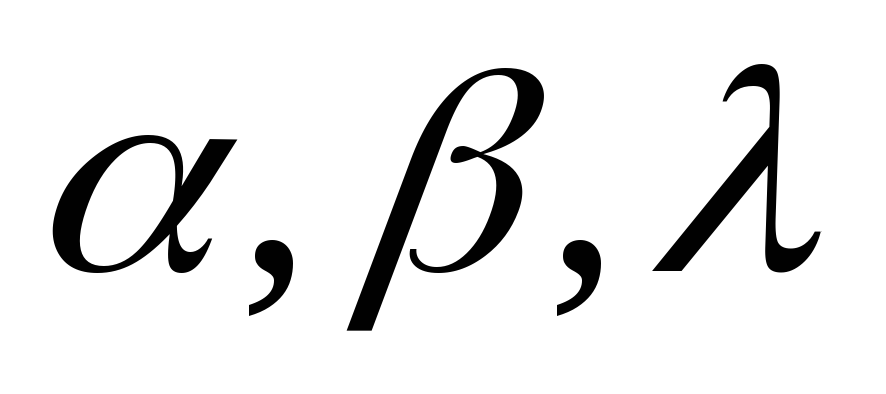 и дан вектор
и дан вектор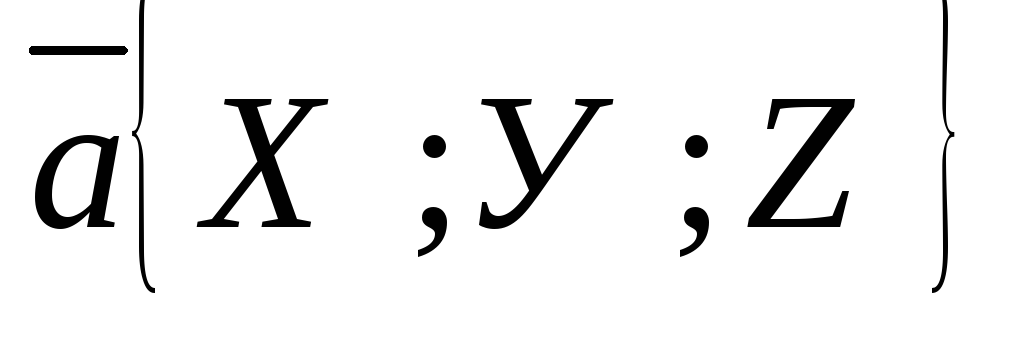 .
Найдём
проекцию
вектора
.
Найдём
проекцию
вектора  на ось х.
на ось х.
На
оси х зададим единичный вектор 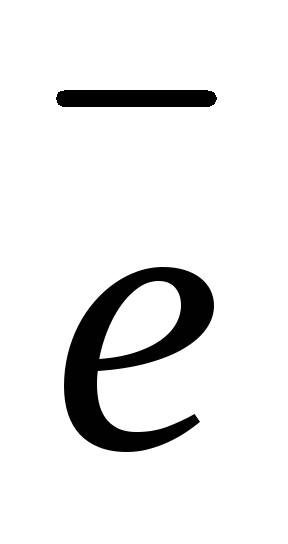
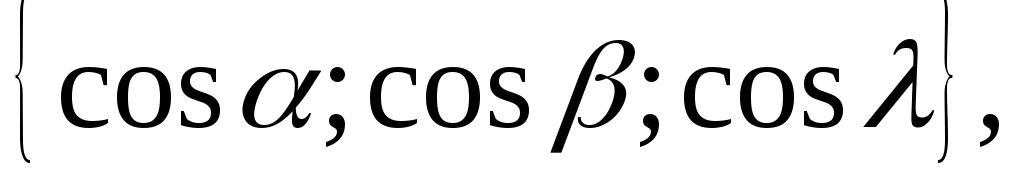
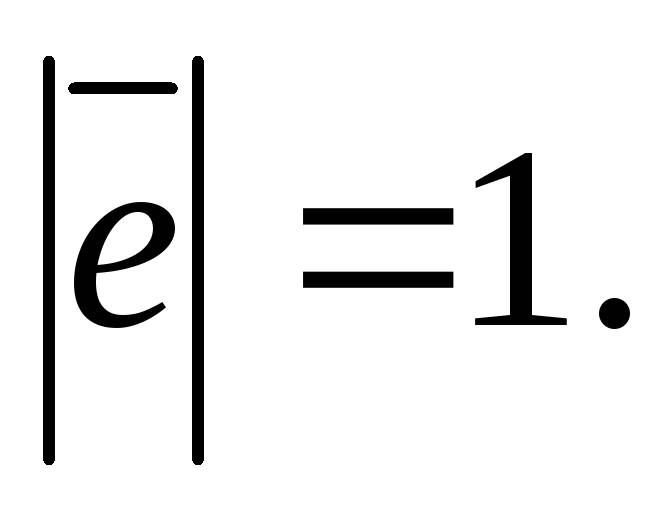
Найдём
пр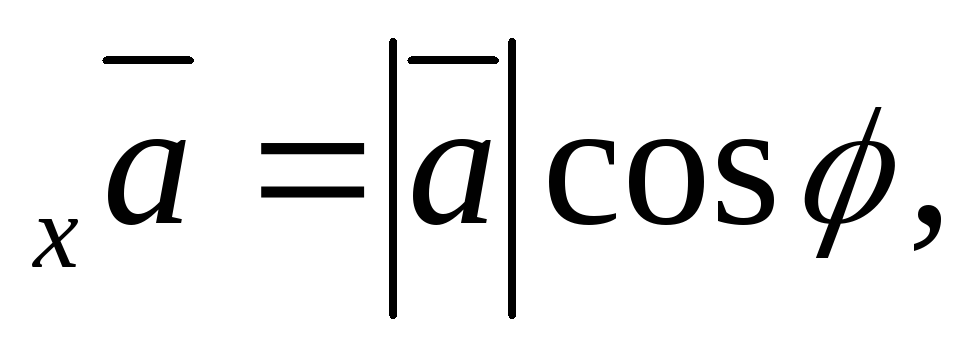
 -угол
между векторами
-угол
между векторами и
и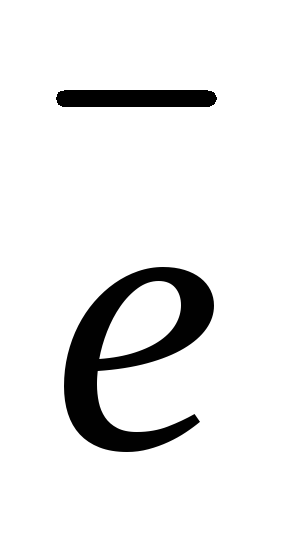 .
.
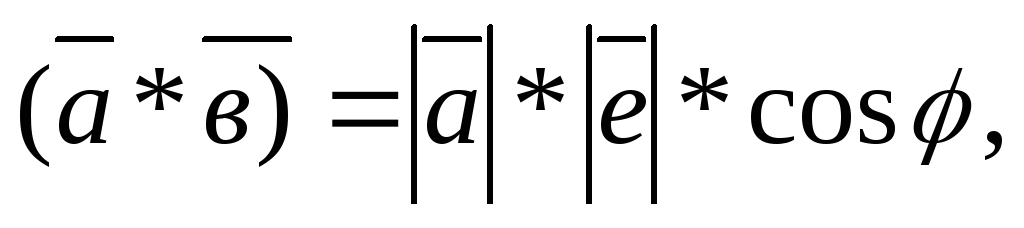 но
т.к
но
т.к 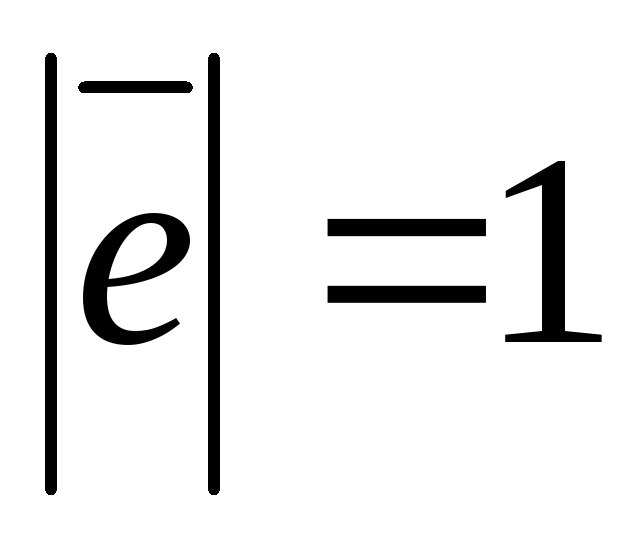 ,
то получим
(
,
то получим
(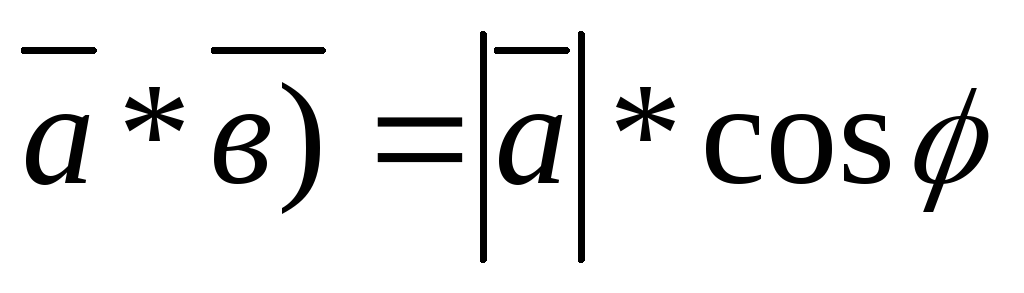 ,
отсюда
,
отсюда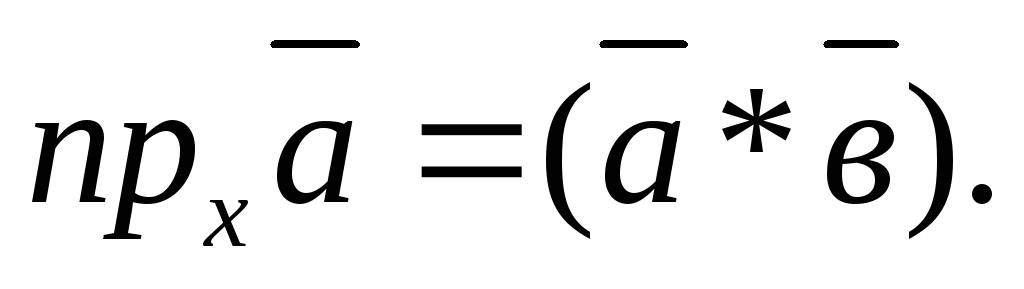 Итак,
Итак, 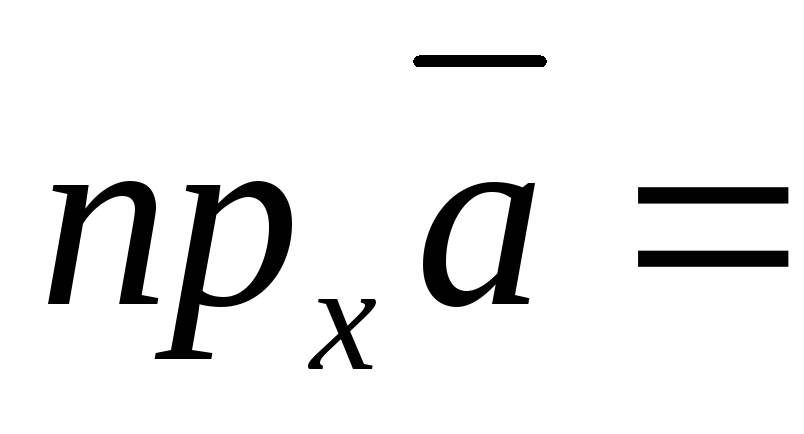 Хcos
Хcos +Уcos
+Уcos +Zcos
+Zcos (3.22)
(3.22)
Пример1: Даны три точки А(1;1;1), В(2;2;1) и С(2;1;2). Найти
косинус угла 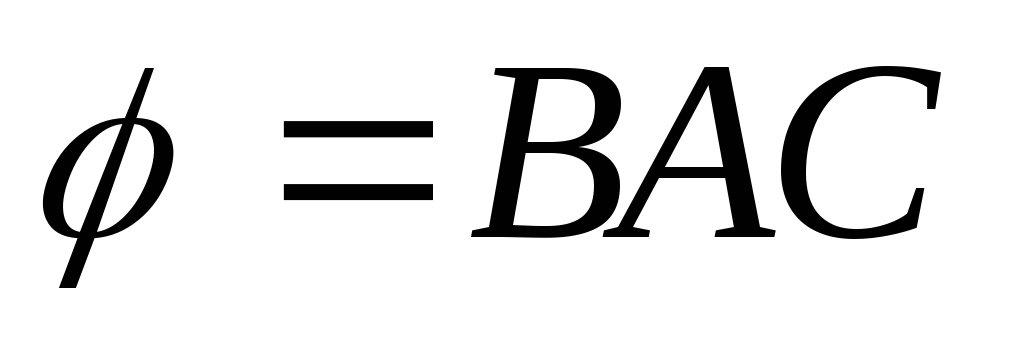
Решение: Найдём векторы 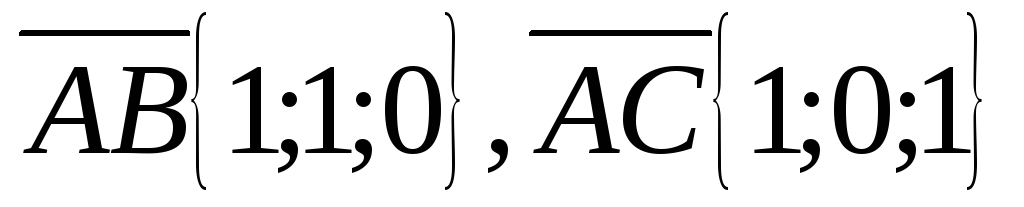 .
На основании формулы (3.21).
.
На основании формулы (3.21).
cos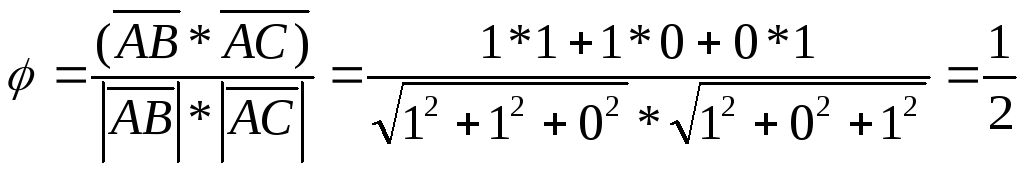
Пример 2: Даны точки А(1;1;1) и В(4;5;3). Найти проекцию вектора АВ на ось х, составляющие с координатными осями равные острые углы.
Решение: Пусть cos ,
cos
,
cos ,
cos
,
cos —
направляющие
косинусы оси х и по условию задачи: cos
—
направляющие
косинусы оси х и по условию задачи: cos =
cos
=
cos =
cos
=
cos .
Зная, что cos
.
Зная, что cos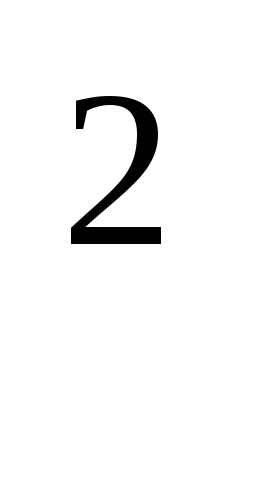
 +cos
+cos
 +cos
+cos
 =1,
имеем cos
cos
=1,
имеем cos
cos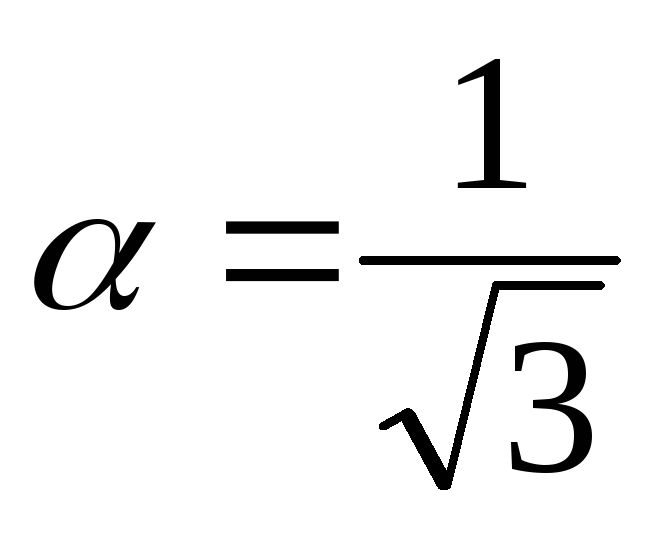 .
Вектор
.
Вектор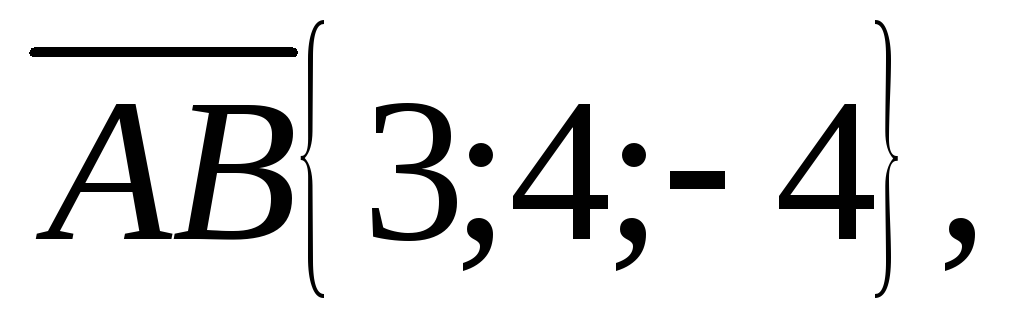 тогда по формуле (3.22):
тогда по формуле (3.22):
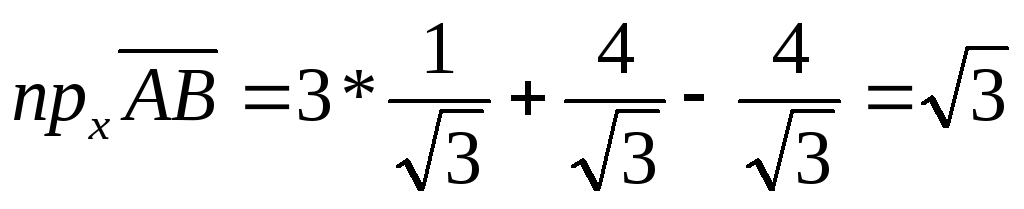
4. Векторное произведение векторов
Определение: Векторным
произведением двух векторов  и
и называется вектор
называется вектор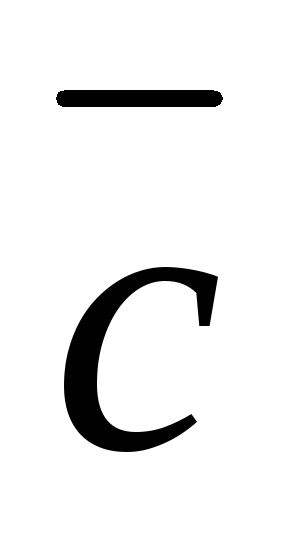 ,
обозначаемый символом
,
обозначаемый символом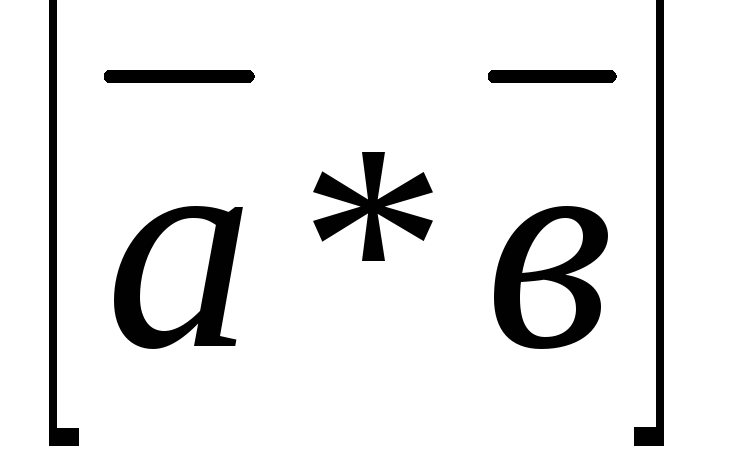 или
или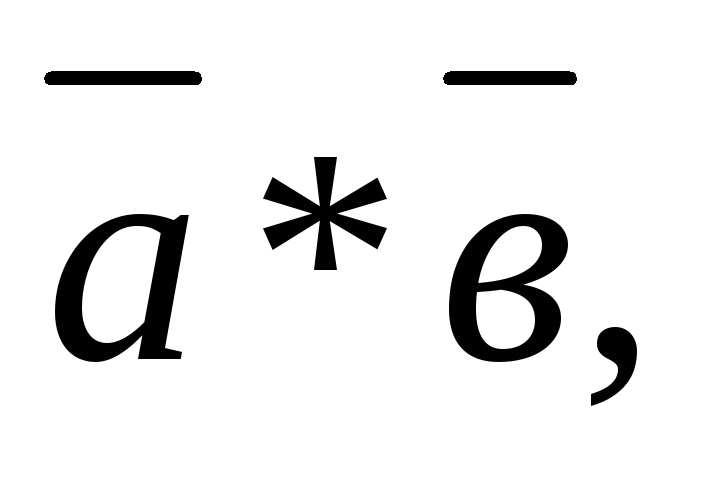 который определяется следующими тремя
условиями:
который определяется следующими тремя
условиями:
Модуль векторного произведения
 =
= равен
равен  где
где угол
между векторами
угол
между векторами и
и ;
;Вектор
 =
= перпендикулярен к каждому из векторов
перпендикулярен к каждому из векторов и
и ;
;Вектор
 направлен
таким образом, чтобы смотря в направлении
от конца вектора
направлен
таким образом, чтобы смотря в направлении
от конца вектора на плоскость вектора
на плоскость вектора и
и кратчайший поворот от
кратчайший поворот от к
к был виден против хода часовой стрелки.
был виден против хода часовой стрелки.
Из определения векторного произведения вытекают следующие свойства:
Если векторы
 и
и коллинеарны, то их векторное произведение
равно нулю.
коллинеарны, то их векторное произведение
равно нулю.Модуль векторного произведения двух векторов
 и
и равен площади параллелограмма
построенного на этих векторах.
равен площади параллелограмма
построенного на этих векторах.При перестановке местами сомножителей векторное произведение меняет свой знак:
Векторное произведение подчиняется распределительному закону:

Векторное произведение подчиняется сочетательному закону по отношению к скалярному множителю:
 где
где  —
число.
—
число.
5. Векторное произведение в координатной форме
Пусть
даны векторы 
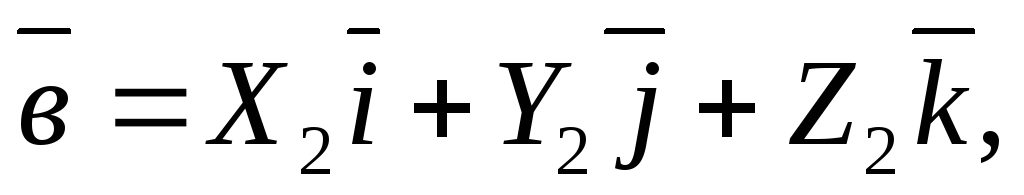
На основании определения и свойств векторного произведения легко показать, что:
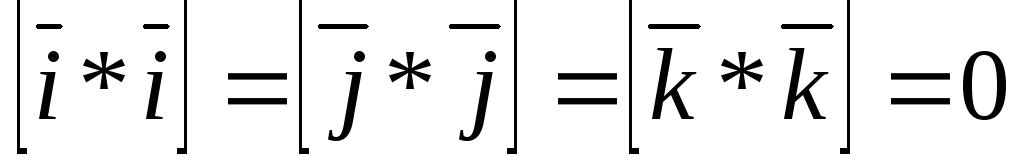
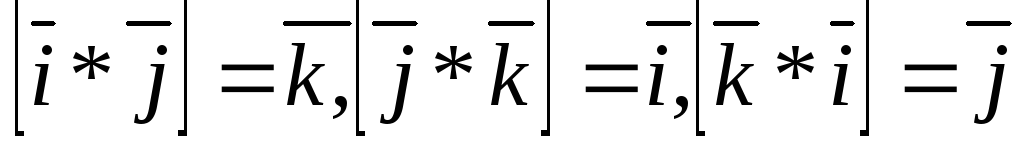 . (3.23)
. (3.23)
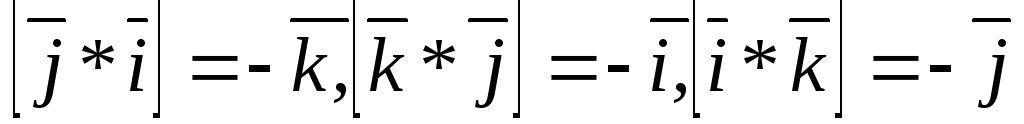 .
.
На основании свойства и (6.1) можно установить, что:
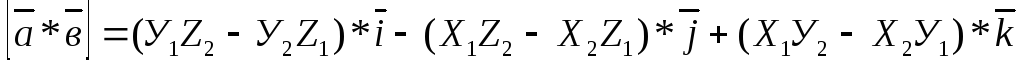 или
или
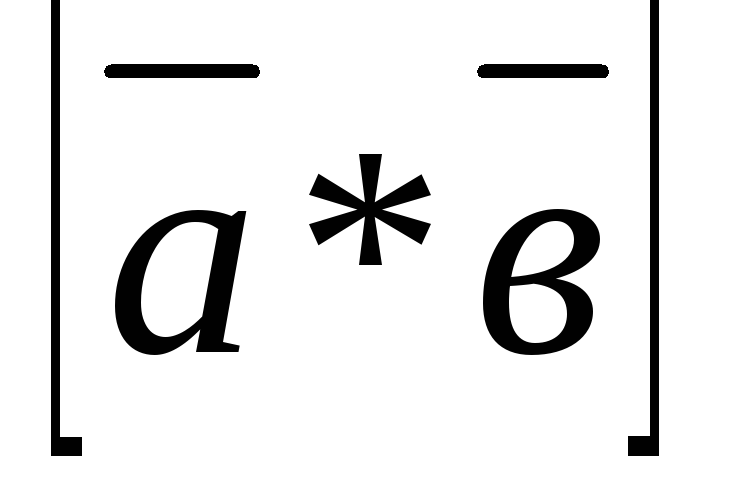 =
=
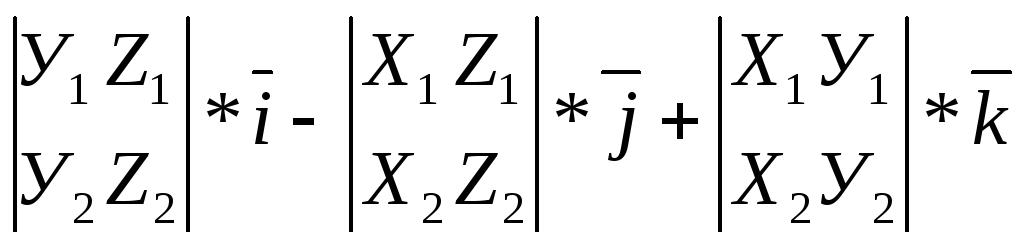 (3.24)
(3.24)
Получим
разложение векторного произведения
по базису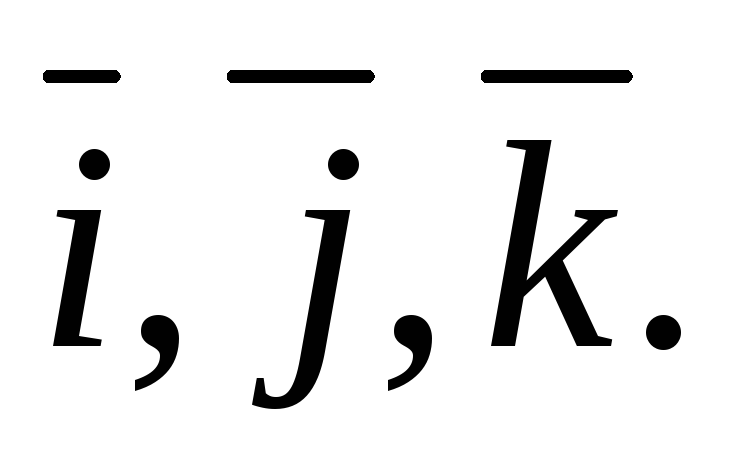 Следовательно координаты векторного
произведения определяются:
Следовательно координаты векторного
произведения определяются:
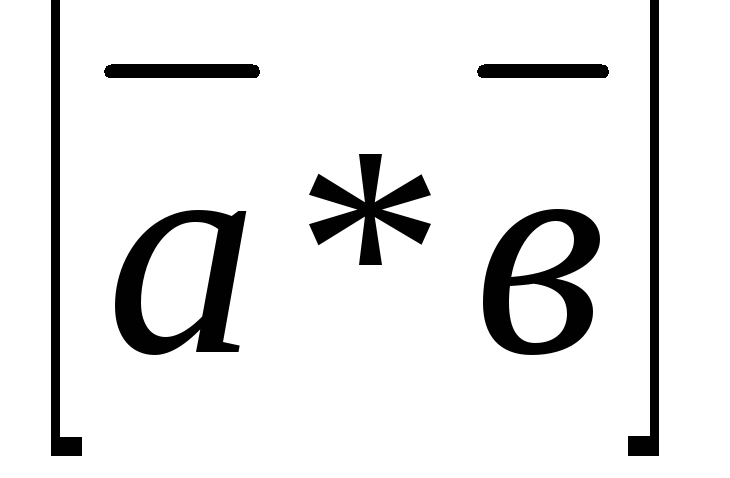 =
=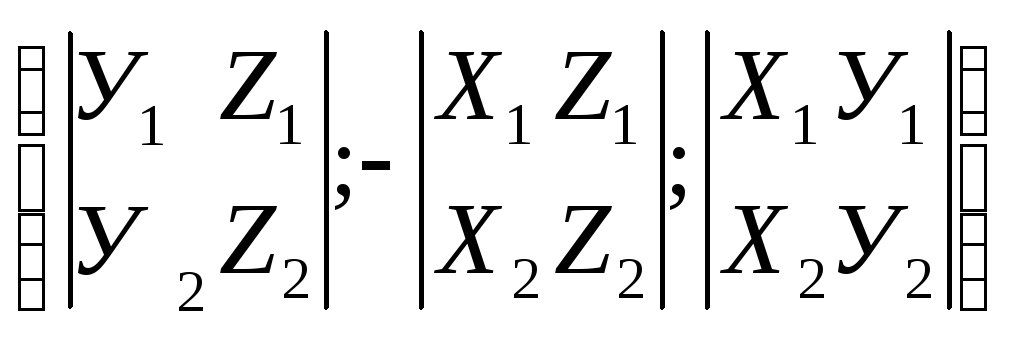 (3.25)
(3.25)
Заметим, что в формуле (3.24) можно придать вид:
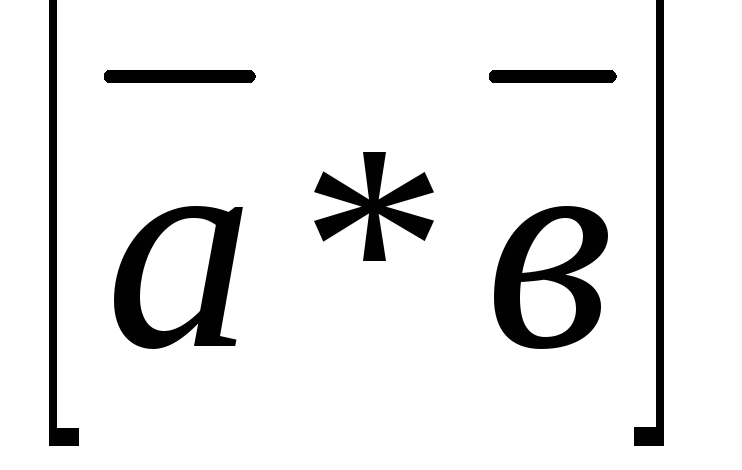 =
=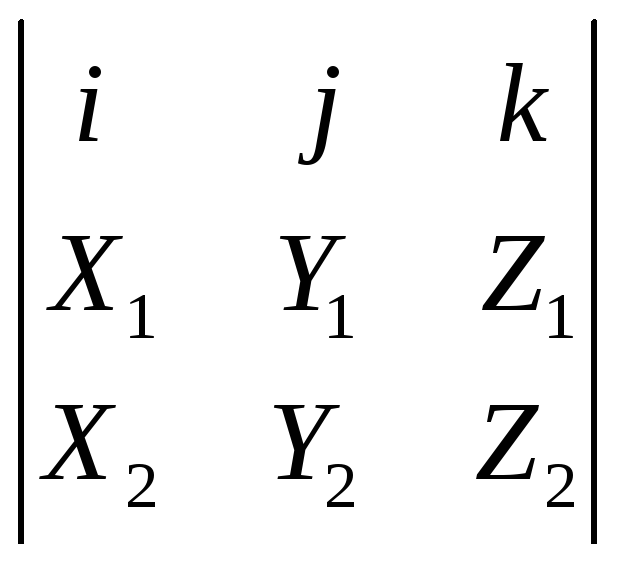 (3.26)
(3.26)
Пример
1: Даны векторы 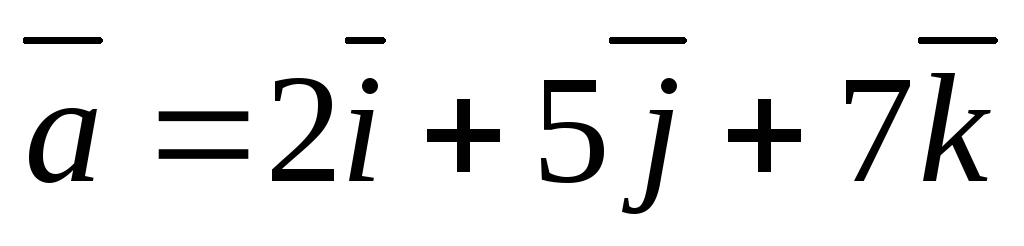 и
и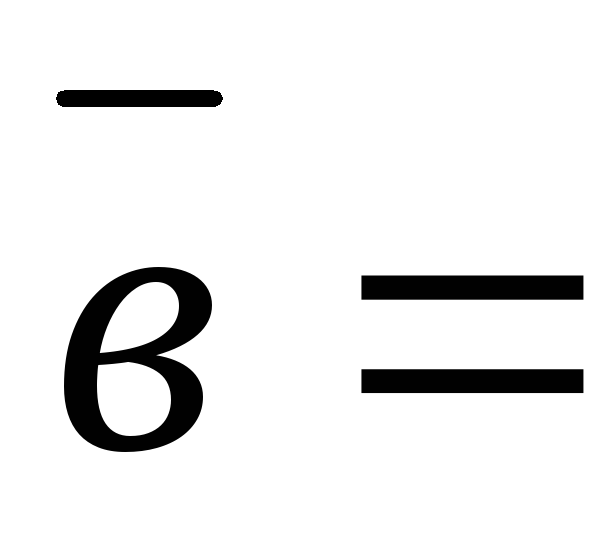
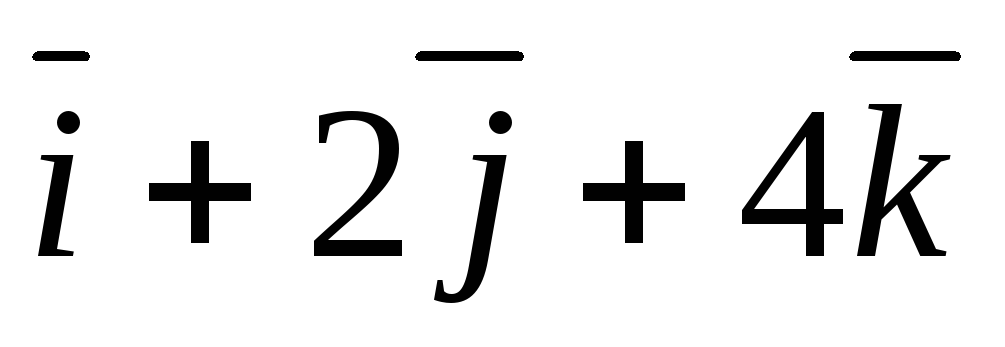 .Разложить
вектор
.Разложить
вектор 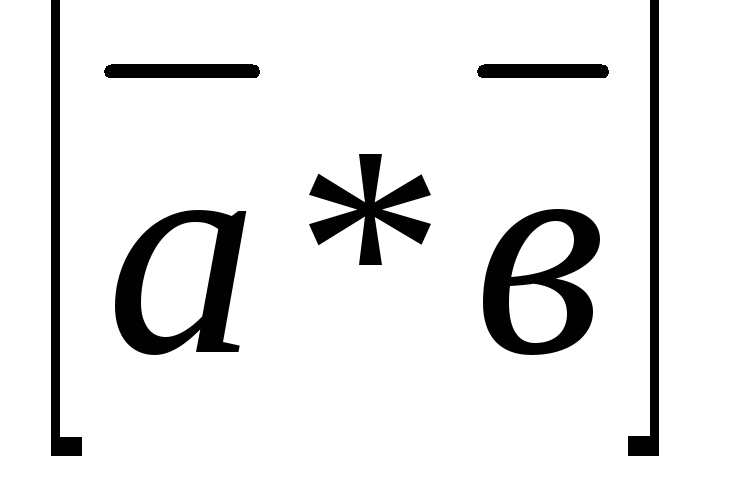 по базису
по базису 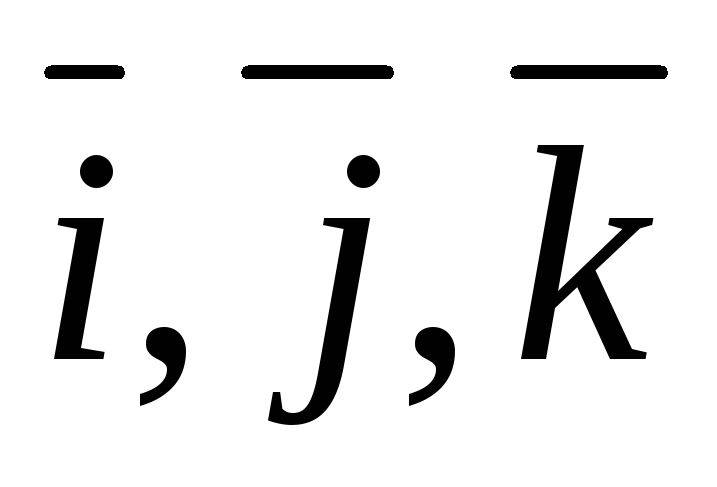 .
.
Решение: Используем формулу (3.25) и получим:
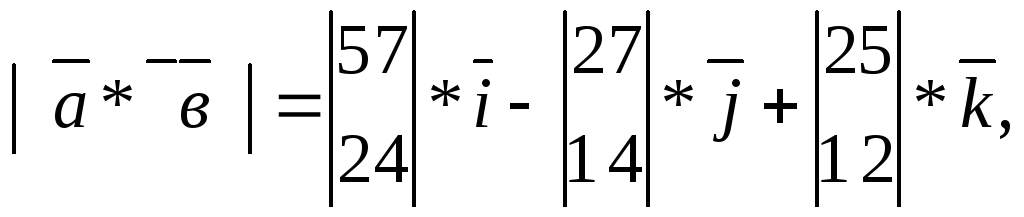 или
или 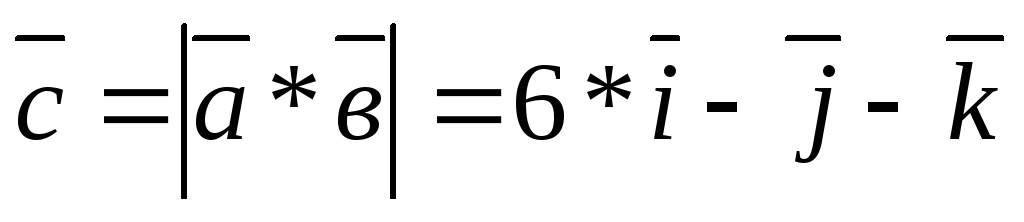
Координаты
векторного произведения 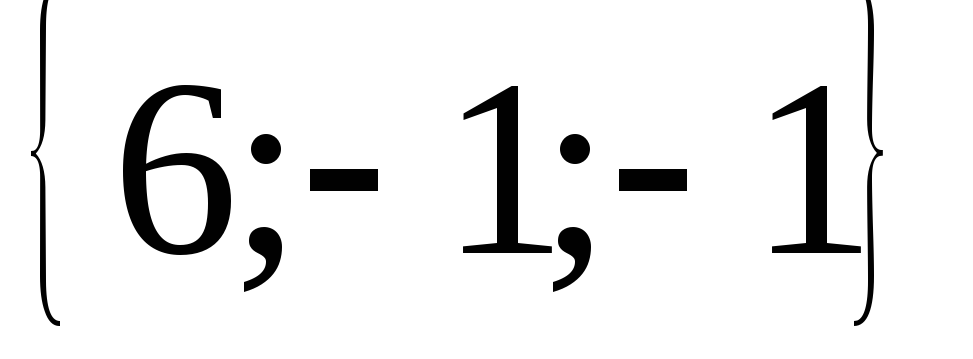
Пример
2: Даны три точки А(1;1;1), В(4;3;5). Найти площадь
S треугольника
АВС.
треугольника
АВС.
Решение: Определим координаты векторов 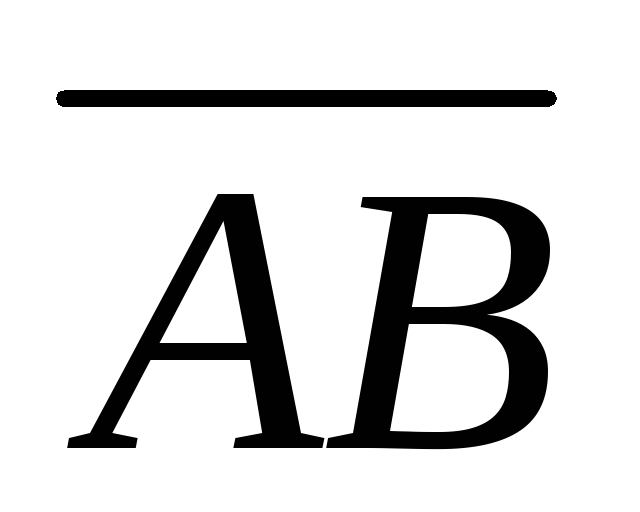 и
и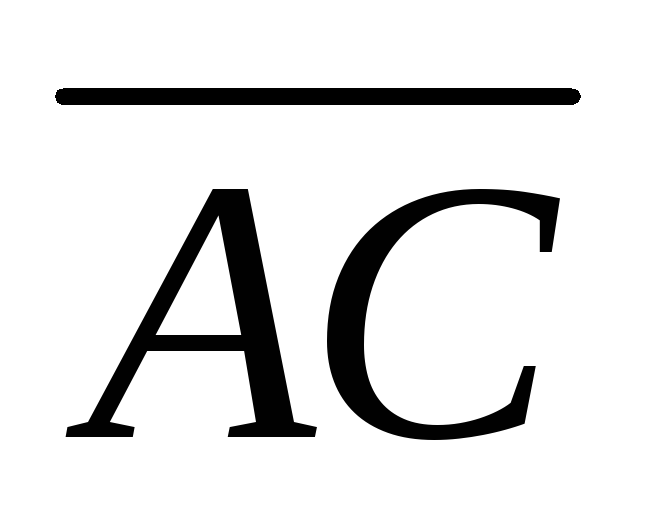 :
: 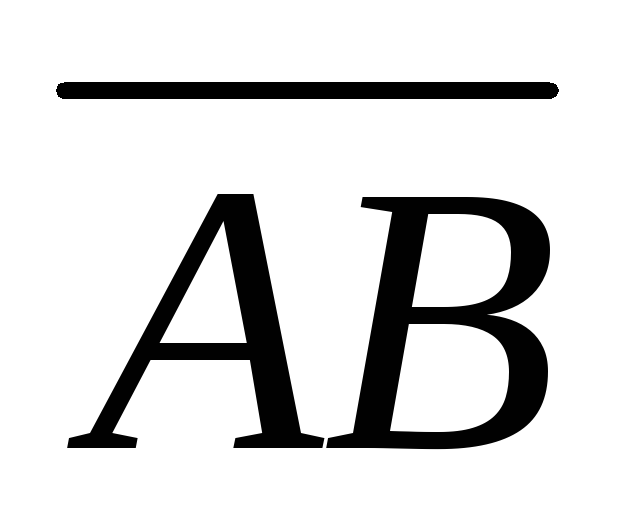
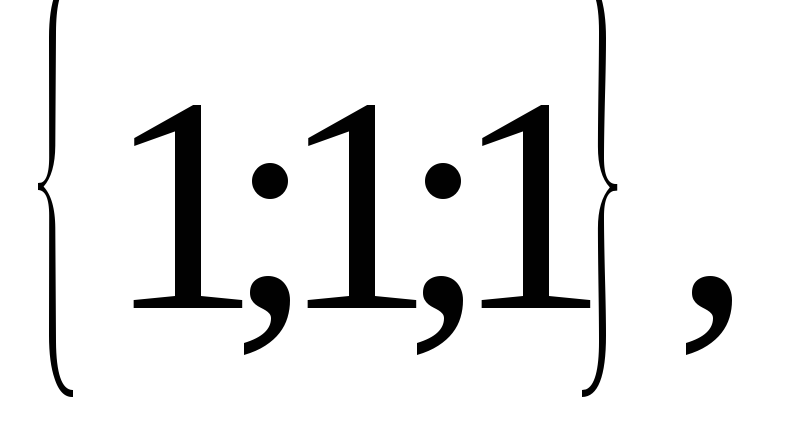
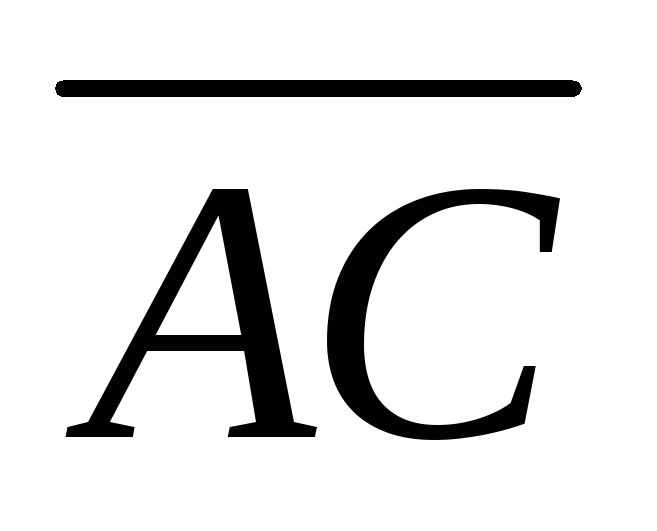
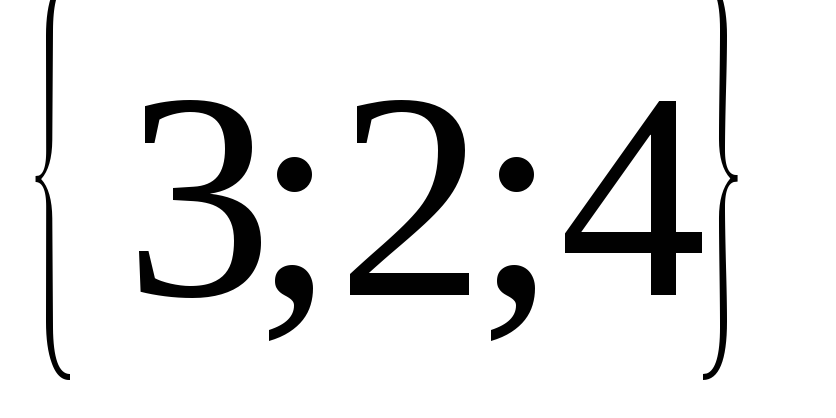 .
Модуль векторного произведения векторов
.
Модуль векторного произведения векторов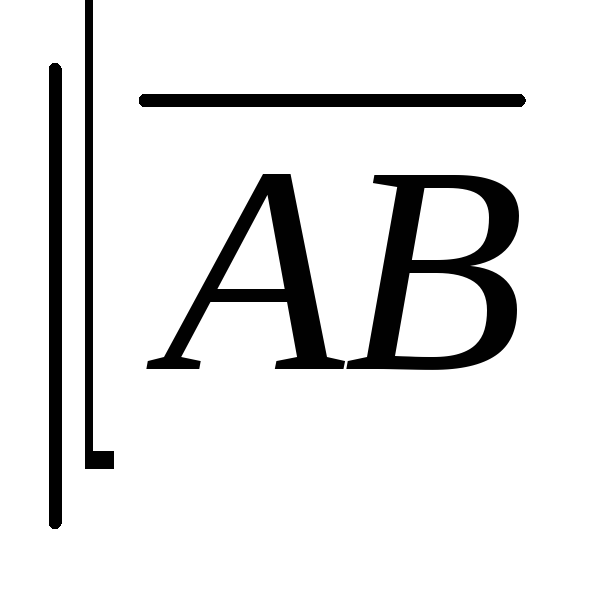
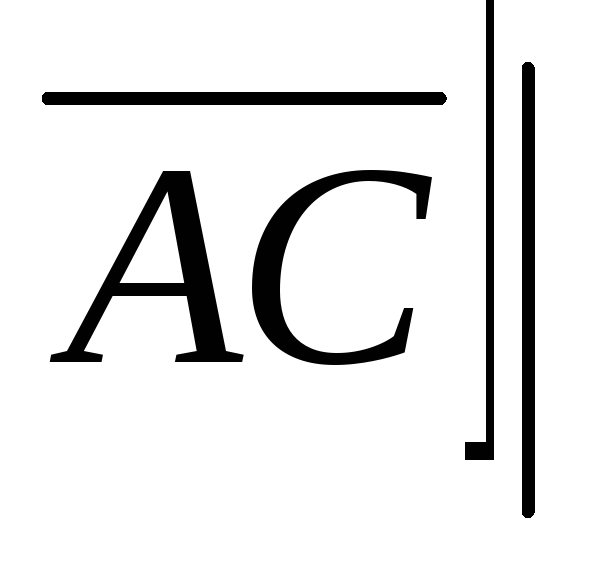 равен площади параллелограмма,
построенного на этих векторах. Площадь
треугольника АВС:
равен площади параллелограмма,
построенного на этих векторах. Площадь
треугольника АВС: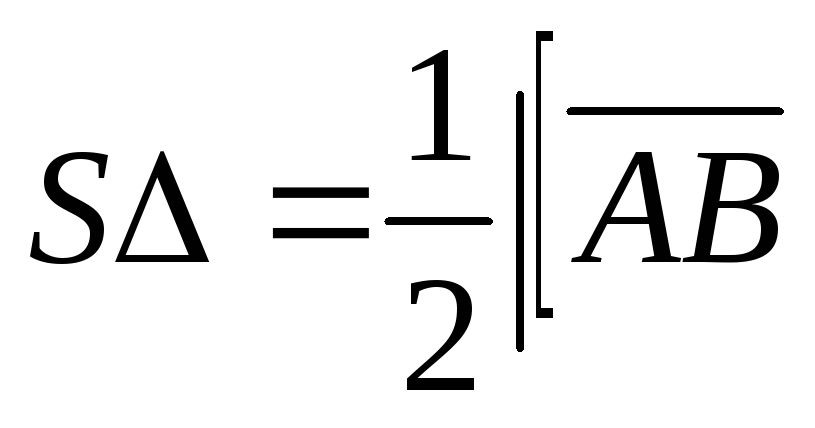
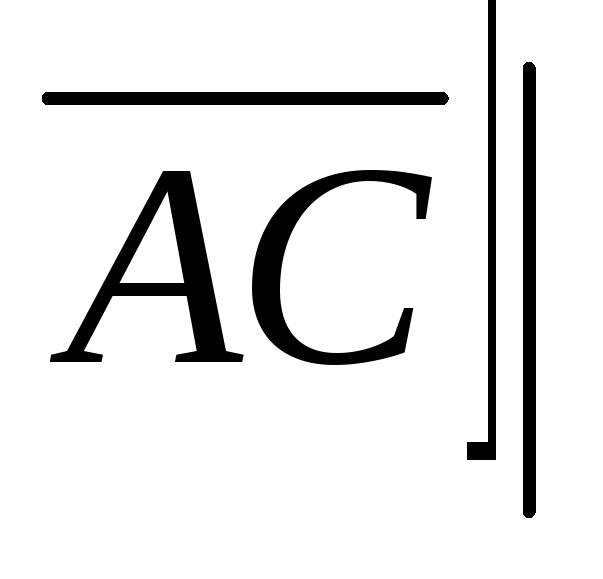 .
По формуле (3.26) найдем координаты.
.
По формуле (3.26) найдем координаты.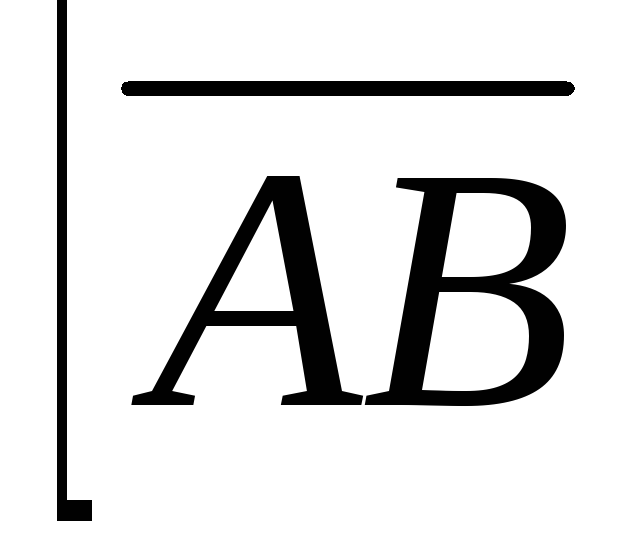
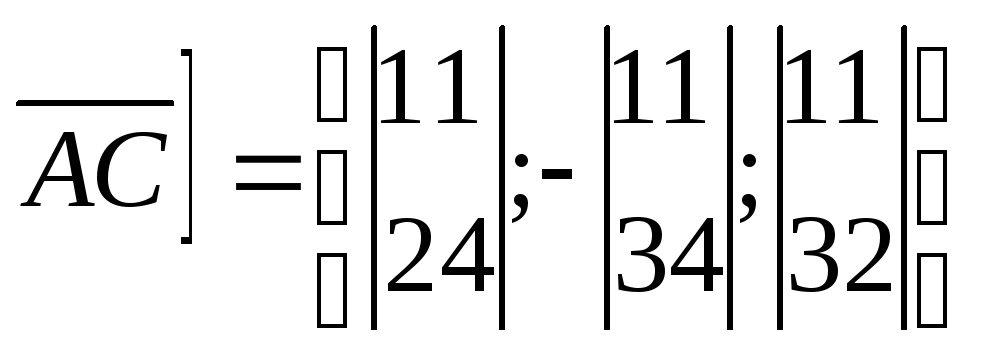 или
или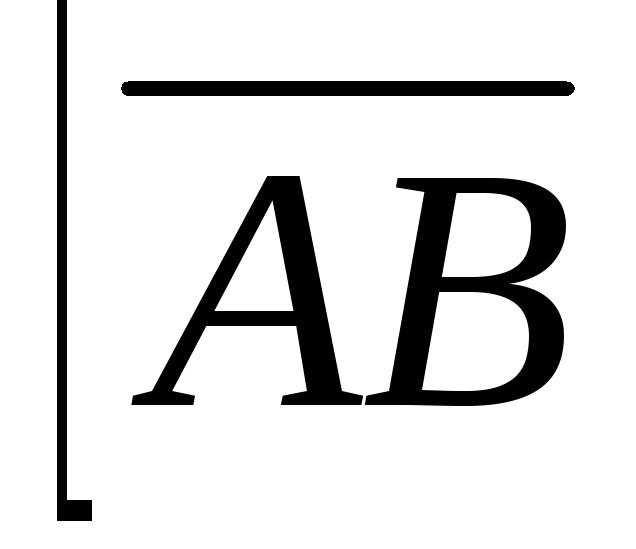
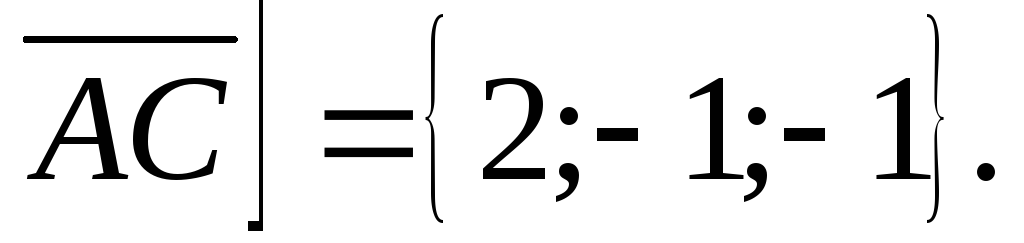
Тогда 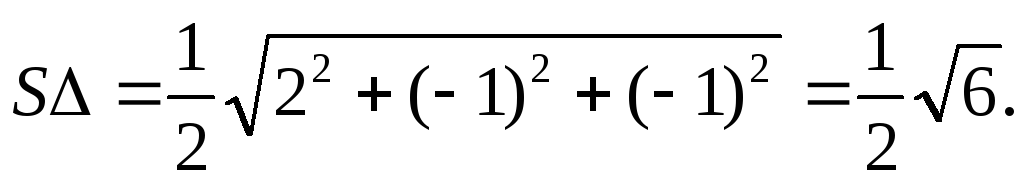
Обсуждение:Скалярное произведение — Википедия
Материал из Википедии — свободной энциклопедии
Уважаемые авторы этой страницы! Как вы думаете, что будут искать 90% посетителей на этой странице? Они будут искать как посчитать скаляр для двух двумерных векторов. Где пример этой самой нужной частности? Посмотрите, как сделана немецкая страница.
Насчёт положительной определённости. А что тогда в пространстве Минковского? Там это разве не скалярное произведение называется?—Begemotv2718 09:09, 21 Янв 2005 (UTC)
Нет охоты этим заниматься, но по-моему то что неправильно определено в начале это не называется скалярным произведением, кроме того лучше бы сделать единые обозначения во всей статье…—Tosha 07:22, 1 октября 2005 (UTC)
В долбаном английском скалярное произведение почему-то делится на dot product и inner product—213.219.95.125 16:46, 23 ноября 2005 (UTC)
- Глянул английские статьи. dot product или scalar product — это стандартное скалярное произведение в Евклидовом пространстве. Т.е. это только скалярное произвдение двух векторов, с результатом — числом. Inner product — это абстрактное скалярное произведение.87.103.193.95 16:14, 20 сентября 2007 (UTC)Артём Камышев
Прочитал статью, так и не понял, что это такое. Нужно добавить примеры. Хотя бы для эвклидовых пространств. Alexsmail 16:25, 27 апреля 2007 (UTC)
Добавил примеры. 81.30.201.52 14:32, 10 мая 2005 (UTC)
Положительная определённость.[править код]
Infovarius, извини — отменил твою правку: всё-таки, когда говорят о скалярном произведении, обычно всё-таки имеют в виду именно положительно определённое; иначе оговаривают явно (иначе, например, косинусов углов нет, и так далее)… Burivykh 18:40, 30 апреля 2009 (UTC)
- Как-то я не помню применения термина «определённость» к скал. произведению — обычно его к норме употребляют? infovarius 13:44, 1 мая 2009 (UTC)
- И к квадратичной форме; а скалярное произведение — это билинейная симметричная форма (что почти то же самое, что и квадратичная). Просто, насколько я знаю, когда говорят «скалярное произведение» — это именно подчёркивает положительную определённость (иначе это просто билинейная симметричная форма). Либо — специально оговаривают незнакоопределённость, подразумевая, что «да, знак может быть разный, так что длину обычным образом определить нельзя, но мы хотим, тем не менее, использовать терминологию и интуицию от евклидова пространства»… Burivykh 22:56, 1 мая 2009 (UTC)
Следует ли нам иметь перенаправление сюда от Внутреннее произведение? Я не совсем силен в терминологии, но как тогда по-русски называется en:Interior product? — Yrogirgtalk 04:39, 23 сентября 2010 (UTC)
На мой взгляд «скалярное произведение» и «внутреннее произведение» синонимы. —Тоша 02:16, 4 октября 2010 (UTC)
Связанные определения[править код]
>>В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия:
Что тогда является определением скалярного произведения в современной аксиоматике? Определение через косинус угла тогда неправомерно (угол вводится далее). Определения через сумму произведений координат концов неправомерно (нужна ортогональная система координат, а понятие «ортогональный» вводится далее). Определение через проекцию неправомерно (для построения проекции нужно знать, что такое прямой угол, а понятие «угол» или «прямой угол» вводится далее).
- определение дано верно, загляните в любой учебник по функану, вобщем надо быстрей удалить эти красные строчки а то они оч раздражают Ivanmipt 04:06, 30 декабря 2013 (UTC)
- >> определение дано верно
- В смысле определение через 3 аксиомы? Okey.
Всё-таки есть проблема в определении. В англоязычной версии статьи сказано предельно ясно «scalar product is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors)». То есть скалярное произведение определено для кортежей одинаковой длины; наличие структуры линейного пространства совсем не обязательно. В данной же статье утверждается, что понятие определено только для векторов. 139.45.252.98 11:17, 22 января 2020 (UTC)
- В Математической энциклопедии сказано: «СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ, внутреннее произведение (а, Ъ) ненулевых векторов a и b, — произведение их модулей на косинус угла φ между ними» (том 4, стр. 1197). Далее в статье Мат. энциклопедии, касаясь обобщений понятия скалярного произведения, также речь идёт о векторах. На мой взгляд, это правильно, потому что определение через кортежи затемняет главное в скалярном произведении — его геометрическую инвариантность. LGB (обс.) 12:25, 22 января 2020 (UTC)


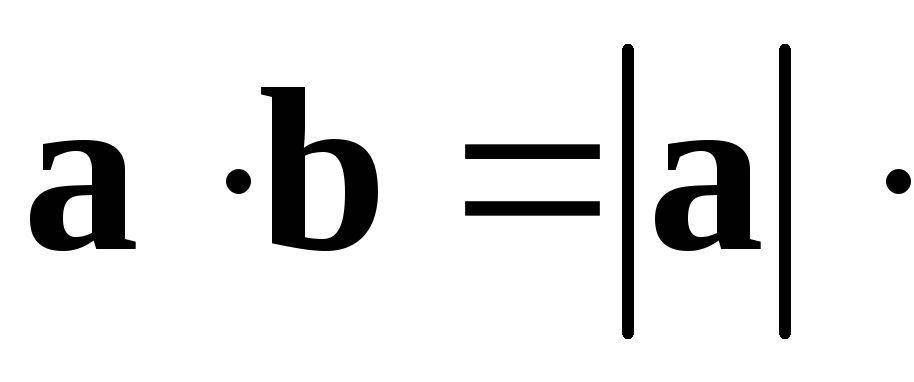 пр
пр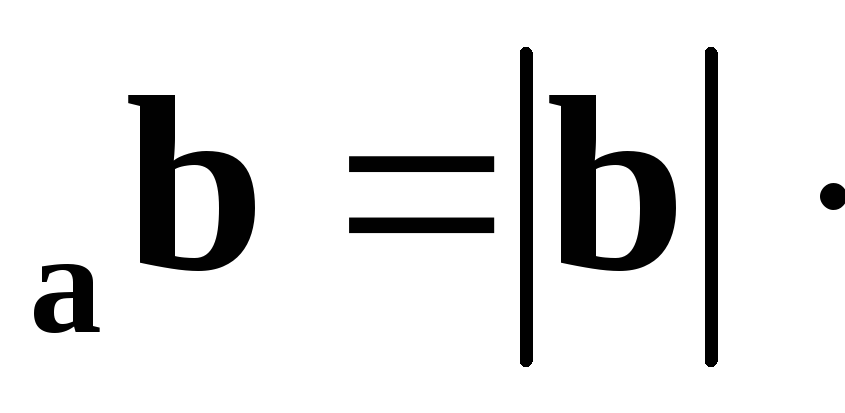 пр
пр
 :
: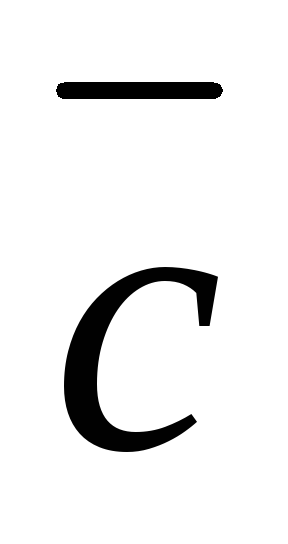 =
=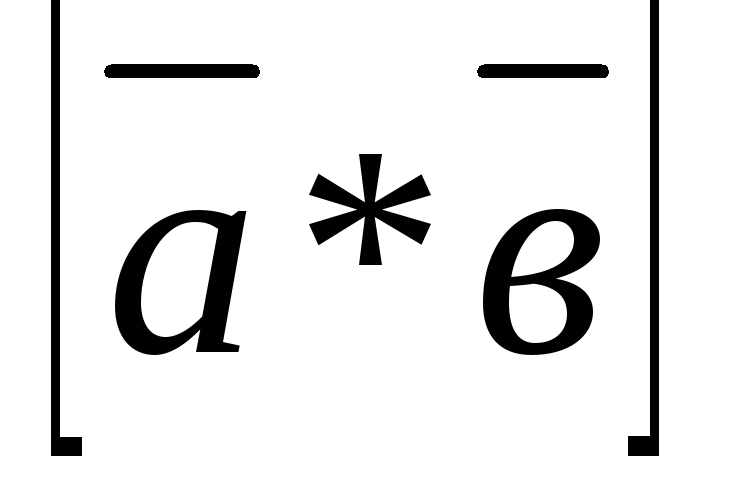 равен
равен 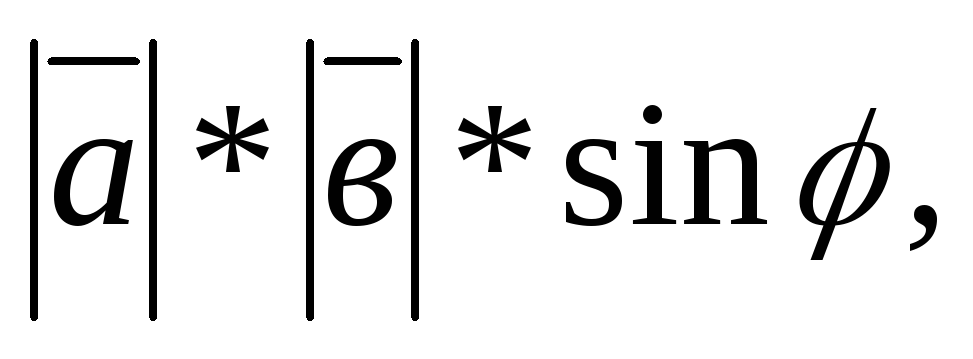 где
где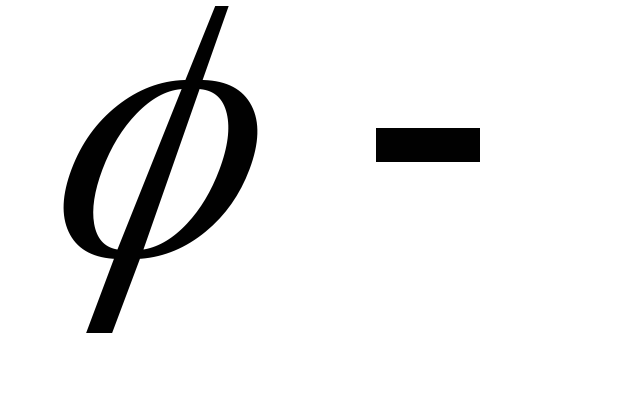 угол
между векторами
угол
между векторами и
и ;
;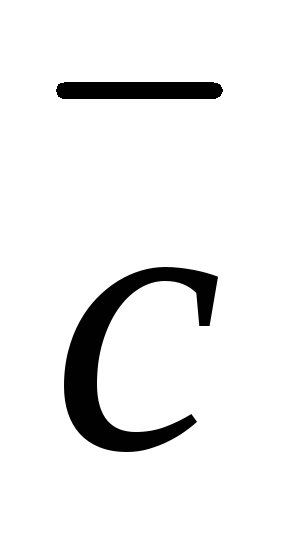 =
=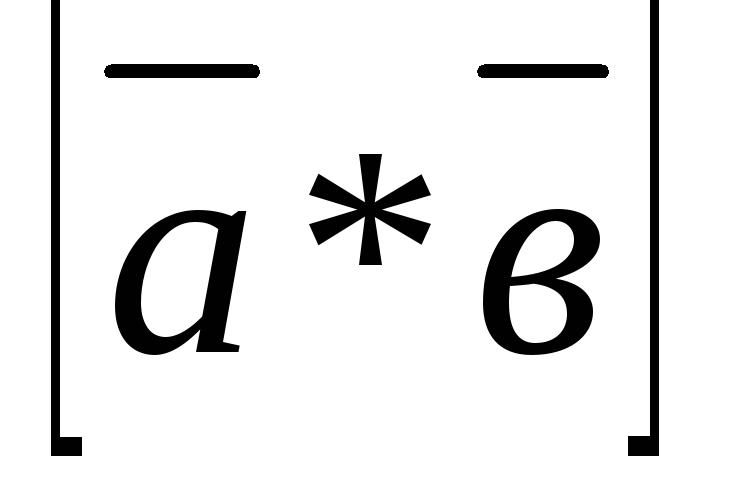 перпендикулярен к каждому из векторов
перпендикулярен к каждому из векторов и
и ;
;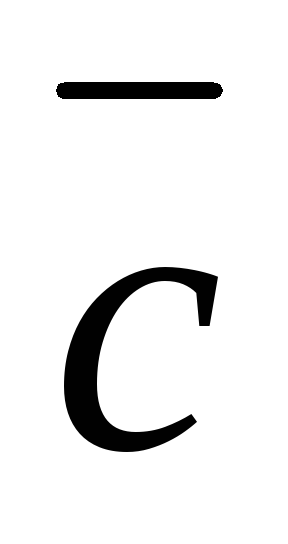 направлен
таким образом, чтобы смотря в направлении
от конца вектора
направлен
таким образом, чтобы смотря в направлении
от конца вектора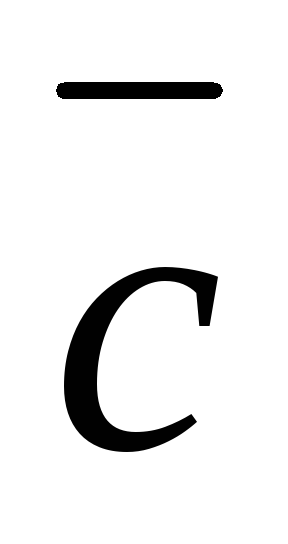 на плоскость вектора
на плоскость вектора и
и кратчайший поворот от
кратчайший поворот от к
к был виден против хода часовой стрелки.
был виден против хода часовой стрелки. и
и коллинеарны, то их векторное произведение
равно нулю.
коллинеарны, то их векторное произведение
равно нулю. и
и равен площади параллелограмма
построенного на этих векторах.
равен площади параллелограмма
построенного на этих векторах.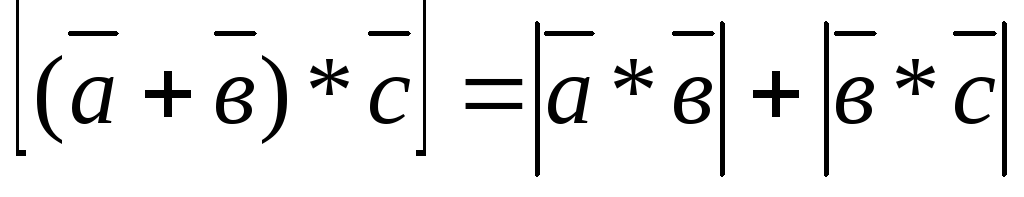
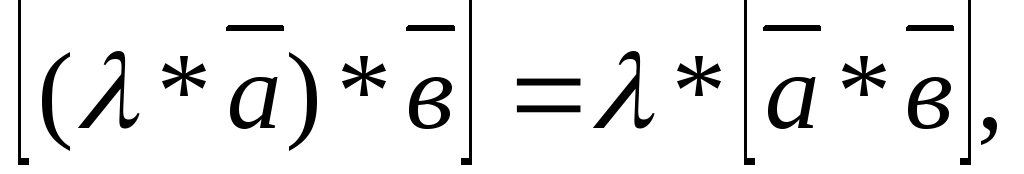 где
где  —
число.
—
число.