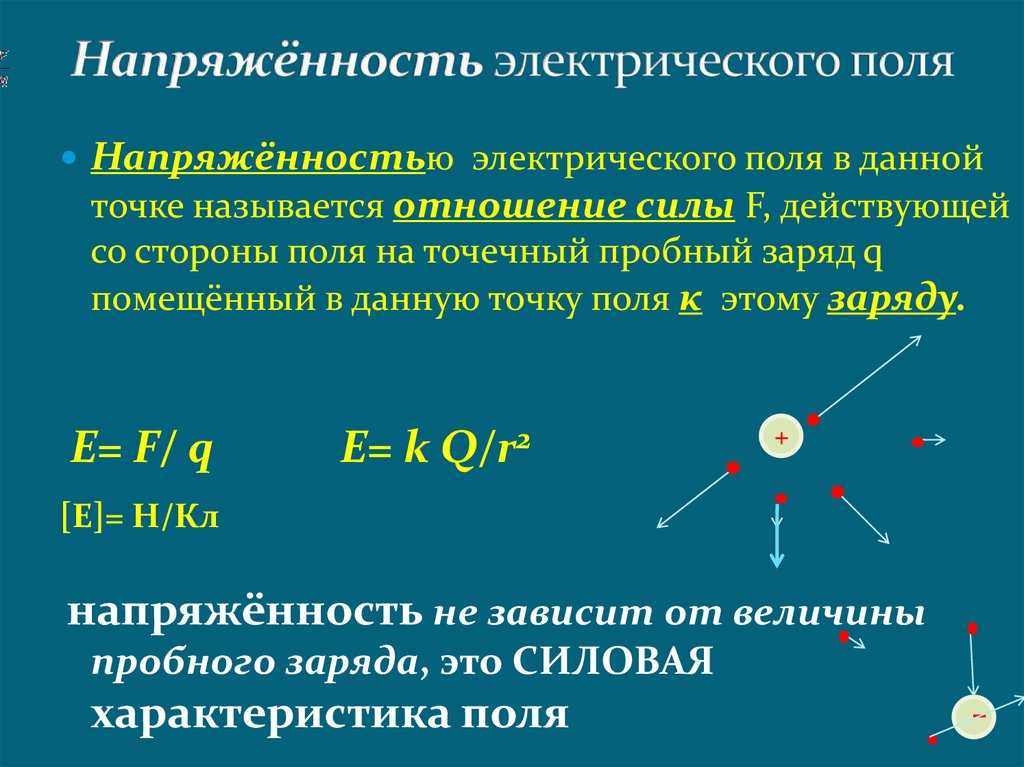
определение характеристики, разность зарядов, размерные единицы

Физика

12.11.21

14 мин.

Вокруг любой обладающей зарядом микрочастицы появляется энергия электростатического поля. Потенциал этой силы определяется характеристикой, описывающей работу, совершаемой для переноса элементарных частиц. При их взаимодействии происходит изменение материи, которое удобно определять, сравнивая отдельные точки в пространстве. Для разности потенциалов даже ввели специальную величину — напряжение.

Оглавление:

• Общие сведения
• Понятие потенциала
• Напряжённость и потенциал
• Простейшие задачи

Общие сведения

Структура твёрдых веществ определяется строением их кристаллической решётки. Состоит она из набора атомов, ионов или молекул. Вокруг узла движутся заряженные вещества. Самой лёгкой из известных элементарных частиц является электрон. Он участвует во всех электрических процессах, возникающих в теле. Так как

атом — электронейтральная частица, то число электронов в нём всегда равняется количеству протонов. Но вместе с тем в теле существуют и свободные частицы. Они не привязаны к атомам и могут перемещаться по кристаллической решётке.

Движение свободных электронов происходит хаотично. При этом они могут сталкиваться с примесями или противоположными им веществами. Многочисленные эксперименты учёных показали, что каждая элементарная частица обладает определённым количеством энергии. Именно она определяет силу взаимодействия между ними. Так, Кулон в 1785 году установил закон, по которому силы влияния двух зарядов друг на друга определяются отношением произведения их энергий и квадратом расстояния между ними.

Фактически физик описал способ нахождения силы притяжения или отталкивания. Этот закон справедлив только для неподвижных зарядов. Но так как сами по себе они существовать не могут, а только когда есть носитель, то правило применимо к элементарным частицам.

В спокойном положении физическое тело находится в состоянии электрического равновесия. Но если к нему приложена внешняя сила, например, деформация или магнитное поле, хаотичное перемещение электронов меняется на упорядоченное. Возникает электрический ток. Характеризуется он силой, которая определяется работой необходимой для переноса частицы из одной точки тела в другую.

Но если таких сил нет, тело всё равно обладает определённой энергией. Отсюда различают два состояния:

• электростатическое — определяется внутренней энергией свободных частиц;
• электромагнитное — возникающее при упорядоченном движении зарядов.

Энергетической характеристикой электростатического поля служит потенциал. Это скалярная величина, специально введённая для определения энергии неподвижного электрона. То есть является отношением потенциальной работы в постоянном поле к заряду. С помощью потенциала можно численно описать материю поля, затрачиваемую на перемещение заряда из произвольной точки в бесконечность.

Понятие потенциала

Пусть существует электростатическое поле, в котором есть пробный заряд q. Под ним понимают минимальную энергию, которой обладают элементарные частицы. Например, заряд протона или электрона. Его значение принимают равным 1,6 * 10^-19 Кл. Этот заряд перемещается в постоянном внутреннем поле из одной точки в другую. Такое движение вызвано отсутствием пары и электрических связей.

Со стороны электростатической энергии действует сила. Её можно обозначить как Fe. С её помощью выполняется работа A, направленная на изменение положения пробной частицы. Это воздействие не зависит от пути, пройденного электроном, а определяется только начальным и конечным положением. Открытое свойство было названо «консервативностью заряда» или «потенциальностью». Нужно отметить, что только электростатическое поле может характеризоваться этой величиной.

Под потенциальной энергией точечного заряда понимают скалярную функцию в электростатике, описываемую в координатах как Eп = Eп (x, y, z). Отсюда следует, что работа, совершаемая для перемещения частицы, обладающей энергией, будет равняться разности значений функций в начальной и конечной точке положения: A = Eп1 — Eп2. Каждый потенциал будет описываться своей координатой.

Eп может быть определена с точностью до постоянной. Для этого необходимо лишь назначить точку отсчёта. Выбирают её в зависимости от решаемой задачи. Ей может быть потенциал:

• земли;
• бесконечно удалённой точки поля;
• отрицательной пластины конденсатора.

Но чаще для удобства принимают ноль. Так как значение энергии зависит от электростатических сил и величины заряда, то различные пробные частицы в одной точке могут иметь разный потенциал. Чтобы избежать недоразумений, к термину было добавлено слово «электрический».

Обозначают эту величину греческой буквой φ (фи). Численно же её находят из отношения: φ = Eп/q. Фактически электрический потенциал является энергетической характеристикой электростатического поля.

В Международной системе измерений принято параметр измерять в вольтах или джоулях, делённых на кулон. Это название для измерения потенциала было выбрано по имени физика Алессандро Вольта, внёсшего огромный вклад в исследование взаимодействия электрических токов и сформулировавшего гипотезу объясняющую магнитные свойства вещества.

Напряжённость и потенциал

Если нет потенциальной энергии, то, естественно, не будет и поля, вызванного этой силой. Электричество может создаваться как положительно заряженной частицей, так и отрицательной. Электростатическая энергия возникает и из совокупности зарядов, имеющих разные знаки. Чтобы можно было определить изменение потенциала, одну из точек считают нулевой. Остальные значения находят относительно этой координаты. Например, в электротехнике за нулевой потенциал принято брать поверхность земли.

Электростатическое поле можно описать с помощью векторной величины напряжённости и скалярной — потенциала. Поэтому между ними должна существовать определённая связь. Если путь перемещения по произвольной траектории обозначить L, то работу на бесконечно малом отрезке можно найти как дифференциал: dA = F * dL. Напряжённость — это величина, пропорциональная силе, действующей на неподвижный заряд и обратно пропорциональна значению энергии частицы: E = F / q. Отсюда следует, что dA = Ei * q * dL. Полная сила, которая воздействует на электрон, выражается формулой Лоренца: F = qE + qV * B, где B — магнитная индукция.

Так как работа, совершаемая при перемещении заряда электростатическим полем, равняется уменьшению потенциальной энергии частицы, изменившей своё положение на dL, то можно записать следующие равенства: dA = — q dφ; Ei * qdL = — qdφ. Отсюда: Ei = — d φ / — dL.

Проекциями напряжённости на оси будут следующие координаты: Ex = -dφ / dx; Ey = -dφ / dx; Ez = -dφ / dx. То есть E = — dφ / dx — dφ / dy — dφ / dz. Градиент этой суммы равен: grad φ = i (dφ / dx) + j (dφ / dy) + k (dφ / dz). Вектор показывает направление возрастания функции. Отсюда связь между потенциалом и напряжённостью будет выглядеть так: E = — grad (φ) = -∇φ, где ∇ — оператор Гамильтона.

Нужно отметить, что разность потенциалов по-другому называется напряжением: φ1 — φ2 = U. Формулу можно представить по-другому: Δφ = ΔW / q. По сути, разница — это приращение потенциала, разница характеризуюется изменением энергии. Отсюда следует, что измеряться напряжение будет в тех же единицах, что и потенциал. Эти выражения действительны лишь при условии, что сторонних сил нет.

Простейшие задачи

Чтобы успешно решать простые задания, связанные с электрическим потенциалом, нужно знать несколько формул.

Но при этом нужно уделять пристальное внимание размерности. Вот несколько типовых примеров, предлагаемых к самостоятельной проработке школьникам:

1. Электрические потенциалы двух изолированных проводников, оторванных от пола, равны 110 B и -110 B. Найти работу, которая совершится при переносе заряда 5 * 10^-4 с одного проводника на другой. Под потенциалом понимается, что для первого тела электростатическое поле равняется 110 вольт, а для второго — 110 В. Для решения примера понадобится воспользоваться двумя формулами: U = φ1 — φ2 и E = A / q. Из второго выражения можно определить работу, а вместо напряжения подставить разность потенциалов: A = q * E = q * (φ1 — φ2) = 5 * 10−4 Кл * (110 В + 110В) = 5 * 10−4 Кл * 220 Дж / Кл = 110 * 10−3 Дж.
2. Какую скорость может сообщить электрону, находящемуся в состоянии покоя, ускоряющая разность потенциалов в 1000 вольт. Масса частицы 9,1 * 10^-31 кг. Для решения этой задачи понадобится взять из справочника значение элементарного заряда: e = 1,6 * 10^-19 Кл. Работа, затрачиваемая на движение, определяется как A = q * U = — e * U. Так как заряд отрицательный, то φ2 должно быть больше φ1. Значит: A = e * Δφ. В то же время затрачиваемая энергия равняется ΔW = (mV² / 2) — 0. Остаётся объединить формулы и выразить искомую величину: V = √(2 * e * Δφ) / m = √ (2 * 1,6 * 10^-19 Кл * В) / 9,1 * 10^-31 кг = 1,9 * 10⁷ м / с.
3. Четыре заряда по 40 нКл расположены по углам квадрата со сторонами 4 см. Определить потенциал поля в центре фигуры. Этой серединой в геометрическом теле будет точка пересечения диагоналей. Решая эту задачу, можно опереться на принцип суперпозиции. Он гласит, что потенциал системы будет равен алгебраической сумме полей каждого заряда в отдельности: φ = Σ4φ1. Потенциал точечного заряда можно найти по формуле φ1 = (k * q) / r, где: r — расстояние до точки, где нужно измерить величину. Отсюда следует: φ = 4√2 * K * q / a = 4√2 * 9 * 109 (Н * м2) / Кл * (40 * 10−9 Кл / 4 * 10−2) м = 36 * √2 кВ = 51 кВ.

Таким образом, решать примеры, связанные с потенциалом несложно. Нужно понимать суть величины и уметь анализировать условие задач. Причём все вычисления должны быть выполнены в СИ.

2. Потенциал электростатического поля

Найдем работу, совершаемую силой электростатического поля, созданного точечным зарядомq, по перемещению пробного заряда из точки 1 в точку 2. Положение этих точек относительно зарядаq определяется радиус-векторами , а положение заряда– радиус-вектором(рис.6).

На основании формул (5) и (4) в любой точке траектории на заряд q_пр действует сила

, (6)

где – напряженность поля зарядаq в месте нахождения заряда .

Работа этой силы при элементарном перемещении заряда

, (7)

где , а работа по перемещению зарядаиз точки 1 в точку 2

. (8)

Из формулы (8) вытекает, что работа силы по перемещению заряда из одной точки электростатического поля в другую не зависит от формы пути, а зависит от координат начального и конечного положений заряда. Следовательно,электростатическое поле точечного заряда является потенциальным, а электростатические силы – консервативными.

Рис. 6. Перемещение пробного заряда в электростатическом

поле заряда qиз точки 1 в точку 2

К такому же выводу мы придем, если будем рассматривать электростатическое поле, созданное не одним зарядом, а системой зарядов.

Из закона сохранения энергии следует, что работа по перемещению заряда в электростатическом поле совершается за счет уменьшения потенциальной энергииэтого заряда в поле:

. (9)

Зная величину в разных точках поля, по формуле (9) удобно определять работу, которую совершат силы поля по перемещению зарядаиз одной точки в другую. Следовательно, для электростатического поля можно ввести понятие энергетической характеристики аналогично тому, как была введена его силовая характеристика – напряженность. Для этого используют отношение, которое уже не зависит от, а определяется только зарядом, создающим поле, и положением точки. Это отношение называетсяпотенциалом:

. (10)

Потенциал j электростатического поля есть физическая величина, численно равная потенциальной энергии, которой обладает точечный единичный положительный заряд, помещенный в данную точку поля..

Единицей потенциала является вольт (В):

.

На основании (9) и (10) можно записать формулу для работы, совершаемой силами электростатического поля по перемещению точечного заряда q из точки поля с потенциалом j₁ в точку с потенциалом j₂:

. (11)

Из выражения (11) вытекает физический смысл разности потенциалов:

разность потенциаловмежду двумя точками электростатического поля численно равна работе, которую совершают силы поля по перемещению точечного единичного положительного заряда из одной точки в другую.

На основании (5), (8) и (11) можно записать

или, (12)

где a – угол между вектором и вектором .

Формула (12) устанавливает связь разности потенциалов между двумя точками электростатического поля с напряженностью этого поля. Соотношение (12) справедливо не только для конечных перемещений, но и для бесконечно малых . Если точки 1 и 2 расположены бесконечно близко друг к другу, то убыль потенциала будет равна его дифференциалу со знаком минус, а в правой части (12) останется лишь подынтегральное выражение

. (13)

Потенциал, как и потенциальная энергия, определяется с точностью до произвольной постоянной С. В теории эту постоянную выбирают так, чтобы потенциал точки был равен нулю при бесконечном удалении ее от заряда, создающего поле . Это означает, что.

Следовательно,

. (14)

Выражение (14) позволяет дать еще одно определение потенциала, чаще используемое при решении задач: потенциал электростатического поля численно равен работе, которую совершает поле над единичным положительным зарядом при удалении его из данной точки на бесконечность.

Эквипотенциальной называется поверхность, все точки которой имеют одинаковый потенциал. С помощью этих поверхностей можно графически изображать электростатические поля.

Выясним, как ориентированы эквипотенциальные поверхности по отношению к линиям напряженности, с помощью которых также графически изображаются электростатические поля. Для этого воспользуемся связью (13) разности потенциалов между двумя точками одной эквипотенциальной поверхности, находящимися на расстояниидруг от друга, с напряженностьюв этом месте:

.

Равенство будет выполняться только в том случае, если уголa между вектором и эквипотенциальной поверхностью будет прямым. Следовательно,вектор всегда перпендикулярен к эквипотенциальным поверхностям и линии напря-женности всегда перпендикулярны к ним. Именно так проведены эквипотенциальные поверхности электростатического поля точечно-го заряда (рис. 7).

Обычно эквипотенциальные поверхности проводят так, чтобы разности потенциалов между любыми соседними поверхностями были одинаковыми. Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряженности в разных точках: там, где эти поверхности гуще, напряженность больше (рис. 7).

Работа сил электростатического поля. Потенциал

Тема: Работа сил электростатического поля. Потенциал электростатического поля. Потенциал электростатического поля точечного заряда. Потенциал электростатического поля системы точечных зарядов

Цель урока: формирование понятия потенциал как энергетической характеристики электростатического поля, представлений об эквипотенциальных поверхностях, умений определять потенциал электростатического поля точечного заряда, равномерно заряженной сферы, системы точечных зарядов, работу сил однородного электростатического поля.

Актуализация опорных знаний

1. Как обнаружить существование электрического поля?

2. Дайте определение напряженности электрического поля? Какова единица напряженности?

3. Как напряженность электрического поля зависит от расстояния?

4. Где начинаются и где заканчиваются линии напряженности электростатического поля?

5. Какое электрическое поле называется однородным?

6. Сформулируйте принцип суперпозиции электростатических полей.

Физический диктант

1. Как называется поле неподвижных зарядов?

2. Что является источником электрического поля?

3. Как называется сила, с которой взаимодействуют заряды?

4. Как называется физическая величина, равная отношению силы, действующей на заряд со стороны электрического поля, к этому заряду?

5. В каких единицах измеряется напряженность?

6. Как направлены силовые линии электрического поля?

7. Как изменится напряженность при увеличении электрического заряда?

8. Как изменится напряженность при увеличении расстояния от точки до заряда?

9. Как изменится сила, действующая на заряд, если напряженность электрического поля увеличить в 2 раза?

10. Какой заряд помещен в электрическое поле, если вектор силы, действующей на заряд, совпадает с вектором напряженности по направлению?

Ответы: электростатическим; заряд; кулоновская; напряженность; В/м; от «+» к «-»; увеличится; уменьшится; увеличится в 2 раза; положительный.

Новый материал

При перемещении тела между двумя точками в гравитационном поле работа силы тяжести не зависит от формы траектории его движения. Силы гравитационного и электрического взаимодействия имеют одинаковую зависимость от расстояния, и векторы сил направлены вдоль прямой, соединяющей точечные тела.

Можно предположить, что при перемещении заряда в электростатическом поле из одной точки в другую работа сил электрического поля не зависит от формы.

На заряд, помещенный в электростатическое поле напряженностью , действует сила , поэтому при его перемещении из А в В полем будет совершаться работа

Найдем работу поля при перемещении заряда по траектории АСВ

Найдем работу поля при перемещении заряда по криволинейной траектории.

Электростатическое поле ‒ это потенциальное поле, т.е. работа по перемещению заряда в этом поле не зависит от формы траектории, а зависит от начальной и конечной координат заряда.

Из механики: работа консервативных сил равна изменению потенциальной энергии, взятому с противоположным знаком:

С другой стороны

Следовательно

Рассмотрим два точечных заряда, расположенных на некотором расстоянии друг от друга.

Потенциальная энергия взаимодействия двух зарядов равна

Если заряды одноименные, то

Если заряды разноименные, то

Рассмотрим несколько точечных зарядов. Потенциальная энергия их взаимодействия равна сумме потенциальных энергий всех пар взаимодействующих зарядов

Введем еще одну характеристику электрического поля.

В точку А однородного электростатического поля с напряженностью помещаем заряд .

Потенциальная энергия заряда в этой точке

Найдем значение величины

В точку А однородного электростатического поля с напряженностью помещаем заряд .

Потенциальная энергия заряда в этой точке

Найдем значение величины

Аналогичный результат мы получим, если будем помещать в эту точку другие заряды. Следовательно, величина

• Не зависит от величины заряда, который мы помещаем в электрическое поле;

• Но зависит от параметров электрического поля

Новая характеристика электрического поля ‒ потенциал поля в данной точке

Потенциал электростатического поля ‒ это скалярная физическая величина, равная отношению потенциальной энергии, которой обладает точечный заряд в данной точке поля, к величине этого заряда.

Потенциал ‒ это энергетическая характеристика электрического поля.

Пусть электрическое поле создано точечным зарядом . В точке А, расположенной на расстоянии от заряда потенциал поля:

Значение потенциала электрического поля, созданного сферой радиуса , имеющего заряд , в точке А на расстоянии от центра сферы, равно

• , если

• , если

Свойства потенциала:

1. Потенциал (как и потенциальная энергия) зависит от выбора нулевого уровня

   1. За нулевой потенциал в технике выбирают:

   2. За нулевой уровень потенциала в физике принимается любая точка, бесконечно удаленная от зарядов, создающих поле

2. Если электрическое поле создано:

   1. Зарядом , то потенциал этого поля

   2. Зарядом , то потенциал этого поля

3. Принцип суперпозиции: потенциал поля, созданного несколькими зарядами, в некоторой точке пространства равен алгебраической сумме потенциалов, создаваемых в этой точке каждым из зарядов в отдельности.

Для графического изображения полей, кроме силовых линий электрического поля, удобно использовать эквипотенциальные поверхности (линии) ‒ поверхности (линии) равного потенциала.

Через каждую точку поля проходит только одна силовая линия и одна эквипотенциальная поверхность, причем в каждой точке поля силовая линия и соответствующая эквипотенциальная поверхность взаимно перпендикулярны.

Докажем факт взаимной перпендикулярности силовой линии и эквипотенциальной поверхности методом от противного. Предположим, что они не перпендикулярны. Тогда при движении заряда вдоль эквипотенциальной поверхности полем совершалась бы работа вследствие того, что существовала бы компонента поля вдоль поверхности. Но в этом случае она не была бы эквипотенциальной, так как ее потенциал не был бы одинаков во всех точках траектории при таком движении. Мы пришли к противоречию, что доказывает истинность исходного утверждения.

Потенциал всякого изолированного проводника можно измерить, сравнивая его с потенциалом Земли. Сделать это можно с помощью прибора, называемого электрометром или электростатическим вольтметром. Один из простейших электрометров ‒ электрометр Брауна ‒ аналогичен по устройству обычному электроскопу. Для определения потенциала заряженного проводника необходимо соединить его со стержнем электрометра, а металлический корпус электрометра соединить с Землей. Часть заряда перейдет на стержень электрометра и на подвижную легкую стрелку, которая, отталкиваясь от стержня, отклонится на некоторый угол и укажет на шкале значение потенциала проводника относительно Земли.

Электрометр Брауна пригоден для измерения разности потенциалов от 1000 до 10000 В. Существуют чувствительные электрометры, при помощи которых можно измерять разности потенциалов от 0,1 до 0,01 В. Напряжения от 0,1 до 1000 В измеряют с помощью бытовых вольтметров.

Во многих установках используются очень высокие разности потенциалов порядка 100 кВ (например, в кинескопе телевизора ~ 25 кВ). При таких разностях потенциачов возникают поля большой напряженности, которые могут ионизировать воздух, т. е. «вырывать» электроны из атомов, образуя большое число свободных заряженных частиц. Воздух становится проводником.. Пробой (искрение) интенсивно возникает на шероховатостях поверхностей и остриях, т. е. местах с малым радиусом кривизны, где напряженность поля становится наибольшей. Поэтому проводники стараются делать как можно более гладкими. Например, при радиусе кривизны 5 мм напряжение пробоя в воздухе, окружающем проводник, составляет ~ 15 кВ Это обстоятельство накладывает ограничения на максимальное значение напряжения, передаваемого по линиям электропередач, так как вследствие пробоя начинаются существенные потери электроэнергии через воздух.

Закрепление изученного

1. Что понимают под работой электростатического поля?

2. Запишите формулу работы электростатического поля по перемещению в нем заряда

3. Как связано изменение потенциальной энергии электростатического поля с совершаемой им работой?

4. От чего зависит работа по перемещению заряда из одной точки поля в другую?

5. Чему равна работа электростатического поля по перемещению заряда по замкнутому контуру?

6. Какие поля называют потенциальными?

7. Как понимать выражение «электростатическое поле потенциально»?

8. Что называют потенциалом электростатического поля?

9. По какой формуле можно определить потенциал электростатического поля?

10. В чем отличие потенциала электростатического поля от напряженности поля?

11. Какие поверхности называют эквипотенциальными?

12. Могут ли эквипотенциальные линии пересекаться?

Домашнее задание

Расчет электрического поля по потенциалу

В этой статье мы узнаем о расчете электрического поля по потенциалу. Мы также выведем связь между электрическим полем и электрическим потенциалом. Электрический потенциал и электрическое поле — сложные, но очень важные темы электростатики. Иногда учащиеся путаются между этими двумя величинами. Хотя и электрическое поле, и потенциал являются величинами, связанными с электростатикой, между ними есть много различий. Электрическое поле является векторной величиной, а электрический потенциал, с другой стороны, является скалярной величиной.

Сначала мы сделаем общий обзор обеих тем, а затем обсудим, как рассчитать напряжение по электрическому полю.

Важные термины и определения

Электрический потенциал

Электрический потенциал – это работа, совершаемая внешним агентом на единицу пробного заряда при перемещении пробного заряда из одной точки в другую в постоянном электрическом поле. Поскольку потенциальная энергия является скалярной величиной, электрический потенциал также является скалярной величиной. Единицей СИ для электрического потенциала является вольт (В).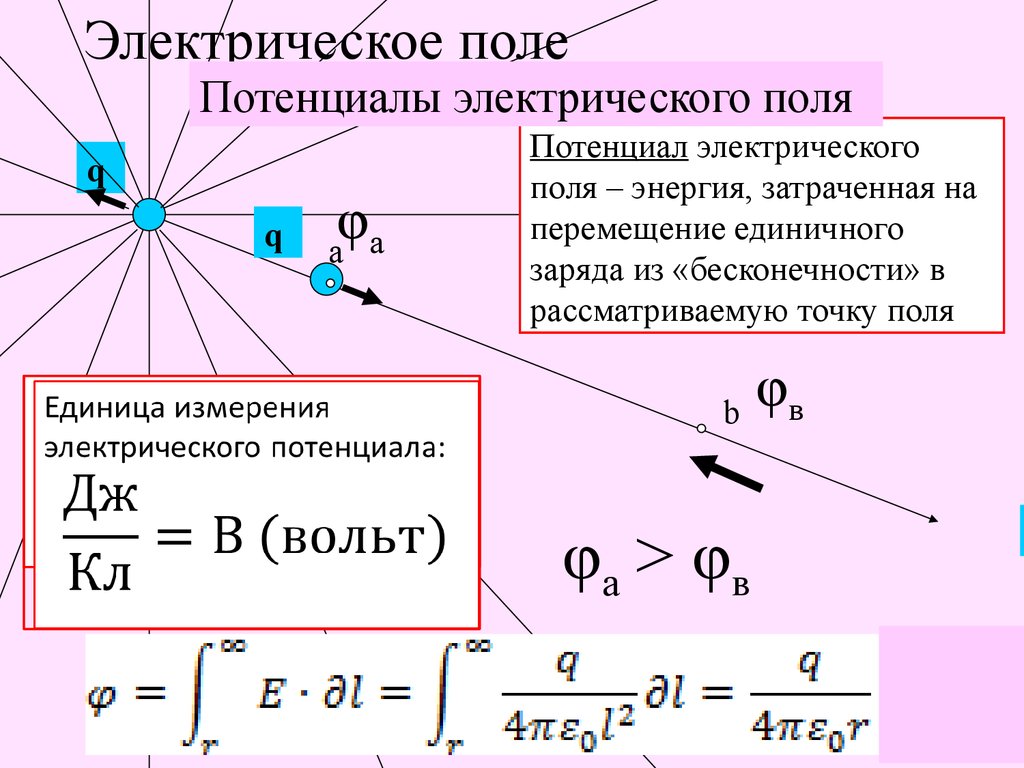 Математически это представляется как,

$V = \frac{W}{Q}$

Где,
$V =$ Электрический потенциал в вольтах
$W =$ Работа в джоулях
$Q =$ Электрический заряд в кулонах

Электрический потенциал к точечному заряду

Электрический потенциал в точке электрического поля определяется как количество работы, совершаемой для перемещения единичного положительного электрического заряда из бесконечности в эту точку.

$V = \frac{Q}{4\pi \epsilon_0 r}$

Где,
Расстояние между зарядом и точкой $= r$
Заряд источника $= Q$
Постоянная Кулона = $\frac{1}{4\pi \epsilon_0 r}$

Если одна точка имеет электрический потенциал 5 вольт, то можно сказать, что она совершает работу 5 джоулей перенести из бесконечности в эту точку заряд в один кулон.

Разность электрических потенциалов

Разность электрических потенциалов определяется как количество работы, необходимой для перемещения единичного заряда из одной точки в другую в электрическом поле. Его также можно определить как разность электрических потенциалов двух заряженных частиц.

Единицей СИ для разности электрических потенциалов является вольт (В).

Таким образом, говорят, что разность потенциалов между двумя точками равна одному вольту, если при перемещении единицы заряда из одной точки в другую совершается работа в один джоуль.

Например, рассмотрим двухэлементные точечные заряды A и B с электрическим потенциалом 10 вольт и 3 вольта соответственно. Затем требуется работа в 7 джоулей, чтобы переместить единичный заряд B в местонахождение заряда A.

Электрическое поле

Электрическое поле — это физическое поле, которое окружает электрически заряженную частицу. В этом поле заряженные частицы воздействуют электромагнитной силой на все другие заряженные частицы, либо притягивая, либо отталкивая их.

Электрическое поле определяется в каждой точке пространства как сила на единицу заряда, которую испытал бы пробный заряд, если бы его удерживали в этой точке.

Производными единицами СИ для электрического поля являются вольты на метр (В/м), что эквивалентно ньютону на кулон (Н/Кл).

Расчет электрического поля по потенциалу

Для расчета напряжения по напряженности электрического поля сначала выведем соотношение между электрическим полем и электрическим потенциалом 9B{\vec E \cdot \vec {dr}}$

Здесь $dr $ обозначает малое расстояние, на которое перемещается единичный положительный заряд. Если электрическое поле между этими точками известно, приведенное выше соотношение можно использовать для вычисления разности потенциалов между двумя точками.

В электрическом поле заряда $+q$, расположенного в точке O, рассмотрим две близлежащие точки $A$ и $B$, как показано на рисунке ниже. Пусть точки A и B разделены $\Delta r$ (т.е. $AB = \Delta r$) на небольшое расстояние. Напряженность электрического поля между точками $A$ и $B$ остается постоянной, так как они находятся очень близко друг к другу. 90$, потому что они действуют по одной и той же линии действия, но в противоположном направлении.

Следовательно,

$E=-\frac{\Delta V}{\Delta r}$

Если мы приблизим точки $A$ и $B$ друг к другу так, что $\Delta r \rightarrow 0 $, то приведенное выше выражение может быть представлено в математической форме, т.е. .

Эта величина $dv/dr$ представляет собой скорость изменения электрического потенциала с расстоянием и называется градиентом потенциала. Отсюда

электрическое поле в любой точке равно отрицательному значению градиента потенциала в этой точке.

Есть преимущество в выражении электрического поля через $V$ (потенциал). Поскольку $V$ является скалярной величиной, анализ электрического поля упрощается. Кроме того, электрический потенциал дает понятие энергии, которое помогает в решении многих проблем. Итак, если известен электрический потенциал в каждой точке области пространства, электрическое поле можно было бы вычислить из потенциала, поскольку электрическое поле $E=-\frac{dV}{dr}$. 92)}{dx}=6x$

При $x=2$ $E = 6 \times (2) = 12 В/м$

Следовательно, электрическое поле $E$ при $(2,1, 2)$ составляет $12 В/м$.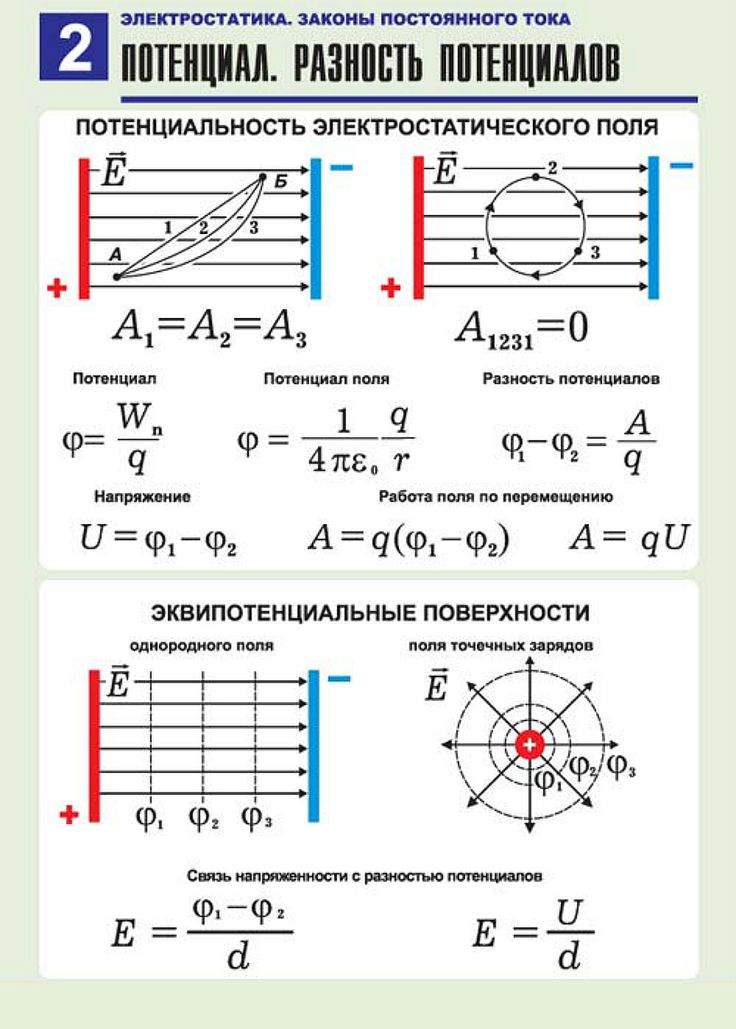

Похожие статьи

• Какой символ и единица измерения используются для напряжения?
• Величина электрического поля
• Разность электрических потенциалов Видеоруководство

Лабораторная работа 1. Электрическое поле и электрический потенциал

Введение

Физики используют понятие поля для объяснения взаимодействия частиц или тел в пространстве, то есть силы «действия на расстоянии» между двумя телами, не находящимися в физическом контакте. Земля изменяет окружающее пространство таким образом, что любое тело, обладающее массой, например Луна, притягивается к ней. Гравитационное поле становится слабее по мере удаления от источника, но никогда полностью не исчезает. Электрон изменяет пространство вокруг себя таким образом, что другие частицы с таким же зарядом отталкиваются, а частицы с противоположным зарядом притягиваются. Как и гравитационное поле, электрическое поле становится слабее по мере удаления от источника, но никогда не исчезает полностью. Любой заряд, помещенный в электрическое поле, будет испытывать силу, как и любая масса, помещенная в гравитационное поле. Как масса в гравитационном поле обладает некоторой потенциальной энергией, так и заряд в электрическом поле. В этой лабораторной работе мы рассмотрим некоторые аспекты электрического поля и электрического потенциала.

Обсуждение принципов

На заряженное тело действует сила

F

всякий раз, когда оно помещено в электрическое поле

E.

Векторная зависимость между силой и электрическим полем определяется выражением

( 1 )

F = qE.

Величина силы, деленная на величину заряда q на теле, численно равна величине электрического поля.

( 2 )

Е =  

Из уравнения

. (1)

F = qE.

, мы видим, что направление вектора электрического поля в любой заданной точке совпадает с направлением силы, действующей полем на положительный пробный заряд, находящийся в этой точке. Положительный пробный заряд будет отталкиваться от положительного заряда и притягиваться к отрицательному. Следовательно, силовые линии электрического поля начинаются на положительных зарядах и заканчиваются на отрицательных. Количество линий, начинающихся с положительного заряда или заканчивающихся отрицательным зарядом, пропорционально величине заряда. Электрическое поле в любой точке касается линий электрического поля. Магнитуда E напряженности электрического поля пропорциональна количеству линий электрического поля на единицу площади, перпендикулярных линиям. Положительный заряд, помещенный в электрическое поле, будет стремиться двигаться в направлении силовых линий электрического поля, а отрицательный заряд будет стремиться двигаться в направлении, противоположном направлению силовых линий электрического поля.

Работа, потенциальная энергия и электростатический потенциал

Работа совершается при перемещении заряженного тела через электрическое поле. Объем работы W done зависит от электрического поля, величины заряда и смещения

d 

, которое заряд совершает через поле. Когда смещение настолько мало, что электрическое поле можно считать однородным в области, через которую движется заряд, работа Вт определяется выражением

( 3 )

Вт = |F||d| cos θ = q|E||d| cos θ  

где θ — угол между векторами поля и смещения или векторами силы и смещения. Отрицательная работа, совершаемая электрической силой, определяется как изменение электрическая потенциальная энергия U тела. Иными словами, это разница потенциальных энергий

ΔU

, связанных с начальным и конечным положениями.

( 4 )

−W = ΔU = (U _{окончательный} − U _{начальный} )

Электростатический потенциал В определяется как электрическая потенциальная энергия тела, деленная на его заряд:

В = U/q

. В терминах электростатического потенциала работа, совершаемая электрическим полем, равна

( 5 )

W = −qΔV

где

ΔV = V _{конечное} — V _{начальное}  

есть разность потенциалов . Величина электрического поля также может быть определена из уравнения

. (3)

Вт = |F||d| cos θ = q|E||d| cos θ  

и

(5)

W = −qΔV

.

( 6 )

E =

ΔV

d cos( θ )

 

3

3 Когда заряженная частица движется в электрическом поле, если ее электрическая потенциальная энергия уменьшается, ее кинетическая энергия увеличивается. Другими словами, полная энергия сохраняется. Положительный заряд, помещенный в электрическое поле, будет стремиться двигаться в направлении поля. Работа, совершаемая электрическим полем, в этом случае будет положительной, поскольку векторы поля и смещения имеют одинаковое направление, а угол между двумя векторами будет равен нулю, как показано на рис. 1 (а). Обратите внимание, что вектор скорости указывает направление вектора смещения заряда.

Рисунок 1 : Движение зарядов в электрическом поле

Из уравнения

. (4)

−W = ΔU = (U _{конечный} − U _{начальный} )

, видим, что изменение электрической потенциальной энергии в этом случае будет отрицательным. Следовательно, он будет терять электрическую потенциальную энергию и приобретать кинетическую энергию. Это говорит нам о том, что электрический потенциал уменьшается в направлении силовых линий электрического поля. Положительный заряд, если он свободно перемещается в электрическом поле, будет перемещаться из точки с высоким потенциалом в точку с низким потенциалом. Теперь рассмотрим отрицательный заряд, помещенный в электрическое поле, как показано на рис. 1(б). Он будет стремиться двигаться в направлении, противоположном электрическому полю, и при этом ускоряться. Работа, совершаемая электрическим полем, будет

( 7 )

W = (−q)Ed cos(180) = qEd

Опять же, обратите внимание, что работа, совершаемая электрическим полем, положительна, и отрицательный заряд будет терять электрическую потенциальную энергию и приобретать кинетическую энергию, когда он движется против поля. Отрицательный заряд, если он свободно перемещается в электрическом поле, будет перемещаться из точки с низким потенциалом в точку с высоким потенциалом. Чтобы переместить положительный заряд против электрического поля, работа должна быть совершена вами или внешней по отношению к полю силой. Заряд вынужден перемещаться из точки с низким потенциалом в точку с высоким потенциалом, а работа, совершаемая внешней силой, отрицательна. Обратное будет верно для отрицательного заряда. Как и в случае гравитационного поля, нулевая точка электрического потенциала выбирается произвольно. В общем случае нулевая точка находится на бесконечности. Очень часто нулевой точкой является земля или проводник, непосредственно соединенный с землей.

Эквипотенциальные линии и линии электрического поля

Рассмотрим поле, создаваемое одиночным точечным зарядом. Точка в этом пространстве вблизи источника поля (т. е. вблизи точечного заряда) и другая точка вдали от источника поля имеют разные потенциалы. Это верно, даже если в двух точках нет зарядов. На рис. 2 точки А и В находятся под разными потенциалами из-за электрического поля положительного заряда.

Рисунок 2 : Электрический потенциал в различных точках поля

Все поля имеют определенные точки с одинаковым потенциалом. Например, когда источником поля является точечный заряд, то любые две точки, находящиеся на одинаковом расстоянии от точечного заряда (точки А и С на рис. 2), будут иметь одинаковый потенциал. Существует бесконечное число точек, лежащих на одной и той же сфере, находящихся на одном и том же расстоянии и имеющих одинаковый потенциал. В трех измерениях эти точки образуют поверхность, называемую эквипотенциальная поверхность . В двух измерениях — скажем, в экваториальной плоскости сферы — окружность (экватор), где сфера пересекает плоскость, представляет собой эквипотенциальную линию ; разность потенциалов между любыми двумя точками на этой прямой равна нулю. Из уравнения

следует (4)

−W = ΔU = (U _{конечная} − U _{начальная} ) 

что при перемещении заряда вдоль «эквипотенциала» (то есть эквипотенциальной линии или поверхности) не совершается никакой работы.

Уравнение (4)

−W = ΔU = (U _{конечное} − U _{начальное} )

также говорит нам о том, что работа не совершается, когда смещение и поле перпендикулярны друг другу. Поэтому векторы электрического поля должны быть перпендикулярны эквипотенциалам.

Рисунок 3 : Линии электрического поля и эквипотенциальные линии

На рис. 3 показаны некоторые линии электрического поля (синие линии со стрелками) для положительного заряда. Пунктирные красные круги — это два из множества эквипотенциальных кругов. В любой заданной точке одной из этих окружностей касательная к окружности будет перпендикулярна направлению линии электрического поля в этой точке. Поскольку непосредственно найти силовые линии электрического поля непросто, в этом эксперименте вы сначала определите местонахождение эквипотенциальных линий, а затем начертите силовые линии, зная, что они перпендикулярны эквипотенциальным линиям.

Цель

Цель этого эксперимента — провести эквипотенциальные линии для четырех различных конфигураций заряда. Затем вы будете использовать эти эквипотенциальные линии для отображения линий электрического поля для каждой конфигурации.

Оборудование

• Картограф научных полей PASCO
• Программное обеспечение Capstone
• Источник питания
• Электроды
• Пробник напряжения

Процедура

Пожалуйста, распечатайте рабочий лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.

Вы будете использовать научный полевой картограф PASCO, который состоит из листа пропитанной углеродом бумаги. Электроды или заряженные тела образованы линией токопроводящих чернил, нанесенной на бумагу и затем высушенной. Вам будут предоставлены четыре конфигурации электродов, уже нарисованные на токопроводящей бумаге, которые соответствуют копиям, приведенным в рабочем листе. Паттерны показаны на рис. 4 ниже.

Рисунок 4 : Шаблоны электродов

1

Не рисуйте на бумаге с углеродной пропиткой.

Вы будете использовать картограф поля, чтобы определить эквипотенциальные точки и перенести эти местоположения в соответствующую копию, представленную на рабочем листе.

Оригинал проводящей бумаги и копия имеют одинаковое количество реперных меток, но на копии они ближе друг к другу, чем на оригинале, т. е. масштаб разный.

2

Вставьте пробник напряжения (штекер с красным и черным проводом) в аналоговый канал А универсального интерфейса PASCO 850 и подключите два провода к выходу 1 интерфейса.

Это будет служить вашим вольтметром.

Ваш интерфейс должен иметь соединения, подобные показанным на рис. 5.

Рисунок 5 : Схема подключения к компьютерному интерфейсу

Рисунок 6 : Фото соединений с компьютерным интерфейсом

Процедура A: Параллельные линии

3

Подсоедините выходные провода сигнального интерфейса «Выход 1» к болтам на токопроводящей бумаге.

Затем подключите – провод (черный) от пробника напряжения к – от выхода 1.

Провод + от датчика напряжения будет размещен в различных местах конфигурации и будет измерять разность потенциалов между этим местом и электродом, подключенным к первому проводу датчика напряжения.

Соединения электродов должны выглядеть так, как показано на рис. 7.

Рисунок 7 : Соединения электродов

4

Откройте соответствующий файл Capstone, связанный с этой лабораторией.

На рис. 8 показан начальный экран в Capstone. Вы увидите окно «Настройка эксперимента», окно «Генератор сигналов» и окно «Цифры».

Рисунок 8 : Открытие экрана Capstone

5

Окно «Генератор сигналов» отображается слева от дисплея напряжения. Установите напряжение постоянного тока на 5 В с помощью кнопок со стрелками вверх/вниз (вверх для увеличения значения и вниз для уменьшения значения) справа от настройки напряжения, как показано на рис. 9.

Рисунок 9 : Окно «Генератор сигналов»

6

Включите генератор сигналов, нажав ВКЛ.

7

Для мониторинга сигнала нажмите Монитор в главном окне.

8

Используйте свободный провод (красный) от сигнального интерфейса, чтобы измерить потенциал в различных точках на бумаге вокруг электродов.

Не проводите пробником напряжения по бумаге, так как это может повредить бумагу.

Поднимайте зонд после каждого измерения, а затем перемещайте его в другое место на бумаге, чтобы выполнить следующее измерение.

Потенциал отображается на вольтметре в Capstone.

9

Поместите щуп в разные точки пространства между двумя параллельными линиями и определите направление увеличения напряжения.

Из этого определите, какая из двух параллельных линий имеет более высокий потенциал, и отметьте это в конфигурации параллельных линий на вашем рабочем листе.

10

При необходимости переориентируйте картографическую бумагу так, чтобы положительная линия была слева, как на рис. 4.

11

Проведите пять эквипотенциальных линий, пока они не закроются или не покинут график. Определите положение щупа по реперным меткам на бумаге и перенесите координаты этого положения на соответствующую копию.

12

На вашем графике должно быть пять эквипотенциальных линий, которые проходят через пространство между электродами и выходят к краям бумаги.

Обязательно пометьте напряжение каждой из эквипотенциальных линий.

13

Измерьте потенциалы в пяти точках A , B , C , D и E . Запишите эти значения напряжения в таблицу данных 1 на рабочем листе.

14

Измерьте расстояние этих пяти точек от положительной линии и запишите их в Таблицу данных 1.

15

Постройте пять линий электрического поля, соединяющих один электрод с другим. Нарисуйте стрелки, указывающие направление линий поля.

16

Выполните расчеты для таблицы данных 2 на рабочем листе.

КПП 1:
Попросите вашего ТА проверить ваши линии поля и расчеты, прежде чем продолжить.

Процедура B: точка и линия

17

Поместите датчик в разные точки пространства между электродами, чтобы определить направление увеличения напряжения.

Исходя из этого, определите окончание конфигурации с высоким потенциалом и отметьте его на копии в своем рабочем листе.

18

При необходимости измените ориентацию картографической бумаги, чтобы она соответствовала показанной для этой конфигурации на рис. 4.

19

Повторите шаги 11 и 12 для конфигурации точек и линий. Определите эквипотенциальные точки по обе стороны от линии, а также вокруг точки.

20

Постройте пять линий электрического поля, соединяющих один электрод с другим, и нарисуйте стрелки, указывающие направление этих силовых линий.

Примечание: Чтобы провести линию, перпендикулярную кривой, рассмотрим касательную к кривой в точке.

21

Измерьте потенциалы в двух точках вдоль линии электрического поля вблизи точки A и по обе стороны от нее. Запишите эти значения напряжения в таблицу данных 3 на рабочем листе.

22

Измерьте расстояние между этими двумя точками и запишите его в рабочий лист.

23

Из значений, полученных на шагах 21 и 22, рассчитайте напряженность электрического поля в точке A , используя уравнение

. (6)

E =

ΔV

d cos( θ )

 

.

24

Повторите шаги с 21 по 23 для остальных четырех местоположений B , C , D и E .

25

Выполните расчеты для таблицы данных 3 на рабочем листе.

КПП 2:
Попросите вашего ТА проверить ваши линии поля и измерения, прежде чем продолжить.

Процедура C: диполь

26

Повторите шаги с 17 по 25 для конфигурации диполя. Определите эквипотенциальные точки в пространстве между двумя точками, а также вокруг точек.

27

Выполните расчеты для таблицы данных 4 на рабочем листе.

КПП 3:
Попросите вашего ТА проверить ваши линии поля и измерения, прежде чем продолжить.

Процедура D: линия и треугольник

28

Повторите шаги с 17 по 25 для конфигурации линии и треугольника.

Определить равнопотенциальные точки в пространстве как внутри треугольника, так и вне его.

29

Выполните расчеты для таблицы данных 5 на рабочем листе.

КПП 4:
Попросите вашего ТА проверить ваши линии поля и измерения.

Трехмерный электростатический анализ методом конечных элементов | by WELSIM — Программное обеспечение для инженерного моделирования

Современные электромагнитные исследования проникли в различные области. В последние годы, с быстрым развитием новых технологий, таких как 5G, электромобили и Интернет вещей, роль электромагнитного анализа становится все более важной. Электромагнитное моделирование широко и успешно применяется во многих аспектах прогнозирования и проектирования электромагнитных характеристик. При разумной настройке модели и параметров электромагнитное моделирование может заменить эксперименты во многих аспектах и ​​оказать большую помощь в быстрой разработке электромагнитных устройств.

Хотя электростатика является относительно более простым видом электромагнитного анализа, она имеет широкий спектр применений и служит основой для других видов электромагнитного анализа. Как важная часть электромагнетизма, электростатика столь же абстрактна и трудна для понимания, как и магнитное поле. В частности, явление электростатической индукции проводников в электростатическом поле также усложняет электростатический анализ.

Используя технологию моделирования конечных элементов, вы можете быстро и точно рассчитать распределение электростатического поля во многих конкретных случаях или условиях. Например, расчет электронных компонентов, таких как анализ емкости и индуктивности, проектирование различных типов кабелей, электромагнитное экранирование, электромагнитная совместимость, проектирование устройств молниезащиты и т. д. имеют множество применений. Электростатическое моделирование становится все более необходимым, особенно с увеличением мощности и рабочего напряжения электрооборудования. Электростатическое моделирование может прогнозировать такие показатели производительности, как изоляция, разряд и вероятность выхода оборудования из строя.

Численные методы трехмерного электростатического анализа

Все расчеты электромагнитного поля основаны на известных уравнениях Максвелла, и полная форма этого уравнения слишком тяжела для расчета электростатического поля. После ряда упрощений и допущений определяющее уравнение электростатического поля можно описать как уравнение Пуассона для электрического потенциала:

Где \phi — электрический потенциал, единицей измерения в международной системе единиц являются вольты, \эпсилон — диэлектрическая проницаемость, \rho — источник заряда, P — вектор поляризации.

В численных методах электромагнетизма обычно используются метод конечных разностей во временной области (FDTD), метод момента (MoM), метод конечных элементов (FEM) и метод разрывов Галеркина (DG). Поскольку электростатическая задача является эллиптической, согласно основному уравнению, МКЭ является одним из лучших способов ее решения. В настоящее время на рынке существует некоторое общее и специальное программное обеспечение для конечных элементов, которое может решать электростатические задачи. WELSIM также поддерживает расчет трехмерных линейных электростатических полей.

Параметром материала, обычно используемым в анализе электростатического поля, является диэлектрическая проницаемость. Диэлектрическая проницаемость в вакууме составляет 8,854e-12 Ф/м. Практическая инженерия также часто использует относительную диэлектрическую проницаемость для представления диэлектрических свойств материалов.

Обычно используемые граничные условия и источник возбуждения:

1) Напряжение

Напряжение, потенциальная величина в основном уравнении, является обычным кусочным граничным условием в электромагнитном анализе. Это граничное условие Дирихле.

2) Нормальная составляющая электрического смещения

Эта нормальная составляющая эквивалентна поверхностной плотности заряда на поверхности. Это редко используется, потому что плотность поверхностного заряда редко известна, если не известно, что она равна нулю. Однако если поверхностная плотность заряда равна нулю, то BC Неймана не нужны, поскольку это естественное граничное условие.

3) Заряд или плотность заряда

Источник электрического поля, обеспечивающий потенциальное возбуждение поля, которое может быть положительным или отрицательным. Как правило, это точечный или сферический заряд.

4) поляризация

В качестве источника электрического поля можно использовать векторную функцию поляризации. Поляризация может быть создана простым вольтовым столбом. Как правило, для определения этого источника требуется заданное положение и размер, а также величина поляризации.

Выполнение трехмерного электростатического анализа с помощью WELSIM

Анализ электростатического поля в WELSIM очень прост и удобен, а результаты распределения электрического поля можно быстро получить с помощью нескольких простых операций.

1) Создайте проект электростатического МКЭ

Создайте новый проект МКЭ и установите для параметра Физический тип значение Электромагнетизм в свойствах проекта МКЭ, а для Типа анализа установите значение по умолчанию Электростатика.

2) Определение материалов

При анализе электростатического поля основным параметром материала является диэлектрическая проницаемость. Здесь мы можем открыть настройку материала воздуха по умолчанию, которая поставляется с системой, где относительная диэлектрическая проницаемость была установлена ​​​​на 1, и вы можете использовать ее напрямую.

3) Построить модель

Создать куб 10x10x10 см3 для имитации распределения электрического поля. И установите материал куба на воздух.

4) Создайте сетку домена

Установите максимальный размер элемента на 0,5 см и нажмите кнопку Mesh. Поскольку решатель электромагнитного поля WelSim автоматически использует единицы более высокого порядка в соответствии с типом анализа, здесь нет необходимости устанавливать элементы более высокого порядка. После того, как построение сетки завершено, генерируется в общей сложности 9484 узла и 54119 элементов Tet4.

5) Наложить граничные условия или источники

Текущая версия WelSim поддерживает граничные условия напряжения, нулевого потенциала (земли) и плотности поверхностного заряда, а также источники точечного заряда, сферического заряда и поляризации для электростатического анализа.

Здесь мы устанавливаем

1) Периферийное нулевое напряжение моделирует поле на бесконечности.

2) Добавьте два точечных заряда и цилиндрическую поляризацию внутри поля.

Точечные заряды 0,1 мКл и -0,1 мКл соответственно, величина поляризации 0,1 мКл/мм2. Положения точечных зарядов и поляризационного цилиндра показаны на рисунках ниже.

6) Решить

Нажмите кнопку Решить, чтобы выполнить вычисление.

7) Оценить результаты расчета.

Добавьте результат напряжения, чтобы быстро оценить значения потенциала. С помощью инструментов постобработки, таких как плоскости отсечения, вы можете визуально проверить распределение внутреннего потенциала внутри поля.