Момент силы и плечо силы
Дано определение момента силы и плеча силы. Определение плеча и момента силы рассмотрено на примерах ОДА человека при выполнении силовых упражнений.
Итак, мы познакомились с рычагом и узнали, что рычаг находится в равновесии (то есть неподвижен), если силы, приложенные к нему обратно пропорциональны их плечам.
F2/F1 = h1/h2
Это условие равновесия имеет один существенный недостаток – оно хорошо работает, если к рычагу приложены только две силы, однако сил может быть и больше. Чтобы преодолеть это препятствие, нужно ввести новую величину, которая называется момент силы.
Давайте представим условие равновесия рычага в следующем виде: F1h1 = F2h2.
Слева от этого равенства представлены показатели, которые характеризуют воздействие первой силы на рычаг, а справа – второй. Именно произведение силы на плечо и является величиной, которая называется моментом силы.
Более подробно функционирование опорно-двигательного аппарата человека и биомеханика мышц описаны в книге:
Биомеханика опорно-двигательного аппарата человека
Определение момента силы
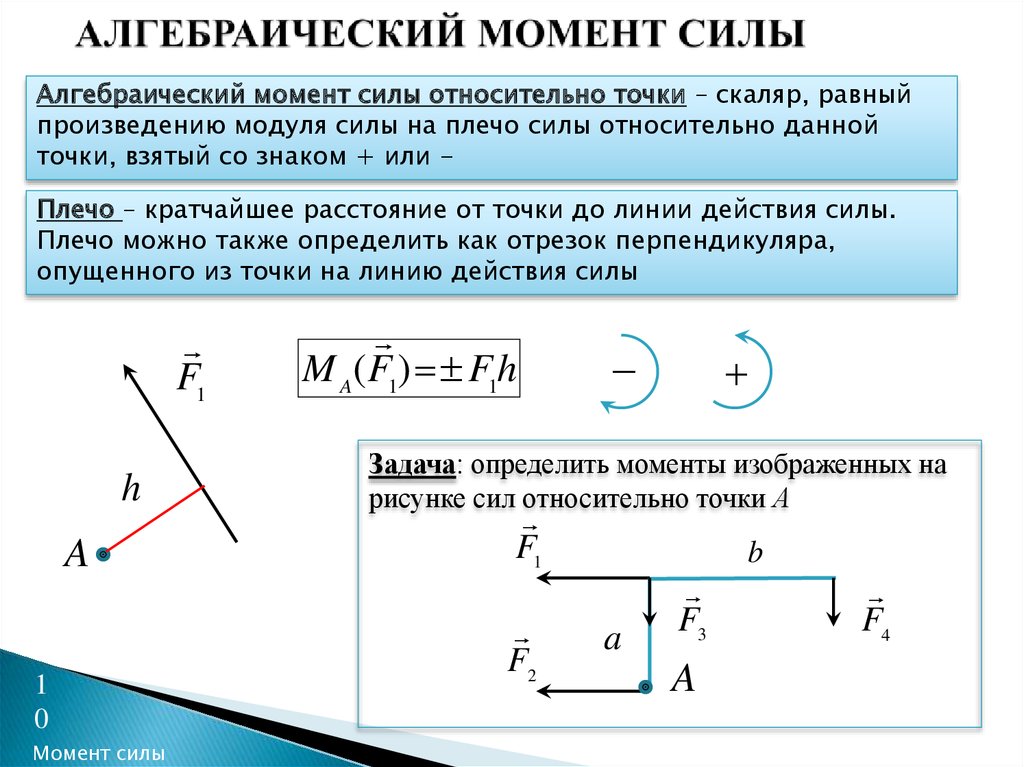
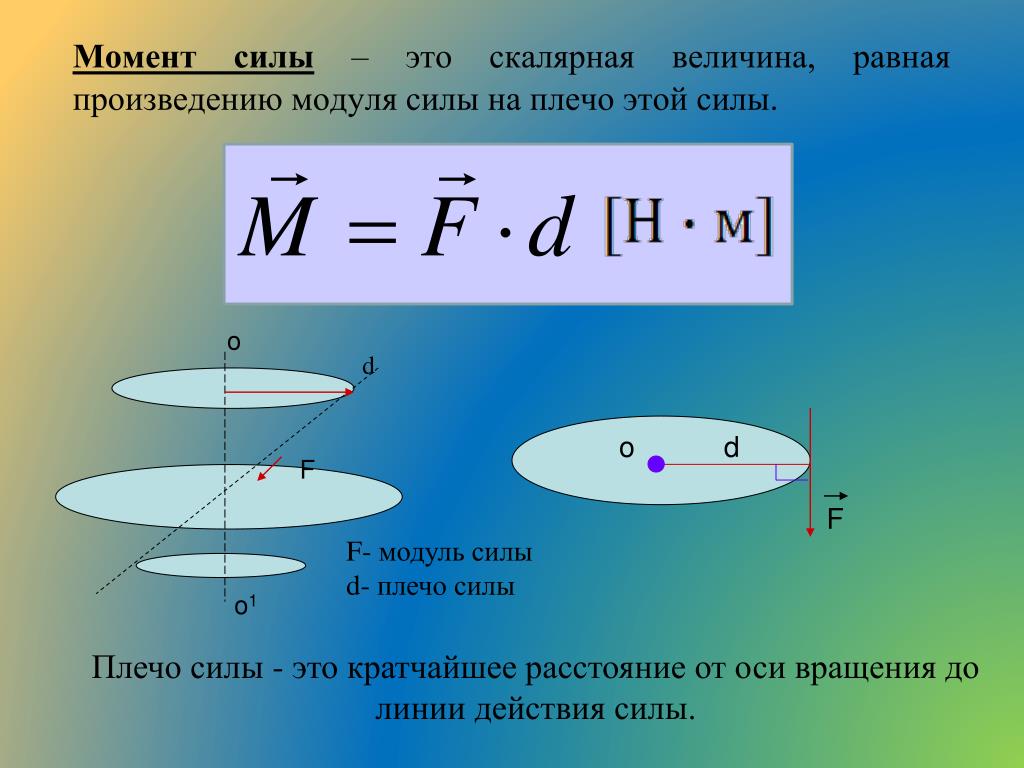
Момент силы относительно оси (М) – векторная величина, характеризующая меру вращательного действия силы. По своему значению момент силы относительно оси равен произведению силы на плечо силы:
М=F*h или Момент силы = сила*плечо силы.
Единица измерения момента силы – Ньютон х метр [Hм].
Момент силы считают положительным, если сила вызывает поворот тела против часовой стрелки, и отрицательным, при повороте тела по часовой стрелке.
Теперь давайте рассмотрим понятие плеча силы более подробно.
Определение плеча силы
Плечо силы относительно оси (h) – это кратчайшее расстояние (длина перпендикуляра) от оси вращения (или центра вращения) до линии действия силы (Рис.1).
Линия действия силы — это прямая, вдоль которой направлен вектор действия силы (она имеет бесконечную длину в обе стороны).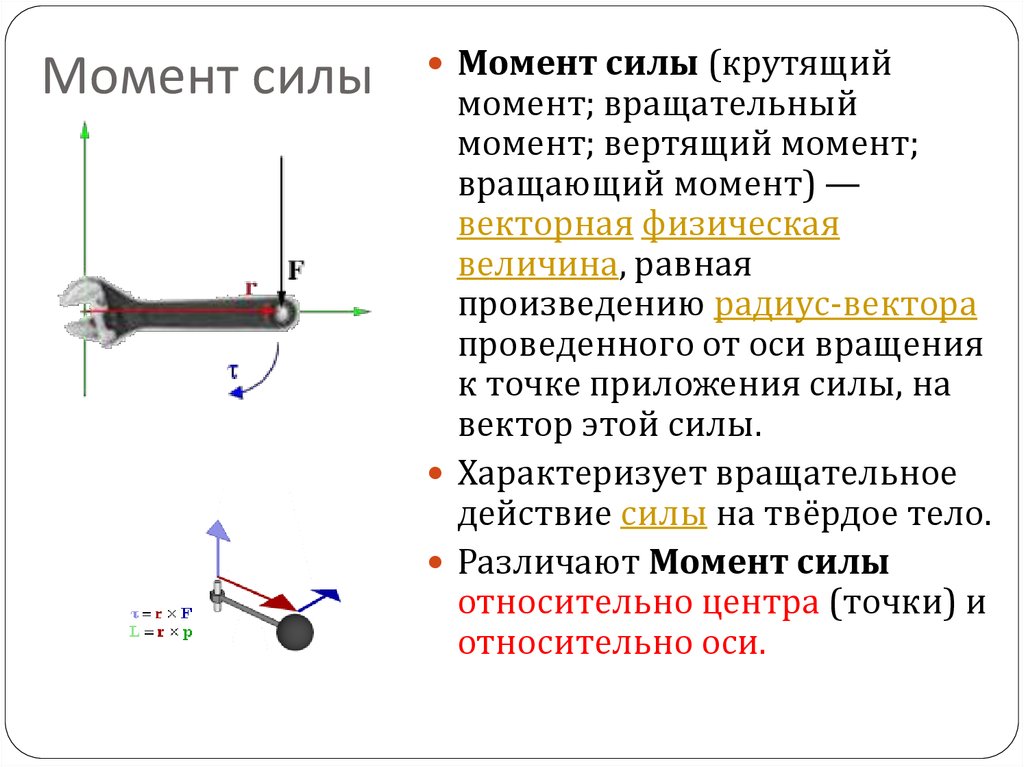
Из определения плеча силы следует, что при прохождении линии действия силы через ось вращения, плечо силы равно нулю.
Рис.1. Определение плеча силыНа рис.2. показаны два статических положения при выполнении жима штанги лежа: начальное (слева) и промежуточное (справа) в момент отрыва штанги от груди. Центром вращения является центр плечевого сустава. Плечо силы тяжести штанги относительно центра плечевого сустава в начальном положении (слева) равно нулю, потому что линия действия силы (она на рисунке показана штриховой линией) проходит через центр вращения (центр плечевого сустава). Плечо силы тяжести штанги в момент отрыва штанги от груди (справа) – это перпендикуляр, проведенный из центра вращения (центра плечевого сустава) до линии действия силы.
Рис. 2. Изменение плеча силы тяжести относительно центра вращения в плечевом суставе при жиме штанги лежа (П.И. Бегун, А.В. Самсонова, 2020)Рассмотрим еще одни пример. На рис.3. изображено статическое удержание гантели, закрепленной в области голеностопного сустава.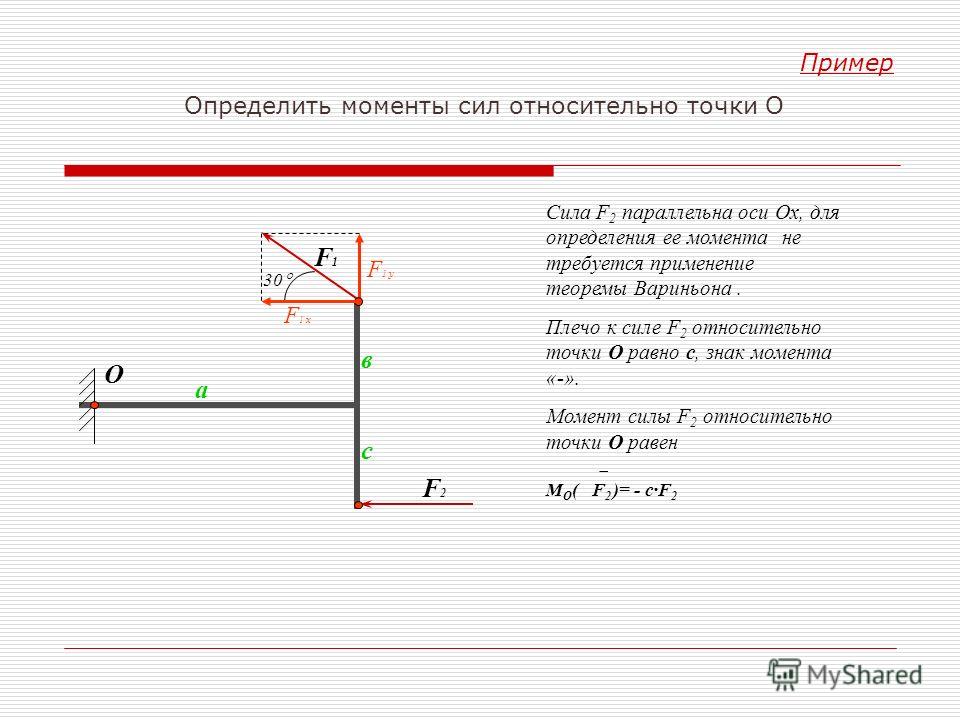
Сила тяжести представлена в виде вектора, направленного вертикально вниз. Линия действия силы тяжести представлена штриховой линией.
Плечо силы тяжести, соответствующее положению (рис. 3. а), равно нулю, так как линия действия силы проходит через ось вращения (центр коленного сустава). Плечо силы не является неизменным, а зависит от расположения голени относительно бедра. Максимальное значение плеча силы тяжести соответствует положению, изображенному на рис. 3.г. Именно это положение труднее всего удерживать длительное время.
Теперь рассчитаем значение момента силы тяжести относительно коленного сустава для положений, изображенных на рис.3. Давайте примем массу гантели равной 15 кг, то есть m = 15 кг, а плечи силы тяжести для положений а-г соответственно равными: а) hтяж =0; б) hтяж = 15 см; в) hтяж =30 см; г) hтяж = 40 см.
Массу голени в данном примере учитывать не будем.
Вначале определим значение силы тяжести гантели. Оно вычисляется по формуле и равно:
Fтяж = m*g = 15*9,8 = 147 H.
Напоминаю, что g – это ускорение свободного падения и оно равно 9,8 м/с2.
Для случая а: момент силы тяжести гантели относительно оси, проходящей через центр коленного сустава будет равен нулю, так как плечо силы тяжести равно нулю.
Для случая б: M= Fтяж*hтяж= 147*15= 2205 Н см
Для случая в: M= Fтяж*hтяж= 147*30= 4410 Н см
Для случая г: M= Fтяж*hтяж= 147*40= 5880 Н см
Таким образом, в положении г) сила тяжести гантели создает наибольший момент силы относительно центра коленного сустава. Удерживать гантель при полностью разогнутой ноге в коленном суставе значительно сложнее, чем при согнутой под углом в 90 градусов.
Если мы хотим учесть влияние момента, который создает сила тяжести, приложенная к голени и стопе относительно оси вращения, проходящей через центр коленного сустава (КС), необходимо определить главный момент силы относительно центра вращения в коленном суставе Мгл.
Главный момент силы (Мгл) равен алгебраической (то есть учитываются знаки моментов сил) сумме моментов силы тяжести голени (Мг, стопы (Мст) и гантели (Мган) относительно оси вращения, проходящей через центр коленного сустава (КС), то есть:
Мгл= Мг + Мст + Мган.
Чтобы пояснить метод расчета главного момента силы рассмотрим следующий пример.
Давайте рассчитаем для положения г (рис. 3г) значения главного момента силы тяжести относительно центра коленного сустава, учитывая массу голени, стопы и гантели. Массу голени примем равной 5 кг, то есть mг = 5 кг, плечо силы тяжести голени примем равным 20 см, то есть hг = 20 см; примем массу стопы равной 2 кг, то есть mст = 2 кг, а плечо силы тяжести стопы примем равным 35 см, то есть hст = 35 см;массу гантели примем равной 15 кг, то есть mган = 15 кг, плечо силы тяжести гантели примем равным 40 см, то есть hган = 40 см
Тогда:
Момент силы тяжести голени равен:Mг=Fг* hг= 5*9,8*20 = 980 Hсм
Момент силы тяжести стопы равен: Mст=Fст* hст=2*9,8*35= 686 Нсм.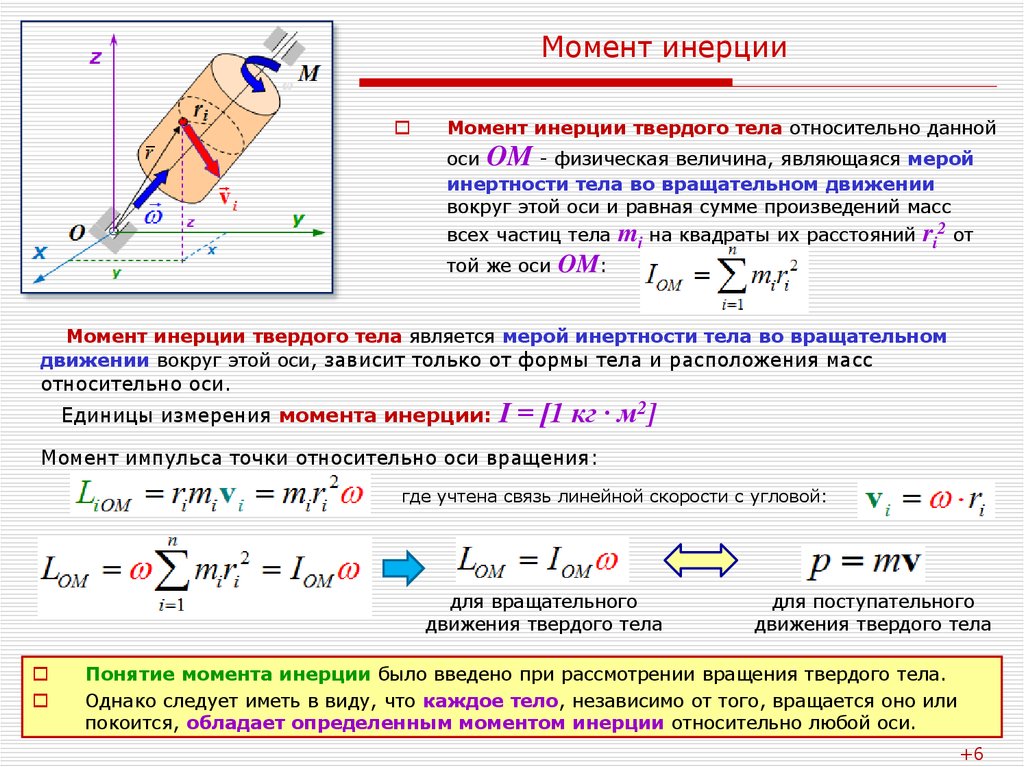
Момент силы тяжести гантели равен: Mган=Fган* hган= 15*9,8*40 = 5580 Нсм.
Главный момент силы тяжести системы «голень-стопа-гантель» равен:
Мгл = Мг + Мст + Мган = 980 + 686+ 5580 = 7546 Нсм.
(Правильнее было бы написать, что Мгл = -7546 Нсм, так как все силы создают момент силы по часовой стрелке, но так как при расчете главного момента не было сил, создающих положительный момент, я использовала абсолютные величины моментов).
Изменение главного момента силы тяжести рассмотрим на следующем примере (рис.4).
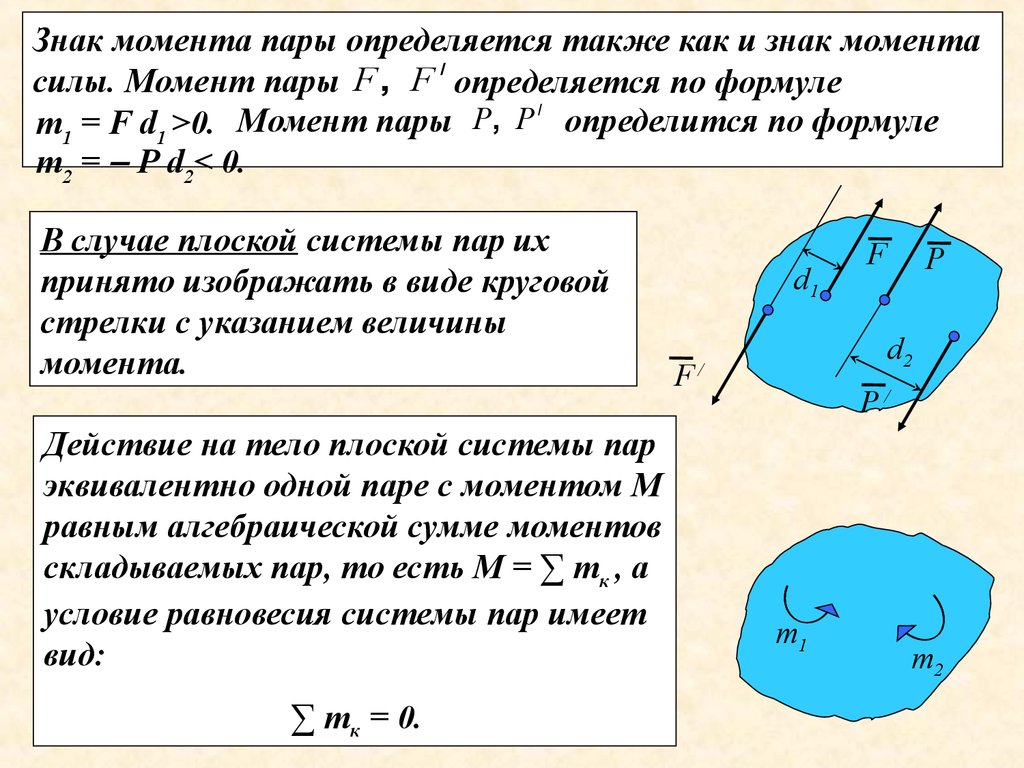
Рис.4. Изменение результирующего момента силы тяжести относительно тазобедренного сустава при различном положении верхних конечностей (Keogh J. W. L., Lake J. P., & Swinton P. A., 2013)Вы хорошо знаете, что выполнение упражнения, показанного на рисунке 4 легче всего выполнять, когда руки вытянуты вдоль туловище (то есть приближены к центру вращения, в данном случае это центр тазобедренного сустава).
Наиболее сложно выполнять это упражнение, когда руки вытянуты за голову. Почему это происходит? Дело в том, что положение рук изменяет главный момент силы тяжести. Главный момент силы тяжести – это сумма момента силы тяжести туловища, момента силы тяжести головы и момента силы тяжести рук. Моменты силы тяжести туловища и головы во всех трех положениях одинаковы, а момент силы тяжести рук меняется. Он тем больше, чем дальше центр тяжести рук расположен от центра вращения (в данном случае тазобедренного сустава), то есть больше плечо силы тяжести рук. Так как мышцам пресса и сгибателям бедра нужно противодействовать большему моменту силы тяжести, когда руки выпрямлены за головой, то и выполнять это упражнение значительно сложнее.
Литература
- Бегун П.И., Самсонова А.В. Биомеханика опорно-двигательного аппарата человека. – Монография. – СПб: Кинетика, 2020.- 179 с.
- Энока Р. Основы кинезиологии. Киев: Олимпийская литература, 1998. – 399 с.
- Keogh J.W.L., Lake J.
P., Swinton P.A. Practical Applications of Biomechanical Principles in Resistance Training: Moments and Moment Arms // Journal of Fitness Research, 2013.– Vol. 2.– N. 2. – P.39-48.
P., Swinton P.A. Practical Applications of Biomechanical Principles in Resistance Training: Moments and Moment Arms // Journal of Fitness Research, 2013.– Vol. 2.– N. 2. – P.39-48.С уважением, А.В.Самсонова
Похожие записи:
Распределение масс в теле человека
Описаны особенности распределения масс в теле человека. Дано понятие геометрии масс тела человека. Показано, что на…
Центр масс и центр тяжести тела
Описаны: центр масс (ЦМ) и центр тяжести (ЦТ) твердого тела. Приведены различные определения ЦМ и ЦТ тела. Показано…
Масса звеньев тела человека и способы ее оценки
Дано определение массы тела, а также описаны методы оценки массы звеньев тела человека, предложенные В. Брауне и О.
Рычаг. Типы (виды) рычагов
Дано определение рычага и типов рычагов. Приведены примеры рычагов первого и второго рода, используемые в быту, технике и…
Метаболический стресс. Накопление лактата в мышцах
Описан механизм влияния метаболического стресса (накопления лактата) на гипертрофию мышечных волокон.
Показано, что накопление лактата приводит к…
Спринтерский бег
Приведена рецензия на книгу В.В.Тюпа и В.Т.Тураева «Бег с максимальной скоростью» зав. кафедрой биомеханики НГУ им. П.Ф.Лесгафта, проф.
определение, формула расчета, пример решения задачи
Типичными задачами раздела физики «Статика» являются проблемы равновесия тел. В этом случае равенство нулю суммы внешних сил является недостаточной информацией для определения состояния рассматриваемого тела, поэтому используют другую величину, которая называется моментом силы. Чему равен он и как его использовать для решения задач на равновесие, рассматривается в этой статье.
Значение понятия
Определение момента силы или кручения, как его часто принято называть, можно дать следующее: это физическая величина, равная произведению действующей силы, приложенной к некоторой точке тела P, на плечо силы, равное расстоянию от оси крепления этого тела O до точки P. Для явного представления данного определения приведем иллюстрацию.
Здесь мы видим, что воздействие силы F на ключ длиною d (плечо) приведет к закручиванию гайки, которая играет роль оси O для данной системы.
В итоге можно записать, что модуль момента силы равен следующему выражению: M = d * F. Откуда видно, чем больше плечо d, тем потребуется меньшая сила F для создания определенного момента кручения M. Единица измерения в СИ для рассматриваемой величины — это ньютоны на метр (Н*м).
M¯ — это вектор
Мы рассмотрели не полностью вопрос, чему равен момент силы относительно оси. Дело в том, что воздействующая сила может быть приложена к рычагу под некоторым углом. И для этого случая не была приведена формула вычисления величины M. На самом деле последняя является вектором, а не скаляром. Она определяется через векторное произведение. Один вектор известен — это внешняя сила F¯. Другим направленным отрезком является OP¯ (в соответствии с точками, введенными в предыдущем пункте). Чему равен силы момент в этом случае? Он может быть записан в виде следующего выражения: M¯ = OP¯ * F¯ (черта над каждым множителем — это значок вектора).
Модуль произведения двух векторов равен абсолютной длине каждого из них на синус угла между ними. Поскольку в пункте выше между силой и плечом угол равен 90o, то векторная формула переводится в скалярный вид путем простого опускания значка вектора. Если же отмеченный угол не является прямым, тогда следует произведение модулей векторов домножить на синус соответствующего угла. Эта ситуация приведена на рисунке ниже.
Здесь видно, что сила F направлена под углом Φ, а это значит, что абсолютное значение момента силы можно рассчитать так:
M = L * F * sin(Φ).
Здесь L уже не является рычагом силы, однако, L * sin(Φ) = d (это равенство следует из определения синуса угла Φ), и скалярное выражение для момента снова можно записать в форме, приведенной в первом пункте статьи.
Направление вектора M¯
Итак, мы научились вычислять, чему момент силы равен относительно оси, но поскольку он является еще и вектором, то следует познакомиться с вопросом, как определять его направление.
Конечно, для этого можно воспользоваться правилом правой руки, которое справедливо для любого векторного произведения, однако результирующий вектор зависит от направления умножаемых отрезков и от порядка их следования в произведении, то есть результатом OP¯ * F¯ и F¯ * OP¯ будут векторы с противоположным направлением.
Поэтому рекомендуется запомнить следующее правило: если представить, что результирующая сила F привела к вращению тела вокруг его оси против часовой стрелки, значит, наблюдатель смотрит на систему с вершины вектора M¯, который в этом случае считается положительным. Наоборот, если сила F должна вызвать вращение тела по часовой стрелке, то наблюдатель смотрит на момент силы вдоль направления его действия, здесь модуль M¯ — это отрицательная величина.
Выше приведен рисунок, на котором показан вектор M¯ с учетом направления вращения в системе. Его модуль, согласно вышесказанному, является положительным, то есть +M.
Системы с несколькими действующими силами
До настоящего времени приводились примеры, в которых вращение осуществляет лишь единственная сила.
В общем случае таких сил может быть несколько. Как вычислять результирующий момент кручения? Величина M является аддитивной, то есть для ее вычисления можно суммировать момент от каждой силы, но при этом следует соблюдать знак (+M или -M).
Решение задачи на равновесие двух тел
Теперь решим простую задачу. Ниже приведен рисунок, где изображено два человека, находящихся в равновесии. Необходимо определить, во сколько раз желтый человек сидит дальше от оси вращения, чем зеленый, зная, что его вес в 1,5 раза меньше веса его напарника.
В первую очередь следует определить, какие силы действуют в системе. Их три: две силы тяжести каждого человека и сила реакции опоры оси. Поскольку плечо для последней равно нулю, то момента кручения она не создает. Остается рассмотреть две силы тяжести.
Так как система находится в равновесии, то общий момент силы тяжести равен нулю. Обозначим P1, P2 и x1, x2 — веса и расстояния от оси для желтого и зеленого человека, соответственно.
Вес желтого человека создает вращение против часовой стрелки, значит, его момент кручения является положительным. Для зеленого человека эта величина будет отрицательной. Тогда имеем: P1 * x1 — P2 * x2 = 0. Откуда получаем: P2 / P1 = x1 / x2 = 1,5.
Таким образом, желтый человек сидит в 1,5 раза дальше от оси, чем зеленый.
Момент силы — онлайн калькулятор
Момент силы — это векторная физическая величина, характеризующая действие силы на механический объект, которое может вызвать его вращательное движение. По другому можно сказать, что момент силы – это произведение силы на плечо этой силы.
В данном обзоре приведен онлайн калькулятор момента силы, теоретические основы и формулы расчета момента силы.
Калькулятор момента силы
Для расчета момента силы (M) необходимо ввести в калькуляторе значения силы (F) и радиус-вектор (r). Также имеется возможность определять силу по известному моменту силы и радиус-вектору, и соответственно радиус-вектор по известной силе и моменту силы.
Определившись с неизвестной величиной, введя известные значения и нажав кнопку «Вычислить», вы получите нужный результат.
| Сила (F) | Ньютон (Н)дина (dyn)килограмм-сила, килопонд (кгс)килоньютон (кН)килофунт-сила (kip)меганьютон (МН)паундаль (pdl)стен (sn)фунт-сила (lbf) | |
| Радиус-вектор (r) | верстадециметрдюйм (in)кабельтовкилометрметрмиллиметрмиляморская милясантиметрфут (ft)ярды | |
| Момент силы (M) | kilopond метровНьютон сантиметров (ССМ)Ньютон-метр (N m)килоньютон метров (кНм)унции силы дюймовунции силы ногфунт-сила дюймовфут-фунт (ft lb) | |
Момент силы — определения и формулы
При вращательном движении линейные кинематические характеристики (пройденный путь s, линейная скорость υ, тангенциальное ускорение aτ) пропорциональны соответствующим угловым характеристикам.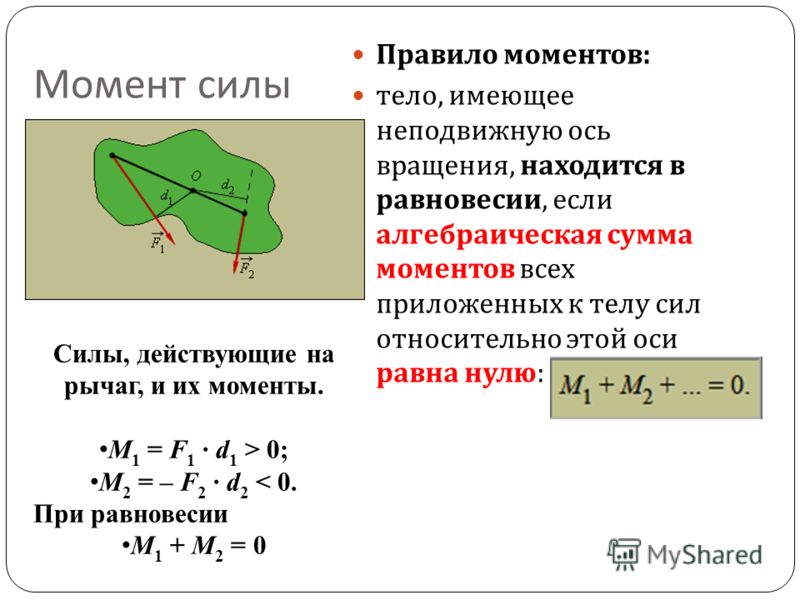
При этом коэффициентом пропорциональности является радиус вращения r. В качестве силовой характеристики вращательного движения вводится понятие момента силы. Следует отличать моменты силы относительно оси и относительно точки.
Момент силы относительно точки O
Моментом силы относительно точки O называется векторное произведение M→ = [r→, F→], где r→ — радиус-вектор, проведенный из этой точки к точке приложения силы. Вектор M→ перпендикулярен плоскости, в которой лежат векторы r→ и F→, и численно равен площади параллелограмма, сторонами которого являются данные векторы M = rFsinφ.
| Направление вектора M→ смотреть с вершины вектора M→. 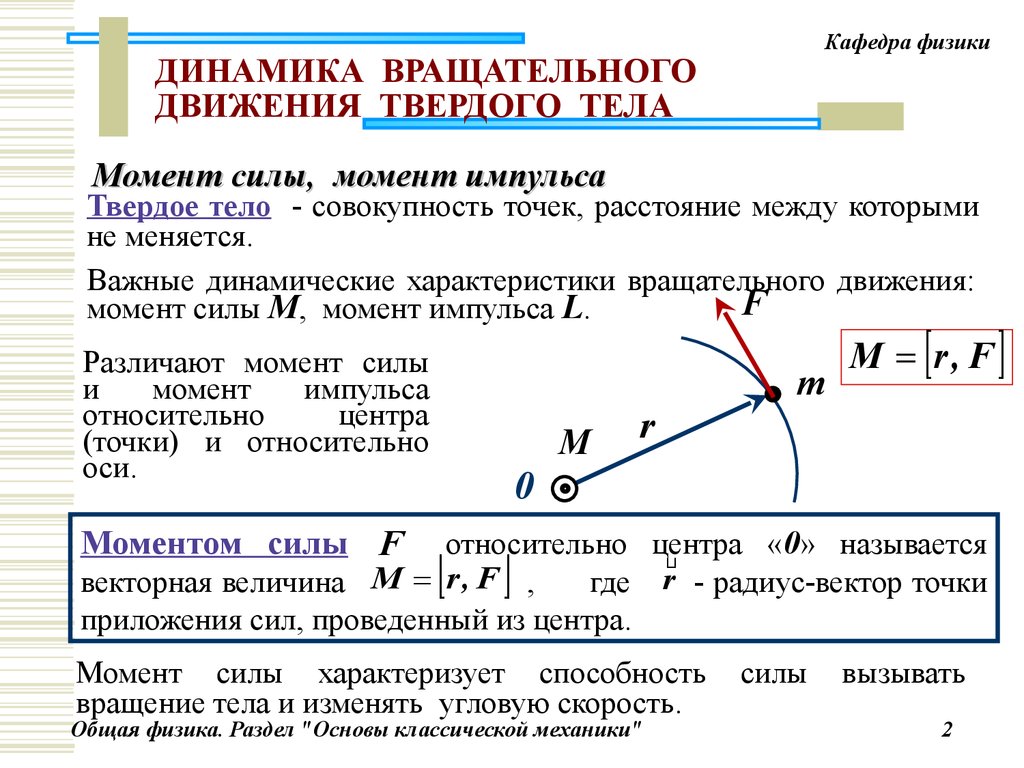 | Иногда удобнее смотреть вслед вектору M→, тогда кратчайший поворот от радиус-вектора r→ к силе F→′ будет происходить по часовой стрелке. На практике удобно определять направление вектора |
Момент силы равен нулю, если равна нулю сила или линия действия силы проходит через точку O.
| Момент силы M→ не изменяется, если вектор F→ (точку приложения силы) переносить вдоль линии действия. Наглядно видно, что площади параллелограммов OABC и OA′B′C равны, поскольку они имеют общее основание OC и высоту d. | Геометрическая сумма моментов нескольких сил, действующих на материальную точку A относительно некоторой точки O, равна моменту суммы этих сил относительно той же точки M→ = [r→, F→] = [r→,(F→1+F→2 +…)] = [r→,F→1]+[r→,F→2]+… |
Момент силы относительно некоторой оси
Моментом силы относительно некоторой оси называют проекцию Mz на данную ось вектора момента этой силы 
Величина Mz не зависит от выбора точки O‘ на оси, поскольку момент силы M при переносе точки приложения силы вдоль линии ее действия не изменяется. Момент силы относительно точки O численно равен моменту этой силы относительно оси OZ, перпендикулярной плоскости, в которой лежат векторы r→ и F→ (а значит и точка O).
Плечо силы — это кратчайшее расстояние между осью и линией действия силы
Рассмотрим действие сил на тело, способное вращаться вокруг неподвижной оси OO′:
Сила F→a, параллельная оси, может только деформировать эту ось.
Вызвать вращение тела вокруг неподвижной оси может только сила или ее составляющая, которая лежит в плоскости, перпендикулярной данной оси, и не совпадает по направлению с радиус-вектором, проведенным в этой плоскости к точке ее приложения. Силу, образующую произвольный угол с осью вращения, можно спроецировать на перпендикулярную плоскость, а затем разложить на тангенциальную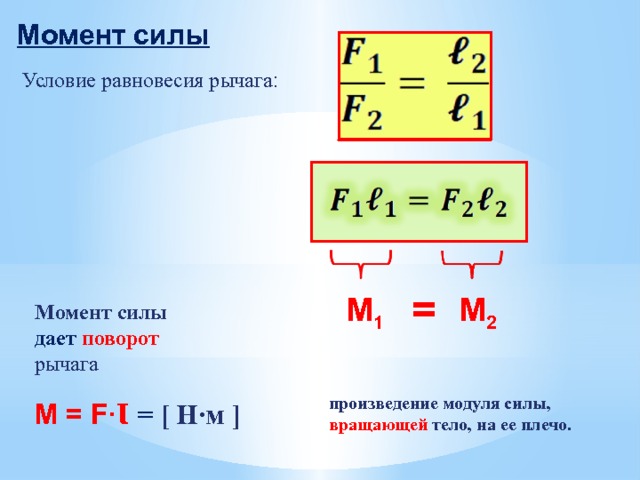 
Калькулятор момента силы | Рассчитать момент силы
✖Сила — это любое взаимодействие, которое, если ему не противостоять, изменит движение объекта. In other words, a force can cause an object with mass to change its velocity.ⓘ Force [F] | Atomic Unit of ForceAttonewtonCentinewtonDecanewtonDecinewtonDyneExanewtonFemtonewtonGiganewtonGram-ForceGrave-ForceHectonewtonJoule per CentimeterJoule per MeterKilogram-ForceKilonewtonKilopondKilopound-ForceKip-ForceMeganewtonMicronewtonMilligrave-ForceMillinewtonNanonewtonNewtonOunce-ForcePetanewtonPiconewtonPondPound Foot на квадратную секундуPoundalPound-ForceStheneTeranewtonTon-Force (Long)Ton-Force (Metric)Ton-Force (Short)Yottanewton | +10% -10% | |
✖Перпендикулярное расстояние между силой и точкой является важным фактором при расчете момента силы.ⓘ Перпендикулярное расстояние между силой и точкой [r 7 0 0 | AlnAngstromArpentAstronomical UnitAttometerAU of LengthBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Ткань)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (ткань)NanometerNautical League UKNau Миля (Международная)Морская миля (Великобритания)ПарсекОкуньПетаметрПикаПикометрПланк ДлинаТочкаПолюсКварталТростник (Длинный)РодРоман АктусВеревкаРусский АрчинПротяженность (Ткань)Радиус СолнцаТераметрТвипВара КастелланаВара КонукераВара Де ТареаЯрдЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
✖Момент силы является произведением силы и перпендикулярного расстояния линии действия силы. | Дин-метр Дин-миллиметрГрам-сила-сантиметрГрам-сила-метрГрам-сила-миллиметрКилограмм-метрКилограмм-сила-сантиметрКилограмм-сила-метрКилограмм-сила-миллиметрКилоньютон-метрНьютон-сантиметрНьютон-метрНьютон-миллиметрУнция-сила-футУнция-сила-футФунт-сила-футФунт-сила-дюйм | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Момент силы Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Сила: 2,5 Ньютон —> 2,5 Ньютон Преобразование не требуется
Перпендикулярное расстояние между силой и точкой: 4 метра —> 4 метра.
Преобразование не требуется
ШАГ 2. Вычисление формулы
ШАГ 3. Преобразование результата в единицу измерения выходного сигнала
10 Ньютон-метр —> преобразование не требуется
< 10+ калькуляторов статики частицФормула момента силы
Момент силы = Сила*Перпендикулярное расстояние между силой и точкой
М = F*r FP
Что такое момент силы?
Момент силы — это мера ее стремления заставить тело вращаться вокруг определенной точки или оси. Чтобы момент развился, сила должна действовать на тело таким образом, чтобы тело начало скручиваться.
Как рассчитать момент силы?
Калькулятор момента силы использует Момент силы = Сила * Перпендикулярное расстояние между силой и точкой для расчета момента силы.
Формула момента силы определяется как произведение силы и перпендикулярного расстояния между точками, в которых вычисляется момент. Момент силы обозначается символом М .
Как рассчитать момент силы с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для момента силы, введите Force (F) & Перпендикулярное расстояние между силой и точкой (r FP ) и нажмите кнопку расчета. Вот как можно объяснить расчет момента силы с заданными входными значениями -> 10 = 2,5*4 .
Часто задаваемые вопросы
Что такое момент силы?
Формула момента силы определяется как произведение силы на перпендикулярное расстояние между точками, в которых вычисляется момент, и представляется как M = F*r FP или Момент силы = Сила*Перпендикулярное расстояние между силой и точкой . Сила — это любое взаимодействие, которое, если ему не противодействовать, изменит движение объекта.
Другими словами, сила может заставить объект с массой изменить свою скорость, а перпендикулярное расстояние между силой и точкой является важным фактором при расчете момента силы.
Как рассчитать момент силы?
Формула момента силы определяется как произведение силы и перпендикулярного расстояния между точками, в которых рассчитывается момент, вычисляется с использованием Момент силы = Сила*Перпендикулярное расстояние между силой и точкой . Чтобы рассчитать момент силы, вам потребуется Сила (F) и Перпендикулярное расстояние между силой и точкой (r FP ) . С помощью нашего инструмента вам нужно ввести соответствующее значение для силы и перпендикулярного расстояния между силой и точкой и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Сколько существует способов расчета момента силы?
В этой формуле момент силы использует силу и перпендикулярное расстояние между силой и точкой.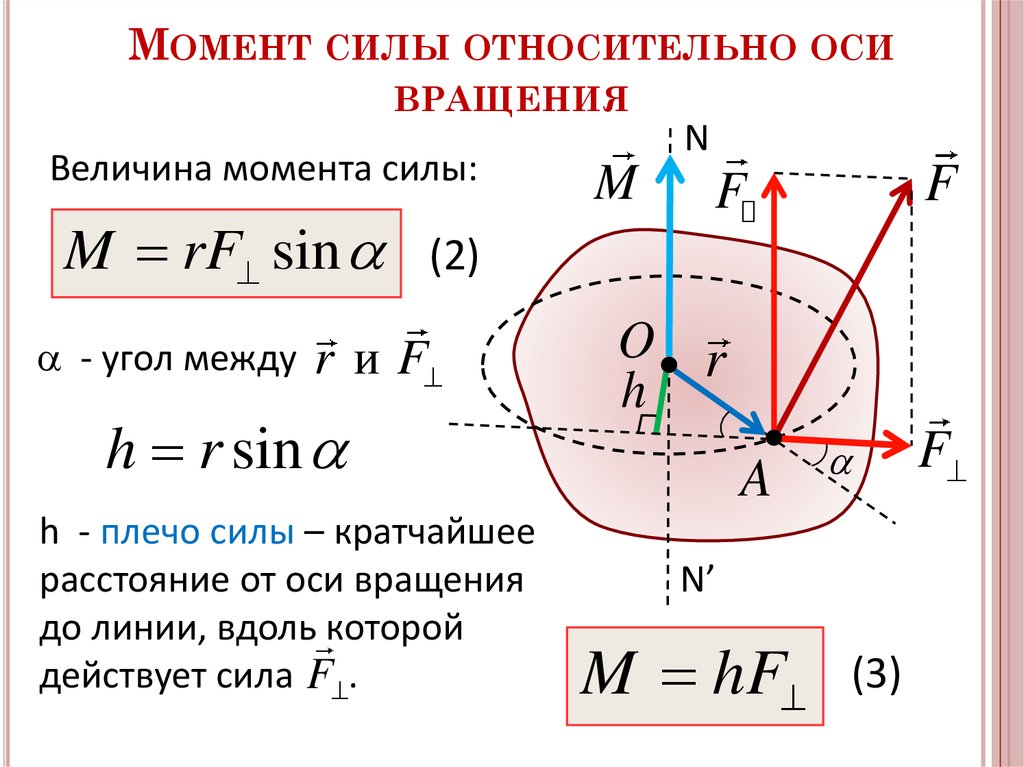
Мы можем использовать 1 другой способ (способы) для вычисления того же самого, который выглядит следующим образом:
- Момент силы = Сила*Перпендикулярное расстояние между двумя силами
Доля
Скопировано!
Давление и моменты — островная физика
Главная >> 9-й год >> Давление и моменты | Гравитация и космос >> |
В этом модуле представлена концепция давления в твердых телах, жидкостях и газах, а также влияние разницы давлений. Моменты охватываются концепцией балансировки объектов.
A — Давление
Цели:
- Вспомнить примеры изменения давления в реальном мире
- Вспомнить единицы измерения давления
- Уметь вычислять давление
Давление является мерой концентрации силы. Если сила сосредоточена в небольшой области (например, в кончике гвоздя), возникает высокое давление.
Если он распространяется на большую площадь (например, на множество гвоздей или на головку канцелярской кнопки), то это означает низкое давление. Чем выше давление, тем больше вероятность того, что сила проникнет через поверхность. Иногда нам нужно высокое давление, если мы хотим забить гвоздь или штифт, а иногда мы хотим максимально снизить давление, используя как можно большую площадь (большие шины, шайбы и т. д.). 92\) также известен как паскаль \((\text{Pa})\) ( в честь Блеза Паскаля, французского математика и ученого.
B — Давление в жидкостях
Цели:
- Описать как давление изменяется с глубиной или высотой
- Объясните, как давление влияет на конструкцию или использование некоторых вещей
Давление под чем-либо обусловлено его весом (силой гравитации, которая тянет его вниз) и площадью контакта. Это наиболее определенно относится к жидкостям и газам, а также к твердым телам. Поскольку изначально предполагалось, что это связано с глубиной воды, оно известно под названием «гидростатическое» давление.
(Гидро из воды и статика означает неподвижность). Давление увеличивается. с глубиной воды, и это легко продемонстрировать с помощью носика.0007
Струя воды из нижней части идет дальше, поскольку она выходит быстрее из-за большего давления, поскольку над ним больше воды. Когда уровень воды падает, скорость водяной струи замедляется, и вода приземляется ближе к бутылке. В качестве примечания: вы можете увеличить дальность и скорость водяной струи, дуя на верхнюю часть днища, так как вы увеличили давление на верхнюю часть воды! |
Получается, что площадь поперечного сечения бутылки на самом деле не имеет значения, так как вес воды над дном увеличивается пропорционально этой площади, поэтому она компенсируется. Давление воды из-за глубины зависит исключительно от глубины воды, плотности воды и силы земного притяжения.
\[гидростатическое\,давление=плотность×g×глубина\]
\[P=\rho gh\]
Вода имеет плотность \(1000\,\text{кг/м}^3\).
Морская вода имеет несколько большую плотность из-за растворенной в ней соли. 92\]
| Моделирование PhET — жидкости и глубина. Это должно показать, что давление на дне жидкости зависит от плотности и глубины жидкости. Площадь и объем значения не имеют. Также обратите внимание, что жидкость находит свой собственный уровень. |
C — Использование давления жидкости
Задачи:
- Объяснить, почему жидкости используются в гидравлических системах
- Описать, как работает гидравлический пресс
- Рассчитать силу, создаваемую гидравлической системой
Одним из лучших способов использования давления жидкости являются гидравлические системы. Название происходит от воды, хотя обычно они заполнены маслом для предотвращения коррозии. Ваш учитель продемонстрирует эту концепцию, используя медицинские шприцы и прозрачные пластиковые пробирки.
Когда один из поршней вдавливается, другой поршень выдвигается, потому что сжимаемая жидкость должна куда-то деваться. Давление, прикладываемое к первому поршню, передается через жидкость и на другой шприц. Преимущество гидравлики в том, что: а) шланги гибкие и могут свободно перемещаться, не влияя на поршни; б) изменение относительных размеров поршней создает простую машину; в) к одному управляющему цилиндру можно подключить несколько цилиндров. Это очень полезно для автомобильных тормозных систем. Одна педаль тормоза управляет 8 тормозными цилиндрами, которые больше по размеру и поэтому выдают большее усилие. Гибкие шланги позволяют использовать рулевое управление и подвеску. 92\]
Это давление передается через жидкость ко второму шприцу. Следовательно, мы можем рассчитать выходную силу, повторно применив то же уравнение, но перестроив его, чтобы получить силу в левой части:
\[F_2=P\times A_2=1,5 \times 8=12\,\text{ N}\]
Таким образом, входная сила \(3\,\text{N}\) выдавала гораздо большую выходную силу \(12\,\text{N}\)
.
Обратите внимание, что поскольку площадь была в четыре раза больше, сила также увеличилась в четыре раза.
Конечно, даром мы ничего не получим. В то время как мы получаем большую силу от этой машины, мы должны переместить поршень на большее расстояние, примерно в четыре раза больше. Это связано с тем, что количество воды, которое перемещается из одного шприца в другой, имеет тот же объем.
D — Моменты
Задачи:
- Вычислить момент силы
- Объяснить, как использовать моменты, чтобы определить, будет ли что-либо уравновешиваться
- Объяснить, как работают рычаги
объект, имеющий точку поворота (точку опоры), то это может привести к вращению объекта. Этот поворотный эффект называется МОМЕНТОМ — по причинам, о которых ваш учитель физики не имеет ни малейшего представления! Так или иначе, этот крутящий момент можно увеличить двумя способами:
- приложить большее усилие (нажать сильнее)
- приложить усилие дальше от точки поворота.
Итак, это дает нам простое уравнение
\[момент=сила \умножить на расстояние\,от\,поворот\]
Единицы измерения: \(\text{(Нм)}\) или \(\text{ (Нсм)}\) в зависимости от того, какие единицы измерения вы используете для расстояния.
| Click to Run |
На основе BELCO и
Royal Gazette четыре новых двигателя MAN 51/60 DF, каждый из которых весит 280 тонн (281 000 кг). Генераторы, прикрепленные к двигателям, весят еще 60 тонн (60 000 кг). Для их перемещения у них есть изготовленный на заказ транспортер весом 59 тонн (59 000 кг), чтобы уменьшить нагрузку на дорогу. Судя по фотографиям, площадь контакта каждого колеса под нагрузкой будет 25 см х 25 см. С каждой стороны 14 комплектов по 8 колес, всего 112 колес. Весь транспортер управляется сложной системой гидравлики, которая поднимает и опускает кузов, управляет колесами, управляет тормозами и приводит в движение колеса.
Действие — Рассчитать давление на дорогу.
Фото двигателя с сайта BELCO. На этом фото генератор не прикреплен к двигателю. Он идет на маховик справа. | Часть грузовика-транспортера. |
Грузовое судно с 400-тонными кранами для подъема тяжелых двигателей и их оборудования. | Один из паровозов стоит на деревянных блоках — почему блоки такие длинные? |
Краны огромны — чтобы предотвратить опрокидывание корабля при повороте двигателей за борт, корабль перемещает водяной балласт в танки на противоположной стороне. В целом, это требует очень тщательного планирования и хорошего знания физики!
Посмотрите на все эти гидравлические шланги и домкраты для подъема, движения и рулевого управления! |
Видео одного из новых паровозов, едущего по Сент-Джонс-роуд мимо Салтуса. |
Прочие ресурсы
Ролик на Youtube, где грузовик пытается наехать на баржу. Здесь не хватает понимания физики. К счастью, водитель выпрыгнул из кабины, когда до него дошло, что грузовик обречен. Ютуб перегружен отказами крана! |
Классное видео, как сделать кран/грейфер с гидравлическим управлением. Обратите внимание на использование рычагов (МОМЕНТЫ) повсюду, а также на простые гидравлические машины. Чтобы не повредить банку, подушечки захвата имеют большие размеры для снижения давления. Практически все, что мы изучили, есть в этом видео! |
РАСЧЕТ СИЛ И МОМЕНТОВ – ЛАБОРАТОРИЯ 4
РАСЧЕТ СИЛ И МОМЕНТОВ – ЛАБОРАТОРИЯ 4РАСЧЕТ СИЛ И МОМЕНТОВ — ЛАБОРАТОРНАЯ 4
Каждой лабораторной группе необходимо:
- Калькулятор (1)
- Рулетка (1)
- Карандаш для кожи (1)
- Текст (1 копия каждого)
- прозрачные пленки и стираемые маркеры, предоставленные преподавателями лаборатории
- Пересмотрите процедуру резистивного теста медиальных мышц задней поверхности бедра (Kendall, McCreary, & Provance, 19). 93, стр. 208), для которого вы построили векторную диаграмму во время лабораторной работы на прошлой неделе. Добавьте следующую информацию к вашей диаграмме.
- Используйте опубликованные антропометрические данные (Smith, Weiss, & Lehmkuhl, 1995, стр. 55) для оценки силы тяжести, действующей на подвижный сегмент, то есть веса подвижного сегмента.
- Предположим, что экзаменатор прикладывает силу в 5 фунтов.
- Оценить расположение латеральной оси коленного сустава (Smith, Weiss, & Lehmkuhl, 1996, рис. 9-3, с. 305).
- Нарисуйте и оцените длину плеча момента для каждого из трех векторов силы на вашей диаграмме. Вы можете использовать рулетку на члене вашей лабораторной группы, когда он или она принимает тестовое положение, или вы можете исследовать лабораторный скелет.
После определения величины (в фунтах) силы тяжести, действующей на подвижный сегмент, и плеча момента силы (в дюймах) по отношению к латеральной оси коленного сустава, рассчитайте момент, который сила тяжести создает вокруг латеральной оси коленного сустава.
. Сделайте то же самое для силы, которую производит экзаменатор. Убедитесь, что обе силы создают моменты разгибателей колена. Рассчитайте величину каждого момента (в дюйм-фунтах). Поскольку оба момента имеют одно и то же направление (удлинение), вы можете сложить их, чтобы получить «чистый» экстензорный момент.Наконец, используйте уравнение вращательного равновесия, чтобы оценить силу, создаваемую мышцей во время резистивного теста. Предположим, что во время теста активна только полусухожильная мышца.
- Повторите процесс, который вы практиковали в предыдущей задаче, анализируя резистивный тест большой ягодичной мышцы (Kendall, McCreary, & Provance, 1993, стр. 226). Проследите или перерисуйте рисунок и используйте его для векторного анализа в сагиттальной плоскости. Нарисуйте отдельные векторы, представляющие три силы, действующие на подвижный сегмент со стороны (1) силы тяжести, (2) большой ягодичной мышцы и (3) сопротивления исследователя. Оцените силы и моменты, используя опубликованные антропометрические данные (Smith, Weiss, & Lehmkuhl, 19). 95, с.55), лабораторные каркасы, рулетки и другие инструменты. Предположим, что исследователь прикладывает силу в 5 фунтов к задней поверхности бедра.
После определения их величин (в фунтах) и плеч моментов (в дюймах) рассчитайте моменты (в дюйм*фунты), создаваемые силами гравитации и силы исследователя вокруг латеральной оси тазобедренного сустава. Убедитесь, что обе силы создают моменты сгибателей бедра, и рассчитайте величину этих моментов.
Осмотрите лабораторный скелет, чтобы оценить плечо момента мышцы. Наконец, используйте уравнение вращательного равновесия, чтобы оценить силу, которую мышца производит во время резистивного теста. Предположим, что во время теста активна только большая ягодичная мышца.
- Получите дополнительную практику в векторном анализе, исследуя активность замкнутой цепи. Нарисуйте в сагиттальной плоскости эффекты гравитации и мышц, когда один из ваших партнеров по лаборатории сидит на поверхности, например на стуле или прикроватном комоде. Сосредоточьтесь на одном голеностопном (голеностопном) суставе.
- Используйте свою диаграмму, чтобы предсказать, вызывает ли сила тяжести тыльное сгибание голеностопного сустава или подошвенное сгибание, когда человек сидит. Подсказка: ваш партнер по лаборатории может сохранять устойчивость, когда он или она сидит, только если положение центра тяжести находится над основанием опоры. Человек наиболее устойчив, когда центр тяжести лежит над центром основания опоры.
- Предсказать, какие мышцы активны.
- Выберите одну из мышц и начертите ее силу, обращая внимание на то, чтобы изобразить ее точку приложения на соответствующем сегменте в этой замкнутой цепи.
- Повторите анализ в сагиттальной плоскости сидя относительно латеральной оси коленного сустава.
Дополнительная задача, которая поможет вам развить навыки анализа человеческого движения: - Для любого из анализов сидения, которые вы выполняли для лодыжки или колена, найдите точку в диапазоне движения, в которой мышца должна производить наибольшую силу.
93, стр. 208), для которого вы построили векторную диаграмму во время лабораторной работы на прошлой неделе. Добавьте следующую информацию к вашей диаграмме.
. Сделайте то же самое для силы, которую производит экзаменатор. Убедитесь, что обе силы создают моменты разгибателей колена. Рассчитайте величину каждого момента (в дюйм-фунтах). Поскольку оба момента имеют одно и то же направление (удлинение), вы можете сложить их, чтобы получить «чистый» экстензорный момент.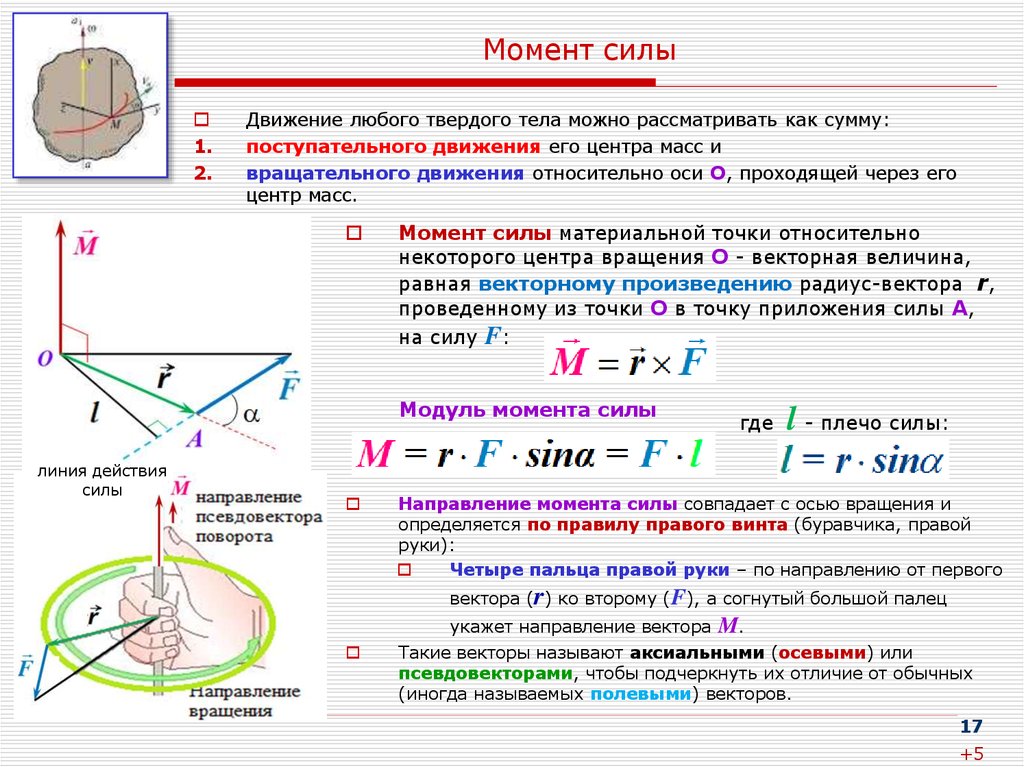
95, с.55), лабораторные каркасы, рулетки и другие инструменты. Предположим, что исследователь прикладывает силу в 5 фунтов к задней поверхности бедра.
Сосредоточьтесь на одном голеностопном (голеностопном) суставе.
