Определение момента инерции твердого тела
Для выполнения этого упражнения необходимо на центр платформы поместить тело с произвольной массой mт. Установка тела проверяется по расположению его относительно концентрических окружностей, нанесенных на платформе. Далее, как в п.1, определяется период колебаний системы – платформа плюс тело и рассчитывается момент инерции Jс системы по формуле: Jc= k(mпл + mтела)Т2,
Момент инерции тела определяется по формуле: Jтела = Jc – Jпл .По данным измерений составить таблицу, аналогичную табл. 1.
Изучение зависимости момента инерции системы (платформа плюс тело) от расположения тела на платформе
По
диаметру платформы поместить два тела
одинаковой формы и массы так, чтобы они
соприкасались в центре платформы.
где m2тел масса двух тел. Тогда момент инерции J2Т двух тел относительно оси вращения платформы будет равен: .
Увеличив расстояние между телами, повторить опыт и сделать вывод о том, как изменяется момент инерции от положения тел на платформе.
Это упражнение можно выполнить, изменяя положение одного тела на платформе (например, параллелепипеда) из вертикального в горизонтальное и наоборот.
Контрольные вопросы
Что называется моментом инерции тела относительно оси вращения? В каких единицах измеряется момент инерции?
Может ли тело иметь несколько моментов инерции?
Как зависит момент инерции от распределения массы?
Как связаны между собой момент силы и момент инерции тела?
Как зависит момент силы от направления приложенной к нему силы и от расстояния от оси вращения до точки приложения силы?
Работа № 5-4 исследование вращательного движения твердых тел с помощью маятника обербека.

Приборы и принадлежности: маятник Обербека с электронным блоком управления, набор грузов.
Описание установки и метода измерений.
Маятник Обербека (рис.1) представляет собой крестовину, состоящую из четырех взаимно перпендикулярных одинаковых стержней 1, которые ввинчены в металлическую втулку 2 радиусом r. Эта крестовина свободно вращается вокруг горизонтальной оси. На стержни надеты одинаковые грузы 3 массой m‘ ,которые могут быть закреплены на различных расстояниях l от оси вращения. На ось вращения маятника посажены два легких шкива 4 с различными радиусами
 Перемещая грузы m‘
по стержням, можно менять момент инерции
маятника. Беря разные грузы m,
а также шкивы разного радиуса, можно
менять момент вращающей силы: M = FR , (1)
Перемещая грузы m‘
по стержням, можно менять момент инерции
маятника. Беря разные грузы m,
а также шкивы разного радиуса, можно
менять момент вращающей силы: M = FR , (1)г де F
Имеющаяся на стойке установки миллиметровая шкала позволяет измерить путь h, проходимый платформой с грузом m при их падении. На верхнем 6 и нижнем 7 кронштейнах расположены фотоэлектрические датчики. При пересечении светового луча движущимся грузом сигнал первого датчика включает электронный секундомер, а сигнал второго датчика выключает его. На индикаторе секундомера 8 высвечивается время t прохождения грузом пути h (расстояния между кронштейнами).
Ускорение a груза может быть найдено на основе закона кинематики равноускоренного движения: (2)
Зная ускорение груза, можно по второму закону Ньютона определить силу Fн натяжения нити: ma = mg — Fн,
где g—
ускорение свободного падения. Тогда Fн= m
(g-a) (3)
Тогда Fн= m
(g-a) (3)
Такая же сила со стороны нити приложена по касательной к шкиву крестовины. Момент этой силы М относительно оси вращения, согласно (1), будет равен: (4)
Этот момент силы в соответствии с основным законом динамики вращательного движения M = I (5)
вызывает ускоренное вращение крестовины с угловым ускорением , (I — момент инерции крестовины относительно оси вращения). Величина может быть определена из взаимосвязи линейного и углового ускорения:
(6)
На основании экспериментальных данных могут быть найдены:
момент силы
 Это позволяет проверить справедливость
основного закона динамики вращательного
движения (5), линейную зависимость от M,
а также определить момент инерции I системы. При этом считается, что силой
трения в подшипнике маятника и силами
сопротивления, действующими на движущиеся
тела, можно пренебречь.
Это позволяет проверить справедливость
основного закона динамики вращательного
движения (5), линейную зависимость от M,
а также определить момент инерции I системы. При этом считается, что силой
трения в подшипнике маятника и силами
сопротивления, действующими на движущиеся
тела, можно пренебречь.Р асстояние l от центра груза до оси вращения определяется (рис.2) по шкале, нанесенной на стержне, и определяется по формуле :
где r = (200,1) мм — радиус втулки,
а = (100,1) мм — цена одного деления шкалы стержня,
l0 = (200,1) мм — размер цилиндрического груза m по его высоте.
Основные данные установки:
радиусы
шкивов R1 = (210,1)
мм и R2 = (440,1)
мм; масса одного груза m
= (1890,01)
г; массы грузов, помещаемых на платформу, m = (410,01)
г; масса платформы равна (530,01)
г.
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 4 из 6Следующая ⇒
Цель работы: определить момент инерции крестовины с грузами, используя законы динамики вращательного движения и сохранения энергии.
Приборы и принадлежности: маятник Обербека, грузы, масштабная линейка, секундомер, штангенциркуль.
Схема экспериментальной установки:
Методика исследования и описание установки Момент инерции твердого тела является физической величиной, характеризующей инертность тела при изменении угловой скорости вращения этого тела ω под действием вращающего момента М. Моментом инерции твердого тела называется скалярная физическая величина равная: , (1) где dV — элемент объема; ρ – плотность; r — расстояние от этого элемента до оси вращения. Из формулы (1) видно, что момент инерции не зависит от характера движения, а зависит от размеров, форм и плотности тела. Момент инерции твердого тела во вращательном движении выполняет ту же роль, что и масса тела при поступательном движении. Проектирование машин и механизмов, имеющих вращающиеся при работе детали, ведется с учетом моментов инерции этих деталей. Для однородного тела правильной геометрической формы момент инерции может быть вычислен теоретически (1). При сложной форме тела и неравномерном распределении плотности вещества в нем теоретическое вычисление момента инерции может быть достаточно сложной задачей. В этих случаях момент инерции определяют опытным путем. В настоящей работе определяется момент инерции крестовины маятника Обербека методом вращения. Подвижная часть маятника Обербека (крестовина) состоит из двухступенчатого блока, насаженного на ось, и четырех спиц с одинаковыми цилиндрическими грузами с массами m1. Грузы m1 можно перемещать, закрепляя в том или ином положении, меняя этим момент инерции крестовины. Центр тяжести системы должен находиться на оси вращения. Крестовина приводится в движение при помощи груза массой m, прикрепленного на нити, накрученной на шкив. Итак, если груз опустить с высоты h, то он будет двигаться с линейным ускорением: , (2) где t — время движения груза на участке длиной h. Крестовина же при этом будет вращаться с угловым ускорением: , (3) где r — радиус шкива, на который наматывается нить. С другой стороны, это ускорение по закону динамики вращательного движения: , (4) , (5) где g — ускорение свободного падения. На основании (2), (3), (4), (5) получаем: . (6) Порядок выполнения работы 1. По указанию преподавателя откройте программу, содержащую блок лабораторных работ по физике, раздел «механика, статистическая физика и термодинамика». Выберите нужную вам лабораторную работу. 2. Еще раз внимательно прочитайте теорию и методику проведения работы. 3. Откройте flash — анимацию, для этого щелкните кнопку «Эксперимент». 4. По указанию преподавателя с помощью мыши задайте параметры экспериментальной установки. 5. Запишите полученные данные в таблицу. 6. Щелкните кнопку «Пуск» для начала эксперимента. Остановите секундомер с помощью мыши в момент касания грузом нулевого уровня. 7. Занесите полученное значение времени в таблицу. 8. Повторите опыт 10 раз, каждый раз вводя параметры установки. 9. При помощи калькулятора произведите вычисления предлагаемых величин. 10. Сделайте вывод о проделанной работе. 11. Ответьте на контрольные вопросы. Обработка результатов измерений 1. Абсолютные погрешности времени определить либо как погрешность многократных измерений, либо как погрешность секундомера (по указанию преподавателя) 2. Момент инерции рассчитывается по формуле (6). 3. Относительные погрешности опытов определяются по формуле . 4. Абсолютные погрешности опытов рассчитать по формуле . Таблица измерений
Контрольные вопросы:
1) Что называется моментом инерции материальной точки и абсолютно твердого тела? 2) Что называется моментом силы относительно неподвижной точки и неподвижной оси, как он направлен, как определяется его модуль? 3) Записать основной закон динамики вращательного движения. 4) Как меняется отношение линейных ускорений груза m, если грузы m1 сдвинуть к центру? 5) Что изменится, если изменить диаметр шкива, на который наматывается нить?
Лабораторная работа №4
⇐ Предыдущая123456Следующая ⇒ Читайте также: Формы дистанционного обучения Передача мяча двумя руками снизу Значение правильной осанки для жизнедеятельности человека Основные ошибки при выполнении передач мяча на месте |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 671; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЁРДОГО ТЕЛА — КиберПедия
МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Цель работы: Определение момента инерции однородного прямоугольного параллелепипеда относительно оси симметрии методом крутильных колебаний.
Приборы и принадлежности:Установка лабораторная „Унифилярный подвес“. Электронный блок ФМ 1/1. Набор грузов. Штангенциркуль. Линейка.
Краткая теория
Моментом инерции твердого тела называется физическая величина, характеризующая распределение масс в теле относительно оси вращения и являющаяся мерой инертности тела при вращательном движении.
Твёрдое тело можно представить как совокупность большого числа материальных точек. В таком случае момент инерции твердого тела относительно оси вращения равен сумме моментов инерции всех образующих его материальных точек относительно этой оси и определяется по формуле
где r- расстояние от данной материальной точки массой до оси вращения, — плотность вещества твердого тела, – объём тела.
Момент инерции тела зависит от его массы, формы, размеров и положения оси вращения.
Найдём момент инерции однородного прямоугольного параллелепипеда относительно оси симметрии Z(рис. 1).
Совместим начало координат с центром масс параллелепипеда, а координатные оси направим параллельно его граням , , .
Для определения момента инерции параллелепипеда относительно оси разобьём его на параллельные слои толщиной , высотой и длиной . Каждый слой разобьём на элементарные объёмы в виде столбиков высотой и площадью основания (рис.1).
Масса каждого элементарного объёма , где – плотность металла, из которого сделан параллелепипед.
Вклад каждого элементарного объёма в общий момент инерции параллелепипеда равен
,(1)
где – расстояние столбика до оси вращения ( ).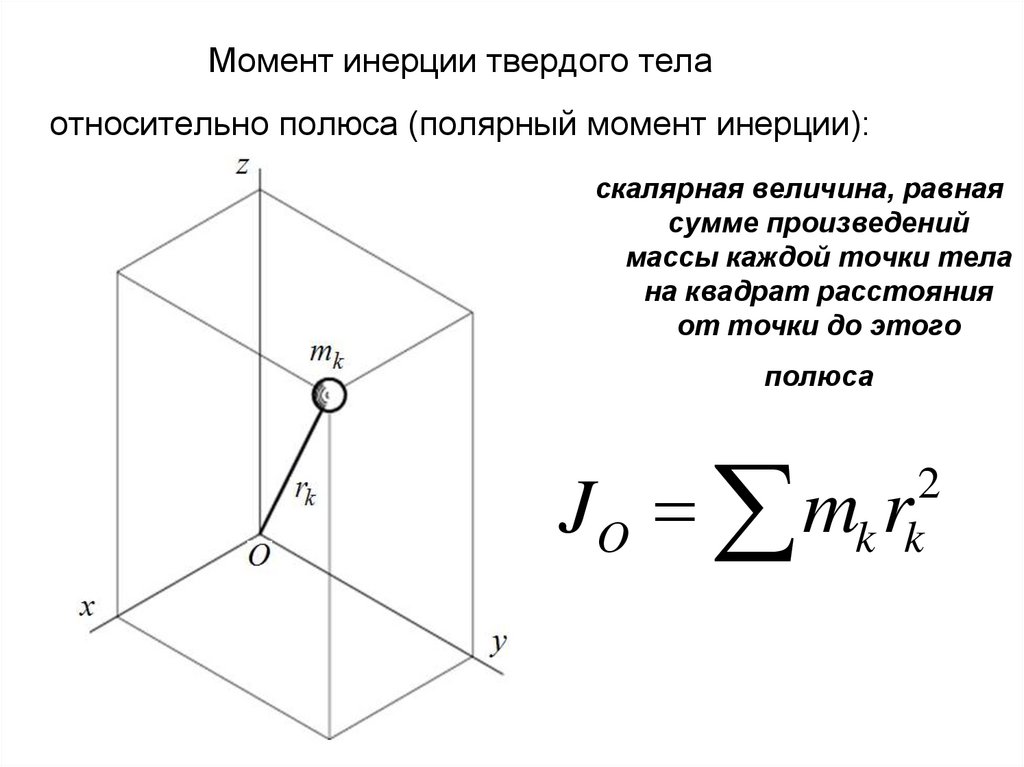
Момент инерции каждого слоя можно найти, проинтегрировав выражение (1) по в пределах от до :
. (2)
Для определения момента инерции всего параллелепипеда нужно выражение (2) проинтегрировать по в пределах от до :
.
Откуда следует окончательное выражение:
. (3)
Полученная формула позволяет вычислить значение момента инерции однородного параллелепипеда относительно оси симметрии .
Однако моменты инерции твёрдых тел относительно заданной оси вращения можно определить и экспериментально.
Для определения момента инерции тела экспериментальным путём в данной лабораторной работе служит установка «Унифилярный подвес» (рис. 2).
Установка состоит из основания 1, вертикальной стойки 2, верхнего 3, нижнего 4 и среднего 5 кронштейнов.
Верхний и нижний кронштейны предназначены для крепления узлов подвески и натяжения стальной проволоки 8, с ней связана металлическая рамка 9, в которой закрепляется исследуемое тело 6.
Если рамку отклонить от положения равновесия и отпустить, она будет совершать колебания. Колебания такого рода называют крутильными. Они происходят под действием упругих сил, возникающих в стальной проволоке 8.
Известно, что период крутильных колебаний относительно оси зависит от момента инерции колеблющейся системы относительно этой оси:
, (4)
где – постоянная момента упругих сил.
Если исследуемое твёрдое тело 6 жёстко закрепить в рамке 9, то для периода колебаний такой системы можно записать:
, (5)
где — момент инерции рамки, а — момент инерции исследуемого тела.
Период колебаний рамки без тела определяется соотношением
. (6)
Решая систему уравнений (5) и (6), получим для выражение
. (7)
Из формулы (7) следует, что если известен момент инерции рамки, то для нахождения момента инерции исследуемого тела достаточно экспериментально определить периоды колебаний унифилярного подвеса с телом и без него.
Момент инерции рамки также можно определить опытным путём. Для этого на ней нужно укрепить грузы 7 (рис 2). В качестве грузов используются два цилиндра. Период крутильных колебаний рамки с цилиндрами:
; (8)
где — момент инерции цилиндра.
Момент инерции цилиндра можно рассчитать с помощью теоремы Штейнера:
, (9)
где – масса цилиндра, – радиус цилиндра, – расстояние от оси цилиндра до оси вращения.
Из формул (6), (8) и (9) для момента инерции рамки следует выражение, в которое входят экспериментально измеряемые величины:
. (10)
Порядок выполнения работы
Ознакомиться с лабораторной установкой «Унифилярный подвес»».
Замечание. В лабораторной установке используется электронный блок ФМ 1/1, представляющий собой электронный секундомер, совмещенный со счетчиком колебаний. Запуск секундомера осуществляется кнопкой «Пуск», остановка — кнопкой «Стоп». Левый дисплей показывает число колебаний. Результаты измерения времени высвечиваются на правом дисплее. Обнуление показаний обоих дисплеев происходит при нажатии кнопки «Сброс».
Левый дисплей показывает число колебаний. Результаты измерения времени высвечиваются на правом дисплее. Обнуление показаний обоих дисплеев происходит при нажатии кнопки «Сброс».
Снять цилиндры с рамки.
1. Рамку без цилиндров отклонить на угол и, нажав кнопку «Сброс» электронного блока, зафиксировать ее.
2. Нажать кнопку «Пуск» и измерить время десяти полных колебаний рамки. Показание таймера занести в табл. 1. Этот опыт проделать три раза.
3. Рассчитать период колебаний рамки по формуле . Результаты занести в табл. 1.
4. Штангенциркулем измерить диаметр одного из цилиндров 7. Записать в табл. 1 значение радиуса цилиндра , расстояние от оси вращения рамки до оси одного из цилиндров и его массу (её значение указано на торце цилиндра).
5. Поместить на рамку цилиндры и, повторив операции, описанные в пункте «2», измерить время десяти полных колебаний. Рассчитать период колебаний рамки с цилиндрами по формуле . Результаты занести в табл. 1.
Результаты занести в табл. 1.
6. По формуле (10) рассчитать момент инерции рамки и записать его в табл. 2.
Замечание: для упрощения дальнейших расчетов рекомендуется вычислить и записать множитель отдельно.
7. Рассчитать абсолютную погрешность по методике обработки воспроизводимых косвенных измерений. При расчете множитель (см. «Замечание») считать константой. Полученный результат занести в табл. 2.
8. Снять цилиндры. Установить исследуемое тело (параллелепипед) в рамку. Определить время десяти полных колебаний, повторив операции пунктов «2»-«3». Вычислить период колебаний рамки с исследуемым телом . Результаты занести в табл. 2.
9. По формуле (7) вычислить экспериментальное значение момента инерции исследуемого тела.
10. Рассчитать абсолютную и относительную погрешности по методике обработки косвенных воспроизводимых измерений. Записать конечный результат и занести в табл. 2.
11. При помощи штангенциркуля определить размеры , , параллелепипеда и по формуле (3) вычислить теоретическое значение момента инерции параллелепипеда (плотность металла = 7900 ). Результаты измерений и вычислений записать в табл. 3.
Результаты измерений и вычислений записать в табл. 3.
12. Сравнить экспериментальное и теоретическое значения момента инерции исследуемого параллелепипеда. Сделать выводы.
Таблица 1
| Ед.изм. | с | c | c | с | c | c | c | c | c | c | кг | м | м |
Таблица 2
Ед. изм. изм.
| с | с | c | с | с | % | ||||
Таблица 3
Контрольные вопросы
1. Момент инерции твёрдого тела относительно оси вращения.
2. Теорема Штейнера.
3. Вывод формулы для расчёта момента инерции прямоугольного параллелепипеда относительно оси симметрии.
4. Вывод формулы для расчета момента инерции рамки по методу крутильных колебаний.
5. Вывод формулы для расчета экспериментального значения момента инерции прямоугольного параллелепипеда методом крутильных колебаний.
ЛАБОРАТОРНАЯ РАБОТА 21-5
Оценка инерции твердого тела с использованием расширенных фильтров Калмана и Савицкого-Голея
На этой странице
АннотацияВведениеЗаключениеСсылкиАвторское правоСтатьи по теме
свойств влияет на точность управления твердым телом. По этой причине для точного управления необходимо получить точные характеристики инерции. Процесс оценки требуется как для шумных гироскопических измерений, так и для временной производной гироскопических измерений. В этой статье предлагается метод оценки для надежных оценок инерционных свойств. Во-первых, уравнения движения Эйлера переформулируются для получения матрицы регрессора. Затем используется расширенный фильтр Калмана для уменьшения шумовых эффектов при измерении угловой скорости гироскопа. Наконец, свойства инерции оцениваются с использованием линейного метода наименьших квадратов. Для получения надежных и точных угловых ускорений используется фильтр Савицки-Голея, основанный на четном числе выборочных данных. Представлены численные примеры, демонстрирующие работоспособность предложенного алгоритма для случая космического корабля. Результаты численного моделирования показывают, что предложенный алгоритм обеспечивает точную оценку инерционных свойств при наличии зашумленных измерений.
Представлены численные примеры, демонстрирующие работоспособность предложенного алгоритма для случая космического корабля. Результаты численного моделирования показывают, что предложенный алгоритм обеспечивает точную оценку инерционных свойств при наличии зашумленных измерений.1. Введение
В динамике вращения твердого тела для достижения целевых ориентаций необходим соответствующий командный крутящий момент для управления ориентацией. Соответственно, необходимо учитывать полный компонент матрицы инерции, который состоит из элементов момента инерции (MOI) и произведения инерции (POI). Существуют различные методы получения инерционных свойств объектов: метод крутильных маятников, использование оборудования, программ автоматизированного проектирования и т.д. Однако эти методы предоставляют информацию о свойствах инерции перед операцией. Для работающего объекта инерционные свойства могут изменяться по нескольким причинам: расход топлива, выплескивание топлива, соединение с другими частями, столкновение с неожиданным объектом и т.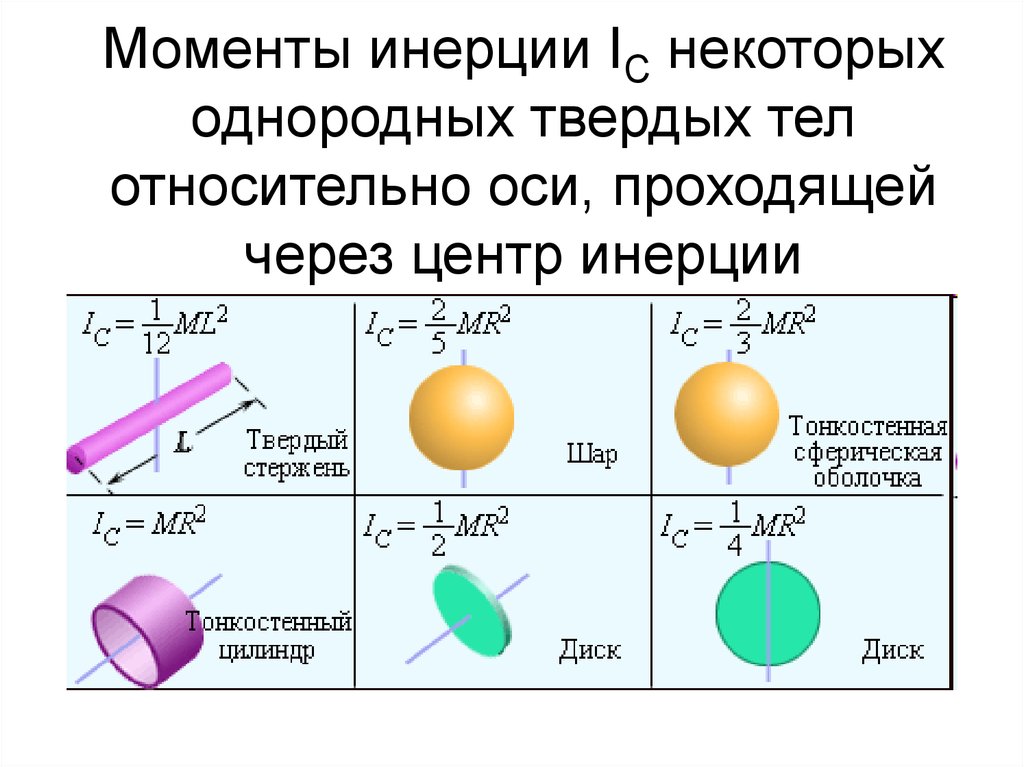 д. Это неизвестное изменение свойств инерции влияет на эффективность управления ориентацией [1, 2]. В частности, инерционные свойства являются чрезвычайно важными параметрами для беспилотных транспортных средств, которые действуют автоматически в непредвиденных условиях. Короче говоря, точные характеристики инерции необходимы для эффективного управления ориентацией.
д. Это неизвестное изменение свойств инерции влияет на эффективность управления ориентацией [1, 2]. В частности, инерционные свойства являются чрезвычайно важными параметрами для беспилотных транспортных средств, которые действуют автоматически в непредвиденных условиях. Короче говоря, точные характеристики инерции необходимы для эффективного управления ориентацией.
Палимака и Берлтон представили метод оценки массовых свойств с использованием метода взвешенных наименьших квадратов [3]. Бергманн и др. разработал метод оценки в реальном времени для асимметричных спутников [4]. Кутлу и др. представил алгоритм оценки инерционных свойств, включая центр масс, с использованием расширенного фильтра Калмана (EKF) [5]. Чжао и др. предложил метод оценивания с использованием дискретного фильтра Калмана для сопряженного управления полетом космических аппаратов [6]. Конти и Соуза представили результат оценки свойств инерции для симулятора управления ориентацией спутника с использованием рекурсивного метода наименьших квадратов (RLS) [7]. Хотя эти исследования включают свойства инерции и центр масс, необходимо учитывать элементы POI, относительно меньшие значения, чем элементы MOI, чтобы избежать снижения точности управления. Ян и др. представил матрицу регрессора, включающую элементы POI, и предложил полный алгоритм оценки инерции на основе RLS [8]. В процессе оценки необходимо использовать угловые ускорения, которые должны быть рассчитаны в общем случае [9].]. Угловые ускорения обычно получают разностным методом: прямой, обратной и центральной разностью. Однако эти методы не годятся в дальнейшем, когда уровни шума при измерениях и время дискретизации недостаточно малы [10]. Ким и др. представил фильтр Савицкого-Голея (SGF) для получения надежных угловых ускорений и впервые применил его для оценки MOI для космических аппаратов [10, 11]. SGF представляет собой простой фильтр сглаживания и дифференцирования, который можно применять к набору последовательных, равномерно распределенных выборочных данных с нечетным числом [11].
Хотя эти исследования включают свойства инерции и центр масс, необходимо учитывать элементы POI, относительно меньшие значения, чем элементы MOI, чтобы избежать снижения точности управления. Ян и др. представил матрицу регрессора, включающую элементы POI, и предложил полный алгоритм оценки инерции на основе RLS [8]. В процессе оценки необходимо использовать угловые ускорения, которые должны быть рассчитаны в общем случае [9].]. Угловые ускорения обычно получают разностным методом: прямой, обратной и центральной разностью. Однако эти методы не годятся в дальнейшем, когда уровни шума при измерениях и время дискретизации недостаточно малы [10]. Ким и др. представил фильтр Савицкого-Голея (SGF) для получения надежных угловых ускорений и впервые применил его для оценки MOI для космических аппаратов [10, 11]. SGF представляет собой простой фильтр сглаживания и дифференцирования, который можно применять к набору последовательных, равномерно распределенных выборочных данных с нечетным числом [11]. Для применения оценки свойств MOI Kim et al. предложил алгоритм оценивания, основанный на линейном методе наименьших квадратов (LLS) [12].
Для применения оценки свойств MOI Kim et al. предложил алгоритм оценивания, основанный на линейном методе наименьших квадратов (LLS) [12].
В данной статье предлагается комбинированный метод получения полных инерционных свойств. Процесс оценки состоит из следующих трех шагов: уменьшение шума, расчет углового ускорения и оценка инерции. Во-первых, шум в измерениях фильтруется с помощью EKF, который обеспечивает наилучшие характеристики в отношении снижения шума [1, 13]. Затем с помощью SGF получают точное угловое ускорение для четного числа выборочных данных. Наконец, полные инерционные свойства оцениваются с помощью LLS на основе предложенной матрицы регрессора в [8]. Эффективность комбинированного метода демонстрируется с использованием проектных параметров одного из уже разработанных корейских научно-технических спутников STSAT-3.
2. Комбинированный метод оценки инерции
2.1. Оценка инерции с использованием линейного метода наименьших квадратов
Вращательная динамика твердого тела описывается как [14] где – вектор угловой скорости твердого тела, – вектор командного крутящего момента, – матрица инерции твердого тела. Соответствующее уравнение измерения выражается как где вектор измерения и вектор ошибки измерения с нулевым средним значением и ковариацией .
Соответствующее уравнение измерения выражается как где вектор измерения и вектор ошибки измерения с нулевым средним значением и ковариацией .
В предположении, что вектор инерции является постоянным в течение интервала интегрирования, (1) выражается как где
Матрицы и в матрице определены следующим образом:
С помощью LLS расчетный вектор инерции получается как
Как показано в (6), матрица состоит из угловых скоростей и ускорений . Следовательно, точные угловые скорости и ускорения приводят к точному расчетному вектору инерции и получаются с использованием EKF и SGF соответственно.
2.2. Шумоподавление с помощью расширенного фильтра Калмана
Угловые скорости, полученные от гироскопических датчиков скорости, включают шумы, вызванные различными источниками, такими как вибрация других частей и характеристики оборудования [13]. EKF хорошо известна как одна из лучших оценок состояния, основанная на снижении уровня шума измерений [13]. Непрерывно-дискретный EKF выбран для обработки нелинейности, присущей (1).
Уравнение (1) преобразуется в дифференциальное уравнение 1-го порядка, где — вектор состояния и — вектор шума состояния с нулевым средним значением и ковариацией . Процесс фильтрации с использованием EKF приведен в таблице 1 [15].
В таблице 1 нижний индекс указывает на шаг дискретного времени, верхний индекс (-) указывает на прогнозируемое состояние, верхний индекс (+) указывает на оцененные состояния и представляет собой матрицы Якоби, представляет собой усиление Калмана, представляет собой ковариационную матрицу и ковариационные матрицы шума состояния и шума измерения соответственно.
2.3. Расчет углового ускорения с использованием фильтра Савицкого-Голея
Савицки и Голей представили упрощенный цифровой фильтр, известный как SGF, для расчета данных сглаживания и дифференцирования с помощью LLS. Нечетное количество точек данных, которые также расположены последовательно и с одинаковым интервалом, необходимо для правильной работы SGF. В [16] обсуждалось применение SGF с использованием четного числа точек данных для преодоления ограничения SGF, которое применимо только к вычислениям с использованием нечетного числа точек данных.
Пусть индекс выборочных данных находится в диапазоне от до . Эти данные располагаются симметрично относительно средней точки выборочных данных. Следовательно, базовая матрица представлена где индексом выборочных данных, является вектором-столбцом базиса и является полиномиальным порядком для отфильтрованных данных. Коэффициенты свертки для дифференцирования th-го порядка получаются как где вектор коэффициентов свертки, порядок дифференцирования, факториал и указывает вектор-столбец матрицы . Например, точка данных дифференцирования 1-го порядка с использованием полинома четвертой степени и 6 выборочных данных задается как
В таблице 2 представлены коэффициенты свертки 1-го дифференцирования полинома четвертой степени по отношению к объему выборочных данных.
3. Численный результат
Параметры моделирования перечислены в таблице 3, а STSAT-3 рассматривается как модель моделирования. Как показано в таблице 4, процесс оценки инерции состоит из следующих трех этапов. Во-первых, шумы измеренных угловых скоростей фильтруются с помощью EKF. Затем угловые ускорения рассчитываются на основе отфильтрованных угловых скоростей с использованием SGF. Наконец, вектор инерции оценивается с использованием LLS и матрицы регрессора. Обратите внимание, что результат оценки получается каждые 40 сек. Объем выборочных данных получается методом автоматического отбора [17]. Как показано на рис. 1, для наилучшей производительности было предоставлено 6 выборочных данных.
Во-первых, шумы измеренных угловых скоростей фильтруются с помощью EKF. Затем угловые ускорения рассчитываются на основе отфильтрованных угловых скоростей с использованием SGF. Наконец, вектор инерции оценивается с использованием LLS и матрицы регрессора. Обратите внимание, что результат оценки получается каждые 40 сек. Объем выборочных данных получается методом автоматического отбора [17]. Как показано на рис. 1, для наилучшей производительности было предоставлено 6 выборочных данных.
Отфильтрованные угловые скорости и границы 3 σ показаны на рисунках 2 и 3 соответственно. На рис. 4 представлены результаты сравнения ошибки углового ускорения, рассчитанной по обратной разнице и SGF. В таблице 5 показан численный результат относительно уменьшенного значения расчетной ошибки углового ускорения. Расчетные угловые ускорения по обратной разнице выражаются следующим образом:
Как показано на рис. 4 и в таблице 5, SGF обеспечивает примерно на 28% более точное угловое ускорение, чем результаты с использованием обратной разности. Результаты оценки показаны на рисунке 5 и в таблице 6 соответственно. Как показано в таблице 6, ошибка оценки вектора инерции находится в пределах 1,0%. Расчетный вектор инерции сходится с истинным вектором инерции примерно на 440 с.
Результаты оценки показаны на рисунке 5 и в таблице 6 соответственно. Как показано в таблице 6, ошибка оценки вектора инерции находится в пределах 1,0%. Расчетный вектор инерции сходится с истинным вектором инерции примерно на 440 с.
4. Заключение
В этой статье предлагается комбинированная методология для оценки свойств полной инерции, которые являются моментом и произведением элементов инерции. Основная идея этого исследования заключается в использовании следующих трех методов: расширенный фильтр Калмана (EKF), фильтр Савицкого-Голея (SGF) и матрица регрессора. Во-первых, с помощью EKF снижается шум измеряемых угловых скоростей. Затем надежное угловое ускорение рассчитывается с использованием SGF на основе четного числа выборочных данных. Наконец, предлагаемая матрица регрессора обеспечивает хороший результат оценки свойств полной инерции с использованием линейного метода наименьших квадратов. Численное моделирование выполнено для оценки точности оценивания предлагаемого подхода.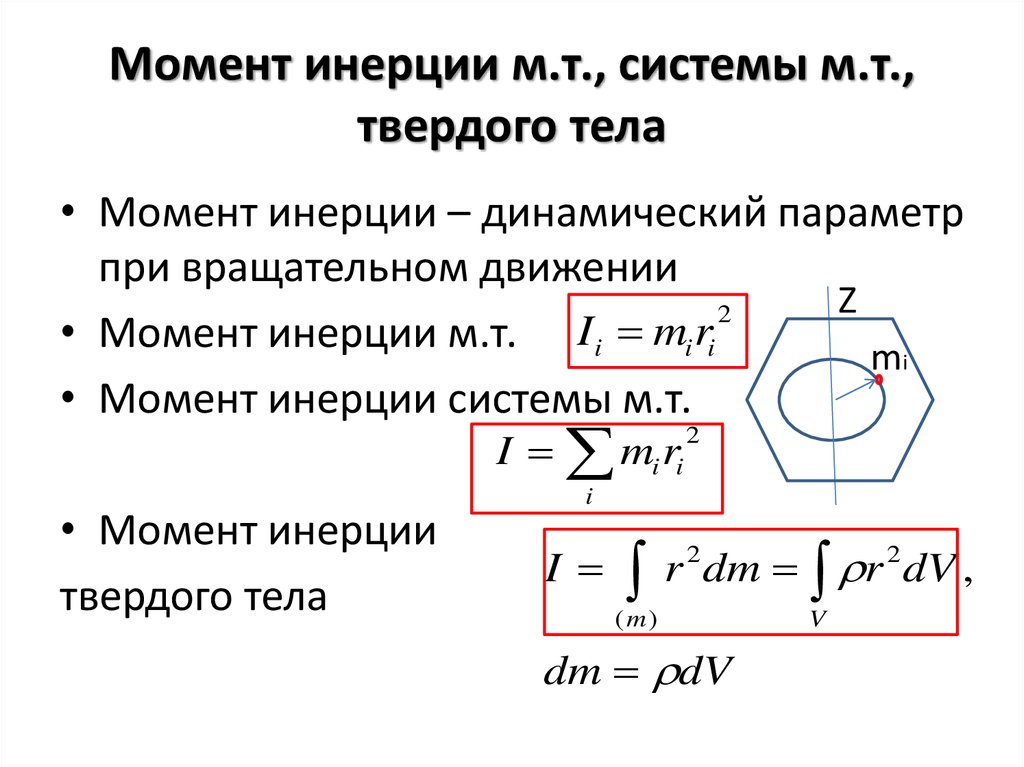 Результат показывает, что предложенный метод способен повысить точность оценки в отношении свойств полной инерции и хорошо отслеживать истинное значение свойств полной инерции.
Результат показывает, что предложенный метод способен повысить точность оценки в отношении свойств полной инерции и хорошо отслеживать истинное значение свойств полной инерции.
Конкурирующие интересы
Авторы заявляют об отсутствии конкурирующих интересов в отношении публикации данной статьи.
Ссылки
Д. Ким, С. Ян, Д.-И. Чеон, С. Ли и Х.-С. О, «Комбинированный метод оценки инерционных свойств STSAT-3», Journal of Mechanical Science and Technology , vol. 24, нет. 8, стр. 1737–1741, 2010.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю. Парк и М. Тахк, «Надежный и оптимальный закон управления ориентацией для космических аппаратов с неопределенностями инерции», Международный журнал KSAA , том. 3, нет. 2, стр. 1–12, 2002 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Дж.
 Палимака и Б. В. Берлтон, «Оценка массовых характеристик космического корабля с использованием данных гироскопа угловой скорости», в Proceedings of the Guidance, Navigation and Control Conference, Guidance, Navigation, and Control and Co-located Conferences ( AIAA/AAS ’92) , Вейл, Колорадо, США, август 1992 г.
Палимака и Б. В. Берлтон, «Оценка массовых характеристик космического корабля с использованием данных гироскопа угловой скорости», в Proceedings of the Guidance, Navigation and Control Conference, Guidance, Navigation, and Control and Co-located Conferences ( AIAA/AAS ’92) , Вейл, Колорадо, США, август 1992 г.Посмотреть по адресу:
Сайт издателя | Академия Google
Е. В. Бергманн, Б. К. Уокер и Д. Р. Леви, «Оценка массовых свойств для управления асимметричными спутниками», Journal of Guidance, Control, and Dynamics , vol. 10, нет. 5, стр. 483–491, 1987.
Посмотреть по адресу:
Сайт издателя | Google Scholar
А. Кутлу, К. Гаджиев и О. Текинальп, «Определение ориентации и идентификация параметров вращательного движения низкоорбитального спутника с помощью данных магнитометра и датчика солнца», в Материалы 3-й Международной конференции по последним достижениям в области космических технологий (RAST ’07) , стр.
 458–461, IEEE, Стамбул, Турция, июнь 2007 г.
458–461, IEEE, Стамбул, Турция, июнь 2007 г.Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю. Чжао, Д. Чжан, Х. Тянь и Х. Ли, «Оценка свойств массы для сопряженного управления полетом», в материалах Международной конференции по компьютерному моделированию и симуляции (ICCMS ’09) , стр. 84–87, Мумбаи, Индия, февраль 2009 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Г. Т. Конти и Л. К. Г. Соуза, «Имитатор спутниковой системы ориентации», Shock and Vibration , vol. 15, нет. 3–4, стр. 395–402, 2008 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
С. Ян, С. Ли, Дж.-Х. Ли и Х.-С. О, «Новый метод оценки инерционных свойств STSAT-3 в реальном времени с использованием данных гироскопа», Труды Японского общества аэронавтики и космических наук , том.
 58, нет. 4, стр. 247–249, 2015.
58, нет. 4, стр. 247–249, 2015.Посмотреть по адресу:
Сайт издателя | Google Scholar
Д. Ким, Д.-Г. Чой и Х.-С. О, «Оценка инерции космического корабля на основе модифицированного закона сохранения углового момента», Journal of Astronomy and Space Science , vol. 27, нет. 4, стр. 353–357, 2010.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Д. Ким, С. Ли и Х. Лигим, «Оценка инерции с использованием фильтра Савицкого-Голея», в Proceedings of the KSAS Fall Conference , стр. 1442–1446, Чеджу, Республика Корея, ноябрь 2014 г. Оценка инерции с использованием комбинации EKF-SGF», Transactions of the Japan Society for Aeronautical and Space Sciences , vol. 59, нет. 3, pp. 189–191, 2016.
Посмотреть по адресу:
Google Scholar
Д.
 Ким, С. Ян и С. Ли, «Оценка инерционных свойств спутника с использованием EKF и SGF», в Материалы Азиатско-Тихоокеанского международного симпозиума по аэрокосмическим технологиям , Кэрнс, Австралия, ноябрь 2015 г. Чеон, С. Ли и Х.-С. О, «Оценка динамических свойств на орбите для STSAT3», в Proceedings of the International Conference on Control, Automation and Systems (ICCAS ’08) , стр. 459–462, COEX, Сеул, Республика Корея, октябрь 2008 г.
Ким, С. Ян и С. Ли, «Оценка инерционных свойств спутника с использованием EKF и SGF», в Материалы Азиатско-Тихоокеанского международного симпозиума по аэрокосмическим технологиям , Кэрнс, Австралия, ноябрь 2015 г. Чеон, С. Ли и Х.-С. О, «Оценка динамических свойств на орбите для STSAT3», в Proceedings of the International Conference on Control, Automation and Systems (ICCAS ’08) , стр. 459–462, COEX, Сеул, Республика Корея, октябрь 2008 г.Посмотреть по адресу:
Сайт издателя | Google Scholar
H. Schaub and J. L. Junkins, Analytical Mechanics of Space Systems , AIAA Education Series, Reston, VA, USA, 2003.
J. L. Crassidis and J. L. , CRC Press, Бока-Ратон, Флорида, США, 2-е издание, 2012 г.
Дж. Луо, К. Ин и Дж. Бай, «Фильтр сглаживания и дифференцирования Савицкого-Голея для данных четных чисел», Signal Processing , том.
 85, нет. 7, стр. 1429–1434, 2005.
85, нет. 7, стр. 1429–1434, 2005.Посмотреть по адресу:
Сайт издателя | Google Scholar
Г. Виво-Труйолс и П. Дж. Шенмакерс, «Автоматический выбор оптимального сглаживания Савицкого-Голея», Analytical Chemistry , vol. 78, нет. 13, стр. 4598–4608, 2006.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Copyright
Copyright © 2016 Donghoon Kim et al. Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Анализ динамических сил
Где k 0 известен как радиус инерции твердого тела относительно к оси, проходящей через 0.
Момент инерция твердого тела относительно центра тяжести будет равна по:
Мы можем написать I 0 как:
С
у я и v i — координаты частицы относительно
до центра тяжести Su i m i = Зв я м я = 0. Следовательно:
Следовательно:
Где k G — радиус вращения вокруг центра тяжести и r G — величина позиционного вектора центра тяжести от 0. Таким образом, мы имеем основную теорему:
6.4.2. Параллельно Теорема оси :
момент инерции тела относительно любой оси равен моменту инерции относительно параллельной оси, проходящей через центр тяжести, плюс произведение масса твердого тела и квадрат расстояния между двумя оси.
В следующем
приведены таблицы моментов инерции некоторых простых тел: Для тел
сложной формы моменты инерции можно вычислить, разделив жесткие
тело в некоторые простые формы и применяя теорему параллельных осей. Обычно, если
используется пакет чертежей с твердотельным моделированием, массы и моменты
инерция деталей может определяться автоматически этими пакетами. В
Как правило, фактически изготовленные детали могут отличаться от чертежей с точки зрения
масса и момент инерции. В случаях, когда момент инерции
требуется существующая часть для определения этих параметров используются экспериментальные методы.
количества.
В случаях, когда момент инерции
требуется существующая часть для определения этих параметров используются экспериментальные методы.
количества.
6.4.3. Ньютона Второй закон движения твердого тела
Согласно Второй закон Ньютона скорость изменения импульса частицы пропорциональна равнодействующей внешней силы, действующей на частицу. Для частицы в твердое тело постоянной массы m i , второй закон Ньютона становится:
(1)
Где F i — внешняя сила, действующая на частицу i и F ji — сила, действующая на частицу i за счет частицы j. F ji широко известен как внутренняя сила . Если мы рассмотрим все частицы внутри твердого тела:
(2)
Отмечая что:
= сумма всех
внешние силы, действующие на твердое тело.
так как F ij + F ji = 0 из-за Ньютона третий закон.
и
.
Таким образом, мы есть Второй закон Ньютона движения для Линейный импульс для жесткой тело, а именно:
(I)
Отсюда уравнения видно, что внутренняя сила не влияет на движение тела. твердое тело, центр тяжести ведет себя так, как если бы вся масса была сосредоточена и результирующая сила S F действовали эта точка. Член m v G известен как линейный импульс твердое тело.
Теперь, если мы возьмем момент сил в уравнении (1) относительно точки 0, мы получить:
(3)
Ускорение точки i, a i , можно записать через ускорение точка 0 и относительные ускорения как:
a i = а 0 + а i/0 = а 0 + а i/0 п + а i/0 т
Где a i/0 t и a i/0 n относительные тангенциальные и нормальные ускорения точки i относительно
точка 0. В векторной записи эти термины задаются как:
В векторной записи эти термины задаются как:
a i/0 t =
а i/0 n = -w 2 r i
Где а и w — угловой ускорение и скорость твердого тела соответственно.
Замена приведенные выше соотношения в уравнение (3) и суммирование для всех частиц в пределах твердое тело дает:
(4)
Отмечая тот:
—
= сумма момент, действующий вдоль оси, проходящей через O (перпендикулярно самолет).
(с F ij = — F ji и эти силы имеют та же линия действий. Сумма будет состоять из термов
терминов в правой части уравнения (4) можно записать как:
(5)
Сейчас:
Следовательно, уравнение (4) упрощается до:
(6)
В целом . Первый срок
в правой части уравнения (v) будет равна нулю, если a 0 =0 или r G =0 или если a 0 и r G параллельны. Ускорение точки 0 равно нулю, если
точка 0 является полюсом ускорения или если твердое тело вращается вокруг
точка 0,
Первый срок
в правой части уравнения (v) будет равна нулю, если a 0 =0 или r G =0 или если a 0 и r G параллельны. Ускорение точки 0 равно нулю, если
точка 0 является полюсом ускорения или если твердое тело вращается вокруг
точка 0,
r G = 0 означает, что точка 0 совпадает с центром тяжести G и a 0 будет параллельна r G только в очень особых случаях. Однако в любом общем случае центр тяжести можно совместить с центр опорной оси. Таким образом, у нас есть Второй закон движения Ньютона для углового Импульс твердого тела, который равен:
(II)
Обратите внимание, что оба
момент внешних сил и момент инерции твердого тела должны
быть относительно оси, проходящей через центр тяжести и
перпендикулярно плоскости движения. Термин I G w известен как угловой момент твердого тела относительно центра
сила тяжести.
6.4.4. Д’Аламбера Принцип
Уравнения I и II можно записать в следующем виде:
(I)
и
(II)
Теперь срок имеет величину силы. Уравнение I является вектором уравнение, которое утверждает, что векторная сумма всех внешних сил плюс фиктивная (несуществующая) сила величины и направления является нуль. Вымышленная сила известна как сила инерции которая будет обозначается F i :
F i имеет то же самое линия действия a G , но в противоположном направлении.
Аналогично,
член имеет величину момента, а уравнение II является вектором
уравнение, которое утверждает, что векторная сумма всех внешних моментов относительно
центр тяжести плюс фиктивный момент величины и направление равны
нуль.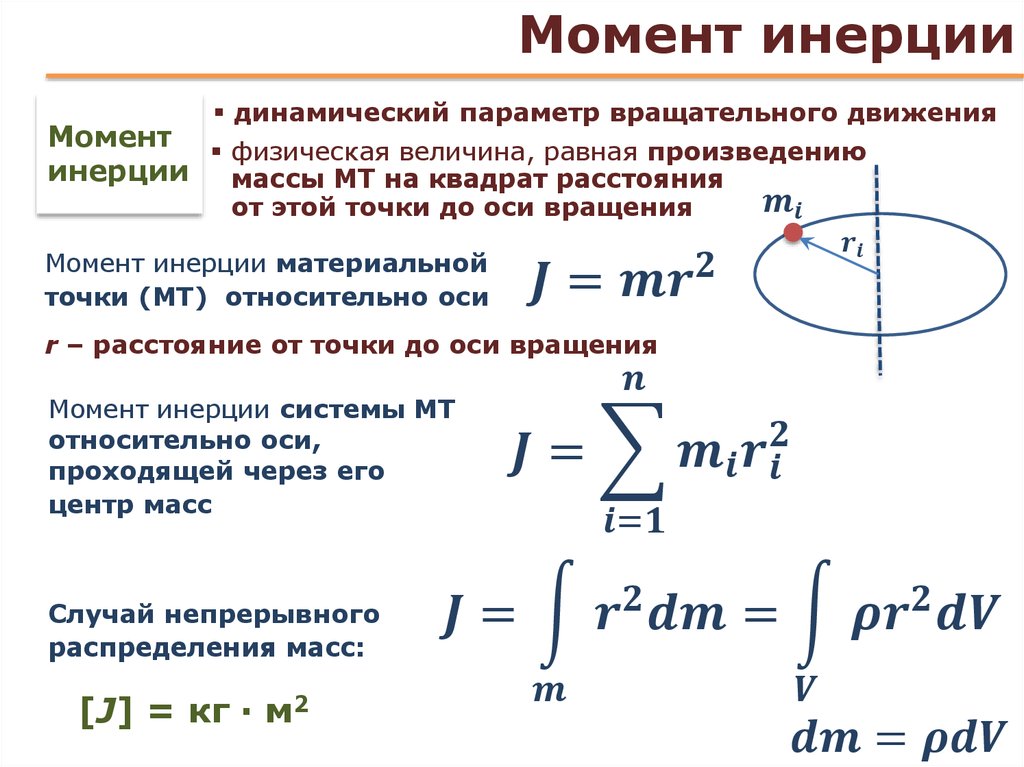 Этот фиктивный момент известен как момент инерции и будет обозначаться как T i :
Этот фиктивный момент известен как момент инерции и будет обозначаться как T i :
T i находится в противоположное направление углового ускорения a . Использование инерции сила и момент инерции. Второй закон Ньютона для твердого тела. с уравнениями:
и
Мы также можем рассматривайте условия инерции, как если бы они были другой внешней силой или моментом, действующим на твердом теле, в этом случае:
и
Где суммирование включает как внешние, так и инерционные силы и моменты. Этот концепция известна как принцип Даламбера, который можно сформулировать как следующим образом:
Даламбера Принцип
В теле, движущемся с известным угловым ускорением и линейным ускорением
центр тяжести, векторная сумма всех внешних сил и инерции
силы, а векторная сумма всех внешних моментов и момента инерции равна
оба по отдельности равны нулю.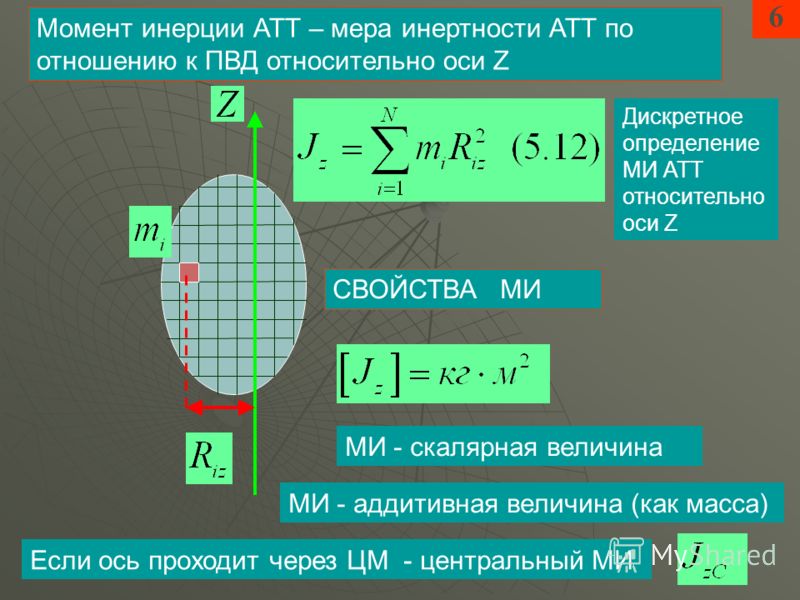
Даламбера Этот принцип очень полезен при анализе динамических сил машин. В отличном многие проблемы, мы знаем характеристики ускорения членов в структура машины, и мы можем определить силы инерции и крутящие моменты. Эти силы инерции и крутящие моменты можно рассматривать как внешние силы. Для этого динамического случая может быть проведена процедура анализа статической силы. Однако никогда нельзя считать силы и моменты инерции реальными силами. Они являются фиктивными силами и никогда не существуют. Ускорение является результатом внешние силы.
В графических решениях удобно заменить силу инерции и момент на эквивалентную результирующую силу инерции.
Рассмотрим твердое тело с a G как ускорение его центр тяжести и a как его угловой ускорение (рис. а). Сила инерции и крутящий момент будут такими, как показано на рисунке. б. Сила инерции и крутящий момент могут быть объединены в одну равнодействующую, R I (Рисунок C) , IF:
и
, где R r — это вектор положения от центра тяжести до точки на линии
действие R i . В таком случае результирующий R i имеет величину и направление силы инерции F i и смещен от центра тяжести на
перпендикулярное расстояние h G такой, что:
В таком случае результирующий R i имеет величину и направление силы инерции F i и смещен от центра тяжести на
перпендикулярное расстояние h G такой, что:
Этот фиктивный сила R i тогда заменит действие силы инерции и крутящий момент
8.2. Динамика одного твердого тела (Часть 1 из 2) – Современная робототехника
8.2. Динамика одиночного твердого тела (часть 1 из 2)
- Описание
- Стенограмма
Это видео знакомит с центром масс твердого тела; его симметричная положительно определенная матрица инерции вращения 3 × 3; главные оси и моменты инерции матрицы инерции; и уравнения, описывающие вращение твердого тела.
Начиная с главы 8.2, мы изучаем метод Ньютона-Эйлера для определения динамики робота. В то время как лагранжева формулировка начинается с потенциальной и кинетической энергии и применяет вариационный подход, основанный на производных, метод Ньютона-Эйлера выводится непосредственно из f равно m-a для твердых тел, из которых состоит робот. Одним из преимуществ этого подхода является то, что мы можем вывести эффективный рекурсивный алгоритм для вычисления динамики роботов с открытой цепью.
Начнем с динамики одиночного твердого тела. Вы можете думать о твердом теле как о наборе точечных масс, которые жестко связаны друг с другом. Мы определяем центр масс как единственную точку в центре тяжести распределения масс и прикрепляем рамку {b} к твердому телу в центре масс. Определение центра масс состоит в том, что сумма взвешенных по массе векторов к точечным массам в системе координат {b} равна нулю.
Определим крутку твердого тела, выраженную в системе {b}, как V_b, состоящую из угловой скорости omega_b и линейной скорости v_b. Тогда линейная скорость массы i равна p_i-dot, равной v_b плюс omega_b, пересекающей p_i. Мы определяем ускорение твердого тела как V_b-dot, и, используя это, мы можем взять производную от p_i-dot, чтобы получить p_i-double-dot. Обратите внимание, что последний член — это омега-b, пересекающая производную по времени от p_i, поэтому мы можем подставить в приведенное выше выражение, чтобы получить это уравнение для p_i-двойной точки. Обратите внимание, что у него есть термины произведения скорости в виде omega_b, пересекающего v_b, и omega_b, пересекающего omega_b и p_i.
Тогда линейная скорость массы i равна p_i-dot, равной v_b плюс omega_b, пересекающей p_i. Мы определяем ускорение твердого тела как V_b-dot, и, используя это, мы можем взять производную от p_i-dot, чтобы получить p_i-double-dot. Обратите внимание, что последний член — это омега-b, пересекающая производную по времени от p_i, поэтому мы можем подставить в приведенное выше выражение, чтобы получить это уравнение для p_i-двойной точки. Обратите внимание, что у него есть термины произведения скорости в виде omega_b, пересекающего v_b, и omega_b, пересекающего omega_b и p_i.
Теперь, принимая за данность, что f равно m-a, мы получаем силу f_i, необходимую для перемещения массы m_i, используя выражение для p_i-двойной точки, которое мы только что получили. Соответствующий момент в кадре {b} равен m_i, равному p_i и f_i, записанному здесь в нашей скобочной записи. Полный рывок F_b, состоящий из момента m_b и силы f_b, необходимой для ускорения тела с ускорением V_b-dot, когда оно движется с поворотом V_b, представляет собой просто сумму сил и моментов, необходимых для отдельных точечных масс. Если мы определим m как общую массу тела, то, используя тот факт, что мы определили рамку {b} как находящуюся в центре масс тела, общая сила f_b будет равна m, умноженному на v_b-точка плюс скобка- omega_b умножить на v_b. Общий момент m_b равен I_b, умноженному на omega_b-dot, плюс квадратная скобка-omega_b, умноженная на I_b, умноженная на omega_b, где I_b называется матрицей инерции. Матрица инерции представляет собой отрицательное значение суммы каждой массы, умноженной на скобку ее положения в квадрате. Мы можем записать матрицу инерции 3 на 3 в терминах ее девяти компонентов с диагональными членами Ixx, Iyy и Izz, а также недиагональными компонентами Ixy, Ixz и Iyz. Эти компоненты рассчитываются, как показано здесь. Например, верхний левый элемент матрицы Ixx называется моментом инерции относительно оси x. Эта инерция становится больше, если масса m_i находится дальше от оси x, где квадрат расстояния от оси x определяется как y_i-квадрат плюс z_i-квадрат. По сути, если масса тела находится далеко от оси x, для ускорения вокруг оси x требуется больший крутящий момент.
Если мы определим m как общую массу тела, то, используя тот факт, что мы определили рамку {b} как находящуюся в центре масс тела, общая сила f_b будет равна m, умноженному на v_b-точка плюс скобка- omega_b умножить на v_b. Общий момент m_b равен I_b, умноженному на omega_b-dot, плюс квадратная скобка-omega_b, умноженная на I_b, умноженная на omega_b, где I_b называется матрицей инерции. Матрица инерции представляет собой отрицательное значение суммы каждой массы, умноженной на скобку ее положения в квадрате. Мы можем записать матрицу инерции 3 на 3 в терминах ее девяти компонентов с диагональными членами Ixx, Iyy и Izz, а также недиагональными компонентами Ixy, Ixz и Iyz. Эти компоненты рассчитываются, как показано здесь. Например, верхний левый элемент матрицы Ixx называется моментом инерции относительно оси x. Эта инерция становится больше, если масса m_i находится дальше от оси x, где квадрат расстояния от оси x определяется как y_i-квадрат плюс z_i-квадрат. По сути, если масса тела находится далеко от оси x, для ускорения вокруг оси x требуется больший крутящий момент.
Недиагональные элементы называются произведениями инерции.
Теперь представьте, что мы заменяем отдельные точечные массы твердого тела непрерывной плотностью массы rho как функцией положения. Тогда элементы матрицы инерции вычисляются как интегралы по объему, а не как суммы, но концептуально разницы нет. В книге можно увидеть несколько упрощенных формул для расчета матрицы инерции некоторых распространенных тел.
Как и матрица масс робота, матрица инерции I_b твердого тела симметрична и положительно определена. Также подобно матрице масс для робота, кинетическая энергия для вращающегося твердого тела составляет половину omega_b-транспонирования, умноженного на I_b, умноженного на omega_b.
Теперь давайте рассмотрим конкретное твердое тело, эллипсоид, с каркасом {b} в центре масс и матрицей инерции I_b, показанной здесь. Теперь рассмотрим то же тело, но с каркасом {p}, также находящимся в центре масс, с другой ориентацией. В этой системе отсчета {p} матрица инерции имеет особенно простой вид со всеми недиагональными элементами, равными нулю. Когда недиагональные элементы равны нулю, оси координат {p}-кадра называются главными осями инерции, а скалярные инерции относительно этих осей называются главными моментами инерции. Вы можете найти главные оси инерции из матрицы инерции для любого кадра {b} в центре масс путем оценки собственных векторов и собственных значений матрицы инерции I_b. Главные оси инерции совмещены с собственными векторами, которые выражены в системе координат {b}, а главные моменты инерции являются собственными значениями. Матрица вращения, выражающая кадр {p} в кадре {b}, R_bp, имеет собственные векторы в качестве своих столбцов.
Когда недиагональные элементы равны нулю, оси координат {p}-кадра называются главными осями инерции, а скалярные инерции относительно этих осей называются главными моментами инерции. Вы можете найти главные оси инерции из матрицы инерции для любого кадра {b} в центре масс путем оценки собственных векторов и собственных значений матрицы инерции I_b. Главные оси инерции совмещены с собственными векторами, которые выражены в системе координат {b}, а главные моменты инерции являются собственными значениями. Матрица вращения, выражающая кадр {p} в кадре {b}, R_bp, имеет собственные векторы в качестве своих столбцов.
Если мы приравняем кинетическую энергию, выраженную в кадрах {p} и {b}, мы можем рассчитать матрицу инерции в кадре {p} как R_bp-транспонирование, умноженное на I_b, умноженное на R_bp. Когда это возможно, предпочтительно выбирать раму корпуса так, чтобы она была совмещена с главными осями инерции, чтобы упростить матрицу инерции. Это также упрощает вращательные уравнения движения.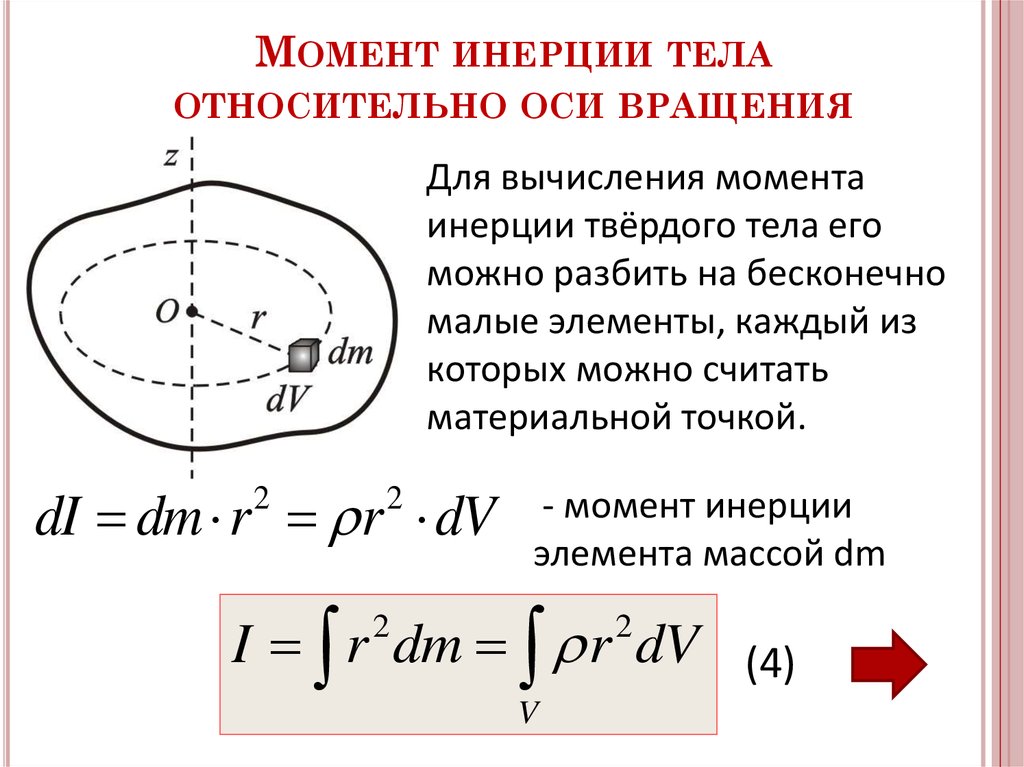


 Все правила по сольфеджио
Все правила по сольфеджио


 Для этого щелкните левой клавишей мыши на экране кнопку «Теория и методика проведения работы».
Для этого щелкните левой клавишей мыши на экране кнопку «Теория и методика проведения работы».

 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.012 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.012 с.)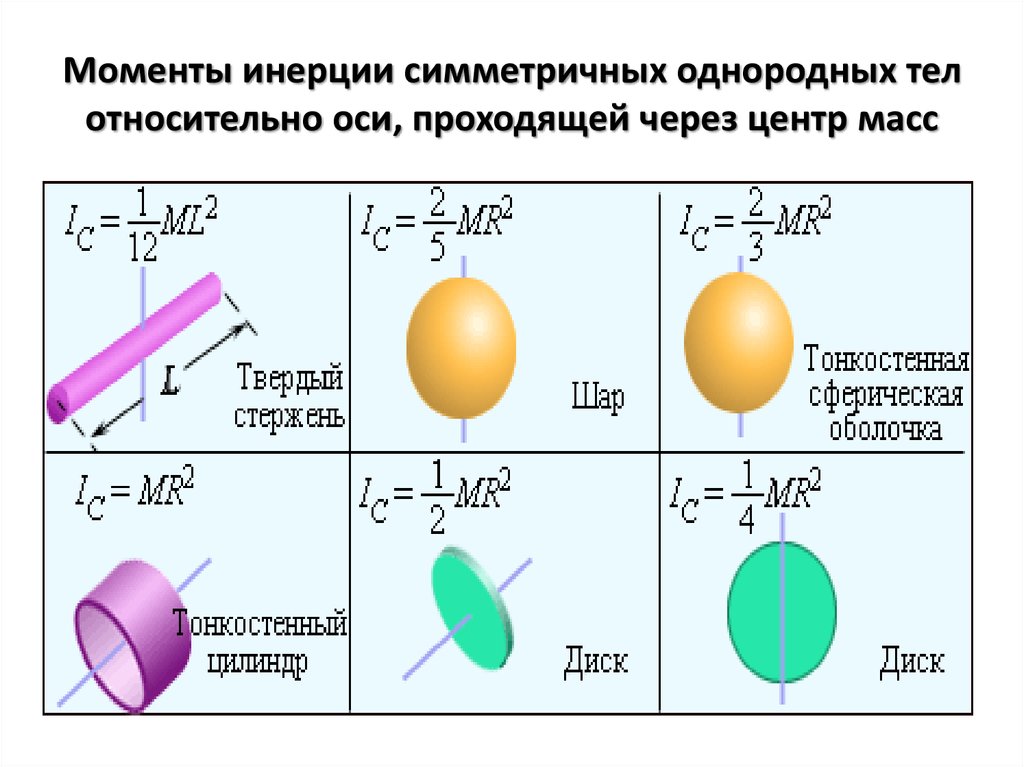 Палимака и Б. В. Берлтон, «Оценка массовых характеристик космического корабля с использованием данных гироскопа угловой скорости», в Proceedings of the Guidance, Navigation and Control Conference, Guidance, Navigation, and Control and Co-located Conferences ( AIAA/AAS ’92) , Вейл, Колорадо, США, август 1992 г.
Палимака и Б. В. Берлтон, «Оценка массовых характеристик космического корабля с использованием данных гироскопа угловой скорости», в Proceedings of the Guidance, Navigation and Control Conference, Guidance, Navigation, and Control and Co-located Conferences ( AIAA/AAS ’92) , Вейл, Колорадо, США, август 1992 г. 458–461, IEEE, Стамбул, Турция, июнь 2007 г.
458–461, IEEE, Стамбул, Турция, июнь 2007 г. 58, нет. 4, стр. 247–249, 2015.
58, нет. 4, стр. 247–249, 2015. Ким, С. Ян и С. Ли, «Оценка инерционных свойств спутника с использованием EKF и SGF», в Материалы Азиатско-Тихоокеанского международного симпозиума по аэрокосмическим технологиям , Кэрнс, Австралия, ноябрь 2015 г. Чеон, С. Ли и Х.-С. О, «Оценка динамических свойств на орбите для STSAT3», в Proceedings of the International Conference on Control, Automation and Systems (ICCAS ’08) , стр. 459–462, COEX, Сеул, Республика Корея, октябрь 2008 г.
Ким, С. Ян и С. Ли, «Оценка инерционных свойств спутника с использованием EKF и SGF», в Материалы Азиатско-Тихоокеанского международного симпозиума по аэрокосмическим технологиям , Кэрнс, Австралия, ноябрь 2015 г. Чеон, С. Ли и Х.-С. О, «Оценка динамических свойств на орбите для STSAT3», в Proceedings of the International Conference on Control, Automation and Systems (ICCAS ’08) , стр. 459–462, COEX, Сеул, Республика Корея, октябрь 2008 г. 85, нет. 7, стр. 1429–1434, 2005.
85, нет. 7, стр. 1429–1434, 2005.