Раздел недели: Обезжиривающие водные растворы и органические растворители. Составы для очистки и обезжиривания поверхности. | |||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Математическая логика. Булева алгебра = алгебра логики. / / Булевы = логические функции. Поделиться:
| ||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. | ||||||||||||||||||||||||||
Справочник по цифровой схемотехнике
Справочник по цифровой схемотехнике
ОглавлениеПРЕДИСЛОВИЕГлава 1. ЧИСЛА И КОДЫ 1.1. СИСТЕМЫ СЧИСЛЕНИЯ 1.3. МАШИННОЕ СЛОВО 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ 1.6. КОД ГРЕЯ 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ Глава 2. АЛГЕБРА ЛОГИКИ 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА 2.4. БУЛЕВА АЛГЕБРА 2.5. СТАНДАРТНЫЕ ФОРМЫ 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ 2.9. КАРТЫ КАРНО Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ 3.1. ЛОГИЧЕСКИЕ СХЕМЫ 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ 4.  1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ 1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ Электронные ключи на биполярных транзисторах. Ключ на биполярном транзисторе с нелинейной обратной связью. Электронные ключи на полезых транзисторах. 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ 6 1. ТРИГГЕРЫ 6.2. РЕГИСТРЫ 6.3. СЧЕТЧИКИ Синхронные счетчики. Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ Глава 8.  КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ Генераторы импульсов на полевых транзисторах. Генераторы импульсов на логических ИМС Генераторы импульсов на основе триггеров. Генераторы импульсов на основе операционных усилителей. Формирователи и генераторы линейно изменяющегося напряжения (ЛИН). 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП 9.3. ЭЛЕМЕНТЫ АЦП 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580 Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813 СПИСОК ЛИТЕРАТУРЫ |
Булева алгебра — законы, правила, теоремы, примеры
Булева алгебра — раздел алгебры, занимающийся логическими операциями над переменными.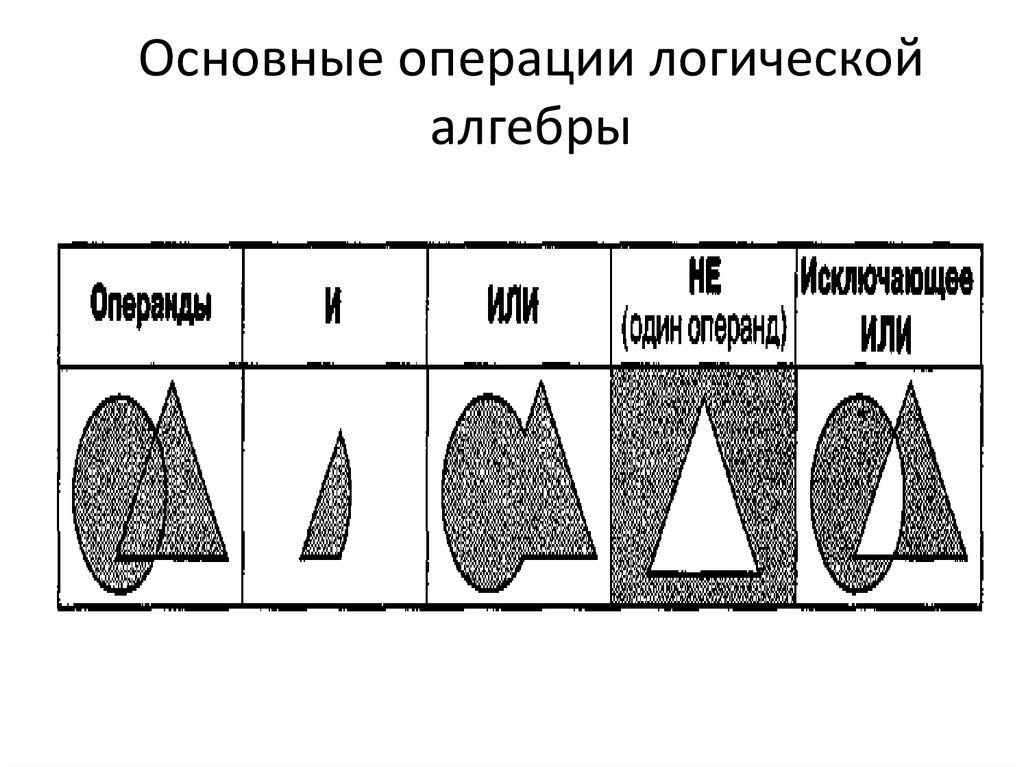 В булевой алгебре может быть только два возможных значения переменных, то есть либо 1, либо 0. Другими словами, переменные могут обозначать только два варианта: истина или ложь. Три основные логические операции булевой алгебры — это конъюнкция, дизъюнкция и отрицание.
В булевой алгебре может быть только два возможных значения переменных, то есть либо 1, либо 0. Другими словами, переменные могут обозначать только два варианта: истина или ложь. Три основные логические операции булевой алгебры — это конъюнкция, дизъюнкция и отрицание.
В элементарной алгебре математические выражения используются в основном для обозначения чисел, тогда как в булевой алгебре выражения представляют значения истинности. Значения истинности используют двоичные переменные или биты «1» и «0» для представления состояния входа, а также выхода. Логические операторы И, ИЛИ и НЕ образуют три основных логических оператора. В этой статье мы узнаем больше об определении, законах, операциях и теоремах булевой алгебры.
| 1. | Что такое булева алгебра? |
| 2. | Выражение булевой алгебры |
| 3. | Булевы алгебраические операции |
4. | Законы булевой алгебры |
| 5. | Теоремы булевой алгебры |
| 6. | Постулаты булевой алгебры |
| 7. | Булева алгебра и логические элементы |
| 8. | Таблица истинности булевой алгебры |
| 9. | Часто задаваемые вопросы по булевой алгебре |
Что такое булева алгебра?
Булева алгебра также известна как бинарная алгебра или логическая алгебра. Основное применение булевой алгебры заключается в том, что она используется для упрощения и анализа различных цифровых логических схем. Диаграммы Венна также можно использовать для визуального представления любой операции булевой алгебры.
Определение булевой алгебры
Булева алгебра может быть определена как тип алгебры, который выполняет логические операции над двоичными переменными. Эти переменные дают истинностные значения, которые могут быть представлены как 0, так и 1. Основными логическими операциями являются конъюнкция, дизъюнкция и отрицание. Логические операторы И, ИЛИ и НЕ используются для представления этих операций соответственно. Более того, эти операции аналогичны пересечению, объединению и дополнению множеств в теории множеств. Вот некоторые из правил булевой алгебры:
Основными логическими операциями являются конъюнкция, дизъюнкция и отрицание. Логические операторы И, ИЛИ и НЕ используются для представления этих операций соответственно. Более того, эти операции аналогичны пересечению, объединению и дополнению множеств в теории множеств. Вот некоторые из правил булевой алгебры:
- Любая используемая переменная может иметь только два значения. Двоичный 1 для HIGH и двоичный 0 для LOW.
- Каждая дополнительная переменная представлена чертой сверху, т. е. дополнение переменной B представлено как B¯. Таким образом, если B = 0, то B¯= 1 и B = 1, то B¯= 0,
- Переменные с ИЛИ представлены знаком плюс (+) между ними. Например, OR для A, B, C представляется как A + B + C.
- Две или более переменных с логическим И представлены точкой между ними, например, A.B.C. Иногда точка может быть опущена, как ABC.
Давайте рассмотрим пример,
Предположим, у нас есть две переменные A = 1 и B = 0. Мы должны выполнить операцию AND. Логическое выражение может быть представлено как A.B = 1.0 = 0.
Логическое выражение может быть представлено как A.B = 1.0 = 0.
Если мы должны выполнить логическую операцию ИЛИ, то логическое выражение задается как A + B = 1 + 0 = 1.
Если мы применим операцию НЕ к обе входные переменные, тогда мы получаем \(\overline{A}\) = 0 и \(\overline{B}\) = 1.
Выражение булевой алгебры
Выражения булевой алгебры — это операторы, в которых используются логические операторы, такие как И, ИЛИ, НЕ, XOR и т. д. Эти логические операторы могут иметь только два выхода: либо истина, либо ложь. В цифровых схемах и логических элементах «1» и «0» используются для обозначения входных и выходных условий. Например, если мы напишем A ИЛИ B, это станет логическим выражением. Существует множество законов и теорем, которые можно использовать для упрощения выражений булевой алгебры, чтобы оптимизировать вычисления, а также улучшить работу цифровых схем.
Булевы алгебраические операции
Существуют три основные операции булевой алгебры. Это конъюнкция, дизъюнкция и отрицание. Логические операторы, эквивалентные этим операциям, приведены ниже.
Это конъюнкция, дизъюнкция и отрицание. Логические операторы, эквивалентные этим операциям, приведены ниже.
- Оператор И: Аналогичен конъюнкции. В логическом выражении «•» используется для представления оператора И. Этот оператор возвращает истину тогда и только тогда, когда все входные операнды истинны.
- Оператор ИЛИ: Этот оператор эквивалентен дизъюнкции. В логическом выражении символ «+» используется для обозначения оператора ИЛИ. Оператор возвращает истину тогда и только тогда, когда истинны один или несколько входных операндов.
- Оператор НЕ: Этот логический оператор сравним с отрицанием. Оператор НЕ возвращает значение true, если входная переменная имеет значение false. Точно так же, если входная переменная ложна, она возвращает истину. Надчеркивание переменной используется для представления этого оператора.
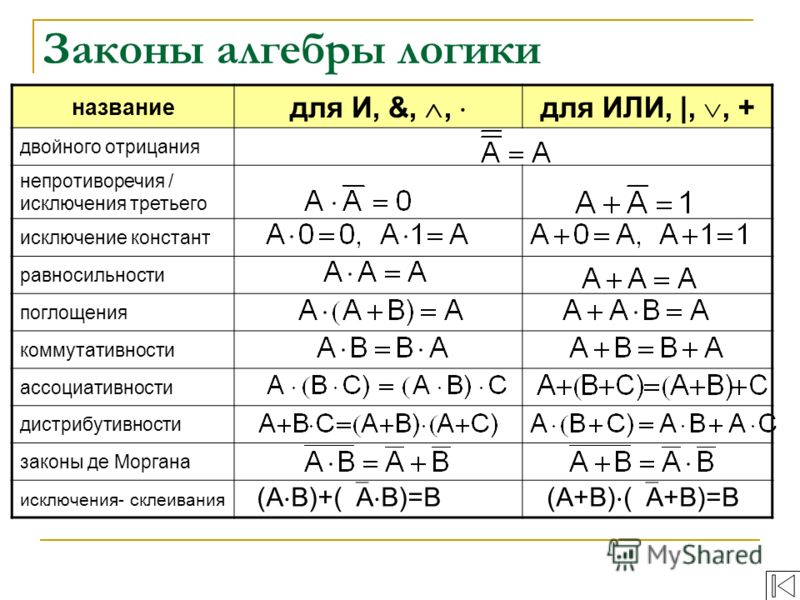
Законы булевой алгебры
Булева алгебра в основном используется для упрощения логических схем. Применяя законы булевой алгебры, мы можем упростить логическое выражение и уменьшить количество логических элементов, которые необходимо использовать в цифровой схеме. Некоторые из важных законов булевой алгебры приведены ниже:
Некоторые из важных законов булевой алгебры приведены ниже:
Распределительный закон
Распределительный закон гласит, что если мы выполним операцию И над двумя переменными и ИЛИ результата с другой переменной, то это будет равно И для ИЛИ третьей переменной с каждой из первых двух переменных. Логическое выражение задается как
A + B.C = (A + B) (A + C)
Таким образом, ИЛИ распределяет по И
Если мы ИЛИ две переменные, то И их результат с другой переменной, то это значение будет равно к ИЛИ И третьей переменной с двумя другими переменными. Это дается:
A .(B+C) = (A.B) + (A.C)
Следовательно, И распределяется по ИЛИ.
Ассоциативный закон
Согласно ассоциативному закону, если более чем две переменные соединены по ИЛИ или по И, то порядок группировки переменных не имеет значения. Результат всегда будет одинаковым. Выражения задаются следующим образом:
A + (B + C) = (A + B) + C
A.(B.C) = (A.B).C
Коммутативный закон
Коммутативный закон утверждает, что если мы поменяем местами порядок операндов (И или ИЛИ) результат логического уравнения не изменится. Это можно представить следующим образом:
Это можно представить следующим образом:
A + B = B + A
A.B = B.A
Закон поглощения
Закон поглощения связывает двоичные переменные и помогает сократить сложные выражения за счет поглощения одинаковых переменных. Есть 4 утверждения, подпадающие под действие этого закона:
- A + A.B = A
- А (А + В) = А
- А + А.В = А + В
- А.(А + В) = А.В
Существуют некоторые свойства и тождества булевой алгебры, которые задаются следующим образом:
- А + 1 = 1
- А + 0 = А
- А . 1 = А
- А . 0 = 0
- А + А = А
- А . А = А
- \(\overline{\overline{A}}\) = А
- А + \(\overline{A}\) = 1
- А . \(\overline{A}\) = 0
Теоремы булевой алгебры
Одной из важнейших теорем булевой алгебры является теорема Де Моргана. Эта теорема состоит из двух утверждений, которые помогают связать операторы И, ИЛИ и НЕ. Два утверждения даны следующим образом:
Два утверждения даны следующим образом:
- Когда две переменные объединяются по И и инвертируются, результат равен ИЛИ каждой инвертированной входной переменной. Логическое выражение: \(\overline{A.B}\) = \(\overline{A}\) + \(\overline{B}\).
- Когда две переменные объединены по ИЛИ и инвертированы, это будет равно И для каждой инвертированной входной переменной. Это определяется как \(\overline{A + B}\) = \(\overline{A}\).\(\overline{B}\)
Постулаты булевой алгебры
Постулаты булевой алгебры — это не законы или теоремы, а истинные утверждения. Этими постулатами являются четыре возможных логических операции ИЛИ и логическое И, а также правила, которым следует оператор НЕ. Ниже приведены постулаты булевой алгебры:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 1
- 0 . 0 = 0
- 0 . 1 = 0
- 1 . 0 = 0
- 1 .
 1 = 1
1 = 1 - \(\overline{1}\) = 0
- \(\overline{0}\) = 1
Булева алгебра и логические элементы
Логический элемент является строительным блоком любой цифровой схемы. Эти логические элементы должны принимать решение об объединении различных входных данных в соответствии с некоторой логической операцией и создавать выходные данные. Логические элементы выполняют логические операции на основе булевой алгебры. Предположим, у нас есть два входа A и B. Пусть выход будет R. Тогда ниже приведены различные типы и символы логических элементов.
И ворота — R = A.B будет логическим выражением. R будет истинным, если оба A и B истинны.
Элемент ИЛИ — логическое уравнение R = A + B. Здесь R будет истинным, если любой из входов A ИЛИ B верен.
вентиль НЕ — также известен как инвертор, а логическое уравнение — R = \(\overline{A}\). Это означает, что вывод истинен только в том случае, если ввод ложен.
вентиль И-НЕ — Это тоже ворота НЕ-И. R = \(\overline{A.B}\) — логическое уравнение. Выход R НЕ будет истинным, если оба A И B верны.
Вентиль ИЛИ — Операция НЕ-ИЛИ приводит к вентилю ИЛИ-НЕ. R = \(\overline{A + B}\) обозначает логическое уравнение и подразумевает, что R истинно, если A и B НЕ истинны.
EX — ворота ИЛИ — Это ворота исключающего ИЛИ. Его можно создать, используя комбинацию вышеупомянутых ворот. R = A ⊕ B — логическое выражение. Это означает, что R истинно, только если истинно либо A, либо B.
EX — вентиль ИЛИ-НЕ — логическое уравнение вентиля исключающее ИЛИ-ИЛИ задается как R = \(\overline{A ⊕ B}\). Это означает, что R истинно, только если оба входа либо истинны, либо ложны.
Таблица истинности булевой алгебры
Таблица истинности булевой алгебры может быть определена как таблица, которая сообщает нам, верно ли логическое выражение для указанных входных переменных.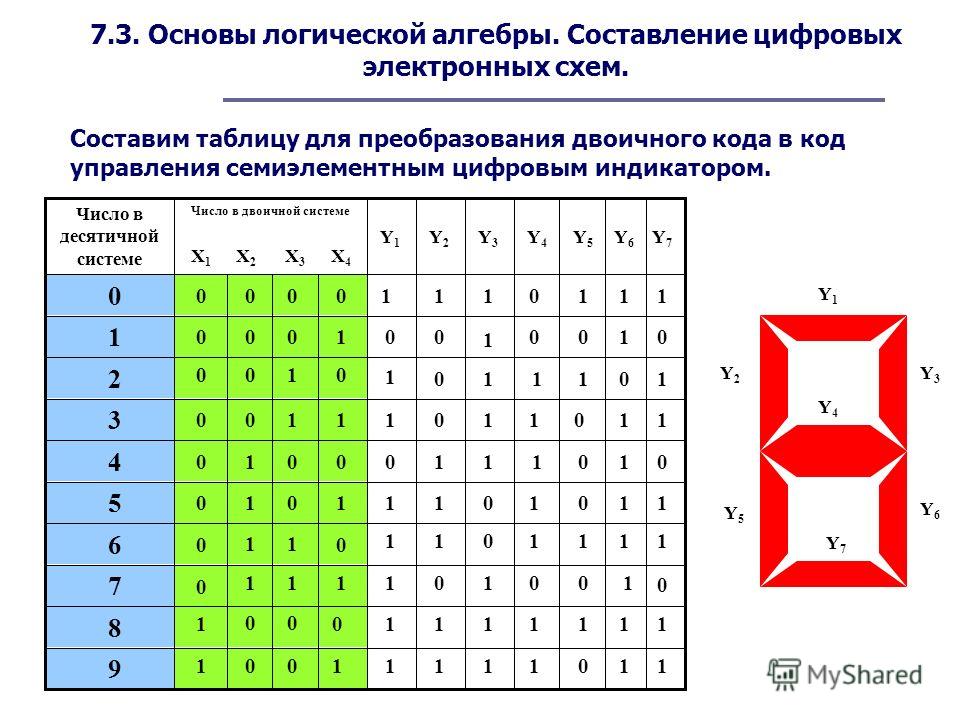 Такая таблица истинности будет состоять только из бинарных входов и выходов. Ниже приведены таблицы истинности для различных логических вентилей.
Такая таблица истинности будет состоять только из бинарных входов и выходов. Ниже приведены таблицы истинности для различных логических вентилей.
И ворота
| А | Б | Р = А.Б. |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Ворота ИЛИ
| А | Б | Р = А + В |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
НЕ ворота
| А | R = \(\overline{A}\) |
| 1 | 0 |
| 0 | 1 |
вентиль И-НЕ
| А | Б | R = \(\overline{A.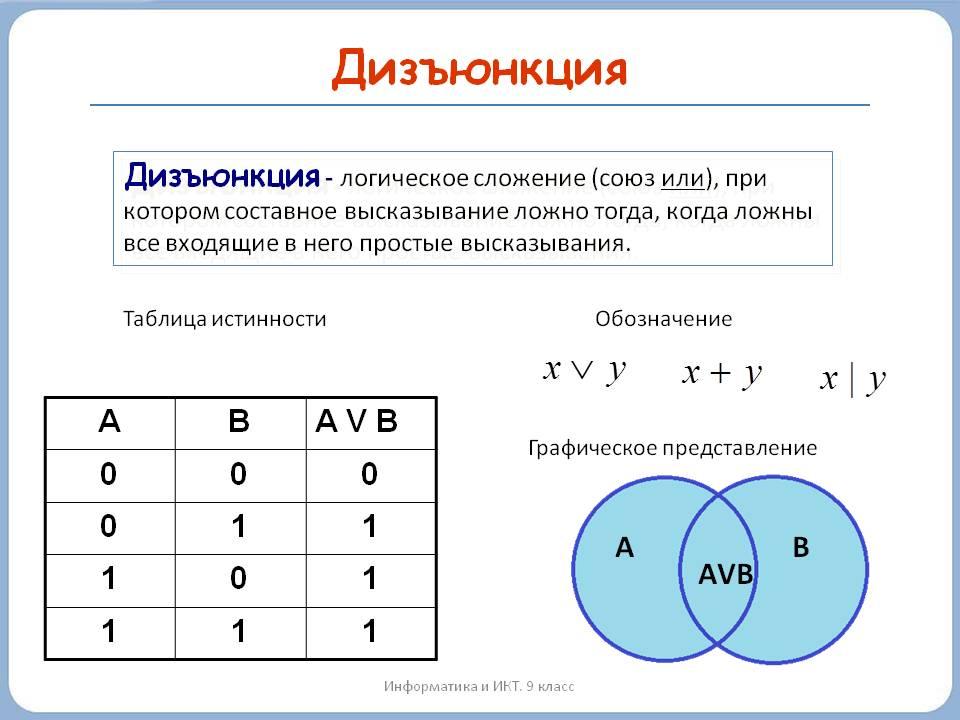 B}\) B}\) |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Ворота NOR
| A | Б | R = \(\overline{A + B}\) |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Ворота EX-OR
| A | Б | Р = А ⊕ В |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Ворота EX — NOR
| A | Б | R = \(\overline{A ⊕ B}\) |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Связанные статьи:
- Наборы
- Калькулятор булевой алгебры
- Дополнение к набору
- Пересечение набора
Часто задаваемые вопросы по булевой алгебре
Что понимается под булевой алгеброй?
Булева алгебра — это тип алгебры, в котором входные и выходные значения могут быть только истинными (1) или ложными (0). Булева алгебра использует логические операторы и используется для построения цифровых схем.
Булева алгебра использует логические операторы и используется для построения цифровых схем.
Что такое правила булевой алгебры?
Основные правила булевой алгебры:
- Любая используемая переменная может иметь только два значения. Двоичный 1 для HIGH и двоичный 0 для LOW.
- Каждая дополнительная переменная представлена чертой сверху, т. е. дополнение переменной B представлено как B¯. Таким образом, если B = 0, то B¯= 1 и B = 1, то B¯= 0,
- Переменные с ИЛИ представлены знаком плюс (+) между ними. Например, OR для A, B, C представляется как A + B + C.
- Две или более переменных с логическим И представлены точкой между ними, например, A.B.C. Иногда точка может быть опущена, как ABC.
Что такое законы булевой алгебры?
Есть четыре основных закона булевой алгебры. Это дистрибутивное право, ассоциативное право, коммутативное право и абсорбционное право. Когда мы упрощаем логическое выражение, эти законы широко используются.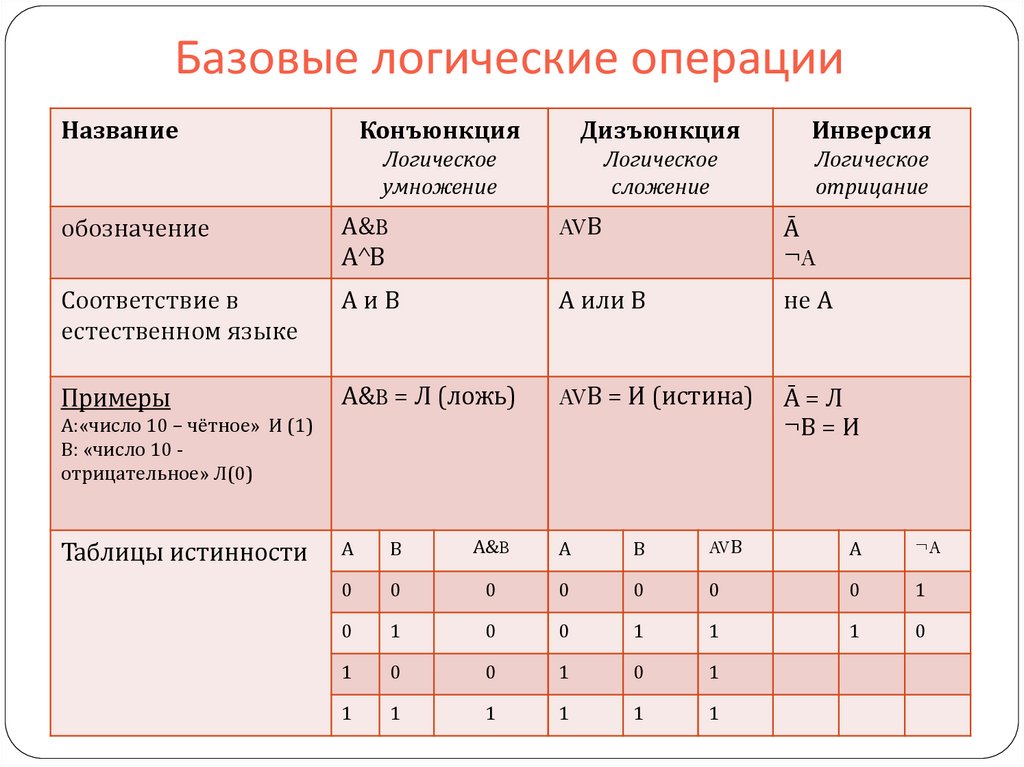
Каковы тождества булевой алгебры?
Важные тождества булевой алгебры приведены ниже:
- A + 1 = 1
- А + 0 = А
- А . 1 = А
- А . 0 = 0
- А + А = А
- А . А = А
- \(\overline{\overline{A}}\) = А
- А + \(\overline{A}\) = 1
- А . \(\overline{A}\) = 0
Как вы занимаетесь булевой алгеброй?
При решении выражения булевой алгебры самое главное помнить законы булевой алгебры, теоремы и связанные с ними тождества. Нам нужно последовательно применять эти правила до тех пор, пока выражение нельзя будет упростить дальше, чтобы получить наш ответ.
Что такое распределительный закон в булевой алгебре?
Закон дистрибутивности в булевой алгебре содержит два утверждения. Два утверждения выглядят следующим образом:
- ИЛИ распределяет по И [A + B.C = (A + B) (A + C)].
- И распределяется по ИЛИ [A .(B+C) = (A.B) + (A.C)]
Что такое закон поглощения в булевой алгебре?
Уравнения булевой алгебры для закона поглощения, которые помогают связать одинаковые переменные, выглядят следующим образом:
- A + A.
 B = A
B = A - А (А + В) = А
- А + А.В = А + В
- А.(А + В) = А.В
Как упростить выражения булевой алгебры?
Мы можем упростить выражения булевой алгебры, используя различные теоремы, законы, постулаты и свойства. В случае цифровых схем мы можем выполнить пошаговый анализ выхода каждого вентиля, а затем применить правила булевой алгебры, чтобы получить максимально упрощенное выражение.
Каковы свойства булевой алгебры?
Булева алгебра имеет три основных свойства, а именно:
- Коммутативное свойство сложения и умножения: порядок переменных может быть изменен на обратный без изменения истинности выражения, т. е. A + B = B + A и AB = BA
- Ассоциативное свойство сложения и умножения: умноженные и добавленные переменные вместе со скобками могут быть изменены без изменения истинности выражения, т. Е. A + (B + C) = (A + B) + C и A (BC) = (AB) C
- Распределительное свойство: выражение, образованное произведением суммы при расширении и переворачивании, показывает, как члены могут быть факторизованы, т.
 е. A(B + C) = AB + BC
е. A(B + C) = AB + BC
Булева алгебра — 1. Операторы и основы
Булева алгебра!
Это действительно логично.
Введение
Мы начнем с рассмотрения того, что такое булева алгебра, а затем рассмотрим некоторые из основных строительных блоков, также называемых операторами. На данном этапе это может показаться немного абстрактным, но как только вы проработаете этот раздел и следующий, он начнет обретать немного больше смысла.
Булева алгебра
Булева алгебра — это способ формального определения или описания конкретной ситуации или процедуры. Мы используем переменных для представления элементов нашей ситуации или процедуры. Переменные могут принимать одно из двух значений. Традиционно это будет True и False . Так, например, у нас может быть переменная X , и мы можем указать, идет ли на улице дождь или нет. Значение X будет:
- True , если на улице идет дождь.
- False , если на улице нет дождя.

Вы должны помнить, что хотя многие вещи в реальном мире существуют в спектре, в булевой алгебре все сводится к черному и белому. Таким образом, у нас может быть, например, небольшой дождь, постоянный дождь или сильный дождь. Однако в булевой алгебре либо идет дождь, либо нет. Это может показаться немного ограничивающим, но такое упрощение вещей на самом деле оказывается весьма мощным.
Можно заменить True и False другими значениями. При работе с компьютерами часто бывает, что True и False заменяются на 1 и 0 . При работе с физическими цепями мы можем заменить True и False на наличие или отсутствие напряжения.
Таким образом, булева алгебра полезна для описания процесса, а затем для создания механизмов, которые могут выполнять эти процессы. Имейте это в виду, когда будете работать над следующими несколькими разделами. Это то, к чему мы движемся.
Основные операции
Выше мы видели, что переменные могут использоваться для представления текущего состояния элементов, которые нас интересуют. Операции позволяют нам затем определить отношения между этими переменными. Есть три основных операции. Они часто используются в логических выражениях, но также используются для создания более сложных операций. Вы, вероятно, обнаружите, что на самом деле использовали эти операции довольно часто, просто вы никогда раньше не думали о них формально.
Операции позволяют нам затем определить отношения между этими переменными. Есть три основных операции. Они часто используются в логических выражениях, но также используются для создания более сложных операций. Вы, вероятно, обнаружите, что на самом деле использовали эти операции довольно часто, просто вы никогда раньше не думали о них формально.
Результат операции аналогичен переменным, может быть только Верно или Ложно .
Я решил всегда писать операции БОЛЬШИМ РЕГИСТРОМ. Поэтому их легко идентифицировать как операции. Многие люди следуют этому соглашению, но это не обязательно. Не стесняйтесь использовать любой метод, который вам больше подходит.
И
Первая операция — И , и это означает почти то же, что и на простом английском языке. Так, например, я могу заявить: «Если снаружи И солнечно, я закончил свою работу, тогда я пойду на пробежку». Чтобы представить это в булевой алгебре, я могу сказать, что:
- x показывает, солнечно на улице или нет.

- y показывает, завершил ли я свою работу или нет.
- z представляет, пойду ли я на пробежку или нет.
А я бы написал так:
x AND y = z
Здесь это представлено визуально. Заштрихованная область — это область, которая представляет И .
А теперь мы представим его с помощью так называемой Таблица истинности . В таблице истинности перечислены все возможные комбинации входных данных для выражения (в данном случае одной операции) и то, каким должен быть результат или вывод.
| Ложь | Ложь | Ложь |
| Правда | Ложь | Ложь |
| Ложь | Правда | Ложь |
| Правда | Правда | Правда |
ИЛИ
ИЛИ тоже самое, что и в простом английском языке. Это означает, что если любая из двух переменных равна True , то результатом будет True . Так, например, я мог бы сказать: «Я вернусь домой с работы раньше, если уйду рано ИЛИ , пробки хорошие».
Так, например, я мог бы сказать: «Я вернусь домой с работы раньше, если уйду рано ИЛИ , пробки хорошие».
Здесь ИЛИ представлены визуально:
И снова таблица истинности:
| Ложь | Ложь | Ложь |
| Правда | Ложь | Правда |
| Ложь | Правда | Правда |
| Правда | Правда | Правда |
Обратите внимание, что И являются Ложными для всех, кроме Истинных и Истинных, в то время как ИЛИ являются Истинными для всех, кроме Ложных и Ложных. Это наблюдение пригодится нам в дальнейшем. На самом деле есть много сокращений и выгодных преимуществ, которые можно получить от поиска подобных шаблонов, поэтому следите за ними.
Not
Not очень похоже на то, как мы используем его в простом английском языке. Он имеет тонкое отличие при использовании в булевой алгебре. Обычно я могу сказать что-то вроде «Я съем десерт, если не наелся». Я также мог бы сказать: «Я съем десерт, если я все еще голоден», что имеет то же значение, но использует противоположное значение. Таким образом, , а не , на самом деле приводит к переворачиванию значения переменной. Если:
Обычно я могу сказать что-то вроде «Я съем десерт, если не наелся». Я также мог бы сказать: «Я съем десерт, если я все еще голоден», что имеет то же значение, но использует противоположное значение. Таким образом, , а не , на самом деле приводит к переворачиванию значения переменной. Если:
- переменная d в настоящее время имеет значение Верно , затем
- выражение не d имеет результат False
Визуально представлено:
И как таблица истинности:
| True | Ложь |
| Ложь | Правда |
Производные операции
Вышеуказанные три операции являются строительными блоками почти всего остального, что мы можем делать в булевой алгебре. Теперь мы представим то, что называется производные операции . По сути, это ярлыки для часто используемых комбинаций основных операций. Как мы узнаем позже, некоторые из этих производных операций очень полезны, когда мы хотим выполнять вычисления и другие вещи.
Исключающее ИЛИ или исключающее ИЛИ
С помощью операции ИЛИ мы увидели, что пока одна из переменных равна True , результатом будет True . Это также было правдой, если оба они были правдой. С операцией XOR теперь мы говорим, что результат будет True, только если одна из двух переменных имеет значение True. То есть одно из них истинно, но истинно только одно из них. Мы можем построить эту операцию из основных операций следующим образом:
g XOR p эквивалентно (g OR p) AND NOT(g AND p)
Когда скобки ( ) используются в выражении, это означает, что мы оцениваем эта часть выражения стоит перед другими частями.
Давайте рассмотрим пример, чтобы лучше понять, что происходит.
Если g истинно, а p ложно, то:
Подставив g и p вместо этих значений, мы получим:
(Истина ИЛИ Ложь) набор скобок (Истина ИЛИ Ложь) И НЕ (Истина И Ложь) оценивается как Истина, поэтому давайте заменим его в выражении, и мы получим:
Истина И НЕ (Истина И Ложь)
Следующий набор скобок Верно И НЕ (Верно И Ложно) оценивается как False, поэтому давайте заменим его в выражении, что также дает нам:
True AND NOT( False )
NOT(False) оценивается как True, поэтому мы можем применить это к выражению, и мы получим :
True и True
И конечный результат True .
Визуально XOR выглядит так:
XOR как таблица истинности:
| Ложь | Ложь | Ложь |
| Правда | Ложь | Правда |
| Ложь | Правда | Правда |
| Правда | Правда | Ложь |
И-НЕ или НЕ-И
НЕ-И фактически противоположно тому, что есть И.
r НЕ-И S эквивалентно НЕ(r И s)
Визуально это выглядит так:
NAND как таблица истинности:
| Ложь | Ложь | Правда |
| Правда | Ложь | Правда |
| Ложь | Правда | Правда |
| Правда | Правда | Ложь |
ИЛИ или НЕ ИЛИ
ИЛИ фактически противоположно ИЛИ.
b NOR k эквивалентно NOT(b OR k)
Визуально это выглядит так:
NOR как таблица истинности:
| Ложь | Ложь | Правда |
| Правда | Ложь | Ложь |
| Ложь | Правда | Ложь |
| Правда | Правда | Ложь |
Сводка
- Переменная
- Элемент внутри логического выражения.



 Введите свой запрос:
Введите свой запрос:
 1 = 1
1 = 1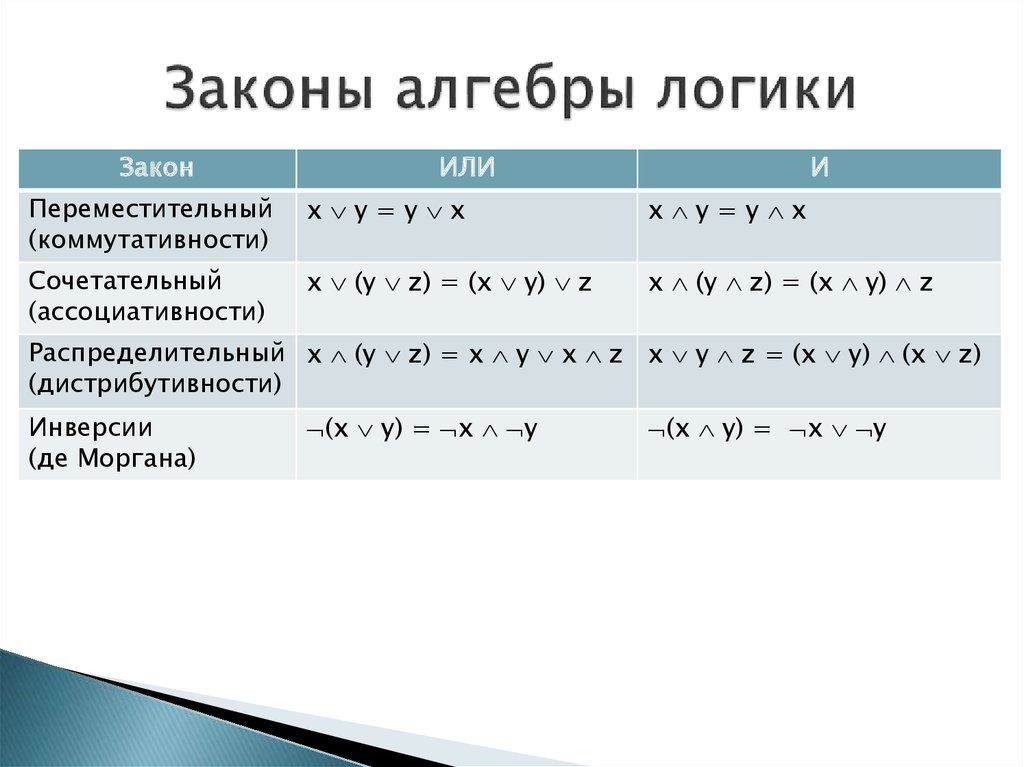 B = A
B = A е. A(B + C) = AB + BC
е. A(B + C) = AB + BC