вычислить онлайн скалярное произведение векторов
Вы искали вычислить онлайн скалярное произведение векторов? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить скалярное произведение, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычислить онлайн скалярное произведение векторов».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычислить онлайн скалярное произведение векторов,вычислить скалярное произведение,вычислить скалярное произведение векторов,вычислить скалярное произведение векторов онлайн,калькулятор векторов скалярное произведение,калькулятор скалярного произведения векторов,калькулятор скалярное произведение векторов,найти скалярное произведение векторов онлайн,найти скалярное произведение векторов онлайн калькулятор,онлайн вычислить скалярное произведение векторов,онлайн калькулятор векторов скалярное произведение векторов,онлайн калькулятор найти скалярное произведение векторов,онлайн калькулятор скалярний добуток векторів,скалярний добуток векторів онлайн калькулятор,скалярное произведение векторов калькулятор,скалярное произведение векторов калькулятор онлайн,скалярное произведение векторов онлайн,скалярное произведение векторов онлайн калькулятор,скалярное произведение калькулятор,скалярное произведение онлайн.
Где можно решить любую задачу по математике, а так же вычислить онлайн скалярное произведение векторов Онлайн?
Решить задачу вычислить онлайн скалярное произведение векторов вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Найти разложение вектора по базису онлайн калькулятор.
 Базис. Разложение вектора по векторам
Базис. Разложение вектора по векторамВ векторном исчислении и его приложениях большое значение имеет задача разложения, состоящая в представлении данного вектора в виде суммы нескольких векторов, называемых составляющими данного
вектора. Эта задача, имеющая в общем случае бесчисленное множество решений, становится вполне определенной, если задать некоторые элементы составляющих векторов.
2. Примеры разложения.
Рассмотрим несколько весьма часто встречающихся случаев разложения.
1. Разложить данный вектор с на два составляющих вектора из которых один, например а, задан по величине и направлению.
Задача сводится к определению разности двух векторов. Действительно, если векторы являются составляющими вектора с, то должно выполняться равенство
Отсюда определяется второй составляющий вектор
2. Разложить данный вектор с на два составляющих, из которых один должен лежать в заданной плоскости а второй должен лежать на заданной прямой а.
Для определения составляющих векторов перенесем вектор с так, чтобы его начало совпало с точкой пересечения заданной прямой с плоскостью (точка О — см. рис. 18). Из конца вектора с (точка С) проведем прямую до
рис. 18). Из конца вектора с (точка С) проведем прямую до
пересечения с плоскостью {В — точка пересечения), а затем из точки С проведем прямую параллельно
Векторы и будут искомыми, т. е. Естественно, что указанное разложение возможно, если прямая а и плоскость не параллельны.
3. Даны три компланарных вектора а, b и с, причем векторы не коллинеарны. Требуется разложить вектор с по векторам
Приведем все три заданных вектора к одной точке О. Тогда в силу их компланарности они расположатся в одной плоскости. На данном векторе с как на диагонали построим параллелограмм, стороны которого параллельны линиям действия векторов (рис. 19). Это построение всегда возможно (если только векторы не коллинеарны) и единственно. Из рис. 19 видно, что
В аудитории находится тележка с шоколадками, и каждому посетителю сегодня достанется сладкая парочка – аналитическая геометрия с линейной алгеброй. В данной статье будут затронуты сразу два раздела высшей математики, и мы посмотрим, как они уживаются в одной обёртке.
Линейная зависимость векторов , линейная независимость векторов , базис векторов и др. термины имеют не только геометрическую интерпретацию, но, прежде всего, алгебраический смысл . Само понятие «вектор» с точки зрения линейной алгебры – это далеко не всегда тот «обычный» вектор, который мы можем изобразить на плоскости или в пространстве. За доказательством далеко ходить не нужно, попробуйте нарисовать вектор пятимерного пространства . Или вектор погоды, за которым я только что сходил на Гисметео: – температура и атмосферное давление соответственно. Пример, конечно, некорректен с точки зрения свойств векторного пространства, но, тем не менее, никто не запрещает формализовать данные параметры вектором. Дыхание осени….
Нет, я не собираюсь грузить вас теорией, линейными векторными пространствами, задача состоит в том, чтобы понять определения и теоремы.
Базис плоскости и аффинная система координат
Рассмотрим плоскость вашего компьютерного стола (просто стола, тумбочки, пола, потолка, кому что нравится). Задача будет состоять в следующих действиях:
1) Выбрать базис плоскости . Грубо говоря, у столешницы есть длина и ширина, поэтому интуитивно понятно, что для построения базиса потребуется два вектора. Одного вектора явно мало, три вектора – лишка.
2) На основе выбранного базиса задать систему координат (координатную сетку), чтобы присвоить координаты всем находящимся на столе предметам.
Не удивляйтесь, сначала объяснения будут на пальцах. Причём, на ваших. Пожалуйста, поместите
, ну, или наоборот: , где – некоторое число, отличное от нуля.
Картинку сего действа можно посмотреть на уроке Векторы для чайников , где я объяснял правило умножения вектора на число.
Будут ли ваши пальчики задавать базис на плоскости компьютерного стола? Очевидно, что нет. Коллинеарные векторы путешествуют туда-сюда по
Такие векторы называют линейно зависимыми .
Справка: Слова «линейный», «линейно» обозначают тот факт, что в математических уравнениях, выражениях нет квадратов, кубов, других степеней, логарифмов, синусов и т.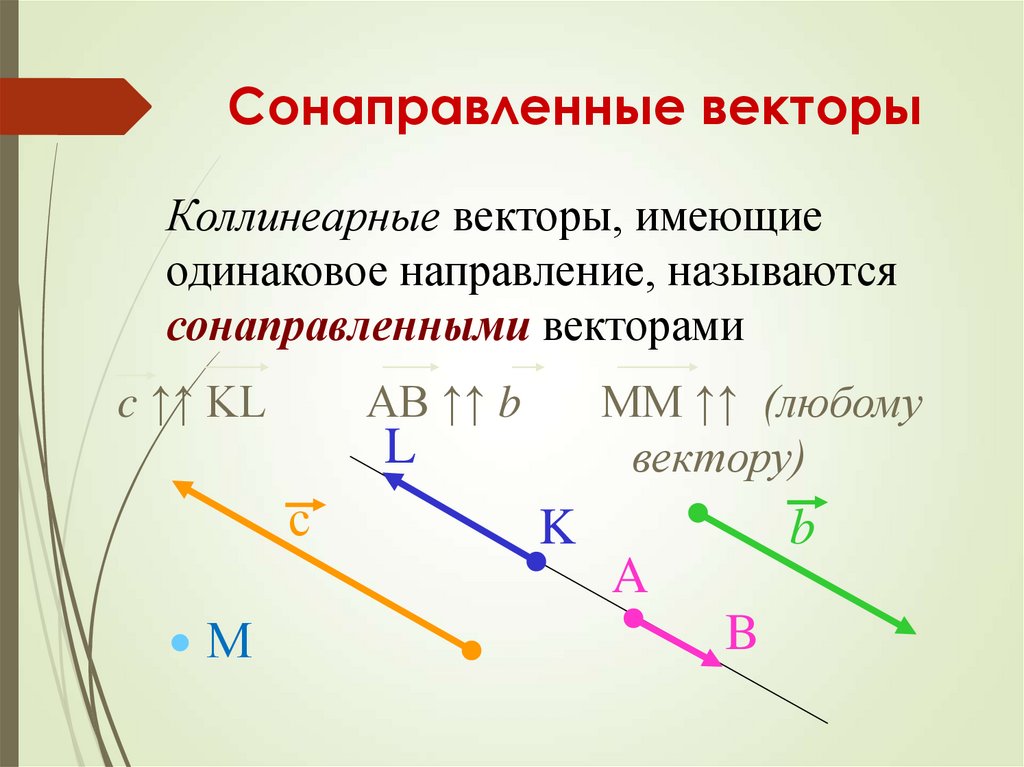 д. Есть только линейные (1-й степени) выражения и зависимости.
д. Есть только линейные (1-й степени) выражения и зависимости.
Два вектора плоскости линейно зависимы тогда и только тогда , когда они коллинеарны .
Скрестите пальцы на столе, чтобы между ними был любой угол, кроме 0 или 180 градусов. Два вектора плоскости
Любой вектор плоскости единственным образом раскладывается по базису :
, где – действительные числа . Числа называют координатами вектора в данном базисе.
Также говорят, что вектор представлен в виде линейной комбинации базисных векторов . То есть, выражение называют разложением вектора по базису или

Например, можно сказать, что вектор разложен по ортонормированному базису плоскости , а можно сказать, что он представлен в виде линейной комбинации векторов .
Сформулируем определение базиса формально: Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов , , при этом любой вектор плоскости является линейной комбинацией базисных векторов.
Существенным моментом определения является тот факт, что векторы взяты в определённом порядке . Базисы – это два совершенно разных базиса! Как говорится, мизинец левой руки не переставишь на место мизинца правой руки.
С базисом разобрались, но его недостаточно, чтобы задать координатную сетку и присвоить координаты каждому предмету вашего компьютерного стола. Почему недостаточно? Векторы являются свободными и блуждают по всей плоскости. Так как же присвоить координаты тем маленьким грязным точкам стола, которые остались после бурных выходных? Необходим отправной ориентир. И таким ориентиром является знакомая всем точка – начало координат. Разбираемся с системой координат:
И таким ориентиром является знакомая всем точка – начало координат. Разбираемся с системой координат:
Начну со «школьной» системы. Уже на вступительном уроке Векторы для чайников я выделял некоторые различия между прямоугольной системой координат и ортонормированным базисом . Вот стандартная картина:
Когда говорят о прямоугольной системе координат , то чаще всего имеют в виду начало координат, координатные оси и масштаб по осям. Попробуйте набрать в поисковике «прямоугольная система координат», и вы увидите, что многие источники вам будут рассказывать про знакомые с 5-6-го класса координатные оси и о том, как откладывать точки на плоскости.
С другой стороны, создается впечатление, что прямоугольную систему координат вполне можно определить через ортонормированный базис . И это почти так. Формулировка звучит следующим образом:
началом координат , и ортонормированный базис задают декартову прямоугольную систему координат плоскости . То есть, прямоугольная система координат однозначно определяется единственной точкой и двумя единичными ортогональными векторами . Именно поэтому, вы видите чертёж, который я привёл выше – в геометрических задачах часто (но далеко не всегда) рисуют и векторы, и координатные оси.
То есть, прямоугольная система координат однозначно определяется единственной точкой и двумя единичными ортогональными векторами . Именно поэтому, вы видите чертёж, который я привёл выше – в геометрических задачах часто (но далеко не всегда) рисуют и векторы, и координатные оси.
Думаю, всем понятно, что с помощью точки (начала координат) и ортонормированного базиса ЛЮБОЙ ТОЧКЕ плоскости и ЛЮБОМУ ВЕКТОРУ плоскости можно присвоить координаты. Образно говоря, «на плоскости всё можно пронумеровать».
Обязаны ли координатные векторы быть единичными? Нет, они могут иметь произвольную ненулевую длину. Рассмотрим точку и два ортогональных вектора произвольной ненулевой длины:
Такой базис называется ортогональным . Начало координат с векторами задают координатную сетку, и любая точка плоскости, любой вектор имеют свои координаты в данном базисе. Например, или . Очевидное неудобство состоит в том, что координатные векторы в общем случае имеют различные длины, отличные от единицы. Если длины равняются единице, то получается привычный ортонормированный базис.
Если длины равняются единице, то получается привычный ортонормированный базис.
! Примечание : в ортогональном базисе, а также ниже в аффинных базисах плоскости и пространства единицы по осям считаются УСЛОВНЫМИ . Например, в одной единице по оси абсцисс содержится 4 см, в одной единице по оси ординат 2 см. Данной информации достаточно, чтобы при необходимости перевести «нестандартные» координаты в «наши обычные сантиметры».
И второй вопрос, на который уже на самом деле дан ответ – обязательно ли угол между базисными векторами должен равняться 90 градусам? Нет! Как гласит определение, базисные векторы должны быть лишь неколлинеарными . Соответственно угол может быть любым, кроме 0 и 180 градусов.
Точка плоскости, которая называется началом координат , и неколлинеарные векторы , , задают аффинную систему координат плоскости :
Иногда такую систему координат называют косоугольной системой.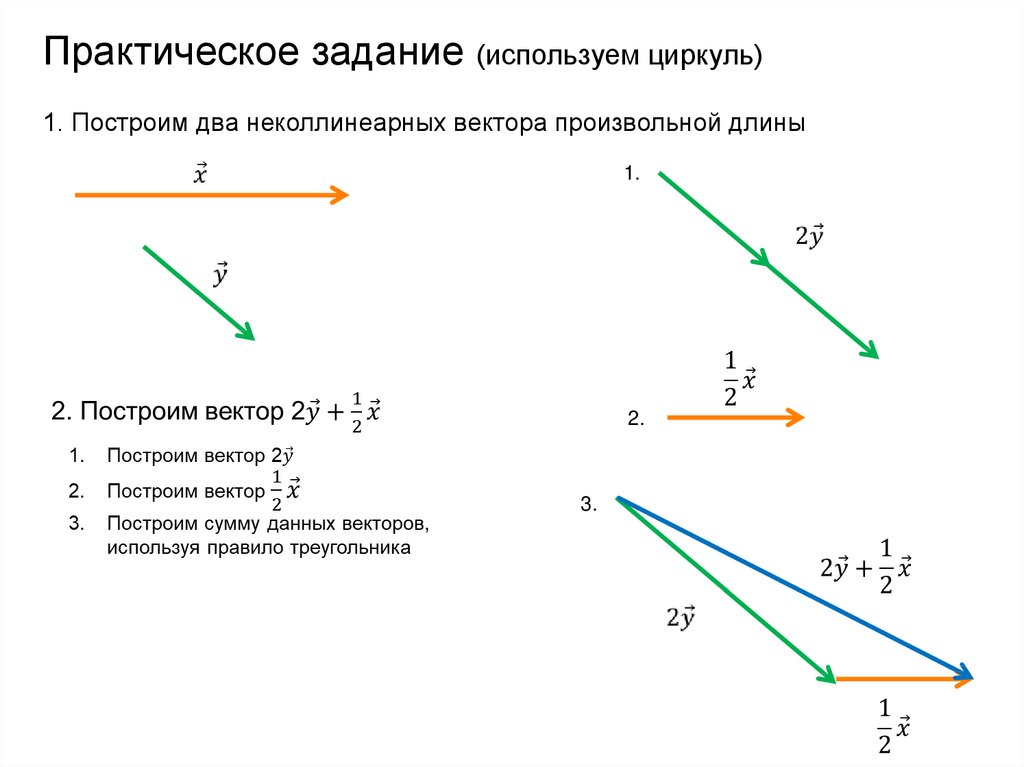 В качестве примеров на чертеже изображены точки и векторы:
В качестве примеров на чертеже изображены точки и векторы:
Как понимаете, аффинная система координат ещё менее удобна, в ней не работают формулы длин векторов и отрезков, которые мы рассматривали во второй части урока Векторы для чайников , многие вкусные формулы, связанные со скалярным произведением векторов . Зато справедливы правила сложения векторов и умножения вектора на число, формулы деления отрезка в данном отношении , а также ещё некоторые типы задач, которые мы скоро рассмотрим.
А вывод таков, что наиболее удобным частным случаем аффинной системы координат является декартова прямоугольная система. Поэтому её, родную, чаще всего и приходится лицезреть. …Впрочем, всё в этой жизни относительно – существует немало ситуаций, в которых уместна именно косоугольная (или какая-набудь другая, например, полярная ) система координат. Да и гуманоидам такие системы могут прийтись по вкусу =)
Переходим к практической части. Все задачи данного урока справедливы как для прямоугольной системы координат, так и для общего аффинного случая. Сложного здесь ничего нет, весь материал доступен даже школьнику.
Сложного здесь ничего нет, весь материал доступен даже школьнику.
Типовая вещь. Для того чтобы два вектора плоскости были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны .По существу, это покоординатная детализация очевидного соотношения .
Пример 1
а) Проверить, коллинеарны ли векторы .
б) Образуют ли базис векторы ?
Решение:
а) Выясним, существует ли для векторов коэффициент пропорциональности , такой, чтобы выполнялись равенства :
Обязательно расскажу о «пижонской» разновидности применения данного правила, которая вполне прокатывает на практике. Идея состоит в том, чтобы сразу составить пропорцию и посмотреть, будет ли она верной:
Составим пропорцию из отношений соответствующих координат векторов:
Сокращаем:
, таким образом, соответствующие координаты пропорциональны, следовательно,
Отношение можно было составить и наоборот, это равноценный вариант:
Для самопроверки можно использовать то обстоятельство, что коллинеарные векторы линейно выражаются друг через друга. В данном случае имеют место равенства . Их справедливость легко проверяется через элементарные действия с векторами:
В данном случае имеют место равенства . Их справедливость легко проверяется через элементарные действия с векторами:
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Исследуем на коллинеарность векторы . Составим систему:
Из первого уравнения следует, что , из второго уравнения следует, что , значит, система несовместна (решений нет). Таким образом, соответствующие координаты векторов не пропорциональны.
Вывод : векторы линейно независимы и образуют базис.
Упрощённая версия решения выглядит так:
Составим пропорцию из соответствующих координат векторов :
, значит, данные векторы линейно независимы и образуют базис.
Обычно такой вариант не бракуют рецензенты, но возникает проблема в тех случаях, когда некоторые координаты равны нулю. Вот так: . Или так: . Или так: . Как тут действовать через пропорцию? (действительно, на ноль же делить нельзя). Именно по этой причине я и назвал упрощенное решение «пижонским».
Ответ: а) , б) образуют.
Небольшой творческий пример для самостоятельного решения:
Пример 2
При каком значении параметра векторы будут коллинеарны?
В образце решения параметр найден через пропорцию .
Существует изящный алгебраический способ проверки векторов на коллинеарность., систематизируем наши знания и пятым пунктом как раз добавим его:
Для двух векторов плоскости эквивалентны следующие утверждения :
2) векторы образуют базис;
3) векторы не коллинеарны;
+ 5) определитель, составленный из координат данных векторов, отличен от нуля .
Соответственно, эквивалентны следующие противоположные утверждения :
1) векторы линейно зависимы;
2) векторы не образуют базиса;
3) векторы коллинеарны;
4) векторы можно линейно выразить друг через друга;
+ 5) определитель, составленный из координат данных векторов, равен нулю .
Я очень и очень надеюсь, что на данный момент вам уже понятны все встретившиеся термины и утверждения.
Рассмотрим более подробно новый, пятый пункт: два вектора плоскости коллинеарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю :. Для применения данного признака, естественно, нужно уметь находить определители .
Решим Пример 1 вторым способом:
а) Вычислим определитель, составленный из координат векторов :
, значит, данные векторы коллинеарны.
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Вычислим определитель, составленный из координат векторов :
, значит, векторы линейно независимы и образуют базис.
Ответ: а) , б) образуют.
Выглядит значительно компактнее и симпатичнее, чем решение с пропорциями.
С помощью рассмотренного материала можно устанавливать не только коллинеарность векторов, но и доказывать параллельность отрезков, прямых. Рассмотрим пару задач с конкретными геометрическими фигурами.
Пример 3
Даны вершины четырёхугольника . Доказать, что четырёхугольник является параллелограммом.
Доказать, что четырёхугольник является параллелограммом.
Доказательство : Чертежа в задаче строить не нужно, поскольку решение будет чисто аналитическим. Вспоминаем определение параллелограмма:
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.
Таким образом, необходимо доказать:
1) параллельность противоположных сторон и ;
2) параллельность противоположных сторон и .
Доказываем:
1) Найдём векторы:
2) Найдём векторы:
Получился один и тот же вектор («по школьному» – равные векторы). Коллинеарность совсем очевидна, но решение таки лучше оформить с толком, с расстановкой. Вычислим определитель, составленный из координат векторов :
, значит, данные векторы коллинеарны, и .
Вывод : Противоположные стороны четырёхугольника попарно параллельны, значит, он является параллелограммом по определению. Что и требовалось доказать .
Больше фигур хороших и разных:
Пример 4
Даны вершины четырёхугольника . Доказать, что четырёхугольник является трапецией.
Для более строгой формулировки доказательства лучше, конечно, раздобыть определение трапеции, но достаточно и просто вспомнить, как она выглядит.
Это задание для самостоятельного решения. Полное решение в конце урока.
А теперь пора потихонечку перебираться из плоскости в пространство:
Как определить коллинеарность векторов пространства?Правило очень похоже. Для того чтобы два вектора пространства были коллинеарны, необходимо и достаточно , чтобы их соответствующие координаты были пропорциональны .
Пример 5
Выяснить, будут ли коллинеарны следующие векторы пространства:
а) ;
б)
в)
Решение:
а) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:
Система не имеет решения, значит, векторы не коллинеарны.
«Упрощёнка» оформляется проверкой пропорции . В данном случае:
– соответствующие координаты не пропорциональны, значит, векторы не коллинеарны.
Ответ: векторы не коллинеарны.
б-в) Это пункты для самостоятельного решения. Попробуйте его оформить двумя способами.
Существует метод проверки пространственных векторов на коллинеарность и через определитель третьего порядка, данный способ освещен в статье Векторное произведение векторов .
Аналогично плоскому случаю, рассмотренный инструментарий может применяться в целях исследования параллельности пространственных отрезков и прямых.
Добро пожаловать во второй раздел:
Линейная зависимость и независимость векторов трехмерного пространства.Пространственный базис и аффинная система координат
Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Я постарался минимизировать конспект по теории, поскольку львиная доля информации уже разжёвана. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.
Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.
Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.
И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний палец . Это будут векторы , они смотрят в разные стороны, имеют разную длину и имеют разные углы между собой. Поздравляю, базис трёхмерного пространства готов! Кстати, не нужно демонстрировать такое преподавателям, как ни крути пальцами, а от определений никуда не деться =)
Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства ? Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными и, совершенно очевидно, что базиса трёхмерного пространства не создают.
Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными и, совершенно очевидно, что базиса трёхмерного пространства не создают.
Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)).
Определение : векторы называются компланарными , если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны.
Три компланарных вектора всегда линейно зависимы , то есть линейно выражаются друг через друга. Для простоты снова представим, что они лежат в одной плоскости. Во-первых, векторы мало того, что компланарны, могут быть вдобавок ещё и коллинеарны, тогда любой вектор можно выразить через любой вектор. Во втором случае, если, например, векторы не коллинеарны, то третий вектор выражается через них единственным образом: (а почему – легко догадаться по материалам предыдущего раздела).
Справедливо и обратное утверждение: три некомпланарных вектора всегда линейно независимы , то есть никоим образом не выражаются друг через друга. И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.
Определение : Базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов , взятых в определённом порядке , при этом любой вектор пространства единственным образом раскладывается по данному базису , где – координаты вектора в данном базисе
Напоминаю, также можно сказать, что вектор представлен в виде линейной комбинации базисных векторов.
Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки и любых трёх линейно независимых векторов:
началом координат , и некомпланарные векторы , взятые в определённом порядке , задают аффинную систему координат трёхмерного пространства :
Конечно, координатная сетка «косая» и малоудобная, но, тем не менее, построенная система координат позволяет нам однозначно определить координаты любого вектора и координаты любой точки пространства. Аналогично плоскости, в аффинной системе координат пространства не будут работать некоторые формулы, о которых я уже упоминал.
Аналогично плоскости, в аффинной системе координат пространства не будут работать некоторые формулы, о которых я уже упоминал.
Наиболее привычным и удобным частным случаем аффинной системы координат, как все догадываются, является прямоугольная система координат пространства :
Точка пространства, которая называется началом координат , и ортонормированный базис задают декартову прямоугольную систему координат пространства . Знакомая картинка:
Перед тем, как перейти к практическим заданиям, вновь систематизируем информацию:
Для трёх векторов пространства эквивалентны следующие утверждения :
1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не компланарны;
4) векторы нельзя линейно выразить друг через друга;
5) определитель, составленный из координат данных векторов, отличен от нуля.
Противоположные высказывания, думаю, понятны.
Линейная зависимость / независимость векторов пространства традиционно проверяется с помощью определителя (пункт 5). Оставшиеся практические задания будут носить ярко выраженный алгебраический характер. Пора повесить на гвоздь геометрическую клюшку и орудовать бейсбольной битой линейной алгебры:
Оставшиеся практические задания будут носить ярко выраженный алгебраический характер. Пора повесить на гвоздь геометрическую клюшку и орудовать бейсбольной битой линейной алгебры:
Три вектора пространства компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю :.
Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (значение определителя от этого не изменится – см. свойства определителей). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.
Тем читателям, которые немножко позабыли методы расчета определителей, а может и вообще слабо в них ориентируются, рекомендую один из моих самых старых уроков: Как вычислить определитель?
Пример 6
Проверить, образуют ли базис трёхмерного пространства следующие векторы:
Решение : Фактически всё решение сводится к вычислению определителя.
а) Вычислим определитель, составленный из координат векторов (определитель раскрыт по первой строке):
, значит, векторы линейно независимы (не компланарны) и образуют базис трёхмерного пространства.
Ответ : данные векторы образуют базис
б) Это пункт для самостоятельного решения. Полное решение и ответ в конце урока.
Встречаются и творческие задачи:
Пример 7
При каком значении параметра векторы будут компланарны?
Решение : Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен нулю:
По существу, требуется решить уравнение с определителем. Налетаем на нули как коршуны на тушканчиков – определитель выгоднее всего раскрыть по второй строке и сразу же избавиться от минусов:
Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению:
Ответ : при
Здесь легко выполнить проверку, для этого нужно подставить полученное значение в исходный определитель и убедиться, что , раскрыв его заново.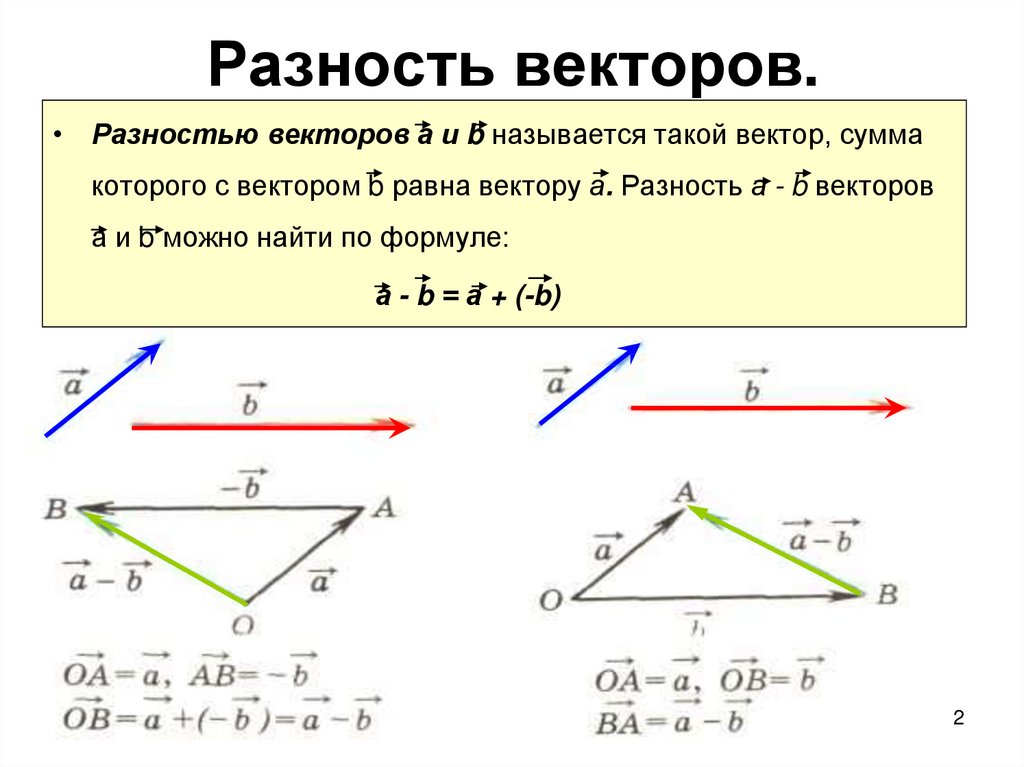
В заключение рассмотрим ещё одну типовую задачу, которая носит больше алгебраический характер и традиционно включается в курс линейной алгебры. Она настолько распространена, что заслуживает отдельного топика:
Доказать, что 3 вектора образуют базис трёхмерного пространстваи найти координаты 4-го вектора в данном базисе
Пример 8
Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе.
Решение : Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора вполне могут образовывать новый базис . И первый этап полностью совпадает с решением Примера 6, необходимо проверить, действительно ли векторы линейно независимы:
Вычислим определитель, составленный из координат векторов :
, значит, векторы линейно независимы и образуют базис трехмерного пространства.
! Важно : координаты векторов обязательно записываем в столбцы определителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения.
Rn,
(МАТЕМАТИКА В ЭКОНОМИКЕ)
Разложение вектора
Разложение вектора а на составляющие — операция замены вектора а несколькими другими векторами аь а2, а3 и т. д., которые при их сложении образуют начальный вектор а; в этом случае векторы db а2, а3 и т. д. называются составляющими вектора а. Иными словами, разложение любого…(ФИЗИКА)
Базис и ранг системы векторов
Рассмотрим систему векторов (1.18) Максимально независимой подсистемой системы векторов (1.I8) называется частичный набор векторов этой системы, удовлетворяющий двум условиям: 1) векторы этого набора линейно независимы; 2) любой вектор системы (1.18) линейно выражается через векторы этого набора….(МАТЕМАТИКА В ЭКОНОМИКЕ)
Представление вектора в разных системах координат.
 Рассмотрим две ортогональные прямолинейные координатные системы с наборами ортов (i, j, к) и (i j», k») и представим в них вектор a . Условно примем, что орты со штрихами отвечают новой системе координат, а без штрихов — старой. Представим вектор в виде разложения по осям как старой, так и новой систем…
Рассмотрим две ортогональные прямолинейные координатные системы с наборами ортов (i, j, к) и (i j», k») и представим в них вектор a . Условно примем, что орты со штрихами отвечают новой системе координат, а без штрихов — старой. Представим вектор в виде разложения по осям как старой, так и новой систем…Разложение вектора в ортогональном базисе
Рассмотрим базис пространства Rn, в котором каждый вектор ортогонален остальным векторам базиса: Ортогональные базисы известны и хорошо представимы на плоскости и в пространстве (рис. 1.6). Базисы такого вида удобны прежде всего тем, что координаты разложения произвольного вектора определяются…(МАТЕМАТИКА В ЭКОНОМИКЕ)
Векторы и их представления в координатных системах
Понятие вектора связывается с определенными физическими величинами, которые характеризуются своей интенсивностью (величиной) и направлением в пространстве. Такими величинами являются, например, сила, действующая на материальное тело, скорость определенной точки этого тела, ускорение материальной частицы. ..
..(МЕХАНИКА СПЛОШНОЙ СРЕДЫ: ТЕОРИЯ НАПРЯЖЕНИЙ И ОСНОВНЫЕ МОДЕЛИ)
Простейшие аналитические представления произвольной эллиптической функции
Представление эллиптической функции в виде суммы простейших элементов. Пусть / (z) есть эллиптическая функция порядка s с простыми полюсами jjt, $s, лежащими в параллелограме периодов. Обозначая через Bk вычет функции относительно полюса мы имеем, что 2 ?л = 0 (§ 1»п. 3, теорема…(ВВЕДЕНИЕ В ТЕОРИЮ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО)
Калькулятор векторного произведения — векторные решения с шагами
Введение в калькулятор векторного произведения
Калькулятор векторного произведения — это онлайн-инструмент для вычисления векторного произведения двух векторов для их умножения. Он использует метод расширения для нахождения векторного произведения двух векторов и строит трехмерную диаграмму относительно заданных векторов. Перекрестное произведение иногда также называют векторным произведением.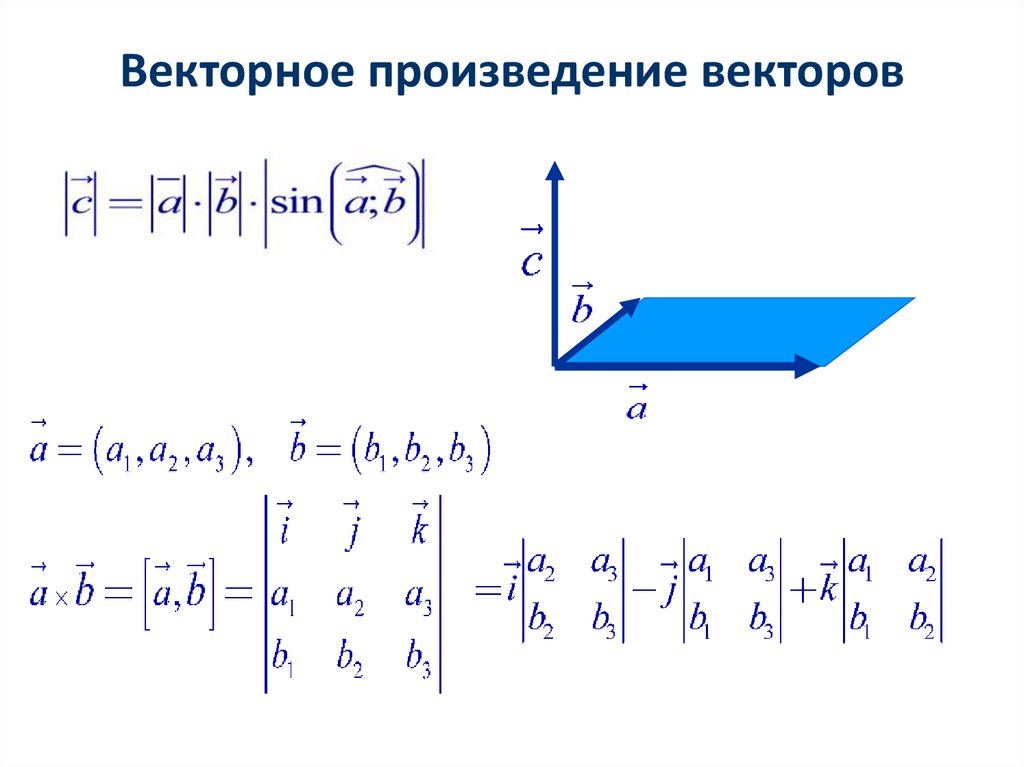
В векторном исчислении основными понятиями являются скаляр и вектор. Вам часто нужно найти равнодействующую двух векторов, перемножив их вместе. Процесс нахождения равнодействующей двух векторов будет проще с помощью инструмента. Вот почему мы представляем инструмент, который может легко оценить векторное произведение двух векторов.
Формула, используемая Калькулятором векторов перекрестного произведения
Калькулятор векторов использует следующие формулы для оценки двух данных векторов:
Векторное произведение двух векторов A и B в трех измерениях может быть записано как:
$$ \vec A \;X\; \vec В \;=\; |А||В|sinθ $$
Где
$$ \vec A \;=\; (а_1,\; а_2,\; а_3) $$ $$ \vec B \;=\; (b_1,\; b_2,\; b_3) $$
A×B — вектор, перпендикулярный к обоим векторам A и B и перпендикулярный плоскости, содержащей их. 92} $$ Пример
Рассмотрим два вектора A и B, которые можно записать как:
A = 2i + 3j — k
B = i — 3j — 2k
Нам нужно найти векторное произведение этих векторов.
Сейчас,
A × B = |i j k 2 3 -11 -3 -2|
А × В = |3 -1 -3 -2|i — |2 -11 -2|j + |2 3 1 -3 |k
А × В = (-6 -3)i-(- 4+1)j+(-6-3)k
A × B = -9i + 3j — 9k = C
Теперь найдем вектор нормали к C.
$$ \шляпа C \;=\; \frac{C}{|C|} $$ $$ |С| знак равно \sqrt{(-92} $$ $$ |С| знак равно \sqrt{171} \;=\; 3 \sqrt{19} $$
Теперь вектор нормали будет
$$ \шляпа C \;=\; (\frac{-3}{\sqrt{19}} \;,\; \frac{1}{\sqrt{19}} \;,\; \frac{-3}{\sqrt{19}}) $$
Как найти векторное произведение двух векторов
Есть несколько шагов для использования этого инструмента. Это:
- Найдите веб-сайт calculatees.com в нужном браузере. И выберите калькулятор векторного векторного произведения из списка доступных инструментов.
- На первом этапе введите значения вектора A в поля X, Y и Z.
- Теперь введите значения вектора B в поля X, Y и Z.

- Нажмите кнопку «Рассчитать».
После нескольких секунд нажатия на кнопку расчета вы получите результаты.
Зачем использовать Калькулятор векторов перекрестного произведения 2?
В математике и физике векторы и скаляры важны для описания величины и направления различных величин. Обычно мы делаем это для 2 векторов. Таким образом, калькулятор произведения можно использовать для нахождения перекрестного произведения и нормализованного вектора для него.
При вычислении векторного произведения иногда забываешь формулу или пропускаешь член, чтобы расширить его. Или иногда вам может потребоваться много времени для вычисления продукта, потому что ручные вычисления могут быть сложными. Вот почему вам нужен этот инструмент, чтобы найти векторное произведение двух векторов.
Преимущества использования Калькулятора перекрестного произведения 2×2
Перекрестное произведение называется векторным произведением. Он представляет собой площадь параллелограмма, стороны которого определяются двумя векторами. Он также имеет множество применений в реальной жизни. Таким образом, векторный калькулятор упрощает поиск результата.
Он также имеет множество применений в реальной жизни. Таким образом, векторный калькулятор упрощает поиск результата.
Есть несколько полезных применений этого инструмента. Это:
- Это экономит ваше время от ручных вычислений, которые являются сложными и трудоемкими.
- Вы можете использовать этот инструмент в образовательных целях и решать множество других реальных задач.
- Этот инструмент можно использовать для вычисления угла между двумя векторами.
- Вам не нужно платить за его использование, потому что это бесплатно. Калькулятор перекрестного произведения
- прост в использовании, поскольку он содержит простые и легкие шаги. Вы должны ввести значения компонентов векторов; это обработает их быстрее и выдаст результат точно.
- Калькулятор векторов перекрестного произведения 2 полностью надежен, потому что в его решении нет шансов на ошибку.
Часто задаваемые вопросы
Что такое векторное произведение?
Произведение векторов — это произведение двух векторов, умноженных для получения результирующего вектора. Крест обозначает его как ‘’. Его формула:
Крест обозначает его как ‘’. Его формула:
$$ \vec A \;X\; \vec В \;=\; |А||В|sinθ $$
В чем разница между векторным и скалярным произведениями?
Разница в том, что векторное произведение двух векторов дает другой вектор. Но скалярное произведение двух векторов дает скалярную величину или число.
Шон Мерфи
Последнее обновление 28 марта 2022 г.Профессиональный автор контента, который любит писать о науке, технологиях и образовании.
Калькулятор умножения матриц | Калькулятор матриц
О нашем калькуляторе умножения матриц
Что такое Матрица?
В математике матрица (множественное число матриц) представляет собой прямоугольный массив или таблицу (см. неправильная матрица) чисел, символов или выражений, расположенных в строках и столбцах. Например, размер приведенной ниже матрицы равен 2 × 3 (читается «два на три»), потому что в ней две строки и три столбца:
неправильная матрица) чисел, символов или выражений, расположенных в строках и столбцах. Например, размер приведенной ниже матрицы равен 2 × 3 (читается «два на три»), потому что в ней две строки и три столбца:
Что такое вектор?
Величина, имеющая направление, величину, особенно определяющую положение одной точки в пространстве относительно другой.
В чем разница между матрицей и вектором?
Вектор — это список чисел (может быть в строке или столбце), а матрица — это массив чисел (одна или несколько строк, один или несколько столбцов).
В математике и физике вектор — это элемент векторного пространства. Для многих конкретных векторных пространств векторы получили определенные имена. Исторически векторы были введены в геометрию и физику до формализации понятия векторного пространства.
Что такое умножение матрицы на вектор?
Жак Филипп Мари Бине — изобретатель метода умножения матриц, который также был признан первым, кто вывел правило умножения матриц в 1812 году.
Поскольку мы рассматриваем векторы как матрицы-столбцы, произведение матрицы на вектор — это просто частный случай матрично-матричного произведения (то есть произведения двух матриц). Как и в случае произведения матрицы на вектор, произведение AB между матрицами A и B определяется только в том случае, если количество столбцов в A равно количеству строк в B.
Когда мы умножаем матрицу на вектор, результатом является другой вектор. Если наши векторы двумерны, мы можем получить графическое представление о взаимосвязи между входным вектором и выходным вектором. Это демонстрируется следующим апплетом. Сплошные стрелки представляют входные векторы.
Калькулятор умножения матриц
Калькулятор определителя матриц или калькулятор умножения матриц — это онлайн-инструмент, который поможет вам вычислить вектор-матрицу, просто введя значения в калькулятор, и он автоматически выдаст вам результаты в долях во-вторых, сэкономив ваше драгоценное время без необходимости вычислять то же самое вручную или около того.
С помощью этого матричного калькулятора вы можете выполнять сверхдлинные расчеты за считанные секунды.
Графическое использование векторной матричной математики.
Графическое программное обеспечение использует математику векторной матрицы для обработки линейных преобразований для визуализации изображений. Квадратная матрица, в которой строк ровно столько, сколько столбцов (вектор), может представлять собой линейное преобразование геометрического объекта. Например, в декартовой плоскости X-Y матрица отражает объект по вертикальной оси Y. В видеоигре это сделало бы перевернутое зеркальное отражение замка, отраженного в озере.
Если в видеоигре есть изогнутые отражающие поверхности, такие как блестящий серебряный кубок, матрица линейного преобразования будет более сложной, чтобы растянуть или уменьшить отражение
Где можно использовать калькулятор умножения матриц?
Матрично-векторный расчет может применяться при изучении электрических цепей, квантовой механики и оптики. Он также используется в робототехнике и автоматизации. Матрицы и обратные матрицы также используются программистами для кодирования и шифрования.
Он также используется в робототехнике и автоматизации. Матрицы и обратные матрицы также используются программистами для кодирования и шифрования.
Матрица Векторная математика имеет множество применений. Математики, ученые и инженеры представляют группы уравнений в виде матриц; тогда у них есть систематический способ делать математику. Компьютеры встроили матрично-векторную арифметику в алгоритмы обработки графики, особенно для визуализации отражения и преломления. Некоторые свойства матрично-векторной математики важны и в математической теории.
Почему умножение матрицы на вектор важно и его актуальность?
Умножение матрицы на вектор играет очень важную роль во многих научных дисциплинах, поскольку оно считается основным инструментом для многих других вычислений в различных областях, таких как сейсмический анализ, различные симуляции (например, галактические симуляции), аэродинамические расчеты. , обработка сигналов и изображений.
Чтобы выполнять сложение, вычитание, умножение и многое другое, мы создали калькулятор сложения матриц, калькулятор вычитания матриц и калькулятор умножения матриц.


