Частные случаи приведения системы сил к точке — КиберПедия

При приведении системы сил к точке возможны следующие ва­рианты:

 

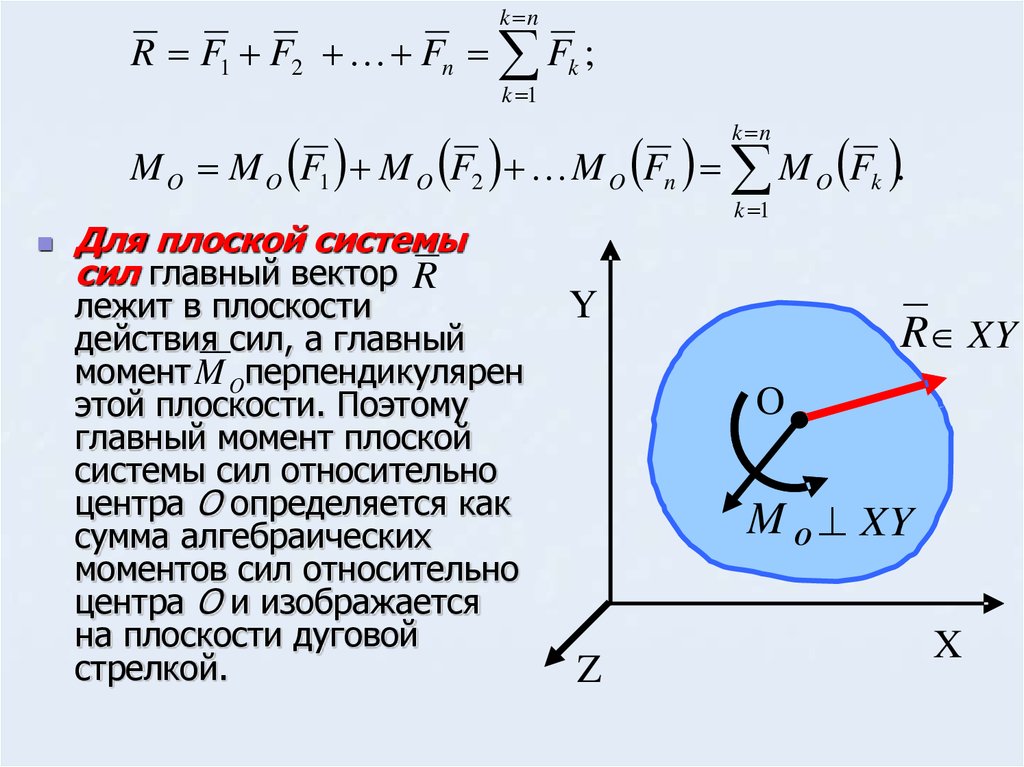
Условие равновесия произвольной плоской системы сил

1. При равновесии главный вектор системы равен нулю (Fгл = 0).

Аналитическое определение главного вектора приводит к выводу:

где Fkx и Fky — проекции векторов на оси координат.

2. Поскольку точка приведения выбрана произвольно, ясно, что
при равновесии сумма моментов сил системы относительно любой
точки на плоскости должна равняться нулю:

 

 

где А и В — разные точки приведения.

38 Лекция 5

Условие равновесия произвольной плоской системы сил может быть сформулировано следующим образом:

Для того чтобы твердое тело под действием произвольной плоской системы сил находилось в равновесии, необходимо и до­статочно, чтобы алгебраическая сумма проекций всех сил систе­мы на любую ось равнялась нулю и алгебраическая сумма момен­тов всех сил системы относительно любой точки в плоскости действия сил равнялась нулю.

Получим основную форму уравнения равновесия:

Теоретически уравнений моментов можно записать бесконечное множество, но практически доказано, что на плоскости можно соста­вить только три независимых уравнения моментов и при этом три точки (центры моментов) не должны лежать на одной линии.

Таким образом, имеем пять независимых уравнений равновесия.

Практически для решения задач на плоскости достаточно трех уравнений равновесия. В каждом конкретном случае используются уравнения с одним неизвестным.

Для разных случаев используются три группы уравнений рав­новесия.

 

Тема 1.4. Плоская система произвольно расположенных сил 39

 

Для частного случая, если уравновешена система параллельных сил, можно составить только два уравнения равновесия:

 

Ось Ох системы координат параллельна линии действия сил.

Примеры решения задач

Пример 1.Найти момент присоединенной пары при переносе силы F3в точку В (рис. 5.3). F1 = 10кН; F₂ = 15кН; F₃ = 18кН; а = 0,2 м.

Решение

Используем теорему Пуансо. Мв(-Рз) = 18 • 0,2 = 3,6кН-м.

Пример 2.Найти главный вектор системы (рис. 5.4).

F1 = 10 кН; F₂ = 16 кН; F₃ = 12 кН; т = 60кН-м.

Решение

Главный вектор равен геометрической сумме сил:

40 Лекция 5

Пример 3.Найти главный момент системы относительно точ­ки В (использовать данные примера 2).

Решение

Главный момент равен алгебраической сумме моментов сил от­носительно точки приведения:

Пример4. К телу приложена уравновешенная система сил (рис. 5.5). Две из них неизвестны. Определить неизвестные силы. F1 = 10kH; F₂ = 16kH.

Наносим оси координат и ис­пользуем уравнения равновесия:

Контрольные вопросы и задания

1. Чему равен главный вектор системы сил?

2. Чему равен главный момент системы сил при приведении ее к точке?

Тема 1.4. Плоская система произвольно расположенных сил 41

3. Чем отличается главный вектор от равнодействующей плос­кой системы произвольно расположенных сил?

Выбрать из предложенных ответов:

— величиной;

— направлением;

— величиной и направлением;

— точкой приложения;

— ничем.

4. Тело движется равномерно и прямолинейно (равновесие). Чему равны главный вектор и главный момент системы?

5. Тело вращается вокруг неподвижной оси.

Чему равны главный вектор и главный момент действующей на него системы сил?

6. Найдите главный вектор и главный момент системы сил, если центр приведения находится в точке А (рис. 5.6).

 

7. Какое еще уравнение равновесия нужно составить, чтобы убедиться в том, что система сил (рис. 5.7) находится в равновесии?

 

 

 

42 Лекция 6

ЛЕКЦИЯ 6

Тема 1. 4. Балочные системы.

Приведение системы сил к данному центру

СТАТИКА
4. Приведение системы сил к данному центру
Момент силы
Виды момента силы
Различают следующие виды момента силы:
а) векторный момент силы относительно центра;
б) алгебраический момент силы относительно центра;
в) момент силы относительно оси.
Векторный момент силы относительно центра.
Опр. Точку, относительно которой берется момент силы
называют моментной точкой (или центром момента).
Опр. Кротчайшее расстояние от линии действия силы до
моментной точки называется плечом силы — h.
центра
Опр. Векторным моментом силы F относительно
(F ),
О называется приложенный в центре О вектор mO
модуль которого равен произведению модуля силы F
на ее плечо h и который направлен перпендикулярно
плоскости, проходящей через центр О и силу, в ту сторону,
откуда сила видна стремящейся повернуть тело вокруг
центра О против хода часовой стрелки.
| mO ( F ) | | F | h.
Алгебраический момент
силы относительно центра
F
mO(F)
О h
А
r
Определение.
Алгебраическим моментом
силы F относительно центра О называется скалярная
величина равная взятому с соответствующим знаком
произведению модуля силы на ее плечо, то есть
mO ( F ) | F | h.
Алгебраический момент имеет знак плюс, если сила
стремится повернуть тело вокруг моментной точки против
хода часовой стрелки
mO ( F1 ) | F1 | h2 0,
и знак минус – когда по ходу часовой стрелки
mO ( F2 ) | F2 | h3 0.
Алгебраический моментом силы
относительно моментной точки О равен
нулю, если линия действия силы проходит
через моментную точку
mO (Q ) 0.
Q
F2
Физический смысл момента силы. Момент силы
характеризует ее вращательный эффект.
h3
О
F1
h2
Примеры вычисления алгебраических моментов сил.
F, Q и Р
1. Найти моменты сил
относительно точки В при
размерах (м), указанных на рисунке.
mB ( F ) F 3,
mB (Q) Q 2,
А
m B ( Р ) 0.
2. Найти момент наклонной
силы F относительно точки
А. Размеры (м) и угол указаны
на рисунке.
m A ( F ) F 3 sin( 600 ),
так как
h = 3 sin 600.
3
3
F
Р
2
Q
2
В
2
1
3
F
А
h
В
Момент силы относительно оси
Опр. Проекция вектора mO (F ),
то есть момента силы F ,
относительно центра О, на какуюнибудь ось z, проходящую через
этот центр, называется
моментом силы F относительно
оси z, т. е.
mZ ( F ) | mO ( F ) | cos( ).
z
F
тZ (F)
mO(F)
Fхуу
О
О1
h
Можно показать, что момент силы F относительно оси z
равен алгебраическому моменту проекции этой силы на
плоскость, перпендикулярную оси z, взятому относительно
точки О1 пересечения оси с этой плоскостью, т.е.
mZ ( F ) | Fху | h.
Знак момента силы относительно оси z определяется также
как и знак алгебраического момента силы.
Момент силы относительно оси
равен 0, если сила лежит в одной
плоскости с осью.
z
F
Q
Задание
Задание
По ребрам прямоугольного
параллелепипеда направлены
силы.
Момент силы относительно
оси ОХ равен…
ВАРИАНТЫ ОТВЕТОВ:
1) F c
2) F b
2
2
3) F с b
4) 0
Задание
Задание
Сила F лежит в плоскости
FOxу
АВСD и приложена в точке В.
Момент силы относительно оси
оy равен…
ВАРИАНТЫ ОТВЕТОВ:
1) F c sin
2) F а sin
3) F b cos
4) F c cos
Понятие пары сил.
Опр. Парой сил называется система двух равных по
модулю, параллельных и направленных в противоположные
стороны сил, действующих на абсолютно твердое тело.
/
Система сил F , F , образующих пару сил, не находится в
равновесии (эти силы не направлены вдоль одной прямой).
Опр. Плоскость, проходящая через линии действия пар сил,
называется плоскостью действия пары.
Опр. Кротчайшее расстояние d
между линиями действия сил пары
называется плечом пары.
d
В
F //
F
А
Виды момента пары.
Различают следующие два вида моментов пары сил:
а) векторный момент;
б) алгебраический момент.
Векторный момент пары.
m
,
Опр. Векторным моментом пары сил называется вектор
модуль которого равен произведению модуля одной из сил пары
на ее плечо и который направлен перпендикулярно плоскости
действия пары в ту сторону, откуда пара видна стремящейся
повернуть тело против хода часовой стрелки: т = F d.
F
d
В
F/
А
т
Выводы:
1. Действие пары сил на твердое тело полностью
характеризуется ее векторным моментом.
2. Две пары сил, имеющие одинаковые векторные моменты
эквивалентны.
3. Векторный момент можно
приложить в любой точке , то есть
это вектор свободный.
В дальнейшем на чертеже пару сил
будем изображать ее векторным
моментом.
F
d
А
В
F/
т
т
т
Теоремы о сложении пар
Теорема 1. Действие на твердое
тело
двух пар сил с моментами m1 и m2
m
можно заменить
m1
одной парой сил
с моментом m, равным
m2
геометрической сумме моментов
складываемых пар
m m1 m2 .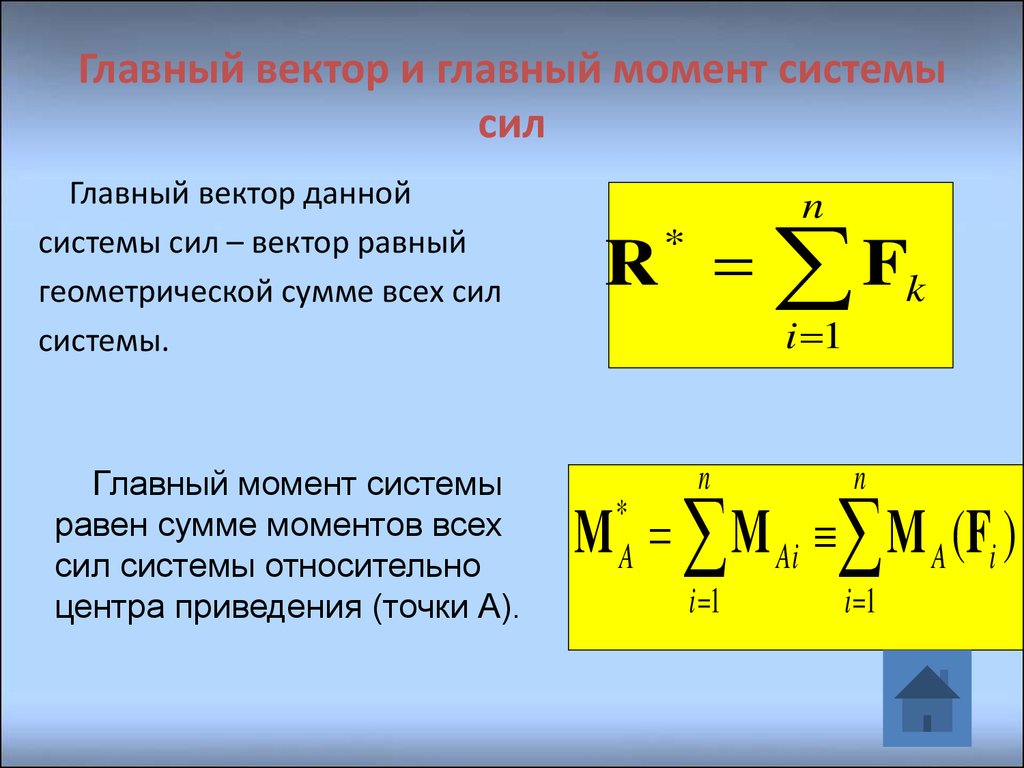
II
I
Теорема 2. Система пар, действующих на абсолютно твердое
тело, эквивалентна одной паре с моментом, равным
геометрической сумме моментов складываемых пар, то есть:
M m1 m2 … mn mk ,
где m1 , m2 ,…, mn – моменты складываемых пар, а М –
момент равнодействующей пары.
Условие равновесия системы пар
При равновесии системы пар момент равнодействующей пары
будет равен нулю, то есть
M mk 0 .
Последнее условие является условием равновесия системы пар.
Алгебраический момент пары
Опр. Алгебраическим моментом пары называется
алгебраическая величина равная взятому с соответствующим
знаком произведение модуля одной из сил пары на ее плечо:
m | F | d F d .
Знак момента пары определяется
также как и знак момента
/
силы. Момент пары F , F определяется
по формуле
/
m1 = F d1 >0. Момент пары Р, Р определится по формуле
m2 = Р d2< 0.
В случае плоской системы пар их
принято изображать в виде круговой
стрелки с указанием величины
момента.
Действие на тело плоской системы пар
эквивалентно одной паре с моментом М
равным алгебраической сумме моментов
складываемых пар, то есть М = ∑ mк , а
условие равновесия системы пар имеет
вид:
∑ mк = 0.
d1
F
F
Р
d2
/
Р/
т1
т2
Задание
Задание
Даны пары сил, у которых F = 3Н, h = 6м,
Q = 2Н, d = 5м.
После сложения, сила результирующей пары
при плече l =10м будет равна …
ВАРИАНТЫ ОТВЕТОВ:
Обоснование ответа.
Момент результирующей пары будет
М = — Р l = — F h — Q d.
Откуда
Р = (F h + Q d)/l = (3 6 + 2 5)/10 = 2,8 Н.
1) 1H
2) 1,8H
3) 2,8H
4) 5H
5) 3,7H
Теорема о параллельном переносе силы
Теорема. Силу, приложенную к абсолютно твердому телу,
можно, не изменяя оказываемого ею действия, переносить из
данной точки в любую другую точку тела, прибавляя
при этом пару с моментом, равным моменту переносимой
силы относительно точки, куда сила переносится.
Доказательство
Пусть
на тело действует сила
F , приложенная в точке А.
т
т
F
/
F
F
/
А
А
В
Действие этой силы на тело
В
F //
не изменится, если в любой
точке тела В приложить
/ //
/ две
//
уравновешенные силы F и F , такие, что F F , F F .
//
Система сил F , F образует пару сил. Векторный момент
этой пары m mB (F ).
F
Таким образом, при переносе силы F из точки А в
произвольную точку В необходимо добавить векторный
момент , направленный перпендикулярно плоскости,
проходящей через линию действия силы F и точку В.
Теорема о приведении системы сил (теорема Пуансо)
Теорема. Любая система сил, действующих на абсолютно
твердое тело, при приведении к произвольно выбранному
центру О заменяется одной силой R, приложенной в центре
приведения О, и одной парой с моментом M О , равным
главному моменту системы сил относительно центра О.
Было установлено, что главный вектор системы сил — R Fk .
Опр. Величина М 0 , равная геометрической сумме моментов
всех сил относительно центра О, называется
главным
моментом системы сил, то есть М 0 m0 ( Fk ).
Пусть к телу приложены силы: F1 , F2 ,…, Fn .
Применим теорему о параллельном переносе сил в точку О.
/ /
/
Заменим «ёжик» сил F1 , F2 ,…, Fn главным вектором R,
а «ёжик» моментов m1 , m2 ,…, mn – главным моментом
М 0 mk .
т1
F1/ А1
т2
тn
О
Аn
F2/
F1
А2
M0
R
F2
О
Fn/
Fn
Замеч1. Сила R не является равнодействующей данной
системы сил, так как заменяет систему сил не одна, а вместе
с парой сил.
Замеч2. Значение
сила R от выбора центра О не зависит.
Значение же М 0 при изменении положения центра может
в общем случае изменяться в следствии изменения значений
моментов отдельных сил. Поэтому всегда необходимо
указывать, относительно какого центра определяется
главный момент.
Следствие из теоремы. Две системы сил, имеющие одинаковые
главные векторы и главные моменты относительно одного и
того же центра, эквивалентны.
Частные случаи приведения системы сил к центру.
1. Если для данной системы сил R 0, a M 0 0, то она
приводится к одной паре сил с моментом М 0 .
2. Если для данной системы сил R 0, a M 0 0, то она
приводится к одной силе, то есть к равнодействующей, равной
R и приложенной в центре О.
Геометрические условия равновесия системы сил
Теорема о равновесии любой системы сил.
Для равновесия любой системы сил необходимо и
достаточно, чтобы главный вектор этой системы сил и ее
главный момент относительно любого центра были равны
нулю, т.е. чтобы выполнялись
условия
(*)
R 0, M 0 0.
Теорема Вариньона о моменте равнодействующей:
Теорема. Если данная система сил
имеет равнодействующую, то
момент равнодействующей
относительно любого центра О равен
сумме моментов сил системы
относительно того же центра, т. е.
m0 ( R) m0 ( Fk ).
z
Fn
C
О
х
F2
R
F1
у

4.3: Эквивалентная система сопряжения сил

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

50587

• Jacob Moore & Contributors
• Pennsylvania State University Mont Alto via Mechanics Map

Каждый набор сил и моментов имеет эквивалентную систему пары сил . Это единственная сила и чистый момент (пара), действующие в одной точке, что статически эквивалентно исходному набору сил и моментов.

Рисунок \(\PageIndex{1}\): Любой набор сил, действующих на тело, можно заменить одной силой и одной парой действующих сил, которые статически эквивалентны исходному набору сил и моментов. Этот набор эквивалентной силы и пары известен как система эквивалентной пары сил.

Чтобы найти эквивалентную систему пары сил, вам просто нужно выполнить следующие шаги.

1. Сначала выберите точку, вокруг которой будет находиться система эквивалентной пары сил. Любая точка будет работать, но точка, которую вы выберете, повлияет на окончательные значения, которые вы найдете для системы эквивалентной пары сил. Традиционно эта точка будет либо центром масс тела, либо некоторой точкой соединения тела.
2. Затем сопоставьте все силы, не действующие через эту точку, с силой и парой, действующей в выбранной вами точке.
3. Чтобы найти «силовую» часть системы эквивалентной пары сил, сложите все векторы сил. Это даст вам величину и направление силы в системе эквивалентной пары сил.
4. Чтобы найти «парную» часть системы эквивалентных пар сил, сложите любые векторы моментов (это могут быть моменты, изначально действующие на тело, или моменты от разложения сил на силы и пары). Это даст вам величину и направление чистого момента (пары) в системе эквивалентной пары сил.

Видеолекция по этому разделу, прочитанная доктором Джейкобом Муром. Источник YouTube: https://youtu.be/bs6Tnlje3IU.

Пример \(\PageIndex{1}\)

Найдите эквивалентную систему пары сил для показанных ниже сил относительно точки A.

Рисунок \(\PageIndex{2}\): схема задачи для примера \(\PageIndex{1 }\). L-образная деталь, два плеча которой соединяются в точке A, испытывает силу, направленную вправо, и момент, направленный против часовой стрелки, относительно конца его вертикального плеча, а также две силы, направленные вниз вдоль его горизонтального плеча.

Решение

Видео \(\PageIndex{2}\): рабочее решение примера проблемы \(\PageIndex{1}\), предоставленное доктором Джейкобом Муром. Источник YouTube: https://youtu.be/cw-rwBZef5w.

---

Эта страница под названием 4.3: Equivalent Force Couple System распространяется по лицензии CC BY-SA 4.0 и была создана, изменена и/или курирована Джейкобом Муром и участниками (Mechanics Map) с помощью исходного контента, который был отредактирован в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Джейкоб Мур и авторы

   Лицензия

   CC BY-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. эквивалентная силовая пара
   2. источник@http://mechanicsmap. psu.edu

Статика: статически эквивалентные системы

Ключевые вопросы

• Что такое эквивалентная система?

• Что такое результирующая сила?

• Что такое результирующий момент?

• Нужно ли учитывать как \(\vec{r}\times\vec{F}\) моменты, так и пары, чтобы найти результирующий момент?

• Как найти простейшую эквивалентную систему?

• Когда простейшей эквивалентной системой будет гаечный ключ?

• Как определить, что две системы нагрузки статически эквивалентны?

Система нагружения представляет собой комбинацию сил и моментов нагрузки, действующих на объект. Она может быть простой, как одна сила, или сложной, как трехмерная комбинация многих векторов силы и момента.

Вы увидите, что любые системы нагружения можно заменить более простой статически эквивалентной системой , состоящей из одной равнодействующей силы в определенной точке и одного равнодействующего момента путем выполнения ряда эквивалентных преобразований. Результирующие системы сил обеспечивают удобное представление сложных силовых взаимодействий в инженерных соединениях, на которые мы будем опираться позже в различных контекстах. Сейчас мы сосредоточимся на деталях сведения системы к одной силе и паре.

В зависимости от исходной системы нагружения результирующая сила, результирующий момент или оба могут быть равны нулю. Если они оба равны нулю, это указывает на то, что объект находится в равновесии при этом условии нагрузки. Если они отличны от нуля, опоры должны будут обеспечить равную и противоположную реакцию, чтобы привести объект в равновесие.

Результирующая сила, действующая на систему, \(\vec{R}\text{,}\) может быть найдена путем сложения отдельных сил, \(\vec{F}_i\text{,}\) таких, что

\begin{уравнение*} \vec{R}=\sum \vec{F} = \vec{F_1}+\vec{F_2}+\vec{F_3}+…\text{.} \end{уравнение*}

Результирующий момент \(\vec{M}_O\text{,}\) относительно точки \(O\text{,}\) можно найти, сложив все моменты \(\vec{M}\ text{,}\) об этой точке, включая моменты \(\vec{r}\times\vec{F}\) и сосредоточенные моменты.

\begin{уравнение*} \vec{M_{O}}=\sum \vec{M}_i =\vec{M_1}+\vec{M_2}+\vec{M_3}+… \end{уравнение*}

Часто удобнее работать со скалярными компонентами результирующих векторов, поскольку они разделяют эффекты по трем координатным направлениям.

\начать{выравнивать*} R_x \amp =\Sigma F_x \amp {M_O}_x \amp = \Sigma M_x\\ R_y \amp =\Sigma F_y \amp {M_O}_y \amp = \Sigma M_y\\ R_z \amp =\Sigma F_z \amp {M_O}_z \amp = \Sigma M_z \конец{выравнивание*}

Рисунок 4.7.1. Статически эквивалентные системы

Системы с силовой парой.

Одно преобразование, которое вы, возможно, хотите, чтобы сделал, — это перемещение отряда в другое место. В то время как скольжение силы вдоль ее линии действия является нормальным, перемещение силы в другую точку меняет свою линию действия и, таким образом, ее вращательное воздействие на объект, поэтому перемещение 9016, а не эквивалентное преобразование.

Рассмотрим консольную балку ниже. На диаграмме (а) нагрузка \(P\) находится на конце балки, а на (б) она перемещена к центру. Внешние эффекты показаны на (c) и (d). Хотя вертикальная сила реакции равна \(P\) в обоих случаях, момент реакции в точке \(O\) равен \(2P\ell\) в первом случае и \(P\ell\) во втором. .

(a) Сила \(P\) на конце балки. (b) Сила \(P\) перемещается к центру балки. (c) FBD и реакции для (a). (d) FBD и реакции для (b). Рисунок 4.7.2. Перемещение силы не является эквивалентным преобразованием

Вы можете переместить силы на новое направление действия эквивалентным образом, если добавите «компенсирующую пару», чтобы аннулировать эффект изменения направления действия. Этого можно добиться с помощью ряда отдельных эквивалентных преобразований, как показано на диаграмме ниже. Чтобы переместить P в другое место, сначала добавьте две равные и противоположные силы там, где вы хотите, чтобы сила была, как в (b). Затем распознайте образовавшуюся пару (с) и замените ее эквивалентным парным моментом.

Результатом этого процесса является эквивалентная силовая пара системы показана на схеме (d), которая статически эквивалентна исходной ситуации на (a).

(a) Исходная ситуация. (b) Добавьте две равные и противоположные силы в средней точке. (c) Распознайте пару. (d) Замените пару, чтобы получить эквивалентную систему сила-пара, с теми же реакциями, что и на рис. 4.7.(c). Рисунок 4.7.3. Эквивалентная система сил-пар

Оценка момента в точке \(O\) at была произвольной. Любая другая точка даст тот же результат. Например, в исходной ситуации (а) сила \(P\) создает момент по часовой стрелке \(M=P\ell\) относительно средней точки. Когда сила перемещается в центр, \(P\) не создает там момента, поэтому для сохранения эквивалентности необходимо добавить компенсационную пару по часовой стрелке с величиной \(P\ell\). Это тот же результат, который мы получили ранее (d). Компенсационная пара была нарисована с центром вокруг средней точки, но это тоже произвольно, потому что сосредоточенные моменты являются свободными векторами и могут быть размещены в любом месте.

Редукция сложной системы.

Любая система нагружения может быть сведена к статически эквивалентной системе, состоящей из одной силы и одного момента в заданной точке с помощью следующей процедуры:

1. Определите результирующий момент относительно указанной точки, учитывая все силы и сосредоточенные моменты в исходной системе.

2. Определите результирующую силу путем сложения всех сил, действующих на исходную систему.

3. Определить результирующий момент относительно точки исходной системы

4. Создайте статически эквивалентную систему, заменив все нагрузки результирующей силой и результирующим моментом в выбранной точке.

Пример 4.7.4. Эксцентричная нагрузка.

Вертикальная колонна поддерживает внецентренную нагрузку, как показано на рисунке.

Замените эту нагрузку эквивалентной системой пары сил, действующей в центре верхней поверхности балки.

Ответ.

\(P = \lb{1200}\) и \(M=\ftlb{900}\) по часовой стрелке

Решение.

Чтобы сместить вертикальную силу \(\inch{9}\) влево, необходимо добавить пару по часовой стрелке \(M\) для сохранения эквивалентности, где

\begin{align*} М \амп = Р д\\ \амп = (\фунт{1200} )(\дюйм{9})\\ \amp = \inlb{10,800}\\ \amp = \ftlb{900}. \end{выравнивание*}

Пример 4.7.5. Эквивалентная система силовой пары.

Заменить систему сил на диаграмме (а) эквивалентной системой сил-пар в точке \(A\text{.}\)

Замените систему пары сил в точке \(A\) одиночной эквивалентной силой и укажите ее местоположение.

(а)

(б)

(в)

Ответ.

\(R = F_1 + F_2\text{,}\) \(M_A = F_1 d_1 + F_2 (d_1 + d_2)\) и \(d = M/R\)

Решение.

Исходная система показана на (а).

Поскольку \(F_1\) и \(F_2\) параллельны, величина равнодействующей силы равна сумме двух величин и направлена ​​вниз.

\begin{уравнение*} Р = Ф_1 + Ф_2 \end{equation*}

Результирующий момент относительно точки \(A\) равен

\begin{equation*} M_A = F_1 d_1 + F_2 (d_1 + d_2)\текст{.} \end{equation*}

Чтобы создать эквивалентную систему (b), результирующая сила и результирующий момент помещаются в точку \(A\text{.}\)

Система в (b) может быть дополнительно упрощена до устранить момент в \(M_A\text{,}\), выполнив процесс в обратном порядке.

В (c) мы поместим результирующую силу \(R\) на расстояние \(d\) от точки \(A\) так, чтобы результирующий момент вокруг точки \(A\) остался прежним. Это расстояние можно найти с помощью \(M = Fd\text{.}\)

\begin{уравнение*} г = М_А/Р \end{equation*}

Все системы в (a), (b) и (c) статически эквивалентны

В этом примере мы начали с двух сил. Мы нашли две различные статически эквивалентные системы; один с силой и парой, другой с одинарной силой. Эта последняя система проще, чем исходная система.

Важно отметить, что статическая эквивалентность применяется только к внешним эффектам. При определении внутренних сил, таких как поперечный и изгибающий момент, описанные в разделе 8.4, или при рассмотрении нежестких тел необходимо использовать исходную систему нагрузки.

Определение эквивалентности.

Две комплексные системы нагружения эквивалентны, если они сводятся к одной и той же равнодействующей силе и к одному и тому же результирующему моменту относительно любой произвольной точки.

Две системы нагружения статически эквивалентны, если

Этот процесс показан в следующем примере.

Пример 4.7.6. Нахождение статически эквивалентных нагрузок.

Какие из трех показанных систем нагрузки статически эквивалентны?

Рисунок 4.7.7.

Отвечать.

(a) и (c) статически эквивалентны

Раствор.

1. Стратегия.

   Оцените результирующую силу и результирующий момент для каждого случая и сравните. Мы решили оценить результирующий момент относительно точки А, хотя любая другая точка будет работать.

2. Для системы (а).

   \начать{выравнивать*} \vec{R} \amp = \langle -10,0 \rangle \lb{}\\ \vec{M_A} \амп =-80+6(10)\\ \amp = \ftlb{-20} \конец{выравнивание*}

3. Для системы (б).

   \начать{выравнивать*} \vec{R}\amp=\langle -20+10,0 \rangle \lb{} \\ \amp = \langle -10,0 \rangle \lb{}\\ \vec{M}_A\amp= -120+12(20)-6(10)\\ \amp = \ftlb{60} \end{выравнивание*}

4. Для системы (в).

   \начать{выравнивать*} \vec{R} \amp =\langle -10,0 \rangle \lb{}\\ \vec{M}_A \amp=-40+20+0(10) \\ \amp = \ftlb{-20} \конец{выравнивание*}

Системы (a) и (c) статически эквивалентны, так как \(\vec{R}\) и \(\vec{M}_A\) одинаковы в обоих случаях. Система (б) не отличается, поскольку ее результирующий момент отличается от двух других.

Любая система нагрузок может быть упрощена до равнодействующей силы \(\vec{R}\text{,}\) и равнодействующей пары \(\vec{M}\text{,}\), действующих в любой произвольной точке \( O\text{.}\) Есть четыре общих особых случая, которые стоит выделить отдельно.

Совпадающие силы.

Когда все силы в системе действуют одновременно, результирующий момент относительно их общей точки пересечения всегда будет равен нулю. Затем нам нужно только найти результирующую силу и поместить ее в точку пересечения. Результирующий момент относительно любой другой точки — это момент равнодействующей силы \(\vec{R}\) относительно этой точки.

Параллельные силы.

Когда все силы в системе параллельны, результирующая сила будет действовать в этом направлении с величиной, равной сумме отдельных величин. Момент вокруг этой оси не создается, но нам нужно найти результирующий момент относительно двух других прямоугольных осей. То есть, если все силы действуют в направлении \(x\), нам нужно только найти результирующую силу в направлении \(x\) и результирующий момент относительно осей \(y\) и \(z\).

Компланарные силы.

Когда все силы в системе компланарны, нам нужно только найти результирующую силу в этой плоскости и результирующий момент относительно оси, перпендикулярной этой плоскости. То есть, если все силы существуют в плоскости \(x\)-\(y\), нам нужно только просуммировать компоненты в направлениях \(x\) и \(y\), чтобы найти результирующую силу \(\vec {R}\text{,}\) и используйте их для определения результирующего момента относительно оси \(z\). Все двумерные задачи попадают в эту категорию.

Гаечный ключ результирующий.

Равнодействующая гаечного ключа является частным случаем, когда равнодействующая момент действует вокруг оси равнодействующей силы. Направления вектора равнодействующей силы и вектора равнодействующей момента совпадают.

Рисунок 4.7.8. Wrench Resultant

Например, если равнодействующая сила действует только в направлении \(x\), а результирующий момент действует только вокруг оси \(x\), это пример равнодействующей гаечного ключа. Повседневным примером является отвертка, в которой и результирующая сила, и ось вращения совпадают с отверткой. Результирующая гаечного ключа считается положительной, если вектор пары и вектор силы указывают в одном направлении, и отрицательной, если они указывают в противоположных направлениях.

Любая трехмерная система пары сил может быть приведена к эквивалентной равнодействующей гаечного ключа, даже если равнодействующая сила и равнодействующий момент изначально не образуют равнодействующую гаечного ключа.

Чтобы найти эквивалентный результирующий ключ:

1. Сначала найдите результирующую силу \(\vec{R}\) и результирующий момент \(\vec{M}\) в произвольной и произвольной точке, \(O\text{.}\). действуют по одной оси.

2. Разложите результирующий момент на скалярные составляющие \(M_\parallel\) и \(M_\perp\text{,}\), параллельные и перпендикулярные оси результирующей силы.

3. Устранить \(M_\perp\), переместив результирующую силу от точки \(O\) на расстояние \(d = M_\perp/R\)

Упрощенная система состоит из момента \(\vec{M}_\parallel\) и силы \(\vec{R}\) и действующего расстояния \(d\) от точки \(O\text{.} \) Поскольку \(\vec{R}\) и \(\vec{M}_\parallel\) действуют вдоль одной и той же оси, система была сведена к равнодействующей гаечного ключа.