PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

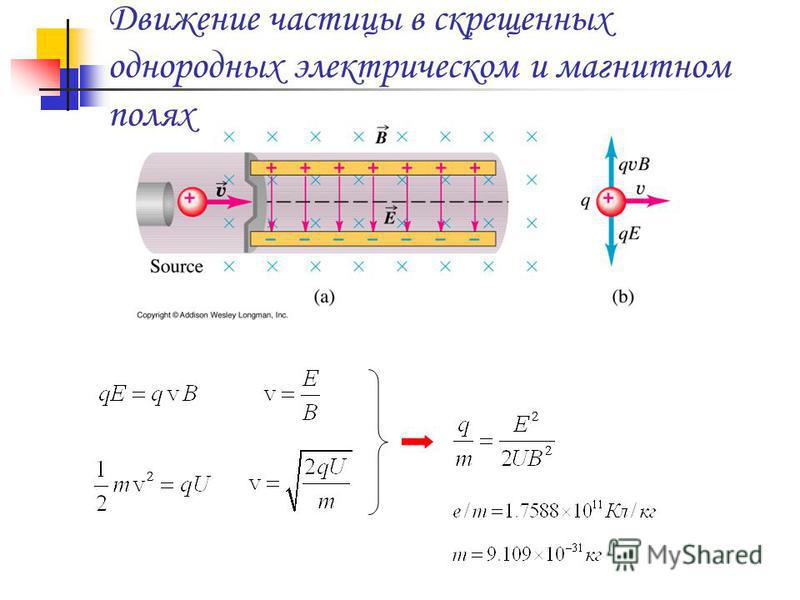
11. Однородное и неоднородные электрические поля

Электромагнитное поле – это итог взаимодействия электрического и магнитного полей, фундаментальное физическое поле, которое возникает вокруг заряженных тел.

Таким образом, электрическое поле – это часть поля электромагнитного, которое в свою очередь порождает электромагнитные волны, распространяющиеся в пространстве со скоростью света. Это не что иное, как возмущения электромагнитного поля.

Электрическое поле создается как неподвижными, так и движущимися зарядами. О наличии электрического поля можно судить, прежде всего, по его способности оказывать силовое действие на электрические заряды, движущиеся и неподвижные, а также по способности индуцировать электрические заряды на поверхности проводящих нейтральных тел.

Напряженность электрического поля. Количественной характеристикой силового действия электрического поля на заряженные тела служит векторная величина E, называемая напряжённостью электрического поля.

E = F / q пр.

Она определяется отношением силы F, действующей со стороны поля на точечный пробный заряд qпр, помещенный в рассматриваемую точку поля, к величине этого заряда.

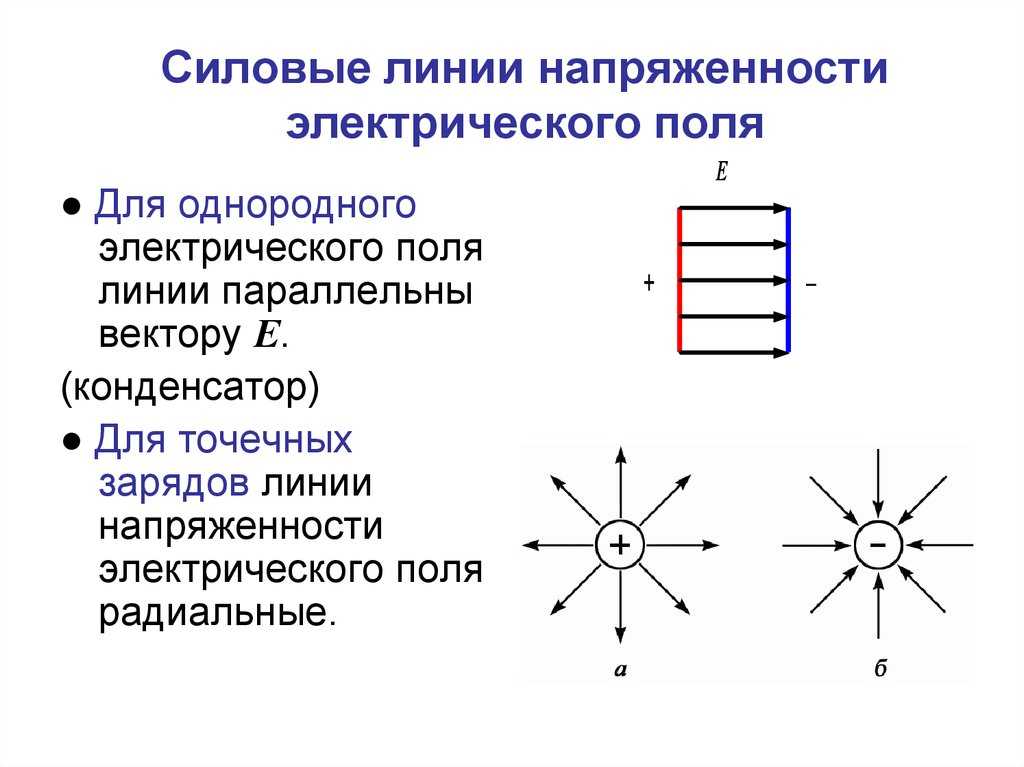
Однородное поле — это электрическое поле, в котором напряжённость одинакова по модулю и направлению во всех точках пространства.

Приблизительно однородным является поле между двумя разноимённо заряженными плоскими металлическими пластинами. В однородном электрическом поле линии напряжённости направлены параллельно друг другу.

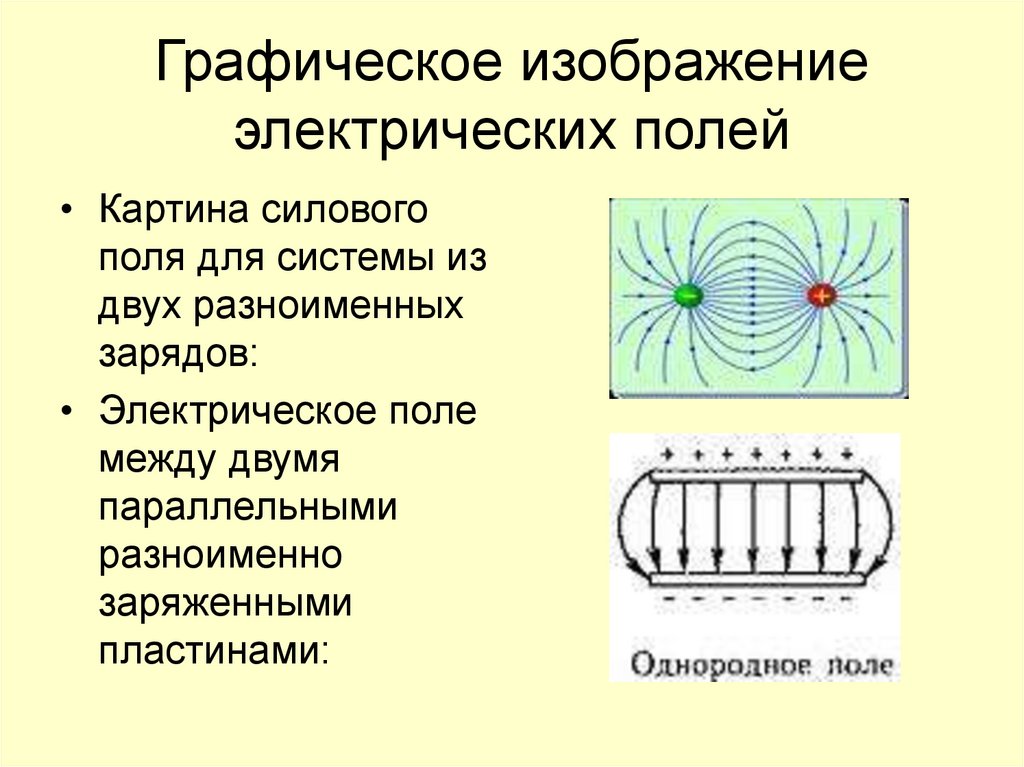
Электрическое поле, в котором напряженность одинакова по модулю и направлению в любой точке пространства, называется однородным электрическим полем.

Приблизительно однородным является электрическое поле между двумя разноименно заряженными плоскими металлическими пластинами. Линии напряженности в однородном электрическом поле параллельны друг другу (рис. 109)

При равномерном распределении электрического заряда q по поверхности площади S поверхностная плотность заряда постоянна и равна

Можно доказать, что напряженность электрического поля бесконечной плоскости с поверхностной плотностью заряда одинакова в любой точке пространства и равна

Формула (17.6) применяется для расчетов напряженности электрического поля около заряженных тел в том случае, когда форма равномерно заряженной поверхности близка к плоскости и расстояние от точки, в которой определяется напряженность поля, до поверхности тела значительно меньше размеров тела и расстояния до края заряженной поверхности.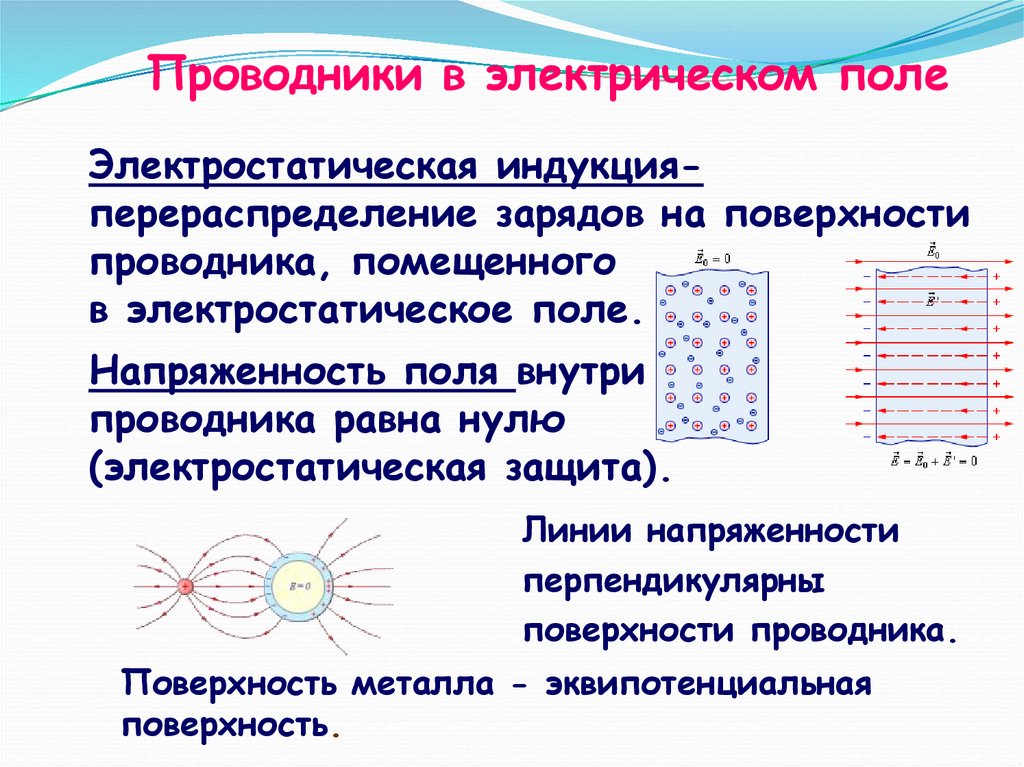

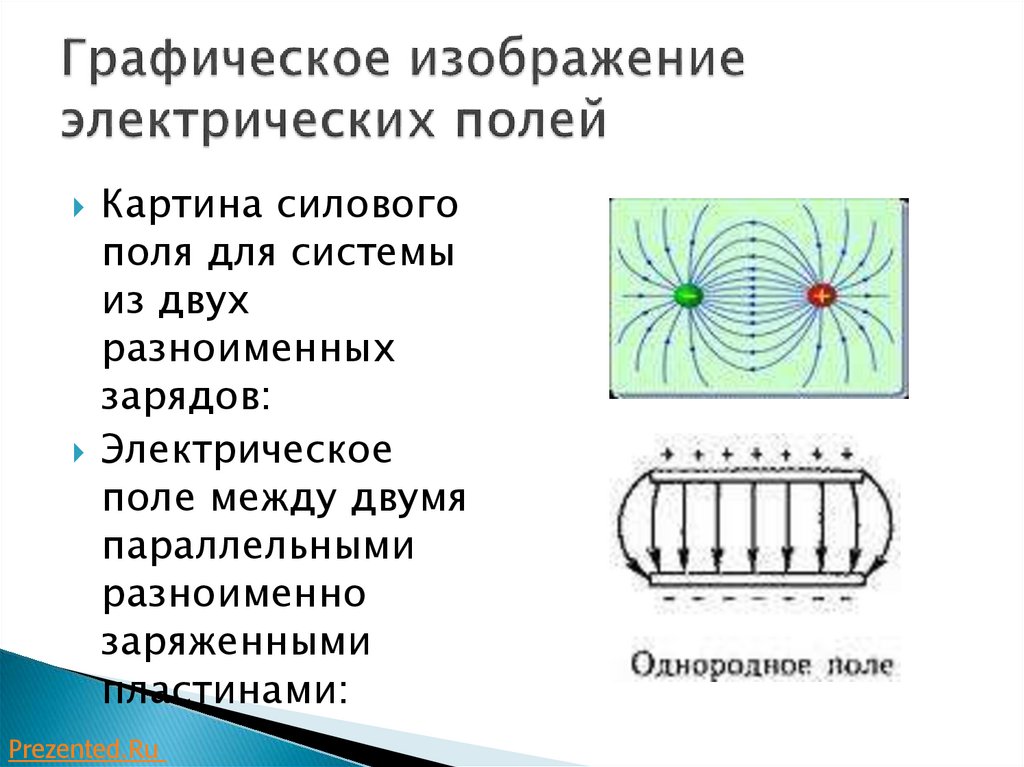
Неоднородное поле

— поле, значение (вектор) которого принимает различные значения и/или направления в разных точках.

Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.

Конденсатор — электрический прибор, состоящий из двух проводящих пластин, разделенных слоем диэлектрика. Конденсаторы служат для накопления зарядов с целью их отдачи в нужный момент времени, а также в цепях переменного тока для деления зарядов (параллельное соединение) и для деления напряжения (последовательное соединение).

— емкость конденсатора (С).

— емкость плоского конденсатора.

Плоский конденсатор. Две плоские параллельные пластины одинаковой площади S, расположенные на расстоянии d друг от друга, образуют плоский конденсатор. Если пространство между пластинами заполнено средой с относительной диэлектрической проницаемостью , то при сообщении им заряда q напряженность электрического поля между пластинами равна , разность потенциалов равна . Таким образом, емкость плоского конденсатора.

19.2 Электрический потенциал в однородном электрическом поле – Физика колледжа

Цели обучения

• Описать взаимосвязь между напряжением и электрическим полем.
• Получите выражение для электрического потенциала и электрического поля.
• Рассчитать напряженность электрического поля с учетом расстояния и напряжения.

В предыдущем разделе мы исследовали взаимосвязь между напряжением и энергией. В этом разделе мы исследуем взаимосвязь между напряжением и электрическим полем. Например, однородное электрическое поле [латекс]\textbf{E}[/латекс] создается путем помещения разности потенциалов (или напряжения) [латекс]\жирный символ{\Delta V}[/латекс] на две параллельные металлические пластины, обозначены A и B.

(См. рис. 1.) Изучив это, мы узнаем, какое напряжение необходимо для создания определенной напряженности электрического поля; это также выявит более фундаментальную связь между электрическим потенциалом и электрическим полем. С точки зрения физика, либо [латекс]\boldsymbol{ \Delta V}[/латекс], либо [латекс]\текстbf{Е}[/латекс] можно использовать для описания любого распределения заряда. [latex]\boldsymbol{ \Delta V}[/latex] наиболее тесно связан с энергией, тогда как [latex]\textbf{E}[/latex] наиболее тесно связан с силой. [латекс]\boldsymbol{\Delta V}[/латекс] это скалярная величина и не имеет направления, тогда как [latex]\textbf{E}[/latex] является векторной величиной , имеющей как величину, так и направление. (Обратите внимание, что величина напряженности электрического поля, скалярная величина, представлена ​​ниже [latex]\textbf{E}[/latex].) Связь между [latex]\boldsymbol{\Delta V}[/latex] а [latex]\textbf{E}[/latex] определяется путем вычисления работы, совершаемой силой при перемещении заряда из точки A в точку B. Но, как отмечалось в главе 19.1 «Электрическая потенциальная энергия: разность потенциалов», это сложный для произвольного распределения заряда, требующий исчисления. Поэтому мы рассматриваем однородное электрическое поле как интересный частный случай.

Рисунок 1. Соотношение между В и E для параллельных проводящих пластин составляет E = В / d . (Обратите внимание, что Δ В = В _AB по величине. Для заряда, который перемещается с пластины A с более высоким потенциалом на пластину B с более низким потенциалом, необходимо включить знак минус следующим образом: –Δ В = В _А – В _В = В _AB . Подробности см. в тексте.)

Работа, совершаемая электрическим полем на рисунке 1 для перемещения положительного заряда [латекс]\boldsymbol{q}[/latex] из A, положительной пластины с более высоким потенциалом, в B, отрицательную пластина, нижний потенциал,

[латекс]\boldsymbol{W = -\Delta \textbf{PE} = -q \Delta V. }[/latex]

Разность потенциалов между точками А и В равна

[латекс]\boldsymbol{- \Delta V = -(V_{\textbf{B}} — V _{\textbf{A}}) = V_{\textbf{A} — V_{\textbf{B}}} = V_{\textbf{AB}}}[/латекс].

Ввод этого в выражение для работы дает

[латекс]\boldsymbol{W = qV _{\textbf{AB}}}[/латекс].

Работа [латекс]\boldsymbol{W = Fd \;\textbf{cos} \theta}[/latex], так как путь параллелен полю, и поэтому [латекс]\boldsymbol{W = Fd}[/ латекс]. Поскольку [латекс]\boldsymbol{F = qE}[/латекс], мы видим, что [латекс]\жирный символ{W = qEd}[/латекс]. Подстановка этого выражения для работы в предыдущее уравнение дает

[латекс]\boldsymbol{qEd = qV _{\textbf{AB}}}[/латекс].

Заряд отменяется, поэтому напряжение между точками A и B равно

[латекс]\begin{array}{l} \boldsymbol{V _{\textbf{AB}} = Ed} \\ \boldsymbol{E = \frac{V _{\textbf{AB}}}{d}} \ end{array}[/latex] [латекс]\}[/латекс] [латекс]\boldsymbol{\textbf{(uniform} \; E \;\textbf{- только поле)}} ,[/latex]

, где [латекс]\boldsymbol{d}[/латекс] — расстояние от А до В или расстояние между пластинами на рисунке 1. Обратите внимание, что приведенное выше уравнение подразумевает, что единицами измерения электрического поля являются вольты на метр. Мы уже знаем, что единицами измерения электрического поля являются ньютоны на кулон; таким образом, справедливо следующее соотношение между единицами:

[латекс]\boldsymbol{1 \;\textbf{N} / \textbf{C} = 1 \;\textbf{V} / \textbf{m}}.[/latex]

Напряжение между точками A и B

[латекс]\begin{array}{l} \boldsymbol{V _{\textbf{AB}} = Ed} \\ \boldsymbol{E = \frac{V _{\textbf{AB }}}{d}} \end{array}[/latex] [латекс]\}[/латекс] [латекс]\boldsymbol{\textbf{(uniform} \; E \;\textbf{- только поле)} } ,[/latex]

где [latex]\boldsymbol{d}[/latex] — расстояние от A до B или расстояние между пластинами.

96 \;\textbf{V} / \textbf{m}}[/latex]. Выше этого значения поле создает в воздухе достаточную ионизацию, чтобы сделать воздух проводником. Это позволяет разряду или искре, которая уменьшает поле. Чему тогда равно максимальное напряжение между двумя параллельными проводящими пластинами, разделенными 2,5 см сухого воздуха?

Стратегия

Заданы максимальное электрическое поле [латекс]\boldsymbol{E}[/латекс] между пластинами и расстояние [латекс]\boldsymbol{d}[/латекс] между ними.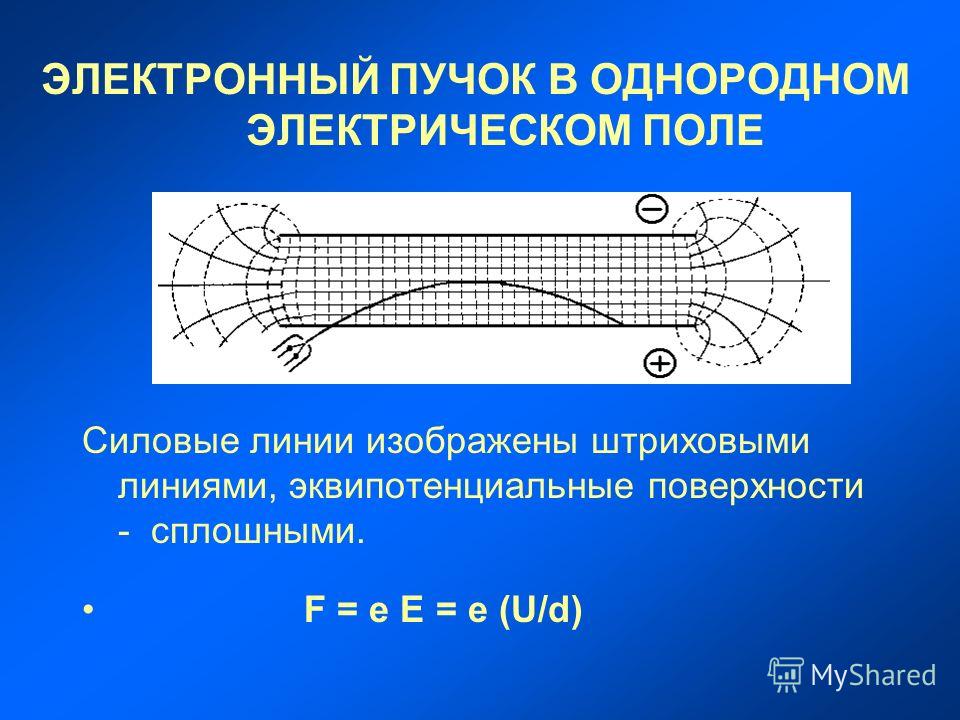 Таким образом, уравнение [латекс]\жирный символ{V_{\textbf{AB}} = Ed}[/латекс] можно использовать для расчета максимального напряжения. 94 \;\textbf{V}}[/latex]

или

[латекс]\boldsymbol{V _{\textbf{AB}} = 75 \;\textbf{кВ}} .[/latex]

( Ответ представлен только двумя цифрами, поскольку максимальная напряженность поля является приблизительной.)

Обсуждение

Одним из следствий этого результата является то, что требуется около 75 кВ, чтобы искровой скачок прошел через 2,5 см (1 дюймов) разрядник или 150 кВ для 5-сантиметровой искры. Это ограничивает напряжения, которые могут существовать между проводниками, например, на линии электропередачи. Меньшее напряжение вызовет искру, если на поверхности есть точки, так как точки создают большее поле, чем гладкие поверхности. Влажный воздух разрушается при более низкой напряженности поля, а это означает, что меньшее напряжение вызовет скачок искры во влажном воздухе. Самые большие напряжения могут быть созданы, например, статическим электричеством, в сухие дни.

Рисунок 2. Искровая камера используется для отслеживания путей высокоэнергетических частиц. Ионизация, создаваемая частицами при их прохождении через газ между пластинами, позволяет проскакивать искре. Искры располагаются перпендикулярно пластинам, следуя линиям электрического поля между ними. Разность потенциалов между соседними пластинами недостаточно высока, чтобы вызвать искры без ионизации, создаваемой частицами в экспериментах на ускорителях (или космическими лучами). (кредит: Дадерот, Wikimedia Commons)

Пример 2: Поле и сила внутри электронной пушки

(a) Электронная пушка имеет параллельные пластины, разделенные расстоянием 4,00 см, и дает электронам энергию 25,0 кэВ. Чему равна напряженность электрического поля между пластинами? б) С какой силой это поле будет действовать на кусок пластика с зарядом [латекс]\boldsymbol{0,500 \;\mu \textbf{C}}[/латекс], который попадет между пластинами?

Стратегия

Поскольку напряжение и расстояние между пластинами заданы, напряженность электрического поля можно рассчитать непосредственно из выражения [латекс]\boldsymbol{E = \frac{V_{\textbf{AB}}}{d} }[/латекс]. 5 \;\textbf{V } / \textbf{м}}.[/латекс] 95 \;\textbf{V} / \textbf{m}) = 0,313 \;\textbf{N}}.[/latex]

Обсуждение

Обратите внимание, что единицами измерения являются ньютоны, поскольку [ латекс]\boldsymbol{ 1 \;\textbf{V} / \textbf{m} = 1 \;\textbf{N} / \textbf{C}}[/latex]. Сила, действующая на заряд, одинакова независимо от того, где находится заряд между пластинами. Это связано с тем, что электрическое поле между пластинами однородно.

В более общих ситуациях, независимо от того, является ли электрическое поле однородным, оно указывает в направлении уменьшения потенциала, потому что сила на положительном заряде направлена ​​в направлении [латекс]\textbf{E}[/латекс], а также в направлении более низкого потенциала [латекс]\boldsymbol{V}[/латекс]. Кроме того, величина [latex]\textbf{E}[/latex] равна скорости уменьшения [latex]\boldsymbol{V}[/latex] с расстоянием. Чем быстрее [латекс]\boldsymbol{V}[/латекс] уменьшается с расстоянием, тем сильнее электрическое поле. В форме уравнения общая связь между напряжением и электрическим полем равна

[латекс]\boldsymbol{E =}[/латекс] [латекс]\boldsymbol{-\frac{\Delta V}{\Delta s}} ,[/latex]

, где [латекс]\жирныйсимвол{\Delta s}[/латекс] — расстояние, на котором происходит изменение потенциала, [латекс]\жирныйсимвол{\Дельта V}[/латекс]. Знак минус говорит нам, что [latex]\textbf{E}[/latex] указывает в сторону уменьшения потенциала. Электрическое поле называется градиентом (по степени или наклону) электрического потенциала.

Связь между напряжением и электрическим полем

В форме уравнения общая взаимосвязь между напряжением и электрическим полем имеет вид ,[/latex]

где [latex]\boldsymbol{\Delta s}[/latex] — расстояние, на котором происходит изменение потенциала [latex]\boldsymbol{ \Delta V}[/latex]. Знак минус говорит нам, что [latex]\textbf{E}[/latex] указывает в сторону уменьшения потенциала. Говорят, что электрическое поле равно градиент (градус или уклон) электрического потенциала.

Для постоянно меняющихся потенциалов [латекс]\boldsymbol{\Delta V}[/латекс] и [латекс]\boldsymbol{\Delta s}[/латекс] становятся бесконечно малыми, и для определения электрического поля необходимо использовать дифференциальное исчисление.

• Напряжение между точками А и В равно

[латекс]\begin{array}{l} \boldsymbol{V _{\textbf{AB}} = Ed} \\ \boldsymbol{E = \frac{V _{\textbf{AB}}}{d}} \end{array}[/latex] [латекс]\}[/латекс] [латекс]\boldsymbol{\textbf{(uniform} \; E \;\textbf{- только поле)}} ,[/latex]

• где [латекс]\жирныйсимвол{d}[/латекс] — расстояние от А до В или расстояние между пластинами.
• В форме уравнения общая связь между напряжением и электрическим полем равна

[латекс]\boldsymbol{E =}[/латекс] [латекс]\boldsymbol{- \frac{\Delta V}{\Delta s}} ,[/latex]

• где [латекс]\boldsymbol{\Delta s}[/латекс] — расстояние, на котором происходит изменение потенциала [латекс]\жирный символ{\Delta V}[/латекс]. Знак минус говорит нам, что [латекс]\текстбф{Е}[/латекс] указывает в направлении убывания потенциала.) Говорят, что электрическое поле представляет собой 93 \;\textbf{V}}[/latex] применяется? б) Насколько близко друг к другу могут располагаться пластины при таком приложенном напряжении?

  6: Напряжение на мембране, образующей клеточную стенку, составляет 80,0 мВ, толщина мембраны 9,00 нм. Что такое напряженность электрического поля? (Значение на удивление большое, но правильное. Мембраны обсуждаются в главе 19.5 «Конденсаторы и диэлектрики» и в главе 20.7 «Нервная проводимость — электрокардиограммы».) Вы можете предположить однородное электрическое поле.

  7: Мембранные стенки живых клеток имеют на удивление большие электрические поля из-за разделения ионов. (Мембраны более подробно обсуждаются в главе 20.7 «Нервная проводимость — электрокардиограммы».) Каково напряжение на мембране толщиной 8,00 нм, если напряженность электрического поля на ней составляет 5,50 МВ/м? Вы можете предположить однородное электрическое поле.

  8: Две параллельные проводящие пластины отстоят друг от друга на 10,0 см, и одну из них принимают за ноль вольт. а) Какова напряженность электрического поля между ними, если потенциал на расстоянии 8,00 см от нулевой пластины (и 2,00 см от другой) равен 450 В? б) Чему равно напряжение между пластинами? 96 \;\textbf{V} / \textbf{m}}[/latex]. а) Какую энергию в кэВ сообщает электрон, если он ускоряется на расстояние 0,400 м? б) На какое расстояние его нужно разогнать, чтобы его энергия увеличилась на 50,0 ГэВ?

   

  скаляр

  физическая величина с величиной, но без направления

  вектор

  физическая величина с величиной и направлением

   

  19.2 Электрический потенциал в однородном электрическом поле — Физика вуза 2е

  Цели обучения

  К концу этого раздела вы сможете:

  • Описать взаимосвязь между напряжением и электрическим полем.
  • Получите выражение для электрического потенциала и электрического поля.
  • Рассчитать напряженность электрического поля с учетом расстояния и напряжения.

  В предыдущем разделе мы исследовали взаимосвязь между напряжением и энергией. В этом разделе мы исследуем взаимосвязь между напряжением и электрическим полем. Например, однородное электрическое поле EE создается путем помещения разности потенциалов (или напряжения) ΔVΔV на две параллельные металлические пластины, обозначенные A и B (см. рис. 19)..5.) Изучив это, мы узнаем, какое напряжение необходимо для создания определенной напряженности электрического поля; это также выявит более фундаментальную связь между электрическим потенциалом и электрическим полем. С точки зрения физики, либо ΔVΔV, либо EE можно использовать для описания любого распределения заряда. ΔVΔV наиболее тесно связано с энергией, тогда как EE наиболее тесно связано с силой. ΔVΔV — скалярная величина, не имеющая направления, а EE — векторная величина, имеющая как величину, так и направление. (Обратите внимание, что величина напряженности электрического поля, скалярная величина, представлена ​​ниже как EE.) Связь между ΔVΔV и EE выявляется путем вычисления работы, совершаемой силой при перемещении заряда из точки A в точку B. Но , как отмечено в книге «Электрическая потенциальная энергия: разность потенциалов», это сложно для произвольного распределения заряда, требующего исчисления. Поэтому мы рассматриваем однородное электрическое поле как интересный частный случай.

  Рисунок 19,5 Соотношение между VV и EE для пластин с параллельными проводниками: E=V/dE=V/d. (Обратите внимание, что Δ В знак равно В АБ Δ В знак равно В АБ по величине. Для заряда, который перемещается с пластины A с более высоким потенциалом на пластину B с более низким потенциалом, необходимо включить знак минус следующим образом: –ΔV=VA–VB=VAB–ΔV=VA–VB=VAB. Подробности см. в тексте.)

  Работа, совершаемая электрическим полем на рис. 19.5 для перемещения положительного заряда q q от A, положительной пластины, с более высоким потенциалом, к B, отрицательной пластине, с более низким потенциалом, составляет

  Вт=–ΔPE=–qΔV.W=–ΔPE=–qΔV.

  19,21

  Разность потенциалов между точками A и B равна

  –ΔV=–(VB–VA)=VA–VB=VAB.–ΔV=–(VB–VA)=VA–VB=VAB.

  19,22

  Ввод этого в выражение для работы дает

  W=qVAB.W=qVAB.

  19,23

  Работа равна W=FdcosθW=Fdcosθ; здесь cosθ=1cosθ=1, так как путь параллелен полю, и поэтому W=FdW=Fd. С F=qEF=qE, мы видим, что W=qEdW=qEd. Подстановка этого выражения для работы в предыдущее уравнение дает

  qEd=qVAB.qEd=qVAB.

  19,24

  Заряд отменяется, поэтому напряжение между точками A и B становится равным

  VAB=EdE=VABd(только однородное-поле),VAB=EdE=VABd(только однородное-поле),

  19. 25

  , где dd — расстояние от А до В или расстояние между пластинами на рис. 19.5. Обратите внимание, что приведенное выше уравнение подразумевает, что единицами измерения электрического поля являются вольты на метр. Мы уже знаем, что единицами измерения электрического поля являются ньютоны на кулон; таким образом, справедливо следующее соотношение между единицами:

  1 Н/З=1 В/м.1 Н/З=1 В/м.

  19,26

  Напряжение между точками A и B

  VAB=EdE=VABd(только для однородного поля), VAB=EdE=VABd(только для однородного поля),

  19,27

  где dd — расстояние от A до B или расстояние между пластинами.

  Пример 19,4

  Какое максимально возможное напряжение между двумя пластинами?

  Сухой воздух поддерживает максимальную напряженность электрического поля около 3,0×106 В/м3,0×106 В/м. Выше этого значения поле создает в воздухе достаточную ионизацию, чтобы сделать воздух проводником. Это позволяет разряду или искре, которая уменьшает поле. Чему тогда равно максимальное напряжение между двумя параллельными проводящими пластинами, разделенными 2,5 см сухого воздуха?

  Стратегия

  Заданы максимальное электрическое поле EE между пластинами и расстояние dd между ними. Таким образом, уравнение VAB=EdVAB=Ed можно использовать для расчета максимального напряжения.

  Решение

  Разность потенциалов или напряжение между пластинами составляет

  VAB=Ed.VAB=Ed.

  19,28

  Ввод заданных значений для EE и dd дают

  VAB=(3,0×106 В/м)(0,025 м)=7,5×104VVAB=(3,0×106 В/м)(0,025 м)=7,5×104 В

  19.29

  или

  VAB=75 кВ.VAB=75 кВ.

  19.30

  (Ответ представлен только двумя цифрами, поскольку максимальная напряженность поля является приблизительной. ) Зазор 2,5 см (1 дюйм) или 150 кВ для искры длиной 5 см. Это ограничивает напряжения, которые могут существовать между проводниками, например, на линии электропередачи. Меньшее напряжение вызовет искру, если на поверхности есть точки, так как точки создают большее поле, чем гладкие поверхности. Влажный воздух разрушается при более низкой напряженности поля, а это означает, что меньшее напряжение вызовет скачок искры во влажном воздухе. Самые большие напряжения могут быть созданы, например, статическим электричеством, в сухие дни.

  Рисунок 19,6 Искровая камера используется для отслеживания путей высокоэнергетических частиц. Ионизация, создаваемая частицами при их прохождении через газ между пластинами, позволяет проскакивать искре. Искры располагаются перпендикулярно пластинам, следуя линиям электрического поля между ними. Разность потенциалов между соседними пластинами недостаточно высока, чтобы вызвать искры без ионизации, создаваемой частицами в экспериментах на ускорителях (или космическими лучами). (кредит: Дадерот, Wikimedia Commons)

  Пример 19,5

  Поле и сила внутри электронной пушки

  (a) Электронная пушка имеет параллельные пластины, разделенные расстоянием 4,00 см, и дает электронам энергию 25,0 кэВ. Чему равна напряженность электрического поля между пластинами? б) С какой силой это поле будет действовать на кусок пластика с зарядом 0,500 мкКл0,500 мкКл, который попадет между пластинами?

  Стратегия

  Поскольку напряжение и расстояние между пластинами заданы, напряженность электрического поля можно рассчитать непосредственно из выражения E=VABdE=VABd. Зная напряженность электрического поля, можно найти силу, действующую на заряд. F=qEF=qE. Поскольку электрическое поле имеет только одно направление, мы можем записать это уравнение в терминах величин: F=qEF=qE.

  Решение для (a)

  Выражение для величины электрического поля между двумя однородными металлическими пластинами:

  E=VABd. E=VABd.

  19,31

  Так как электрон является однозарядным и имеет энергию 25,0 кэВ, разность потенциалов должна быть 25,0 кВ. Вводя это значение для VABVAB и расстояния между пластинами 0,0400 м, получаем

  E=25,0 кВ0,0400 м=6,25×105 В/м.E=25,0 кВ0,0400 м=6,25×105 В/м.

  19,32

  Решение для (б)

  Величина силы, действующей на заряд в электрическом поле, получается из уравнения

  F=qE.F=qE.

  19,33

  Подставляя известные значения, получаем 0,313 Н.

  19,34

  Обсуждение

  Обратите внимание, что единицами измерения являются ньютоны, поскольку 1 В/м=1 Н/Кл1 В/м=1 Н/Кл. Сила, действующая на заряд, одинакова независимо от того, где находится заряд между пластинами. Это связано с тем, что электрическое поле между пластинами однородно.

  В более общих ситуациях, независимо от того, является ли электрическое поле однородным, оно указывает в направлении уменьшения потенциала, потому что сила на положительном заряде направлена ​​в направлении EE, а также в направлении более низкого потенциала VV.