Непрерывный сигнал — Википедия

Материал из Википедии — свободной энциклопедии

.ts-Боковая_навигационная_таблица-preTitle{padding-top:0}.mw-parser-output .ts-Боковая_навигационная_таблица-image{padding:0.4em 0 0.4em}.mw-parser-output .ts-Боковая_навигационная_таблица-title{padding:0.2em 0.4em 0.2em;font-size:125%;line-height:1.15em;font-weight:bold;background:#cfe3ff}.mw-parser-output .ts-Боковая_навигационная_таблица-above,.mw-parser-output .ts-Боковая_навигационная_таблица-below{padding:0.2em 0.4em 0.2em;font-weight:bold}.mw-parser-output .ts-Боковая_навигационная_таблица-heading{padding:0.2em 0;font-weight:bold;background:#eaf3ff}.mw-parser-output .ts-Боковая_навигационная_таблица-list{padding:0.2em 0}]]>

Непрерывная волна или непрерывный сигнал ( CW) — это электромагнитная волна с постоянными амплитудой, частотой и, в математическом анализе, с бесконечной продолжительностью. Понятие непрерывной волны также использовалось для первых методов радиопередачи, в которой волна-носитель выключалась и включалась. Информация передавалась с помощью переменной длины периодов включения и выключения сигнала, например азбукой Морзе в ранних радиосистемах. В начале беспроводной телеграфии с помощью радио передачи CW волны также назывались «незатухающими волнами», чтобы отличить этот метод от передачи затухающей волны.

• Apurba Das: Signal Conditioning: An Introduction to Continuous Wave Communication and Signal Processing. Springer,2012 год,ISBN = 978-3-642-28818-0

INFOблог: Непрерывные и дискретные сигналы

В предыдущем посте мы рассматривали различные определения понятия «информация» и пришли к выводу, что информация может быть определена множеством разных способов в зависимости от выбранного подхода. Но об одном мы можем говорить однозначно: информация — знания, данные, сведения, характеристики, отражения и т.д. — категория нематериальная. Но мы живем в мире материальном. Следовательно, для существования и распространения в нашем мире информация должна быть связана с какой-либо материальной основой. Без нее информация не может передаваться и сохраняться.

Тогда материальный объект (или среда), с помощью которого представляется та или иная информация будет являться носителем информации, а изменение какой-либо характеристики носителя мы будем называть сигналом.
Например, представим равномерно горящую лампочку, она не передает никакой информации. Но, если мы будем включать и выключать лампочку (т.е. изменять ее яркость), тогда с помощью чередований вспышек и пауз мы сможем передать какое-нибудь сообщение (например, посредством азбуки Морзе). Аналогично, равномерный гул не дает возможности передать какую-либо информацию, однако, если мы будем изменять высоту и громкость звука, то сможем сформировать некоторое сообщение (что мы и делаем с помощью устной речи).

При этом сигналы могут быть двух видов: непрерывный (или аналоговый) и дискретный.
В учебнике даны следующие определения.

Непрерывный сигнал принимает множество значений из некоторого диапазона. Между значениями, которые он принимает, нет разрывов.
Дискретный сигнал принимает конечное число значений. Все значения дискретного сигнала можно пронумеровать целыми числами.

Немного уточним эти определения.
Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала.

Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала.

Графики этих сигналов выглядят следующим образом

Примерами непрерывных сигналов могут быть музыка, речь, изображения, показания термометра (высота столба ртути может быть любой и представляет собой ряд непрерывных значений).

Примерами дискретных сигналов могут быть показания механических или электронных часов, тексты в книгах, показания цифровых измерительных приборов и т.д.

Вернемся к примерам, рассмотренным в начале сообщения — мигающая лампочка и человеческая речь. Какой из этих сигналов является непрерывным, а какой дискретным? Ответьте в комментариях и аргументируйте свой ответ. Можно ли непрерывную информацию преобразовать в дискретную? Если да — приведите примеры.

Чем отличается непрерывный сигнал от дискретного

Для связи и передачи сообщений используют сигналы, которые отличаются друг от друга. Существуют непрерывные (НС) и дискретные сигналы (ДС).

Особенности непрерывного сигнала

Если дискретный сигнал квантуется как по времени, так и по уровню, то его называют цифровым сигналом

Сигнал считается непрерывным, если в заданных пределах он может иметь любое значение. С математической точки зрения это означает, что НС можно представить в виде непрерывной функции. Примерами такого сигнала является получаемый с микрофона сигнал о давлении на его мембрану звуковой волны или сигнал от термопары об измеряемой температуре.

Аналоговые системы для передачи информации, использующие НС, имеют следующие недостатки:

• пониженную помехозащищённость — это свойство связано с тем, что из-за непрерывности системы помеху, попавшую в сигнал, невозможно отличить от самого сигнала;
• затруднения при передаче сигналов управления;
• трудности при сопряжении с компьютером и другими цифровыми устройствами;
• трудности шифрования.

Что такое дискретный

Дискретность применяется в вычислительной технике для пакетной передачи данных

Дискретный сигнал — тот, который в некотором интервале может принимать определённое число значений. К таким сигналам относятся показания цифровых часов или приборов, а также тексты в книгах.

Благодаря достижениям в цифровой технике большинство электронных устройств в настоящее время являются цифровыми и работают с ДС. В то же время физические сигналы в природе имеют аналоговый вид. Преобразование НС в дискретный вид производится путём дискретизации его с помощью специальных устройств (АЦП). Обратное преобразование сигнала производится с помощью ЦАП.

Достоинствами цифровых систем, работающих на ДС, являются:

• высокая помехозащищённость и возможность работы каналов связи при больших шумах;
• простота передачи команд управления каналами;
• возможность цифровой обработки сигналов;
• лёгкость засекречивания.

Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер — цифровая машина, то есть внутреннее представление информации в нём дискретно. Дискретизация входных сигналов (если она непрерывна) позволяет сделать их пригодными для дискретной обработки.

Отличия двух видов сигналов

Все значения дискретного сигнала можно пронумеровать целыми числами

Основным отличием непрерывного сигнала от ДС является то, что он может иметь в заданном диапазоне любое значение, тогда как ДС может принимать только определённые значения.

К недостаткам систем, использующих ДС, можно отнести:

• увеличение полосы частот, требуемой для передачи сообщений;
• для обеспечения точного воспроизведения непрерывного сигнала при дискретизации требуется значительное количество уровней квантования и высокая частота;
• требование синхронизации;
• плохая совместимость с уже имеющимися аналоговыми системами.

Различные процессы могут быть описаны с помощью непрерывных или дискретных сигналов. Непрерывный сигнал может иметь любое значение из некоторого диапазона величин, тогда как для дискретного сигнала возможные его значения определены заранее. Во многих случаях при использовании цифровых методов обработки информации полезно преобразовать непрерывные сигналы в дискретные.

непрерывный сигнал — это… Что такое непрерывный сигнал?



непрерывный сигнал

Сигнал, описываемый непрерывной функцией времени.

Политехнический терминологический толковый словарь. Составление: В. Бутаков, И. Фаградянц. 2014.

• непрерывный режим
• неприводимые диаграммы фейнмана

Смотреть что такое «непрерывный сигнал» в других словарях:

• непрерывный сигнал

  — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN continuous signal …   Справочник технического переводчика

• непрерывный сигнал — 06.01.20 непрерывный сигнал [ continuous wave]: Непрерывный гармонический сигнал заданной частоты, поступающий от устройства считывания/опроса и обеспечивающий электропитание пассивной радиочастотной метки, не подвергнутый амплитудной и/или… …   Словарь-справочник терминов нормативно-технической документации

• непрерывный сигнал — analoginis signalas statusas T sritis Standartizacija ir metrologija apibrėžtis Signalas, išreiškiamas laiko funkcija, kartojančia atitinkamo dydžio kitimo dėsnį. atitikmenys: angl. analog signal; analogue signal vok. analoges Signal, n;… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• непрерывный сигнал — analoginis signalas statusas T sritis fizika atitikmenys: angl. analog signal; analogue signal vok. analoges Signal, n; Analogsignal, n rus. аналоговый сигнал, m; непрерывный сигнал, m pranc. signal analogique, m; signal analogue, m …   Fizikos terminų žodynas

• непрерывный сигнал — tolydusis signalas statusas T sritis fizika atitikmenys: angl. analog signal; analogue signal; continuous signal vok. analoges Signal, n; kontinuierliches Signal, n; stetiges Signal, n rus. аналоговый сигнал, m; непрерывный сигнал, m pranc.… …   Fizikos terminų žodynas

• непрерывный сигнал — аналоговый сигнал …   Словарь русских синонимов по технологиям автоматического контроля

• Сигнал бедствия — У этого термина существуют и другие значения, см. Сигнал (значения). Часы радиста. Цветными секторами на циферблате обозначены трехминутные периоды радиомолчания, когда все служебные станции должны прослушивать частоты сигналов бедствия:… …   Википедия

• аналоговый сигнал — непрерывный сигнал …   Словарь русских синонимов по технологиям автоматического контроля

• аналоговый сигнал — analoginis signalas statusas T sritis Standartizacija ir metrologija apibrėžtis Signalas, išreiškiamas laiko funkcija, kartojančia atitinkamo dydžio kitimo dėsnį. atitikmenys: angl. analog signal; analogue signal vok. analoges Signal, n;… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• аналоговый сигнал — analoginis signalas statusas T sritis fizika atitikmenys: angl. analog signal; analogue signal vok. analoges Signal, n; Analogsignal, n rus. аналоговый сигнал, m; непрерывный сигнал, m pranc. signal analogique, m; signal analogue, m …   Fizikos terminų žodynas

Непрерывные сигналы.

В качестве непрерывных сигналов в системах передачи данных чаще всего используются электромагнитные процессы, изменяющиеся по гармоническому закону:

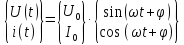
Таких сигналов характерными параметрами являются амплитуда, частота, фаза.

Гармонические сигналы в чистом виде практически не пригодны для передачи информации.

Потому что если известны исходные параметры такого процесса в начальный момент времени, то параметры этого процесса фактически будут известны в в любой последующий момент времени.

Лекция №4

Дискретные сигналы

Такого типа сигналы реализуются в виде кратковременных отклонений, используемого физического процесса от исходного стационарного состояния.

Если в качестве дискретного сигнала использовать кратковременное воздействие электрического тока или напряжения, то такие сигналы называются видеоимпульсами.

Если импульс сигнала характеризуется кратковременным высокочастотным процессом, то такой сигнал называется радиоимпульсом.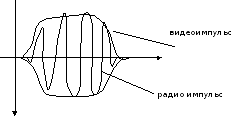

При этом огибающая радиоимпульса рассматривается как видеоимпульс.

Форма этих сигналов может быть различна, а именно прямоугольной, трапециидальной, треугольной, пилообразной, колоколообразной, экспоненциальной.

Информационные признаки сигналов, используемых в системах передачи данных (спд)

Для кодирования информации, передаваемой с помощью импульсных сигналов и для обеспечения возможности их последовательности кодирования при приеме принято использовать определенные импульсные признаки.

К числу основных импульсных отличительных признаков относятся следующие:

а) полярные признаки – отличительным признаком в этом случае является полярность передаваемых сигналов 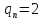. Импульсные сигналы с полярными признаками могут использоваться только в проводных линиях связи. Надежность систем используемых такие признаки достаточно высока, потому что такие системы весьма помехоустойчивы и не реагируют на изменение амплитуды передаваемых импульсов, а также на колебания параметров линии связи;

б) амплитудные признаки – отличительным признаком является амплитуда передаваемых сигналов 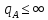. Так как на практике трудно различать сигналы, отличающиеся друг от друга по амплитуде на незначительную величину, особенно при наличии помех в канале связи, то реально используемые системы в которых число амплитудных признаков;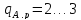

в) временные признаки – отличительным признаком сигналов данного типа является длительность импульсов

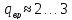
г) фазовые признаки – в этом случае отличительным признаком является фаза импульса

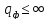
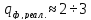
д) частотные признаки – отличительным признаком сигналов в этом случае является частота следования импульсов

Сообщения и их виды

Величины, характеризующие тот или иной информационный процесс, как правило имеют случайный характер, то есть не могут быть заранее известными.

Если случайная величина (температура в химическом реакторе) может принимать только конченое число значений, то ее называют дискретной по множеству.

Если же случайная величина может принимать бесконечное число своих значений, то ее называют непрерывной по множеству.

В общем случае получаемые сообщения представляют собой некоторую функцию времени. По виду получающейся функции все сообщения можно классифицировать следующим образом:

1 – непрерывные про множеству и времени (непрерывные) – в этом случае функция характеризующая передаваемое сообщение имеет непрерывное множество значений и меняется с течением времени

Такого рода сообщения характерны для телеизмерений.

2 – непрерывные по времени и дискретные по множеству сигналы

X(t)

3 – непрерывные по множеству и дискретные по времени сигналы

4 – дискретные по множеству и времени

1.3 Сигналы непрерывные и дискретные. Преобразование сигналов.

Информация (сообщения и сигналы) может существовать в двух формах: непрерывной и дискретной.

В большинстве случаев информация о протекании того или иного физического процесса вырабатывается соответствующими датчиками в виде сигналов, непрерывно изменяющихся во времени. Такой сигнал можно представить в виде непрерывной функции Х(t) непрерывного аргументаt– функции, которая может принимать любые вещественные значения в интервале (X_min,X_max) для любых значений аргументаtв интервале (0, Т) (рис. 1.10а). Множество значений непрерывной функции бесконечно.

Дискретные сообщения и сигналы состоят из конечного множества элементов, поступающих последовательно во времени. Набор элементов (символов) составляет алфавит источника дискретной информации. Обычно элементами дискретных сигналов являются последовательности чисел.

Для передачи информации по каналу связи и ее дальнейшей обработки средствами вычислительной техники непрерывный сигнал преобразуют в дискретный. Это преобразование осуществляется с помощью специальных устройств – преобразователей непрерывных сигналов и может быть выполнено дискретизацией во времени, квантованием по уровню или одновременно дискретизацией во времени и квантованием по уровню. При этом соответственно возможны три разновидности сигналов.

Дискретизация во временисостоит в преобразовании непрерывного сигнала Х(t) непрерывного аргументаt(рис. 1.10а) в непрерывный сигнал Х(t_i) дискретного аргументаt_iс шагом дискретизации ∆t(рис. 1.10б). Сигнала Х(t_i) может принимать любые значения в интервале (X_min,X_max), но лишь на дискретном множестве значений аргументаt_i(t₁,t₂, …,t_к) в интервале (0, Т). Какой бы малый шаг дискретизации не выбирался, множество значений дискретной функции будет конечно (ограничено). Примером такого сигнала может быть последовательность импульсов, модулированных по амплитуде. Рассмотренная дискретизации является равномерной, т.к. длительность шага дискретизации ∆t_i=constна всем интервале (0, Т). Дискретизация может быть и неравномерной, если длительность шага ∆t_iразлична (∆t_i=var). Методы изменения шага ∆t_iмогут быть адаптивными, когда он изменяется в зависимости от текущего изменения параметров сигнала, и программируемыми, когда он изменяется в соответствии с заранее установленной программой или оператором, на основе анализа поступающей информации. Очевидно, что каждый вид дискретизации имеет свои преимущества и недостатки. Все же в основном, применяется равномерная дискретизация, так как алгоритмы и аппаратура для ее реализации существенно проще. Однако очевидно, что при этом в случае медленно изменяющихся сигналов возможны «лишние» отсчеты, т.е. избыточность информации.

К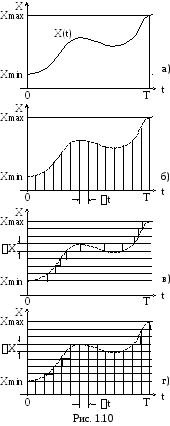вантование по уровнюсостоит в преобразовании непрерывных значений сигнала Х(t_i) в дискретные значения. При этом образуется дискретный сигнал непрерывного аргумента; соседние значения сигнала различаются на элементарную величину ∆Х – квант (рис. 1.10в). Значения, которые может принимать сигнал Х(t), образуют дискретный ряд заранее заданных чисел Х₁, Х₂,…Х_кили уровней 1, 2, 3, 4 и т.д.; значение аргументаtможет быть любым в интервале (0,Т). Примером такого сигнала может быть сигнал на выходе проволочного потенциометра, выходное напряжение которого квантуется за счет скачков сопротивления при перемещении движка с витка на виток. Можно отметить, что квантование по уровню может быть и неравномерным, если ∆Х=var. В основном, используется равномерное квантование — ∆Х=const.

С

Преобразование непрерывного сигнала в дискретный

овместное применение операции дискретизации во времени и квантования по уровнюпозволяет преобразовать непрерывный сигнал Х(t) в дискретный по координатам Х иt(рис. 1.10г). При этом образуется дискретный сигнал дискретного аргумента. Значения сигнала Х(t) и аргументаtобразуют дискретные ряды чисел Х₁, Х₂, …Х_киt₁,t₂, …t_к, заполняющие интервалы (Х_min,Х_max) и (0,Т) соответственно.

Первые две из рассмотренных разновидностей принадлежат дискретно-непрерывным сигналам, а третья – дискретному сигналу. Последний называется также цифровым, так как дискретные значения сигнала обычно представляются в цифровой форме.

Рассмотрим некоторые вопросы, связанные с точностью представления непрерывных сигналов Х(t) в результате дискретизации во времени и квантования по уровню.

В результате дискретизации во времени исходный непрерывный сигнал Х(t) представляется конечной последовательностью отдельных значений Х(t_i), измеренных с шагом дискретизации ∆t=t_i-t_i-1. По значениям Х(t_i) можно восстановить исходный сигнал Х(t) с некоторой погрешностью. Функцию Х(t), полученную в результате восстановления (интерполяции) по значениям Х(t_i), называют воспроизводящей. При дискретизации возникает вопрос о точности преобразования, которая очевидно зависит от частоты отсчетов функцииf_k=1/∆t_i, т.е. от выбранного шага дискретизации ∆t_i. С одной стороны, очевидно, что с уменьшением (увеличением) ∆t_iточность преобразования будет расти (уменьшаться) за счет увеличения (уменьшения) количества отсчетов. С другой стороны, очевидно, что нет смысла стремиться всегда брать отсчеты как можно чаще, независимо от вида сигнала Х(t), так как в случае медленно изменяющегося сигнала Х(t) два соседних значения Х(t_i) и Х(t_i+1) могут быть настолько связаны (коррелированны) между собой, что по одному из них Х(t_i) можно прогнозировать другое Х(t_i+1), т.е. никакой новой информации о сигнале при его последующем восстановлении по отсчетам это не дает. Проблема обеспечении точности дискретизации может быть сформулирована следующим образом: с каким максимальным интервалом необходимо брать отсчеты значений сигнала Х(t_i), чтобы не пропустить существенных его изменений или, другими словами, какое минимальное количество отсчетов необходимо брать для обеспечения заданной точности воспроизведения сигнала Х(t). От этого, в конечном счете, зависит количество информации, которую надо хранить и преобразовывать в вычислительном устройстве.

Возможны различные пути решения указанной проблемы.

В общем виде задача о представлении некоторого сигнала, являющегося непрерывной функцией времени, в виде конечного числа значений, взятых для дискретных значений времени, решена В.А. Котельниковым. В двух теоремах В.А. Котельников применительно к системе передачи сообщений по линии связи определил, как следует выбрать частоту дискретизации, обеспечивающую по полученным дискретным данным последующее воспроизведение исходного сигнала с заданной точностью.

Теорема 1. Любую функцию Х(t), имеющую спектр частот от 0 доf_m, можно представить суммой функцииsinx/x, т.е. рядом:

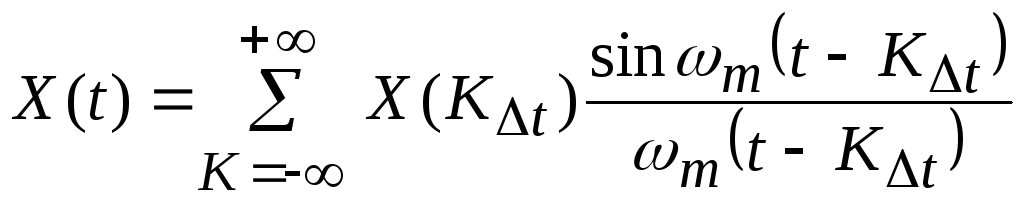, (1.51)

где K– целое число,

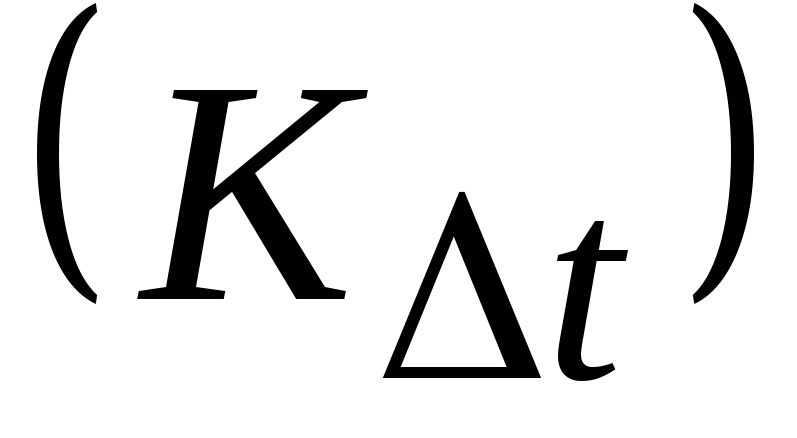– отсчеты мгновенных значений функции Х(t) с шагом дискретизации ∆t,

ω_m= 2πf_m,f_m– максимальная частота в спектре частот сигнала Х(t), Гц

ω_m– круговая частота.

Из этой теоремы может быть сделан и обратный вывод: любая функция, представленная рядом Котельникова (1.51), имеет спектр, состоящий из частот от 0 до f_m.

Теорема 2. Любая функция Х(t), содержащая частоты от 0 доf_m, полностью определяется дискретными значениями этой функции, следующими друг за другом с частотой 2f_m, т.е. через интервал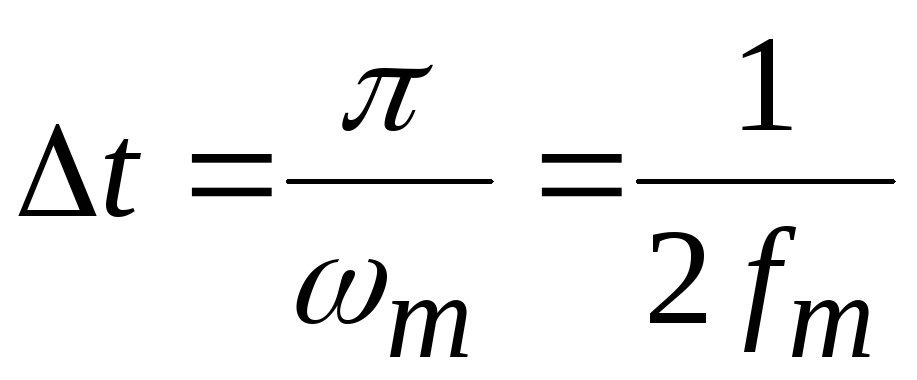сек. Таким образом, передачу непрерывного сигнала Х(t) с ограниченным спектром частот, поступающего от какого-либо датчика, можно свести к передаче последовательности дискретных чисел – значений этого сигнала, взятых через интервал времени 1/2f_m; число этих значений равно 2f_m. Через полученные значения ординат, при обработке результатов измерений, можно провести единственным способом воспроизводящую непрерывную функцию. Поэтому, проще говоря, нет смысла брать отсчеты чаще, чем интервал 1/2f_m, так как никакой новой информации о функции при ее последующем восстановлении по отсчетам это не дает. Следует подчеркнуть, что сказанное справедливо только в том случае, если в получаемой информации действительно отсутствует частоты вышеf_m.

Теоремы В.А. Котельникова, являющиеся основой современной теории передачи сообщений, очень удобны для исследования всевозможных линий связи, вследствие того, что для этих линий известны частотные характеристики, а спектр передаваемых сигналов ограничен. Другое дело – реальные сигналы, имеющие конечную длительность Т. Для их точного представления, в отличие от моделей сигналов с ограниченным спектром (1.51), необходим спектр, который простирался бы от нуля до бесконечности. Теоретически, чтобы избежать погрешности дискретизации, для такого спектра требуется бесконечно большая частота взятия отсчетов. Практически выбирают такую частоту дискретизации, при которой погрешность не превышает заданной величины В этой связи теорему 2 В.А. Котельникова можно рассматривать как приближенную для функций с неограниченным спектром. На практике частоту отсчетов часто определяют как 2f_mk, т.е. интервал между отсчетами

(1.52)

где f_m– максимальная допустимая частота в спектре сигнала Х(t)

k– коэффициент запаса (обычно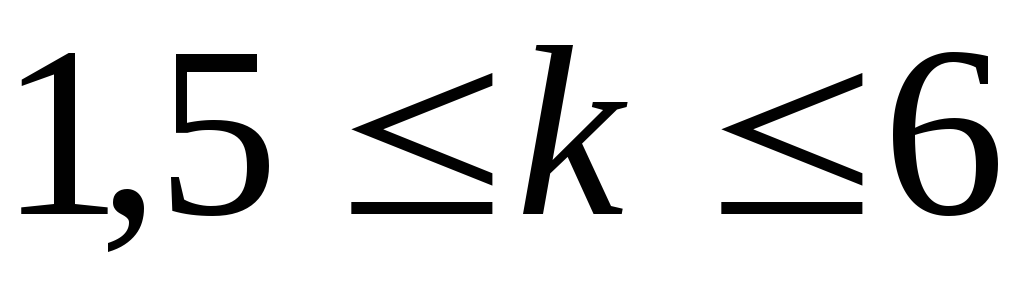). Так как безграничный частотный спектр заменяется ограниченным, вне которого спектральная плотность принимается равной нулю, то погрешность дискретизации будет определяться соотношением составляющих, лежащих внутри спектра и вне его.

Другой, практически легко реализуемый путь определения оптимального интервала дискретизации ∆tнепрерывного сигнала Х(t) заключается в построении автокорреляционной функции сигнала и нахождении интервала корреляции τ_к .Дискретные отсчеты, взятые через интервал ∆t=τ_к, будут независимыми и информативными; для их обработки могут быть использованы методы математической статистики.

В случае, когда непрерывный сигнал Х(t) представлен своими дискретными значениями, полученными при равномерной или неравномерной дискретизации, он может быть заменен некоторой приближающей (аппроксимирующей) зависимостью. В общем случае исходный сигнал может быть аппроксимирован специальной функцией или полиномом, график которого проходит через известные дискретные значения. Наиболее часто используются степенные алгебраические полиномы, но так как обычно исходный сигнал задается в графическом или табличном, а не в аналитическом виде, то проведение аппроксимации полиномами с порядком выше первого затруднительно. При аппроксимации полиномом первого порядка все точки кривой, соответствующие дискретным моментам времени, соединяются отрезками прямых (кусочно-линейная аппроксимация). Алгебраические полиномы удобны для программирования и обработки с помощью вычислительной техники

При квантовании исходного сигнала по уровню возникает погрешность квантования. Так как в процессе преобразования значение сигнала Х(t) обычно отображается ближайшим уровнем квантования Х_m, то все значения, кроме кратныхХ, представляются с некоторой погрешностью, максимальное значение которой равно 0,5.

В заключение этого параграфа отметим, что дискретизация и квантование находят широкое применение в преобразователях информации, используемых для связи вычислительных устройств с реальными объектами.

Аналоговые, дискретные и цифровые сигналы

DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов

Распространяется под лицензией LGPL v3

Страница проекта на GitHub.

Содержание

Вводные понятия Дискретизация аналоговых сигналов. Математическая модель дискретного сигнала Размерность дискретного сигнала Преобразование Фурье решетчатой функции Спектральная плотность дискретного сигнала Размерность спектра дискретного сигнала Список литературы Обнаружили ошибку? Выделите ее мышью и нажмите

Вводные понятия

Рисунок 1. Аналоговый, дискретный и цифровой сигналы

Сигнал называют аналоговым, если он определен на непрерывной оси времени , и в каждый момент может принимать произвольные значения. Аналоговый сигнал может быть представлен непрерывной, или кусочно-непрерывной функции переменной . Пример аналогового сигнала показан на рисунке 1.

Если сигнал принимает произвольные значения только в фиксированные моменты времени ,  — целое число, то такой сигнал называется дискретным. Наиболее широкое распространение получили дискретные сигналы, определенные на равноотстоящей сетке , где  — интервал дискретизации. При этом в моменты дискретизации дискретный сигнал может принимать произвольные значения. Если значения дискретного сигнала  также берутся на фиксированной сетке значений, и при этом сами значения могут быть представлены числом конечной разрядности в одной из систем счисления, то такой дискретный сигнал называется цифровым . Часто говорят, что цифровой сигнал представляет собой квантованный по уровню дискретный сигнал. Примеры дискретного и цифрового сигналов также показаны на рисунке 1. Тонкая разница между дискретными и цифровыми сигналами дает возможность их отождествлять практически во всех прикладных задачах. Аналоговый сигнал может быть описан функцией времени, в то время как дискретный и цифровой сигналы могут быть заданы вектором отсчетов :

(1)

Вектор отсчетов цифрового сигнала может быть помещен в память вычислительного устройства с возможность многократной перезаписи и копирования без потери точности, в то время как перезапись и копирование аналоговых сигналов неизбежно сопровождается потерей части информации. Кроме того, обработка цифровых сигналов позволяет добиться потенциально-возможных характеристик устройств, ввиду возможности выполнения вычислительных операций без потерь, или с пренебрежимо малыми потерями качества.

Указанные преимущества определили повсеместное распространение цифровых систем хранения и обработки сигналов. Но цифровые сигналы также имеют и недостатки по сравнению с аналоговыми.

Во-первых нет возможности передавать цифровые сигналы «как есть», поскольку передача сигналов чаще всего происходит при использовании электромагнитных и акустических волн, которые являются непрерывными во времени. Поэтому для передачи цифровых сигналов требуются дополнительные методы цифровой модуляции, а также цифро-аналоговые преобразователи (ЦАП).

Другим недостатком цифровых сигналов является меньший динамический диапазон сигнала (т.е. отношение самого большого значения к самому маленькому), из-за квантования сигнала на фиксированной сетке значений.

Дискретизация аналоговых сигналов. Математическая модель дискретного сигнала

В данном параграфе мы рассмотрим способ выборки дискретных значений аналогового сигнала. Структурная схема устройства дискретизации показана на рисунке 2. Данное устройство называется аналого-цифровой преобразователь (АЦП), потому что оно преобразует аналоговый сигнал в набор оценок дискретных значений , где  — целое число, взятых через равноотстоящие промежутки времени .

Рисунок 2. Структурная схема аналого-цифрового преобразователя

Временны́е осциллограммы, поясняющие принцип работы устройства показаны на рисунке 3 (см. [1, стр. 475–476], или [2, стр. 438]).

Рисунок 3. Временны́е осциллограммы АЦП

На входе АЦП имеется аналоговый сигнал . Генератор импульсов формирует равноотстоящие стробирующие импульсы , которые управляют ключом, в результате чего на вход усилителя подаются короткие выборки сигнала длительности , взятые через интервал дискретизации .

Оценка дискретного сигнала может быть представлена в виде

(2)

где  — прямоугольный импульс длительности единичной амплитуды, который мы уже рассматривали в предыдущих разделах.

Интегрируя на каждом интервале длительности стробирующего импульса получим оценку значения сигнала в момент времени . При конечной величине мы можем говорить об оценке значения сигнала в момент времени  с некоторой погрешностью, ввиду изменения сигнала на интервале . Поэтому мы используем шапочку над обозначением , чтобы подчеркнуть приближенную оценку.

При уменьшении длительности погрешность оценки будет уменьшаться, и в пределе мы можем получить дискретный сигнал как:

(3)

где  — смещенная на дельта-функция Дирака, которую мы подробно рассматривали в параграфе ранее.

Бесконечная сумма смещенных дельта-функций называется решетчатой функцией и обозначается [3, стр. 77]:

(4)

где индекс указывает временной интервал следования дельта-функций.

Тогда математической моделью дискретного сигнала будет произведение исходного аналогового сигнала на решетчатую функцию:

(5)

Заметим, что (5) уже не является приближенной оценкой, а представляет собой истинную модель дискретного сигнала.

Графически модель дискретного сигнала , с использованием решетчатой функции показана на рисунке 4.

Рисунок 4. Модель дискретного сигнала
на основе решетчатой функции

Для получения численных значений дискретного сигнала необходимо проинтегрировать дискретный сигнал (5) в окрестности :

(6)

где  — конечный интервал интегрирования дискретного сигнала в окрестности .

В дальнейшем мы будем широко использовать данную модель дискретного сигнала для перехода от методов анализа и обработки аналоговых сигналов, к цифровым.

Размерность дискретного сигнала

Пусть исходный аналоговый сигнал описывает изменение напряжения во времени и имеет размерность вольт . Вспомним, что дельта-функция Дирака имеет размерность, обратную размерности ее аргумента. Тогда решетчатая функция , согласно (4) имеет размерность , а размерность дискретного сигнала (5) будет .

Заметим, что значения дискретного сигнала, полученные из (6) как результат интегрирования дискретного сигнала в окрестности момента времени , будут иметь размерность исходного сигнала .

Преобразование Фурье решетчатой функции

В данном разделе мы проанализируем спектральную плотность решетчатой функции . Для начала рассмотрим как периодический сигнал. Тогда можно представить в виде разложения в ряд Фурье:

(7)

где , рад/с — частота дискретизации,

(8)

Тогда (7) с учетом (8):

(9)

Заметим, что знак аргумента комплексной экспоненты выражения (9) можно изменить, потому что суммирование ведется от минус бесконечности до бесконечности с положительными и отрицательными . Тогда:

(10)

Выражение (10) представляет как бесконечную сумму комплексных экспонент.

Рассмотрим теперь преобразование Фурье решетчатой функции:

(11)

Поменяем операции интегрирования и суммирования и применим фильтрующее свойство дельта-функции:

(12)

Выражение (12) также представляет собой бесконечную сумму комплексных экспонент. Учтем, что и получим:

(13)

Сравнивая (13) с (10) можно заключить, что:

(14)

Таким образом, спектральная плотность решетчатой функции представляет собой также решетчатую функцию.

Период повторения дельта-функций в частотной области равен , при этом дельта-функции масштабируются в раз, как это показно на рисунке 5.

Рисунок 5. Решетчатая функция:
а — временно́е представление; б — спектральная плотность

Заметим, что умножение на в частотной области изменяет размерность спектральной плотности , в результате чего спектральная плотность переходит в безразмерный спектр (что не удивительно, потому что исходная решетчатая функция — периодическая).

Спектральная плотность дискретного сигнала

Пусть дан аналоговый сигнал , спектральная плотность которого равна . В данном параграфе мы рассмотрим процесс равноотстоящей дискретизации сигнала в частотной области.

Преобразование Фурье дискретного сигнала (5) равно:

(15)

Применим свойство преобразования Фурье произведения сигналов, тогда представляет собой свертку спектральной плотности решетчатой функции и спектральной плотности исходного сигнала :

(16)

Преобразуем (16), используя фильтрующее свойство дельта-функции:

(17)

Уравнение (17) задает спектральную плотность дискретного сигнала как бесконечную сумму масштабированных копий спектральной плотности , отстоящих друг от друга на рад/с по частоте, как это показано на рисунке 6.

Рисунок 6. Спектральная плотность дискретного сигнала

Заметим, что мы не накладываем никаких ограничений ни на интервал дискретизации , ни на сигнал , ни на спектральную плотность . Вне зависимости от частоты дискретизации рад/с, и формы , спектральная плотность дискретного сигнала всегда будет представлять собой сумму масштабированных копий , отстоящих друг от друга на величину частоты дискретизации рад/с.

Размерность спектра дискретного сигнала

Проанализируем выражение (17) на предмет размерности , в предположении, что исходный аналоговый сигнал имеет размерность :

(18)

Таким образом, из (18) можно заключить, что при дискретизации сигнала, его спектральная плотность переходит в спектр, а размерность  спектра дискретного сигнала совпадает с размерностью исходного аналогового сигнала .

Если аналоговый сигнал описывает изменения напряжения во времени и измеряется в единицах вольт, то при дискретизации аналогового сигнала, получим дискретные отсчеты, также измеряемые в вольт, и спектр дискретного сигнала также будет измеряться в единицах вольт. Тогда функцию  мы можем назвать спектром, а не спектральной плотностью.

Главный вывод: преобразование Фурье дискретного сигнала не изменяет размерности дискретных отсчетов сигнала, в отличии от преобразования Фурье аналогового сигнала, которое возвращает спектральную плотность .

Выводы

В данном разделе мы ввели понятие дискретного и цифрового сигналов. Мы опеределили, что дискретный сигнал может быть представлен как результат произведения решетчатой функции и аналогового сигнала.

Были детально рассмотрены свойства решетчатой функции и показано, что спектральная плотность решетчатой функции также представляет собой масштабированную по амплитуде решетчатую функцию.

В результате свойств решетчатой функци получили, что спектральная плотность дискретного сигнала представляется бесконечной суммой копий спектральных плотностей исходного сигнала, отставленных дург от друка на величину равную частоте дискретизации.

Смотри также

Представление периодических сигналов рядом Фурье
Некоторые свойства разложения периодических сигналов в ряд Фурье
Свойства преобразования Фурье
Спектральные плотности некоторых сигналов
Информация была полезна? Поделитесь с друзьями!

Список литературы

[1] Гоноровский И.С. Радиотехнические цепи и сигналы Москва, Советское радио, 1977, 608 c.

[2] Баскаков, С.И. Радиотехнические цепи и сигналы Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4

[3] Bracewell, R. The Fourier Transform and Its Applications McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6

© Бахурин Сергей 2015 — 2020. Все права защищены. Любое копирование материалов сайте без разрешения автора запрещено.