Нч фильтр: Что такое фильтр нижних частот? Руководство по основам пассивных RC фильтров — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Нч фильтр в категории «Техника и электроника»

Пассивный регулятор низких частот НЧ фильтр кроссовер эквалайзер для авто сабвуфера

На складе в г. Одесса

Доставка по Украине

296 грн

Купить

Регулятор низких частот пассивный, фильтр НЧ для сабвуфера автомобильного, кроссовер эквалайзер, металлический

На складе в г. Одесса

Доставка по Украине

380 грн

Купить

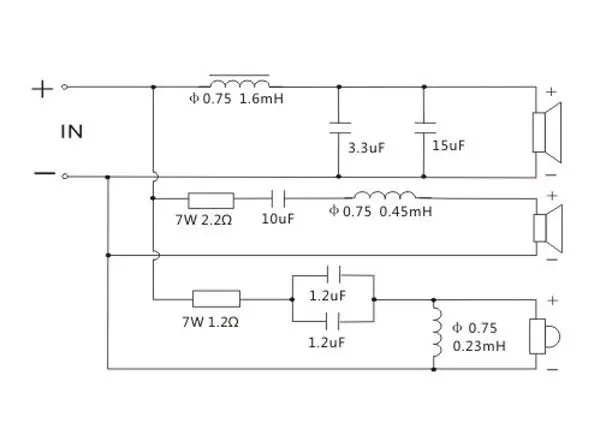
Пассивный 2-Х полосный кроссовер фильтр НЧ и ВЧ звука 4-8 Ом 60Вт

На складе в г. Кропивницкий

Доставка по Украине

по 100 грн

от 2 продавцов

100 грн

Купить

Пассивный 3-Х полосный кроссовер фильтр НЧ, СЧ и ВЧ звука 4-8 Ом 150Вт

На складе в г. Кропивницкий

Доставка по Украине

по 220 грн

от 2 продавцов

220 грн

Купить

Пассивный 3-Х полосный кроссовер фильтр НЧ, СЧ и ВЧ звука 4-8 Ом 120Вт

На складе

Доставка по Украине

по 220 грн

от 2 продавцов

220 грн

Купить

Активный 3-х полосный фильтр (НЧ,СЧ,ВЧ) на TL074 (TL084), +/-5. ..15В.

На складе в г. Софиевская Борщаговка

Доставка по Украине

82 грн

Купить

Фильтр НЧ для сабвуфера NE5532. DC 9-32В

На складе в г. Тернополь

Доставка по Украине

300 грн

Купить

Фильтр НЧ для сабвуфера NE5532 DC 9-15В плата

Доставка из г. Полтава

по 338.1 грн

от 2 продавцов

338.10 грн

Купить

Фильтр НЧ для сабвуфера NE5532 DC 9-15В плата

Доставка из г. Полтава

338.10 грн

Купить

Фильтр НЧ для сабвуфера NE5532. Двухполярное 9-15В

На складе в г. Тернополь

Доставка по Украине

225 грн

Купить

Фильтр НЧ для сабвуфера NE5532 DC 9-15В плата

Доставка из г. Полтава

338.10 грн

Купить

Плата сабвуфера Аудио усилитель 100W на базе TPA3116D2, фильтр НЧ, D класс

Доставка из г. Черновцы

1 139.33 грн

Купить

Активный фильтр низких частот PM40 (CROSSOVER) Акция! Цена снижена

Доставка по Украине

1 890 грн

Купить

КИТ, набор фильтр активный 3-х полосный на TL074, +12. ..30В, K248.

На складе в г. Софиевская Борщаговка

Доставка по Украине

115 грн/комплект

Купить

Плата активный 3-х пол. фильтр (НЧ,СЧ,ВЧ) на TL084

На складе в г. Софиевская Борщаговка

Доставка по Украине

29 грн

Купить

Смотрите также

Фильтр НЧ для сабвуфера NE5532 2.1-канальный. DC 10-24В

На складе в г. Тернополь

Доставка по Украине

345 грн

Купить

Фильтр НЧ для сабвуфера NE5532. DC 10-24В

На складе в г. Тернополь

Доставка по Украине

225 грн

Купить

Низкочастотный фильтр для сабвуфера с регулировкой частоты среза, уровня громкости, предусилитель темброблок

Доставка из г. Киев

260 грн

Купить

Фильтр частот 2-х полосый — Нч и Вч F2

Недоступен

548 грн

Смотреть

Темброблок + фильтр НЧ для усилителя 2.1 на NE5532

Недоступен

1 053 грн

Смотреть

Аудио усилитель TPA3116D2, 100Вт сабвуфер, фильтр НЧ, D класс

Недоступен

420 грн

Смотреть

Темброблок + фильтр НЧ для усилителя 2. 1 на NE5532

Недоступен

1 053 грн

Смотреть

Фильтр НЧ для сабвуфера NE5532. DC 10-24В

Недоступен

225 грн

Смотреть

Темброблок + фильтр НЧ для усилителя 2.1 на NE5532

Недоступен

1 053 грн

Смотреть

Фильтр НЧ для сабвуфера NE5532 2.1-канальный. DC 10-24В

Недоступен

345 грн

Смотреть

Кросовер 200 вт двух полосний фильтр НЧ ВЧ разделительный 3000Hz

Недоступен

585 грн

Смотреть

Фильтр частот 2-х полосый — Нч и Вч F15-2

Недоступен

530 грн

Смотреть

Аудио усилитель для сабвуфера 100w, TPA3116D2, фильтр НЧ, D класс

Недоступен

340 грн

Смотреть

Активный НЧ фильтр для сабвуфера, регулировка частоты среза, уровня громкости, предусилитель кроссовер NE5532

Недоступен

330 грн

Смотреть

1. Расчет и исследование нч-фильтров.

ФНЧ1

коэффициенты фильтра рассчитываются по формулам :

Таким образом, коэффициент a_k (k=0,. ..,N) зависит от отношения частоты среза к частоте дискретизации. Поэтому при расчетах удобно использовать относительную частоту среза:

; .

Рассчитаем коэффициенты фильтра в соответствии с вариантом задания:

, ;

, .

уравнение фильтра:

аналитическое выражение частотной характеристики фильтра :

С помощью программы Matlab вычислить коэффициенты нерекурсивного фильтра нижних частот. Сопоставить (в табличной форме) расчетные и вычисленные с помощью программы Matlab коэффициенты фильтра, построить графики импульсного отклика, АЧХ и ФЧХ фильтра.

Рисунок 1 – расчет коэффициентов фильтра с помощью Matlab

Рисунок 2 – амплитудно- и фазово-частотная характеристики фильтра

Рисунок 3 – импульсная характеристика фильтра

Рисунок 4 – структурная схема фильтра

Приведем в таблице коэффициенты фильтра расчетные и вычисленные в Matlab.

Таблица 1 — Коэффициенты фильтра

Коэффициенты фильтра	Расчётные	Вычисленные
а₀	0.166	0.166
а₁	0.159	0.159
а₂	0.137	0.137
а₃	0.106	0.106
а₄	0. 069	0.068
а₅	0.032	0.0318
а₆	0.00019	0

ФНЧ2:

коэффициенты фильтра :

а₀=0,24, а₁=0,224, а₂=0,158, а₃=0,075, а₄=0, а₅=-0,045, а₆=-0,052

уравнение фильтра:

Аналитическое выражение частотной характеристики фильтра :

Рисунок 5 – расчет коэффициентов фильтра с помощью Matlab

Рисунок 6 – амплитудно- и фазово-частотная характеристики фильтра

Рисунок 7 – импульсная характеристика фильтра

Рисунок 8 – структурная схема фильтра

Приведем в таблице коэффициенты фильтра расчетные и вычисленные в Matlab.

Таблица 2 — Коэффициенты фильтра

Коэффициенты фильтра	Расчётные	Вычисленные в Matlab
а₀	0,24	0,24
а₁	0,224	0,224
а₂	0,158	0,158
а₃	0,075	0,075
а₄	0	0
а₅	-0,043	-0,043
а₆	-0,052	-0,052

По результатам расчета ФНЧ₁ и ФНЧ₂рассчитать (без компьютера) коэффициенты полосового фильтра с частотами среза f _c1 и f_c2 (f _c1 < f_c2).

За основу берется ФНЧ с частотой среза _в, которая соответствует верхней частоте среза искомого ПФ. Из спектра этого ФНЧ вычитается спектр другого ФНЧ с меньшей (нижней) частотой среза 

н. В результате останется спектр полосового фильтра с зоной прозрачности (пропускания) между _н и _в. Искомые коэффициенты ПФ рассчитываются по формуле:

а_к,ПФ = а_{к,ФНЧ(в)} — а_{к,ФНЧ(н)}

С помощью программы Matlab произвести расчет коэффициентов этого же полосового цифрового фильтра и построить графики его импульсной и частотной характеристик. Сопоставить (в табличной форме) расчетные и вычисленные с помощью программы Matlab коэффициенты полосового фильтра

Рисунок 9 – расчет коэффициентов фильтра с помощью Matlab

Рисунок 10 – амплитудно- и фазово-частотная характеристики фильтра

Рисунок 11 – импульсная характеристика фильтра

Рисунок 12 – структурная схема фильтра

Приведем в таблице коэффициенты фильтра расчетные и вычисленные в Matlab.

Таблица 3 — Коэффициенты фильтра

Коэффициенты фильтра	расчётные	Вычисленные в Matlab
а₀	0,82	0,82
а₁	0,066	0,066
а₂	0,02	0,02
а₃	-0,03	-0,03
а₄	-0,068	-0,068
а₅	-0,075	-0,075
а₆	-0,053	-0,053

Синтезировать входной сигнал в виде аддитивной смеси гармонического сигнала с шумом.

Частота гармонического сигнала , амплитуда A=1, длительность . Шум – с нормальным распределением, нулевым средним значением и единичным стандартным отклонением. Произвести фильтрацию смеси сигнала с шумом, рассчитанным полосовым фильтром. Построить графики фильтруемой смеси и результата фильтрации.

Рисунок 13 – Simulink-модель фильтрации смеси сигнала с шумом

Рисунок 14 – отфильтрованный сигнал

Сгенерировать и профильтровать (рассчитанным полосовым фильтром) сигнал в виде последовательности знакоположительных прямоугольных импульсов амплитудой A=1, длительностью , следующих с частотой . Относительная длительность импульсов . Построить графики фильтруемой смеси и результата фильтрации.

Рисунок 15 – Simulink-модель фильтрации сигнала с шумом

Рисунок 16 – отфильтрованный сигнал

Ответы на контрольные вопросы

Нерекурсивный цифровой фильтра — это фильтр, который не имеет обратной связи.
Отличительной особенностью НЦФ является зависимость выходного сигнала y(n) только от входных сигналов в настоящий момент времени x(n) и предыдущие моменты x(n-k).
Его характеризует число задержек.
Тем, что выходной сигнал в момент времени n можно вычислить только тогда, когда станут известными “будущие” входные отсчеты. Это означает необходимость задержки выходного сигнала фильтра относительно входного.
Последовательность отсчетов, соответствующих весовым коэффициентам фильтра a_k , конечна, поэтому НЦФ имеет конечный импульсный отклик и называется фильтром с конечной импульсной характеристикой (КИХ-фильтром или FIR (finite impulse response filtre) фильтром).
Относительная частота среза — это отношение верхней частоты (частоты среза) спектра аналогового сигнала к частота дискретизации сигнала, выраженное в радианах.

7.Всечастотный фильтр (ВФ) – это фильтр, который пропускает без ослабления все частоты.

Вывод

В результате проведения работы были синтезированы и рассчитаны рекурсивные и нерекурсивные фильтры низких частот. В результате работы, рассчитанные вручную коэффициенты совпадают с полученными с помощью компьютера. Дискретное преобразование Фурье, используемое во всех непараметрических методах спектрального оценивания, подразумевает периодическое продолжение анализируемого фрагмента сигнала. При этом на стыках фрагментов могут возникать скачки, приводящие к появлению боковых лепестков значительного уровня в спектральной области. Для ослабления этого эффекта сигнал перед выполнением ДПФ умножают на спадающую от центра к краям весовую функцию (окно). В результате величина скачков на стыках сегментов уменьшается, меньше становится и уровень нежелательных боковых лепестков спектра — платой за это является некоторое расширение спектральных пиков. Помимо спектрального анализа весовые функции применяются при синтезе нерекурсивных фильтров путем обратного преобразования Фурье желаемой частотной характеристики. В этом случае они позволяют увеличить подавление сигнала в полосе задерживания фильтра за счет некоторого расширения полосы пропускания.

Фильтр нижних частот — MATLAB & Simulink

Фильтр нижних частот — это фильтр, который пропускает сигналы ниже частоты среза (известной как полоса пропускания) и ослабляет сигналы выше частоты среза (известной как полоса задерживания).

Фильтры нижних частот, особенно фильтры скользящего среднего или фильтры Савицкого-Голея, часто используются для очистки сигналов, удаления шума, создания эффекта сглаживания, выполнения усреднения данных и разработки дециматоров и интерполяторов. Фильтры нижних частот производят медленные изменения выходных значений, чтобы было легче увидеть тенденции и повысить общее отношение сигнал/шум с минимальным ухудшением сигнала.

Сглаживание сигналов с использованием фильтра Савицкого-Голея и фильтра скользящего среднего.

Вы можете использовать MATLAB ^® для проектирования фильтров на основе конечной импульсной характеристики (FIR) и на основе бесконечной импульсной характеристики (IIR), двух распространенных методов фильтрации нижних частот.

КИХ-фильтры очень привлекательны, поскольку они по своей природе стабильны. Они могут иметь линейную фазу, которая вносит задержку в отфильтрованный сигнал при сохранении формы сигнала. Тем не менее, эти фильтры могут иметь длительные переходные характеристики и могут оказаться дорогостоящими в вычислительном отношении в некоторых приложениях. КИХ-фильтры полезны в аудио, биомедицинских, радиолокационных и других приложениях, где форма сигнала предоставляет полезную информацию. Общие методы проектирования низкочастотных КИХ-фильтров включают окно Кайзера, метод наименьших квадратов и аппаратную рябь.

Технические характеристики проекта и отклик низкочастотного КИХ-фильтра Кайзера в MATLAB.

БИХ-фильтры полезны, когда вычислительные ресурсы ограничены. Однако стабильные причинно-следственные БИХ-фильтры не имеют идеально линейной фазы. БИХ-фильтры обычно используются для выравнивания звука, обработки сигналов биомедицинских датчиков, интеллектуальных датчиков IoT/IIoT и высокоскоростных телекоммуникационных/радиочастотных приложений. Методы проектирования фильтров на основе БИХ включают фильтры Баттерворта, Чебышева (тип I и тип II) и эллиптические.

Технические характеристики конструкции и характеристика фильтра нижних частот Чебышева типа I IIR в MATLAB.

Функция lowpass в Signal Processing Toolbox™ особенно полезна для быстрой фильтрации сигналов. Вы можете использовать designfilt и другие функции, зависящие от алгоритма ( oil, fir1 ), когда требуется больший контроль над такими параметрами, как тип фильтра, порядок фильтра и затухание. Для получения дополнительной информации о дизайне фильтра смотрите Signal Processing Toolbox™.

`Примеры и инструкции`

Практическое введение в проектирование цифровых фильтров - Пример
Практическое введение в цифровую фильтрацию - Пример
Сглаживание сигнала - Пример
Галерея дизайна фильтров - Пример

`Справочник по программному обеспечению`

Реализация фильтра и анализ - Документация
Конструкция КИХ-фильтра - Концепция
Дизайн БИХ-фильтра - Концепция
Начало работы с Signal Processing Toolbox - Документация
Фильтрация Савицкого-Голея - Документация
Медианная фильтрация - Документация

См. также: графические процессоры для алгоритмов обработки сигналов в MATLAB, Системный инструментарий DSP, фильтр верхних частот, конструкция фильтра, квантование

`Фильтры нижних и верхних частот`

 Фильтры нижних и верхних частот 
  Next:  Полосовые и задерживающие фильтры  Up:  Таксономия фильтров  Предыдущий:  Таксономия фильтров  Содержимое   Индекс  На сегодняшний день наиболее частой целью использования фильтра является извлечение либо
низкочастотная или высокочастотная часть звукового сигнала, ослабляющая
остальные. Это достигается с помощью  низкочастотный  или  высокочастотный  фильтр.
  Рисунок 8.2:  Терминология для описания АЧХ низкочастотных и
фильтры верхних частот. По горизонтальной оси отложена частота, по вертикали
ось усиление. Показан фильтр нижних частот; фильтр верхних частот имеет то же самое
функции переключались справа налево.
 В идеале фильтр нижних или верхних частот должен иметь частотную характеристику
1 до (или до) указанной частоты среза и ноль после нее; но
такие фильтры не могут быть реализованы на практике. Вместо этого мы пытаемся найти
возможные приближения к этому идеальному отклику. Чем больше дизайнерских усилий
и время вычислений, которое мы вкладываем в это, тем ближе мы можем добраться.
 На рис. 8.2 показана частотная характеристика фильтра нижних частот.
фильтр. Спектр частот разделен на три полосы, обозначенные на
Горизонтальная ось.  полоса пропускания  это область (полоса частот), через которую фильтр должен пропускать входной сигнал.
на его выходе с единичным коэффициентом усиления.
Для фильтра нижних частот (как показано) полоса пропускания достигает частоты
ноль до определенного предела частоты. Для фильтра верхних частот полоса пропускания
появится в правой части графика и будет простираться от
ограничение частоты до максимально возможной частоты. Любой
полоса пропускания реализуемого фильтра будет лишь приблизительно плоской;
отклонение от плоскостности называется  пульсация  ,
и часто определяется путем предоставления отношения между самым высоким и самым низким усилением
в полосе пропускания, выраженное в децибелах. Идеальный фильтр нижних или верхних частот
будет иметь пульсацию 0 дБ.
  полоса задерживания  фильтра нижних или верхних частот – это область спектра (частота
диапазон), в котором фильтр не предназначен для передачи входных данных.  затухание в полосе задержания  это разница в децибелах между самым низким коэффициентом усиления в полосе пропускания
и максимальное усиление в полосе задерживания. В идеале это было бы
быть бесконечным; чем выше, тем лучше.
 Наконец, реализуемый фильтр, частотная характеристика которого всегда
непрерывная функция частоты, всегда нуждается в области или частоте
полоса, в которой усиление падает от усиления в полосе пропускания до полосы задерживания
прирост; это называется  переходная полоса  .