Как вычислить скалярное произведение в R » finnstats
Скалярное произведение, иногда называемое скалярным произведением, представляет собой алгебраическую операцию, которая возвращает одно целое число из двух чисел одинаковой длины.
Допустим, у нас есть два вектора x и y, и нам нужно получить их скалярное произведение.
Учитывая, что
x = [x1, x2, x3] Когда вектор y = [y1, y2, y3], скалярное произведение векторов x и y, сокращенно x.y, вычисляется следующим образом:
x · у = х1 * у1 + х2 * у2 + х3 * у3
Например, если x = [12, 15, 16] и y = [14, 13, 12], то скалярное произведение x и y будет равно:
x. y = 12*14 + 15*13 + 16*12
x·y = 168 + 195 + 192
x ·y = 555
Сумма произведений соответствующих элементов в двух векторах есть скалярное произведение/ скалярное произведение.
Как в R вычислить скалярное произведение?
В R есть два простых метода вычисления скалярного произведения двух векторов.
Способ 1: Используйте %*%
В следующем коде показано, как создать скалярное произведение между двумя векторами в R, используя функцию процентов * процентов:
Давайте создадим два вектора
a <- c(12, 15, 16) b <- c(14, 13, 12)
Теперь мы вычисляем скалярное произведение между приведенными выше векторами
a %*% b
[1] [1,] 555
Результат скалярного произведения — 555.
Эта функция также применима к столбцам фрейма данных:
Приведенные выше данные мы можем присвоить «данным» в качестве фрейма данных.
data<- data.frame(a=c(12, 15, 16), b=c(14, 13, 12))
Для вычисления скалярного произведения между столбцами 'a' и 'b' данных кадра, мы можем использовать ту же функцию процентов * процентов.
данные$a %*% данные$b
[1] [1,] 555
Подход 2: использование функции dot()
Метод dot() из библиотеки pracma также можно использовать для вычисления скалярного произведения между двумя векторами.
библиотека (пракма)
Мы можем использовать те же векторы, что и в подходе2.
а <- с(12, 15, 16) b <- c(14, 13, 12)
Теперь мы можем вычислить скалярное произведение между векторами на основе точечной функции.
точка(a, b)
[1] 555
Скалярное произведение двух векторов снова равно 555.
Подход 3: Использование функции dot()
R обеспечивает очень эффективный способ вычисления скалярного произведения двух векторов. Этого можно добиться, используя метод dot() из библиотеки геометрии.
Синтаксис: точка(x, y, d = NULL)
Параметры:
x: Матрица векторов
y: Матрица векторов
d: Размерность, по которой вычисляется скалярное произведение ) [1] 555
Ответ такой же, как в подходах 1 и 2.
Подход 4: Используйте функцию sum()
a <- c(12, 15, 16) b <- c(14, 13, 12)
сумма(a*b) [1] 555
Да, простой и мощный метод.
Подход 5: Использование собственной функции
Давайте создадим функцию и рассчитаем скалярное произведение.
mydot <- function(x, y){ # x и y могут быть векторами или матрицами
result <- t(x)%*%y # %*% — оператор умножения матриц
print(result) # t(x) обозначает транспонирование x
} mydot(a,b)
[1] [1,] 555
Во всех подходах ответ один.
Биномиальное распределение в R-Quick Guide »
Подпишитесь на нашу рассылку!
[newsletter_form type="minimal"]
1.4.1 Карточки со скалярным произведением Ирины Солошенко
Скалярное произведение
- Скалярное произведение двух векторов определяется как .
- Скалярное произведение и равно AB, если векторы имеют одинаковое направление, нулю, если векторы перпендикулярны, и -AB, если векторы направлены в противоположные стороны.
- Скалярный продукт подчиняется дистрибутивному свойству: .
- В компонентной форме скалярное произведение двух векторов равно
примечание 1
- До сих пор мы обсуждали, как масштабировать, складывать и вычитать векторы.
 А умножение?
А умножение? - Это определение скалярного произведения или скалярного произведения. Эту формулу можно рассматривать как определение умножения между двумя векторами и .
- Вам может быть интересно: почему в формуле есть множитель cos θ?
- Вот ситуация, которая объясняет определение. Предположим, что такой объект, как игуанодон, может свободно двигаться в горизонтальном направлении. Когда на него действует сила, он движется, что приводит к некоторому смещению. Произведение вектора толчка (технически называемого вектором силы) и вектора смещения связано с тем, какая работа выполняется, толкая объект.
- Но если сила не направлена в том же направлении, что и смещение, часть силы теряется — поскольку объект может свободно перемещаться только горизонтально, только составляющая силы, параллельная смещению, действительно что-то делает. Эта компонента имеет величину q. Тогда имеет смысл, что произведение должно равняться q. - Эти три примера иллюстрируют, как скалярное произведение двух векторов может быть положительным, нулевым или отрицательным.

- В общем случае, если два вектора указывают примерно в одном направлении (угол между ними меньше 90°), их скалярное произведение положительно. Если они перпендикулярны, скалярное произведение равно нулю. Если они указывают примерно в противоположных направлениях (угол между ними больше 90°), скалярное произведение отрицательно.
примечание 2
- Что, если два рассматриваемых вектора находятся в компонентной форме?
- Свойство распределения можно использовать для получения формулы скалярного произведения двух векторов в компонентной форме. Начните с того, что запишите произведение и умножьте его, чтобы получить четыре члена. Тогда используйте тот факт, что и для упрощения.
- Полученная формула проста и легко запоминается.
- Этот пример демонстрирует одно из многих применений скалярного произведения. Предположим, вам даны два вектора в компонентной форме. Как найти угол между ними?
- Чтобы решить эту задачу, объедините две формулы скалярного произведения.
 Результатом является формула для желаемого угла с точки зрения компонентов и величин двух векторов.
Результатом является формула для желаемого угла с точки зрения компонентов и величин двух векторов.
Какое утверждение о векторе А неверно
Значение Ay отрицательное.
Какая часть выражения соответствует проекции вектора B в направлении вектора A
B cos θ
Угол между двумя векторами равен 175,0°. Чему равно скалярное произведение этих двух векторов, если их величины равны 4000 см и 3000 см?
−11,95
Какое из следующих утверждений о скалярном произведении двух векторов неверно? Предположим, что одна линия сетки является одной единицей.
Скалярное произведение двух векторов является положительным значением.
Какой из следующих вариантов ответа, относящихся к скалярному произведению двух векторов, неверен?
Все значения Ax, Bx, Ay и By больше 0.
Какое из следующих утверждений о скалярном произведении двух векторов неверно?
Значение A до двух значащих цифр равно 7,2. Значение B до двух значащих цифр равно 3,5.


 А умножение?
А умножение?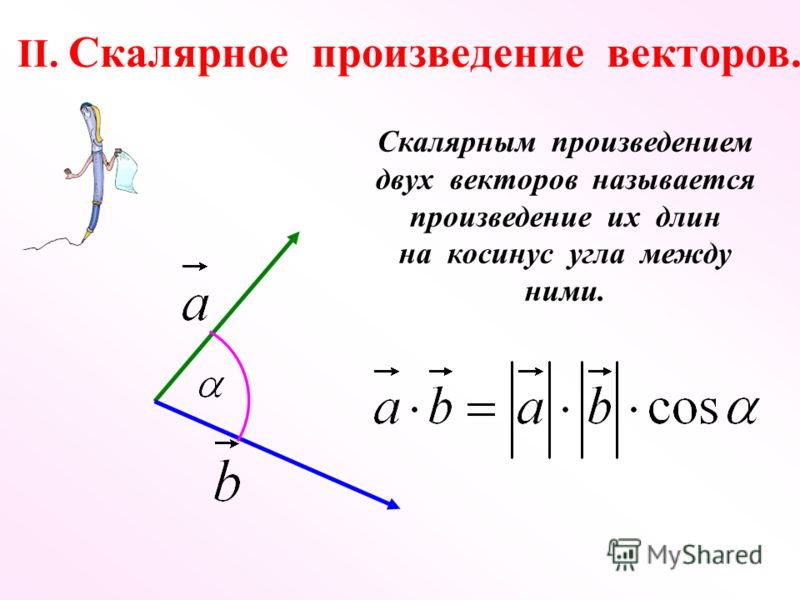
 Результатом является формула для желаемого угла с точки зрения компонентов и величин двух векторов.
Результатом является формула для желаемого угла с точки зрения компонентов и величин двух векторов.