Синонимы и антонимы «напряжение» — анализ и ассоциации к слову напряжение. Морфологический разбор и склонение слов

• Перевод
• Ассоциации
• Анаграммы
• Антонимы
• Синонимы
• Гиперонимы
• Морфологический разбор
• Склонения
• Спряжения

Перевод слова напряжение

Мы предлагаем Вам перевод слова напряжение на английский, немецкий и французский языки.
Реализовано с помощью сервиса «Яндекс.Словарь»

• На английский
• На немецкий
• На французский

• voltage — вольтаж
  • выходное напряжение — output voltage
• tension — напряженность, стресс, нагрузка
  • нервное напряжение — nervous tension
  • остаточное напряжение — residual stress
  • напряжение глаз — eye strain
• pressure — давление
  • эмоциональное напряжение — emotional pressure
• exertion — усилие
  • стенокардия напряжения — angina of exertion
• suspense — неизвестность
  • держать в напряжении — keep in suspense
• tense — время
• pull — натяжение, растяжка
• straining
• potential — потенциал
• intension — намерение
• struggle — борьба
• rush — прилив

• Spannung — напряженность, нагрузка
  • электрическое напряжение — elektrische Spannung
• Stress — нагрузка
  • большое напряжение — Menge Stress
  • снижение напряжения — Verringerung der Belastung
• Streß — нагрузка
• Anstrengung — нагрузка
  • умственное напряжение — geistige Anstrengung
• Intensität — напряженность
• Mühe — усилие
• Bemühung — усилие

• tension — давление, вольтаж, напряженность, ток
  • стабилизатор напряжения — stabilisateur de tension
  • высокое напряжение — haut voltage
  • эмоциональное напряжение — stress émotionnel
  • остаточные напряжения — contraintes résiduelles
  • внутреннее напряжение — effort intérieur
• charge — нагрузка
• potentiel — сила
• érection — установка
• contraction — сжатие
• défense — защита
• distension — растяжение
• RAT
• contention

Связь с другими словами

Слова заканчивающиеся на -напряжение:

• бионапряжение
• перенапряжение

Какой бывает напряжение (прилагательные)?

Подбор прилагательных к слову на основе русского языка.

внутреннейполноймышечнойсильнойвыдержавшейвысокойтребующеймеханическойвозникающейопаснойфизическойприливнойдополнительнойогромнойподающейбольшейснимающейхроническойэкологическоймалейшейвнешнейнервнойтермическойэмоциональноймускульнойостаточнойколоссальнойвозможнойненужнойзначительнойзаметнойлюбойпсихологическойисполненнойгравитационнойскрывающейвзрослойновойлокальнойкрайнейместнойнеучтеннойизбыточнойэкономическойгигантскойразличнойнаибольшейподспуднойнестоящейнеобходимойоблегчающейвызывающейсейсмическойгеологическойотрицательнойдесятикратнойтоническойстраннойумственнойтончайшейэлектрическойлишеннойсоциальнойправильной

Что может напряжение? Что можно сделать с напряжением (глаголы)?

Подбор глаголов к слову на основе русского языка.

находитьсяждатьболетьсмотретьследитьзаболетьразболетьсявсматриватьсякружитьсяпроизнестиожидатьоказатьсяисчезнутьсказатьзамеретьлопнутьдрожатьспроситьотпуститьловитьразрядитьвзмокнутьсжатьпребыватьстоитьвглядыватьсявыдаватьпробежатьвслушиватьсясуметьзакружитьсяраскалыватьсяпоявитьсясестьпорождатьвыступитьулыбнутьсястоятьвыпрямитьсяуйтиповернутьдержатьнаблюдатьснятьприложитьначинатьпокинутьдостичьвыговоритьсидетьвыдавитьдобавлятьсяслушатьприслушиватьсясправлятьсясжиматьприжиматьсяпровестипропускатьчувствоватьсядуматьусилитьсясдерживатьобвести

Ассоциации к слову напряжение

голоспахкомнаталицовоздухсетьзалглазмышцателоотношениелобгрудьплечоожиданиерукачреслработаспинастолобществошеяпомощьголоваобластьдействительностьгорлоконецтолпаборттечениедоматмосфераживотбойуголокногамостикразговорстранавыходмускулгенераторприсутствиекабинетэлектросетьпределгородлиниялагерпозапопыткамозгдушсемьяподъеммужчинагруппагостинаякорпустысячасторонасознаниеконструкция

Синонимы слова напряжение

домогательствозаботанатугапопыткапреследованиестараниестремлениетрудолюбиеусердиеусилиенадсада

Гипонимы слова напряжение

1. эрекция

Сфера употребления слова напряжение

ТехникаСтроительствоЭлектротехникаЭлектроникаНефть и газ

Морфологический разбор (часть речи) слова напряжение

Часть речи:

существительное

Род:

женский

Число:

единственное

Одушевленность:

неодушевленное

Падеж:

именительный

Склонение существительного напряжение

Падеж	Вопрос	Ед. число	Мн. число
Именительный	(кто, что?)	напряжение	напряжения
Родительный	(кого, чего?)	напряжения	напряжений
Дательный	(кому, чему?)	напряжению	напряжениям
Винительный	(кого, что?)	напряжение	напряжения
Творительный	(кем, чем?)	напряжением	напряжениями
Предложный	(о ком, о чём?)	напряжении	напряжениях

Предложения со словом напряжение

Пожалуйста, помогите нашему роботу осознать ошибки. Их пока много, но с вашей помощью их станет гораздо меньше. Вот несколько предложений, которые он сделал.

1. Выдержавшая напряжение внезапно поддалась под дипломатическим нажимом

0

0

2. Ненужная напряжение мало прожила без благородного отца

0

0

3. Исполненная напряжение точно ожидала от полного мужчины

0

0

4. Облегчающая напряжение неожиданно застыла в собственном седле

1

0

Определения слов

wordmap

Даже самые эрудированные люди могут попасть в ситуацию, когда они никак не могут вспомнить или подобрать нужное слово. Оно может долго крутится хаотично в голове, не давая им покоя. Такое может случиться с каждым. На сайте WordMap можно воспользоваться удобной функцией подбор слов по маске, работа с которой построена очень просто, или просто подобрать существительно или прилагательное, с которым слово чаще всего употребляется (например: какой бывает музыка).

Вспомнить все

Имея под рукой компьютер и интернет сегодня можно найти абсолютно любую информацию.

При работе с текстовыми документами функция определение слов, имеющаяся на сайте WordMap, поможет найти подходящие слова для описания какого-либо объекта или события. Достаточно просто ввести его в соответствующее поле и нажать кнопку «Поиск». После этого остается только выбрать самое подходящее слово из предоставленного списка.

Как работать с маской

Любите тренировать мозговую активность, разгадывая кроссворды, но никак не можете справиться с некоторыми словами? Тогда используйте функцию маски. Можно задать подбор слов по буквам. В поисковую строку вводим все известные буквы. За место неизвестных ставим «*». Например, И***дром (по маске всего 8 букв). Неизвестна 2,3 и 4. После поиска на сайте видим ответ: ипподром.

Неизвестные буквы могут находиться в любом месте слова. Вариантов может быть несколько. Например, набираем: ма**ер. Нажимаем «Поиск». Получаем следующие варианты: маклер, маркер, мастер, маузер. Из полученного списка уже можно выбрать подходящий по смыслу вариант для своего текста.

Читать сухой текст не всегда приятно. Особенно это касается информационных и развлекательных материалов, где нужно красиво и живо подать текст. Используя возможности сайта, можно осуществить подбор прилагательных для слова. Они помогут описать все события красочно и ярко.

Удобство онлайн поиска

Искать на просторах сети нужные слова — дело довольно долгое и не всегда удачное. Поэтому для удобства пользователей существуют специальные сервисы. WordMap — один из них. Сайт устроен понятно для любого человека. Для начала работы на нем регистрация не требуется.

Преимущества сайта

• В обеспечении функционала задействованы новейшие разработки. Искусственный интеллект работает с большой базой русского языка. Она собрана и сгруппирована языковедами за многие годы. Поэтому функции «слово по маске», «синонимы», «подбор существительных для слова» и другие работают, опираясь на нее.
• Поисковая строка расположена в удобном месте страницы сайта.
  Есть подсказки, которые помогают пользователю работать со словами.
• За время использования сервиса можно расширить свой кругозор и улучшить грамотность.

Подбирая любые слова и определения к ним, легко сделать текст насыщенным и интересным. Используйте сервис не только для работы, но и для познавательной игровой активности.

Только что искали:

дом 1 секунда назад

бардаченко 1 секунда назад

алтасина 4 секунды назад

уключины 5 секунд назад

пившикон 5 секунд назад

дома христиан 5 секунд назад

представляемая 6 секунд назад

прижимай 6 секунд назад

мрочек-дроздовский петр николаевич 6 секунд назад

норманн 7 секунд назад

шврейцака 7 секунд назад

бумажник 10 секунд назад

терновский александр сергеевич 10 секунд назад

мартышка 11 секунд назад

построенные города 15 секунд назад

Ваша оценка

Закрыть

Спасибо за вашу оценку!

Закрыть

Последние игры в словабалдучепуху

Имя	Слово	Угадано	Время	Откуда
Игрок 1	контрабанда	20 слов	1 час назад	176. 115.129.97
Игрок 2	серебрильщик	6 слов	1 час назад	176.115.129.97
Игрок 3	привет	0 слов	2 часа назад	46.98.111.8
Игрок 4	слова	0 слов	11 часов назад	81.88.144.196
Игрок 5	непрошибаемость	202 слова	11 часов назад	95.24.168.205
Игрок 6	монтировщица	41 слово	19 часов назад	95.68.114.220
Игрок 7	желторотость	44 слова	19 часов назад	95.68.114.220
Играть в Слова!

Имя	Слово	Счет	Откуда
Игрок 1	татор	57:56	9 часов назад	82. 215.98.67
Игрок 2	слово	54:53	9 часов назад	82.215.98.67
Игрок 3	тулуз	47:45	9 часов назад	85.93.58.63
Игрок 4	коник	47:53	10 часов назад	85.93.58.63
Игрок 5	вечер	14:18	10 часов назад	176.59.115.237
Игрок 6	кристадин	60:57	10 часов назад	194.85.94.236
Игрок 7	календула	46:53	11 часов 13 секунд назад	88.200.230.5
Играть в Балду!

Имя	Игра	Вопросы	Откуда
Карина	На одного	10 вопросов	13 часов назад	83. 220.237.247
Анна	На одного	10 вопросов	18 часов назад	62.118.80.106
Анна	На одного	10 вопросов	18 часов назад	62.118.80.106
Ритка	На одного	20 вопросов	20 часов назад	176.116.165.103
Светлана	На одного	15 вопросов	1 день назад	176.59.109.211
Sliv	На одного	10 вопросов	2 дня назад	185.90.101.73
Зоро	На одного	10 вопросов	3 дня назад	109.167.132.152
Играть в Чепуху!

Напряжение: смысл, примеры, силы и физика

Напряжение — это не просто чувство, которое вы испытываете, когда собираетесь сдавать тест. Что касается физики, напряжение — это тип силы. Сила натяжения действует аналогично другим приложенным силам, например, если вы должны тянуть коробку по полу. Однако вместо того, чтобы тянуть коробку руками, вы будете тянуть коробку веревкой, шнуром, цепью или подобным предметом, чтобы это считалось натяжением. Поскольку напряжение похоже на приложенную силу, для него нет конкретного уравнения или формулы. Примером натяжения является ситуация, когда собака тянет поводок, пока вы берете ее на прогулку, — поводок тянет вас вперед с силой натяжения.

Определение напряжения

Напряжение убивает меня! Что такое напряжение? Натяжение — это тип контактной силы, возникающей при использовании веревки или шнура.

В физике мы определяем натяжение как силу, возникающую, когда веревка, шнур или подобный предмет натягивает объект. На противоположных сторонах веревки действуют две силы, создающие натяжение.

Натяжение представляет собой тянущую силу (потому что вы не можете толкать веревкой) и действует в направлении веревки. Мы считаем напряжение a контактная сила , так как веревка должна коснуться объекта, чтобы оказать на него силу.

Натяжение в физике

Следует отметить, что натянутая веревка прикладывает одинаковую силу к каждому прикрепленному объекту. Например, когда мы упомянули прогулку с собакой, мы описали, как собака, дергающая за поводок, приложит к вам силу натяжения. Если бы нас интересовали только силы, действующие на вас, это все, что нас интересовало бы. Но что, если бы мы также захотели узнать силы, действующие на собаку? Мы заметим, что, когда собака тянет поводок, есть сила, удерживающая — или тянущая — ее тоже. Сила натяжения, тянущая вас вперед, такая же (имеет ту же величину), что и сила натяжения, удерживающая его назад. Как показано ниже, мы можем нанести на поводок две стрелки, чтобы показать эти две силы.

Силы натяжения

Натяжение в результате межатомных электрических сил. Межатомные электрические силы являются причиной всех контактных сил. Для натяжения веревка состоит из множества атомов и молекул, связанных вместе. По мере того как веревка становится натянутой под действием силы, одна из связей между атомами растягивается все дальше друг от друга на микроскопическом уровне. Атомы хотят оставаться рядом в своем естественном состоянии, поэтому электрические силы, удерживающие их вместе, возрастают. Все эти крошечные силы складываются вместе, чтобы создать одну силу натяжения. Этот принцип делает стрелки на рис. 1 более понятными: если собака и человек тянут поводок наружу, силы, удерживающие поводок вместе, направлены на поводок.

Уравнение натяжения

Не существует специального уравнения для силы натяжения, как для сил трения и упругости. Вместо этого нам нужно использовать диаграмму свободного тела и Второй закон движения Ньютона для решения напряженности.

Нахождение натяжения с помощью диаграммы свободного тела и второго закона Ньютона

Диаграммы свободного тела помогают визуализировать силы, действующие на объект. Для ящика, тянущегося по полу веревкой, как показано на рисунке ниже,

Рис. 2 – Веревка, тянущая коробку

мы бы добавили стрелки для всех сил, действующих на коробку.

Рис. 3 — Здесь представлены все силы, действующие на коробку.

Эта цифра включает все силы, которые могут действовать в данной ситуации, включая трение \(F_\text{f} \), гравитацию \(F_g\), нормальное \(F_\text{N} \) и напряжение \(Т\).

Помните: всегда отводите стрелки силы натяжения от объекта. Напряжение — это сила притяжения, поэтому сила всегда будет направлена ​​наружу.

Второй закон движения Ньютона утверждает, что ускорение объекта зависит от силы, действующей на объект, и массы объекта

Следующее уравнение:

$$\sum \vec F =m\vec a \mathrm{,}$$

является результатом второго закона Ньютона.

Это уравнение применимо к каждому направлению, поэтому обычно мы хотим включить одно для направления \(y\) и одно для направления \(x\). В нашем примере на рисунках выше нет никакого напряжения, действующего в направлении \(y\), поэтому для определения напряжения мы можем сосредоточиться на направлении \(x\), где у нас есть сила трения, действующая влево и напряжение, действующее вправо. Выбирая право быть положительным, наше результирующее уравнение выглядит так:

$$-F_\text{f} + T =ma\mathrm{.}$$

Затем мы можем переставить для решения натяжения:

$$T=ma+F_\text{f} \mathrm{ .}$$

Если коробка находится на поверхности без трения, сила трения равна нулю, поэтому натяжение будет равно произведению массы коробки на ускорение коробки.

Примеры натяжения

В задачах по физике вы можете увидеть множество реальных сценариев, связанных с натяжением, таких как:

• Автомобили, буксирующие прицепы
• Перетягивание каната
• Шкивы и канаты
• Тренажерный зал

Это может показаться очень разными сценариями, но для решения каждого из них вы будете использовать один и тот же метод. Ниже приведены некоторые проблемы, с которыми вы можете столкнуться, и способы их решения.

Веревка между двумя объектами

Теперь давайте все перемешаем и сделаем пример с двумя объектами, соединенными веревкой.

Рис. 4 – Веревка между двумя объектами.

На приведенном выше рисунке показана веревка между двумя ящиками и одним тянущим ящиком 2 вправо. Как мы упоминали в случае с собачьим поводком, натяжение, действующее на коробку 1, такое же, как и на коробку 2, поскольку это та же самая веревка. Поэтому на рисунке мы обозначили их одинаково \(T_1 \).

В любой задаче мы можем выбрать, какой объект или группу объектов анализировать на диаграмме свободного тела. Допустим, мы хотели найти \(T_1\) и \(T_2\). Мы могли бы начать с просмотра поля 1, потому что это более простая сторона, и мы ищем только одно неизвестное. На следующем рисунке показана диаграмма свободного тела для ящика 1:

Рис. 5 — Диаграмма свободного тела ящика 1.

Поскольку натяжение действует только в направлении \(x\), мы можем пренебречь действующими силами в \(y\)-направлении. Выбрав положительное значение, уравнение второго закона Ньютона будет выглядеть так:

$$-F_{\text{f}1} +T_1 = m_1 a\mathrm{.}$$

Затем мы можем переставить переменные для решения \(T_1 \)

$$T_1 = m_1 a + F_{\text{f}1}\mathrm{;}$$

, чтобы найти \(T_2 \), мы могли посмотреть силы только на поле 2, показанном здесь:

Рис. 6 — Диаграмма свободного тела из поля 2.

Снова игнорируя \(y\)-направление, уравнение для \(x\)-направления выглядит следующим образом:

$$-T_1 — F_{\text{f}2} + T_2 = m_2 a\mathrm{.}$$

Поскольку мы знаем, что \(T_1 \) одинаково для каждого блока, мы можем взять \(T_1 \), который мы узнали из блока 1, и применить его к блоку 2 путем замены

$$-(m_1 a + F_{\text{f}1}) — F_{\text{f}2} +T_2 = m_2 a$$

и тогда мы можем найти \(T_2 \),

$$T_2 = (m_2 + m_1 )a ​​+ F_{\text{f}1} + F_{\text{f}2}\mathrm{.}$$

Однако, если нам не нужно известно \(T_1 \), мы всегда можем смотреть на оба ящика вместе, как если бы они были одним целым. Ниже мы можем увидеть, как выглядит диаграмма свободного тела, когда вы группируете два ящика:

Рис. 7 — Диаграмма свободного тела обоих ящиков вместе.

Если мы напишем уравнение второго закона Ньютона для направления \(x\), мы получим

$$-(F_{\text{f}1} + F_{\text{f}2})+T_2 = (m_1 +m_2 )a$$

и может переставить его, чтобы найти \(T_2 \ ),

$$T_2 = (m_1 + m_2 )a + F_{\text{f}1} + F_{\text{f}2}\mathrm{.}$$

Мы можем видеть, что это дает тот же результат, что и при рассмотрении квадратов по отдельности, а затем составлении уравнений вместе. Любой метод работает для поиска \(T_2 \) (вы можете решить, какой из них проще, и использовать любой из них), но иногда переменную, которую вам нужно найти, можно найти, только сосредоточившись на одном конкретном объекте.

Тяга под углом

Теперь давайте сделаем пример со всеми любимыми: углы.

Рис. 8 — Натяжение каната под углом.

На рисунке выше веревка тянется за ящик под углом, а не вдоль горизонтальной поверхности. В результате коробка скользит по поверхности горизонтально. Чтобы найти натяжение, мы использовали бы суперпозицию сил , чтобы разделить угловую силу на часть силы, действующую в направлении \(х\), и часть силы, действующую в направлении \(у\). )-направление.

Рис. 9 — Диаграмма свободного тела с разделением натяжения на компоненты \(x\) и \(y\).

Это показано красным на рисунке выше на диаграмме свободного тела. Тогда мы можем написать отдельное уравнение для направления \(x\) и направления \(y\) в соответствии с диаграммой свободного тела.

\(T_x = T\cos{\theta}\) и \(T_y = T\sin{\theta}\).

В этом примере теперь у нас есть некоторое напряжение, действующее в направлении \(y\), поэтому мы не хотим игнорировать гравитационную и нормальную силы, как мы делали в примерах выше. Так как коробка не ускоряется в направлении \(y\), сумма сил в направлении \(y\) равна нулю

$$F_\text{N} + T\sin{\theta} -F_g =0\mathrm{,}$$

и перестановка для нахождения \(T\) дает

$$T=\frac{ F_g — F_\text{N} }{\sin{\theta}}\\\mathrm{. }$$

Направление \(x\) похоже на то, что мы сделали выше, но только с \(x\) составляющая угловой силы натяжения:

$$-F_\text{f} + T\cos{\theta} = ma\mathrm{.}$$

Затем переставляем, чтобы найти \( T\):

$$T=\frac{ma+F_\text{f}}{\cos{\theta}}\\\mathrm{.}$$

Оба этих результата дадут вам одно и то же значение для \(T\), поэтому в зависимости от того, какую информацию вы получили, вы можете либо сосредоточиться только на \(x\)-направлении, только на \(y\)-направлении, либо на обоих.

Свободно висящий объект

Когда объект висит на веревке, как показано ниже,

Рис. 10 — Объект, висящий на веревке

, единственными силами, действующими на него, являются гравитационная сила, тянущая его вниз, и сила натяжения удерживая его.

Это показано на диаграмме свободного тела ниже.

Рис. 11. Схема свободного тела объекта, подвешенного на веревке

Полученное уравнение будет выглядеть следующим образом:

$$T-F_g =ma\mathrm{. }$$

Если мы перестроим, чтобы найти \(T\) и подставим \(mg\) вместо гравитационной силы, мы получим

$$T=ma +mg\mathrm{.}$$

Если объект не ускоряется , напряжение и гравитационная сила были бы равны и противоположны, поэтому \(T=mg\).

Натяжение за наклонную поверхность

Когда к ящику на наклонной поверхности прикладывается натяжение, мы используем ту же стратегию, что и при натяжении веревки под углом.

Рис. 12 – Натяжение объекта на склоне

Сначала начните с диаграммы свободного тела.

Рис. 13 — Схема натяжения свободного тела на наклонной поверхности

При работе с наклонной поверхностью помните, что нормальная сила всегда действует перпендикулярно поверхности, а сила тяжести (вес) всегда действует прямо вниз .

Вместо того, чтобы разбивать силу натяжения на компоненты \(x\) и \(y\), мы хотим разбить гравитационную силу на компоненты. Если мы наклоним нашу систему координат, чтобы она соответствовала углу поверхности, как показано ниже, мы увидим, что натяжение действует в новом направлении \(x\), а нормальная сила действует в новом направлении \(y\)- направление. Гравитационная сила — единственная сила под углом, так что мы разделили бы ее на компоненты, следующие новым направлениям \(x\) и \(y\), показанным ниже красным.

Рис. 14 — Диаграмма свободного тела с новой системой координат и гравитационной силой, разделенной на компоненты \(x\) и \(y\)

Тогда мы применим второй закон Ньютона в каждом направлении, как и в любой другой задаче.

Подвешивание на двух веревках

Когда объект подвешен на нескольких веревках, натяжение неравномерно распределяется между веревками, если только они не находятся под одинаковыми углами.

Рис. 15. Объект, подвешенный на двух веревках

В этом примере мы подставим действительные числа, чтобы найти \(T_1 \) и \(T_2 \). 92}=0\mathrm{.}$$

Мы можем решить эти два уравнения и два неизвестных алгебраически любым удобным для нас способом. В этом примере мы решим первое уравнение для \(T_1 \) и заменим его вторым. Решение для \(T_1 \) дает

$$\begin{align*} \frac{1}{\sqrt{2}} T_1 &= \frac{1}{2} T_2 \\ T_1 &= \frac{ \sqrt{2}}{2} T_2 \mathrm{,} \\ \end{align*}$$

и подстановка этого во второе уравнение для нахождения \(T_2 \) дает

$$\begin{align *} \frac{\sqrt{2}}{2} T_2 \times \frac{1}{\sqrt{2}} + \frac{\sqrt{3}}{2} T_2 — 147,15\,\mathrm{ N} &= 0 \\ \frac{1+\sqrt{3}}{2} T_2 &= 147,15\,\mathrm{N} \\ T_2 &= 107,72\,\mathrm{N. } \\ \end {выравнивание*}$$

Затем подстановка \(T_2 \) обратно в первое уравнение для решения для \(T_1 \) дает нам окончательный ответ

$$\begin{align*} T_1 &= 107,72\,\mathrm{N} \ раз \frac{\sqrt{2}}{2} \\ T_1 &= 76,17\,\mathrm{N.} \\ \end{align*}$$

Блок, наклон и подвешенный объект

Пример На изображении ниже сочетается многое из того, что мы обсуждали в каждом из приведенных выше примеров.

Рис. 17. Наклон, блок и подвешенный объект

На следующем рисунке показано, как будут выглядеть силы, воздействующие на каждый объект, учитывая, что сила трения может действовать в противоположном направлении в зависимости от того, как движется система .

Рис. 18. Силы, показанные для приведенного выше сценария

Ниже приведены советы, которые мы узнали в каждой из вышеперечисленных задач, которые также применимы к этой:

• Мы можем смотреть на один объект отдельно и выполнять отдельные диаграмма тела и уравнения второго закона Ньютона.
• Веревка оказывает одинаковое натяжение на каждый объект.
• Мы можем наклонить нашу систему координат. У нас даже может быть своя система координат для каждого объекта, если мы будем анализировать силы, воздействующие на каждый объект в отдельности. В этом случае мы бы изолировали коробку 2 и наклонили систему координат, чтобы она соответствовала углу поверхности, но когда мы смотрим на коробку 1 отдельно, мы сохранили бы стандартную систему координат.
• Мы можем разделить силы на составляющую \(x\) и составляющую \(y\). В этом случае, как только мы наклоним систему координат ящика 2, мы разделим гравитационную силу ящика на составляющие.

Натяжение — основные выводы

• Натяжение — это сила, возникающая, когда веревка (или аналогичный предмет) натягивает объект.
• Натяжение вызвано межатомными электрическими силами, пытающимися удержать атомы веревки вместе.
• Уравнение для силы натяжения отсутствует.
• Используйте диаграммы свободного тела и второй закон Ньютона для определения натяжения.

4 типа напряженности, которые нужно включить в каждую историю, которую вы пишете | Мишель Рене Миллер

Четыре типа драматического напряжения и как их использовать

Мишель Рене Миллер

·

Читать

Опубликовано в

·

7 мин чтения

·

1 августа 2020 г.

Фото Джоша Уилберна на Unsplash

На этой неделе подписчик рассылки Sowmya задал мне вопрос о типах напряженности, которые следует включить в историю. Меня сразу же вдохновило написать свой первый пост о создании напряжения, потому что это такой ценный инструмент для писателей!

Нарастание напряжения — это фраза, используемая в творческом письме, чтобы рассказать о конфликте, который возникает у главных героев. Чтобы создать напряжение в истории, нужно дать вашим читателям повод для страха. Не боится , а боится за.

Итак, что я имею в виду? Ну, бояться чего-то, значит бояться, что это может как-то навредить вам .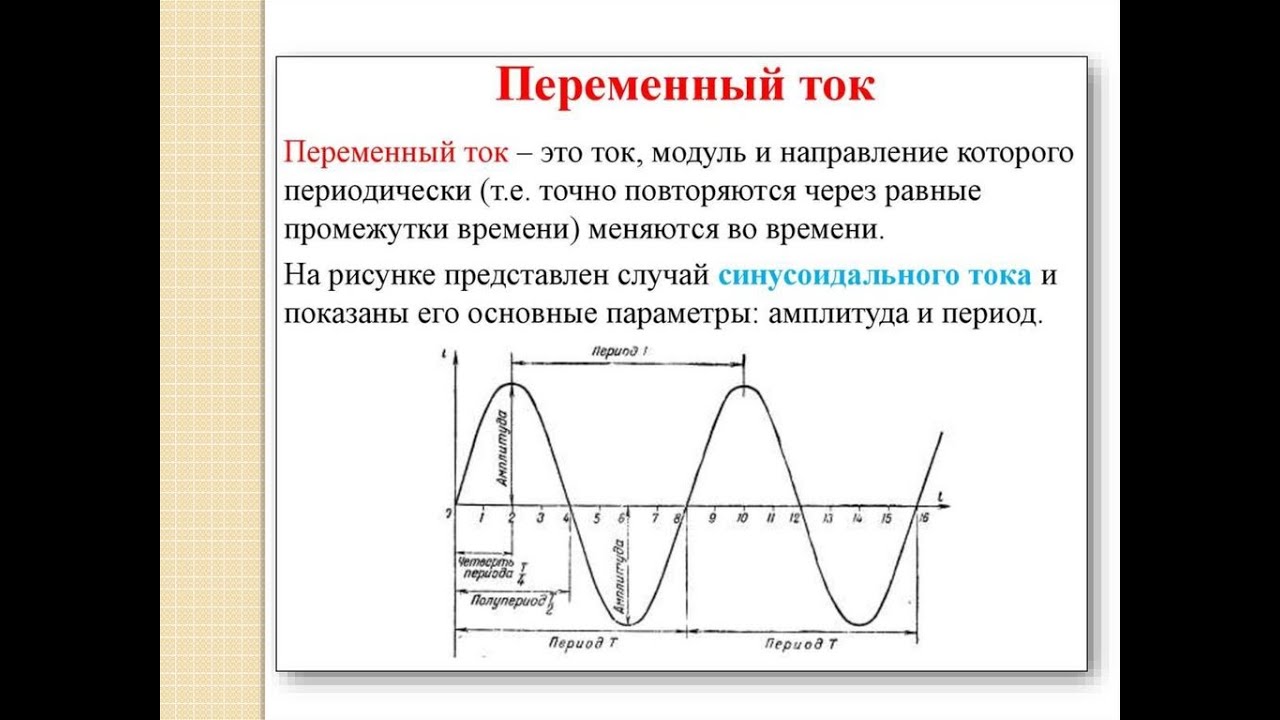 Но бояться за что-то значит бояться, что это могут пострадать.

При написании сюжета вы хотите, чтобы ваши читатели беспокоились о том, что что-то может помешать тому, чего хочет главный герой. Ваш персонаж хочет долго и счастливо? Напряжение в истории может быть связано с драконом, охраняющим замок, или с комой, из которой принцесса может так и не выйти.

Прежде чем мы углубимся в то, как можно создать напряжение, давайте посмотрим на напряжение в популярных литературных произведениях.

Большинство из нас знакомы с пьесой Уильяма Шекспира « Ромео и Джульетта », так что давайте посмотрим на типы напряжения в ней.

С самого начала между персонажами выстраивается напряжение, потому что нам сразу показывают две семьи, которые презирают друг друга, но конечно Ромео влюбляется в Джульетту с первого взгляда на сцене. Так что теперь боимся за Ромео. Как он может любить Капулетти? Что скажет его семья? Будет ли он изгнан? Сохранится ли их любовь?

Здесь с самого начала возникает много вопросов. Напряжение заставит ваших читателей задавать себе вопросы об исходе напряженной ситуации.

В конце пьесы Джульетта без сознания, но Ромео думает, что она мертва. Использование здесь драматической иронии также создает напряжение. Мы хотим кричать на Ромео, чтобы он не убивал себя, потому что Джульетта просто не умерла. Опять же, нам остается только гадать, что, черт возьми, собирается делать Ромео. Мы на краю нашего места, ожидая увидеть, действительно ли он убивает себя. Как только он это делает, наше внимание переключается на Джульетту, чтобы посмотреть, что она будет делать.

Лексика: Драматическая ирония: Когда читатель знает правду, а персонажи нет.

Теперь давайте поговорим о различных типах натяжения, когда их использовать и как они могут выглядеть.

Возможно, вы слышали о четырех типах драматического напряжения:

1. Отношения
2. Задача
3. Сюрприз
4. Тайна

Итак, давайте разберем каждый из них.

Это напряжение, которое мы все ощущаем в повседневной жизни. Это может быть и самое увлекательное чтение, потому что это похоже на сплетни и драму, с которыми мы сталкиваемся каждый день.

Точка напряжения здесь между двумя персонажами. Как и в нашем примере «Ромео и Джульетта », между семьями существует напряженность. Отношения между нашими двумя семьями, мягко говоря, не очень хорошие. Они смертельные враги.

Вы могли видеть это напряжение между главным героем и антагонистом. Мы болеем за успех главного героя, но антагонист продолжает мешать.

Это напряжение часто встречается в любовных историях. Есть ли у главного героя любовный интерес? «Они будут, не так ли?» троп является распространенным источником напряженности в отношениях.

Споры друзей, дисциплинарные взыскания родителей, пассивная агрессия, молчаливое обращение — все это примеры напряженности в отношениях.

Так зачем вообще использовать это напряжение?

Напряжение в отношениях помогает персонажам почувствовать себя реальными людьми, что, конечно же, является целью написания персонажей. Если ваш персонаж движется по своей истории, никогда не вступая в спор, никогда не бодаясь и не имея мнения, отличного от чьего-то еще, это очень нереально.

Каждый день у нас возникают трения с другими людьми. Пролистывание социальных сетей и просмотр политического поста, с которым вы не согласны, вызывает напряженность в отношениях. Как давно вы в последний раз ссорились с кем-то? Это часть нашей повседневной жизни, поэтому она должна быть частью повседневной жизни ваших персонажей.

Это напряжение я чувствую прямо сейчас, когда пишу этот пост. Вы, вероятно, чувствуете это каждый день на работе или в школе.

Напряжение задачи связано с тем, что пытается выполнить ваш главный герой. Он может быть в меньшем или большем масштабе. Возможно, в этой главе они пытаются найти ответ на проблему, но главная цель истории — спасти мир.

Если ваш персонаж может легко достичь своих целей, это хорошо для него, но не для читателя. Никто не хочет читать историю, в которой все сыграно идеально. Опять же, когда вы в последний раз получали то, что хотели, без особых усилий?

Зачем нам такое напряжение?

Чтобы сделать историю реалистичной, вашему главному герою нужно поставить несколько препятствий на своем пути. Какие препятствия мешают им спасти мир? Возможно, они думали, что метеор упадет на Землю, но оказалось, что на самом деле это инопланетный космический корабль, которому теперь нужна армия для борьбы.

Вы также можете сделать так, чтобы они внутренне боролись, чтобы что-то завершить. Как я уже сказал, сейчас я чувствую напряженность задачи, но не из-за каких-то непредвиденных препятствий. Я это чувствую, потому что уже поздно, я работал целый день, и иногда трудно объяснить литературную тактику. Напряжение, которое я сейчас чувствую, полностью внутреннее.

Ваш персонаж может страдать депрессией или тревожностью, поэтому ему будет сложнее выполнять определенные задания. Или, может быть, они просто устали после долгого дня, и их задача требует больше энергии.

Есть много способов помешать главному герою выполнить задание, так что проявите творческий подход!

Этот тип напряжения, пожалуй, самый очевидный. Люди, которые говорят, что любят сюрпризы, говорят только о подарках или отдыхе. Никто не любит сюрпризов.

Здесь у нас есть два разных типа сюрпризов. Читатель может быть удивлен сюжетным поворотом, а главный герой может быть удивлен новыми событиями по мере их развития.

Вы помните какое-то время назад, где-то в 2012 году, наверное, когда люди кричали «поворот сюжета!» когда они узнали что-то новое? Так рад, что мы как общество вышли из этой фазы. Но это также показывает, что на самом деле все может быть поворотом сюжета.

Конечно, некоторые из них будут иметь больший вес, чем другие, но я пытаюсь сказать, что напряжение не должно быть большим драматическим изменением в истории.

Ваше удивление может варьироваться от того, что мамы нет дома, когда она обычно бывает, до метеора, который на самом деле является инопланетным космическим кораблем.

Итак, зачем использовать это напряжение?

Если подумать, не проходит и дня, чтобы мы не были чем-то удивлены. Сегодня я был удивлен, когда случайно удалил часы работы на своем ноутбуке. Иногда я с удивлением слышу, что полицейские убили еще одного темнокожего мужчину.

Сюрпризы бывают разных размеров, но случаются они каждый день.

Опять же, как и в случае с другими событиями, вы должны включать в свои истории сюрпризы, чтобы они казались реалистичными. История, которая разыгрывается именно так, как ожидалось, не стоит читать. Ваши читатели не хотят иметь возможность предсказывать все, что произойдет дальше, это неинтересно.

Этот тип напряжения также довольно распространен и его легко понять.

Король ужасов, Стивен Кинг, отлично помогает читателю постоянно думать: «Что, черт возьми, происходит?»

Это напряжение продвигает читателя вперед по сюжету. Тайна настолько заманчива, что они не могут не узнать, что произошло. Этого можно достичь, нарастив другие напряжения до клиффхэнгера, который затем разрешается позже. У вас может быть одна всеобъемлющая загадка, которая разыгрывается до кульминации истории. И у вас могут быть загадки поменьше, которые будут всплывать на протяжении всей истории. Все эти версии мистики привлекут внимание вашего читателя.

Зачем использовать мистику в рассказе?

Опять же, тайны случаются каждый день в нашей жизни, и часто в меньшем масштабе. «Как моя ручка исчезла в моем одеяле?» это то, что я часто переживаю снова и снова, как будто это День сурка.

Эмоциональная загадка, которая может быть связана с напряжением в отношениях, — это «Почему они сказали это мне? Почему они так со мной поступили?» тайна.

Иногда мы становимся более крупными, более прискорбными загадками, такими как «Почему они должны были умереть такими молодыми?»

Есть и более важные загадки, такие как «Кто убил этого человека?» или «Как это здание сгорело?»

Загадки случаются постоянно, поэтому не включать их в историю значит делать вашу историю нереалистичной.