{2}}\rbrack\) .

Напряженность электрического поля «выходит» из положительного заряда и «входит» в отрицательный.

Принцип суперпозиции полей: если в точке пространства несколько заряженных частиц создают поля, напряженности которых равны \(\overrightarrow{Е_{1}}\) и \(\overrightarrow{Е_{2}}\), то результирующая напряженность поля в этой точке равна векторной сумме полей \(\overrightarrow{Е} = \overrightarrow{Е_{1}} + \overrightarrow{Е_{2}}\) .

При этом вектора могут иметь разную длину. Чтобы определить ее, нужно сравнить модули зарядов, их знаки и расстояние от каждого заряда до точки, где ищется напряженность.

Если поместить заряженное тело в электрическое поле (внешнее или поле соседнего заряда), то заряженное тело начнет двигаться в соответствии с правилами, описанными выше. Но само движение тела возможно только за счет действия на него силы, которая называется электрическая и находится как:

\(\overrightarrow{F} = q\overrightarrow{Е}\), где:

F – электрическая сила, с которой поле действует на заряд [Н],

q – заряд [Кл],

E – напряженность поля [Н/Кл]

Электростатический потенциал точечного заряда выражается формулой:

\(\varphi = \frac{\text{kq}}{R}\), где

q ― заряд [Кл];

R ― расстояние от заряда до точки, в которой проводятся измерения [м];

k ― коэффициент пропорциональности равный 9 ∙ 10⁹ \(\lbrack\frac{Н \bullet м^{2}}{Кл^{2}}\rbrack\).

Для потенциала так же справедлив принцип суперпозиции: потенциал поля, созданного в точке несколькими точечными зарядами, равен сумме потенциалов полей, создаваемых в этой точке каждым зарядом по отдельности:

φ = φ₁ + φ₂ + φ₃ + … +φ_n

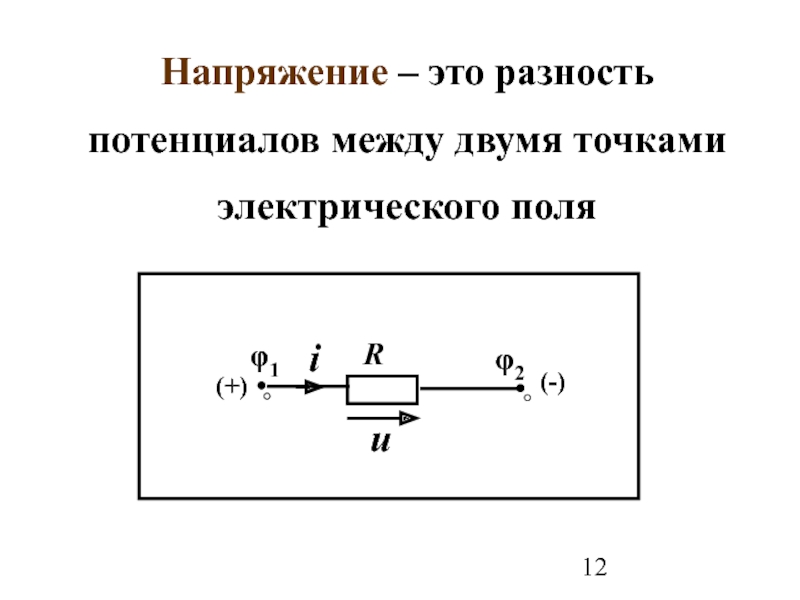
Разность потенциалов между двумя точками в постоянном электрическом поле определяется выражением ∆φ = — Ed

∆φ ― разность потенциалов [В];

E ― напряженность однородного электрического поля [В/м];

d ― расстояние между точками, между которыми определяется разность потенциалов. [м].

Работа совершаемая электрическими силами определяется через разность потенциалов, как A = — ∆φ ∙ q:

А — работа [Дж];

∆φ — разность потенциалов [В];

q — заряд [Кл].

Работа не зависит от траектории, а зависит только от начального и конечного положения тела.

\(A_{1} = A_{2} = A_{3}\) .

Напряженность электрического поля | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Загрузка…

Тема:

Напряженность и потенциал электрического поля

Раздел:

Электричество

Действие электрического поля на заря­женное тело может иметь разную интен­сивность. Сила, характеризующая это дейст­вие, будет зависеть не только от заряда тела, но и от характеристик поля. Тем не менее, в каждом отдельном случае для дан­ной точки поля она будет пропорциональ­ной значению электрического заряда. Отно­шение силы к заряду в данной точке поля всегда будет постоянным. То есть

F₁ / q₁ = F₂ / q₂ = F₃ / q₃ = … = F / q,

где F— сила, действующая на заряженное тело;

q — значение электрического заряда тела.

Сила взаимодействия электри­чески заряженного тела с элект­рическим полем пропорциональ­на его заряду.

В электрическом поле другого источника или в другой точке данного поля это со­отношение также будет справедливым, но его значение может быть другим.

Для исследования электричес­кого поля используют тела ма­лых размеров (точечные).

Отношение F / q будет индивидуальным для каждой точки поля и будет характеризовать силовое действие поля. Это стало основа­нием для введения физической величины, которая характеризует силовое действие электрического поля. Такая физическая ве­личина называется

напряженностью элект­рического поля, и ее значение устанавли­вается на основании соотношения

Загрузка…

E̅ = F̅ / q.

Напряженность электрического поля — это физическая величина, которая является си­ловой характеристикой электрического поля и равняется силе, действующей на точечное тело, имеющее единичный электрический за­ряд.

Точечное тело, имеющее поло­жительный единичный электри­ческий заряд, называют проб­ным зарядом, или пробным те­лом.

Напряженность является векторной вели­чиной и определяет не только значение силы, действующей на заряженное тело, но и ее направление.

Для измерения напряженности электри­ческого поля применяются специальные еди­ницы измерения. В соответствии с опре­делением Материал с сайта http://worldofschool.ru

[E] = 1 Н / 1 Кл = 1 Н/Кл.

Собственного наименования эта единица не имеет и читается как «ньютон на кулон». В практике применяют другую единицу напряженности — 1 В/м. Ее читают как «вольт на метр». По размеру эти две единицы одинаковые.

Если напряженность в разных точках по­ля имеет разные значения, то это поле на­зывают неоднородным.

На этой странице материал по темам:

• Какое свойство электрического поля описывает напряженность

• Гдз по физике напряженность электрического поля

• Напряженность электрического поля е [b/м].

  f_1/q_1 =f_2/q_2 =f_3/q_3 =e ⃗

• Яку властивість електричного поля описує напруженість

• Конспект по теме напряженность электрического поля

Вопросы по этому материалу:

• Какое свойство электрического поля описывает напряженность?

• Какую физическую величину называют напряженностью электри­ческого поля?

• Какие единицы измерения напряженности электрического поля?

Материал с сайта http://WorldOfSchool.ru

19.2 Электрический потенциал в однородном электрическом поле – Колледж физики, главы 1-17

19 Электрический потенциал и электрическое поле

Цели обучения

• Описать взаимосвязь между напряжением и электрическим полем.
• Получите выражение для электрического потенциала и электрического поля.
• Рассчитать напряженность электрического поля с учетом расстояния и напряжения.

В предыдущем разделе мы исследовали взаимосвязь между напряжением и энергией. В этом разделе мы исследуем взаимосвязь между напряжением и электрическим полем. Например, однородное электрическое поле [латекс]\textbf{E}[/латекс] создается путем помещения разности потенциалов (или напряжения) [латекс]\жирный символ{\Delta V}[/латекс] на две параллельные металлические пластины, обозначены A и B. (См. рис. 1.) Изучив это, мы узнаем, какое напряжение необходимо для создания определенной напряженности электрического поля; это также выявит более фундаментальную связь между электрическим потенциалом и электрическим полем. С точки зрения физики, либо [латекс]\boldsymbol{ \Delta V}[/латекс], либо [латекс]\текстbf{Е}[/латекс] можно использовать для описания любого распределения заряда. [latex]\boldsymbol{ \Delta V}[/latex] наиболее тесно связан с энергией, тогда как [latex]\textbf{E}[/latex] наиболее тесно связан с силой. [латекс]\boldsymbol{\Delta V}[/латекс] равно

скалярная величина и не имеет направления, в то время как [latex]\textbf{E}[/latex] является векторной величиной , имеющей как величину, так и направление. (Обратите внимание, что величина напряженности электрического поля, скалярная величина, представлена ​​ниже [latex]\textbf{E}[/latex].) Связь между [latex]\boldsymbol{\Delta V}[/latex] а [latex]\textbf{E}[/latex] определяется путем вычисления работы, совершаемой силой при перемещении заряда из точки A в точку B. Но, как отмечалось в главе 19.1 «Электрическая потенциальная энергия: разность потенциалов», это сложный для произвольного распределения заряда, требующий исчисления. Поэтому мы рассматриваем однородное электрическое поле как интересный частный случай.

Рисунок 1. Соотношение между В и E для параллельных проводящих пластин составляет E = В / d . (Обратите внимание, что Δ В = В _AB по величине. Для заряда, который перемещается с пластины A с более высоким потенциалом на пластину B с более низким потенциалом, необходимо включить знак минус следующим образом: –Δ В = В _А – В _В = В _AB . Подробности см. в тексте.)

Работа, совершаемая электрическим полем на рисунке 1 для перемещения положительного заряда [латекс]\boldsymbol{q}[/latex] из A, положительной пластины с более высоким потенциалом, в B, отрицательную пластина, нижний потенциал,

[латекс]\boldsymbol{W = -\Delta \textbf{PE} = -q \Delta V.}[/latex]

Разность потенциалов между точками А и В равна

[латекс]\boldsymbol{- \Delta V = -(V_{\textbf{B}} — V_{\textbf{A}}) = V_{\textbf{A} — V_{\textbf{B}}} = V_{\textbf{AB}}}[/латекс].

Ввод этого в выражение для работы дает

[латекс]\boldsymbol{W = qV _{\textbf{AB}}}[/латекс].

Работа [латекс]\boldsymbol{W = Fd \;\textbf{cos} \theta}[/latex], так как путь параллелен полю, и поэтому [латекс]\boldsymbol{W = Fd}[/ латекс]. Поскольку [латекс]\boldsymbol{F = qE}[/латекс], мы видим, что [латекс]\boldsymbol{W = qEd}[/латекс]. Подстановка этого выражения для работы в предыдущее уравнение дает

[латекс]\boldsymbol{qEd = qV _{\textbf{AB}}}[/латекс].

Заряд отменяется, поэтому напряжение между точками A и B равно

[латекс]\begin{array}{l} \boldsymbol{V _{\textbf{AB}} = Ed} \\ \boldsymbol{E = \frac{V _{\textbf{AB}}}{d}} \ end{array}[/latex] [латекс]\}[/латекс] [латекс]\boldsymbol{\textbf{(uniform} \; E \;\textbf{- только поле)}} ,[/latex]

, где [латекс]\boldsymbol{d}[/латекс] — расстояние от А до В или расстояние между пластинами на рисунке 1. Обратите внимание, что приведенное выше уравнение подразумевает, что единицами измерения электрического поля являются вольты на метр. Мы уже знаем, что единицами измерения электрического поля являются ньютоны на кулон; таким образом, справедливо следующее соотношение между единицами:

[латекс]\boldsymbol{1 \;\textbf{N} / \textbf{C} = 1 \;\textbf{V} / \textbf{m}}.[/latex]

Напряжение между точками A и B

[латекс]\begin{array}{l} \boldsymbol{V _{\textbf{AB}} = Ed} \\ \boldsymbol{E = \frac{V _{\textbf{AB }}}{d}} \end{array}[/latex] [латекс]\}[/латекс] [латекс]\boldsymbol{\textbf{(uniform} \; E \;\textbf{- только поле)} } ,[/latex]

где [latex]\boldsymbol{d}[/latex] — расстояние от A до B или расстояние между пластинами.

96 \;\textbf{V} / \textbf{m}}[/latex]. Выше этого значения поле создает в воздухе достаточную ионизацию, чтобы сделать воздух проводником. Это позволяет разряду или искре, которая уменьшает поле. Каково же тогда максимальное напряжение между двумя параллельными проводящими пластинами, разделенными 2,5 см сухого воздуха?

Стратегия

Заданы максимальное электрическое поле [латекс]\boldsymbol{E}[/латекс] между пластинами и расстояние [латекс]\boldsymbol{d}[/латекс] между ними. Таким образом, уравнение [латекс]\жирный символ{V_{\textbf{AB}} = Ed}[/латекс] можно использовать для расчета максимального напряжения. 94 \;\textbf{V}}[/latex]

или

[латекс]\boldsymbol{V_{\textbf{AB}} = 75 \;\textbf{кВ}} .[/latex]

( Ответ представлен только двумя цифрами, поскольку максимальная напряженность поля является приблизительной.)

Обсуждение

Одним из следствий этого результата является то, что требуется около 75 кВ, чтобы искра перескочила через 2,5 см (1 дюймов) разрядник или 150 кВ для 5-сантиметровой искры. Это ограничивает напряжения, которые могут существовать между проводниками, например, на линии электропередачи. Меньшее напряжение вызовет искру, если на поверхности есть точки, так как точки создают большее поле, чем гладкие поверхности. Влажный воздух разрушается при более низкой напряженности поля, а это означает, что меньшее напряжение вызовет скачок искры во влажном воздухе. Наибольшие напряжения могут быть созданы, скажем, статическим электричеством в сухие дни.

Рисунок 2. Искровая камера используется для отслеживания путей высокоэнергетических частиц. Ионизация, создаваемая частицами при их прохождении через газ между пластинами, позволяет проскакивать искре. Искры располагаются перпендикулярно пластинам, следуя линиям электрического поля между ними. Разность потенциалов между соседними пластинами недостаточно высока, чтобы вызвать искры без ионизации, создаваемой частицами в экспериментах на ускорителях (или космическими лучами). (кредит: Дадерот, Wikimedia Commons)

Пример 2: Поле и сила внутри электронной пушки

(a) Электронная пушка имеет параллельные пластины, разделенные расстоянием 4,00 см, и дает электронам энергию 25,0 кэВ. Чему равна напряженность электрического поля между пластинами? б) С какой силой это поле будет действовать на кусок пластика с зарядом [латекс]\boldsymbol{0,500 \;\mu \textbf{C}}[/латекс], который попадет между пластинами?

Стратегия

Поскольку напряжение и расстояние между пластинами заданы, напряженность электрического поля можно рассчитать непосредственно из выражения [латекс]\boldsymbol{E = \frac{V_{\textbf{AB}}}{d} }[/латекс]. Когда напряженность электрического поля известна, сила, действующая на заряд, определяется с помощью [латекс]\жирныйсимвол{\текстбф{F} = q \текстбф{Е}}[/латекс]. Поскольку электрическое поле имеет только одно направление, мы можем записать это уравнение в терминах величин: [латекс]\boldsymbol{F = q \; Е}[/латекс].

Решение для (a)

Выражение для величины электрического поля между двумя однородными металлическими пластинами:

[латекс]\boldsymbol{E =}[/латекс] [латекс]\boldsymbol{ \frac{ V_{\textbf{AB}}}{d}}[/латекс]. 5 \;\textbf{V } / \textbf{м}}.[/латекс] 95 \;\textbf{V} / \textbf{m}) = 0,313 \;\textbf{N}}.[/latex]

Обсуждение

Обратите внимание, что единицы измерения — ньютоны, поскольку [ латекс]\boldsymbol{ 1 \;\textbf{V} / \textbf{m} = 1 \;\textbf{N} / \textbf{C}}[/latex]. Сила, действующая на заряд, одинакова независимо от того, где находится заряд между пластинами. Это связано с тем, что электрическое поле между пластинами однородно.

В более общих ситуациях, независимо от того, является ли электрическое поле однородным, оно указывает в направлении уменьшения потенциала, потому что сила на положительном заряде направлена ​​в направлении [латекс]\textbf{E}[/латекс], а также в направлении более низкого потенциала [латекс]\boldsymbol{V}[/латекс]. Кроме того, величина [latex]\textbf{E}[/latex] равна скорости уменьшения [latex]\boldsymbol{V}[/latex] с расстоянием. Чем быстрее [латекс]\boldsymbol{V}[/латекс] уменьшается с расстоянием, тем сильнее электрическое поле. В форме уравнения общая связь между напряжением и электрическим полем равна

[латекс]\boldsymbol{E =}[/латекс] [латекс]\boldsymbol{-\frac{\Delta V}{\Delta s}} ,[/latex]

, где [латекс]\жирныйсимвол{ \Delta s}[/латекс] — расстояние, на котором происходит изменение потенциала, [латекс]\жирныйсимвол{\Дельта V}[/латекс]. Знак минус говорит нам, что [latex]\textbf{E}[/latex] указывает в направлении уменьшения потенциала. Говорят, что электрическое поле представляет собой градиент (по степени или наклону) электрического потенциала.

Связь между напряжением и электрическим полем

В форме уравнения общая взаимосвязь между напряжением и электрическим полем имеет вид ,[/latex]

где [latex]\boldsymbol{\Delta s}[/latex] — расстояние, на котором происходит изменение потенциала [latex]\boldsymbol{ \Delta V}[/latex]. Знак минус говорит нам, что [latex]\textbf{E}[/latex] указывает в направлении уменьшения потенциала. Говорят, что электрическое поле равно градиент (градус или уклон) электрического потенциала.

Для постоянно меняющихся потенциалов [латекс]\boldsymbol{\Delta V}[/латекс] и [латекс]\boldsymbol{\Delta s}[/латекс] становятся бесконечно малыми, и для определения электрического поля необходимо использовать дифференциальное исчисление.

• Напряжение между точками A и B составляет

  [латекс]\begin{array}{l} \boldsymbol{V _{\textbf{AB}} = Ed} \\ \boldsymbol{E = \frac{V _{\textbf{AB}}}{d}} \ end{array}[/latex] [latex]\}[/latex] [latex]\boldsymbol{\textbf{(uniform} \; E \;\textbf{- только поле)}} ,[/latex]

  , где [латекс]\boldsymbol{d}[/латекс] — расстояние от А до В или расстояние между пластинами.

• В форме уравнения общая связь между напряжением и электрическим полем выглядит следующим образом:

  [латекс]\boldsymbol{E =}[/латекс] [латекс]\boldsymbol{- \frac{\Delta V}{\Delta s}} ,[/latex]

  , где [латекс]\boldsymbol{\Delta s}[/латекс] — расстояние, на котором происходит изменение потенциала, [латекс]\жирный символ{\Delta V}[/латекс]. Знак минус говорит нам, что [латекс]\текстбф{Е}[/латекс] указывает в направлении убывания потенциала.) Говорят, что электрическое поле представляет собой 93 \;\textbf{V}}[/latex] применяется? б) Насколько близко друг к другу могут располагаться пластины при таком приложенном напряжении?

  6: Напряжение на мембране, образующей клеточную стенку, составляет 80,0 мВ, толщина мембраны 9,00 нм. Что такое напряженность электрического поля? (Значение на удивление большое, но правильное. Мембраны обсуждаются в главе 19.5 «Конденсаторы и диэлектрики» и в главе 20.7 «Нервная проводимость — электрокардиограммы».) Вы можете предположить однородное электрическое поле.

  7: Мембранные стенки живых клеток имеют на удивление большие электрические поля из-за разделения ионов. (Мембраны более подробно обсуждаются в главе 20.7 «Нервная проводимость — электрокардиограммы».) Каково напряжение на мембране толщиной 8,00 нм, если напряженность электрического поля на ней составляет 5,50 МВ/м? Вы можете предположить однородное электрическое поле.

  8: Две параллельные проводящие пластины отстоят друг от друга на 10,0 см, и одну из них принимают за ноль вольт. а) Какова напряженность электрического поля между ними, если потенциал на расстоянии 8,00 см от нулевой пластины (и 2,00 см от другой) равен 450 В? б) Чему равно напряжение между пластинами? 96 \;\textbf{V} / \textbf{m}}[/latex]. а) Какую энергию в кэВ сообщает электрон, если он ускоряется на расстояние 0,400 м? б) На какое расстояние его нужно разогнать, чтобы его энергия увеличилась на 50,0 ГэВ?

   

  скаляр

  физическая величина с величиной, но без направления

  вектор

  физическая величина с величиной и направлением

   

  19.2 Электрический потенциал в однородном электрическом поле — Физика вуза 2е

  Цели обучения

  К концу этого раздела вы сможете:

  • Описать взаимосвязь между напряжением и электрическим полем.
  • Получите выражение для электрического потенциала и электрического поля.
  • Рассчитать напряженность электрического поля с учетом расстояния и напряжения.

  В предыдущем разделе мы исследовали взаимосвязь между напряжением и энергией. В этом разделе мы исследуем взаимосвязь между напряжением и электрическим полем. Например, однородное электрическое поле EE создается путем помещения разности потенциалов (или напряжения) ΔVΔV на две параллельные металлические пластины, обозначенные A и B (см. рис. 19)..5.) Изучив это, мы узнаем, какое напряжение необходимо для создания определенной напряженности электрического поля; это также выявит более фундаментальную связь между электрическим потенциалом и электрическим полем. С точки зрения физики, либо ΔVΔV, либо EE можно использовать для описания любого распределения заряда. ΔVΔV наиболее тесно связано с энергией, тогда как EE наиболее тесно связано с силой. ΔVΔV — скалярная величина, не имеющая направления, а EE — векторная величина, имеющая как величину, так и направление. (Обратите внимание, что величина напряженности электрического поля, скалярная величина, представлена ​​ниже как EE.) Связь между ΔVΔV и EE выявляется путем вычисления работы, совершаемой силой при перемещении заряда из точки A в точку B. Но , как отмечено в книге «Электрическая потенциальная энергия: разность потенциалов», это сложно для произвольного распределения заряда, требующего исчисления. Поэтому мы рассматриваем однородное электрическое поле как интересный частный случай.

  Рисунок 19,5 Соотношение между VV и EE для пластин с параллельными проводниками: E=V/dE=V/d. (Обратите внимание, что Δ В «=» В АБ Δ В «=» В АБ по величине. Для заряда, который перемещается с пластины A с более высоким потенциалом на пластину B с более низким потенциалом, необходимо включить знак минус следующим образом: –ΔV=VA–VB=VAB–ΔV=VA–VB=VAB. Подробности см. в тексте.)

  Работа, совершаемая электрическим полем на рис. 19.5 для перемещения положительного заряда q q от A, положительной пластины, с более высоким потенциалом, к B, отрицательной пластине, с более низким потенциалом, составляет

  Вт=–ΔPE=–qΔV.W=–ΔPE=–qΔV.

  19,21

  Разность потенциалов между точками A и B равна

  –ΔV=–(VB–VA)=VA–VB=VAB.–ΔV=–(VB–VA)=VA–VB=VAB.

  19,22

  Ввод этого в выражение для работы дает

  W=qVAB.W=qVAB.

  19,23

  Работа равна W=FdcosθW=Fdcosθ; здесь cosθ=1cosθ=1, так как путь параллелен полю, и поэтому W=FdW=Fd. С F=qEF=qE, мы видим, что W=qEdW=qEd. Подстановка этого выражения для работы в предыдущее уравнение дает

  qEd=qVAB.qEd=qVAB.

  19,24

  Заряд отменяется, поэтому напряжение между точками A и B становится равным

  VAB=EdE=VABd(только однородное-поле),VAB=EdE=VABd(только однородное-поле),

  19.25

  , где dd — расстояние от А до В или расстояние между пластинами на рис. 19.5. Обратите внимание, что приведенное выше уравнение подразумевает, что единицами измерения электрического поля являются вольты на метр. Мы уже знаем, что единицами измерения электрического поля являются ньютоны на кулон; таким образом, справедливо следующее соотношение между единицами:

  1 Н/З=1 В/м.1 Н/З=1 В/м.

  19,26

  Напряжение между точками A и B

  VAB=EdE=VABd(только для однородного поля),VAB=EdE=VABd(только для однородного поля),

  19,27

  где dd — расстояние от A до B или расстояние между пластинами.

  Пример 19,4

  Какое максимально возможное напряжение между двумя пластинами?

  Сухой воздух поддерживает максимальную напряженность электрического поля около 3,0×106 В/м3,0×106 В/м. Выше этого значения поле создает в воздухе достаточную ионизацию, чтобы сделать воздух проводником. Это позволяет разряду или искре, которая уменьшает поле. Каково же тогда максимальное напряжение между двумя параллельными проводящими пластинами, разделенными 2,5 см сухого воздуха?

  Стратегия

  Заданы максимальное электрическое поле EE между пластинами и расстояние между ними dd. Таким образом, уравнение VAB=EdVAB=Ed можно использовать для расчета максимального напряжения.

  Решение

  Разность потенциалов или напряжение между пластинами составляет

  VAB=Ed.VAB=Ed.

  19,28

  Ввод заданных значений для EE и dd дают

  VAB=(3,0×106 В/м)(0,025 м)=7,5×104VVAB=(3,0×106 В/м)(0,025 м)=7,5×104 В

  19.29

  или

  VAB=75 кВ.VAB=75 кВ.

  19.30

  (Ответ приводится только из двух цифр, поскольку максимальная напряженность поля является приблизительной.) Зазор 2,5 см (1 дюйм) или 150 кВ для искры длиной 5 см. Это ограничивает напряжения, которые могут существовать между проводниками, например, на линии электропередачи. Меньшее напряжение вызовет искру, если на поверхности есть точки, так как точки создают большее поле, чем гладкие поверхности. Влажный воздух разрушается при более низкой напряженности поля, а это означает, что меньшее напряжение вызовет скачок искры во влажном воздухе. Наибольшие напряжения могут быть созданы, скажем, статическим электричеством в сухие дни.

  Рисунок 19,6 Искровая камера используется для отслеживания путей высокоэнергетических частиц. Ионизация, создаваемая частицами при их прохождении через газ между пластинами, позволяет проскакивать искре. Искры располагаются перпендикулярно пластинам, следуя линиям электрического поля между ними. Разность потенциалов между соседними пластинами недостаточно высока, чтобы вызвать искры без ионизации, создаваемой частицами в экспериментах на ускорителях (или космическими лучами). (кредит: Дадерот, Wikimedia Commons)

  Пример 19,5

  Поле и сила внутри электронной пушки

  (a) Электронная пушка имеет параллельные пластины, разделенные расстоянием 4,00 см, и дает электронам энергию 25,0 кэВ. Чему равна напряженность электрического поля между пластинами? б) С какой силой это поле будет действовать на кусок пластика с зарядом 0,500 мкКл0,500 мкКл, который попадет между пластинами?

  Стратегия

  Поскольку напряжение и расстояние между пластинами заданы, напряженность электрического поля можно рассчитать непосредственно из выражения E=VABdE=VABd. Зная напряженность электрического поля, можно найти силу, действующую на заряд. F=qEF=qE. Поскольку электрическое поле имеет только одно направление, мы можем записать это уравнение в терминах величин: F=qEF=qE.

  Решение для (a)

  Выражение для величины электрического поля между двумя однородными металлическими пластинами:

  E=VABd.E=VABd.

  19,31

  Так как электрон является однозарядным и имеет энергию 25,0 кэВ, разность потенциалов должна быть 25,0 кВ. Вводя это значение для VABVAB и расстояния между пластинами 0,0400 м, получаем

  E=25,0 кВ0,0400 м=6,25×105 В/м.E=25,0 кВ0,0400 м=6,25×105 В/м.

  19,32

  Решение для (б)

  Величина силы, действующей на заряд в электрическом поле, получается из уравнения

  F=qE.F=qE.

  19,33

  Подстановка известных значений дает 0,313 Н.

  19,34

  Обсуждение

  Обратите внимание, что единицами измерения являются ньютоны, поскольку 1 В/м=1 Н/Кл1 В/м=1 Н/Кл.