Задача из раздела «Частично заполненные таблицы истинности логических выражений»
В статье показано решение одной задачи, которую меня попросили посмотреть.
Постановка задачи
Логическая функция $F$ задаётся выражением $(x \equiv (w \lor y)) \lor ((w \rightarrow z ) \land (y \rightarrow w))$.
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции $F$.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных $x$, $y$, $z$, $w$.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $?$ | $?$ | $?$ | $?$ | $F$ |
| 1 | 1 | 0 | ||
| 1 | 0 | |||
| 1 | 1 | 0 |
В ответе напишите буквы $w$, $x$, $y$, $z$ в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т.
Решение
Разбор выражения
Выражение $(x \equiv (w \lor y)) \lor ((w \rightarrow z) \land (y \rightarrow w))$ состоит из двух частей, соединенных операцией дизъюнкцией (логическое «ИЛИ»).
Так как в таблице все строки таблицы истинности равны $0$ (последний столбец), то, значит, обе части выражения $x \equiv (w \lor y)$ и $(w \rightarrow z) \land (y \rightarrow w)$ должны быть равные $0$, так как, если бы кто-то них был равен $1$, то выражение стало бы равным $F = 1$.
Чаще всего в выражениях используется переменная $w$, поэтому её и будем анализировать.
Первый случай
Пусть $w = 0$.
Тогда выражение $x \equiv (w \lor y)$ примет вид: $x \equiv (0 \lor y)$. Тут возможно два варианта:
Пусть $y = 0$.
Тогда $0 \lor y = 0 \lor 0 = 0$. Значит, чтобы $x \equiv 0$ было ложным, нужно, чтобы $x = 1$.
Пусть $y = 1$.
Тогда $0 \lor y = 0 \lor 1 = 1$.
Значит, чтобы $x \equiv 1$ было ложным, нужно, чтобы $x = 0$.
Рассмотрим вторую часть выражения $(w \rightarrow z) \land (y \rightarrow w)$, которое также должно быть ложным. Так как мы считаем, что $w = 0$, то оно превращается в $(0 \rightarrow z) \land (y \rightarrow 0)$.
Так как две импликации соединены конъюнкцией, то для того, чтобы выражение было ложным, достаточно ложности хотя бы одной импликации.
Надо помнить, что импликация бывает ложной только в одном случае: $1 \rightarrow 0 = 0$.
Отсюда следует, что $(0 \rightarrow z)$ не может быть ложным ни при каких значениях $z$. Значит ложным должна быть импликация $y \rightarrow 0$. А это возможно только в случае, если $y = 1$.
Выше при рассматривании выражения $x \equiv (w \lor y)$ мы рассматривали два случая: когда $y = 0$ и когда $y = 1$. Но после рассмотрения выражения $(w \rightarrow z) \land (y \rightarrow w)$ вариант $y = 0$ можно исключить.
Из этих размышлений можно формулировать следующий вывод.
Вывод 1
Если $w = 0$, то $y = 1$, $x = 0$.
Второй случай
Пусть $w = 1$.
Тогда выражение $x \equiv (w \lor y)$ пр имеет вид: $x \equiv (1 \lor y)$. Так как в правой части используется дизъюнкция, то правая часть всегда будет истинной при любых значениях $y$. Значит, чтобы выражение было ложным, левая часть должна быть ложной, то есть $x = 0$.
Рассмотрим выражение $(w \rightarrow z) \land (y \rightarrow w)$, которое также должно быть ложным. Так как мы считаем, что $w = 1$, то оно превращается в $(1 \rightarrow z) \land (y \rightarrow 1)$.
Из свойств импликации следует, что вторая импликация никогда не может быть ложной. Следовательно, для ложности выражения необходима ложность первой импликации $1 \rightarrow z$, а это возможно только в случае $z = 0$.
Из вышесказанного можно сформулировать следующий вывод:
Вывод 2
Если $w = 1$, то $x = 0$, $z = 0$.
Эти два вывода будем использовать для анализа таблицы истинности.
Разбор таблицы истинности
В предыдущей части мы взяли за основу переменную $w$.
Её и возьмём для анализа таблицы истинности.
Первый столбец
Пусть $w$ располагается в первом столбце таблицы истинности:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $w$ | $?$ | $?$ | $?$ | $F$ |
| 1 | 1 | 0 | ||
| 0 | ||||
| 1 | 1 | 0 |
По второму выводу следует, что, если $w = 1$, то минимум две переменных должно быть равно $0$ ($x = 0$, $z = 0$).
Так как в первой строке $w = 1$, а четвертый столбец занят $1$, то, значит, второй и третий столбец должны быть равны $0$. И какой-то из этих столбцов будет содержать переменную $x$, а какой-то $z$.
То есть, из первой строки следует, что, если, первый столбец равен $1$, то второй и третий равны $0$.
Но третья строка также содержит значение $w = 1$, а третий столбец содержит значение, равное $1$. А согласно первой строке, там должен находится $0$.
Мы пришли к противоречию. Значит, $w$ не может располагаться в первом столбце.
Второй столбец
Пусть $w$ располагается во втором столбце таблицы истинности:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $?$ | $w$ | $?$ | $?$ | $F$ |
| 1 | 1 | 0 | ||
| 0 | ||||
| 1 | 1 | 0 |
Пусть в первой строке $w = 1$:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $?$ | $w$ | $?$ | $?$ | $F$ |
| 1 | 1 | 1 | 0 | |
| 1 | 0 | |||
| 1 | 1 | 0 |
Но это невозможно, так как для этого случая нам нужно два столбца, равных $0$, а такой может быть только один.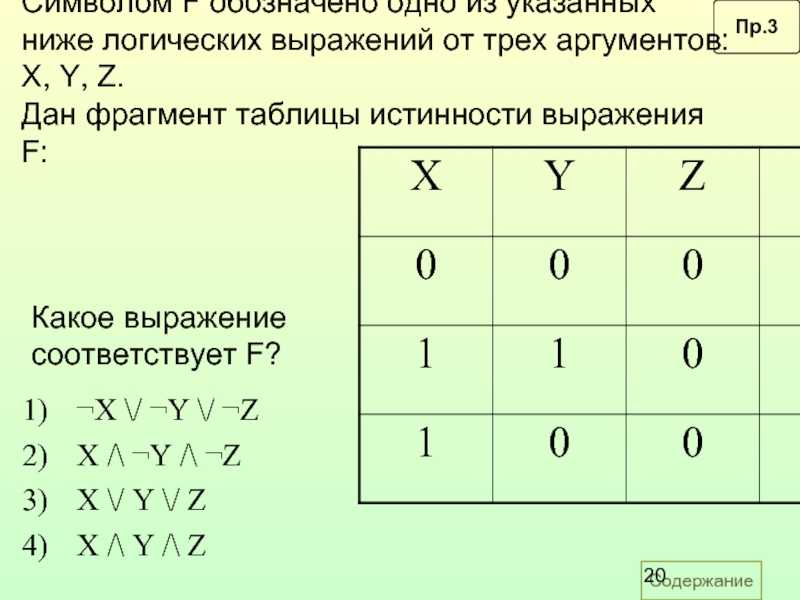
Пусть в первой строке $w = 0$:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $?$ | $w$ | $?$ | $?$ | $F$ |
| 1 | 0 | 1 | 0 | |
| 1 | 0 | |||
| 1 | 1 | 0 |
Если $w = 0$, то по первому выводу $y = 1$, $x = 0$. Так как у нас в первой строчке все заполненные столбцы равны $1$, то $x$ может располагаться только в третьем столбце, и там будет значение $0$:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $?$ | $w$ | $x$ | $?$ | $F$ |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | |||
| 1 | 1 | 0 |
Но согласно первому и второму выводу $x$ всегда равен $0$, а в третьей строчке мы видим, что в третьем столбце $1$.
Мы пришли к противоречию. Значит, $w$ не может располагаться во втором столбце.
Третий столбец
Пусть $w$ располагается в третьем столбце таблицы истинности:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $?$ | $?$ | $w$ | $?$ | $F$ |
| 1 | 1 | 0 | ||
| 1 | 0 | |||
| 1 | 1 | 0 |
Так как согласно обоим выводам $x = 0$, то только во втором столбце может располагаться $x$, так как во всех остальных есть хотя бы одна $1$:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $?$ | $x$ | $w$ | $?$ | $F$ |
| 1 | 0 | 1 | 0 | |
| 0 | 1 | 0 | ||
| 1 | 0 | 1 | 0 |
Рассмотрим последнюю строчку.
В ней $w = 1$, следовательно, нужно два столбца, равных $0$. Второй занят для $x$, первый содержит $1$. Значит, $z = 0$ может располагаться только в четвертом столбце. А первый столбец тогда будет закреплен за оставшейся переменной $y$:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $y$ | $x$ | $w$ | $z$ | $F$ |
| 1 | 0 | 1 | 0 | |
| 0 | 1 | 0 | ||
| 1 | 0 | 1 | 0 | 0 |
Так как в первой строке только одно значение $0$, то $w$ может быть равен только $0$, так как при $w = 1$ нужно два нулевых значения:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $y$ | $x$ | $w$ | $z$ | $F$ |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | ||
| 1 | 0 | 1 | 0 | 0 |
Во второй строчке $z = 1$, следовательно, w может быть равен только $0$:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $y$ | $x$ | $w$ | $z$ | $F$ |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | ||
| 1 | 0 | 1 | 0 | 0 |
А из первого вывода следует, что $y = 1$ в таком случае:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $y$ | $x$ | $w$ | $z$ | $F$ |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
Мы получили таблицу истинности с двумя одинаковыми строчками, что невозможно.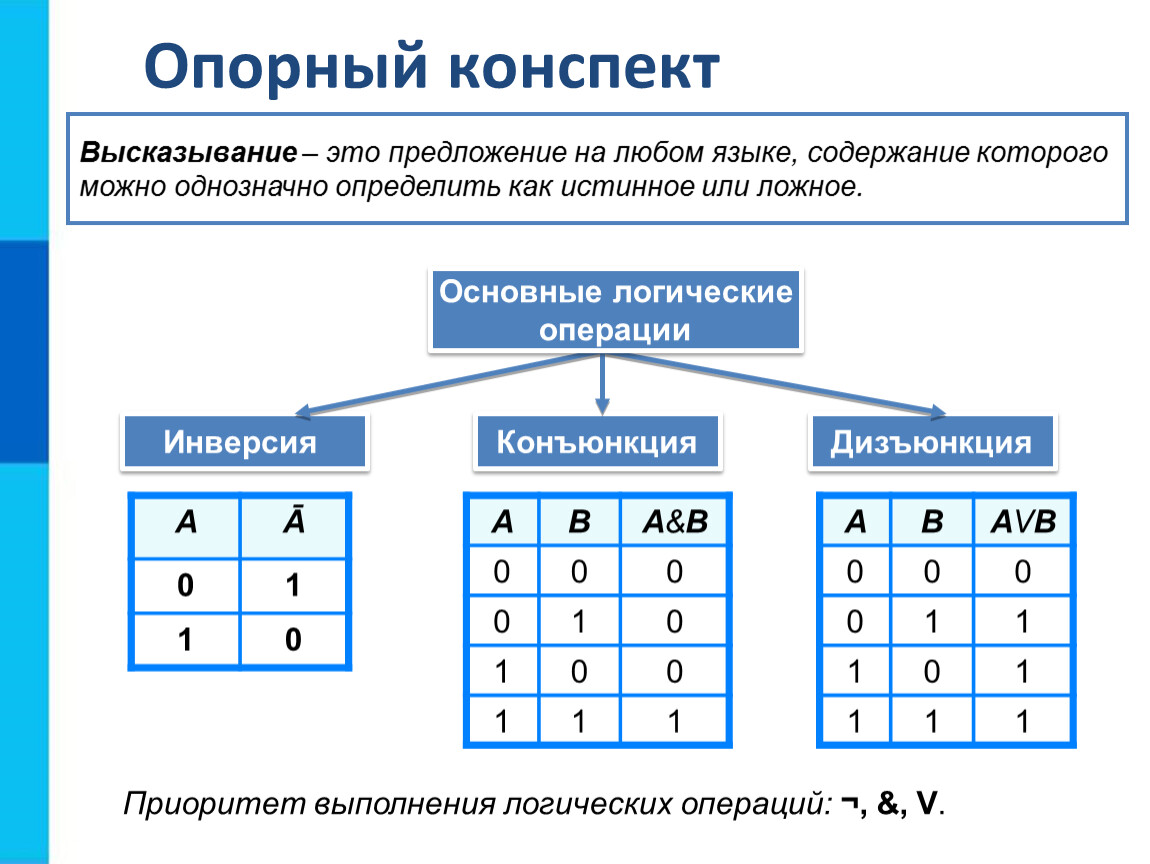
Мы пришли к противоречию. Значит, $w$ не может располагаться в третьем столбце.
Четвертый столбец
Пусть $w$ располагается в четвертом столбце таблицы истинности:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $?$ | $?$ | $?$ | $w$ | $F$ |
| 1 | 1 | 0 | ||
| 1 | 0 | |||
| 1 | 1 | 0 |
Так как из двух выводов следует, что $x = 0$, то для этого есть только второй столбец, как мы выяснили выше. Следовательно, таблица истинности примет вид:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $?$ | $x$ | $?$ | $w$ | $F$ |
| 1 | 0 | 1 | 0 | |
| 0 | 1 | 0 | ||
| 1 | 0 | 1 | 0 |
Из второго вывода следует, что если $w = 1$, то $z = 0$.
В первой строчке в первом столбце стоит $1$, во втором столбце находится $x$. Следовательно, для $z$ остается только третий столбец, а $y$ следом уходит в первый столбец:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $y$ | $x$ | $z$ | $w$ | $F$ |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | ||
| 1 | 0 | 1 | 0 |
Можно на этом остановиться, то разберем все строчки таблицы истинности на всякий случай.
Во второй строке $w = 1$. Значит, по второму выводу $z = 0$:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $y$ | $x$ | $z$ | $w$ | $F$ |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 0 |
Если во второй строке $y = 1$, то получим две одинаковые строчки в таблице истинности, что допустить нельзя.
Проверим наше главное выражение $(x \equiv ( w \lor y)) \lor ((w \rightarrow z ) \land (y \rightarrow w))$ для второй строчки при $y = 0$: $(0 \equiv ( 1 \lor 0)) \lor ((1 \rightarrow 0 ) \land (0 \rightarrow 1)) = (0 \equiv 1) \lor (0 \land 1) = 0 \lor 0 = 0$. То есть получаем ложное выражение, как нам и нужно. Следовательно, мы можем вот так заполнить вторую строчку:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $y$ | $x$ | $z$ | $w$ | $F$ |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 |
Осталась последняя строка.
Пусть $w = 0$.
Тогда $(x \equiv ( w \lor y)) \lor ((w \rightarrow z ) \land (y \rightarrow w)) = (0 \equiv ( 0 \lor 1)) \lor ((0 \rightarrow 1 ) \land (1 \rightarrow 0)) = (0 \equiv 1) \lor (1 \land 0) = 0 \lor 0 = 0$.
Пусть $w = 1$.
Тогда $(x \equiv ( w \lor y)) \lor ((w \rightarrow z ) \land (y \rightarrow w)) = (0 \equiv ( 1 \lor 1)) \lor ((1 \rightarrow 1 ) \land (1 \rightarrow 1)) = (0 \equiv 1) \lor (1 \land 1) = 0 \lor 1 = 1$.
Получается, что при $w = 1$ мы получаем истину, хотя должны были получить ложь. А при $w = 0$ получаем ожидаемую ложь. Следовательно, $w = 0$:
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| $y$ | $x$ | $z$ | $w$ | $F$ |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
То есть мы смогли расставить все переменные по столбцам и получить однозначную заполненную таблицу истинности.
Ответ
$yxzw$
ЕГЭ по информатике задание 2 — Информатика в школе
Главная » ЕГЭ
Опубликовано: Рубрика: ЕГЭАвтор: amlesson
Тема: «Построение и анализ таблиц истинности логических выражений»
Логическая функция F задаётся выражением:
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных w, x, y, z.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 1 | 1 | |
| 0 | 0 | 1 | ||
| 1 | 1 | 1 |
РЕШЕНИЕ
Задание №2 ЕГЭ по информатике подразумевает знание принципов алгебры логики и анализ таблиц истинности логических выражений
Строим таблицу истинности для данного логического выражения:
У нас имеется 4 переменные (x,y,z,w), по формуле N= 2^i , вычисляем количество строчек со значениями в данной таблицы( 2^4 = 16).
не z)
Отметим все истинные выражения зеленым цветом
| № строки | x | y | z | w | | 1 скобка | 2 скобка | 1 ≡ 2 | |
| (x ^ y ^ ) | (y v z v ) | F | |||||||
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 2 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 3 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 5 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 6 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 7 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 8 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 9 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 10 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 11 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 12 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 13 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 14 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 15 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 16 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
Выписываем «зеленые» строчки в отдельную найденную таблицу
| № строки | x | y | z | w | F |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 1 | 0 | 0 | 1 | 1 |
| 3 | 1 | 1 | 0 | 0 | 1 |
| 4 | 1 | 1 | 0 | 1 | 1 |
Сравниваем с исходной таблицей
| № строки | Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
| ??? | ??? | ??? | ??? | F | |
| 1 | 1 | 1 | 1 | 1 | |
| 2 | 0 | 0 | 1 | ||
| 3 | 1 | 1 | 1 |
Из показаний данных таблиц мы можем понять, что z обязательно должен стоять на 3 позиции.
| № строки | Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
| ??? | ??? | Z | ??? | F | |
| 1 | 1 | 1 | 0 | 1 | 1 |
| 2 | 0 | 0 | 0 | 1 | |
| 3 | 1 | 0 | 1 | 1 |
Далее находим совпадающие строки из таблиц:
найденной(4 строка) и исходной(1 строка)
найденной(2 строка) и исходной(3 строка)
| № строки | x | y | z | w | F |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 1 | 0 | 0 | 1 | 1 |
| 3 | 1 | 1 | 0 | 0 | 1 |
| 4 | 1 | 1 | 0 | 1 | 1 |
| № строки | Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
| ??? | ??? | Z | ??? | F | |
| 1 | 1 | 1 | 0 | 1 | 1 |
| 2 | 0 | 0 | 0 | 1 | |
| 3 | 1 | 0 | 0 | 1 | 1 |
Остается найти 2 строку исходной таблицы.
Анализируем найденную таблицу. Нам подходит только 1 строка, если подставить W на первое место
| № строки | Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
| W | ??? | Z | ??? | F | |
| 1 | 1 | 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 0 | 0 | 1 |
| 3 | 1 | 0 | 0 | 1 | 1 |
Далее, методом подбора, подставим X на второе место, а Y на 4 и решаем логическое выражение
| № строки | Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
| W | X | Z | Y | F | |
| 1 | 1 | 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 0 | 0 | 1 |
| 3 | 1 | 0 | 0 | 1 | 0 |
Видим, что в 3 строке исходной таблицы не совпадений, поэтому меняем местами X и Y
| № строки | Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
| W | Y | Z | X | F | |
| 1 | 1 | 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 0 | 0 | 1 |
| 3 | 1 | 0 | 0 | 1 | 1 |
и получаем ответ: wyzx
Ответ: wyzx
0 2 502 просмотров
Раздел 4: Частичные таблицы истинности
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1046
- P.
D. Магнус - Университет Олбани, Государственный университет Нью-Йорка через Плодовитость
D. МагнусЧтобы показать, что предложение является тавтологией, нам нужно показать, что оно равно 1 в каждой строке. Итак, нам нужна полная таблица истинности. Однако, чтобы показать, что предложение не является тавтологией, нам нужна только одна строка: строка, на которой предложение равно 0. Поэтому, чтобы показать, что что-то не является тавтологией, достаточно указать одну строку . таблица частичной истинности — независимо от того, сколько букв в предложении может быть в нем.
Рассмотрим, например, предложение ( \(U\) & \(T\) ) → ( \(S\) & \(W\) ). Мы хотим показать, что это , а не тавтологией, предоставив частичную таблицу истинности. Мы заполняем 0 для всего предложения. Главной связкой предложения является условная. Чтобы условие было ложным, антецедент должен быть истинным (1), а консеквент должен быть ложным (0). Итак, мы заносим это на стол:
| \(С\) | \(Т\) | \(У\) | \(Вт\) | (\(U\) & \(T\))→(\(S\) & \(W\)) |
| 1 0 0 |
Чтобы (\(U\) &\(T\)) было истинным, должны быть истинными и \(U\), и \(T\).
| \(С\) | \(Т\) | \(У\) | \(Вт\) | (\(U\) & \(T\))→(\(S\) & \(W\)) |
| 1 | 1 | 1 1 1 0 0 |
Теперь нам просто нужно сделать (\(S\)&\(W\)) ложным. Для этого нам нужно сделать хотя бы одно из \(S\) и \(W\) ложным. Мы можем сделать и \(S\), и \(W\) ложными, если захотим. Важно только то, что в этой строке все предложение оказывается ложным. Приняв произвольное решение, закончим таблицу таким образом:
| \(С\) | \(Т\) | \(У\) | \(Вт\) | (\(U\) & \(T\))→(\(S\) & \(W\)) |
| 1 | 1 | 0 | 1 1 1 0 0 0 0 |
Чтобы показать, что что-то является противоречием, требуется полная таблица истинности.
Показать, что что-то равно , а не , противоречие требует только однострочной таблицы частичной истинности, где предложение истинно в этой одной строке.
Предложение условно, если оно не является ни тавтологией, ни противоречием. Таким образом, чтобы показать, что предложение условно, требуется двухстрочная таблица частичной истинности: предложение должно быть истинным в одной строке и ложным в другой. Например, мы можем показать, что приведенное выше предложение зависит от этой таблицы истинности:
.| \(С\) | \(Т\) | \(У\) | \(Вт\) | (\(U\) & \(T\))→(\(S\) & \(W\)) |
0 0 | 1 1 | 1 0 | 0 0 | 1 1 1 0 0 0 0 0 0 1 1 0 0 0 |
Обратите внимание, что есть много комбинаций значений истинности, которые сделали бы предложение истинным, поэтому есть много способов, которыми мы могли бы написать вторую строку.
Чтобы показать, что предложение является , а не контингентным, требуется предоставить полную таблицу истинности, потому что это требует показать, что предложение является тавтологией или что оно является противоречием. Если вы не знаете, является ли конкретное предложение контингентным, то вы не знаете, нужна ли вам полная или частичная таблица истинности. Вы всегда можете начать работу над полной таблицей истинности. Если вы закончите ряды, которые показывают, что предложение является условным, вы можете остановиться. Если нет, то заполните таблицу истинности. Даже если две тщательно отобранные строки покажут, что условное предложение является условным, нет ничего плохого в том, чтобы заполнить больше строк.
Чтобы показать, что два предложения логически эквивалентны, необходимо предоставить полную таблицу истинности. Чтобы показать, что два предложения логически не эквивалентны, требуется всего лишь однострочная таблица частичной истинности: Составьте таблицу так, чтобы одно предложение было истинным, а другое — ложным.
Чтобы показать, что набор предложений непротиворечив, необходимо предоставить одну строку таблицы истинности, в которой все предложения истинны. Остальная часть таблицы не имеет значения, поэтому подойдет однострочная таблица частичной истинности. С другой стороны, чтобы показать, что набор предложений несовместим, требуется полная таблица истинности: вы должны показать, что в каждой строке таблицы хотя бы одно из предложений ложно.
Чтобы показать, что аргумент действителен, требуется полная таблица истинности. Чтобы показать, что аргумент недействителен , требуется только предоставить однострочную таблицу истинности: если вы можете создать строку, в которой все посылки верны, а заключение ложно, то аргумент недействителен.
Вот таблица, в которой показано, когда требуется полная таблица истинности, а когда частичная таблица истинности.
тавтология?
противоречие? контингент
?
аналог?
соответствует?
действителен?
| ДА | НЕТ |
полная таблица истинности полная таблица истинности двухстрочная таблица частичной истинности полная таблица истинности однострочная таблица частичной истинности полная таблица истинности | однострочная таблица частичной истинности однострочная таблица частичной истинности полная таблица истинности однострочная таблица частичной истинности полная таблица истинности однострочная таблица частичной истинности |
Таблица 3.
2: Вам нужна полная или частичная таблица истинности? Это зависит от того, что вы пытаетесь показать.
Эта страница под названием Раздел 4: Частичные таблицы истинности распространяется по лицензии CC BY-SA и была создана, изменена и/или курирована П.Д. Магнус (Плодовитость).
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ПД Магнус
- Лицензия
- CC BY-SA
- Теги
Таблицы истинности :: Вычислительное ядро K-State
Ресурсы
- Слайды
Видеоскрипт
Обзор
Теперь, когда мы рассмотрели некоторые операторы и некоторые правила, управляющие булевой алгеброй, давайте рассмотрим пример некоторой булевой логики. Много раз, что вы увидите в компьютерных науках, особенно когда вы имеете дело с булевой логикой и сложными алгоритмами, наши таблицы истинности, таблицы истинности демонстрируют все различные варианты для каждой логической переменной внутри оператора логической логики, а также как то, что на самом деле производят эти конкретные факты для этих переменных. Итак, давайте посмотрим на пример, который мы уже сделали с end. Итак, мы уже изучили утверждения A, B и C. Вы уже видели, как выглядит диаграмма Венна для этого, но мы также можем исследовать, как это выглядит снова здесь, всего за секунду, но давайте посмотрим во всех возможных значениях, которые мы могли бы фактически ввести для A, B и C.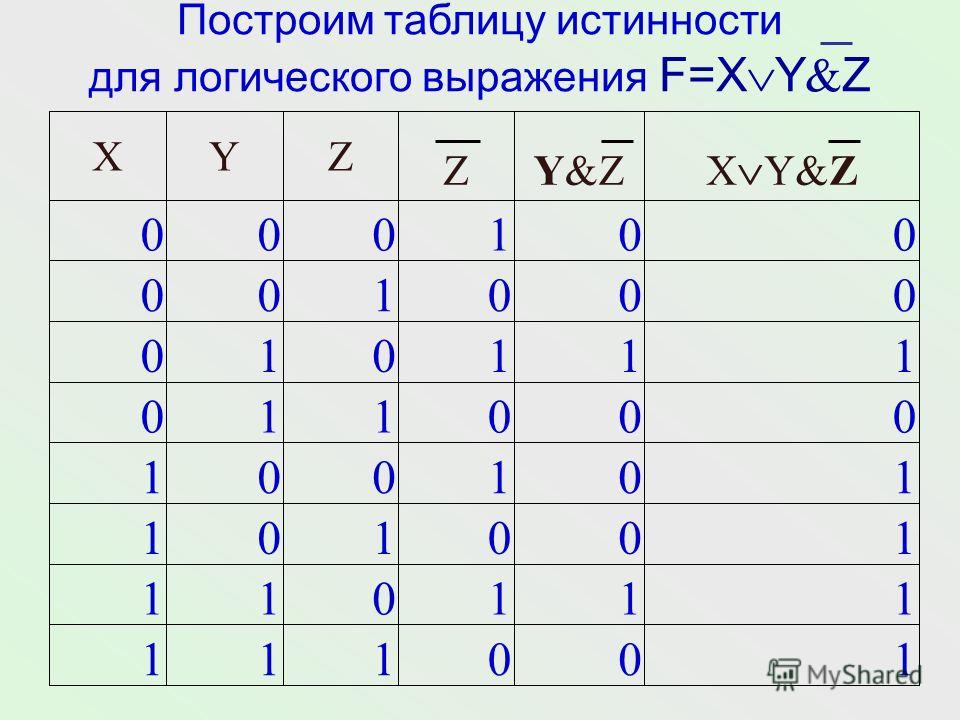
И если вы помните, у нас будет только два двоичных значения: либо единица, либо ноль, либо истина, либо ложь. Теперь оба работают как синонимы. И то, и другое вы найдете в таблицах истинности. И на самом деле, в примерах, с которыми вы будете работать, мы действительно используем единицы и нули для истинности и ложности. Итак, если вы помните, единица означает истину, ноль означает ложь. Но давайте посмотрим, как мы можем заполнить нашу таблицу истинности этими конкретными значениями. Теперь я собираюсь пойти дальше и использовать T для истинного и ложного. Но, как вы можете себе представить, вы можете заменить единицу на истину и ноль на ложь, и все будет идентично.
Итак, что мы на самом деле должны начать с нашей таблицы истинности здесь, поскольку каждый из наших столбцов здесь представляет каждую из наших переменных или каждый из наших фактов как часть нашего логического логического утверждения. простой способ заполнить это, мы собираемся заполнить все различные возможности.
Итак, если мы тщательно пройдемся по каждой из наших переменных, вы можете обнаружить, что каждая из них имеет два возможных значения. И затем, если мы умножим это, если это степень двойки, у нас будет восемь возможных результатов или комбинаций этих значений. Вы заметите, что в моей таблице истинности восемь разных строк. Это будет представлять все различные комбинации, которые у меня есть для этого оператора логической логики. Теперь, как правило, когда мы пытаемся выяснить, сколько различных комбинаций у нас есть, количество вариантов, которые у нас есть для нашей переменной, в степени количества переменных, которые у нас есть на самом деле, так что в этом случае будет два в степени три . Итак, два раза, два раза. Чтобы написать два раза два, четыре раза два равно восьми. Это общее количество возможных комбинаций истин или наших фактов, которые мы на самом деле могли бы получить из этого утверждения логической логики.
Заполнение таблицы истинности
Итак, давайте остановимся на этом и соответствующим образом заполним нашу таблицу истинности.
Самый простой способ начать работу с нашей таблицей истинности — сначала перейти на один столбец вниз, потому что есть своего рода общая схема, которой вы можете следовать при ее заполнении. Если мы просто заполним половину наших строк значением false, а затем половину строк значением true, мы сможем это решить. Таким образом, столбец заполняется довольно легко. Этот шаблон, которому вы можете следовать для второго столбца, работает как таковой, если вы просто заполните половину ложных значений или половину строк, которые были ложными в первом столбце, истинными, а половину из них ложными и подобными шаблон для наборов истин здесь внизу. Итак, если я нарисую воображаемую линию прямо здесь, посередине, мы можем попытаться сначала заполнить все ложные значения. Итак, я хочу заполнить половину из них ложным, а половину — истинным. Итак, давайте сначала начнем с false. Итак, ложь, ложь, а затем Истина, правда. Здесь, внизу, я собираюсь сделать то же самое. ложный, ложный, истинный, истинный.
И я собираюсь продолжить ту же схему, где я собираюсь заполнить половину того, что я только что заполнил и увидел, ложными, а половину того, что я только что заполнил, истинным. Итак, для этого набора ложных значений здесь у меня будет ложное истинное. С набором у меня будет false true. Теперь этот шаблон не всегда верен, особенно когда вы начинаете добавлять четвертый столбец. Но с тремя переменными довольно легко заполнить, используя этот конкретный шаблон. Но если вы обнаружите, что заполняете таблицу истинности для более чем трех фактов, все, что мы на самом деле делаем, — это исчерпывающее выписывание всех различных комбинаций истинных и ложных значений или каждого набора переменных. Теперь давайте пройдемся и попробуем оценить вывод здесь или нашу таблицу истинности. Это конкретное утверждение довольно легко сделать с a, b и c. Поскольку мы уже видели, что с оператором and обе части оператора должны быть истинными, чтобы все операторы были оценены как истинные.
Итак, в моем выводе здесь я собираюсь написать, что этот набор фактов оценивает этот ряд фактов для нашего оператора логической логики выше.
Так что я просто поставлю здесь номера строк 123. А затем давайте напишем наш вывод. Здесь, таким образом, ложь, ложь и ложь будут оцениваться как ложь, потому что ни одна из сторон не является истинной, а похожие идентификаторы здесь, ложь и ложь, являются ложными. И правда. также Ложь. Ложь и правда есть Ложь. Ложь и Ложь. Ложь и правда. И заметьте, я оцениваю это слева направо, справа, потому что мое утверждение — это a, b и c, поэтому я сначала оцениваю A и B, а затем добавляю этот результат к C. Итак, ложно и правда есть Ложь. Ложь и правда есть ложь. правда и ложь есть ложь, ложь и ложь есть ложь. правда и ложь есть ложь, ложь и правда есть ложь. Правда и правда есть правда. Но истинное и ложное есть ложное. Правда и правда есть правда, правда и правда есть правда. Теперь в нашей таблице истинности у нас есть завершенная оценка того, что на самом деле могут охватывать наши утверждения логической логики A, B и C, так что у нас есть все различные комбинации значений или истинность A, B и C.
И затем мы также оценили эти значения истинности как часть нашего вывода. Итак, теперь мы знаем, когда это утверждение верно, а когда ложно.
Диаграмма Венна
В лекции в предыдущем видео мы видели, как выглядел оператор AND для нашей диаграммы Венна. Итак, давайте нарисуем это здесь, просто чтобы у нас снова было то, на что это похоже, и или утверждение точно так же, как у нас было в нашей таблице истинности, мы только собираемся заполнить то место, где истинное B истинно, а C истинно, где, по сути, это означает, что выходные данные нашей таблицы стран верны. Итак, если я просто поставлю здесь a, b и c, а затем мы также вспомним, у нас есть квадрат снаружи, который представляет все, что не является A, B или C. Я приведу вам еще несколько примеров этого. или там, где я на самом деле дам вам таблицу истинности, тогда вы попытаетесь сгенерировать оператор булевой логики, диаграмму Венна и даже некоторые логические вентили.
Логические элементы
Но давайте попробуем нарисовать логические элементы и для этого.
