Формула действующего значения силы тока и напряжения. Действующие значения силы тока и напряжения

Физический смысл данных понятий примерно таков же, как физический смысл средней скорости или других величин, усредненных по времени. В различные моменты времени сила переменного тока и его напряжение принимают разные значения, поэтому говорить о силе переменного тока вообще можно лишь условно.

Вместе с тем совершенно очевидно, что различные токи имеют различные энергетические характеристики – они производят разную работу за один и тот же промежуток времени. Произведенная током работа принята за основу при определении действующего значения силы тока. Задаются определенным промежутком времени и рассчитывают работу, совершенную переменным током за этот промежуток времени. Затем, зная эту работу, производят обратное вычисление: узнают силу постоянного тока, который произвел бы аналогичную работу за тот же промежуток времени. То есть производят усреднение по мощности. Вычисленная сила гипотетически протекающего через тот же проводник постоянного тока, производящего ту же самую работу и есть – действующее значение исходного переменного тока. Аналогично поступают и с напряжением. Данный расчет сводится к определению величины такого интеграла:

Откуда берется данная формула? Из хорошо известной формулы для мощности тока, выражаемой через квадрат его силы.

Действующие значения периодических и синусоидальных токов

Вычислять действующее значение для произвольных токов – занятие малопродуктивное. Зато для периодического сигнала данный параметр может оказаться весьма полезным. Известно, что любой периодический сигнал может быть разложен в спектр. То есть, представлен как конечная или бесконечная сумма синусоидальных сигналов. Поэтому для определения величины действующего значения такого периодического тока нам нужно знать, как вычислять действующее значение простого синусоидального тока. В итоге, сложив действующие значения нескольких первых гармоник с максимальной амплитудой, мы получим приближенное значение действующего значения тока для произвольного периодического сигнала. Подставляя в вышеприведенную формулу выражение для гармонического колебания, получим такую приближенную формулу.

Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля.

В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются

периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, — периодом Т. Для периодического тока имеем

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i — мгновенное значение тока ;

u – мгновенное значение напряжения ;

е — мгновенное значение ЭДС ;

р — мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ).

Амплитуда тока;

Амплитуда напряжения;

Амплитуда ЭДС.

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи.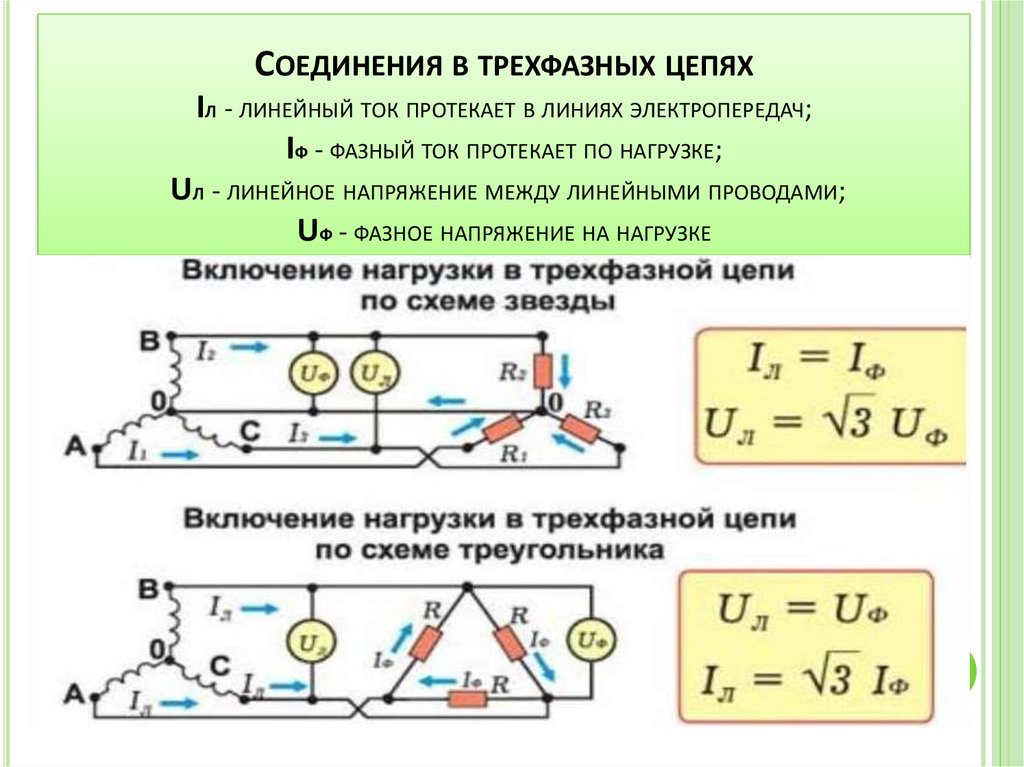 Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:

Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t =0): и —начальной фазой ( ).

Величину , характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода

Т изменяется на рад., то угловая частота есть, гдеf– частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .

Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:

Векторное изображение синусоидально изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное

) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:

Каждый из этих токов синусоидален и может быть представлен уравнением

Результирующий ток также будет синусоидален:

Определение амплитудыи начальной фазыэтого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

.

Построение векторной диаграммы в масштабе позволяет определить значения ииз диаграммы, после чего может быть записано решение для мгновенного значенияпутем формального учета угловой частоты:.

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т.

д.) нельзя судить по амплитуде этого тока.

Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.

Действующее значение переменного тока — это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.

Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.

Мощность Р постоянного тока I, проходящего через сопротивление r, будет Р = Р 2 r.

Мощность переменного тока выразится как средний эффект мгновенной мощности I 2 r за целый период или среднее значение от (Im х sinωt) 2 х rза то же время.

Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √M,

Величина I называется действующим значением переменного тока.

Среднее значение i2 при переменном токе определим следующим образом.

Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.

Действующее значение переменного тока

Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода, будучи возведены в квадрат, дают положительные величины.

Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно1/2I 2 m. Следовательно, М = 1/2I 2 m

Так как действующее значение I переменного тока равно I = √M, то окончательно I = Im / √2

Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:

U = Um / √2,E= Em / √2

Действующие значения переменных величин обозначаются прописными буквами без индексов (I, U, Е).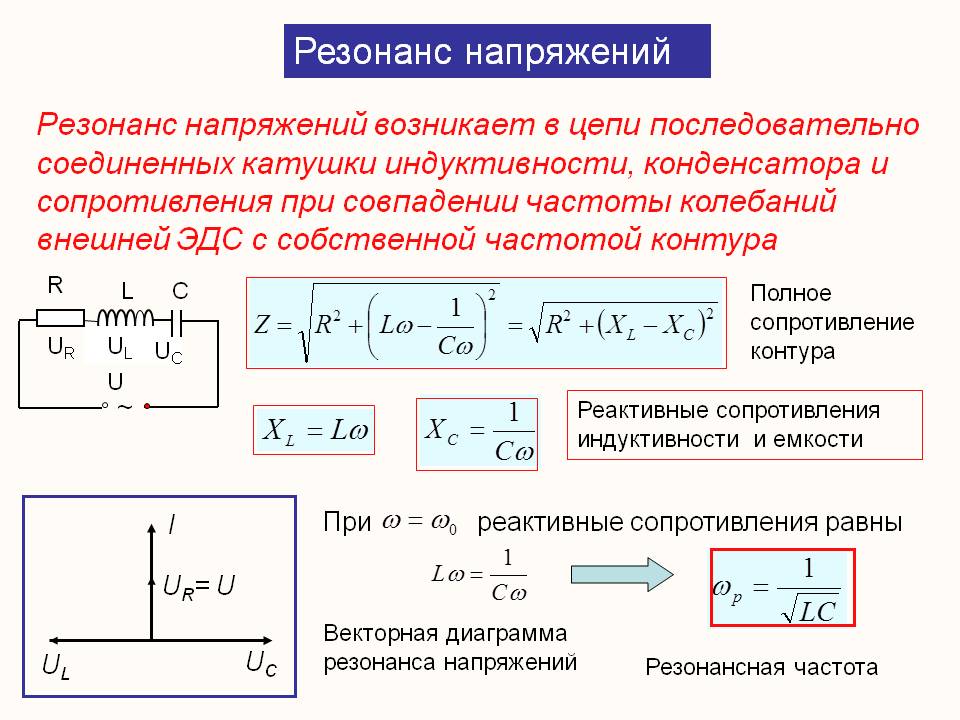

На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения.

При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √2 раз. От этого расположение векторов на диаграмме не изменяется.

Метод измерения действующего значения напряжения с применением МК / Хабр

    В данном посте речь пойдет об одном из вариантов измерения действующего значения напряжения и частоты сети на 8-ми битном микроконтроллере PIC18. При желании, можно метод перенести на любой другой МК, вплоть до всеми любимых ARDUINO (если они поддерживают реализацию прерываний по таймеру с частотой 5-10 кГц).
    Также, рассматриваемый метод позволяет измерять частоту сетевого напряжения без использования внешних дополнительных средств, таких как компараторы. Но, при этом приходится жертвовать либо временными ресурсами МК, либо точностью измерения частоты.
    Почему важно измерять действующее значение, а не какое либо другое, например, средневыпрямленное? Большинство “китайских” электронных вольтметров измеряют сетевое напряжение по средневыпрямленному значению. Методика измерения следующая: за период сетевого напряжения делается выборка из N значений амплитуды напряжения, результаты суммируются (без знака), делятся на N (усредняются), после чего полученный результат умножается на коэффициент

    Указанный коэффициент определяет зависимость действующего значения синусоидального (!) сигнала от средневыпрямленного.
    Такая методика измерения проста, не требует много ресурсов микроконтроллера (как временных, так и ресурсов памяти). Основным недостатком такой методики измерения является большая ошибка измерения на несинусоидальных сигналах.
    Как все знают, изменение сигнала сетевого напряжения подчиняется синусоидальному закону (вследствие применения синхронных генераторов на электростанции), с частотой изменения сигнала 50 Гц (60 Гц). Однако, на практике вследствие влияния сторонних факторов (в основном подключение к сети мощных нелинейных нагрузок), а также применения инверторов с квазисинусоидальным выходным напряжением (см. рисунок), синусоида напряжения либо значительно искажается, либо заменятся прямоугольными импульсами. В таких случаях указанный выше метод измерения даст очень большую погрешность (например, в квазисинусоидальных инверторах выходное напряжение, измеренное “китайским» вольтметром может быть равно 180-200В, в то время как действующее напряжение будет равно 220В ).

    Например, напряжение у меня дома

    Почему важно измерять именно действующее значение напряжения (тока)? Потому что именно действующие (еще называют его эффективными) значения напряжения и тока определяют работу электрической системы (грубо говоря, электронагреватель выделяет тепло в прямой зависимости от действующих значений напряжения и тока сети).
    Действующее значение измеряемой периодической величины рассчитывается по формуле

    Или после дискретизации получим

    Т.е. нам нужно делать выборку ряда значений за период сетевого напряжения, просуммировать значения квадратов точек выборки, поделить на количество точек за период (при определении количества точек выборки не забываем про теорему Котельникова-Шеннона), и взять квадратный корень из полученного результата.
    Вроде бы ничего сложного, если бы не но:
      1)  Каждый период точки выборки набираются заново, что увеличивает погрешность измерения;
      2)  В реальной сети, около нуля напряжения, могут встречаться как “нулевые полки”, так и повторные переходы через ноль напряжения, что значительно внесет погрешность в измерение.
    С первым пунктом будем бороться измерением измерением суммы квадратов точек выборки за каждый полупериод, после чего суммируя n-ую сумму квадратов с (n+1)-й и откидывая (n-1)-ую.
    Со вторым пунктом будем бороться введением зон нечувствительности по напряжению (введем границы напряжения перехода через ноль с положительной и отрицательной сторон) обычно 5-10 В в обе стороны, а также зон нечувствительности по частоте (ограничим допустимую частоту сигнала напряжения).

    Таким образом, мы получим рассчитанное значение действующего значения сетевого напряжения за период на каждом полупериоде сетевого напряжения.

    Частота напряжения вычисляется по формуле:

где Fд — частота дискретизации (для удобства и увеличения точности измерения частоты выбрана равной 10 кГц (период выборки — 100 мкс)).
    Теперь рассмотрим структурную схему измерительной части (в реальной схеме следует добавить фильтрующие и защитные элементы).

Внимание! В данном методе измерения не реализована гальваническая развязка микроконтроллера от сети.     Гальваноразвязка реализуется на стороне цифрового интерфейса передачи данных от микроконтроллера. 2/R) — чтобы не превышала допустимой мощности резисторов. Плечи дифференциального усилителя тоже делаем равными. Тогда, напряжение в точке 1 рассчитывается по формуле:

А напряжение в точке 1 будет иметь вид:

    Также, половина опорного напряжения подается на один из каналов АЦП. Это позволяет в постоянном режиме (например, один раз за период) определять положение уровня нуля измеряемого напряжения.
Т.е. мы обошлись операционным усилителем с однополярным питанием, и наш входной сигнал в точке 1 изменяется от 0 до Uоп. Такой способ дает достаточно точные результаты, по сравнению, например, с выпрямлением напряжения с помощью диодов.
    Расчет делителя и коэффициента АЦП сводится к следующему:

где A и В — замеры АЦП (за вычетом измеренного значения нуля сигнала — AN1) для текущего и предыдущего полупериодов; N1, N2 — число замеров для текущего и предыдущего полупериодов; Nadс — разрядность АЦП; U’оп — опорное напряжение за вычетом зон нелинейности (нечувствительности) операционного усилителя (обычно 0,6 В).
    Расчет делителя удобно проводить считая сигнал постоянным, приведенным к амплитуде синусоидального, а не синусоидальным. Тогда действующее значение сигнала равно амплитудному и равно значению каждого замера.
Например, нужно рассчитать делитель для измерения максимального значения 420В переменного тока:

Сопротивление Ra выбирается в диапазоне от 500 кОм до 1500 кОм. По выбранному сопротивлению Ra рассчитывается Rb.
    В итоге, алгоритм расчета действующего значения напряжения и частоты примет вид:

При этом часть затратных расчетов (деление, извлечение корня) можно перенести из прерывания в основную программу.

    При расчете действующих значений на 8-ми битном МК целесообразно пользоваться целочисленными методами (с использованием масштабных коэффициентов) не прибегая к расчетам с плавающей запятой, а также упрощать по возможности арифметические операции (деление, изъятие квадратного корня и проч.). Это значительно экономит ресурсы МК.

Что такое размах сигнала?

По

• Гэвин Райт

Что такое размах (размах)?

Размах (pk-pk) — это разница между самым высоким и самым низким значениями сигнала. В переменном токе (AC) значение размаха в два раза превышает пиковое значение или в 2,828 раза превышает среднеквадратичное значение (RMS). Пиковое напряжение обозначается как V _ПП .

Разница между размахом, пиком, амплитудой и среднеквадратичным значением

При питании от сети переменного тока (AC) напряжение повышается и понижается по плавной синусоидальной волне. Напряжение увеличивается до максимального положительного напряжения, возвращается к нулю, затем к максимальному отрицательному значению и снова к нулю, чтобы начать сначала. Поскольку напряжение меняется со временем, существуют различные способы его выражения в зависимости от того, какой аспект вы пытаетесь подчеркнуть.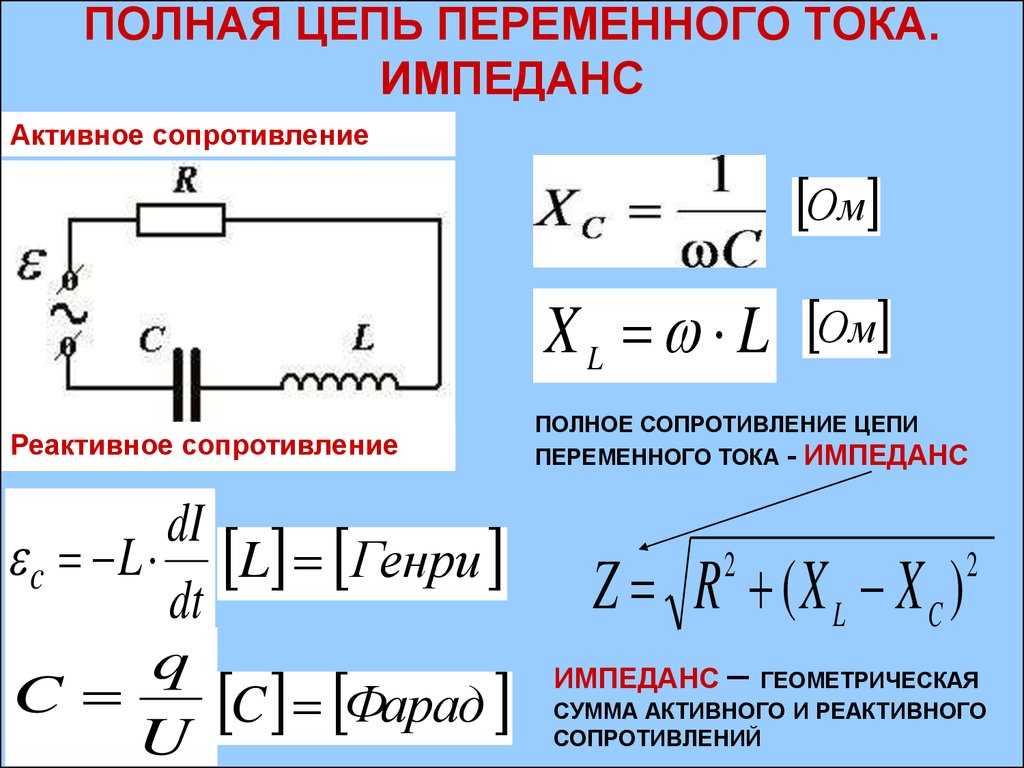

Пиковое напряжение, обозначенное как В _P — максимальное значение напряжения по сравнению с нулевым напряжением. Амплитуда аналогична пиковому значению, поскольку она выражает самое высокое значение сигнала. Значения пика и амплитуды чаще используются при анализе формы сигнала и реже при работе с электричеством переменного тока.

Размах напряжения, показанный как V _PP , представляет собой разницу между самым высоким и самым низким значениями напряжения переменного тока. В приложениях переменного тока значение размаха будет в два раза больше пикового значения. Значение размаха больше используется при анализе формы сигнала или при проектировании усилителей и реже при работе с электричеством переменного тока.

Размах — это разница между самым высоким и самым низким значениями сигнала. Форма волны показывает, как переменный ток (AC) изменяется во времени.

Среднеквадратичное (RMS) напряжение, выраженное как V _RMS , является эквивалентным напряжением постоянного тока (DC) мощности переменного тока. Поскольку напряжение переменного тока со временем повышается и понижается, оно не всегда обеспечивает пиковую максимальную мощность. Среднеквадратичное значение дает эффективное напряжение переменного тока для расчета мощности и других расчетов.

Например, среднеквадратичное значение используется при расчете закона Ома для переменного тока. Пиковое значение равно удвоенному квадратному корню из двух V _RMS или примерно 2,8284 V _RMS . RMS чаще всего используется в электрических работах переменного тока.

Чтобы проиллюстрировать разницу между пиковым, размахом и среднеквадратичным напряжением, мы можем использовать стандартную электроэнергию для жилых домов Северной Америки. Большинство людей знают только, что это 120 вольт, но могут не знать, какого типа. Это 120 вольт RMS (V _RMS ). Это удобно для расчета мощности электроприборов.

120 В _RMS равно пиковому напряжению 170 вольт (V _P ), поэтому из стены может выходить до 170 вольт. 170 В _P равно 340 вольт от пика до пика (V _PP ), что является разницей между +170 В и -170 В.

Математически это можно выразить так:

В _PP = 2 x В _P = 2 √ 2 x В _СКЗ

См. также: сопротивление , ампер , полное сопротивление , реактивное сопротивление , осциллограф

Последнее обновление: октябрь 2022 г.

Продолжить чтение О размахе (pk-pk)

• Обеспечение энергоснабжения центра обработки данных с помощью регулярного обслуживания ИБП

• Основы инфраструктуры центра обработки данных предотвращают простои

• Что нужно знать об управлении питанием пограничных устройств

• Влияние типов шума в системах передачи данных на сеть

• Бесперебойное питание в центре обработки данных: выбор между устойчивостью и безотказной работой

СИЭМ

Управление информацией и событиями безопасности (SIEM) — это подход к управлению безопасностью, который объединяет функции управления информацией о безопасности (SIM) и управления событиями безопасности (SEM) в одной системе управления безопасностью.

Сеть

• сетевой трафик

  Сетевой трафик — это объем данных, которые перемещаются по сети в любое заданное время.

• динамический и статический

  В общем, динамический означает «энергичный, способный к действию и/или изменению или сильный», тогда как статический означает «неподвижный или фиксированный».

• MAC-адрес (адрес управления доступом к среде)

  MAC-адрес (адрес управления доступом к среде) — это 12-значное шестнадцатеричное число, назначаемое каждому устройству, подключенному к сети.

Безопасность

• контрольная сумма

  Контрольная сумма — это значение, представляющее количество битов в передаваемом сообщении, которое используется ИТ-специалистами для обнаружения …

• информация о безопасности и управление событиями (SIEM)

  Управление информацией о безопасности и событиями (SIEM) — это подход к управлению безопасностью, объединяющий информацию о безопасности . ..

• Злая Корпорация

  Evil Corp — международная сеть киберпреступников, использующая вредоносное ПО для кражи денег с банковских счетов жертв и для …

ИТ-директор

• зеленые ИТ (зеленые информационные технологии)

  Green IT (зеленые информационные технологии) — это практика создания и использования экологически устойчивых вычислений.

• ориентир

  Контрольный показатель — это стандарт или точка отсчета, которые люди могут использовать для измерения чего-либо еще.

• пространственные вычисления

  Пространственные вычисления широко характеризуют процессы и инструменты, используемые для захвата, обработки и взаимодействия с трехмерными данными.

HRSoftware

• самообслуживание сотрудников (ESS)

  Самообслуживание сотрудников (ESS) — это широко используемая технология управления персоналом, которая позволяет сотрудникам выполнять множество связанных с работой . ..

• платформа обучения (LXP)

  Платформа обучения (LXP) — это управляемая искусственным интеллектом платформа взаимного обучения, предоставляемая с использованием программного обеспечения как услуги (…

• Поиск талантов

  Привлечение талантов — это стратегический процесс, который работодатели используют для анализа своих долгосрочных потребностей в талантах в контексте бизнеса …

Служба поддержки клиентов

• BOPIS (купить онлайн, забрать в магазине)

  BOPIS (купить онлайн, забрать в магазине) — это бизнес-модель, которая позволяет потребителям делать покупки и размещать заказы в Интернете, а затем забирать …

• аналитика в реальном времени

  Аналитика в реальном времени — это использование данных и связанных с ними ресурсов для анализа, как только они поступают в систему.

• маркетинг баз данных

  Маркетинг баз данных — это систематический подход к сбору, консолидации и обработке данных о потребителях.

Эффективное напряжение МОП-транзистора Калькулятор

✖Напряжение на оксиде из-за заряда на границе оксид-полупроводник, а третий член обусловлен плотностью заряда в оксиде.ⓘ Напряжение на оксиде [В GS ]		AbvoltAttovoltCentivoltDecivoltDekavoltEMU of Electric PotentialESU of Electric PotentialFemtovoltGigavoltHectovoltKilovoltMegavoltMicrovoltMillivoltNanovoltPetavoltPicovoltPlanck VoltageStatvoltTeravoltVoltWatt per AmpereYoctovoltZeptovolt	+10% -10%
✖Threshold voltage of transistor is the minimum gate to source voltage that необходим для создания проводящего пути между клеммами истока и стока. Это важный фактор для поддержания энергоэффективности.ⓘ Пороговое напряжение [В T ]		AbvoltAttovoltCentivoltDecivoltDekavoltEMU of Electric PotentialESU of Electric PotentialFemtovoltGigavoltHectovoltKilovoltMegavoltMicrovoltMillivoltNanovoltPetavoltPicovoltPlanck VoltageStatvoltTeravoltVoltWatt per AmpereYoctovoltZeptovolt	+10% -10%

✖Эффективное напряжение или напряжение перегрузки называется превышением напряжения на оксиде над тепловым напряжением. ⓘ Эффективное напряжение MOSFET [В или ]

AbvoltAttovoltCentivoltDecivoltDekavoltEMU электрического потенциалаESU электрического потенциалаFemtovoltGigavoltHectovoltKilovoltMegavoltMicrovoltMillivoltNanovoltPetavoltPicovoltPlanck VoltageStatvoltTeravoltVoltWatt per AmpereYoctovoltZeptovolt

⎘ Копировать

👎

Формула

Перезагрузить

👍

Эффективное напряжение MOSFET Solution

ШАГ 0: Сводка предварительного расчета

ШАГ 1: Преобразование входных данных в базовую единицу

Напряжение на окисле: 2 В —> 2 В Преобразование не требуется
Пороговое напряжение: 50 В —> 50 В Преобразование не требуется

ШАГ 2: Вычисление формулы

ШАГ 3: Преобразование результата в единицу измерения

-48 Вольт —> Преобразование не требуется

< 10+ MOS Калькуляторы полевых транзисторов (MOSFET)

Ток, протекающий через индуцированный канал в транзисторе

Выходной ток = (Подвижность электронов на поверхности канала * Оксидная емкость * (Ширина канала / Длина канала) * Эффективное напряжение или напряжение перегрузки) * Напряжение между стоком и истоком Идти

Проводимость канала MOSFET с использованием Vgs

Проводимость канала = Подвижность электронов на поверхности канала * Оксидная емкость * (Ширина канала / Длина канала) * (Эффективное напряжение или перенапряжение — пороговое напряжение) Идти

Проводимость канала МОП-транзисторов

Проводимость канала = Подвижность электронов на поверхности канала * Емкость оксида * (Ширина канала / Длина канала) * Напряжение на оксиде Идти

Величина электронного заряда в канале MOSFET

Электронный заряд в канале = оксидная емкость * ширина канала * длина канала * эффективное напряжение или напряжение перегрузки Идти

Ток стока, когда полевой МОП-транзистор работает как источник тока, управляемый напряжением

Ток стока = 1/2 * Параметр крутизны процесса * Коэффициент сжатия * (Напряжение на оксиде — пороговое напряжение) ^ 2 Идти

Параметр крутизны MOSFET

Параметр крутизны MOSFET = Подвижность электронов на поверхности канала * Оксидная емкость * Коэффициент сжатия Идти

Электронная скорость дрейфа канала в транзисторе NMOS

Скорость дрейфа электронов = подвижность электронов на поверхности канала * электрическое поле по длине канала Идти

Параметр крутизны процесса MOSFET

Параметр крутизны процесса = Подвижность электронов на поверхности канала * Оксидная емкость Идти

Электрическое поле по длине канала NMOS-транзистора

Электрическое поле по длине канала = напряжение между стоком и истоком/длина канала Идти

Эффективное напряжение MOSFET

Эффективное напряжение или напряжение перегрузки = напряжение на оксиде — пороговое напряжение. Идти

Эффективное напряжение формулы MOSFET

Эффективное напряжение или напряжение перегрузки = напряжение на оксиде — пороговое напряжение.
В _ов = В _ГС -В _Т

Что такое пороговое напряжение?

Значение напряжения на оксиде, при котором в области канала накапливается достаточное количество подвижных электронов для образования проводящего канала, называется пороговым напряжением и обозначается как V _t .

Объясните весь процесс формирования области канала MOSFET конденсатора с плоскими пластинами.

Затвор и область канала МОП-транзистора образуют плоский конденсатор с
оксидный слой действует как диэлектрик конденсатора. Положительное напряжение затвора вызывает накопление положительного заряда на верхней пластине конденсатора (электроде затвора). Соответствующий отрицательный заряд на нижней пластине формируется электронами в индуцированном канале. Таким образом, электрическое поле развивается в вертикальном направлении. Именно это поле управляет количеством заряда в канале и, таким образом, определяет проводимость канала и, в свою очередь, ток, который будет течь через канал при приложении напряжения.

Как рассчитать эффективное напряжение MOSFET?

Калькулятор эффективного напряжения MOSFET использует Эффективное напряжение или напряжение перегрузки = Напряжение на оксиде. Пороговое напряжение для расчета эффективного напряжения или напряжения перегрузки. Эффективное напряжение MOSFET представляет собой превышение напряжения оксида над пороговым напряжением и представляет собой величину. что определяет заряд в канале. Эффективное напряжение или напряжение перегрузки обозначается цифрой 9.0380 В _ов символ.

Как рассчитать эффективное напряжение МОП-транзистора с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для эффективного напряжения MOSFET, введите напряжение на оксиде (V _GS ) и пороговое напряжение (V _T ) и нажмите кнопку расчета. Вот как можно объяснить расчет эффективного напряжения MOSFET с заданными входными значениями -> -48 = 2-50 .

Часто задаваемые вопросы

Что такое эффективное напряжение MOSFET?

Эффективное напряжение МОП-транзистора представляет собой превышение напряжения оксида над пороговым напряжением и является величиной, определяющей заряд в канале, и представляется как В _ov = В _GS -V _T или Эффективное напряжение или напряжение перегрузки = Напряжение на оксиде — пороговое напряжение . Напряжение на оксиде из-за заряда на границе оксид-полупроводник, а третий член обусловлен плотностью заряда в оксиде. Пороговое напряжение транзистора — это минимальное напряжение затвор-исток, необходимое для создания проводящего пути между истоком. и сливные терминалы. Это важный фактор для поддержания энергоэффективности.

Как рассчитать эффективное напряжение МОП-транзистора?

Эффективное напряжение МОП-транзистора представляет собой превышение напряжения оксида над пороговым напряжением и является величиной, определяющей заряд в канале, который рассчитывается с использованием Эффективное напряжение или напряжение перегрузки = Напряжение на оксиде — пороговое напряжение . Чтобы рассчитать эффективное напряжение MOSFET, вам нужно напряжение на оксиде (V _GS ) и пороговое напряжение (V _T ) . С помощью нашего инструмента вам нужно ввести соответствующее значение для напряжения на оксиде и порогового напряжения и нажать кнопку расчета.