Направление силы Лоренца – определение действия и примеры с правилом левой руки

4.6

Средняя оценка: 4.6

Всего получено оценок: 92.

Обновлено 22 Января, 2021

4.6

Средняя оценка: 4.6

Всего получено оценок: 92.

Обновлено 22 Января, 2021

На заряд, движущийся в магнитном поле, со стороны этого поля действует сила, называемая силой Лоренца. При этом направление этой силы не совпадает с направлением магнитных линий поля. Поговорим о методике определения этого направления.

Сила Лоренца

Долгое время магнетизм и электричество считались малосвязанными явлениями. Лишь к середине XIX в. опыты Х. Эрстеда и А. Ампера выявили такую связь. На основе исследований А. Ампера, Ж. Био, Ф. Савара, П. Лапласа были выведены законы, точно описывающие связь между электрическим током, возникающим магнитным полем и величину силы взаимодействия между ними.

Рис. 1. Взаимодействие проводника с током тока и магнита.

Силу, с которой магнитное поле действует на проводник с током, назвали силой Ампера.

Однако механизм ее возникновения был раскрыт лишь к концу XIX в. Х. Лоренцем. К этому времени уже установили, что электрический ток представляет собой упорядоченное движение заряженных частиц, и магнитное поле действует именно на заряженные частицы. Силы, с которыми магнитное поле действует на каждый из движущихся зарядов, сливаются в одну общую силу, которая и является силой Ампера.

Следовательно, сила Ампера — это проявление более общей силы, названной впоследствии силой Лоренца. Формула силы Лоренца:

$$F_L = qvB sin \alpha$$

Рис. 2. Сила Лоренца.

Направление силы Лоренца

В формулу силы Лоренца входит важный параметр — угол $\alpha$. Это угол между векторами скорости движения заряда и магнитной индукцией. Присутствие этого элемента в формуле неслучайно. Дело в том, что направление действия силы Лоренца не совпадает ни с вектором скорости движения заряда, ни с вектором магнитной индукции.

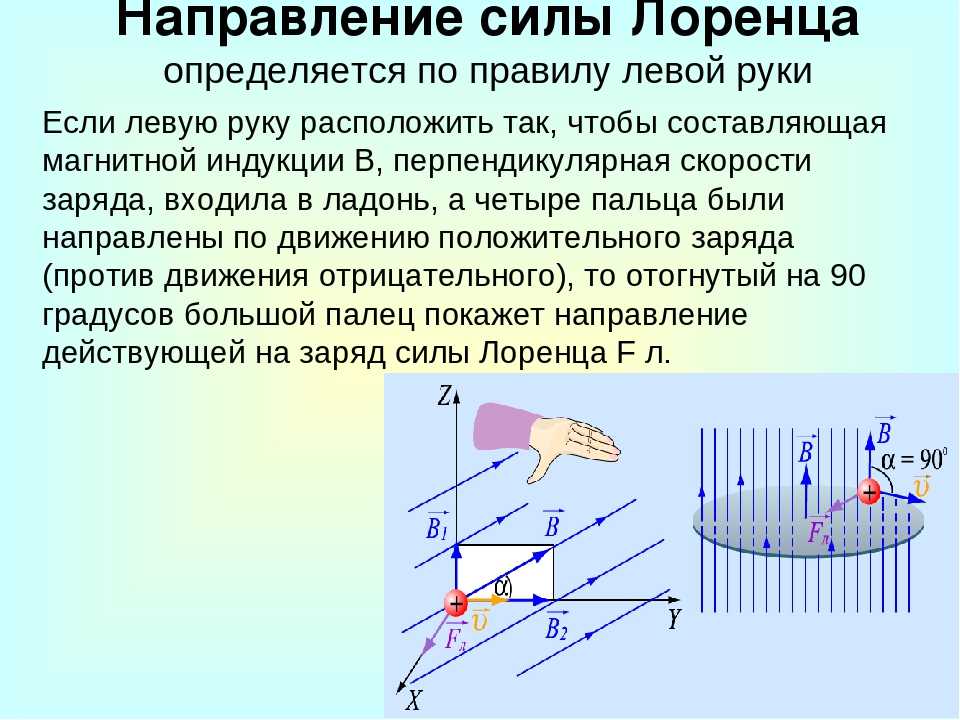
Сила Лоренца направлена перпендикулярно плоскости, образованной вектором скорости движения заряда и вектором магнитной индукции.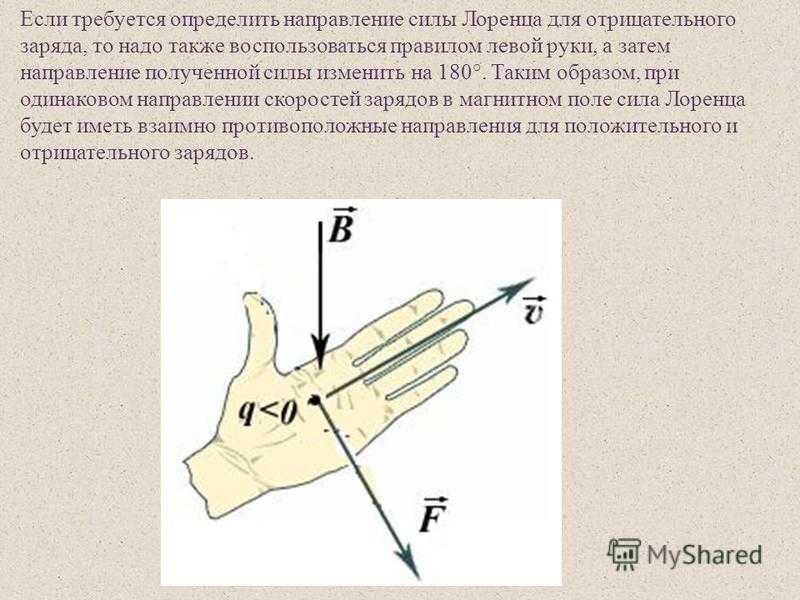 Для определения этого направления принято мнемоническое правило левой руки: если четыре вытянутых пальца левой руки указывают направление движения положительного заряда, а линии магнитного поля входят в ладонь, «прокалывая» ее, то отставленный большой палец покажет направление силы Лоренца.

Примеры использования правила левой руки

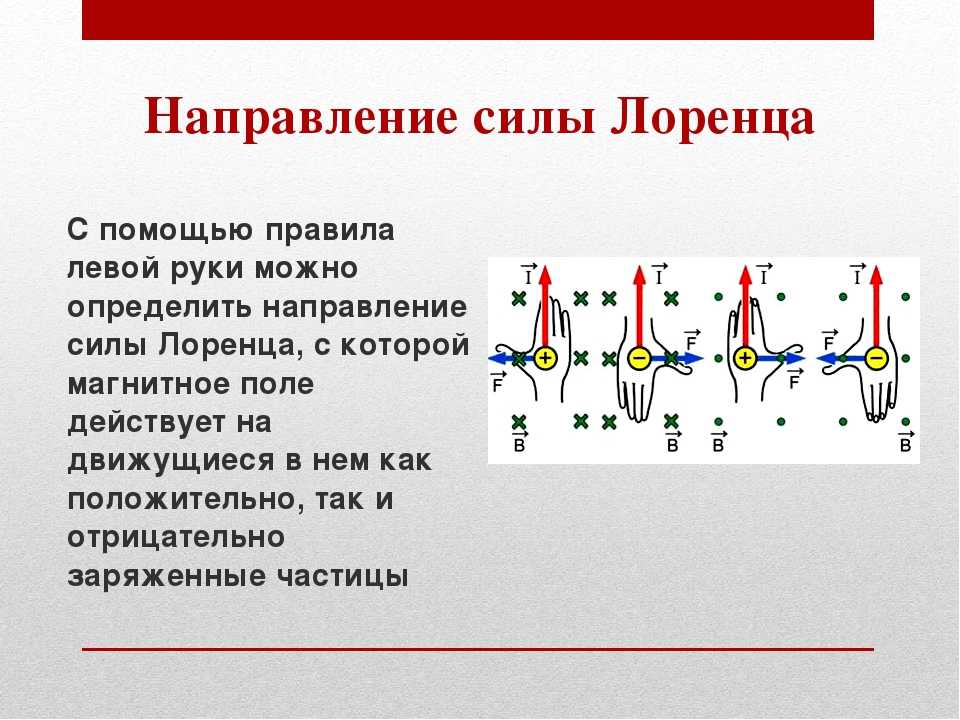
Рассмотрим конкретные примеры, в которых сила Лоренца определяется по правилу левой руки.

Допустим, протон движется вперед, северный магнитный полюс находится внизу, южный — вверху, куда будет направлена сила Лоренца?

Правило левой руки определено для положительно заряженной частицы. Протон — положительно заряжен, следовательно четыре пальца надо расположить по направлению его скорости — то есть, вперед. Линии магнитной индукции выходят из северного полюса и приходят к южному. Следовательно, в рассматриваемом случае они направлены снизу вверх. Располагаем руку ладонью вниз, чтобы магнитные линии входили в ладонь (четыре пальца по-прежнему направлены вперед).

Отставленный большой палец левой руки покажет направо. Туда и будет направлена сила Лоренца при описываемых условиях.

Другой пример. Пусть электрон движется справа налево, северный полюс будет сверху. Куда направлена сила Лоренца?

Электрон заряжен отрицательно, для электрона четыре пальца должны быть направлены против его движения, то есть, направо. Ладонь при этом должна смотреть вверх. Отставленный большой палец укажет направление вперед. Это и будет направление силы Лоренца в данном случае.

Сила Лоренца перпендикулярна плоскости, образованной векторами движения заряда и магнитной индукции. Если эти вектора лежат на одной прямой, то плоскости они не образуют — величина силы Лоренца равна нулю, и ее направление определить невозможно.

Рис. 3. Правило левой руки.

Что мы узнали?

Сила Лоренца действует на заряд, движущийся в магнитном поле. Эта сила направлена перпендикулярно плоскости, образованной векторами скорости и магнитной индукции. Для удобного определения направления силы Лоренца используется мнемоническое правило левой руки.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.6

Средняя оценка: 4.6

Всего получено оценок: 92.

---

А какая ваша оценка?

Сила Лоренца — Студопедия

Поделись  

— сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.

где q — заряд частицы;

V — скорость заряда;

B — индукции магнитного поля;

a — угол между вектором скорости заряда и вектором магнитной индукции.

Направление силы Лоренца определяется по правилу левой руки:

Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца:

.

Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию).

Если заряженная частица движется параллельно силовым линиям магнитного поля, то Fл = 0 , и заряд в магнитном поле движетсяравномерно и прямолинейно.

Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной:

и создает центростремительное ускорение равное:

В этом случае частица движется по окружности.

.

Согласно второму закону Ньютона: сила Лоренца равнв произведению массы частицы на центростремительное ускорение:

тогда радиус окружности:

а период обращения заряда в магнитном поле:

Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды. Если внести проводник с током в магнитное поле (фиг.96,а), то мы увидим, что в результате сложения магнитных полей магнита и проводника произойдет усиление результирующего магнитного поля с одной стороны проводника (на чертеже сверху) и ослабление магнитного поля с другой стороны проводника (на чертеже снизу). В результате действия двух магнитных полей произойдет искривление магнитных линий и они, стремясь сократиться, будут выталкивать проводник вниз (фиг. 96, б).

Направление силы, действующей на проводник с током в магнитном поле, можно определить по «правилу левой руки». Если левую руку расположить в магнитном поле так, чтобы магнитные линии, выходящие из северного полюса, как бы входили в ладонь, а четыре вытянутых пальца совпадали с направлением тока в проводнике, то большой отогнутый палец руки покажет направление действия силы. Сила Ампера , действующая на элемент длины проводника, зависит: от величины магнитной индукции В, величины тока в проводнике I, от элемента длины проводника и от синуса угла а между направлением элемента длины проводника и направлением магнитного поля.

Эта зависимость может быть выражена формулой:

Для прямолинейного проводника конечной длины, помещенного перпендикулярно к направлению равномерного магнитного поля, сила, действующая на проводник, будет равна:

Из последней формулы определим размерность магнитной индукции.

Так как размерность силы:

т. е. размерность индукции такая же, какая была получена нами из закона Био и Савара.

Тесла (единица магнитной индукции)

Тесла, единица магнитной индукции Международной системы единиц, равная магнитной индукции, при которой магнитный поток сквозь поперечное сечение площадью 1 м2 равен 1 веберу. Названа по имени Н. Тесла. Обозначения: русское тл, международное Т. 1 тл = 104 гс(гаусс).

Магни?тный моме?нт, магни?тный дипо?льный моме?нт — основная величина, характеризующая магнитные свойства вещества.

Магнитный момент измеряется в А⋅м² или Дж/Тл (СИ), либо эрг/Гс (СГС), 1 эрг/Гс = 10^-3 Дж/Тл. Специфической единицей элементарного магнитного момента является магнетон Бора. В случае плоского контура с электрическим током магнитный момент вычисляется как

,

где — сила тока в контуре, — площадь контура, — единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.

Для произвольного замкнутого контура магнитный момент находится из:

,

где — радиус-вектор, проведенный из начала координат до элемента длины контура

В общем случае произвольного распределения токов в среде:

,

где — плотность тока в элементе объёма .

Итак, на контур с током в магнитном поле действует вращающий момент. Контур ориентируется в данной точке поля только одним способом. Примем положительное направление нормали за направление магнитного поля в данной точке. Вращающий момент прямо пропорционален величине тока

I, площади контура S и синусу угла между направлением магнитного поля и нормали .

здесь М – вращающий момент, или момент силы, – магнитный момент контура (аналогично – электрический момент диполя).

В неоднородном поле ( ) формула справедлива, если размер контура достаточно мал (тогда в пределах контура поле можно считать приближенно однородным). Следовательно, контур с током по-прежнему стремится развернуться так, чтобы его магнитный момент был направлен вдоль линий вектора .

Но, кроме того, на контур действует результирующая сила (в случае однородного поля и . Эта сила действует на контур с током или на постоянный магнит с моментом и втягивает их в область более сильного магнитного поля.

Работа по перемещению контура с током в магнитном поле.

Нетрудно доказать, что работа по перемещению контура с током в магнитном поле равна , где и — магнитные потоки через площадь контура в конечном и начальном положениях. Эта формула справедлива, если ток в контуре постоянен, т.е. при перемещении контура не учитывается явление электромагнитной индукции.

Формула справедлива и для больших контуров в сильно неоднородном магнитном поле (при условии

I=const).

Наконец, если контур с током не смещать, а изменять магнитное поле, т.е. изменять магнитный поток через поверхность, охватываемую контуром, от значения до то для этого надо совершить ту же работу . Эта работа называется работой изменения магнитного потока, связанного с контуром. Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, которая равна

(1)

где B_n=Вcosα — проекция вектора В на направление нормали к площадке dS (α — угол между векторами n и В), dS = dSn — вектор, у которого модуль равен dS, а направление его совпадает с направлением нормали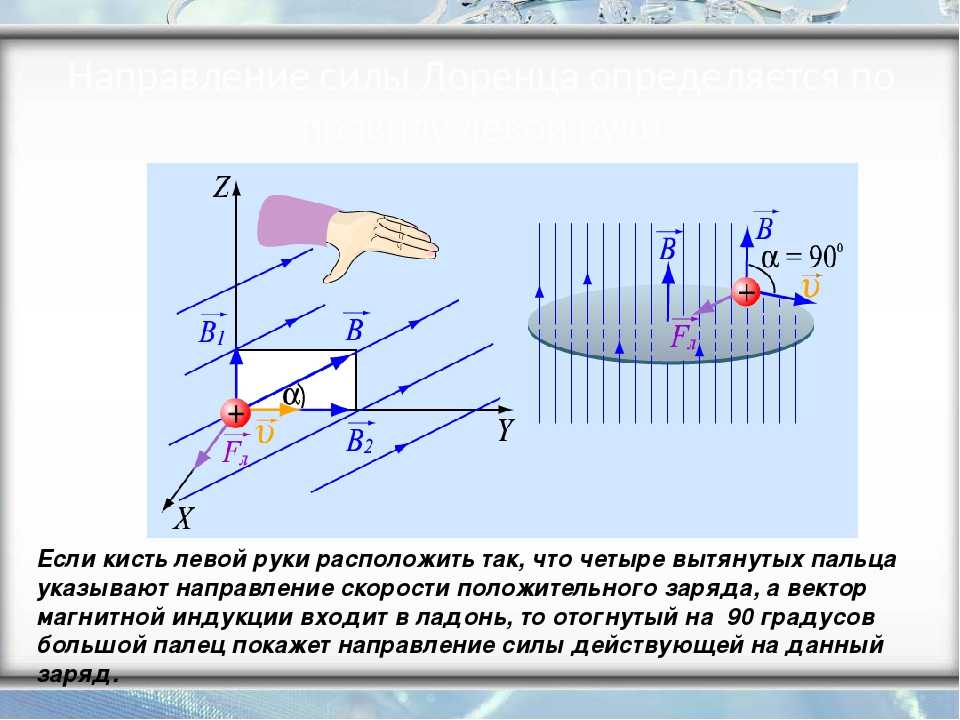

n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cosα (задается выбором положительного направления нормали n). Поток вектора В обычно связывают с контуром, по которому течет ток. В этом случае положительное направление нормали к контуру нами задавалось: оно связывается с током правилом правого винта. Значит, магнитный поток, который создается контуром, через поверхность, ограниченную им самим, всегда положителен.

Поток вектора магнитной индукции Ф_B через произвольную заданную поверхность S равен

(2)

Для однородного поля и плоской поверхности, которая расположена перпендикулярно вектору В, B_n=B=const и

Из этой формулы задается единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, который проходит сквозь плоскую поверхность площадью 1 м², который расположен перпендикулярно однородному магнитному полю и индукция которого равна 1 Тл (1 Вб=1 Тл•м²).

Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:

(3)

Эта теорема является отражением факта, что магнитные заряды отсутствуют, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

Следовательно, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные формулы.

В качестве примера найдем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью μ, равна

Магнитный поток сквозь один виток соленоида площадью S равен

а полный магнитный поток, который сцеплен со всеми витками соленоида и называемый потокосцеплением,



Определение правила правой руки в физике.

(существительное)

Направление угловой скорости ω и углового момента L, на которое указывает большой палец правой руки, когда вы сгибаете пальцы в направлении вращения.

• Направление магнитной силы: правило правой руки

  • правая рука правило используется для определения направления магнитной силы на положительном заряде.
  • Направление магнитной силы F перпендикулярно плоскости, образованной v и B, как определено справа рука правило , что показано на рисунке выше.
  • правая рука правило гласит: чтобы определить направление магнитной силы на положительно движущемся заряде, ƒ, направьте большой палец правой руки в направлении v, пальцы в направление B, а перпендикуляр к ладони указывает в направлении F.
  • Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B, и соответствует справа рука правило –1 (RHR-1) как показано.
  • Применить правую ручную правило для определения направления магнитной силы на заряд

• Угловые величины как векторы

  • Для угловых величин направление вектора определяется с помощью Право Рука Правило , показанное на .
  • правая ручная Правило можно использовать для определения направления как углового момента, так и угловой скорости.
  • Используя правую руку правило , ваша правая рука будет захватывать шест так, чтобы ваши четыре пальца (указательный, средний, безымянный и мизинец) следовали направлению вращения.
  • На рисунке (b) показано правое — ручное правило .
  • Определить направление вектора с помощью Право Рука Правило

• Электродвигатели

  • Направление силы Лоренца перпендикулярно как направлению тока, так и магнитного поля и может быть найдено с помощью правого — ручного правила , показанного на .
  • Используя правую руку , направьте большой палец в направлении тока, а указательный палец укажите в направлении магнитного поля.

• Величина магнитной силы

  • Направление магнитной силы $F$ перпендикулярно плоскости, образованной $v$ и $B$, как определено правой рукой правилом , которое показано на рисунке 1 .
  • В нем говорится, что для определения направления магнитной силы на положительный движущийся заряд вы указываете большим пальцем правой руки в направлении $v$, пальцами в направлении $B$ и перпендикуляр к ладони указывает в направлении $F$.
  • Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B, и следует вправо влево правилу –1 (RHR-1), как показано.

• Закон Ампера: магнитное поле, создаваемое длинным прямым проводом

  • Как показано, направление магнитного поля можно определить с помощью правой руки правила — указывая большим пальцем в направлении тока, сгиб пальцев указывает направление магнитного поля вокруг прямой провод.
  • Направление магнитного поля можно определить по правой ручной правилу .

• Магнитное воздействие на проводник с током

  • Направление магнитной силы можно определить с помощью правой руки правила , продемонстрированного в .

• Электрические силы против магнитных сил

  • $E=\слева | \frac{F}{q} \ вправо 9{2}}$
  • Направление F можно легко определить с помощью правой руки правила .
  • Магнитное поле также может быть создано током с линиями поля, представленными в виде концентрических окружностей вокруг провода с током. Магнитная сила в любой точке в этом случае может быть определена с помощью правой ручной правила , и будет перпендикулярно как току, так и магнитному полю.
  • Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B, и следует вправо влево правилу –1 (RHR-1), как показано.

• Угловые и линейные величины

  • Чтобы устранить эту двусмысленность, в физике принято использовать правую руку правило : согните пальцы вашей правой руки в направлении кругового движения, а ваш большой палец будет указывать на направление векторов угловой скорости и импульса.
  • При определении направления углового вектора используйте правую правило руки : согните пальцы правой руки в направлении кругового движения, а большой палец указывает в направлении вектора.

• Электрические токи и магнитные поля

  • Другая версия правой руки правила вытекает из этого исследования и применима для любого сегмента тока — направьте большой палец в направлении тока, а пальцы согните в направлении созданных петель магнитного поля. этим.
  • правая рука правило может дать вам направление силы на проводе, как показано на рисунке выше.
  • правое ручное правило можно использовать для определения направления силы на проводнике с током, помещенном во внешнее магнитное поле.
  • (b) Правая Рука Правило 2 гласит, что если правая рука большой палец указывает в направлении тока, то пальцы скручиваются в направлении поля.
  • Это правило согласуется с полем, отображаемым для длинного прямого провода, и действительно для любого текущего сегмента.

• ЭДС движения

  • ( правая ручная правило требует, чтобы I вращался против часовой стрелки, что, в свою очередь, означает, что вершина стержня положительна, как показано.)
  • (a) ЭДС движения = Bℓv индуцируется между рельсами, когда этот стержень движется вправо в однородном магнитном поле.
  • Право Рука Правило задает показанное направление тока, а полярность стержня будет управлять таким током.

22.4: Напряженность магнитного поля — сила, действующая на движущийся заряд в магнитном поле

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

2698

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Описывать влияние магнитных полей на движущиеся заряды.
• Используйте правило правой руки 1, чтобы определить скорость заряда, направление магнитного поля и направление магнитной силы, действующей на движущийся заряд.
• Рассчитайте магнитную силу, действующую на движущийся заряд.

Каков механизм, посредством которого один магнит воздействует на другой? Ответ связан с тем фактом, что весь магнетизм вызван током, потоком заряда. Магнитные поля воздействуют на движущиеся заряды , и поэтому они воздействуют на другие магниты, все из которых имеют движущиеся заряды.

Правило правой руки 1

Магнитная сила, действующая на движущийся заряд, является одной из самых фундаментальных известных. Магнитная сила так же важна, как электростатическая или кулоновская сила. И все же магнитная сила более сложна как по количеству воздействующих на нее факторов, так и по своему направлению, чем относительно простая кулоновская сила. Величина магнитной силы \(F\) на заряде \(q\), движущемся со скоростью \(v\) в магнитном поле напряженностью \(B\), определяется выражением

\[F = qvB\sin \theta,\]

где \(\theta\) — угол между направлениями \(\bf{v}\) и \(\bf{B}\). Эту силу часто называют силой Лоренца . Фактически именно так мы определяем напряженность магнитного поля \(B\)-in через силу, действующую на заряженную частицу, движущуюся в магнитном поле. Единица СИ для напряженности магнитного поля \(B\) называется тесла (T) в честь эксцентричного, но гениального изобретателя Николы Теслы (1856–1943). Чтобы определить, как тесла относится к другим единицам СИ, мы решаем 9{-5} T\), или 0,5 G.

Направление магнитной силы \(\bf{F}\) перпендикулярно плоскости, образованной \(\bf{v}\) и \( \bf{B}\), как определено правилом правой руки 1 (или RHR-1), которое показано на рисунке \(\PageIndex{1}\). RHR-1 утверждает, что для определения направления магнитной силы на положительно движущемся заряде вы указываете большим пальцем правой руки в направлении \(v\), пальцами в направлении \(\bf{B }\), а перпендикуляр к ладони указывает в направлении \(\bf{F}\). Один из способов запомнить это состоит в том, что существует одна скорость, и поэтому ее представляет большой палец. Есть много линий поля, поэтому пальцы представляют их. Сила направлена ​​в том направлении, куда вы бы толкнули ладонью. Сила, действующая на отрицательный заряд, направлена ​​прямо противоположно силе на положительном заряде.

Рисунок \(\PageIndex{1}\): Магнитные поля воздействуют на движущиеся заряды. Эта сила является одной из самых основных известных.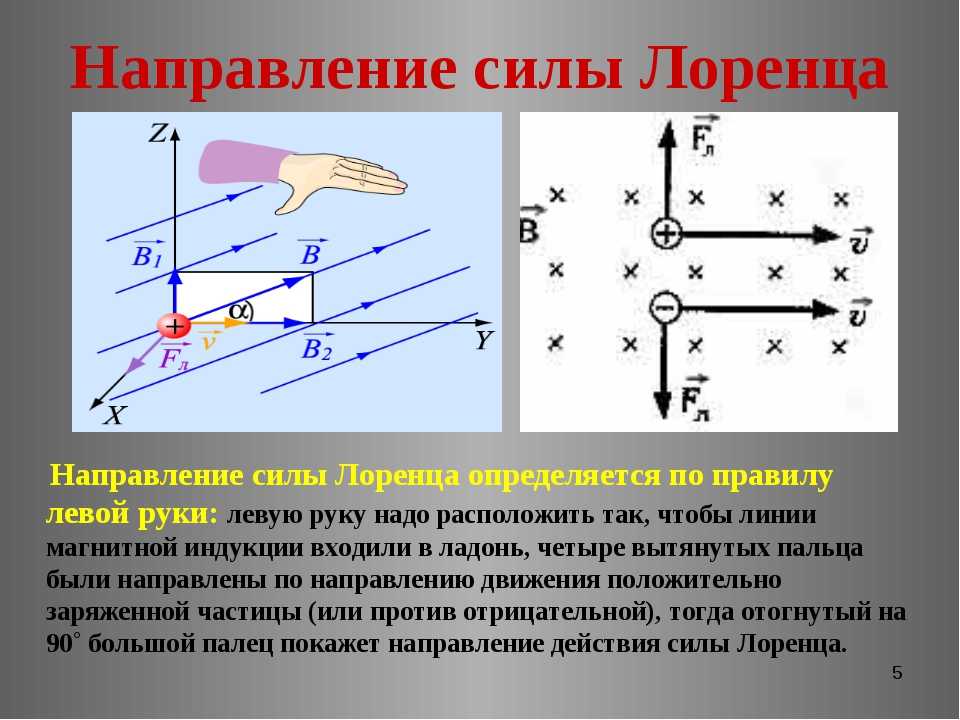 Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной \(\bf{v}\) и \(\bf{B}\), и следует правилу правой руки-1 (RHR-1), как показано . Величина силы пропорциональна \(q\), \(v\), \(B\) и синусу угла между \(\bf{v}\) и \(\bf{B} \).

ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ЗАРЯДЫ И МАГНИТЫ

На статические заряды не действует магнитная сила. Однако на движущиеся заряды действует магнитная сила. Когда заряды неподвижны, их электрические поля не действуют на магниты. Но когда заряды движутся, они создают магнитные поля, которые воздействуют на другие магниты. При относительном движении возникает связь между электрическим и магнитным полями — одно влияет на другое.

Пример \(\PageIndex{1}\): расчет магнитной силы: магнитное поле Земли на заряженном стеклянном стержне

За исключением компаса, вы редко видите или лично испытываете силы, связанные с небольшим магнитным полем Земли. Чтобы проиллюстрировать это, предположим, что в физической лаборатории вы натираете стеклянную палочку шелком, помещая на нее положительный заряд в 20 нКл.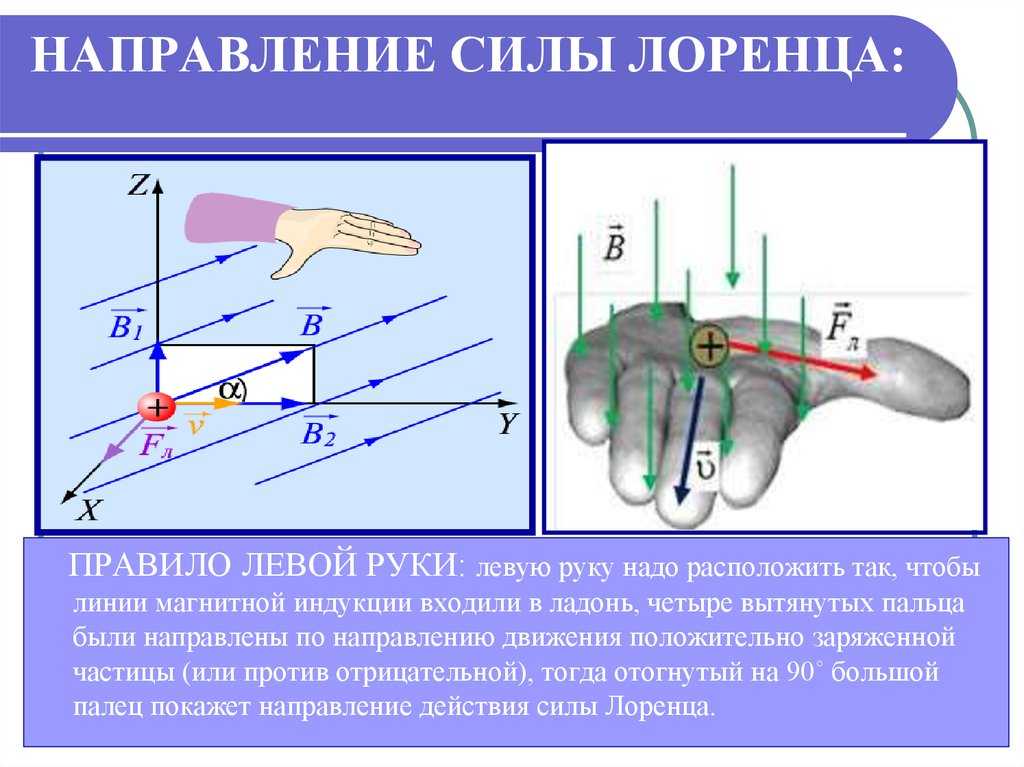 Вычислите силу, действующую на стержень со стороны магнитного поля Земли, если бросить его с горизонтальной скоростью 10 м/с строго на запад в месте, где поле Земли направлено строго на север параллельно земле. (Направление силы определяется правилом правой руки 1, как показано на рисунке \(\PageIndex{2}\)).

Рисунок \(\PageIndex{2}\): Положительно заряженный объект, движущийся строго на запад в области, где магнитное поле Земли направлено строго на север, испытывает силу, направленную строго вниз, как показано. Отрицательный заряд, движущийся в том же направлении, почувствовал бы силу прямо вверх.

Стратегия

Нам известны заряд, его скорость, напряженность и направление магнитного поля. Таким образом, мы можем использовать уравнение \(F = qvB \sin\theta\), чтобы найти силу.

Раствор

9{-11} Н . \end{align*}\]

Обсуждение

Этой силой можно пренебречь на любом макроскопическом объекте, что согласуется с опытом.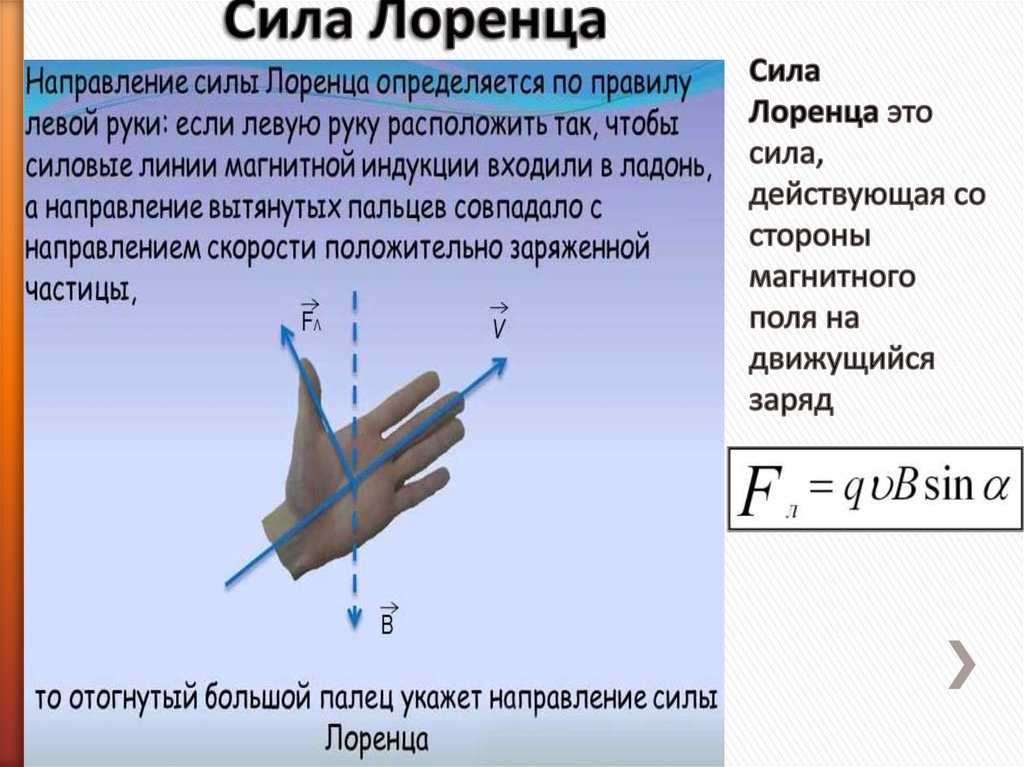 (Оно вычисляется только с точностью до одной цифры, поскольку поле Земли меняется в зависимости от местоположения и выражается только одной цифрой.) Однако магнитное поле Земли оказывает очень важное влияние, особенно на субмикроскопические частицы. Некоторые из них рассматриваются в следующем разделе.

Резюме

• Магнитные поля воздействуют на движущийся заряд q , величина которого равна \[F = qvB sin \theta , \nonumber \], где \(\theta\) — угол между направлениями \(v\) и \(B\).
• Единицей СИ для напряженности магнитного поля \(B\) является тесла (Тл), которая связана с другими единицами соотношения \[1 T = \frac{1N}{C \cdot м/с} = \frac{1 N}{А \cdot м}. \номер\]
• Направление силы, действующей на движущийся заряд, определяется правилом правой руки 1 (RHR-1): Направьте большой палец правой руки в направлении \(v\), остальные пальцы в направлении \( B\), а перпендикуляр к ладони указывает в направлении \(F\).
• Сила перпендикулярна плоскости, образованной \(\mathbf{v}\) и \(\mathbf{B}\).