Сила Лоренца | Формулы и расчеты онлайн

Сила Лоренца действующая на электрон

В частном случае носителем заряда является электрон. Тогда в формулу (5) в качестве Q следует подставить

\[ е = — 1.602 · 10^{-19} Кл. \]

При определении направления движения электронов с помощью правила левой руки следует учитывать, что направление движения электронов противоположно техническому направлению тока.

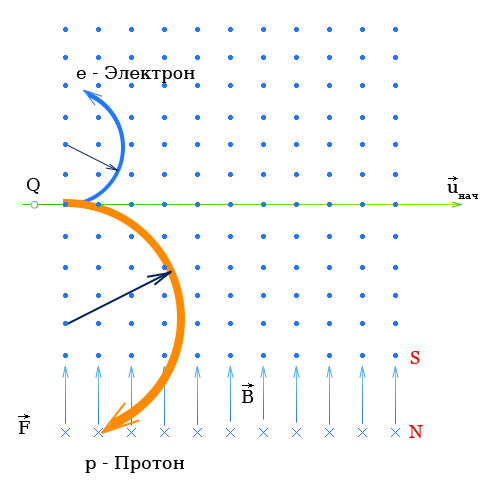
Сила Лоренца действующая на электрон и протон

Величина и направление силы Лоренца определяются соотношением

\[ \vect{F_{L}}= e \vect{v} × \vect{B} \]

где $\vect{v}$, $\vect{B}$ и $\vect{F}$ образуют правую систему.

Для электронов, движущихся перпендикулярно магнитному полю, формула упрощается:

\[ F_{L} = evB \]

Так как сила действует перпендикулярно скорости и направлению поля, она создает центростремительное ускорение, т.е. изменяет направление скорости, не меняя ее величины. Поэтому электрон движется в магнитном поле по окружности.

Вычислить, найти силу Лоренца действующую на электрон или протон

Радиус траектории электрона в магнитном поле

Для определения радиуса круговой траектории электрона приравняем силу Лоренца и центростремительную силу.

Если

r	радиус круговой траектории электрона,	метр
me	9,11 · 10-31 кг — масса электрона,	кг
e	1,602 · 10-19 Кл — элементарный электрический заряд,	Кулон
v	скорость электрона,	м/с
B	магнитная индукция,	Тесла

то, приравнивая обе силы, получаем

\[ evB = \frac{m_{e} · v^{2}}{r} \]

и, следовательно,

\[ r = \frac{m_{e} · v}{eB} \]

Сила Лоренца действующая на протон

Электрический заряд протона равен по модулю заряду электрона, но имеет положительный знак.

\[ p = + 1.602 · 10^{-19} Кл. \]

При определении направления движения протонов с помощью правила левой руки направление движения протонов совпадает с техническим направлением тока и с картинкой.

Таким образом электрон и протон влетая в магнитное поле в одном направлении будут отклоняться в разные стороны.

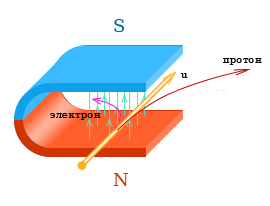
Сила Лоренца действующая на протон

Величина силы действующая на электрон и на протон будет одинакова (определяется формулой №3), но поскольку протон гораздо тяжелее электрона, радиус закручивания для протона будет больше.

Радиус траектории протона в магнитном поле

Если

r	радиус круговой траектории протона,	метр
mp	1,67 · 10-27 кг — масса протона,	кг
p	1,602 · 10-19 Кл — элементарный электрический заряд,	Кулон
v	скорость протона,	м/с
B	магнитная индукция,	Тесла

Радиус траектории для протона будет вычисляться по аналогичной формуле

\[ r = \frac{m_{p} · v}{pB} \]

Из этой формулы видно что при одинаковых скоростях электрона и протона радиус траектории протона будет значительно больше, чем у электрона пропорционально отношению масс этих частиц

В помощь студенту

Сила Лоренца	стр. 665

Магнитная сила Лоренца. Формула. Электрон. Индукция магнитного поля. Правило руки буравчика

Как уже было сказано ранее, магнитное поле действует на движущийся заряд. В ряде экспериментов было показано, что при влёте в магнитное поле заряженной частицы, её траектория искривляется (т.е. отклоняется от прямой). Вследствие знания второго закона Ньютона и наличия центростремительного ускорения (т.к. тело движется по кривой), такое движение объясняется наличием силы — силы Лоренца.

Значение модуля этой силы:

(1)

Рис. 1. Сила Лоренца

Направление силы Лоренца — перпендикуляр к касательной траектории (т.е. перпендикуляр к скорости в данный момент). Однако в плоскости рисунка возможны два направления для перпендикуляра. Какое из них выбрать — вопрос заряда и правила левой руки. Пусть положительный заряд

влетает в магнитное поле перпендикулярно линиям магнитной индукции () со скоростью . Поле направлено перпендикулярно поверхности «на нас». Тогда, согласно правилу левой руки, сила Лоренца направлена как показано на рисунке 1. Дальнейшее движение заряда, в нашем случае, — движение по окружности.

В случае, если движущийся заряд будет отрицательным, направление силы изменяется на противоположное.

Правило левой руки для силы Лоренца: ориентируем руку так, чтобы линии магнитной индукции входили в ладонь. Четыре пальца руки сонаправляем с вектором скорости частицы, тогда противопоставленный большой палец указывает на направление силы Лоренца для положительно заряженной частицы. Направление силы Лоренца для отрицательно заряженной частицы противоположно.

Задачи на силу Лоренца можно условно разделить на два типа:

• направление скорости перпендикулярна линиям магнитной индукции (тогда задача сводится к записи второго закона Ньютона и плану решения задач по динамике) и фактически рисунка 1,
• направление скорости составляет угол  с линиями магнитной индукции. Тогда заряженное тело будет двигаться по спирали (рис. 2).

Рис. 2. Сила Лоренца (Спираль)

Для решения второго типа задач рассматривается логика движения тела, брошенного под углом к горизонту. Т.е. мысленно разделяем движение на две оси (вдоль и перпендикулярно полю) и анализируем движение: одно — движение по окружности, второе — прямолинейное.

Вывод: задачи на силу Лоренца (1) практически идентичны друг другу. Обычно решаются через второй закон Ньютона и определение центростремительного ускорения. Надо чётко различать задачи, в которых частица движется в магнитном поле перпендикулярно линиям магнитной индукции (тогда тело движется по окружности) или влетает в поле под углом к линиям магнитной индукции (тогда частица движется по винтовой траектории).

Поделиться ссылкой:

Понравилось это:

Нравится Загрузка…

Формула силы Лоренца в физике

Определение и формула силы Лоренца

Определение

Сила , действующая на движущуюся заряженную частицу в магнитном поле, равная:

называется силой Лоренца (магнитной силой).

Исходя из определения (1) модуль рассматриваемой силы:

где – вектор скорости частицы, q – заряд частицы, – вектор магнитной индукции поля в точке нахождения заряда, – угол между векторами и . Из выражения (2) следует, что если заряд движется параллельно силовым линиям магнитного поля,то сила Лоренца равна нулю. Иногда силу Лоренца стараясь выделить, обозначают, используя индекс:

Направление силы Лоренца

Сила Лоренца (как и всякая сила) – это вектор. Ее направление перпендикулярно вектору скорости и вектору (то есть перпендикулярно плоскости, в которой находятся векторы скорости и магнитной индукции) и определяется правилом правого буравчика (правого винта) рис.1 (a). Если мы имеем дело с отрицательным зарядом, тонаправление силы Лоренца противоположно результату векторного произведения (рис.1(b)).

вектор направлен перпендикулярно плоскости рисунков на нас.

Следствия свойств силы Лоренца

Так как сила Лоренца направлена всегда перпендикулярно направлению скорости заряда, то ее работа над частицей равна нулю. Получается, что воздействуя на заряженную частицу при помощи постоянного магнитного поля нельзя изменить ее энергию.

Если магнитное поле однородно и направлено перпендикулярно скорости движения заряженной частицы, то заряд под воздействием силы Лоренца будет перемещаться по окружности радиуса R=const в плоскости, которая перпендикулярна вектору магнитной индукции. При этом радиус окружности равен:

где m – масса частицы,|q|- модуль заряда частицы, – релятивистский множитель Лоренца, c – скорость света в вакууме.

Сила Лоренца — это центростремительная сила. По направлению отклонения элементарной заряженной частицы в магнитном поле делают вывод о ее знаке (рис.2).

Формула силы Лоренца при наличии магнитного и электрического полей

Если зар

Сила Лоренца | Все формулы

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng! 
Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА

Сила Лоренца — Сила, с которой, электромагнитное поле действует на точечную заряженную частицу

Направление силы Лоренца определяется по правилу левой руки — Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление

силы Лоренца

Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы.

Рассмотрим 2 вида движения заряженных частиц:

1) Если заряженная частица движется параллельно силовым линиям магнитного поля, то Сила Лоренца равняется нулю Fл = 0 , и заряд в магнитном поле движется равномерно и прямолинейно.

2) Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной и равна :

Радиус данной окружности будет равен:

В формуле мы использовали :

— Сила Лоренца

— Заряд электрона

— Скорость заряда

— Магнитная индукция

— Угол между вектором магнитной индукцией и вектором скорости

— Центростремительное ускорение

— Радиус окружности

Формула силы Лоренца

ОПРЕДЕЛЕНИЕ

Сила Лоренца – сила, действующая на точечную заряженную частицу, движущуюся в магнитном поле.

Она равна произведению заряда, модуля скорости частицы, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и скоростью движения частицы.

   

Здесь – сила Лоренца, – заряд частицы, – модуль вектора индукции магнитного поля, – скорость частицы, – угол между вектором индукции магнитного поля и направления движения.

Единица измерения силы – Н (ньютон).

Сила Лоренца — векторная величина. Сила Лоренца принимает своё наибольшее значение когда векторы индукции и направления скорости частицы перпендикулярны ().

Направление силы Лоренца определяют по правилу левой руки:

Если вектор магнитной индукции входит в ладонь левой руки и четыре пальца вытянуты в сторону направления вектора движения тока, тогда отогнутый в сторону большой палец показывает направление силы Лоренца.

В однородном магнитном поле частица будет двигаться по окружности, при этом сила Лоренца будет центростремительной силой. Работа при этом не будет совершаться.

Примеры решения задач по теме «Сила Лоренца»

ПРИМЕР 1

Задание	Найти силу Лоренца, действующую на частицу с зарядом 10 Кл, движущаяся со скоростью 9 м/с под углом к вектору магнитной индукции.Индукция магнитного поля равна 3 Тл.
Решение	Подставим значения в формулу:
Ответ	Сила Лоренца приблизительно равна 233,83 ньютон.

ПРИМЕР 2

Задание	Под действием силы Лоренца частица массы m с зарядом q движется по окружности. Магнитное поле однородно, его напряжённость равна B. Найти центростремительное ускорение частицы.
Решение	Вспомним формулу силы Лоренца:     Кроме того, по 2 закону Ньютона:     В данном случае сила Лоренца направлена к центру окружности и ускорение, ею создаваемое, направлено туда же, то есть это и есть центростремительное ускорение. Значит:     Осталось узнать α. Обратим внимание на рисунок. – это угол между вектором скорости и направлением вектора магнитной индукции. Нетрудно увидеть, что эти векторы перпендикулярны, т.е. .     Значит:
Ответ

Понравился сайт? Расскажи друзьям!

Сила Лоренца — Вікіпедія

Си́ла Ло́ренца — сила, що діє на рухомий електричний заряд, який перебуває в електромагнітному полі.

F=qE+q[v×B]{\displaystyle \mathbf {F} =q\mathbf {E} +{q}[\mathbf {v} \times \mathbf {B} ]}.

Тут F{\displaystyle \mathbf {F} } — сила, q{\displaystyle q} — величина заряду, E{\displaystyle \mathbf {E} } — напруженість електричного поля, v{\displaystyle \mathbf {v} } — швидкість руху заряду, B{\displaystyle \mathbf {B} } — вектор магнітної індукції^[1]. Іноді силою Лоренца називають лише другу складову цього виразу — силу, яка діє на заряд, що рухається, з боку магнітного поля (F=q[v×B]{\displaystyle \mathbf {F} ={q}[\mathbf {v} \times \mathbf {B} ]}).

Електричне поле діє на заряд із силою, направленою вздовж силових ліній поля. Магнітне поле діє лише на рухомі заряди. Сила дії магнітного поля перпендикулярна до силових ліній поля й до швидкості руху заряду.

Названа на честь Гендрика Лоренца, який розробив це поняття 1895 року.

Виведення із використанням закону Кулона та спеціальної теорії відносності[ред. | ред. код]

Попередні перетворення[ред. | ред. код]

Попередні перетворення  

Перетворення Лоренца для радіус-вектора:

 r′=r+Γu(u⋅r)c2−γut{\displaystyle \ \mathbf {r} ‘=\mathbf {r} +\Gamma \mathbf {u} {\frac {(\mathbf {u} \cdot \mathbf {r} )}{c^{2}}}-\gamma \mathbf {u} t},

 γ=11−u2c2{\displaystyle \ \gamma ={\frac {1}{\sqrt {1-{\frac {u^{2}}{c^{2}}}}}}}

 Γ=γ−1u2c2=γ21+γ{\displaystyle \ \Gamma ={\frac {\gamma -1}{\frac {u^{2}}{c^{2}}}}={\frac {\gamma ^{2}}{1+\gamma }}}

 u{\displaystyle \ \mathbf {u} } — відносна швидкість між двома інерціальними системами відліку.

При  t=0{\displaystyle \ t=0} вираз перетворюється у наступний:

 r′=r+Γu(u⋅r)c2(.1){\displaystyle \ \mathbf {r} ‘=\mathbf {r} +\Gamma \mathbf {u} {\frac {(\mathbf {u} \cdot \mathbf {r} )}{c^{2}}}\qquad (.1)}.

Якщо піднести ліву і праву частину до квадрату, можна буде отримати:

r′2=r2+γ2c2(u⋅r)2(.2){\displaystyle \mathbf {r} ‘^{2}=\mathbf {r} ^{2}+{\frac {\gamma ^{2}}{c^{2}}}(\mathbf {u} \cdot \mathbf {r} )^{2}\qquad (.2)}.

Виведення.  

r′2=r2+2Γ(u⋅r)2c2+Γ2u2(u⋅r)2c4=r2+(u⋅r)2u2[2(γ−1)+(γ−1)2]=r2+(u⋅r)2c2[(γ−1)c2u2(γ+1)]={\displaystyle \mathbf {r} ‘^{2}=\mathbf {r} ^{2}+2\Gamma {\frac {(\mathbf {u} \cdot \mathbf {r} )^{2}}{c^{2}}}+\Gamma ^{2}u^{2}{\frac {(\mathbf {u} \cdot \mathbf {r} )^{2}}{c^{4}}}=\mathbf {r} ^{2}+{\frac {(\mathbf {u} \cdot \mathbf {r} )^{2}}{u^{2}}}\left[2(\gamma -1)+(\gamma -1)^{2}\right]=\mathbf {r} ^{2}+{\frac {(\mathbf {u} \cdot \mathbf {r} )^{2}}{c^{2}}}\left[{\frac {(\gamma -1)c^{2}}{u^{2}}}(\gamma +1)\right]=}

=|Γ=γ−1u2c2=γ21+γ|=|r|2+(u⋅r)2c2γ2{\displaystyle =\left|\Gamma ={\frac {\gamma -1}{\frac {u^{2}}{c^{2}}}}={\frac {\gamma ^{2}}{1+\gamma }}\right|=|\mathbf {r} |^{2}+{\frac {(\mathbf {u} \cdot \mathbf {r} )^{2}}{c^{2}}}\gamma ^{2}}.

Якщо скалярно домножити  (.1){\displaystyle \ (.1)} на  u{\displaystyle \ \mathbf {u} }, то можна буде отримати:

 (u⋅r′)=(u⋅r)+Γ|u|2c2(u⋅r)=(u⋅r)(1+γ−1)=γ(u⋅r)(.3){\displaystyle \ (\mathbf {u} \cdot \mathbf {r} ‘)=(\mathbf {u} \cdot \mathbf {r} )+\Gamma {\frac {|\mathbf {u} |^{2}}{c^{2}}}(\mathbf {u} \cdot \mathbf {r} )=(\mathbf {u} \cdot \mathbf {r} )(1+\gamma -1)=\gamma (\mathbf {u} \cdot \mathbf {r} )\qquad (.3)}.

Накінець,

 (v′⋅r′)=(r⋅v)γ(1−(v⋅u)c2)−γ(r⋅u)(.4){\displaystyle \ (\mathbf {v} ‘\cdot \mathbf {r} ‘)={\frac {(\mathbf {r} \cdot \mathbf {v} )}{\gamma (1-{\frac {(\mathbf {v} \cdot \mathbf {u} )}{c^{2}}})}}-\gamma (\mathbf {r} \cdot \mathbf {u} )\qquad (.4)}.

Виведення.  

 (r′⋅v′)=([r+Γuc2(u⋅r)]⋅v+Γuc2(u⋅v)−γuγ(1−(u⋅v)c2))=(r⋅v)γ(1−(u⋅v)c2)+Γc2(u⋅r)(u⋅v)(2+Γ2u2c2)−γ(u⋅r)(1+Γu2c2)γ(1−(u⋅v)c2)={\displaystyle \ (\mathbf {r} ‘\cdot \mathbf {v} ‘)=\left(\left[\mathbf {r} +{\frac {\Gamma \mathbf {u} }{c^{2}}}(\mathbf {u} \cdot \mathbf {r} )\right]\cdot {\frac {\mathbf {v} +{\frac {\Gamma \mathbf {u} }{c^{2}}}(\mathbf {u} \cdot \mathbf {v} )-\gamma \mathbf {u} }{\gamma \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}\right)={\frac {(\mathbf {r} \cdot \mathbf {v} )}{\gamma \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}+{\frac {{\frac {\Gamma }{c^{2}}}(\mathbf {u} \cdot \mathbf {r} )(\mathbf {u} \cdot \mathbf {v} )\left(2+{\frac {\Gamma ^{2}u^{2}}{c^{2}}}\right)-\gamma (\mathbf {u} \cdot \mathbf {r} )\left(1+{\frac {\Gamma u^{2}}{c^{2}}}\right)}{\gamma \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}=}

 =|2+Γ2u2c2=γ+1=γ2Γ,1+Γu2c2=γ|=(r⋅v)γ(1−(u⋅v)c2)−γ2(r⋅u)(1−(u⋅v)c2)γ(1−(u⋅v)c2)=(r⋅v)γ(1−(u⋅v)c2)−γ(r⋅u){\displaystyle \ =\left|2+{\frac {\Gamma ^{2}u^{2}}{c^{2}}}=\gamma +1={\frac {\gamma ^{2}}{\Gamma }},\quad 1+{\frac {\Gamma u^{2}}{c^{2}}}=\gamma \right|={\frac {(\mathbf {r} \cdot \mathbf {v} )}{\gamma \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}-{\frac {\gamma ^{2}(\mathbf {r} \cdot \mathbf {u} )\left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}{\gamma \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}={\frac {(\mathbf {r} \cdot \mathbf {v} )}{\gamma \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}-\gamma (\mathbf {r} \cdot \mathbf {u} )}.

Вираз для перетворення 3-вектора сили при переході до нової ІСВ:

 Fγ(1−(v⋅u)c2)=F′+γu(F′⋅v′)c2+Γu(u⋅F′)c2(.5){\displaystyle \ {\frac {\mathbf {F} }{\gamma (1-{\frac {(\mathbf {v} \cdot \mathbf {u} )}{c^{2}}})}}=\mathbf {F} ‘+\gamma {\frac {\mathbf {u} (\mathbf {F} ‘\cdot \mathbf {v} ‘)}{c^{2}}}+\Gamma \mathbf {u} {\frac {(\mathbf {u} \cdot \mathbf {F} ‘)}{c^{2}}}\qquad (.5)}.

Власне, сила Лоренца[ред. | ред. код]

Базовим виразом для аналізу взаємодії заряда  Q{\displaystyle \ Q} із деяким пробним зарядом  q{\displaystyle \ q} є закон Кулона: для статичних зарядів у вакуумі відносно інерціальної системи відліку, що перебуває у спокої, можна записати, що сила їхньої взаємодії дорівнює

 F=qQ|r|3r{\displaystyle \ \mathbf {F} ={\frac {qQ}{|\mathbf {r} |^{3}}}\mathbf {r} }.

Для того, щоб визначити, як буде виглядати ця сила в інерціальній системі відліку, що рухається, можна розглянути наступний «віртуальний» експеримент.

Нехай у вакуумі знаходяться два заряди, скріплені пружинкою. Заряди розглядаються відносно інерціальної системи відліку, у якій вони перебувають у спокої протягом досить великого проміжку часу. Пружинка забезпечує статичність зарядів, а розтяг пружинки чисельно характеризує силу взаємодії зарядів. Якщо прибрати пружинку й розглянути деяке мале відхилення від статичного стану, наприклад, одного заряду, то можна проаналізувати час, за який другий заряд «відчує» зміну стану першого, тим самим експериментально визначивши швидкість розповсюдження взаємодії між зарядами. Проте в рамках експерименту (заряди скріплені пружинкою) про швидкість розповсюдження взаємодії нічого не можна сказати, оскільки система є статичною. Таким чином, закон Кулона, який описує взаємодію статичних зарядів, не несе, без додаткових припущень, жодної інформації про швидкість розповсюдження взаємодії між зарядами. А отже, релятивістський та класичний опис взаємодії зарядів у статичному випадку збігаються.

Для подальшого аналізу взаємодії цих зарядів можна розглянути їх відносно інерційної системи відліку, що довільно рухається. У такому разі, система вже не буде статичною, а це означає, що можна оцінити швидкість розповсюдження взаємодії. Якщо припустити, що виконується аксіома абсолютності одночасності, то швидкість розповсюдження взаємодії нескінченна, а це, загалом, означає, що до закона Кулона застосовуються перетворення Галілея, що залишають його інваріантним відносно вибору інерціальної системи відліку. А якщо припустити, що аксіома абсолютності одночасності не виконується, то швидкість розповсюдження взаємодії скінченна, і це означає, що до закону Кулона застосовуються перетворення Лоренца, які не залишають вираз для сили Кулона інваріантним відносно вибору інерційної системи відліку.

Саме останньому випадку і присвячені наступні викладки.

Можна записати вираз для сили Кулона точкового заряду  Q{\displaystyle \ Q} відносно системи відліку K’, що рухається у вакуумі зі швидкістю  u{\displaystyle \ \mathbf {u} } відносно системи  S{\displaystyle \ S}, у якій заряд  Q{\displaystyle \ Q} перебуває у спокої, а заряд  q{\displaystyle \ q} рухається із швидкістю  v{\displaystyle \ \mathbf {v} } відносно нього. Перед цим треба ввести постулат про інваріантність заряду,  Q′=Q{\displaystyle \ Q’=Q}. Тоді

 F′=qQ|r′|3r′(.6){\displaystyle \ \mathbf {F} ‘={\frac {qQ}{|\mathbf {r} ‘|^{3}}}\mathbf {r} ‘\qquad (.6)}.

Якщо підставити  (.6){\displaystyle \ (.6)} у  (.5){\displaystyle \ (.5)}, то, з урахуванням попередніх перетворень  (.1)−(.4){\displaystyle \ (.1)-(.4)}, можна буде отримати вираз для сили  F′{\displaystyle \ \mathbf {F} ‘}, що діє на заряд  q{\displaystyle \ q} у системі  S{\displaystyle \ S} відносно системи відліку S′{\displaystyle S’}:

 F=qQγ(r2+γ2(r⋅u)2c2)32[r+1c2[v×[u×r]]](.7){\displaystyle \ \mathbf {F} ={\frac {qQ\gamma }{\left(\mathbf {r} ^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}\right)^{\frac {3}{2}}}}\left[\mathbf {r} +{\frac {1}{c^{2}}}[\mathbf {v} \times [\mathbf {u} \times \mathbf {r} ]]\right]\qquad (.7)}.

Виведення.  

 Fγ(1−(v⋅u)c2)=Qq|r′|3[r′+γu(r′⋅v′)c2+Γu(u⋅r′)c2]=Qq|r′|3[r+Γu(u⋅r)c2+γuc2((u⋅r)γ(1−(u⋅v)c2)−γ(u⋅r))+Γγu(u⋅r)c2]={\displaystyle \ {\frac {\mathbf {F} }{\gamma (1-{\frac {(\mathbf {v} \cdot \mathbf {u} )}{c^{2}}})}}={\frac {Qq}{|\mathbf {r} ‘|^{3}}}\left[\mathbf {r} ‘+\gamma \mathbf {u} {\frac {(\mathbf {r} ‘\cdot \mathbf {v} ‘)}{c^{2}}}+\Gamma \mathbf {u} {\frac {(\mathbf {u} \cdot \mathbf {r} ‘)}{c^{2}}}\right]={\frac {Qq}{|\mathbf {r} ‘|^{3}}}\left[\mathbf {r} +\Gamma \mathbf {u} {\frac {(\mathbf {u} \cdot \mathbf {r} )}{c^{2}}}+\gamma {\frac {\mathbf {u} }{c^{2}}}\left({\frac {(\mathbf {u} \cdot \mathbf {r} )}{\gamma (1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}})}}-\gamma (\mathbf {u} \cdot \mathbf {r} )\right)+\Gamma \gamma \mathbf {u} {\frac {(\mathbf {u} \cdot \mathbf {r} )}{c^{2}}}\right]=}

 Qq|r′|3(1−(u⋅v)c2)[r(1−(u⋅v)c2)+Γu(u⋅r)c2(1+γ)−uc2γ2(u⋅r)+γuc2(v⋅r)]=|Γ(1+γ)=γ2|={\displaystyle \ {\frac {Qq}{|\mathbf {r} ‘|^{3}\left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}\left[\mathbf {r} \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)+\Gamma \mathbf {u} {\frac {(\mathbf {u} \cdot \mathbf {r} )}{c^{2}}}(1+\gamma )-{\frac {\mathbf {u} }{c^{2}}}\gamma ^{2}(\mathbf {u} \cdot \mathbf {r} )+\gamma {\frac {\mathbf {u} }{c^{2}}}(\mathbf {v} \cdot \mathbf {r} )\right]=|\Gamma (1+\gamma )=\gamma ^{2}|=}

 =Qq|r′|3(1−(u⋅v)c2)[r(1−(u⋅v)c2)+γ2uc2(u⋅r)−uc2γ2(u⋅r)+γuc2(v⋅r)]=Qq|r′|3(1−(u⋅v)c2)[r(1−(u⋅v)c2)+uc2(v⋅r)]={\displaystyle \ ={\frac {Qq}{|\mathbf {r} ‘|^{3}\left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}\left[\mathbf {r} \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)+\gamma ^{2}{\frac {\mathbf {u} }{c^{2}}}(\mathbf {u} \cdot \mathbf {r} )-{\frac {\mathbf {u} }{c^{2}}}\gamma ^{2}(\mathbf {u} \cdot \mathbf {r} )+\gamma {\frac {\mathbf {u} }{c^{2}}}(\mathbf {v} \cdot \mathbf {r} )\right]={\frac {Qq}{|\mathbf {r} ‘|^{3}\left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}\left[\mathbf {r} \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)+{\frac {\mathbf {u} }{c^{2}}}(\mathbf {v} \cdot \mathbf {r} )\right]=}

 =|u(v⋅r)=[v×[u×r]]+r(u⋅r)|=Qq|r′|3(1−(u⋅v)c

Сила Лоренца — это… Что такое Сила Лоренца?

Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью заряд лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического и магнитного полей. Выражается в СИ как:

Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено Хевисайдом^[2].

Макроскопическим проявлением силы Лоренца является сила Ампера.

Уравнение (единицы СИ)

Заряженная частица

Сила Лоренца f действующая на заряженную частицу (заряда q) при движении (с постоянной скоростью v). E поле и B поле меняются в пространстве и во времени.

Сила F действующая на частицу с электрическим зарядом q, движущуюся с постоянной скоростью v, во внешнем электрическом E и магнитном B полях, такова:

где × векторное произведение. Все величины выделенные жирным являются векторами. Более явно:

где r — радиус-вектор заряженной частицы, t — время, точкой обозначена производная по времени.

Непрерывное распределение заряда

Сила Лоренца (на единичный 3-объём) f действующая на непрерывное распределение заряда (зарядовая плотность ρ) при движении. 3-плотность потока J соответствует движению заряженного элемента dq в объеме dV .

Для непрерывного распределения заряда, сила Лоренца принимает вид:

где dF — сила, действующая на маленький элемент dq.

Ковариантная запись

4-сила выражается через вектор 4-скорости частицы по формуле

, где  — 4-сила, q — заряд частицы,  — тензор электромагнитного поля,  — 4-скорость.

Частные случаи

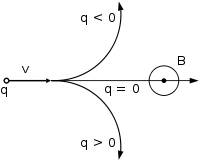Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)

В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:

Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости , намного меньшей скорости света, круговая частота не зависит от :

Если заряженная частица движется в магнитном поле так, что вектор скорости составляет с вектором магнитной индукции угол , то траекторией движения частицы является винтовая линия с радиусом и шагом винта :

Применение силы Лоренца

Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне

В электроприборах

Основным применением силы Лоренца (точнее, её частного случая — силы Ампера) являются электрические машины (электродвигатели и генераторы). Сила Лоренца широко используется в электронных приборах для воздействия на заряженные частицы (электроны и иногда ионы), например, в телевизионных электронно-лучевых трубках, а также в масс-спектрометрии и МГД генераторах.

В ускорителях заряженных частиц

Сила Лоренца также используется в ускорителях заряженных частиц, задавая орбиту, по которой движутся эти частицы.

В вооружении

• См. рельсотрон, или, как его ещё называют, рэйлган («рельсовая пушка»)

Другие применения

Примечания

1. ↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
2. ↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.

См. также