Напишите формулу закона Кулона.
Стр 1 из 4Следующая ⇒
F1= 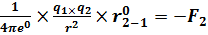
Какое явление определяется с помощью закона Кулона?
Ответ: силу взаимодействия между неподвижными электрическими зарядами.
Каковы формы проявления электромагнитного поля?
Ответ: действие на магнитную стрелку (её отклонение)
При каких условиях электрическое поле называют электростатическим?
Ответ: при условии, что поле создается неподвижными зарядами.
Что произойдет с силой взаимодействия между двумя зарядами если их из воздуха перенести в воду?
Ответ: уменьшиться в E раз.
1.1.6. Величина одного заряда 2.10-5 Кл, другого -4.10-4 Кл. Определить силу взаимодействия между ними, если они помещены в керосин (ε = 2) и находится на расстоянии 10 см друг от друга.
| Дано: | Решение: |
| q1=2×10-5Кл q2=-4×10-4Кл r=10см=0.1м ɛ=2 ф/м | F1= 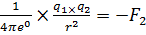 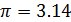 F1= F1=  × × 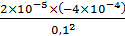 |
| Найти: | |
| F — ? | |
| Ответ: | -3,2×10-7H |
1.1.7. Определите силу взаимодействия между электрическими зарядами q1= 5.10-4 Кл и q2 = 2.10-5 Кл, находящимися в дистиллированной воде (ε =81) на расстоянии 5 см друг от друга.
Выберите правильный ответ:
1.1.8. Два заряда, находящихся на расстоянии 10 см друг от друга, помещены в керосин (ε = 2). Как изменится сила взаимодействия этих зарядов в вакууме? Если взаимное расположение этих зарядов сохраняется.
a) увеличится в два раза;
b) не изменится;
c) уменьшится в два раза.
1.1.9. Расстояние между электрическими зарядами возросло в три раза. Как должны изменится величины зарядов q1и q2, чтобы сила взаимодействия между ними возросла в девять раз?
a) увеличиться в три раза;
b) уменьшиться в три раза;
c) увеличиться в девять раз.
Электрическое поле каких зарядов изображено на рисунке?
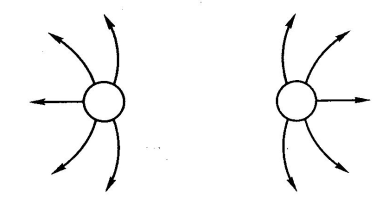
Ответ: одноименные заряды .
Потенциал и напряженность электрического поля
1.2.1. Сформулируйте определения:
Потенциал электрического поля –это отношение потенциальной энергии зарядов поля к этому заряду.
Напряжение— это физическая величина, характеризующая работу электрическое поле по перемещению электрического заряда (разность потенциалов).
Напряженность электрического поля -это физическая величина определяемая силой с которой поле действует на единичный точечный заряд помещенный в эту точку.
В каких единицах измеряется электрический потенциал?
Ответ: Вольт (В)
1.2.3. Как определить работу по переносу заряда из одной точки электрического поля в другую?Ответ: A=q(φ1-φ2)
1.2.4. Определите потенциал точки электрического поля, в которую из бесконечности внесен заряд q= 3.10-6 Кл, если при этом силами поля совершена работа А = 6.10-6 Дж.
| Дано: | Решение: |
| q= 3.10-6 Кл
1.2.5. | 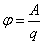 φ=
φ= 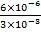 =2B =2B
|
| Найти: | |
| φ-? | |
| Ответ: | 2 B |
1.2.5. Потенциал электрического поля в точке А составляет 60 В, а в точке Б – 7 В. Заряд q = 6 Кл перенесен из точки А в точку Б. Какая при этом совершена работа.
| Дано: | Решение: |
| q = 6 Кл
φ | А=q(φa-φб) A =6×(60-7)=318(Дж) |
| Найти: | |
| A — ? | |
| Ответ: | 318(Дж) |
1.2.6. Вычислите напряженность двух различных электрических полей, действующих на заряд q = 0,004 Кл с силами F1 = 0,018 Н и F2 = 0,012 Н.
| Дано: | Решение: |
| q = 0,004 Кл F1 = 0,018 Н 1.2.7. F2 = 0,012 Н | E=  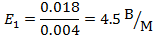 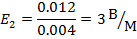 |
| Найти: E1-? E2-? | |
| Ответ: | 4,5B/м; 3 B/м |
Определите напряженность электрического поля плоского конденсатора, если расстояние между пластинами 2 мм, а напряжение 220 В.
| Дано: | Решение: |
| d=2мм=2×10-3м U=220 В | E=  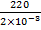 =1,1×105 B/м =1,1×105 B/м
|
| Найти: | |
| E — ? | |
| Ответ: | 1,1×105 B/м |
Электрическая емкость
От чего зависит емкость конденсатора?
Ответ: от геометрических размеров и диэлектрика
Как влияет диэлектрик на емкость конденсаторов?
Ответ: С увеличением диэлектрической проницаемости диэлектрика емкость увеличивается.
В каком случае необходимо применять последовательное соединение конденсаторов?
Ответ: если нужно уменьшить емкость конденсатор
1.3.4. Заполните таблицу.
| 0,0015 Ф | 33 мкФ | 0,047 мкФ | 100 пФ | 6,8 нФ | 820 пФ |
| 1500 мкФ | 3,3×10-5Ф | 47000 пФ | 10-4 мкФ | 6800 пФ | 0,82 нФ |
Определите эквивалентную емкость соединения конденсаторов, схема которых приведена на рисунке, если все конденсаторы имеют емкость по 5 мкФ.
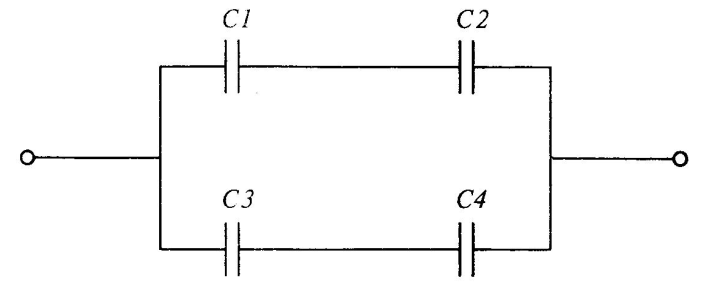
| Дано: | Решение: |
| С1=С2=С3=С4= =5 мкФ | С1,2= 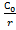 C1,2=
C1,2=  = 2,5 мкФ
С3,4 = = 2,5 мкФ
С3,4 =  = 2,5 мкФ
Сэкв = С1,2+С3,4;
С = 2,5 мкФ
Сэкв = С1,2+С3,4;
С |
| Найти: | |
| Сэк — ? | |
| Ответ: | 5 мкФ |
1.3.6. Конденсатор имеет две пластины. Площадь каждой пластины составляет 15 см2. Между пластинами помещен диэлектрик – слюда толщиной 0,02 см. Определите емкость этого конденсатора.
| Дано: | Решение: |
| E=7 S=15см2 d=0,02см | С = 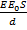 С =
С = 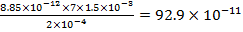 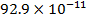 =9 пФ =9 пФ
|
| Найти: | |
| С — ? | |
| Ответ: | 9 пФ |
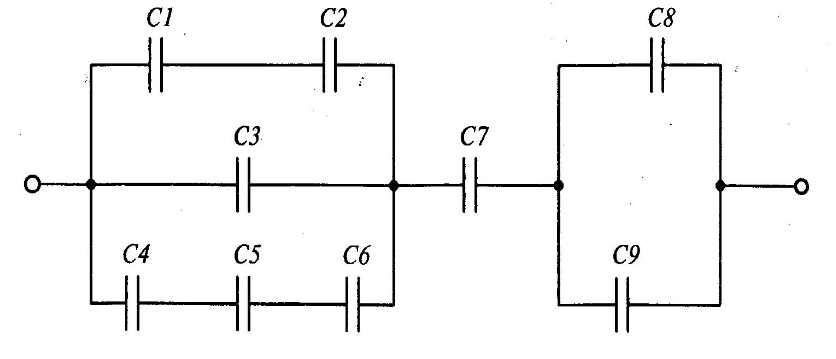
Определите эквивалентную емкость конденсаторов, схема включения которых представлена на рисунке, если все конденсаторы имеют емкость по 10 мкФ.
Рекомендуемые страницы:
Закон Кулона | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Известно, что каждое заряженное тело имеет электрическое поле. Можно также утверждать, что если есть электрическое поле, то есть заряженное тело, которому принадлежит это поле. Итак, если рядом находятся два заряженных тела с электрическими зарядами, то можно сказать, что каждое из них находится в электрическом поле соседнего тела. А в таком случае на первое тело будет действовать сила
F1 = q1E2,
где q1 — заряд первого тела; E2 — напряженность поля второго тела. На второе тело, соответственно, будет действовать сила
F2 = q2E1,
где q2— заряд первого тела; E1 — напряженность поля второго тела.
Электрически заряженное тело взаимодействует с электрическим полем другого заряженного тела.
Если эти тела небольшие (точечные), то
E1 = k • q1 / r2,
E2 = k • q2 / r2,
Силы, действующие на каждое из взаимодействующих заряженных тел, можно рассчитать, зная лишь их заряды и расстояние между ними.
Подставим значения напряженности и получим
F1 = k • q1q2 / r2 и F2 = k • q2q1 / r2.
Значение каждой силы выражается лишь через значение зарядов каждого тела и расстояние между ними. Таким образом, определять силы, действующие на каждое тело, можно, пользуясь лишь знаниями об электрических зарядах тел и расстоянии между ними. На этом основании можно сформулировать один из фундаментальных законов электродинамики — закона Кулона.
Закон Кулона. Сила, действующая на неподвижное точечное тело с электрическим зарядом в поле другого неподвижного точечного тела с электрическим зарядом, пропорциональна произведению значений их зарядов и обратно пропорциональна квадрату расстояния между ними.
В общем виде значение силы, о которой идет речь в формулировке закона Кулона, можно записать так:
F = k • q1q2 / r2,
В формуле для расчета силы взаимодействия записаны значения зарядов обоих тел. Поэтому можно сделать вывод, что по модулю обе силы равны. Тем не менее, по направлению — они противоположные. В случае если заряды тел одноименные, тела отталкиваются (рис. 4.48). Если заряды тел разноименные, то тела притягиваются (рис. 4.49). Окончательно можно записать:
F̅1 = —F̅2.
| Рис. 4.48. Силы взаимодействующих одноименно заряженных тел имеют противоположные направления. |
| Рис. 4.49. Силы взаимодействующих разноименно заряженных тел имеют противоположные направления. |
Записанное равенство подтверждает справедливость III закона динамики Ньютона для электрических взаимодействий. Поэтому в одной из распространенных формулировок закона Кулона говорится, что
сила взаимодействия двух заряженных точечных тел пропорциональна произведению значений их зарядов и обратно пропорциональна квадрату расстояния между ними.
Если заряженные тела находятся в диэлектрике, то сила взаимодействия будет зависеть от диэлектрической проницаемости этого диэлектрика
F = k • q1q2 / εr2.
Для удобства расчетов, базирующихся на законе Кулона, значение коэффициента k записывают иначе:
k = 1 / 4πε0.
Величина ε0 называется электрической постоянной. Ее значение вычисляется в соответствии с определением:
9 • 109 Н•м2/Кл2 = 1 / 4πε0,
ε0 = (1 / 4π) • 9 • 109 Н•м2/Кл2 = 8,85 • 10-12 Кл2/Н•м2. Материал с сайта http://worldofschool.ru
Таким образом, закон Кулона в общем случае можно выразить формулой
F = (1 / 4πε0) • q1q2 / εr2.
Закон Кулона является одним из фундаментальных законов природы. На нем базируется вся электродинамика, и не отмечено ни единого случая, когда бы нарушался закон Кулона. Существует единственное ограничение, которое касается действия закона Кулона на различных расстояниях. Считается, что закон Кулона действует на расстояниях больше 10-16 м и меньше нескольких километров.
При решении задач необходимо учитывать, что закон Кулона касается сил взаимодействия точечных неподвижных заряженных тел. Это сводит все задачи к задачам о взаимодействии неподвижных заряженных тел, в которых применяется два положения статики:
- равнодействующая всех сил, действующих на тело, равна нулю;
- сумма моментов сил равна нулю.
В подавляющем большинстве задач на применение закона Кулона достаточно учитывать лишь первое положение.
На этой странице материал по темам:Есть ли ограничение относительно действия закона кулона
Закон кулона можно записать в виде f k q1 q2/r 2
Физика реферат: закон кулона
Учитывает ли закон кулона действие окружающей среды на взаимодействующие. тела
Как происходит взаимодействие между заряженными телами?
Почему можно говорить о взаимодействии заряженных тел?
Какие ограничения существуют в формулировке закона Кулона относительно взаимодействующих тел?
Как формулируется закон Кулона?
Учитывает ли закон Кулона действие окружающей среды на взаимодействующие тела?
Есть ли ограничение относительно действия закона Кулона?
Закон Кулона и его полевая трактовка
Историческая справка
Закон Кулона входит в число основных экспериментальных фактов, находящихся в основании теории б электричестве. Этот закон для определения силы взаимодействия точечных зарядов $q_1\ $ и $q_2$, которые находятся на расстоянии $r$, имеет вид:
где ${\varepsilon }_0=8,8\cdot {10}^{-12}\frac{Ф}{м}$.
Этот закон установлен Ш. Кулоном в 1785 г. экспериментально. Кулон измерял силы взаимодействия заряженных тел. Точность опытов была плохой, только аналогии с силами тяготения дала уверенность в том, что закон в виде (1) справедлив. С результатами эксперимента, обычно сравнивают следствия из закона Кулона, и на этой основе делается вывод о точности и границах применения данного закона. Первая проверка закона была проведена Кавендишем за 13 лет до Кулона. Кавендиш работ не публиковал, но надо отметить, что его метод был более точным, чем эксперименты Кулона. Позднее опыты по проверке закона Кулона проводил Максвелл. Эти опыты подтвердили справедливость закона Кулона с большой точностью. В соответствии с современными представлениями электромагнитные взаимодействия осуществляются посредством фотонов. Вследствие чего вопрос о справедливости закона Кулона сводится к вопросу о равенстве массы фотона нулю. Все частицы обладают корпускулярными и волновыми свойствами. Энергия фотона (${\varepsilon }_{\nu }=h\nu $) и ${\varepsilon }_{\nu }=m_{\nu }c^2$, где $m_{\nu }$ — масса фотона, $h$ — постоянная Планка. Масса $m_{\nu}$ больше массы покоя, если у фотона масса отлична от нуля. Следовательно, если найти верхний предел для $m_{\nu }$, получим ограничение для массы покоя фотона. Если существование электромагнитных волн с большой длиной волны (а лучше бесконечной) доказать, то можно утверждать, что $m_{\nu }$ очень мало. Наиболее длинные электромагнитные волны, которые удалось наблюдать на сегодняшний момент, образуются в виде стоячих волн в пространстве между поверхностью Земли и ионосферой. Они носят имя Шумана, а точнее называются резонансами Шумана. Минимальный резонанс Шумана соответствует частоте $\nu $=8Гц. С учетом расстояния от поверхности Земли было получено, что $m_{\nu }
Для малых расстояний закон Кулона проверяется в экспериментах, связанных с элементарными частицами. Уже опыты Резерфорда доказали, что закон Кулона справедлив с большой точностью на расстоянии ${10}^{-15}м$.
До работ Фарадея закон Кулона трактовался с позиций дальнодействия, то есть считалось, что одно тело действует на другое без посредников (действие на расстоянии). В первой половине 18 века сложился другой взгляд на механизм взаимодействия, в соответствии с которым существует посредник, осуществляющий непрерывную передачу сил.(теория близкодействия). Поначалу таким посредником назначили, так называемый Мировой эфир. Состояние которого характеризовали некоторыми механическими свойствами. Попытка математического описания механической картины передачи электрических взаимодействий была сделана Максвеллом. Он пытался представить электромагнитные силы в виде механических сил, которые вызываются натяжением и давлением в эфире. Позже Максвелл перешел к феноменологической формулировке взаимодействия и охарактеризовал состояние среды с помощью векторов: напряженности электростатического поля ($\overrightarrow{E}$), электрического смещения ($\overrightarrow{D}$), напряженности магнитного поля ($\overrightarrow{H}$), магнитной индукции ($\overrightarrow{B}$), которым не дал никакой механической интерпретации. В 1864 г. Максвелл сформулировал уравнения электромагнитного поля (уравнения Максвелла). Надежда на механическое толкование электромагнитных взаимодействий умерла. Поле стало основной сущностью, посредством которого осуществляется электромагнитное взаимодействие. Оно характеризуется величинами, которые не могут интерпретироваться в рамках механики. После того как Герц записал уравнения Максвелла в современном виде стало очевидно, что поле существует в пространстве и времени наряду с материей.
Полевая трактовка закона Кулона
Пусть мы имеем два точечных заряда $q_1\ (точка\ 1)\ $ и $q_2$(точка 2).Тогда ${\overrightarrow{F}}_{12}$- сила, с которой заряд $q_1$ действует на заряд $q_2$. ${\overrightarrow{F}}_{21}$- сила, с которой заряд $q_2$ действует на заряд $q_1$. ${\overrightarrow{r}}_{12}$- вектор из точки (1) в точку (2), ${\overrightarrow{r}}_{21}$ — вектор из точки (2) в точку (1). Исходя из принятых нами обозначений, запишем закон Кулона:
По своему физическому содержанию формулы (2) и (3) различны. Они определяют силы, которые действуют на второй (2) и первый (3) заряды, то есть описывают силы в разных точках пространства. Механизм же возникновения этих сил одинаков. Заряды вокруг себя создают электрическое поле. Это поле принято характеризовать напряженностью ($\overrightarrow{E}$). Напряженностью электрического поля является физическая величина, которая равна отношению силы, с которой действует поле на положительный заряд, помещенный в данную точку поля к заряду. Соответственно, с учетом (2,3), запишем:
Соответственно:
Формула (4) описывает напряженность электрического поля, которое образуется зарядом $q_1.$ Формула (5) характеризует силу, с которой поле с напряженностью ${\overrightarrow{E}}_2$ действует на заряд, который находится в точке поля. Действие одного заряда на другой делится на:
- Точечный заряд создает вокруг себя электрическое поле, напряженность которого равна: \[\overrightarrow{E}=\frac{1}{4\pi {\varepsilon }_0}\frac{q}{r^2}\frac{\overrightarrow{r}}{r}\ \left(8\right),\]
- На точечный заряд q, который находится в точке поля с напряженностью $\overrightarrow{E}$, действует сила равная: \[\overrightarrow{F}=q\overrightarrow{E}\ \left(9\right).\]
где $\overrightarrow{r}$- радиус — вектор, проведенный из точки нахождения заряда до точки, в которой определяется напряженность.
Эти два утверждения дают полевую трактовку Закона Кулона.
Если имеется несколько источников поля (количество зарядов $N$), то результирующую силу, действующую на пробный заряд $q$ можно найти как:
\[\overrightarrow{F}=\sum\limits^N_{i=1}{\overrightarrow{F_{ia}}}\left(10\right),\]где $\overrightarrow{F_{ia}}$ — сила, с которой N зарядов действуют на заряд $q$.
Закон Кулона в формуле (1) записан для вакуума, если мы имеем дело с какой-то средой, ее диэлектрические свойства характеризует диэлектрическая проницаемость среды ($\varepsilon $), тогда уравнение (1) примет вид:
\[\overrightarrow{F}=\frac{1}{4\pi {\varepsilon \varepsilon }_0}\frac{q_1q_2\overrightarrow{r}}{r^3}\ \left(11\right).\]Пример 1
Задание: Три одинаковых точечных заряда величиной $q$ поместили в вершинах равностороннего треугольника. Найдите величину точечного заряда $Q$, который надо поместить в центр масс треугольника, чтобы система находилась в состоянии равновесия.
Решение:

Рис. 1
Для определенности допустим, что заряды в вершинах треугольника отрицательные, тогда на пересечении медиан (в центре масс) положительный.
Рассмотрим силы, которые действуют на заряд ${-q}_1$. Это будут три силы Кулона, две — отталкивания, со стороны зарядов в вершинах и одна — притяжения со стороны «центрального». Тогда условие равновесия сил запишем в виде:
\[\overrightarrow{F_{12}}+\overrightarrow{F_{13}}+\overrightarrow{F_{10}}=0\ \left(1.1\right).\]Выберем ось OX, как указано на рис.1, найдем проекцию уравнения (1) на эту ось:
\[F_{12}{cos \left(\frac{\alpha }{2}\right)\ }+F_{13}{cos \left(\frac{\alpha }{2}\right)\ }-F_{10}=0\ \left(1.2\right),\]где $\alpha $- угол треугольника (так как треугольник равносторонний, следовательно, $\alpha =60{}^\circ $).
Так как по условию задачи треугольник равносторонний, заряды в вершинах одинаковые и равны q, то $F_{12}=F_{13}$, а по закону Кулона:
\[F_{12}=F_{13}=\frac{q^2}{4 \pi \varepsilon \varepsilon_0a^2}\ \left(1.3\right),\]где a — сторона треугольника. Для силы $F_{10}$ по закону Кулона получим:
\[F_{10}=\frac{qQ}{4\pi \varepsilon \varepsilon_0r^2}\ \left(1.4\right).\]В таком случае выражение (1.2) запишем в виде:
\[\frac{2q^2}{4\pi {\varepsilon \varepsilon }_0a^2}{cos \left(\frac{\alpha }{2}\right)\ }=\frac{qQ}{4\pi {\varepsilon \varepsilon }_0r^2}\ \left(1.5\right),\]где точка пересечения медиан делит их в соотношении 2:1, если считать от вершины, следовательно:
\[r=\frac{2}{3}{acos \left(\frac{\alpha }{2}\right)\ }\left(1.6\right).\]Подставляем (1.6) в (1.5) выражаем $Q$, получаем:
\[Q=\frac{8qcos^3\left(\frac{б}{2}\right)}{9}\]Ответ: $Q=\frac{8qcos^3\left(\frac{\alpha }{2}\right)}{9}$ (Кл).
Пример 2
Задание: Положительный точечный заряд 1 Кл находится на плоскости XOY в точке, которая определена радиус — вектором$\overrightarrow{{\ r}_1}=4\overrightarrow{i}+6\overrightarrow{j}$,(м) где $i$ и $j$ — орты осей. Найдите модуль напряженности электрического поля E в точке с радиус-вектором $\overrightarrow{{\ r}_2}=16\overrightarrow{i}-\overrightarrow{j}\ (м)$.
Решение:
Найдем разность векторов $\overrightarrow{{\ r}_2}$-$\overrightarrow{{\ r}_1}$, получим:
\[\overrightarrow{{\ r}_2}-\overrightarrow{{\ r}_1}=12\overrightarrow{i}-\overrightarrow{7j}\ \left(2.1\right).\]Из закона Кулона выражение для напряженности электростатического поля может быть записано как:
\[E=\frac{1}{4\pi {\varepsilon }_0}\frac{q}{r^2}=k\frac{q}{r^2}\ \left(2.2\right),\]где $k=9•{10}^9\frac{Нм^2}{{Кл}^2}$
Найдем $r$, получим:
\[r=\left|\overrightarrow{{\ r}_2}-\overrightarrow{{\ r}_1}\right|=\sqrt{{12}^2+7^2}\approx 13,89\ (м)\]Вычислим напряженность (модуль), получим:
\[E=9\cdot {10}^9\frac{1}{193}\approx 4,7{\cdot 10}^7\ \left(\frac{В}{м}\right).\]Ответ: Напряженность поля в заданной точке $4,7{\cdot 10}^7\frac{В}{м}$.
Обсуждение:Закон Кулона — Википедия
Материал из Википедии — свободной энциклопедии
Примечательно что закон Кулона Кулон переоткрыл сам того не зная. В 1771 к аналогичному выводу пришел Кавендиш Генри (10.10.1731—24.2.1810). Но Кавендиш не счёл целесообразным это публиковать. И вообще был очень замкнутым человеком.
Сейчас смог найти под рукой только
Храмов Ю. А. Физики: Биографический справочник. — 2-е изд., испр. и дополн. — М.: Наука, Главная редакция физико-математической литературы, 1983.
- может Кавендиш тоже переоткрыл :)—Berserkerus 22:50, 18 мая 2007 (UTC)
- а вообще-то англичане славились научно-технологическим шпионажем. не удивлюсь что Кавендиш на самом деле был после и просто проверял инфу —Berserkerus 22:52, 18 мая 2007 (UTC)
Вывод закона Кулона в квантовой теории поля. ВП:ОРИС?[править код]
Хотелось бы увидеть ВП:АИ для этого раздела. К квантовой теории поля подобный «квазиквантовый оценочный подход» отношения не имеет. Фразы типа: «Решение данной задачи невозможно без изучения статистической физики и квантовой теории поля. Поэтому просто приведем готовые результаты и выведем закон силы…» делают сомнительным ценность подобного «вывода». Излучение абсолютно чёрного тела к вакууму взаимодействия электронов с виртуальными фотонами имеет крайне отдалённое отношение (достаточно спросить — какова его температура?). Гремучая смесь из классической силы, соотношения неопределённости и фактов теории излучения делает всё это крайне подозрительным. —Source 18:02, 4 мая 2010 (UTC)
Источник, в котором обсуждается квантовый вывод закона Кулона[править код]
См. книгу: Д. Фриш, А. Торндайк, «Элементарные частицы», М., 1966, Атомиздат, пер. с англ. В.В. Емельяновой, под ред. И.И. Тугова, УДК 539.12 (023). Квантовый вывод закона Кулона обсуждается на стр. 98-102 в гл. 8 «Изучение сил между элементарными частицами», параграф «Квантовая теория сил, пропорциональных 1r2{\displaystyle {\frac {1}{r^{2}}}}. Если хотите, могу отсканировать эти страницы и переслать Вам по e-mail.
- Если не затруднит. Я с интересом посмотрю. В свободном доступе этой книги я не нашёл. E-mail на моей странице. К слову, иногда заходите и на свою страниц обсуждения (или нажимайте список наблюдения). Удаление произошло после отсутствия Вашего ответа там, и обсуждения этой проблемы с другим участником. —Source 17:05, 5 мая 2010 (UTC)
- Ну, и у меня небольшие претензии оформительского характера. Прошу ссылки на литературу оформить как принято в Вики и стиль статьи на более энциклопедический поправить. Сейчас он скорее журнальный. —Dodonov 17:32, 5 мая 2010 (UTC)
Курица или яйцо?[править код]
Касательно всего «вывода», дождусь обещанной Вами книги. Однако, уже вторая фраза: «Строго обоснованные расчеты осуществляются путем построения диаграмм Фейнмана [2] и здесь для простоты опущены.» ставит в тупик. Вы действительно считаете, что для обоснования («вывода») закона Кулона подходит квантовая электродинамика? На самом деле, ситуация в точности обратная. Классический закон Кулона (экспериментальный факт) + СТО = Уравнения Максвелла. Уравнения Максвелла + Квантовая механика = Квантовая электродинамика (КЭД). Это конечно упрощённая схема, но другой нет! Обратное движение от (КЭД) к закону Кулона вполне уместно, но уже как поправки к его классической версии (бегущая константа связи, свойства вакуума и т.п.). Вот это, действительно, стоит отразить в статье.
Вообще, «вывод» закона Кулона тема достаточно скользкая. Есть экспериментальный факт. Это, как говаривал Фандорин — раз. Существуют рассуждения связанные с размерностью пространства (площадь сферы = r^2). Однако, они фактически подменяют закон Кулона эквивалентным законом Гаусса в интегральной форме, поэтому выводом не являются. Это — два. Существуют различные соображения выделенности силы 1/r^2 среди других функций (замкнутость траекторий, дополнительный закон сохранения и т.п.). Но они не являются выводом, а относятся к оборотам «интересно заметить». Наконец существуют различные модельные выводы (типа Теория гравитации Лесажа), но они не выдерживают критики. Недавно видел статьи посвящённые выводу из энтропийных соображений. Но выглядят они тоже не очень убедительно. Поэтому, при всём моём личном желании получить закон Кулона из первых принципов, приходится пока признавать правоту Ньютона, касательно не измышления гипотез.—Source 18:10, 5 мая 2010 (UTC)
- Добавил про отклонения от закона Кулона вследствие нелинейных эффектов КЭД, буду благодарен за уточнения Raoul NK 11:55, 6 мая 2010 (UTC)
- Очень хорошо написано. Я там формулу, как мне кажется, в более понятном виде привёл и ссылок немного поставил. —Source 12:34, 6 мая 2010 (UTC)
- Спасибо за уточнение, сейчас ещё поищу ссылки на потенциал в сильных внешних полях, может, у Вас что-нибудь есть? Raoul NK 14:14, 6 мая 2010 (UTC)
- Классическая монография: Гриб А.А., Мамаев С.Г., Мостепаненко В.М. «Вакуумные квантовые эффекты в сильных полях» (есть на homelinux). Но она не числится в списке моих любимых книг 🙂 —Source 14:25, 6 мая 2010 (UTC).
- Кулоновского потенциала я там, к сожалению, не нашёл. Нагуглил ссылку на расчёт потенциала во внешнем магнитном поле, а вот во внешнем электрическом — упс 🙁 Raoul NK 15:15, 6 мая 2010 (UTC)
- Классическая монография: Гриб А.А., Мамаев С.Г., Мостепаненко В.М. «Вакуумные квантовые эффекты в сильных полях» (есть на homelinux). Но она не числится в списке моих любимых книг 🙂 —Source 14:25, 6 мая 2010 (UTC).
- Спасибо за уточнение, сейчас ещё поищу ссылки на потенциал в сильных внешних полях, может, у Вас что-нибудь есть? Raoul NK 14:14, 6 мая 2010 (UTC)
- Очень хорошо написано. Я там формулу, как мне кажется, в более понятном виде привёл и ссылок немного поставил. —Source 12:34, 6 мая 2010 (UTC)
Да, в книге Фриша и Торндайка «Элементарные частицы» закон Кулона в этом месте не упоминается и не обсуждается. Авторы обсуждают не закон Кулона, а точку зрения на закон обратных квадратов для электрических сил с позиций квантовой электродинамики. Извините. Я исправил свою ошибку.
Здраствуйте. После первой формулы: «В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:» идёт пояснение переменных и постоянных используемых в этой формуле. Так, вот цитирую: «(Вектор r12)- радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами -r12)». Возможно правильней будет «расстоянию между зарядами — q1 и q2» ? —spiker01 17:07, 29 мая 2011 (UTC)

