Site Loader
Posted on 12.07.2023

Сопротивление при соединении проводников | Частная школа. 8 класс

Конспект по физике для 8 класса «Сопротивление при последовательном и параллельном соединении проводников». Как найти общее сопротивление цепи, состоящей из последовательно соединённых проводников. Как найти общее сопротивление цепи, состоящей из параллельно соединённых проводников.

Конспекты по физике    Учебник физики    Тесты по физике

Рассмотрим участок цепи AB, представляющий собой последовательное соединение двух резисторов с сопротивлениями R1 и R2.

В соответствии с законом Ома полное сопротивление рассматриваемого участка U = IR, где U — общее напряжение на участке цепи АВ, равное сумме напряжений на каждом из резисторов: U = U1 + U2.

I — сила тока на участке цепи АВ. Она одинакова на всём участке и равна силе тока I1 и I2

в каждом из резисторов. Поэтому можно записать:
IR = IR1 + IR2,
IR = I(R1 + R2).

Следовательно, R = R1 + R2.

Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников.

При последовательном соединении нескольких проводников общее сопротивление цепи равно сумме сопротивлений отдельных проводников:

R = R1 + R2 + … Rn.

Способ последовательного подключения всё новых участков цепи реализован в работе реостата, о котором говорилось на предыдущих уроках. Передвигая ползунок реостата, мы увеличиваем или уменьшаем число витков проволоки, включённых последовательно в цепь. При этом сопротивление цепи соответственно увеличивается или уменьшается.

При последовательном соединении проводников их общая длина увеличивается. Поэтому сопротивление цепи становится больше сопротивления любого из проводников.

СОПРОТИВЛЕНИЕ ПРИ ПАРАЛЛЕЛЬНОМ СОЕДИНЕНИИ

Рассмотрим участок цепи CD, представляющий собой параллельное соединение двух резисторов с сопротивлениями R1 и R2.

В соответствии с законом Ома I = U/R, где R — общее сопротивление рассматриваемого участка цепи; U — общее напряжение на участке цепи CD, равное напряжениям U

1 и U2 на каждом из резисторов; I — сила тока на участке цепи CD, она равна сумме токов в каждом из резисторов:  I = I1 + I2.

Поэтому можно записать:

где R1 и R2 — сопротивления первого и второго резисторов соответственно.

Учитывая, что U = U1 = U2, получаем

Следовательно,

Для рассмотренного случая двух резисторов, соединённых параллельно

, общее сопротивление цепи можно вычислить по формуле

Таким образом, общее сопротивление цепи при параллельном соединении нескольких резисторов можно вычислить из формулы

Уменьшение общего сопротивления проводников при их параллельном соединении объясняется тем, что общая площадь поперечного сечения проводников на данном участке цепи увеличивается.

В используемых на практике электрических цепях часто встречается смешанное соединение проводников, включающее в себя как последовательные, так и параллельные участки.

При расчёте таких цепей сначала вычисляют необходимые величины на каждом из участков цепи, а затем находят её общие параметры.

 

Вы смотрели Конспект по физике для 8 класса «Сопротивление при последовательном и параллельном соединении проводников».

Вернуться к Списку конспектов по физике (Оглавление).

Просмотров: 6 661

Решение задач по теме: «Смешанное соединение проводников» 8 класс онлайн-подготовка на Ростелеком Лицей

Необходимые для решения задач формулы и факты

 

Под соединением проводников подразумевается соединение резисторов – приборов, сделанных на основе сопротивления проводников. На предыдущих уроках были рассмотрены параллельное и последовательное соединения. На данном уроке будут рассмотрены задачи на смешанное соединение проводников, то есть когда в цепи присутствует и последовательное, и параллельное соединение.

 

Для решения задач сначала рассмотрим формулы для связи различных величин при параллельном и последовательном соединениях:

 

Если проводники соединены последовательно, то сила тока в них одинакова и равна силе тока в цепи. При этом общее напряжение в цепи будет состоять из суммы напряжений на каждом проводнике. А если говорить о сопротивлении этого участка цепи, в котором проводники соединены последовательно, то оно равно сумме сопротивлений проводников.

В параллельном соединении все по-другому. Сила тока в каждой ветке этой цепи будет различной, при этом общая сила тока в цепи будет вычисляться как сумма сил токов в проводниках. Напряжение на проводниках, соединенных последовательно, будет одинаковым. Общее сопротивление этого участка цепи, так называемое «эквивалентное сопротивление» R, будет вычисляться по следующей формуле: .

Также стоит отметить, что параллельное соединение обычно применяется при включении бытовых приборов, а последовательное – для того, чтобы создать длинную неразветвленную цепь.

 

Задача №1

 

 

Рассмотрим следующую задачу. Участок цепи состоит из двух последовательно соединенных сопротивлений, каждое из которых равно 1 Ом. К этим двум резисторам параллельно подключают еще одно сопротивление, значение которого составляет 2 Ом. Всю эту цепь подключают к источнику тока, который создает на концах данного соединения напряжение 2,4 В. Необходимо определить силу тока во всей электрической цепи (рис. 1).

 

Рис. 1. Условия и рисунок задачи № 1

Как видим, резисторы R1 и R2 соединены последовательно, резистор R3 – параллельно к ним. Источник дает напряжение 2,4 В, соответственно, на участке АВ напряжение будет также 2,4 В. Сила тока, которую требуется найти, – это сила тока, протекающая через амперметр А.

Такое соединение проводников называется неразветвленным. В промышленности обычно изготавливается набор резисторов с четко определенными сопротивлениями, но для экспериментов могут понадобиться любые различные сопротивления. Тогда с помощью таких схем можно создавать нужное сопротивление для эксперимента или прибора.

Далее требуется определить эквивалентное сопротивление неразветвленной части. Сначала посмотрим, чему равно сопротивление R’ участка цепи АВ, который содержит только резисторы R1 и R2. Они соединены последовательно, тогда R′=R1+R2=2 [Ом]. Теперь можно перерисовать электрическую цепь, заменив сопротивления R1 и R2 эквивалентным им сопротивлением R’ (рис. 2).

Рис. 2. Первая замена эквивалентным сопротивлением

Теперь можно сказать, что участок АВ включает в себя не три, а два сопротивления: R3 и R’. Эти два сопротивления соединены параллельно, соответственно, можно найти общее сопротивление электрической цепи по формуле . Выразив R и подставив значения , получаем:

Стоит отметить, что сопротивления были соединены, но общее сопротивление получилось все равно равным 1 Ом. Теперь электрическую цепь можно заменить следующей (рис. 3):

Рис. 3. Вторая замена эквивалентным сопротивлением

На рис. 3 сопротивление R=1 Ом называется эквивалентным сопротивлением, поскольку три сопротивления были заменены на одно. Чтобы рассчитать силу тока в цепи, надо использовать закон Ома для участка цепи: . Напряжение на сопротивлении R – это напряжение на участке АВ (Рис. 1), которое, в свою очередь, равно 2,4.Тогда . Это и будет значение силы тока в электрической цепи, которое покажет амперметр.

 

Задача №2

 

 

Теперь рассмотрим задачу, в которой также будет три сопротивления, но соединены они будут по-другому (рис. 4):

 

Рис. 4. Условие задачи № 2

Два сопротивления R1 и R2 соединены параллельно (R1=R2=2 Ом), к ним еще последовательно присоединено сопротивление R3=1 Ом. Амперметр показывает силу тока в цепи, равную I=0,5 А. Требуется определить напряжение на концах участка этой цепи, то есть на участке АВ.

Для начала определим сопротивление участка цепи, содержащего сопротивления R1 и R2. Эти два сопротивления соединены параллельно, значит, их эквивалентное сопротивление R’ можно найти из формулы . Подставляя значения, получаем:

Теперь можно сказать, что цепь включает в себя только два сопротивления: R’и R3, которые соединены последовательно.

Рис. 5. Замена параллельного соединения эквивалентным сопротивлением

В задаче требуется определить напряжение.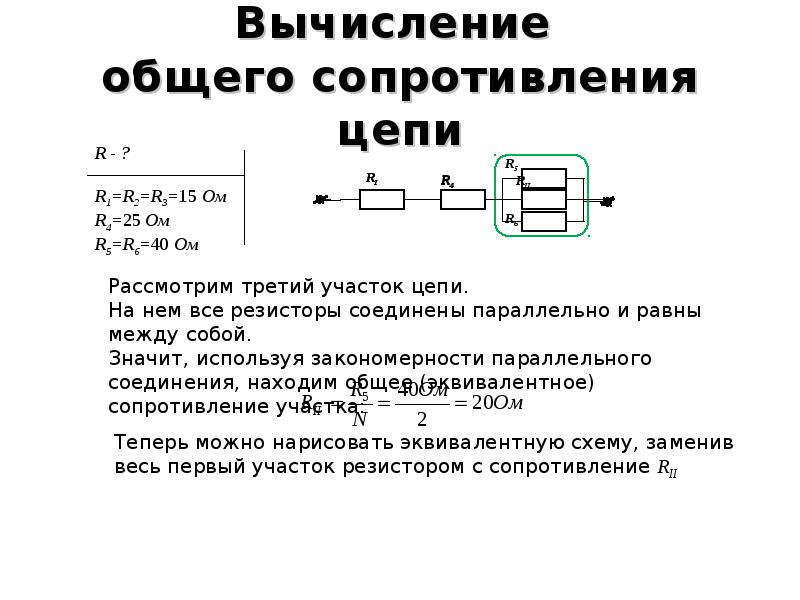 Для этого используется прибор, который называется вольтметр. В цепь он включается параллельно. И рассмотрим участок цепи, в котором все три сопротивления уже заменены эквивалентным.

Рис. 6. Включение вольтметра в цепь

Вольтметр включен в месте, соответствующем участку АВ на рис. 4. Соответственно, он измеряет напряжение на это участке цепи. Чтобы найти значения этого напряжения, требуется сначала найти эквивалентное сопротивление. Сопротивления R’ и R3 соединены последовательно (рис. 5), значит, эквивалентное сопротивление определяется по формуле:

Теперь из закона Ома для участка цепи можно найти напряжение:

Значит, вольтметр должен будет показать значения напряжения в 1 В.

 

Расчет более сложных цепей

 

 

На уроке были рассмотрены соединения только трех сопротивлений, когда они были последовательные, к ним параллельно подключается третий, или когда два соединены параллельно, а к ним последовательно подключают третье сопротивление.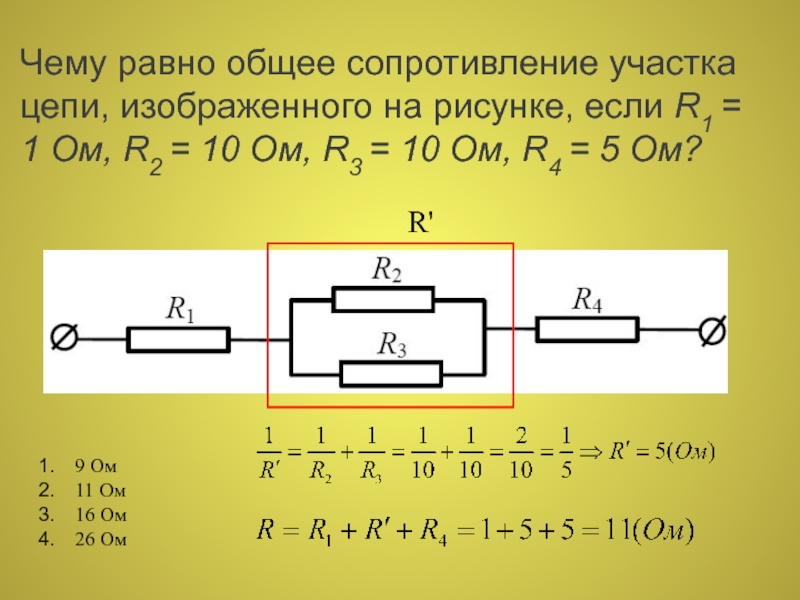

Но реальные схемы значительно сложнее. Они содержат огромное количество различных элементов, сопротивлений, поэтому имеются достаточно сложные методы расчетов электрических цепей.

 

Впервые расчетами таких сложных электрических цепей озадачились ученые приблизительно в XIX веке, и появились новые правила, которые используются и по сей день. Немецкий ученый Кирхгоф разработал возможность расчета электрических сложных цепей, поэтому правила, которые используют для сложных цепей, называются «правилами Кирхгофа».

На следующих уроках будет рассмотрено понятие мощности и работы силы тока.

 

Список литературы

  1. Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.
  2. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
  3. Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

  1. Festival.
    1september.ru (Источник)
  2. Electroandi.ru (Источник)
  3. Bocharova.ucoz.ru (Источник)

 

Домашнее задание

  1. Стр. 117: задачи № 4, 5. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
  2. В каком случае эквивалентное сопротивление будет больше: если три проводника с сопротивлениями 1 Ом каждый соединить параллельно или последовательно?
  3. Два сопротивления R1=1 Ом и R2= 2 Ом соединены последовательно, к ним параллельно присоединено сопротивление 3 Ом. Чему равно эквивалентное сопротивление?
  4. Сколько различных цепей можно составить из трех резисторов с сопротивлениями 1 Ом каждый так, чтоб их эквивалентные сопротивления была различными?

 

 

21.1: Резисторы последовательно и параллельно

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    2688
    • OpenStax
    • OpenStax

    Цели обучения

    К концу этого раздела вы сможете:

    • Нарисовать цепь с параллельными и последовательными резисторами.
    • Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
    • Сравните способ расчета общего сопротивления резисторов, включенных последовательно и параллельно.
    • Объясните, почему общее сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
    • Рассчитайте общее сопротивление цепи, содержащей смесь резисторов, соединенных последовательно и параллельно.

    Большинство цепей имеют более одного компонента, называемого резистором , который ограничивает поток заряда в цепи. Мера этого предела потока заряда называется сопротивлением

    . Простейшими комбинациями резисторов являются последовательное и параллельное соединения, показанные на рисунке \(\PageIndex{1}\). Общее сопротивление комбинации резисторов зависит как от их отдельных значений, так и от того, как они соединены.

    Рисунок \(\PageIndex{1}\): (a) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.

    Резисторы серии

    Когда резисторы серии относятся к серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый

    током , должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, в землю, то \(R_{1}\) на рисунке \(\PageIndex{1}\)(a) может быть сопротивлением стержня отвертки, \ (R_{2}\) сопротивление его ручки, \(R_{3}\) сопротивление тела человека и \(R_{4}\) сопротивление ее обуви.

    На рисунке \(\PageIndex {2}\) показаны резисторы, последовательно подключенные к источнику напряжения . Кажется разумным, что общее сопротивление представляет собой сумму отдельных сопротивлений, учитывая, что ток должен последовательно проходить через каждый резистор. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев высокоомную обувь на резиновой подошве. Это могло бы быть недостатком, если бы одним из сопротивлений был неисправный высокоомный шнур для устройство, которое уменьшило бы рабочий ток.) ​​

    Рисунок \(\PageIndex{2}\): Три резистора, соединенные последовательно с батареей (слева), и эквивалентное одиночное или последовательное сопротивление (справа).

    Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потери электроэнергии, называемые падением напряжения , в каждом резисторе на рисунке \(\PageIndex {2}\).

    Согласно Закону Ома , падение напряжения \(В\) на резисторе при протекании через него тока рассчитывается по уравнению \(V=IR\), где \(I\) равно току в амперах (А) и \(R\) сопротивление в омах\((\Омега)\). Другой способ думать об этом состоит в том, что \(V\) — это напряжение, необходимое для того, чтобы ток \(I\) протекал через сопротивление \(R\).

    Таким образом, падение напряжения на \(R_{1}\) равно \(V_{1}=IR_{1}\), на \(V_{2}=IR_{2}\) и на \ (R_{3}\) равно \(V_{3}=IR_{3}\). Сумма этих напряжений равна выходному напряжению источника; то есть

    \[V=V_{1}+V_{2}+V_{3}.\]

    Это уравнение основано на законах сохранения энергии и заряда. Электрическая потенциальная энергия может быть описана уравнением \(\mathrm{PE}=qV\), где \(q\) — электрический заряд, а \(V\) — напряжение. Таким образом, энергия, подаваемая источником, равна \(qV), а энергия, рассеиваемая резисторами, равна

    \[qV_{1}+qV_{2}+qV_{3}.\]

    СОЕДИНЕНИЯ: ЗАКОНЫ СОХРАНЕНИЯ

    Выводы выражений для последовательного и параллельного сопротивления основаны на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно связаны со всеми электрическими явлениями и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.

    Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения энергии. Таким образом, \(qV=qV_{1}+qV_{2}+qV_{3}\). Заряд \(q\) отменяется, что дает \(V=V_{1}+V_{2}+V_{3}\), как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для накопления заряда, нет места для утечки заряда, и заряд сохраняется.)

    Теперь подстановка значений отдельных напряжений дает

    \[V=IR_{1}+IR_{2}+IR_{3}=I(R_{1}+R_{2}+R_{3}). \]

    Обратите внимание, что для эквивалентного последовательного сопротивления \(R_{\mathrm{S}}\) мы имеем

    \[V=IR _{\mathrm{S}}.\]

    Это означает, что общее или эквивалентное последовательное сопротивление \(R_{\mathrm{S}}\) трех резисторов равно \(R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}\).

    Эта логика действительна в целом для любого количества последовательно соединенных резисторов; таким образом, полное сопротивление \(R_{\mathrm{S}}\) последовательного соединения равно

    \[R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}+\dots ,\]

    как предложено. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого из них, а последовательные сопротивления просто складываются.

    Пример \(\PageIndex{1}\): расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи

    Предположим, что выходное напряжение батареи на рисунке \(\PageIndex{2}\) равно \(12,0\mathrm{V}\), а сопротивления равны \(R_{1}=1,00\Омега\), \(R_{2}=6,00\Омега\) и \(R_{3}= 13.0\Омега\). а) Чему равно полное сопротивление? б) Найдите силу тока. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.

    Стратегия и решение для (a)

    Общее сопротивление представляет собой просто сумму отдельных сопротивлений, определяемую следующим уравнением:

    \[R_{\mathrm{S}}=R_{1}+R_ {2}+R_{3}\]

    \[=1,00\Омега + 6,00\Омега + 13,0\Омега\]

    \[=20,0 \Омега. \]

    Стратегия и решение для (b)

    Ток определяется по закону Ома \(V=IR\). Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:

    \[I=\dfrac{V}{R_{\mathrm{S}}}=\dfrac{12,0\Omega}{20,0\Omega}=0,600 \mathrm{A}.\]

    Стратегия и решение для (c)

    Падение напряжения или \(IR\) на резисторе определяется законом Ома. Ввод тока и значения первого сопротивления дает

    \[V_{1}=IR_{1}=(0,600\mathrm{A})(1,0\Omega)=0,600\mathrm{V}.\]

    Аналогично,

    \[V_{2}=IR_{2}=(0,600\mathrm{A})(6,0\Omega)=3,60\mathrm{V}\]

    и

    \[V_{3}= IR_{3}=(0,600\mathrm{A})(13,0\Omega)=7,80\mathrm{V}.\]

    Обсуждение для (c)

    Три капли \(IR\) добавляются к \(12.0\mathrm{V}\), как и предполагалось:

    \[V_{1}+V_{2}+V_ {3}=(0,600+3,60+7,80)\mathrm{V}=12,0\mathrm{V}.\]

    Стратегия и решение для (d)

    Самый простой способ расчета мощности в ваттах (Вт) рассеивается на резисторе в цепи постоянного тока, чтобы использовать закон Джоуля , \(P=IV\), где \(P\) — электрическая мощность. В этом случае через каждый резистор протекает одинаковый полный ток. Подставив закон Ома \(V=IR\) в закон Джоуля, мы получим мощность, рассеиваемую первым резистором, как 9{2}}{R}\), где \(V\) — падение напряжения на резисторе (не полное напряжение источника). Будут получены одинаковые значения.

    Стратегия и решение для (e)

    Самый простой способ рассчитать выходную мощность источника — использовать \(P=IV\), где \(V\) — напряжение источника. Это дает

    \[P=(0,600\mathrm{A})(12,0\mathrm{V})=7,20 \mathrm{W}.\]

    Обсуждение для (e)

    Обратите внимание, по совпадению, что общая мощность, рассеиваемая резисторами, также составляет 7,20 Вт, как и мощность, выдаваемая источником. то есть

    \[P_{1}+P_{2}+P_{3}=(0,360 +2,16+4,68)\mathrm{W}=7,20\mathrm{W}.\]

    Мощность – это энергия в единицу времени ( Вт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.

    ОСНОВНЫЕ ХАРАКТЕРИСТИКИ РЕЗИСТОРОВ В СЕРИИ

    1. Последовательные сопротивления добавляют: \(R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}+\dots\)
    2. Один и тот же ток протекает через каждый резистор последовательно.
    3. Отдельные последовательно соединенные резисторы не получают общее напряжение источника, а делят его.

    Резисторы, включенные параллельно

    На рисунке \(\PageIndex{3}\) показаны резисторы, соединенные параллельно , подключенные к источнику напряжения. Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление. Таким образом, к каждому резистору приложено полное напряжение источника.

    Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен). Например, автомобильные фары, радиоприемник и т. д. соединены параллельно, так что они используют полное напряжение источника и могут работать совершенно независимо.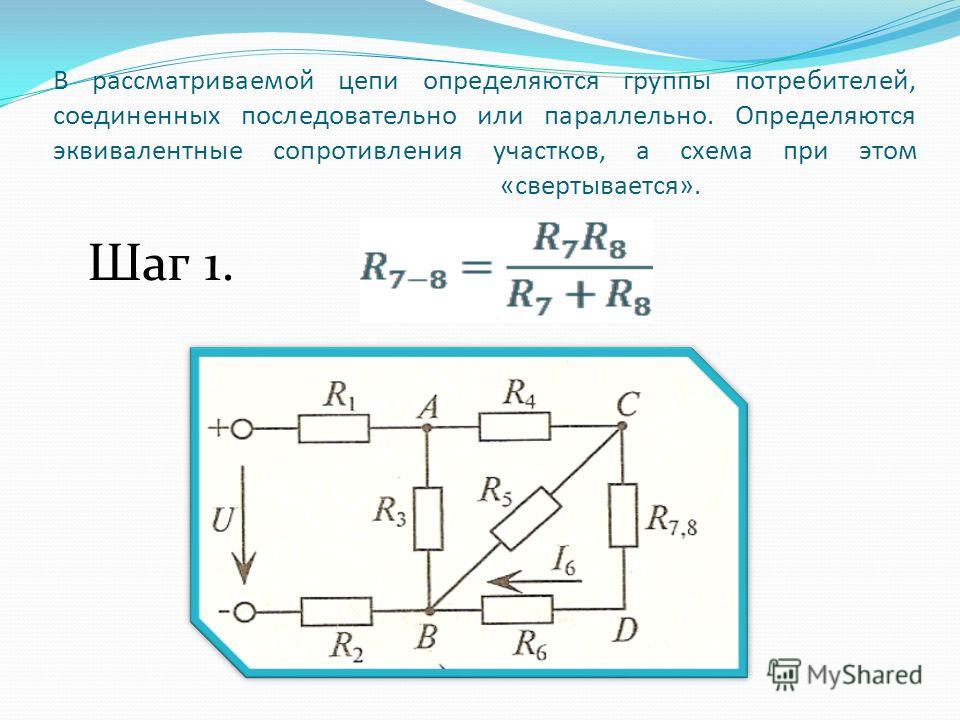 То же самое верно и в вашем доме, или в любом здании. (См. рисунок \(\PageIndex{3}\)(b).)

    Рисунок \(\PageIndex{3}\): (a) Три резистора, подключенные параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление. (b) Установка электроснабжения в доме. (кредит: Dmitry G, Wikimedia Commons)

    Чтобы найти выражение для эквивалентного параллельного сопротивления \(R_{\mathrm{p}}\), давайте рассмотрим протекающие токи и то, как они связаны с сопротивлением. Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны \(I_{1}=\dfrac{V}{R_{1}}\), \(I_{2}=\dfrac{ V}{R_{2}}\) и \(I_{3}=\dfrac{V}{R_{3}}\). Сохранение заряда подразумевает, что полный ток \(I\), производимый источником, представляет собой сумму этих токов:

    \[I=I_{1}+I_{2}+I_{3}.\]

    Подстановка выражений для отдельных токов дает

    \[I=\dfrac{V}{R_{1}} +\dfrac{V}{R_{2}}+\dfrac{V}{R_{3}}=V(\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}} +\dfrac{1}{R_{3}}). \]

    Обратите внимание, что закон Ома для эквивалентного единичного сопротивления дает

    \[I=\dfrac{V}{R_{\mathrm{p}}}= V(\dfrac{1}{R_{\mathrm{p}}}).\]

    Члены в скобках в последних двух уравнениях должны быть равны. Обобщая на любое количество резисторов, общее сопротивление \(R_{\mathrm{p}}\) параллельного соединения связано с отдельными сопротивлениями как

    \[\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{ R_{3}}+\dots\]

    Это соотношение приводит к тому, что общее сопротивление \(R_{\mathrm{p}}\) меньше, чем наименьшее из отдельных сопротивлений. (Это видно в следующем примере.) Когда резисторы соединены параллельно, от источника протекает больший ток, чем для любого из них по отдельности, и поэтому общее сопротивление ниже.

    Пример \(\PageIndex{2}\): расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи

    Пусть выходное напряжение батареи и сопротивления при параллельном соединении на рисунке \(\PageIndex{3}\) будут такими же, как при рассмотренном ранее последовательном соединении: \(V=12. 0\mathrm{V},\: R_ {1}=1,00\Омега\: R_{2}=6,00\Омега\) и \(R_{3}=13,0\Омега\). а) Чему равно полное сопротивление? б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна общему выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.

    Стратегия и решение для (a)

    Общее сопротивление для параллельной комбинации резисторов определяется с помощью приведенного ниже уравнения. Ввод известных значений дает

    \[\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac {1}{R_{3}}=\dfrac{1}{1.00\Omega}+\dfrac{1}{6.00\Omega}+\dfrac{1}{13.0\Omega}.\]

    Таким образом,

    \[\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1,00}{\Omega}+\dfrac{0,1667}{\Omega}+\dfrac{0,07692}{\Omega}=\ dfrac{1.2436}{\Omega}.\]

    (Обратите внимание, что в этих вычислениях каждый промежуточный ответ показан с дополнительной цифрой. )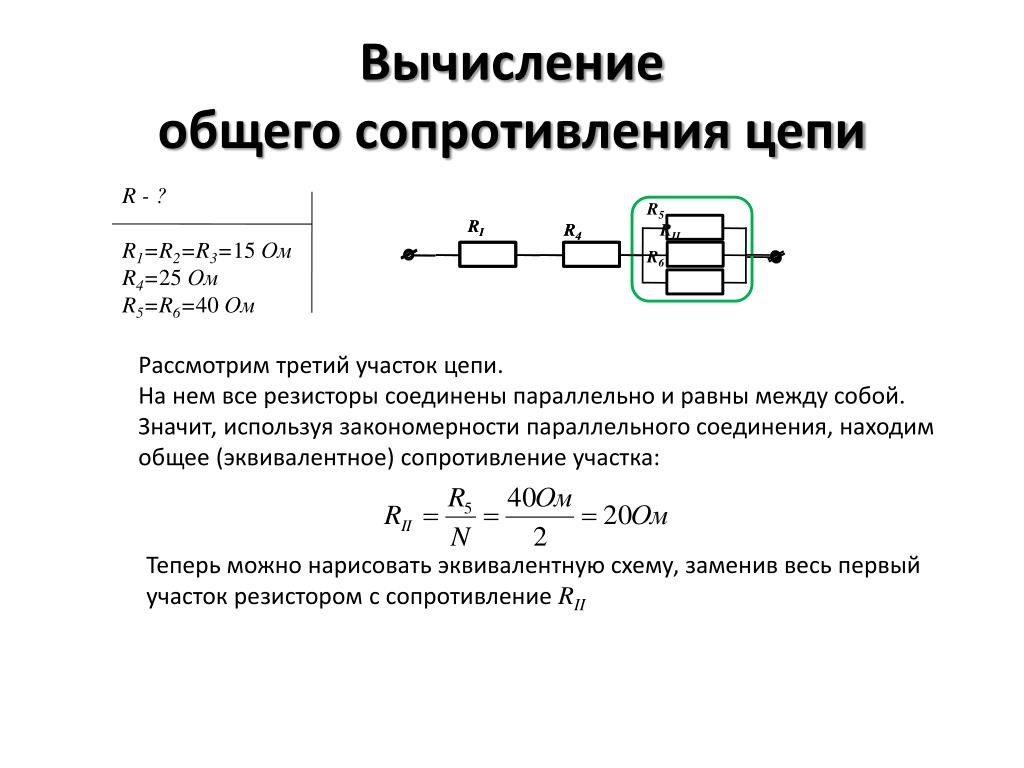

    Мы должны инвертировать это, чтобы найти полное сопротивление \(R_{\mathrm{p}}\). Это дает

    \[R_{\mathrm{p}}=\dfrac{1}{1,2436}\Omega=0,8041\Omega.\]

    Общее сопротивление с правильным количеством значащих цифр равно \(R_{\ матрм{р}}=0,804\Омега\).

    Обсуждение для (a)

    \(R_{\mathrm{p}}\), как и предполагалось, меньше наименьшего индивидуального сопротивления.

    Стратегия и решение для (b)

    Полный ток можно найти из закона Ома, подставив \(R_{\mathrm{p}}\) вместо полного сопротивления. Это дает

    \[I=\dfrac{V}{R_{\mathrm{p}}}=\dfrac{12,0\mathrm{V}}{0,8041 \Omega}=14,92 \mathrm{A}.\]

    Обсуждение для (б)

    Ток \(i\) для каждого устройства намного больше, чем для тех же устройств, соединенных последовательно (см. предыдущий пример). Цепь с параллельными соединениями имеет меньшее общее сопротивление, чем резисторы, соединенные последовательно.

    Стратегия и решение для (c)

    Отдельные токи легко рассчитать по закону Ома, поскольку на каждый резистор подается полное напряжение. Таким образом,

    \[I_{1}=\dfrac{V}{R_{1}}=\dfrac{12.0\mathrm{V}}{1.00\Omega}=12.0\mathrm{A}.\]

    Аналогично,

    \[I_{2}=\dfrac{V}{R_{2}}=\dfrac{12.0\mathrm{V}}{6.00\Omega}=2.00\mathrm{A}\]

    и

    \[I_{3}=\dfrac{V}{R_{3}}=\dfrac{12.0\mathrm{V}}{13.0\Omega}=0,92\mathrm{A}.\]

    9{2}}{13.0\Omega}=11.1\mathrm{W}.\]

    Обсуждение для (d)

    Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к одному и тому же напряжению. источник.

    Стратегия и решение для (e)

    Общая мощность также может быть рассчитана несколькими способами. Выбор \(P=IV\) и ввод общего тока дает

    \[P=IV=(14,92\mathrm{A})(12,0\mathrm{V})=179\mathrm{W}.\]

    Обсуждение для (е)

    Суммарная мощность, рассеиваемая резисторами, также составляет 179 Вт:

    \[P_{1}+P_{2}+P_{3}=144\mathrm{W}+24.0\mathrm{W}+11.1\mathrm {W}=179\mathrm{W}. \]

    Это согласуется с законом сохранения энергии.

    Общее обсуждение

    Обратите внимание, что и токи, и мощности при параллельном соединении больше, чем у тех же устройств, соединенных последовательно.

    ОСНОВНЫЕ ХАРАКТЕРИСТИКИ РЕЗИСТОРОВ, ПОДКЛЮЧЕННЫХ ПАРАЛЛЕЛЬНО

    1. Параллельное сопротивление находится из \(\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1}{R_{1}}+\dfrac{1 }{R_{2}}+\dfrac{1}{R_{3}}+\dots\), и оно меньше любого отдельного сопротивления в комбинации.
    2. К каждому параллельно подключенному резистору приложено одинаковое полное напряжение источника. (Системы распределения электроэнергии чаще всего используют параллельные соединения для питания множества устройств, обслуживаемых одним и тем же напряжением, и позволяют им работать независимо.)
    3. Параллельные резисторы не получают суммарный ток каждый; они его делят.

    Комбинации последовательного и параллельного соединения

    Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения. Они часто встречаются, особенно когда учитывается сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.

    Комбинации последовательного и параллельного соединений можно привести к одному эквивалентному сопротивлению с помощью метода, показанного на рисунке \(\PageIndex{4}\). Различные части идентифицируются как последовательные или параллельные, сокращаются до их эквивалентов и далее сокращаются до тех пор, пока не останется единственное сопротивление. Процесс скорее трудоемкий, чем сложный.

    Рисунок \(\PageIndex{4}\): Эта комбинация семи резисторов имеет как последовательные, так и параллельные части. Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единственное эквивалентное сопротивление.

    Простейшая комбинация последовательного и параллельного сопротивлений, показанная на рисунке \(\PageIndex{5}\), также является наиболее поучительной, поскольку она встречается во многих приложениях. Например, \(R_{1}\) может быть сопротивлением проводов от автомобильного аккумулятора до его электрических устройств, которые включены параллельно. \(R_{2}\) и \(R_{3}\) могут быть стартером и освещением салона. Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.

    Пример \(\PageIndex{3}\): расчет сопротивления, падения \(IR\), тока и рассеиваемой мощности: объединение последовательных и параллельных цепей

    На рисунке \(\PageIndex{5}\) показаны резисторы из предыдущие два примера подключены по-другому — комбинация последовательного и параллельного. Мы можем рассматривать \(R_1\) как сопротивление проводов, ведущих к \(R_2\) и \(R_3\). а) Найдите полное сопротивление. (б) Что такое падение \(IR\) в \(R_1\)? (c) Найдите ток от \(I_2\) до \(R_2\). (d) Какая мощность рассеивается \(R_2\)?

    Рисунок \(\PageIndex{5}\). Эти три резистора подключены к источнику напряжения так, что \(R_2\) и \(R_3\) параллельны друг другу, а эта комбинация последовательно с \(R_1\).

    Стратегия и решение для (a)

    Чтобы найти общее сопротивление, заметим, что \(R_2\) и \(R_3\) параллельны, а их комбинация \(R_p\) последовательно с \(R_1 \). Таким образом, полное (эквивалентное) сопротивление этой комбинации равно \[R_{tot} = R_1 + R_2.\]

    Сначала находим \(R_p\), используя уравнение для параллельных резисторов и вводя известные значения: \[\ dfrac{1}{R_p} = \dfrac{1}{R_2} + \dfrac{1}{6,00 \, \Omega} + \dfrac{1}{13,0 \, \Omega} = \dfrac{0,2436}{\ Омега}.\]

    Инвертирование дает \[R_p = \dfrac{1}{0,2436}\Omega = 4,11 \, \Omega.\] Таким образом, общее сопротивление равно \[R_{tot} = R_1 + R_p = 1,00 \Omega + 4,11 \Omega. = 5,11 \, \Омега.\]

    Обсуждение для (а)

    Суммарное сопротивление этой комбинации является промежуточным между чисто последовательными и чисто параллельными значениями (\(20,0 \, \Омега\) и \(0,804 \, \Omega\) соответственно), найденные для тех же резисторов в двух предыдущих примерах.

    Стратегия и решение для (b)

    Чтобы найти падение \(IR\) в \(R_1\), заметим, что полный ток \(I\) протекает через \(R_1\). Таким образом, его \(IR\) падение равно \[V_1 = IR_1.\]. Мы должны найти \(I\), прежде чем мы сможем вычислить \(V_1\). Полный ток \(I\) находится по закону Ома для цепи. То есть \[I = \dfrac{V}{R_{tot}} = \dfrac{12,0 \, V}{5,11 \, \Omega} = 2,35 \, A.\]. Вводя это в выражение выше, мы получить \[V_1 = IR_1 = (2,35 \, A)(1,00 \, \Omega) = 2,35 \, V.\]

    Обсуждение для (б)

    Напряжение на \(R_2\) и \(R_3\) меньше общего напряжения на величину \(V_1\). Когда сопротивление проводов велико, это может существенно повлиять на работу устройств, представленных \(R_2\) и \(R_3\).

    Стратегия и решение для (c)

    Чтобы найти ток через \(R_2\), мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение \(V_p\), потому что оно применяется к параллельной комбинации резисторов. 2(6,00 \, \ омега) = 15,5\, Вт.\]

    Обсуждение для (d)

    Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.

    Практические выводы

    Одним из следствий последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемые на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение \(IR\) в проводах также может быть значительным.

    Например, когда вы роетесь в холодильнике и включается двигатель, освещение холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).

    То, что происходит в таких сильноточных ситуациях, показано на рисунке \(\PageIndex{6}\). Устройство, представленное \(R_3\), имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение \(IR\) в проводах, представленных \(R_1\), уменьшая напряжение на лампочке (которое равно \(R_2\)), которая затем заметно тускнеет.

    Рисунок \(\PageIndex{6}\): Почему при включении крупного электроприбора свет тускнеет? Ответ заключается в том, что большой ток, потребляемый двигателем электроприбора, вызывает значительное (IR) падение напряжения в проводах и снижает напряжение на лампе.

    Упражнение \(\PageIndex{1}\)

    Можно ли любую произвольную комбинацию резисторов разбить на последовательные и параллельные комбинации? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательных и параллельных соединений.

    Ответить

    Нет, существует множество способов соединения резисторов, не являющихся комбинациями последовательного и параллельного соединения, включая петли и соединения. В таких случаях правила Кирхгофа, которые будут представлены в Правилах Кирхгофа, позволят вам проанализировать схему.

    Стратегии решения проблем для последовательных и параллельных резисторов

    1. Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает в себя список известных проблем, поскольку они помечены на вашей принципиальной схеме.
    2. Определите, что именно нужно определить в задаче (идентифицируйте неизвестные). Письменный список полезен.
    3. Определите, подключены ли резисторы последовательно, параллельно или как последовательно, так и параллельно. Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
    4. Используйте соответствующий список основных функций для последовательных или параллельных соединений, чтобы найти неизвестные. Есть один список для серий и другой для параллельных. Если в вашей задаче сочетаются последовательные и параллельные соединения, уменьшите ее пошагово, рассмотрев отдельные группы последовательных или параллельных соединений, как это делается в этом модуле и в примерах. Специальное примечание: при нахождении \(R_p\) необходимо соблюдать осторожность.
    5. Проверить разумность и последовательность ответов. Единицы и численные результаты должны быть разумными. Например, общее последовательное сопротивление должно быть больше, тогда как общее параллельное сопротивление должно быть меньше. Мощность должна быть больше для тех же устройств, соединенных параллельно, по сравнению с последовательными и т.д.

    Резюме

    • Общее сопротивление электрической цепи с последовательно соединенными резисторами представляет собой сумму отдельных сопротивлений: \(R_s = R_1 + R_2 + R_3 + ….\)
    • Через каждый резистор в последовательной цепи протекает одинаковый ток.
    • Падение напряжения или рассеиваемая мощность на каждом отдельном резисторе в серии различны, и их общая сумма составляет входную мощность источника питания.
    • Общее сопротивление электрической цепи с параллельно соединенными резисторами меньше наименьшего сопротивления любого из компонентов и может быть определено по формуле: \(\dfrac{1}{R_p} = \dfrac{1}{R_1 } +\dfrac{1}{R_2} + \dfrac{1}{R_3} + . …\)
    • К каждому резистору в параллельной цепи приложено одинаковое полное напряжение источника.
    • Ток, протекающий через каждый резистор в параллельной цепи, различен в зависимости от сопротивления.
    • Если более сложное соединение резисторов представляет собой комбинацию последовательного и параллельного сопротивления, его можно свести к единому эквивалентному сопротивлению, обозначив различные его части как последовательные или параллельные, сведя каждую к эквиваленту и продолжая до тех пор, пока в конечном итоге не будет достигнуто единое сопротивление .

    Глоссарий

    Серия
    последовательность резисторов или других компонентов, включенных в цепь один за другим
    резистор
    Компонент, обеспечивающий сопротивление току, протекающему по электрической цепи
    сопротивление
    , вызывающий потерю электроэнергии в цепи
    Закон Ома
    соотношение между током, напряжением и сопротивлением в электрической цепи: V=IR
    напряжение
    электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например батареей
    падение напряжения
    потеря электроэнергии при протекании тока через резистор, провод или другой компонент
    текущий
    поток заряда через электрическую цепь, проходящий через заданную точку измерения
    Закон Джоуля
    Соотношение между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемое как: \(P_e = IV\)
    параллельный
    соединение резисторов или других компонентов в электрической цепи таким образом, что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы

    Эта страница под названием 21. 1: Резисторы в последовательном и параллельном соединении распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Автор
        ОпенСтакс
        Лицензия
        СС BY
        Версия лицензии
        4,0
        Программа OER или Publisher
        ОпенСтакс
        Показать оглавление
        нет
      2. Теги
        1. Текущий
        2. Закон Джоуля
        3. Закон Ома
        4. параллельно
        5. сопротивление
        6. Резистор
        7. Резисторы параллельно
          8. Резисторы
        8. в серии
        9. серия
        10. источник@https://openstax. org/details/books/college-physics
        11. падение напряжения

      Как рассчитать общее сопротивление параллельной цепи?

      от Veerendra

      Как рассчитать общее сопротивление параллельной цепи?

      Эффективное сопротивление резисторов, соединенных параллельно

      1. В параллельной цепи есть три важные характеристики :
        (a) Разность потенциалов одинакова на каждом резисторе.
        (б) Ток, который проходит через каждый резистор, обратно пропорционален сопротивлению резистора.
        (в) Полный ток в цепи равен сумме токов, проходящих через резисторы в ее параллельных ветвях.
      2. Когда два или более сопротивления соединены между двумя общими точками так, что к каждой из них приложена одинаковая разность потенциалов, говорят, что они соединены параллельно.
        Когда такая комбинация сопротивлений подключена к батарее, все сопротивления имеют одинаковую разность потенциалов на своих концах.
      3. Вывод математического выражения для параллельной комбинации:
        Пусть V будет разностью потенциалов между двумя общими точками A и B. Тогда из закона Ома
        Ток, проходящий через R 1 ,     I 1 = V/ R 1             … (i)
        Ток, проходящий через R 2 ,     I 2 = V/R 2           … (ii)
        Ток, проходящий через R 3 ,     I 3 = V/R 3          … (iii)
        4. 9 0003 Если R — эквивалентное сопротивление, то по закону Ома полный ток, протекающий через цепь, определяется выражением
        I = V/R                                   … (v)
      4. Подставляя значения I , I 1 , I 2 и I 3  в уравнении (v),
        \( \frac{\text{V}}{\text{R}}=\frac{\text{V}}{{{\text{R}}_{\text{1}} }}+\frac{\text{V}}{{{\text{R}}_{\text{2}}}}+\frac{\text{V}}{{{\text{R}} _{\text{3}}}}\text{ }……..\text{ (vi)} \)
      5. Отменив общий V-член, получим
        \( \frac{\text{1}}{ \text{R}}=\frac{\text{1}}{{{\text{R}}_{\text{1}}}}+\frac{\text{1}}{{{\text {R}}_{2}}}+\frac{\text{1}}{{{\text{R}}_{3}}} \)
        Эквивалентное сопротивление параллельной комбинации сопротивлений меньше чем каждое из всех отдельных сопротивлений.
      6. Эквивалентная схема показана на рис.

      Важные результаты о параллельном соединении:

      1. Полный ток в цепи равен сумме токов, протекающих через нее.
      2.  В параллельной комбинации резисторов напряжение (или разность потенциалов) на каждом резисторе одинаково и равно приложенному напряжению, т. е. В 1 = В 2 = В 3 = В. через каждый резистор обратно пропорциональна его сопротивлению, таким образом, чем выше сопротивление резистора, тем ниже будет ток, протекающий через него.

      Люди также спрашивают

      • Чем отличаются последовательные и параллельные цепи?
      • Как рассчитать общее сопротивление последовательной цепи?
      • Что такое электрический ток?
      • Что такое электрическое поле и как оно создается?
      • Какая связь между электрическим током и разностью потенциалов?
      • Электродвижущая сила, внутреннее сопротивление и разность потенциалов элемента/батареи
      • Связь между передаваемой энергией, током, напряжением и временем
      • Номинальная мощность и энергопотребление различных электроприборов

      Задачи параллельных цепей с решениями
      1. Три резистора, R 1 , R 2 и R 3 , подключены параллельно аккумулятор, как показано на рисунке.

        Вычислите
        (a) разность потенциалов на каждом резисторе,
        (b) эффективное сопротивление цепи, R,
        (c) ток, I, в цепи,
        (d) токи, I 1 , I 2 и I 3 , проходящие через каждый резистор.
        Решение:
        (a) Поскольку это параллельная цепь, разность потенциалов на каждом резисторе составляет 6 В, такая же, как и разность потенциалов на батарее, которая составляет 6 В. : рабочий лист комбинационных цепей с ответами, сложные задачи на последовательные и параллельные цепи, последовательный и параллельный ток, вывод параллельной комбинации, формула эффективного сопротивления, электричество, определение эквивалентного сопротивления, задачи на эквивалентное сопротивление, как рассчитать общее сопротивление параллельной цепи ?, как найти эквивалентное сопротивление, как решить проблемы с последовательной параллельной цепью, определение параллельной цепи, примеры параллельных цепей, проблемы с параллельной цепью с решениями, параллельная комбинация, параллельное сочетание сопротивления, последовательное и параллельное резисторы, проблемы с последовательными и параллельными цепями и ответы, определение последовательной цепи, схема последовательной цепи, проблемы последовательной цепи с решениями, последовательная цепь против параллельной цепи.

      alexxlab

      Добавить комментарий

      Ваш адрес email не будет опубликован. Обязательные поля помечены *