Момент инерции стержня, теория и примеры

Определение и общие понятия момента инерции стержня

Это скалярная (в общем случае тензорная) физическая величина, которую определяют как сумму произведений масс материальных точек () на которые разбивают тело на квадраты расстояний () от них до оси вращения:

   

Если тело рассматривают как непрерывное, то суммирование в формуле (1) заменяют на интегрирование, массы элементов тела обозначают как , тогда J тела, вращающегося около оси:

   

где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела. Для однородного тела выражение (2) представим как:

   

Формула для вычисления момента инерции однородного стержня

Определим формулу для вычисления момента инерции однородного стержня, вращающегося относительно оси (), которая проходит перпендикулярно стержню и идет через его один конец. Масса стержня равна m, длина l (рис.1).

Выделим в объеме стержня материальную точку (), которая находится от оси вращения на расстоянии r. Ее момент инерции равен:

   

Будем считать, что толщина стержня много меньше, чем его длина, тогда массу можно считать распределенной по длине стержня

   

Обозначим линейную плотность стержня как , тогда:

   

где – объем, стержня, который занимает наша материальная точка. Для нахождения момента инерции всего стержня проинтегрируем выражение (4), учитывая (6) и то, что :

   

Зная из (5), что:

   

формулу (7) перепишем в виде:

   

Мы получили, что момент инерции стержня вращающегося относительно оси, перпендикулярной ему и проходящей через один их его концов равен:

   

Для того чтобы получить момент инерции относительно оси, перпендикулярной стержню и проходящей через центр масс стержня (), следует рассмотреть интеграл:

   

в котором расстояние изменяется в пределах: :

   

Формула (11) дает момент инерции относительно оси, перпендикулярной стержню и проходящей через его центр масс.

Примеры решения задач

Момент инерции — это… Что такое Момент инерции?

У этого термина существуют и другие значения, см. Момент.

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.

Осевой момент инерции

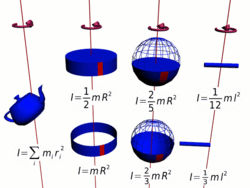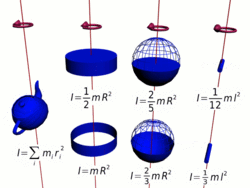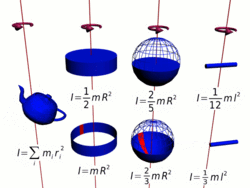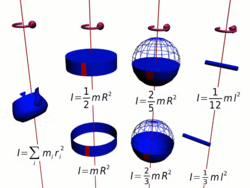Осевые моменты инерции некоторых тел.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где:

• m_i — масса i-й точки,
• r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

,

где:

Если тело однородно, то есть его плотность всюду одинакова, то

Теорема Гюйгенса-Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела

J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

,

где  — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

Осевые моменты инерции некоторых тел

Вывод формул

Тонкостенный цилиндр (кольцо, обруч)

Вывод формулы  

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ_i. Тогда

Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

Толстостенный цилиндр (кольцо, обруч)

Вывод формулы  

Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R₁, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит

Момент инерции толстого кольца найдём как интеграл

Поскольку объём и масса кольца равны

получаем окончательную формулу для момента инерции кольца

Однородный диск (сплошной цилиндр)

Вывод формулы  

Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R₁ = 0), получим формулу для момента инерции цилиндра (диска):

Сплошной конус

Вывод формулы  

Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен

где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят

Интегрируя, получим

Сплошной однородный шар

Вывод формулы  

Разобъём шар на тонкие диски толщиной

dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле

Масса и момент инерции такого диска составят

Момент инерции сферы найдём интегрированием:

Тонкостенная сфера

Вывод формулы  

Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:

Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.

Тонкий стержень (ось проходит через центр)

Вывод формулы  

Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

Интегрируя, получим

Тонкий стержень (ось проходит через конец)

Вывод формулы  

При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен

Безразмерные моменты инерции планет и их спутников^[1][2]

Безразмерные моменты инерции планет и их спутников

Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса

r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr²). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. ^[3][4]

Центробежный момент инерции

Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:

где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.

Ось OX называется главной осью инерции тела, если центробежные моменты инерции J_xy

и J_xz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.

Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.

Геометрический момент инерции

Геометрический момент инерции — геометрическая характеристика сечения вида

где  — расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси.

Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.

Единица измерения СИ — м⁴. В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см⁴.

Из него выражается момент сопротивления сечения:

.

Центральный момент инерции

Центральный момент инерции (или момент инерции относительно точки O) — это величина

,

где:

Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .

Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:

(1),

где  — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:

,
.

Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где  — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины  — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:

,

откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на

и произведя замены:

,

получаем канонический вид уравнения эллипсоида в координатах :

Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:

См. также

Примечания

Литература

• Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
• Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
• Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
• Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
• Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
• Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
• Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.

Ссылки

Читать книгу Сопротивление материалов. Шпаргалка для студентов Романа Сиренко : онлайн чтение

22. Статический момент сечения

Расчеты на прочность показывают, что напряжение и деформации, возникающие в твердом теле, зависят от внутренних силовых факторов и геометрических характеристик поперечного сечения. При растяжении, например, напряжение зависит от площади поперечного сечения, и, так как напряжение в этом случае распределяется по сечению равномерно, не зависит от формы сечения. При кручении напряжения зависят от размеров и формы сечения из-за неравномерного распределения напряжений. В расчетные формулы бруса при кручении входят полярный момент инерции I_p и полярный момент сопротивления W_p – геометрические характеристики сечения. Проводя расчеты на прочность бруса при изгибе, необходимо знать моменты инерции и моменты сопротивления сечения относительно осей, проходящих через центр тяжести бруса. Возьмем для рассмотрения некоторое сечение бруса площадью A и ось, проходящую через центр тяжести этого тела. Статическим моментом плоского сечения относительно некоторой оси x называется сумма произведений площадей элементарных площадок, из которых состоит сечение, на расстояния этих площадок до оси, проходящей через центр тяжести. Аналогично для оси y.

Статический момент измеряется в кубических метрах. Он может быть положительным, отрицательным или равным нулю в зависимости от выбранной оси. Если известны статические моменты и площадь сечения, то координаты центра тяжести могут быть определены как отношение статического момента к площади поперечного сечения. И наоборот, если координаты центра тяжести сечения известны – x_c, y_c, статический момент равен произведению площади сечения на расстояния от центра тяжести до оси.

S_x = Ay_c

S_y = Ax_c

Из полученных соотношений видно, что в случае, когда ось проходит через центр тяжести, статический момент равен нулю.

В случае, когда сечение можно рассматривать как n-ное количество составляющих частей с известными площадями A_i и координатами центров тяжести x_i, y_i, положение всего центра тяжести можно определить как сумму произведений:

Каждое слагаемое в числителе определяет статический момент данного участка относительно выбранной оси.

23. Момент инерции сечения

Осевым (или экваториальным) моментом инерции плоского сечения относительно некоторой оси x называется сумма произведений площадей элементарных площадок, из которых состоит сечение на квадрат расстояния этих площадок до оси, проходящей через центр тяжести. Таким образом, осевые моменты представляют собой интегралы по всей площади сечения.

Полярным моментом инерции относительно некоторой точки (полюса) называется сумма произведений площадей элементарных площадок, из которых состоит сечение, на квадрат расстояния этих площадок до выбранной точки.

Центробежным моментом инерции относительно некоторых двух взаимно перпендикулярных осей называется сумма произведений элементарных площадок, из которых состоит сечение, на расстояния этих площадок до этих осей.

Моменты инерции измеряются в м⁴. Осевые и полярный моменты инерции могут быть только положительными, так как при любом знаке координаты в формуле берется квадрат этой координаты. Центробежный момент инерции может быть положительным, отрицательным и равным нулю.

Сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей равна полярному моменту инерции относительно точки, где эти оси пересекаются.

I_ρ = I_x +I_y

Действительно, ρ – это расстояние от элементарной площадки сечения до некоторой точки, он определяется как гипотенуза треугольника со сторонами x и y.

ρ² = x² + y²

Подставим это соотношение в выражение для полярного момента инерции и получим:

24. Моменты инерции простых сечений

Рассмотрим моменты инерции некоторых простых фигур.

Круг. I_ρ = I_x +I_y. Так как круг – симметричная фигура, то I_x= I_y. Следовательно, I_ρ = 2I_x. Исходя из определения полярного момента инерции и соотношения для полярного момента инерции и осевых моментов инерции в случае круга имеем:

Для кольца диаметром d и внутренним диаметром d₀

Полукруг. Главные центральные оси представляют собой ось симметрии этого полукруга и перпендикулярную ей ось. Для полукруга момент инерции в два раза меньше, чем момент инерции круга для той же самой оси. Если обозначить x₁ ось основания, то

Из соотношения, связывающего моменты инерции параллельных осей, одна из которых является центральной, и, зная значение ординаты центра тяжести полукруга y_c ≈ 0.424r можно определить моменты инерции полукруга:

Прямоугольник. Определим момент инерции I_x1, совпадающий с основанием прямоугольника, и рассмотрим сечение A как сумму элементарных прямоугольников шириной b и высотой dy₁, A = bdy₁

Для моментов инерции параллельных осей, одна из которых является центральной, I_x = I_x1 – a²A. В данном случае расстояние a = h / 2, A = bh, момент инерции относительно осей x и y

I_x = bh³ / 12

I_y = hb³ / 12

В частном случае квадрата

I_x = I_y = b⁴ / 12

Для треугольника вычислим момент инерции I_x1, относительно оси x₁, совпадающей с основанием, и для этого рассмотрим сечение как сумму элементарных прямоугольников шириной b. После выполнения математических преобразований найдем значение I_x= bh³ / 12. Момент инерции относительно центральной оси равен I_x = I_x1 — a²b, в данном случае a = h / 3, A = (1 / 2)bh. В итоге получим:

I_x = bh³ / 12 – (h / 3)³(1 / 2)bh = bh³ / 36

В общем случае ось x не является главной и

I_y = bh³ / 48

25. Зависимость между моментами инерции относительно параллельных осей

Установим зависимость между моментами инерции относительно параллельных осей, одна из которых является центральной. Для этого рассмотрим сечение площадью А. (Рис. 10) Предположим, что известны координаты центра тяжести сечения C и моменты инерции I_xc, I_yc относительно центральных осей x_c, y_c. В таком случае можно определить моменты инерций относительно осей x и y, параллельных центральным и удаленным от центральных на расстояние a и b соответственно. Запишем соотношение для координат параллельных осей:

x = x_c + b

y = y_c + a

Тогда момент инерции сечения относительно оси x запишется в виде:

В этом выражении первое слагаемое представляет собой момент инерции относительно оси x_c, во втором слагаемом интеграл представляет статический момент (а относительно центральной оси статический момент всегда равен нулю), третье слагаемое – это площадь сечения, умноженная на квадрат расстояния между осями а. Таким образом:

I_x = I_xc + a²A

I_y = I_yc + b²A

Момент инерции относительно какой-либо оси равен сумме момента инерции относительно центральной оси, параллельной данной, и произведения площади сечения фигуры на квадрат расстояния между осями.

Мы получили соотношение для моментов инерции относительно центральных осей при переходе к параллельным им нецентральным. Эти соотношения носят также название формул параллельного переноса.

Из полученных формул понятно, что момент инерции относительно центральной оси всегда меньше, чем момент инерции любой параллельной ей нецентральной.

Рис. 10

26. Главные оси инерции и главные моменты инерции

Через любую точку плоскости сечения можно провести бесчисленное множество пар взаимно перпендикулярных осей. Так как сумма двух осевых моментов инерции сечения представляет собой полярный момент и является постоянной величиной, то, перемещая систему координат, можно подобрать такое положение осей, в котором один из выбранных моментов инерции будет максимальным, а второй – минимальным. Рассмотрим зависимость между моментами инерции относительно осей x₀, y₀ и моментами инерции относительно осей x и y, повернутыми на угол α относительно x₀, y₀. Найдем такие значения угла α, при которых моменты инерции перпендикулярных осей примут свои максимальное и минимальное значения. Для этого найдем первую производную по углу поворота от I_x, I_y и приравняем ее нулю (математическое правило нахождения экстремумов функции).

После преобразований соотношение примет вид:

Полученная формула определяет положение двух взаимно перпендикулярных осей, момент инерции относительно одной из которых максимален, момент инерции относительно другой минимален. Такие оси носят название главных осей инерции. Моменты инерции относительно таких осей называются главными моментами инерции. При этом центробежный момент равняется нулю.

Оси, проходящие через центр тяжести сечения, носят название центральных осей. В практических расчетах интерес представляют главные моменты инерции относительно центральных осей, их называют главными центральными моментами инерции, а такие оси – главными центральными осями. Так как интерес представляют только центральные оси, то для краткости их называют просто главными осями, и осевые моменты инерции, вычисленные относительно таких осей называют просто главными моментами инерции.

Одной из главных осей инерции является ось, проходящая через центр симметрии плоскости сечения, вторая – перпендикулярная ей. Ось симметрии и любая перпендикулярная ей образуют систему главных осей. Если сечение имеет несколько осей симметрии (например, круг, квадрат, равносторонний треугольник), то все центральные оси являются главными и все центральные моменты равны.

27. Вычисление моментов инерции сложных сечений

Для нахождения момента инерции сложного сечения площадью A сечение разбивают на простые A₁, A₂, … A_n, для которых моменты инерции находятся по готовым формулам или таблицам.

Момент инерции сложной фигуры находится как сумма моментов инерции, составляющих простых фигур.

I_x = I_x1 + I_x2 +… + I_xn

Момент инерции представляет собой интеграл по площади поверхности сечения,

для интеграла справедливо:

Следовательно, можно записать, что:

Другими словами, момент инерции составного сечения относительно некоторой оси складывается из моментов инерции составляющих этого сечения относительно той же самой оси.

При решении задач такого рода придерживаются следующего алгоритма. Находят центр тяжести плоского сечения и определяют главные центральные оси. Из таблиц или с помощью готовых формул вычисляют значения моментов инерции составляющих частей относительно собственных центральных осей, параллельных главным центральным осям сечения. При помощи формул параллельного переноса вычисляют значения моментов инерции составляющих частей сечения относительно главных осей сечения. Путем суммирования определяют значения главных центральных моментов инерции.

Это правило справедливо также для центробежного момента инерции.

28. Понятие о крутящем моменте

Кручение – это один из видов деформации бруса, при котором в поперечном сечении бруса возникает один внутренний силовой фактор, называемый крутящим моментом Мк. Такой вид деформации возникает, когда на брус действует пара сил, называемых скручивающими моментами М, приложенных перпендикулярно его продольной оси.

Нагруженный вращающими моментами брус называется валом. Сумма вращающих моментов, действующих на вал, равна нулю, если вал вращается равномерно. Вращающий момент можно определить по формуле, с условием, что известны передаваемая мощность P и угловая скорость w.

При известной частоте вращения вала угловая скорость может быть записана в виде

Следовательно, выражение для вращающего момента можно записать в виде:

В практических расчетах реальный объект заменяется расчетной схемой. Для упрощения задачи предполагается, что вращательные моменты сосредоточены в среднем сечении деталей, а не распределены по их поверхности. В сечении произвольного вала крутящий момент можно определить, используя метод сечений, когда вал мысленно рассекается плоскостью. Одну из частей отбрасывают и заменяют ее влияние крутящим моментом Мк, затем определяют его из уравнений равновесия. Числовое значение крутящего момента складывается из сумм вращающих моментов, находящихся по одну сторону сечения.

В поперечных сечениях бруса при кручении возникают только касательные напряжения, нормальные силы параллельны продольной оси бруса и их моменты равны нулю. Следовательно, можно сформулировать определение для крутящего момента таким образом: крутящий момент – это результирующий момент внутренних касательных сил, возникающих в поперечном сечении бруса относительно его продольной оси.

При расчетах на прочность в случае кручения бруса необходимо найти опасное сечение бруса. Если размеры поперечного сечения вдоль оси бруса неизменны, то опасными считаются сечения с максимальным крутящим моментом. Для нахождения опасных сечений строятся эпюры крутящих моментов (графики изменения крутящих моментов по длине бруса). При построении эпюров принято считать, что крутящий момент положителен, если его направление совпадает с направлением часовой стрелки, если смотреть на проведенное сечение. Это предположение условно, так как знак крутящего момента не имеет физического смысла.

29. Определение напряжений при кручении круглого вала

При изучении кручения валов имеют место следующие предположения:

– гипотеза плоских сечений: плоские поперечные сечения бруса после деформации также остаются плоскими и направленными по нормали к его оси, поворачиваясь на некоторый угол относительно этой оси;

– радиусы поперечных сечений не искривляются, и их длина остается постоянной;

– вдоль оси бруса расстояния между поперечными сечениями остаются постоянными.

Исходя из перечисленных предположений кручение круглого вала можно рассматривать как чистый сдвиг. Полученные на основе этих предположений формулы подтверждаются экспериментально.

Рассмотрим кручение участка бруса круглого сечения с радиусом r длиной dz. Один из концов будем считать неподвижно закрепленным.

Рис. 11

При повороте на угол a в поперечном сечении угол сдвига, лежащий на поверхности такого вала, определяется по формуле:

Отношение полного угла закручивания на участке вала к его длине называется относительным углом закручивания.

Мысленно выделим в рассматриваемом участке вала цилиндр с радиусом ρ, угол сдвига для поверхности этого цилиндра определяется аналогично:

Согласно закону Гука в случае сдвига касательные напряжения равны:

Таким образом, при кручении касательные напряжения прямо пропорциональны расстоянию от центра тяжести сечения, причем у центра тяжести касательные напряжения равны нулю. Приближаясь к поверхности вала, они принимают свои максимальные значения.

30. Вычисление моментов, передаваемых на вал

Рассмотрим кручение участка круглого вала диметром r и длиной dz. Выделим в нем цилиндр диаметра ρ. Так как кручение представляет собой чистый сдвиг, нормальные напряжения равны нулю, а касательные напряжения при повороте на угол α распределяются следующим образом:

Крутящий момент определяется как:

А – площадь сечения. Подставив в это выражение касательное напряжение и учитывая, что интеграл от радиуса по площади сечения представляет собой полярный момент инерции сечения , получим:

Подставив это выражение в формулу для касательных напряжений, получим:

Таким образом, касательные напряжения определяются как произведение крутящего момента и радиуса, отнесенное к полярному моменту сечения. Ясно, что для точек, удаленных от оси на одинаковые расстояния, касательные напряжения равны, максимальные значения напряжения имеют точки, расположенных на поверхности вала.

Здесь  – полярный момент сопротивления при кручении.

Для круглого сечения

Условие прочности при кручении выглядит следующим образом:

[τ] – максимально допускаемое касательное напряжение.

Эта формула позволяет также определять допускаемый крутящий момент или подбирать допустимый диаметр вала.

31, Деформация при кручении. Потенциальная энергия

В процессе кручения вращающие моменты поворачиваются вместе с сечением на какой-то угол и при этом совершают работу, которая так же, как и при других видах деформации, расходуется на создание в теле, подвергающемся деформации, определенного запаса потенциальной энергии и определяется по формуле:

Это соотношение следует из линейной зависимости крутящего момента М_к от угла поворота φ.

Рис. 12

При воздействии нагрузки крутящий момент постепенно нарастает, при этом в соответствии с законом Гука пропорционально увеличивается угол поворота. Работа, совершаемая крутящим моментом, равна потенциальной энергии деформации согласно закону сохранения энергии, следовательно,

Если в полученное соотношение подставить известную формулу для угла закручивания, то выражение примет вид:

При ступенчатом изменении крутящего момента или поперечного сечения бруса потенциальная энергия представляет собой сумму:

Если же крутящий или полярный моменты (или оба одновременно) непрерывно изменяются по длине участков бруса, то потенциальная энергия представляет интеграл по длине

32. Расчет винтовых цилиндрических пружин

В машиностроении и приборостроении широко используются винтовые пружины, которые могут иметь цилиндрическую, конусовидную или фасонную. Чаще всего применяются пружины цилиндрической формы, изготовленные из проволоки круглого поперечного сечения: пружины растяжения (изготавливаются без просветов между витками) и пружины сжатия (с просветом). Для упрощения расчета пружин на жесткость и прочность будем считать, что угол наклона витков настолько мал, что им можно пренебречь и считать сечение вдоль оси пружины поперечным для витка. Из условий равновесия для отсеченной части пружины ясно, что в сечении возникают два внутренних силовых фактора: поперечная сила Q_y = F и крутящий момент М_к = FD / 2, т. е. в сечении витка возникают только касательные напряжения. Будем считать, что касательные напряжения, связанные с поперечной силой, распределены по сечению равномерно, а касательные силы, связанные с наличием крутящего момента, распределены по линейному закону и достигают своих максимальных значений в крайних точках сечения. Наиболее напряженной окажется точка, расположенная ближе всего к оси пружины, напряжение для нее равно:

Отношение диаметра пружины к диаметру проволоки называют индексом пружины,

c_n = D / d

Если считать что напряжения в витке возникают только от кручения, и пренебречь вторым слагаемым, формула запишется в следующем виде:

Полученная формула приближенна из-за пренебрежения влиянием поперечной силы и из-за того, что не учтена кривизна витков. Введем поправочный коэффициент К, зависящий от индекса пружины и угла наклона витков. Тогда условие прочности примет вид:

При воздействии нагрузки пружина изменяет свою длину. Это изменение называется осадкой пружины λ. Определим, чему равна осадка, если витки испытывают только кручение. Согласно формуле Клапейрона работа внешних статических сил равна:

Потенциальная энергия деформации

В данном случае

где l – длина рассматриваемого участка пружины;

n – число витков.

Выполнив подстановку и математические преобразования, получим, что:

33. Перемещения и напряжения в винтовых пружинах

Винтовые пружины широко используются в машиностроении как амортизирующие устройства или устройства обратной подачи. Расчет винтовых пружин хорошо демонстрирует метод определения перемещений. Винтовые пружины подразделяются на пружины растяжения, сжатия и кручения. Пружины растяжения и сжатия нагружаются силами, действующими вдоль оси пружины, пружины кручения нагружаются моментами, расположенными в плоскости, перпендикулярной оси пружины.

Витую пружину можно рассматривать как пространственно изогнутый стержень с осью, имеющей винтовую форму. Форма пружины характеризуется следующими параметрами: диаметром пружины D, числом витков n, углом подъема θ и шагом пружины s, определяемым формулой:

s = πDtgθ

Обычно шаг пружины значительно меньше, чем πD, угол θ достаточно мал (меньше 5°).

Рассмотрим пружину растяжения-сжатия. Под воздействием внешней нагрузки Р в каждом поперечном сечении возникает результирующая внутренняя сила Р и момент М = РD / 2, лежащий в плоскости действия сил Р. На Рис. 13 изображены силы, действующие в поперечном сечении пружины.

Рис. 13

Проекции полной силы и момента относительно системы координат, связанной с сечением, описываются следующими соотношениями:

M_к = (PD / 2) × cosθ,

M_изг= (PD / 2) × sinθ,

Q = P × cosθ,

N = P × sinθ.

Предположим, что сила Р равна 1, тогда соотношения для сил и моментов примут вид:

M_к1 = (D / 2) × cosθ,

M_изг1 = (D / 2) × sinθ,

Q₁ = cosθ,

N₁ = sinθ.

Найдем осевое перемещение в пружине, пользуясь интегралом Мора. С учетом малости перемещений, вызванных нормальной и поперечными силами, а также осевого перемещения, в данном случае интеграл Мора запишется следующим образом:

где произведение в знаменателе представляет собой жесткость пружины на кручение;

l – длина рабочей части пружины;

l ≈ πDn

Вследствие малости угла наклона витков θ полагаем, что cos θ = 1, тогда

Напряжения в винтовых пружинах, работающих на сжатие-растяжение или кручение, определяются следующим образом:

Момент инерции — это… Что такое Момент инерции?

У этого термина существуют и другие значения, см. Момент.

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.

Осевой момент инерции

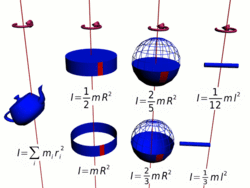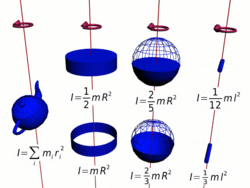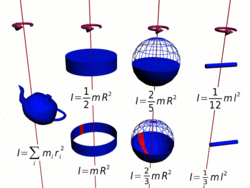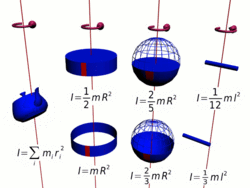Осевые моменты инерции некоторых тел.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где:

• m_i — масса i-й точки,
• r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

,

где:

Если тело однородно, то есть его плотность всюду одинакова, то

Теорема Гюйгенса-Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

,

где  — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

Осевые моменты инерции некоторых тел

Вывод формул

Тонкостенный цилиндр (кольцо, обруч)

Вывод формулы  

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ_i. Тогда

Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

Толстостенный цилиндр (кольцо, обруч)

Вывод формулы  

Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R₁, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит

Момент инерции толстого кольца найдём как интеграл

Поскольку объём и масса кольца равны

получаем окончательную формулу для момента инерции кольца

Однородный диск (сплошной цилиндр)

Вывод формулы  

Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R₁ = 0), получим формулу для момента инерции цилиндра (диска):

Сплошной конус

Вывод формулы  

Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен

где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят

Интегрируя, получим

Сплошной однородный шар

Вывод формулы  

Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле

Масса и момент инерции такого диска составят

Момент инерции сферы найдём интегрированием:

Тонкостенная сфера

Вывод формулы  

Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:

Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.

Тонкий стержень (ось проходит через центр)

Вывод формулы  

Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

Интегрируя, получим

Тонкий стержень (ось проходит через конец)

Вывод формулы  

При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен

Безразмерные моменты инерции планет и их спутников^[1][2]

Безразмерные моменты инерции планет и их спутников

Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr²). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. ^[3][4]

Центробежный момент инерции

Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:

где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.

Ось OX называется главной осью инерции тела, если центробежные моменты инерции J_xy и J_xz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.

Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.

Геометрический момент инерции

Геометрический момент инерции — геометрическая характеристика сечения вида

где  — расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси.

Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.

Единица измерения СИ — м⁴. В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см⁴.

Из него выражается момент сопротивления сечения:

.

Центральный момент инерции

Центральный момент инерции (или момент инерции относительно точки O) — это величина

,

где:

Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .

Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:

(1),

где  — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:

,
.

Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где  — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины  — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:

,

откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на

и произведя замены:

,

получаем канонический вид уравнения эллипсоида в координатах :

Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:

См. также

Примечания

Литература

• Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
• Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
• Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
• Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
• Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
• Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
• Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.

Ссылки