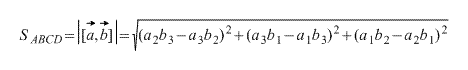Векторное произведение векторов через координаты. Онлайн калькулятор.
Данный калькулятор вычислит векторное произведение векторов через их координаты и даст подробное решение всех этапов вычисления. Для записи десятичной дроби используйте точку либо запятую (например, 1.12 или 1,12), для ввода обыкновенных дробей воспользуйтесь знаком «/» (например, 1/2 или 3/4)
Результатом векторного произведения двух векторов будет являться вектор, перпендикулярный обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами.
Как найти векторное произведения векторов
Пример №1Найдем векторное произведение векторов пространства. Координаты обоих векторов заданны точками.
Координаты точки А вектора AB: (7; 0.2 ; 69)
Координаты точки B вектора AB: (-1 ; 0 ; 2/8)
Координаты точки C вектора CD: (-4 ; -6 ; 2)
Координаты точки D вектора CD: (3 ; 0 ; 9)
Решение:
| i̅ | j̅ | k̅ |
| ABx | ABy | ABz |
| CDx | CDy | CDz |
i̅ (AByCDz — CDy
Вычислим координаты первого вектора по двум точкам A и B:
AB = {xB — xA ; yB — yA; zB — zA} = {-1 — 7 ; 0 — 0.2 ; 2/8 — 69} = {-8 ; -1/5 ; -275/4}
Вычислим координаты второго вектора по двум точкам C и D:
CD = {xD — xC ; yD — yC; zD — zC} = {3 — (-4) ; 0 — (-6) ; 9 — 2} = {7 ; 6 ; 7}
ABx = -8ABy = -1/5
AB
CDx = 7
CDy = 6
CDz = 7
N̅ = [AB × CD] = i̅ (-1/5 ⋅ 7 — 6 ⋅ (-275/4)) — j̅ (-8 ⋅ 7 — 7 ⋅ (-275/4)) + k̅ (-8 ⋅ 6 — 7 ⋅ (-1/5)) = i̅ (-7/5 — (-825/2)) — j̅ (-56 — (-1925/4)) + k̅ (-48 — (-7/5)) = (4111/10)i̅ — (1701/4)j̅ — (233/5)k̅
N̅ = [AB × CD] = (4111/10)i̅ — (1701/4)j̅ — (233/5)k̅
N̅ = {4111/10 ; -1701/4 ; -233/5}
N̅ = {411.1 ; -425.25 ; -46.6}
Пример №2
Найдем векторное произведение векторов пространства.
Координаты вектора a: (5 ; 1 ; 7)
Решение:
N̅ = [a × b] = = i̅ — j̅ + k̅ = i̅ aybz — i̅ azby — j̅ axbz + j̅ azbx + k̅ axby — k̅ aybx =i̅ (aybz — byaz) — j̅ (axbz — bxaz) + k̅ (axby — bxay)ax = 5
a
az = 7
bx = 2
by = 4
bz = 6
N̅ = [a × b] = i̅ (1 ⋅ 6 — 4 ⋅ 7) — j̅ (5 ⋅ 6 — 2 ⋅ 7) + k̅ (5 ⋅ 4 — 2 ⋅ 1) = i̅ (6 — 28) — j̅ (30 — 14) + k̅ (20 — 2) = -22i̅ -16j̅ +18k̅
N̅ = [a × b] = -22i̅ -16j̅ +18k̅
N̅ = {-22 ; -16 ; 18}
Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Векторы представляют собой особый раздел аналитической геометрии, который в том числе оказал значительное влияние на развитие физики. Сам по себе вектор выглядит как отрезок, который имеет начало и имеет конец, определен заданной конечными точками длиной этого отрезка. Но внутри вектора кроется множество других скрытых функций, за счет того что вектор задает направление. Поэтому если для отрезка не имеет значения какая точка названа началом, а какая концом, и чаще просто применяется принцип чтения «слева направо», то для векторов AB и BA – это диаметрально противоположные понятия.
Итак, в векторе присутствует две важных составляющих – это его длина и направление. Тем не менее, координатами вектора задается не его фактическая длина, а местоположение на плоскости или в пространстве. Поэтому длина вектора, иначе называемая модуль вектора, вычисляется, используя прямоугольный треугольник с осями координат. Дальнейшие действия с вектором также чаще используют именно его координаты, нежели фактическую длину. Работе с векторами можно провести аналогию с целыми числами, — как только появляются отрицательные числа на числовой оси, приходится не только считать значение примера, но и все время обращать внимание на знаки. Так и с векторами, во всех действиях – будь то сложение, вычитание, умножение скалярное или векторное и другие действия, приходится не только учитывать реальные масштабы вектора – координаты, длина или угол, но и принимать в расчет его направление. К слову, направления векторов также находят отражение в знаках – обратный изначальному вектор всегда будет со знаком «минус».
В данном разделе разложены все основные действия с векторами, такие как нахождение длины вектора, координат вектора, сложение векторов, вычитание векторов, скалярное произведение векторов, векторное произведение векторов, смешанное произведение трех векторов, вычисление угла между векторами и другие. Все расчет можно произвести для векторов на плоскости или для векторов в пространстве. Также доступен векторный калькулятор, который вычисляет все возможные параметры одного и более векторов, с заданными координатами точек вектора.
Векторное произведение векторов | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Векторное произведение векторов по определению возможно только в трехмерном пространстве, где у каждого вектора указаны три координаты (i,j,k). Векторное произведение векторов отличается от скалярного тем, что оно представляет собой не просто число, но вектор, имеющий свое собственное направление. Это третье направление и обуславливает трехмерность системы.
Векторное произведение двух векторов 
и 
на графике выглядит следующим образом – из точки начала двух векторов проводится третий вектор-произведение 
, направленный вверх при умножении первого вектора на второй или вниз при умножении второго вектора на первый. Соответственно, направление и знак вектора взаимосвязаны, поэтому обратное векторное произведение векторов будет отрицательным.
Вычислить векторное произведение векторов можно, умножив их длины на синус угла между ними. Эта же самая формула определяет площадь параллелограмма, образованного сторонами и . =[
]=|||| sinα |
|=Sпар. Таким образом, если векторы и коллинеарны, то синус угла между ними равен нулю, и векторное произведение коллинеарных векторов тоже равно нулевому вектору. Из этого следует, что векторное умножение вектора самого на себя тоже дает нулевой вектор. Если векторы
ортогональны, то их векторное произведение равно произведению их длин, так как синус угла в 90 градусов равен 1.Векторное произведение векторов, онлайн калькулятор
Наш онлайн калькулятор позволяет найти векторное произведение двух векторов всего за пару минут. Для вычисления векторного произведения выберите форму представления векторов (через координаты или по точкам), заполните все элементы и нажмите кнопку «Вычислить», калькулятор выдаст пошаговое решение и ответ! Каждый шаг будет детально расписан, это поможет вам понять, как был получен ответ и, при необходимости, проверить свое решение.
Форма представления векторов:
координатами точками
Формула : |
| Понравился сайт? Расскажи друзьям! | |||
Векторное произведение векторов онлайн
Вычисление векторного произведения векторов онлайн.
Выберите необходимые вам размерность векторов и форму их представления
Форма представления первого вектора:
КоординатамиТочками
Форма представления второго вектора:
КоординатамиТочками
Введите значения векторов.
Первый вектор
Второй вектор
Вводить можно числа или дроби. Например: 1.5 или 1/7 или -1/4 и т.д.
Получить ответВоспользуйтесь также:
Скалярное произведение векторов
Смешанное произведение векторов
Проверка образуют ли вектора базис
Разложение вектора по заданному базису
Векторное произведение векторов онлайн
Векторное произведение
Векторным произведением вектора
a
на векторb
называется векторc
, длина которого численно равна площади параллелограмма построенного на векторахa
иb
, направленный перпендикулярно к плоскости этих векторов так, чтоб наименьшее вращение от вектораa
кb
, если смотреть с конца вектораc
, осуществлялось против часовой стрелки (то есть по правилу правого буравчика).Векторное произведение двух векторов
a
={x1; y1; z1}
иb
={x2; y2; z2}
, заданных в декартовой системе координат можно вычислить, используя следующие формулы:|
a ×b = |
i | j | k |
= i(y1z2 — z1y2) — j(x1z2 — z1x2) + k(x1y2 — y1x2) |
x1 | y1 | z1 |
||
x2 | y2 | z2 |
a
×b
={y1 z2 — z1 y2; z1 x2 — x1 z2; x1 y2 — y1 x2}
Векторное произведение векторов онлайн
Векторное произведение векторов представляет собой вектор, который удовлетворяет следующим условиям.
Величина этого вектора равна произведению модулей (длин) исходных векторов на синус угла между ними:
Этот вектор перпендикулярен каждому из исходных векторов:
Вектор направлен таким образом, что если смотреть с конца этого вектора, то кратчайший поворот от вектора к вектору осуществляется против часовой стрелки (т.е. тройка векторов а × b, , является правой).
Реклама
Векторное произведение обладает следующими свойствами:
Антикоммутативность:
Ассоциативность, относительно числового множителя (α):
Дистрибутивность:
Векторное произведение векторов вычисляется по формуле:
Наш онлайн калькулятор находит векторное произведение векторов с описанием подробного хода решения на русском языке.
Векторное произведение двух векторов. Он-лайн калькулятор.
Векторное произведение двух векторов. Он-лайн калькулятор.
|
Векторное произведение двух векторов а и b — это операция над ними, определенная лишь в трехмерном пространстве, результатом которой является вектор со следующими свойствами: Для большей ясности приведем пример — на рисунке справа вектор [a,b] — векторное произведение векторов а и b. Как сказано в определении, мы привели все три вектора к общему началу, и тогда, если смотреть на вектора a и b с конца вектора [a,b], кратчайший поворот от вектора а до вектора b будет против часовой стрелки . |
Очевидно, что в случае векторного произведения, имеет значение порядок, в котором берутся вектора, более того,
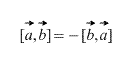
Так же, непосредственно из определения следует, что для любого скалярного множителя k (числа) верно следующее:
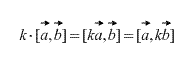
Векторное произведение коллинеарных векторов равно нулевому вектору. Более того, векторное произведение двух векторов равно нулю тогда и только тогда, когда они коллинеарны. (В случае, если один из них нулевой вектор необходимо вспомнить, что нулевой вектор коллинеарен любому вектору по определению).
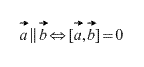
Векторное произведение обладает распределительным свойством, то есть
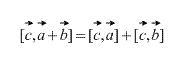
Выражение векторного произведения через координаты векторов.
Пусть даны два вектора
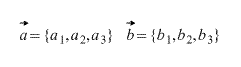
(как найти координаты вектора по координатам его начала и конца — см. статью Скалярное произведение векторов, пункт Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами.)
Тогда
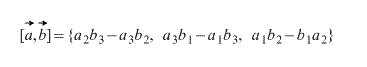
Зачем нужно векторное произведение?
Существует множество способов применения векторного произведения, например, как уже написано выше, вычислив векторное произведение двух векторов можно выяснить, коллинеарны ли они.
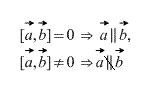
Или же его можно использовать как способ вычисления площади параллелограмма, построенного на этих векторах. Исходя из определения, длина результирующего вектора и есть площадь данного параллелограмма.
|
|
Он-лайн калькулятор векторного произведения.
Чтобы найти скалярное произведение двух векторов с помощью данного калькулятора, нужно ввести в первую строку по порядку координаты первого вектора, во вторую- второго. Координаты векторов могут быть вычислены по координатам их начала и конца (см. статью Скалярное произведение векторов, пункт Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами. )
