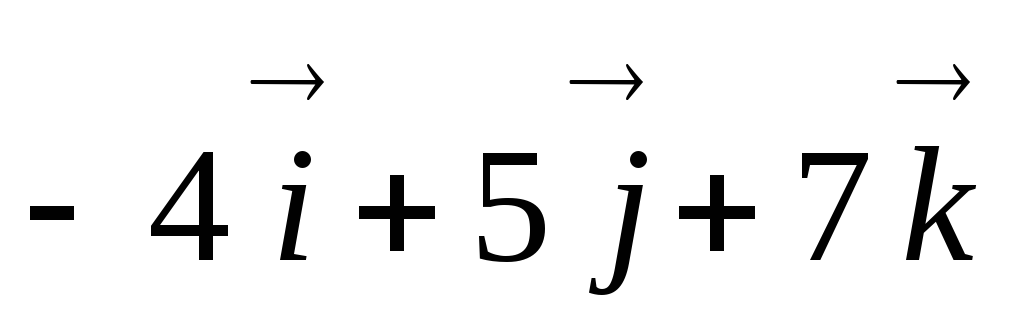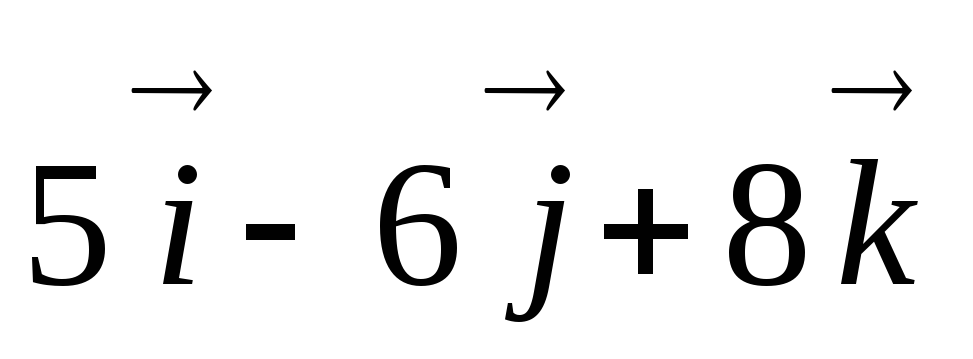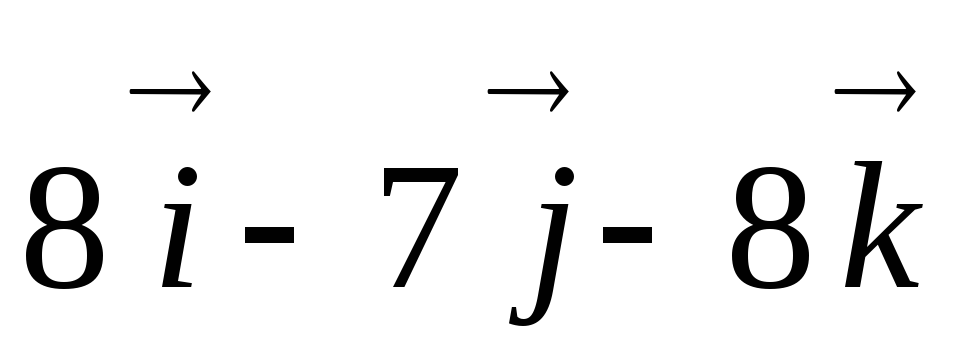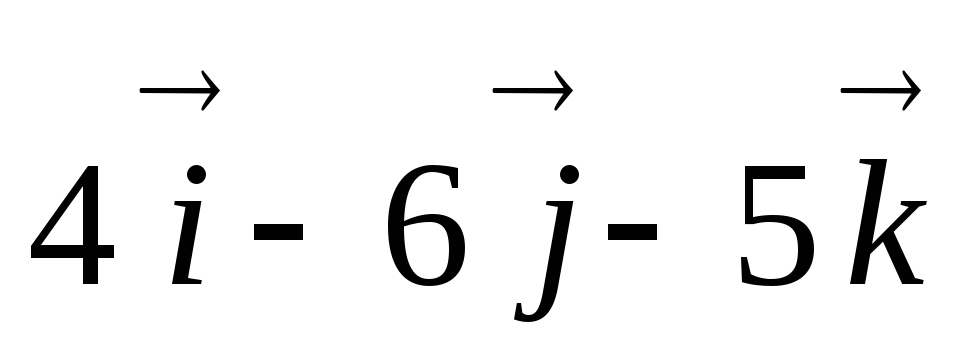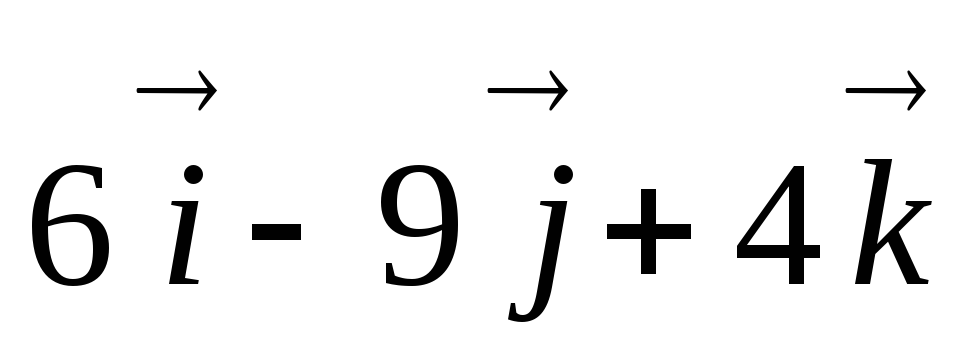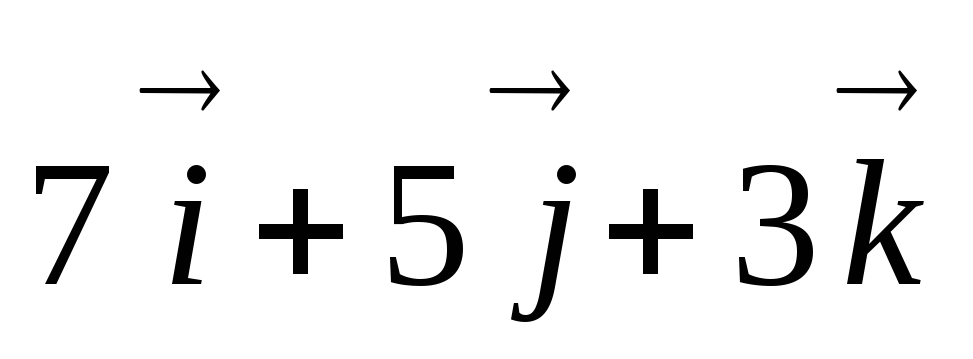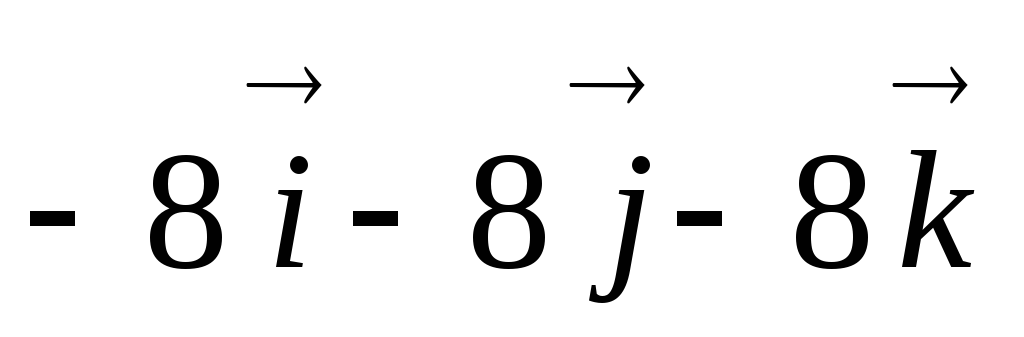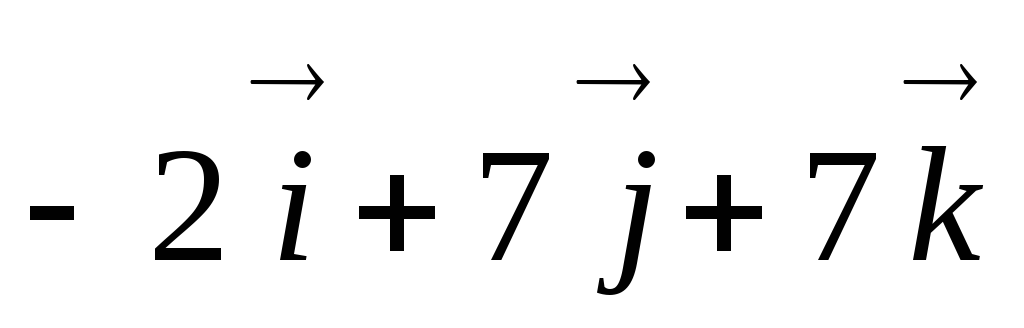Главный вектор плоской системы произвольно расположенных сил равен векторной сумме всех сил системы и приложен в центре приведения.
Графически главный вектор выражается замыкающей стороной силового многоугольника, построенного на данных силах.
Аналитически модуль главного вектора можно вычислить по формуле:
Fгл = √[(ΣX)2 + (Y)2] (здесь и далее √ — знак корня),
а направляющий косинус – по формуле cos (Fгл, x) = FглХ / Fгл.
Плоская система пар эквивалентна одной паре, момент которой равен алгебраической сумме моментов данных пар, следовательно,
Мгл = m1 = m2 + m3 +….+ mn = MO(F1) + MO(F2) + MO(F3) +….+ MO(Fn), или
Мгл = ΣМO(Fi).
Эту пару с моментом Мгл
Главный момент плоской системы произвольно расположенных сил равен алгебраической сумме моментов всех сил системы относительно центра приведения.
Таким образом, всякая плоская система сил в общем случае эквивалентна системе, состоящей из силы и пары сил, следовательно, теорема доказана.
Не следует считать, что главный вектор и главный момент имеют чисто формальное значение, введенной для удобства доказательства, и что их можно найти только с помощью вычислений. Нередко отдельно действующие на тело силы определить трудно или даже невозможно, а главный вектор или главный момент этих сил найти сравнительно легко. Так, например, число точек контакта и модули сил трения между вращающимся валом и подшипником скольжения, как правило, неизвестны, но главный момент этих сил можно определить простым измерением.
***
Свойства главного вектора и главного момента
Свойства главного вектора и главного момента заключаются в следующем:
1. модуль и направление главного вектора данной системы не зависят от выбора центра приведения, так как при любом центре приведения силовой многоугольник, построенный на данных силах, будет один и тот же;
2. величина и знак главного момента в общем случае зависят от выбора центра приведения (кроме случая, рассмотренного далее, когда Fгл = 0, а Мгл ≠ 0), так как при перемене центра приведения изменяются плечи сил, а их модули остаются неизменными;
3. главный вектор и равнодействующая системы сил векторно равны, но в общем случае не эквивалентны. Пусть известны главный вектор Fгл и главный момент Мгл
Определим равнодействующую этой системы.
Пользуясь известным свойством пары сил, преобразуем главный момент Мгл так, чтобы силы пары F и FΣ(рис. 4б) были равны по модулю и параллельны главному вектору Fгл:
F = FΣ = Fгл; Мгл = М(F, FΣ),
причем сила F приложена в точке О противоположно Fгл
Далее систему (Fгл, F), как взаимно уравновешенную, отбросим:
(Fгл,Мгл) = (Fгл,F,FΣ) ≡ FΣ.
В результате получим одну силу FΣ, эквивалентную главному вектору и главному моменту, т. е. равнодействующую системы, причем FΣ = Fгл.
Модуль равнодействующей можно определить по формуле:
FΣ = √[(ΣX)2 + (Y)2] = Fгл,
а положение линии действия равнодействующей определяется плечом d по формуле:
d = Мгл / Fгл.
В результате можно считать установленным, что главный вектор и равнодействующая векторно равны, но не эквивалентны.
4. главный вектор и равнодействующая эквивалентны лишь в частном случае, когда главный момент системы равен нулю. Это возможно лишь в случае, когда центр приведения находится на линии действия равнодействующей. Из приведенного выше рисунка видно, что момент равнодействующей FΣ относительно центра приведения О равен моменту Мгл пары (FΣ,F), т.е. главному моменту данной системы:
МО(FΣ) = М(FΣ,F) = Мгл.
Так как Мгл = ΣМО(Fi), а за центр приведения можно взять любую точку плоскости действия сил данной системы, то всегда имеем:
М(FΣ) = ΣМ(Fi).
Полученная формула является математическим выражением теоремы о моменте равнодействующей.
Теорема:момент равнодействующей силы относительно какой-либо точки, расположенной в плоскости действия сил, равен алгебраической сумме моментов составляющих сил относительно той же точки.
Теорему о моменте равнодействующей впервые доказал французский ученый
Применим доказанную теорему для определения положения линии действия равнодействующей FΣ плоской системы n параллельных сил:
(F1 + F2 + F3 +….+ Fn) ≡ FΣ.
Выберем какую-либо точку О плоскости действия сил за центр моментов и согласно теореме Вариньона запишем:
ΣМO(Fi) = МO(FΣ
Из последнего равенства определяем плечо d:
d = ΣМO(Fi) / FΣ = ΣМO(Fi) / ΣFi, так как FΣ = ΣFi.
Чтобы установить, в какую сторону от точки О следует на перпендикуляре к линиям действия сил отложить плечо d, следует учесть направление вектора FΣ
***
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Частные случаи приведения системы сил к точке — КиберПедия
При приведении системы сил к точке возможны следующие варианты:
Условие равновесия произвольной плоской системы сил
1. При равновесии главный вектор системы равен нулю (Fгл = 0).
Аналитическое определение главного вектора приводит к выводу:
где Fkx и Fky — проекции векторов на оси координат.
2. Поскольку точка приведения выбрана произвольно, ясно, что
при равновесии сумма моментов сил системы относительно любой
где А и В — разные точки приведения.
38 Лекция 5
Условие равновесия произвольной плоской системы сил может быть сформулировано следующим образом:
Для того чтобы твердое тело под действием произвольной плоской системы сил находилось в равновесии, необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил системы на любую ось равнялась нулю и алгебраическая сумма моментов всех сил системы относительно любой точки в плоскости действия сил равнялась нулю.
Получим основную форму уравнения равновесия:
Теоретически уравнений моментов можно записать бесконечное множество, но практически доказано, что на плоскости можно составить только три независимых уравнения моментов и при этом три точки (центры моментов) не должны лежать на одной линии.
Таким образом, имеем пять независимых уравнений равновесия.
Практически для решения задач на плоскости достаточно трех уравнений равновесия. В каждом конкретном случае используются уравнения с одним неизвестным.
Для разных случаев используются три группы уравнений равновесия.
Тема 1.4. Плоская система произвольно расположенных сил 39
Для частного случая, если уравновешена система параллельных сил, можно составить только два уравнения равновесия:
Ось Ох системы координат параллельна линии действия сил.
Примеры решения задач
Пример 1.Найти момент присоединенной пары при переносе силы F3в точку В (рис. 5.3). F1 = 10кН; F2 = 15кН; F3 = 18кН; а = 0,2 м.
Решение
Используем теорему Пуансо. Мв(-Рз) = 18 • 0,2 = 3,6кН-м.
Пример 2.Найти главный вектор системы (рис. 5.4).
F1 = 10 кН; F2 = 16 кН; F3 = 12 кН; т = 60кН-м.
Решение
Главный вектор равен геометрической сумме сил:
40 Лекция 5
Пример 3.Найти главный момент системы относительно точки В (использовать данные примера 2).
Решение
Главный момент равен алгебраической сумме моментов сил относительно точки приведения:
Пример4. К телу приложена уравновешенная система сил (рис. 5.5). Две из них неизвестны. Определить неизвестные силы. F1 = 10kH; F2 = 16kH.
Наносим оси координат и используем уравнения равновесия:
Контрольные вопросы и задания
1. Чему равен главный вектор системы сил?
2. Чему равен главный момент системы сил при приведении ее к точке?
Тема 1.4. Плоская система произвольно расположенных сил 41
3. Чем отличается главный вектор от равнодействующей плоской системы произвольно расположенных сил?
Выбрать из предложенных ответов:
— величиной;
— направлением;
— величиной и направлением;
— точкой приложения;
— ничем.
4. Тело движется равномерно и прямолинейно (равновесие). Чему равны главный вектор и главный момент системы?
5. Тело вращается вокруг неподвижной оси.
Чему равны главный вектор и главный момент действующей на него системы сил?
6. Найдите главный вектор и главный момент системы сил, если центр приведения находится в точке А (рис. 5.6).
7. Какое еще уравнение равновесия нужно составить, чтобы убедиться в том, что система сил (рис. 5.7) находится в равновесии?
42 Лекция 6
ЛЕКЦИЯ 6
Тема 1.4. Балочные системы.
Определение главного вектора и главного момента плоской системы произвольно расположенных сил
Цель работы — произвести графическое и аналитическое приведение (упрощение) плоской системы произвольно расположенных сил к данной точке; проверить опытным путем главный момент и величину главного вектора; выявить признаки уравновешенной системы сил.

Рисунок 9
. Теоретическое обоснование. В реальных условиях к телу могут быть приложены силы, произвольно расположенные на плоскости. На рис. 9, а показана система сил, линии действия которых не пересекаются в одной точке и не параллельны между собой. Это и есть признаки произвольно расположенной системы сил. Исследование такой системы сил начинают с приведения сил к точке, лежащей в той же плоскости.
В общем случае данная система сил заменяется эквивалентной системой, состоящей из одной силы — главного вектора R‘ и одной пары, момент которой называют главным м о м е н т о м MQ заданной системы сил относительно центра приведения О (рис. 9, б).
Приведение плоской системы сил к данной точке можно производить двумя способами: графическим и аналитическим.
Последовательность действий при определении главного вектора аналогична той, которая указана в табл. 1 и 2. Определение главного момента системы сил основано на правиле сложения пар сил: момент результирующей пары равен алгебраической сумме моментов заданных сил относительно точки 0:
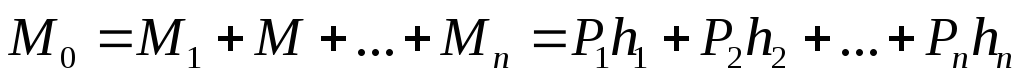
где Мо — главный момент, Нм; Pi — заданные силы, Н; hi— отрезки перпендикуляров, опущенных из точки приведения на линию действия сил, м, см, мм.
Последовательность действий приведения к точке плоской системы произвольно расположенных сил указана в табл. 5
Таблица 5
Последовательность действий приведения к точке плоской системы произвольно расположенных сил
№п/п | Наименование операций | |
1 | Изобразить схематически тело и заданные силы | |
2 | Выбрать
точку приведения 0 в
плоскости
действия сил. Приложить в
точке О две
противоположные силы | |
3 | Из точки приведения O восстановить перпендикуляры к линии действия каждой силы. Отметить отрезки этих перпендикуляров ht как плечи сил относительно точки 0. Отметить черточками силы, образующие пару. Величину плеча hi измерить по чертежу или вычислить аналитически | |
4 | Для системы сходящихся сил, приведенных к точке О, построить силовой многоугольник и найти главный вектор R‘ как геометрическую сумму этих сил (см. табл. 1) или вычислить величину и направление главного вектора методом проекции л , _ I оглавного вектора методом Проекций | |
5 | Произвести алгебраическое сложение моментов пар сил, т.е. найти главный момент системы сил относительно выбранного центра приведения. | |
6 | Для
случая, когда | |
При приведении сил к какой-либо точке, плоскости могут встретиться следующие случаи:
а) система
сил приводится к главному вектору и
главному моменту: 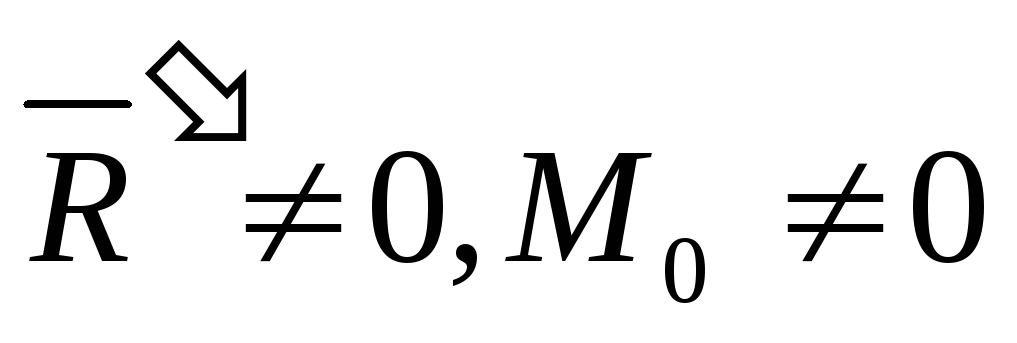
б) система .сил приводится к одной равнодействующей — главному вектору системы:

в) система
приводится к паре сил, момент которой
равен главному
моменту: 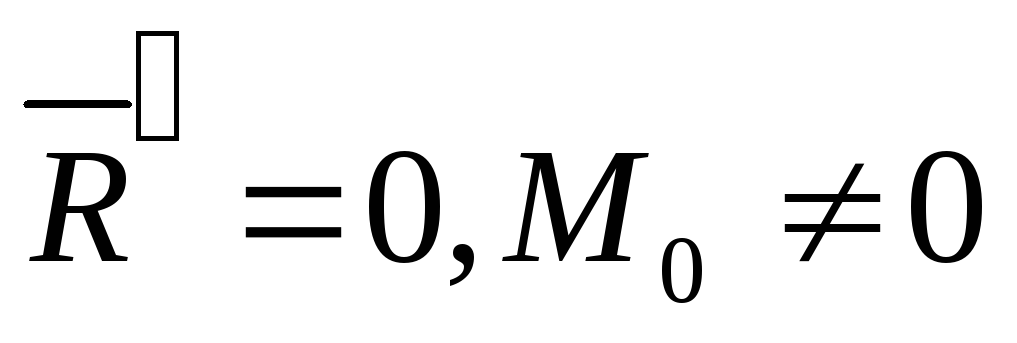
На
рис. 9, б показан
главный вектор 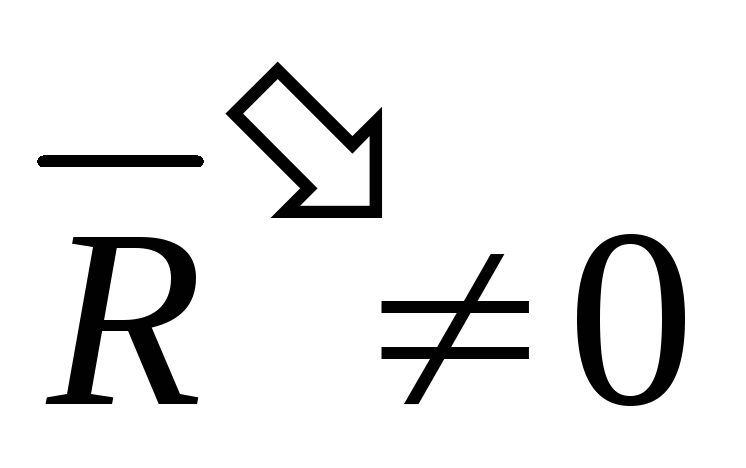 и
главный момент
и
главный момент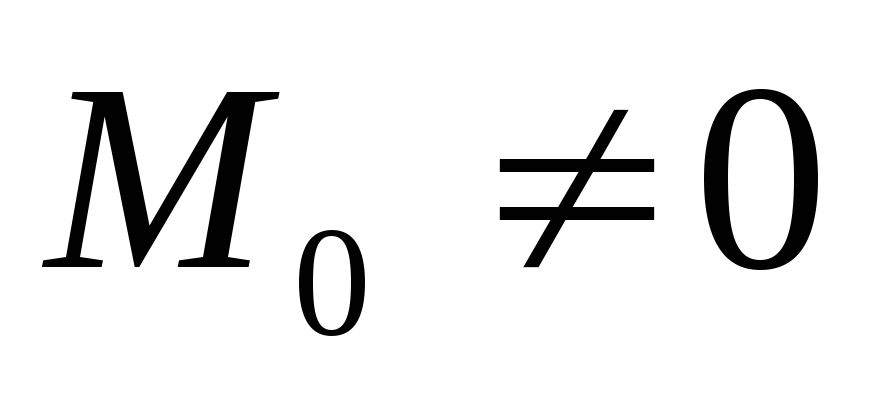
Произведем
эквивалентное преобразование главного
момента таким
образом, чтобы модуль сил, образующих
пару, был равен модулю
главного вектора. При этом плечо пары 
Расположим пару
сил так, чтобы сила была направлена в
сторону, противоположную главному
вектору. При этом в точке О окажутся две
силы 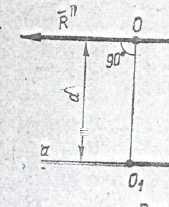 взаимно
противоположные, равные по модулю и
направленные по одной прямой. Так как
эти силы уравновешены, их можно отбросить.
Следовательно, относительно точки О1 система сил приведена к одной
равнодействующей.
взаимно
противоположные, равные по модулю и
направленные по одной прямой. Так как
эти силы уравновешены, их можно отбросить.
Следовательно, относительно точки О1 система сил приведена к одной
равнодействующей.
Таким образом, в том случае, когда главный вектор и главный момент не равны нулю, можно найти такую линию, вдоль которой вся система сил может быть уравновешена одной силой.
Необходимым
и достаточным условием равновесия
системы сил, произвольно
расположенных в плоскости, является
равенство нулю главного вектора и
главного момента относительно любого
центра приведения: 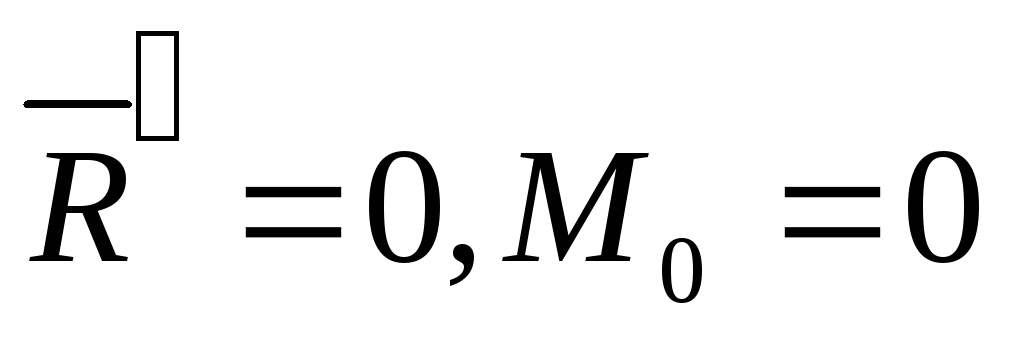 .
.
Экспериментальная проверка правильности определения главного вектора и главного момента плоской системы произвольно расположенных сил может быть произведена на установке, позволяющей воспроизвести заданные силы и пары сил и находить величину и направление уравнивающей силы.
Установка для испытания. Схема установки показана на рис. 8. Основными деталями установки являются диск 1 с отверстиями и грузики 2, создающие заданную систему сил. Требуемое направление сил достигается установкой подвижных блоков 4, через которые перекинуты гибкие нити, соединенные с грузиками и крючками 3, вставленными в отверстия диска. Главный вектор уравновешивается реакцией пальца 5. Уравновешивающий момент создается грузом, установленным таким образом, чтобы момент его относительно точки оси вращения диска был равен главному моменту системы сил относительно этой же точки и направлен противоположно.
Порядок выполнения работы. Ознакомиться с устройством установки для экспериментального исследования плоской системы произвольно расположенных сил. В отчет записать величину и направление сил, образующих данную систему. Система сил выбирается по табл. 6 в соответствии с вариантом задания. Центр приведения для всех вариантов задания — точка О.
Построить в масштабе заданную систему сил. Произвести все необходимые построения для определения главного вектора и главного момента относительно данной точки в той последовательности, которая указана в табл. 5. Определить графически величину и угол наклона главного вектора, численное значение и направление, главного момента.
Вычислить величину и направление главного вектора и главного момента аналитически. Сравнить результаты, полученные графическим и аналитическим способами. Расхождение между величинами, полученными двумя различными способами, не должно превышать 10%, в противном случае нужно проверить построения и вычисления и выявить ошибку.
В
зависимости от значений главного вектора
и главного момента
определить уравновешивающую систему
сил. В том случае, если главный
вектор и главный момент порознь не равны
нулю, т. е. 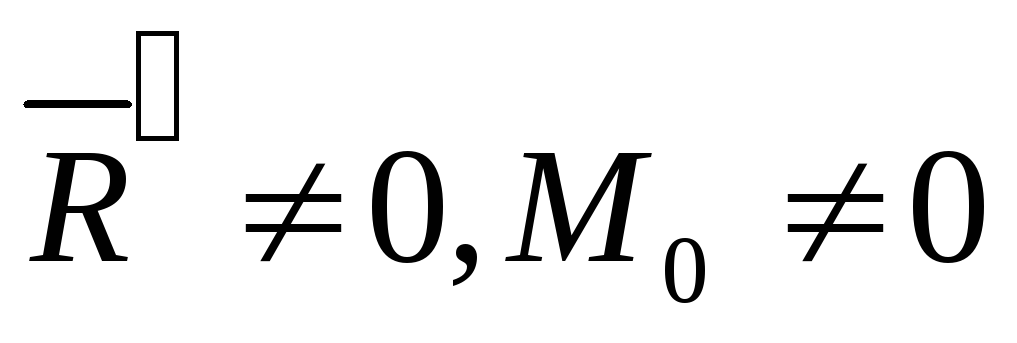 , найти
линию действия равнодействующей силы.
, найти
линию действия равнодействующей силы.
Произвести экспериментальную проверку полученных результатов. В данной работе центром приведения выбирается точка О, лежащая на оси неподвижного пальца 5 (см. рис. 8). На этом же пальце свободно установлен диск /, поэтому главный вектор всегда будет уравновешен реакцией пальца.
Чтобы уравновесить главный момент, следует при помощи груза приложить к диску момент, численно равный главному моменту Мо, но направленный в противоположную сторону.
Если
главный вектор и главный момент не равны
нулю 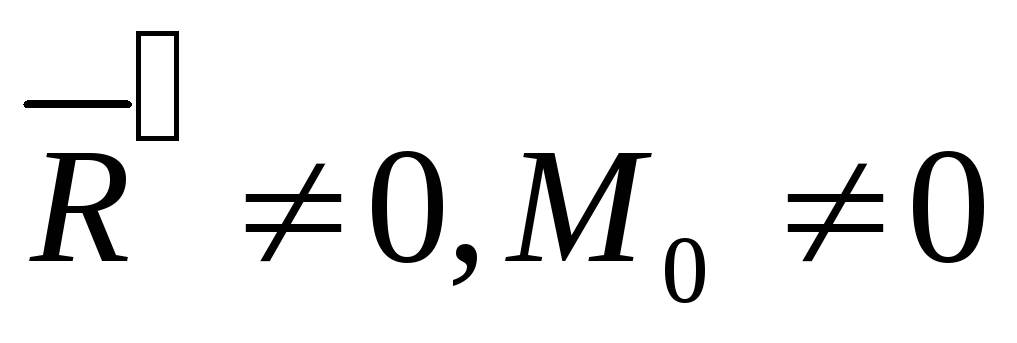 , заданную
систему сил можно уравновесить одной
силой (см.
табл. 5, п. 6). В этом случае при помощи
груза 6, крючка
3 и
подвижного блока 4 (см.
рис. 8) к диску 1 прикладывается
.уравновешивающая сила требуемой
величины и направления. Отчет
о работе. 1. Номер варианта задания (по
табл. 1.6)… Масштаб
сил КР=...Н/мм;
масштаб линейных размеров. Изображение
заданной системы сил. Данные:
, заданную
систему сил можно уравновесить одной
силой (см.
табл. 5, п. 6). В этом случае при помощи
груза 6, крючка
3 и
подвижного блока 4 (см.
рис. 8) к диску 1 прикладывается
.уравновешивающая сила требуемой
величины и направления. Отчет
о работе. 1. Номер варианта задания (по
табл. 1.6)… Масштаб
сил КР=...Н/мм;
масштаб линейных размеров. Изображение
заданной системы сил. Данные:
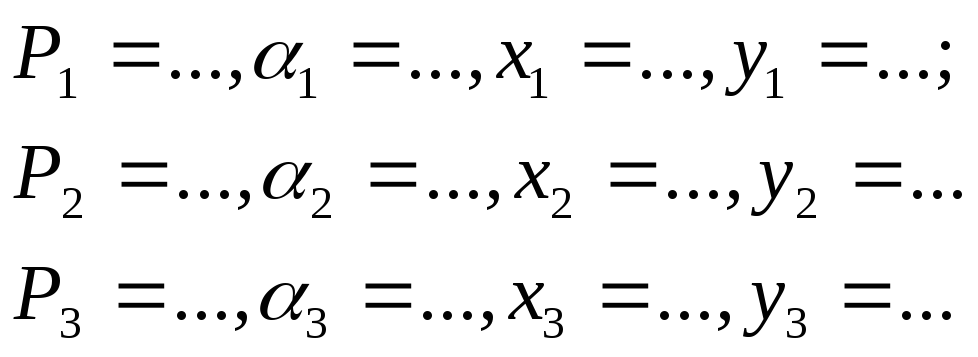
Точка приведения…
2. Приведение заданной системы сил к точке (см. табл. 5) — графическое, аналитическое.
3. Величина и направление главного вектора и главного момен-■а, определенных графическим и аналитическим способами:
4. Сравнение результатов, полученных графическим и аналитическим способами:
5. Определение положения линии действия равнодействующей силы R (см. табл. 1.5, п. 6) для случая, когда.
Вычисление расстояния от центра приведения до линии действия равнодействующей;
6. Схема прибора для экспериментальной проверки главного
вектора R‘ и главного момента М0.
7. Вывод о соответствии результатов, полученных расчетным и
опытным путями.
8. Ответы на контрольные вопросы.
Яблонский. Задание С.6. Приведение системы сил к простейшему виду. Определить главный вектор R*и главный момент M0 заданной системы сил относительно
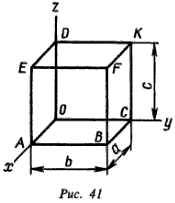
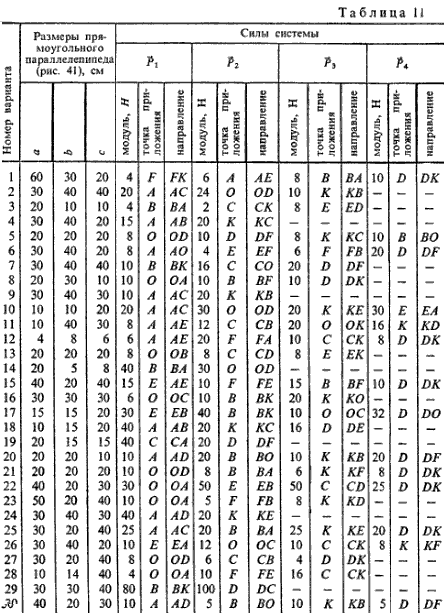
Яблонский. Задание С.6. Приведение системы сил к простейшему виду.Определить главный вектор R*и главный момент M0 заданной системы сил относительно центра O и установить, к какому простейшему виду приводится эта система. Размеры параллелепипеда (рис. 41), а также модули и направления сил указаны в табл. 11.
При выполнении задания необходимо сделать следующее.
1. Изобразить заданную систему сил, выполнив построение параллелепипеда в масштабе, показав ∠ xOy на чертеже равным 135°; сокращение размеров по оси Ox принять равным 1:2.
2. Выбрав систему координатных осей, определить модуль и направление главного вектора заданной системы сил по его проекциям на координатные оси и изобразить R*на чертеже.
3. Вычислить главный момент заданной системы сил относительно центра O по его проекциям на координатные оси и изобразить Mo на чертеже.
4. Вычислить наименьший главный момент заданной системы сил.
5. На основании результатов вычислений главного вектора и наименьшего главного момента M*установить, к какому простейшему виду приводится заданная система сил. При этом необходимо сделать следующее:
а) если заданная система сил приводится к паре сил, то показать момент этой пары, приложив его к точке O;
б) если заданная система сил приводится к равнодействующей, то найти уравнение линии действия равнодействующей, определить точки пересечения этой линией координатных плоскостей и изобразить R на чертеже;
в) если заданная система сил приводится к динаме (силовому винту), то найти уравнения центральной оси, определить точки пересечения этой осью координатных плоскостей и изобразить R*и M*на чертеже.
Пример решения;
Вариант 1;
Вариант 2;
Вариант 3;
Вариант 4;
Вариант 5;
Вариант 6;
Вариант 7;
Вариант 8;
Вариант 9;
Вариант 10;
Вариант 11;
Вариант 12;
Вариант 13;
Вариант 14;
Вариант 15;
Вариант 16;
Вариант 17;
Вариант 18;
Вариант 19;
Вариант 20;
Вариант 21;
Вариант 22;
Вариант 23;
Вариант 24;
Вариант 25;
Вариант 26;
Вариант 27;
Вариант 28;
Вариант 29;
Вариант 30;
Для просмотра изображения в полном размере нажмите на него
Для просмотра изображения в полном размере нажмите на него
5. Задание с2. Определение главного вектора и главного момента произвольной пространственной системы сил
К параллелепипеду
ОАВСDEKL
(рис. С2а), стороны которого равны l1, l2и l3приложены
сосредоточенные силы F1и F2 и линейная
равномерно распределенная нагрузка
интенсивностью q.
Размеры сторон, точки приложения сил 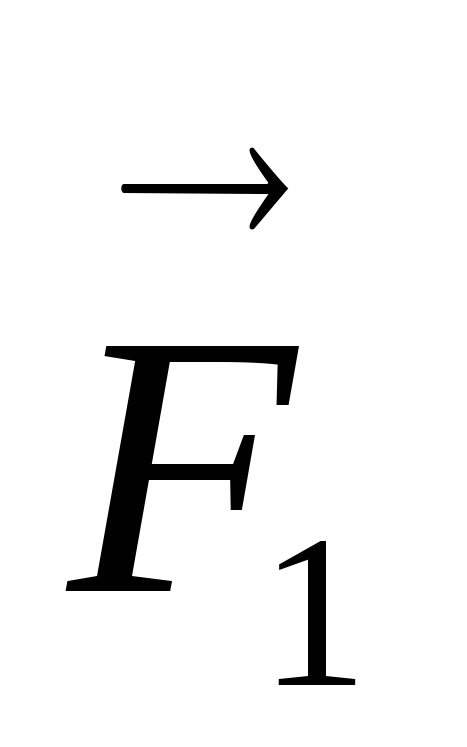 и
и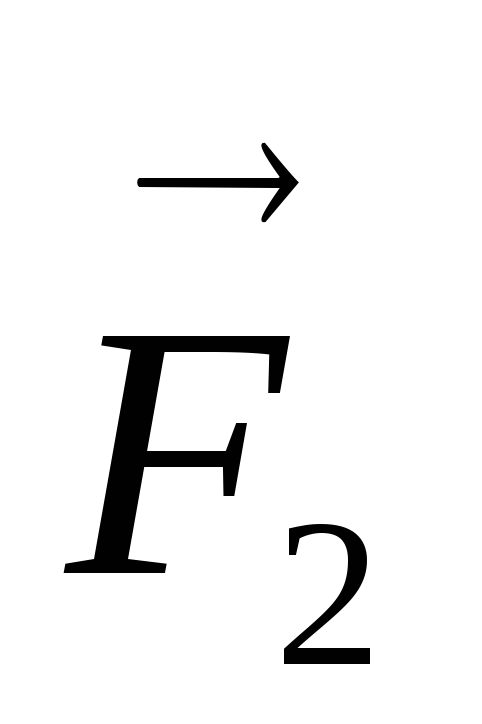 ,
ребро, к которому приложена равномерно
распределенная нагрузка и направление
действия этой нагрузки указаны в таблице
С2-1. Также в этой таблице дана точка
параллелепипеда, к которой направлена
сила
,
ребро, к которому приложена равномерно
распределенная нагрузка и направление
действия этой нагрузки указаны в таблице
С2-1. Также в этой таблице дана точка
параллелепипеда, к которой направлена
сила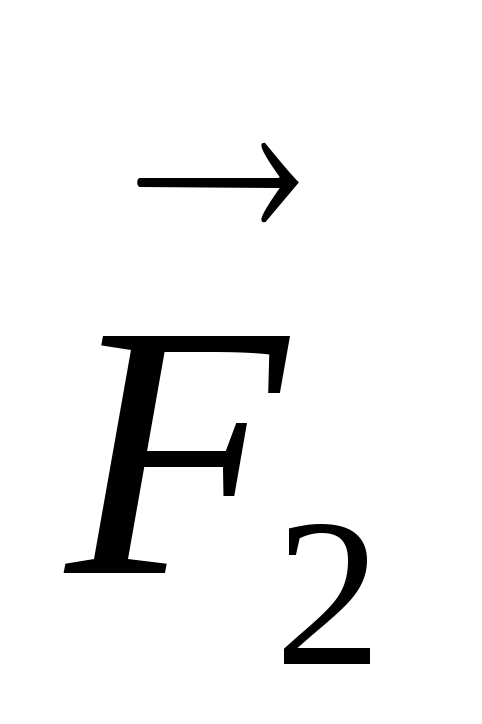 .
В таблице С2-2 приведены значения силF1и F2и интенсивность q равномерно распределенной нагрузки.
.
В таблице С2-2 приведены значения силF1и F2и интенсивность q равномерно распределенной нагрузки.
Определить главный вектор R и главный момент M системы заданных сил.
Таблица С2-1
Цифра шифра “б” | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 3 | 2 | 1 | 2 | 3 | 4 |
| 2 | 1 | 2 | 2 | 2 | 4 | 2 | 1 | 4 | 3 |
| 2 | 3 | 1 | 3 | 4 | 3 | 3 | 4 | 1 | 2 |
Точка
приложения силы | D | L | B | L | D | K | L | B | D | L |
Точка
приложения силы | K | D | L | K | B | L | A | L | K | B |
Распределенная нагрузка приложена к ребру | BC | AB | DE | AO | KL | BC | DE | EK | AB | EK |
Направление действия распределенной нагрузки |
|
|
|
|
|
|
|
|
|
|
Точка,
к которой направлена сила | A | C | E | A | D | C | K | E | A | E |
Примечание: Указанное стрелкой направление действия равномерно распределенной нагрузки означает, что нагрузка действует:
—  вертикально вниз;
вертикально вниз;
—  вертикально вверх;
вертикально вверх;
—  горизонтально слева направо;
горизонтально слева направо;
—  горизонтально справа налево.
горизонтально справа налево.
Таблица С2-2
Цифра шифра “а” |
| F2, Н | q, Н/м |
0 |
| 6 | 2,5 |
1 |
| 7 | 3,0 |
2 |
| 8 | 3,5 |
3 |
| 9 | 4,0 |
4 |
| 10 | 4,5 |
5 |
| 5 | 1,5 |
6 |
| 6 | 2,0 |
7 |
| 7 | 2,5 |
8 |
| 8 | 3,0 |
9 |
| 9 | 3,5 |

Рис. С2а
Для решения задачи С2 необходимо знать и уметь:
1. Вычислять проекции
силы на координатные оси в случае задания
силы через единичные векторы (орты
осей). Например, если сила 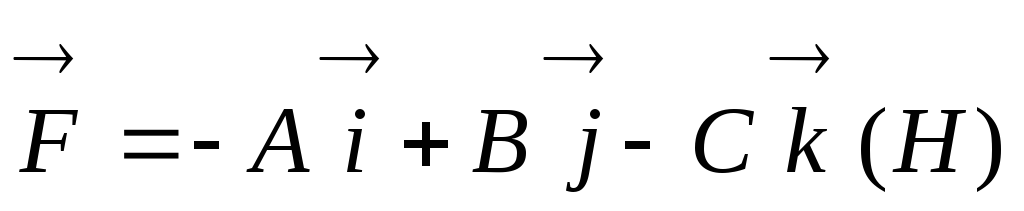 ,
то ее проекции равны:Fx= — A,
H;
Fy= B,
H; Fz= — C,
H.
,
то ее проекции равны:Fx= — A,
H;
Fy= B,
H; Fz= — C,
H.
2. Определять модуль главного вектора через проекции сил на координатные оси:

где проекции главного вектора Rx, Ry и Rz равны алгебраической сумме всех действующих сил на соответствующие оси координат, т.е.:
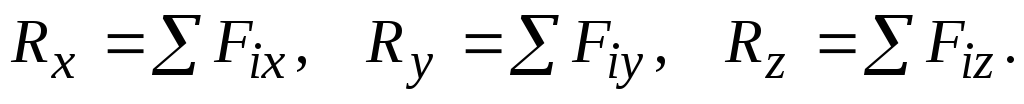
3. Находить направление главного вектора через направляющие косинусы:
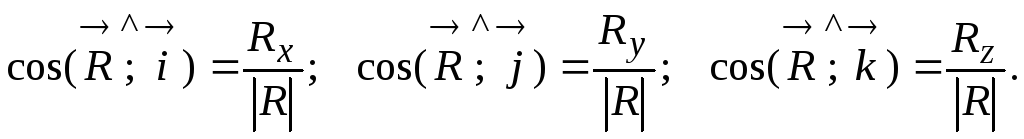
4. Вычислять проекции главного момента на координатные оси, как алгебраическую сумму моментов всех сил, приложенных к рассматриваемому
телу, относительно соответствующей оси:
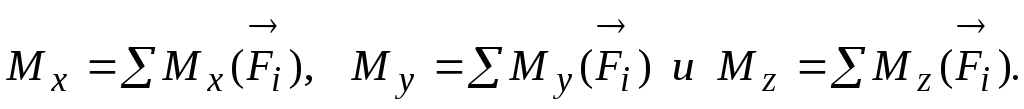
5. Определять модуль и направление главного момента по формулам:

и
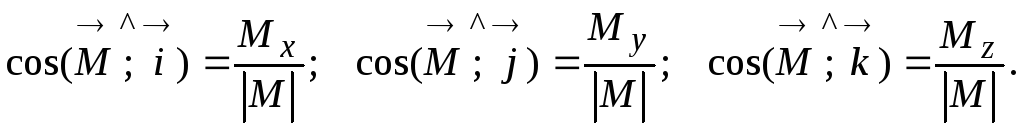
6. Вычислять момент силы относительно точки: моментом силы относительно точки называется величина, равная взятому с соответствующим знаком произведению модуля силы на плечо. Плечо силы – кратчайшее расстояние от рассматриваемой точки до линии действия силы.
Момент силы относительно точки имеет знак «плюс», если эта сила стремится повернуть тело вокруг рассматриваемой точки против хода часовой стрелки, и знак «минус» — если по ходу часовой стрелки.
Момент силы относительно точки равен нулю, если линия действия силы проходит через данную точку.
7. Находить момент силы относительно оси по правилу: моментом силы относительно оси называется скалярная величина, равная моменту проекции этой силы на плоскость, перпендикулярную этой оси, относительно точки пересечения данных оси и плоскости. Момент имеет знак «плюс», если с положительного конца рассматриваемой оси мы видим, что сила стремится повернуть тело против хода часовой стрелки. В противном случае момент силы относительно данной оси имеет знак “минус”.
При вычислении момента силы относительно оси возможны следующие частные случаи:
Если сила параллельна оси, то ее момент относительно этой оси равен нулю.
Если линия действия силы пересекает ось, то ее момент относительно данной оси равен нулю.
8. Вычислять момент силы при помощи теоремы Вариньона о моменте равнодействующей: момент равнодействующей относительно любого центра равен алгебраической сумме моментов составляющих сил относительно того же центра.
Пример решения задачи С2.
Дано: 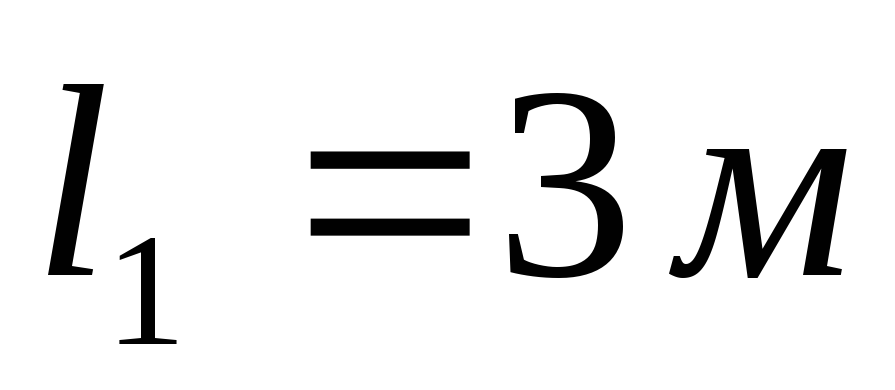 ;
; ;
; ;
;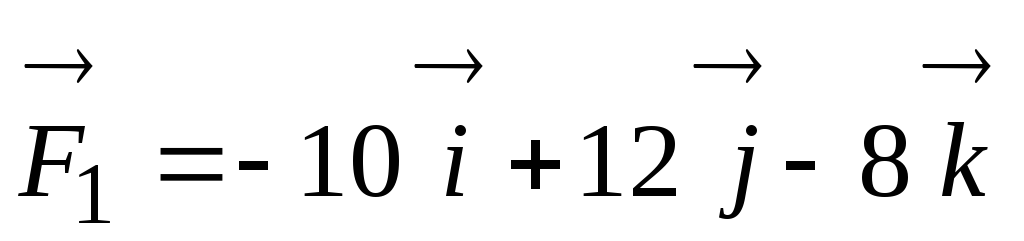 ,
Н;
,
Н;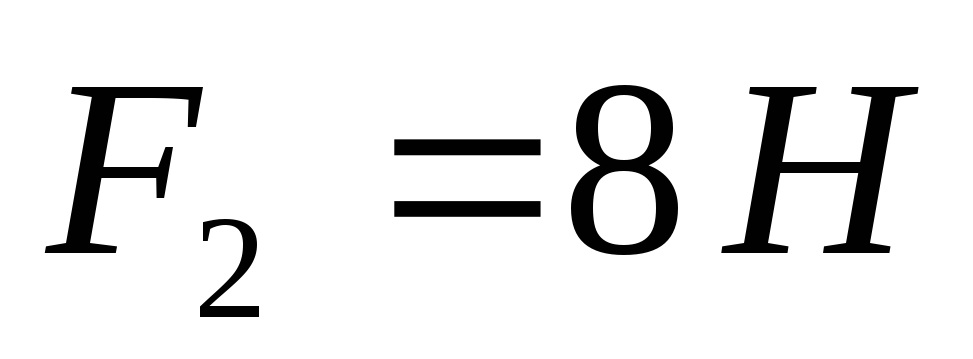 ;
;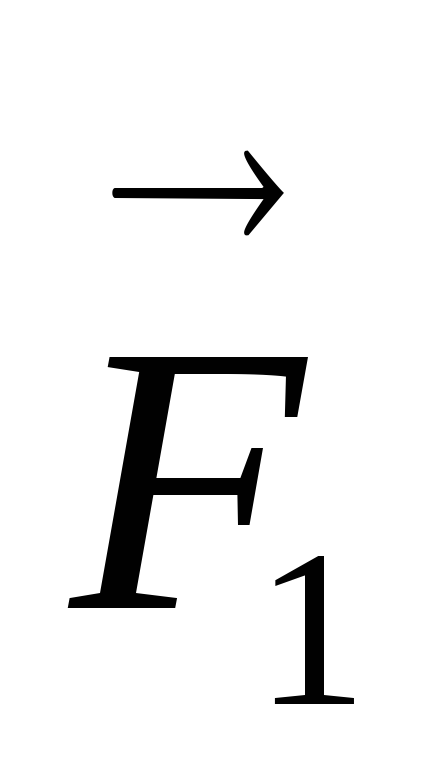 приложена к точке
L;
приложена к точке
L; 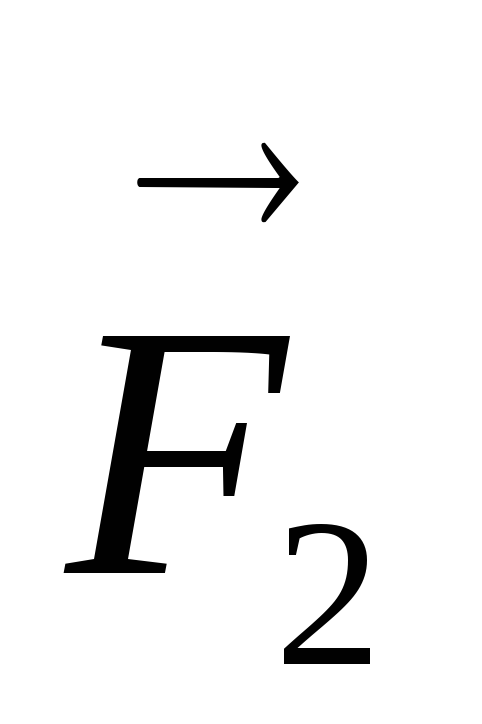 приложена к точке
В;
приложена к точке
В;  направлена от
точки В к точке Е;
направлена от
точки В к точке Е; 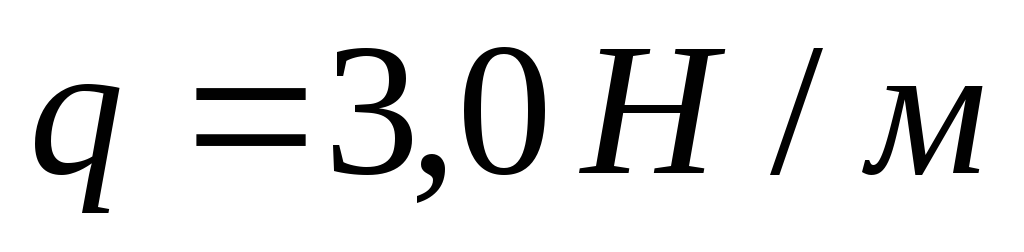 ;
распределенная нагрузка приложена к
ребруDE;
направление нагрузки – “
;
распределенная нагрузка приложена к
ребруDE;
направление нагрузки – “ ”.
”.
Найти:  и
и .
.
Решение.
1
Рис. С2б
. Изображаем на рисунке (рис. С2б) параллелепипедOABCDEKL в соответствии с условием задачи. Выбираем систему координат OXУZ. Прикладываем к точке L проекции силы :
: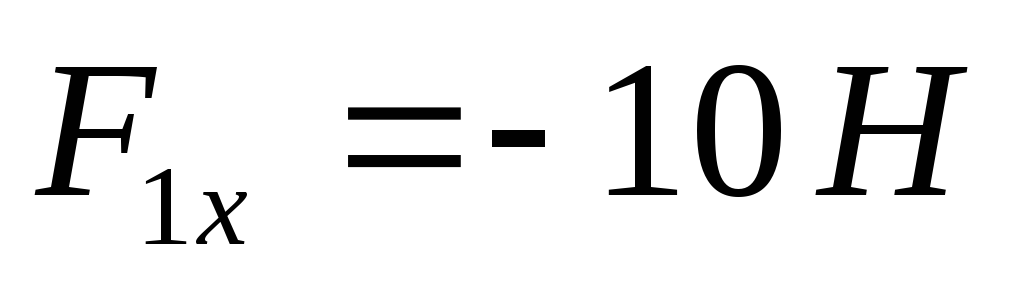 ;
;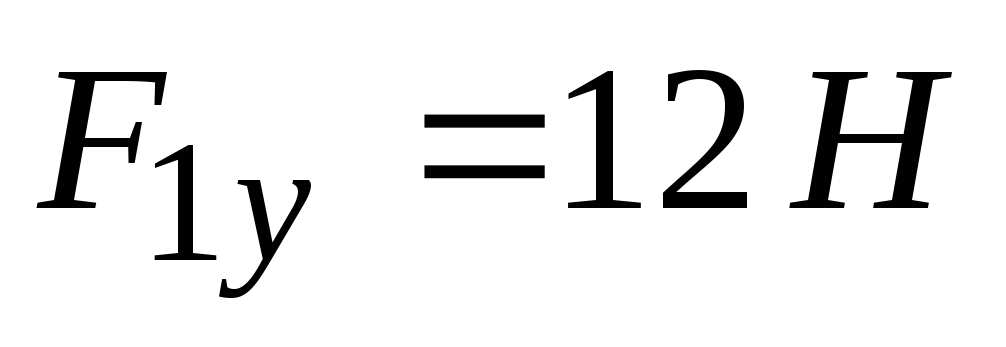 и
и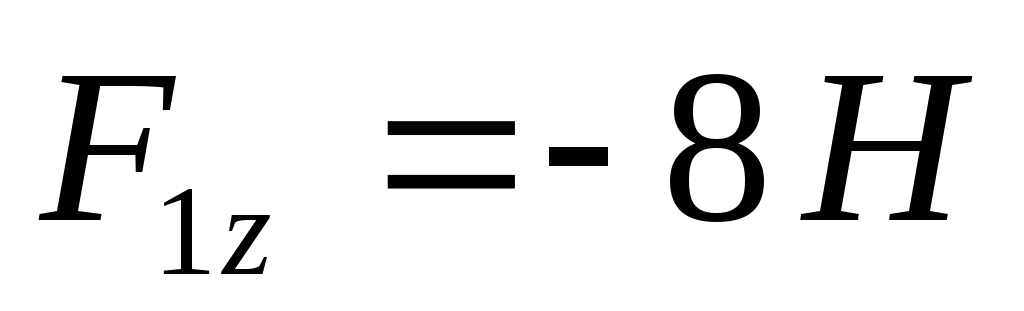 .Показываем силу
.Показываем силу  ,
приложенную к точке В и направленную
от точки В к точке Е. К ребруDE
прикладываем равномерно распределенную
нагрузку интенсивностью
,
приложенную к точке В и направленную
от точки В к точке Е. К ребруDE
прикладываем равномерно распределенную
нагрузку интенсивностью  ,
направленную горизонтально слева
направо.
,
направленную горизонтально слева
направо. 2. Заменяем равномерно
распределенную нагрузку сосредоточенной
силой, равной  .
Сила
.
Сила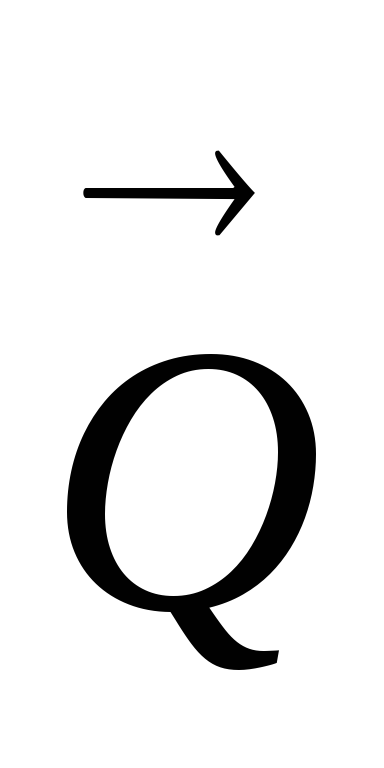 направлена горизонтально и приложена
к середине ребраDE
(см. рисунок).
направлена горизонтально и приложена
к середине ребраDE
(см. рисунок).
3. Вычисляем косинусы
и синусы углов α и β, необходимые для
определения проекций силы 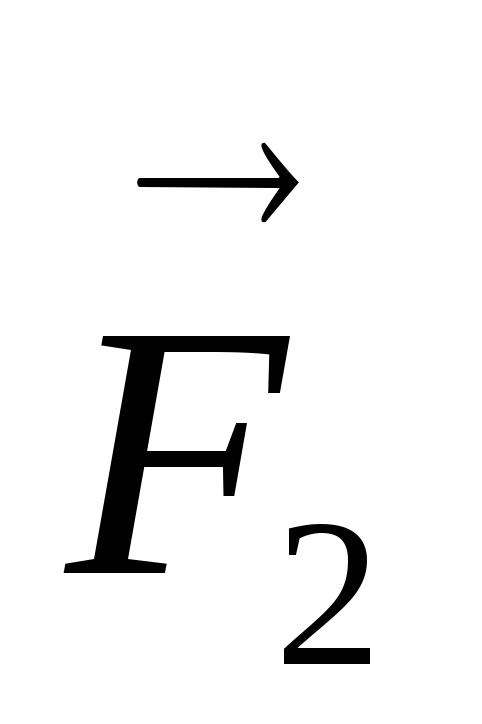 на выбранную систему координат:
на выбранную систему координат:
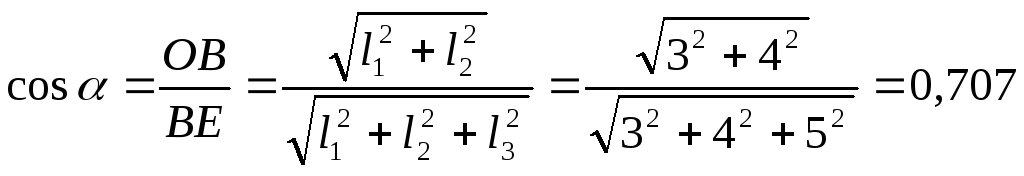 .
.
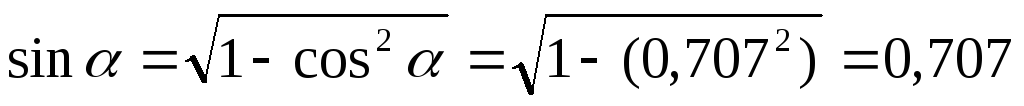 .
.
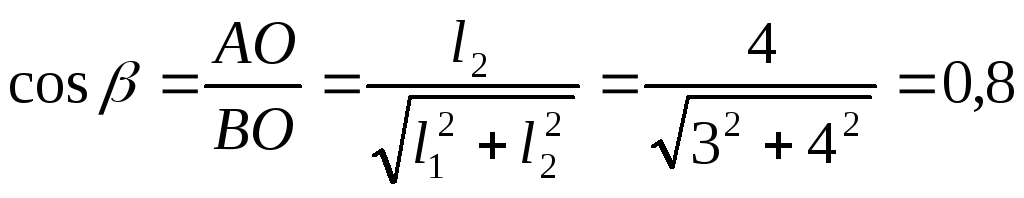 .
.
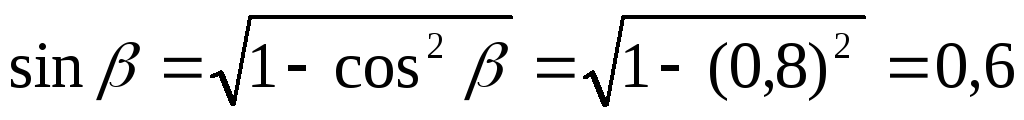 .
.
4. Определяем проекции главного вектора на оси координат:
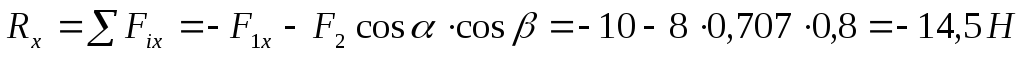 ;
;
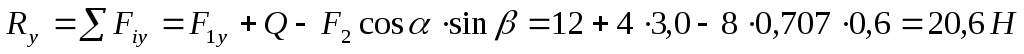 ;
;
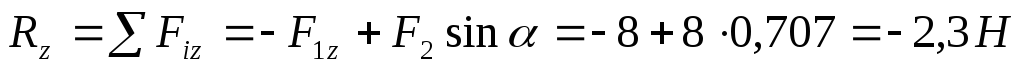 .
.
При нахождении
проекции силы  на оси Х и У пользуемся правилом двойного
проектирования: вначале силу
на оси Х и У пользуемся правилом двойного
проектирования: вначале силу проектируем на плоскость ХОУ, а затем
эту проекцию проектируем на соответствующую
координатную ось.
проектируем на плоскость ХОУ, а затем
эту проекцию проектируем на соответствующую
координатную ось.
5. Находим главный вектор:
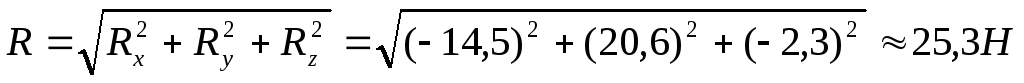 .
.
6. Вычисляем направляющие косинусы главного вектора:

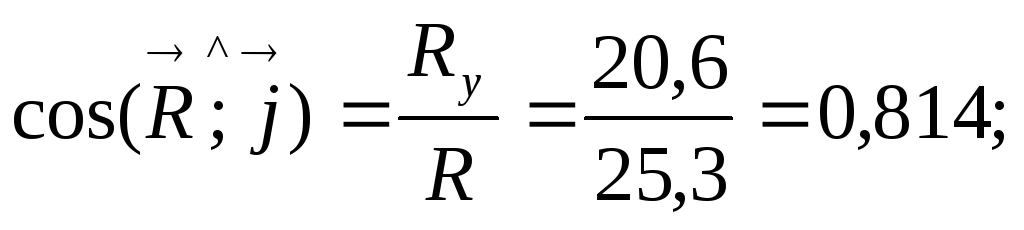

7. Определяем проекции главного момента относительно координатных осей:
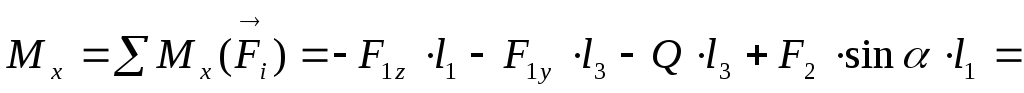



При вычислении
моментов сил относительно осей учитываем,
что момент силы относительно оси равен
нулю, если сила параллельна оси и если
линия действия силы пересекает
рассматриваемую ось. Так, например,
момент силы  относительно осиZ
равен нулю потому, что линия действия
силы
относительно осиZ
равен нулю потому, что линия действия
силы 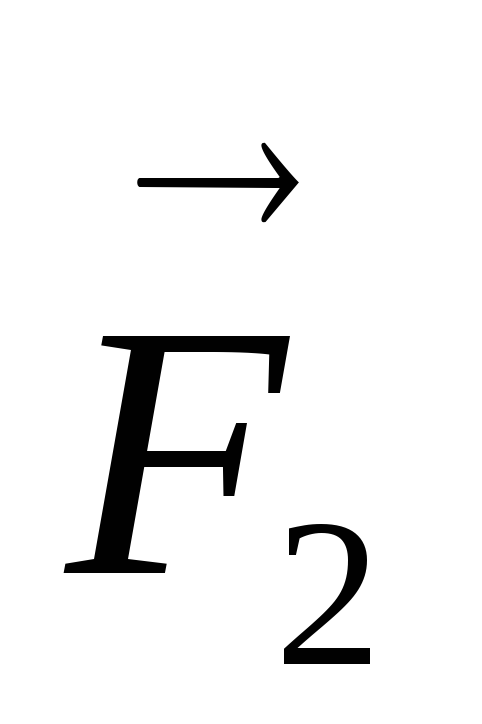 пересекает осьZ.
пересекает осьZ.
Определение знака
момента проиллюстрируем на примере
вычисления момента проекции 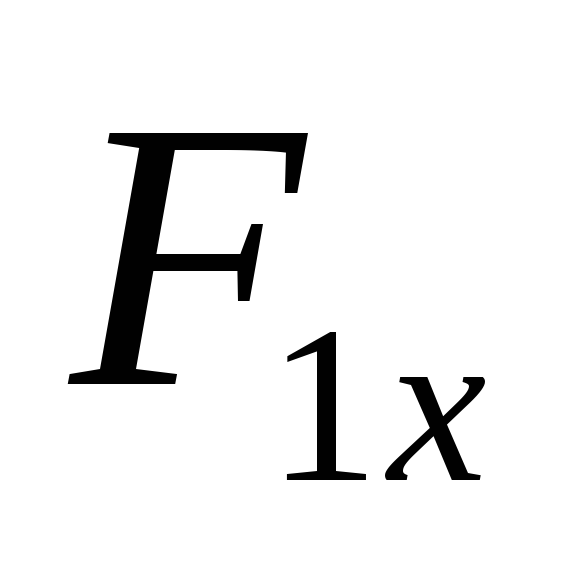 относительно оси ОУ: наблюдая со стороны
положительного конца оси ОУ видим, что
проекция
относительно оси ОУ: наблюдая со стороны
положительного конца оси ОУ видим, что
проекция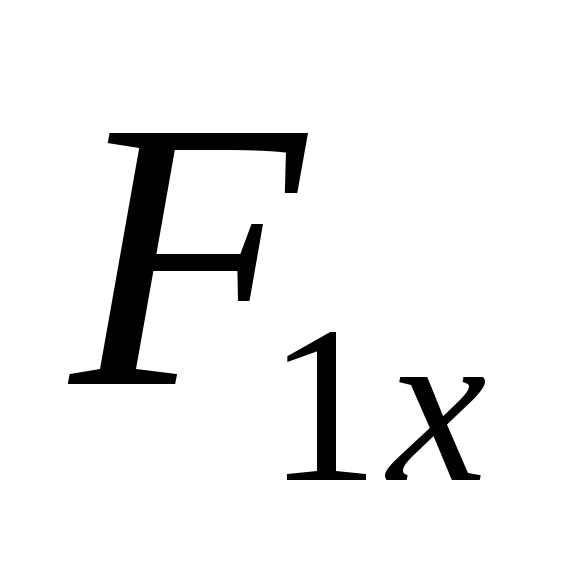 стремиться повернуть параллелепипед
относительно этой оси по ходу часовой
стрелки, следовательно, знак момента
проекции
стремиться повернуть параллелепипед
относительно этой оси по ходу часовой
стрелки, следовательно, знак момента
проекции относительно оси ОУ отрицательный.
относительно оси ОУ отрицательный.
8. Находим главный момент:

9. Вычисляем направляющие косинусы главного момента:
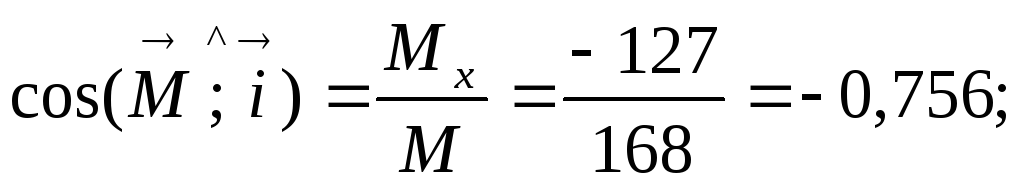
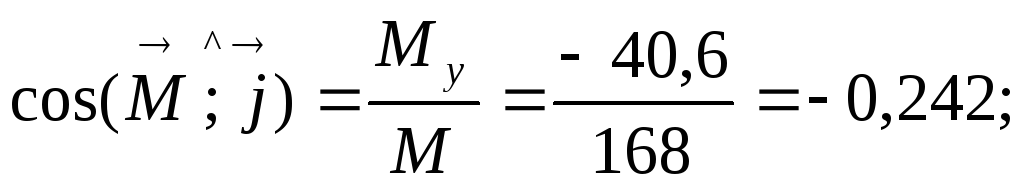
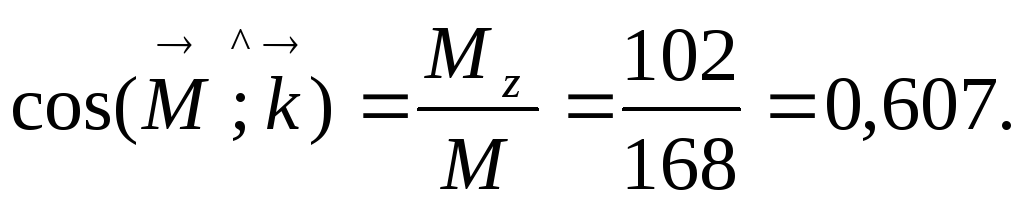
Ответ: 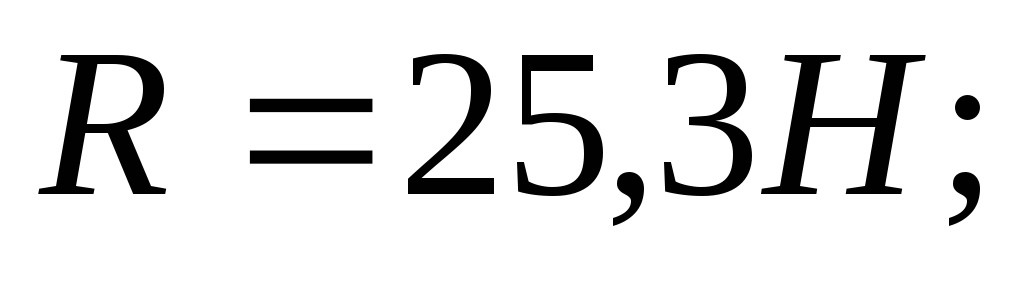
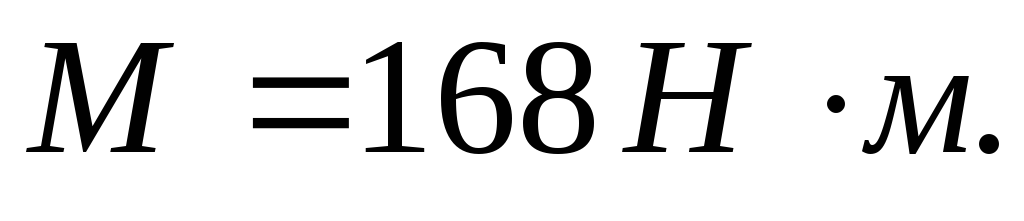


 и
и 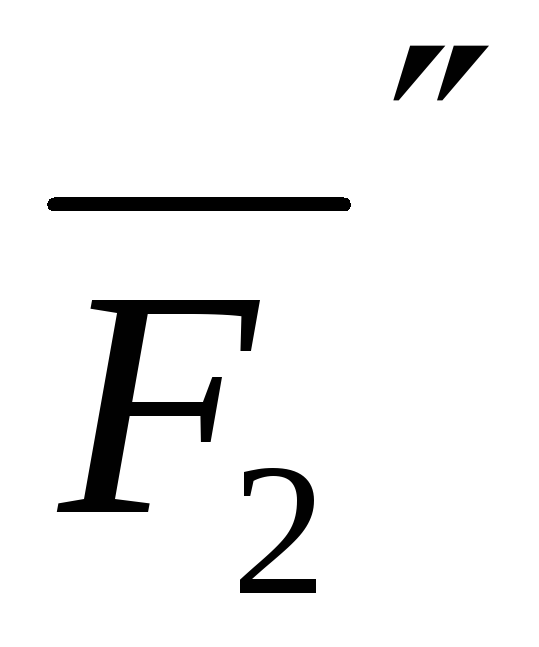 ,
равные по модулю силе
,
равные по модулю силе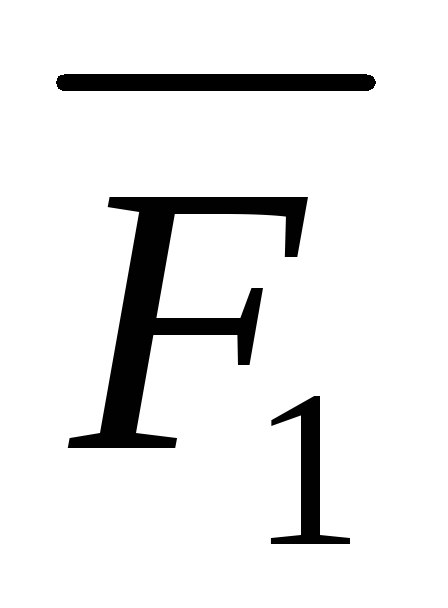 и
направленные параллельно ей. Аналогичные
операции произвести для
всех п сил
и
направленные параллельно ей. Аналогичные
операции произвести для
всех п сил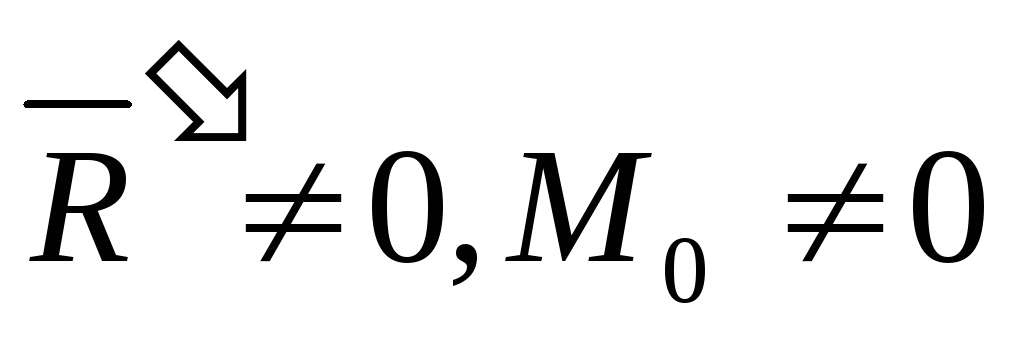 к
к восстановить
перпендикуляр длиной
восстановить
перпендикуляр длиной 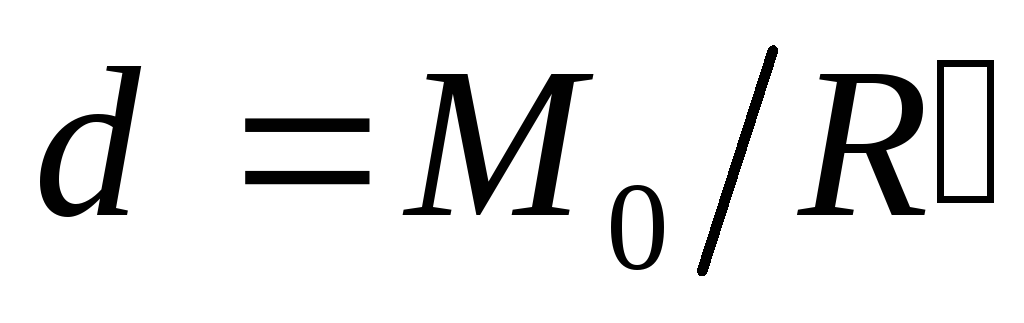 ,
через конец этого отрезка провести
линию, параллельную
,
через конец этого отрезка провести
линию, параллельную  ,
и на этой линии отложить вектор
равнодействующей силы
,
и на этой линии отложить вектор
равнодействующей силы  ,
причем линия
,
причем линия  должна располагаться относительно
точки О так, чтобы равнодействующая
сила
должна располагаться относительно
точки О так, чтобы равнодействующая
сила  создавала
момент такого же направления, как М0
создавала
момент такого же направления, как М0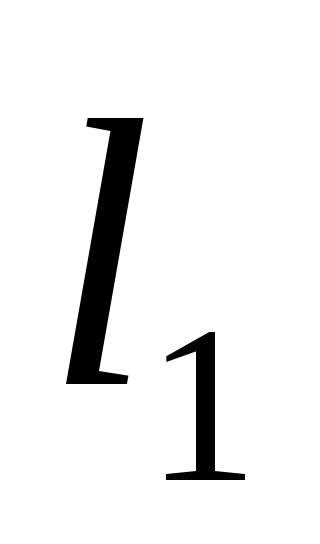 ,
м
,
м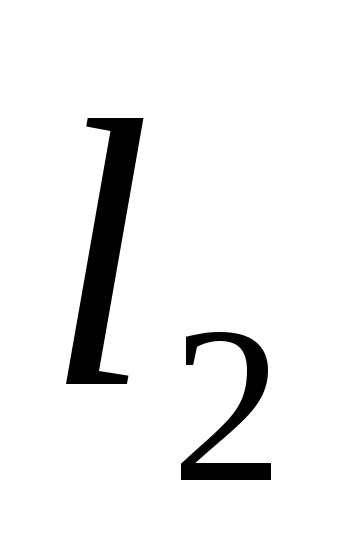 ,
м
,
м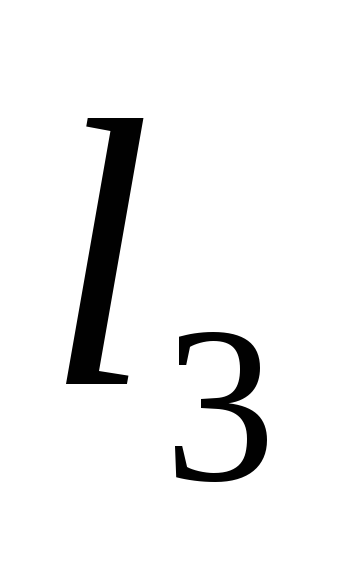 ,
м
,
м
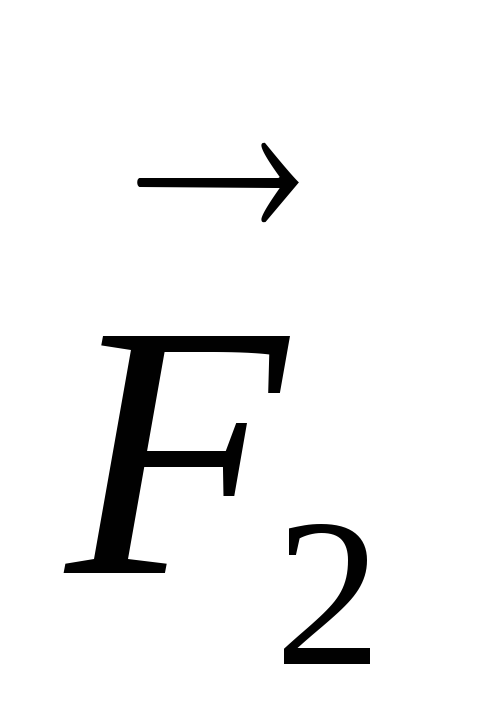






 ,
Н
,
Н