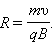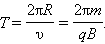ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД. СИЛА ЛОРЕНЦА — Студопедия
Электрический ток — это упорядоченно движущиеся наряженные частицы. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника. Найдем силу, действующую на одну частицу.
Модульсилы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной  , к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:
, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:

Рассмотрим отрезок тонкого прямого проводника с током (рис. 1.23). Пусть длина отрезка  и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля
и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля 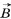
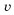 следующей формулой:
следующей формулой:
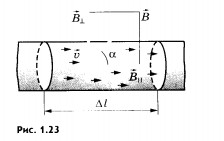
Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен:
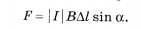
Подставляя в эту формулу выражение (1.4) для силы тока, получаем:
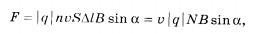
где N = nS  — число заряженных частиц в рассматриваемом объеме. Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:
— число заряженных частиц в рассматриваемом объеме. Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:
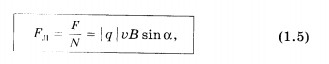
где 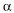
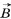 и
и  . Ее направление определяется с помощью того же правила левой руки, что и направление силы Ампера: если левую руку распололсить так, чтобы составляющая магнитной индукции
. Ее направление определяется с помощью того же правила левой руки, что и направление силы Ампера: если левую руку распололсить так, чтобы составляющая магнитной индукции 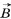 , перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° большой палец укажет направление действующей на заряд силыЛоренца
, перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° большой палец укажет направление действующей на заряд силыЛоренцаЭлектрическое поле действует на заряд q с силой 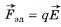 . Следовательно, если есть и электрическое поле, и магнитное поле, то суммарная сила
. Следовательно, если есть и электрическое поле, и магнитное поле, то суммарная сила  , действующая на заряд, равна:
, действующая на заряд, равна:
 =
= 
 л.
л.
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работы. Согласно теореме о кинетической энергии (см. учебник физики для 10 класса) это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.
Движение заряженной частици в однородном магнитном поле. Рассмотрим движение частицы с зарядом q в однородном магнитном поле 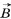
 (рис. 1.25).
(рис. 1.25). 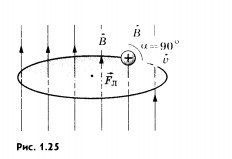
Сила Лоренца зависит от модулей векторов скорости частицы и индукции магнитного поля.
Так как магнитное поле не меняет модуль скорости движущейся частицы, то остается неизменным и модуль силы Лоренца. Эта сила перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы. Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что частица равномерно движется по окружности радиусом r. Определим этот радиус.
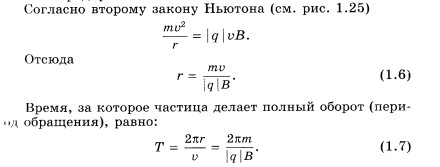
Использование действия магнитного поля на движущийся заряд. Действие магнитного поля на движущийся заряд широко используют в современной технике. Достаточно упомянуть телевизионные трубки (кинескопы), в которых летящие к экрану электроны отклоняются с помощью магнитного поля, создаваемого особыми катушками.

Сила Лоренца используется и ускорителе заряженных частиц (циклотрон) для получения частиц с большими энергиями. Циклотрон состоит из двух полых полуцилиндров (дуантов) 3, находящихся в однородном магнитном поле (рис. 1.26). Между дуантами создается переменное электрическое поле. Согласно формуле (1.6) при увеличении скорости частицы / радиус окружности (траектории 2), по которой движется частица, увеличивается. Период обращения частицы не зависит от скорости (см. формулу (1.7)), и, следовательно, через полпериода, вследствие изменения направления электрического поля, частица снова оказывается в ускоряющем ее поле и т. д. На последнем витке частица вылетает из циклотрона.
На действии магнитного поля основано также и устройство приборов, позволяющих разделять заряженные частицы по их уденьиым зарядам, т. е. по отношению заряда частицы к ее массе, и по полученным результатам точно определять массы частиц. Такие приборы получили название масс-электрографов.
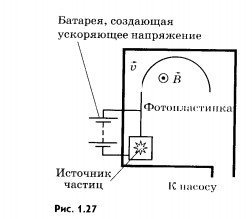
На рисунке 1.27 изображена принципиальная схема простейшего масс-электрографа. Вакуумная камера прибора помещена в магинитое поле (вектор индукции 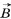 перпендикулярен рисунку). Ускорение электрическим полем заряженные частицы (электроны или ионы), описав дугу, попадают на фотопластинку, где оставляют след, позволяющий с высокой точностью измерить радиус траектории r. По этому радиусу определяется удельный заряд иона. Зная заряд иона, легко вычислить его массу.
перпендикулярен рисунку). Ускорение электрическим полем заряженные частицы (электроны или ионы), описав дугу, попадают на фотопластинку, где оставляют след, позволяющий с высокой точностью измерить радиус траектории r. По этому радиусу определяется удельный заряд иона. Зная заряд иона, легко вычислить его массу.
На движущуюся заряженную часчицу со стороны магнитного поля действует сила Лоренца. Эта сила перпендикулярна скорости и не совершает работы.

1. Чему равен модуль силы Лоренца!
2. Как движется заряженная частица в однородном магнитном поле, если начальная скорость частицы перпендикулярна линиям магнитной индукции!
Действие магнитного поля на движущийся электрический заряд
1. «Модели эфиров»
Если бы Андре Мари Ампер (рис. 1) знал о действии электрического тока, то продвинулся гораздо дальше в своих открытиях.

Рис. 1. Андри Мари Ампер (Источник)
Как и многие учёные того периода Ампер придерживался «модели эфира»: электрический ток – эфир, некая жидкость, которая протекает по проводникам. Именно отсюда и сам термин «электрический ток» — то, что течёт. Только в самом конце XIX века – вначале ХХ модели эфиров стали отходить, а на смену им стали появляться новые модели адекватнее отражающие наблюдаемые явления. В частности были открыты катодные лучи, была выявлена радиоактивность, проведены исследования Фарадея по электролизу – всё это наводило на мысль о существовании заряжённых частиц, которые как-то движутся.
2. Электронная модель Хендрика Лоренца
Серьёзную модель предложил учёный Хендрик Лоренц (рис. 2) так называемую «электронную модель». При образовании кристаллической решётки металлов, от каждого атома металла отрывается по одному внешнему электрону, таким образом, в узлах кристаллической решётки находятся положительные ионы, а в объёме этой решётки почти свободно могут двигаться электроны (рис. 3).

Рис. 2. Хендрик Лоренц (Источник)
Такая модель является достаточно устойчивой, потому что действуют электростатические силы между положительно заряжённой решёткой и электронным окружением. Именно поэтому металлы достаточно прочны для разряжения, но в то же время, ковки.
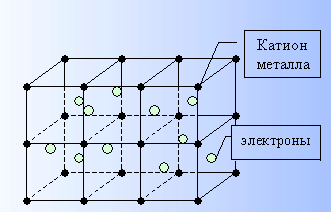
Рис. 3. Кристаллическая решетка (Источник)
Модель, предложенная Лоренцом, хороша хотя бы тем, что достаточно легко объясняла возникновение электрического тока в металлах. При обычных условиях эти электроны находятся в беспорядочном движении вокруг кристаллической решётки. И только при подаче разности потенциалов на конце проводника, когда внутри проводника появляется электрическое поле, кроме этой хаотической составляющей появляется другая – упорядоченная составляющая или направленное движение. Именно это движение, согласно модели Лоренца, представляет собой электрический ток.
Так, со стороны магнитного поля 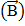 на проводник с током (I), действует сила Ампера
на проводник с током (I), действует сила Ампера 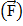 перпендикулярная направлению тока и направлению линии магнитного поля. (Рис. 4)
перпендикулярная направлению тока и направлению линии магнитного поля. (Рис. 4)
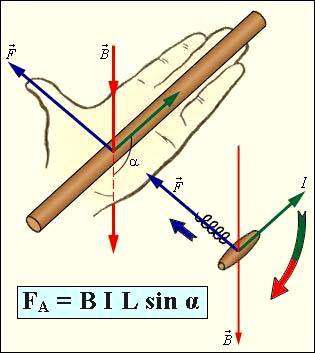
Рис. 4. Направленное движение (Источник)
«Если электрический ток представляет собой направленное движение зарядов, то не будет ли со стороны магнитного поля действовать такая же сила» — примерно, так рассуждал Лоренц. В выражение для силы Ампера (1.1.) вместо силы тока подставим определение силы тока – отношение перенесенного заряда в проводнике ко времени, за которое было осуществлено данное перенесение.
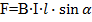 (1.1)
(1.1)
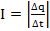 (1.2)
(1.2)
Также заметим, что отношение элемента длины проводника к интервалу времени – скорость движения заряда.
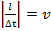 (1.3)
(1.3)
Тогда выражение принимает вид (6.4.). Модуль силы равен произведению величины магнитной индукции поля на количество переносимого через проводник заряда на скорость частиц, которые переносят заряд и на синус угла между направлением движения заряда и направлением вектора магнитной индукции.
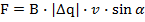 (1.4)
(1.4)
Учтём, что носителями электрического тока в проводнике являются электроны, величина зарядов которых одинакова. Поэтому можно записать, что совокупный заряд, переносимый через поперечное сечение проводника – произведение элементарного заряда на количество электронов переносимых через поперечное сечение проводника.
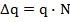 (1.5)
(1.5)
 (1.6)
(1.6)
Вывод приведенной формулы был сугубо формальным, однако, даже такой вывод позволял предположить, что не только на проводник с током, но и на отдельный заряд в магнитном поле будет действовать сила со стороны этого поля. Предположим, что число зарядов равно единице и этот заряд движется не внутри кристаллической решётки, а в свободном пространстве. Возникает вопрос: что произойдёт с этим зарядом, если он войдёт в область, где существует однородное магнитное поле? Согласно нашей гипотезе, на частицу, движущуюся в однородном магнитном поле, должна действовать сила, которая перпендикулярна скорости этой частицы (поскольку именно так будет направлен электрический ток, связанный с движением этих частиц) и перпендикулярна линиям магнитного поля. Величина этой силы будет определяться так:
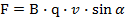
3. Проверка гипотезы Лоренца – принцип работы электронно-лучевой трубки
Открытие катодных лучей, а также радиоактивности позволили проверить экспериментально гипотезу Лоренца. Воспользуемся электронно-лучевой трубкой (рис. 5)
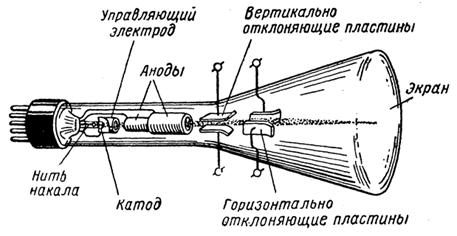
Рис. 5. Электронно-лучевая трубкой (Источник).
В вакуумной трубке размещены две пластины: анод и катод. На катод подаётся отрицательный потенциал, на анод – положительный. Для того чтобы в трубке возникли свободные электроны, катод нагревается нитью накала. Свободные электроны металлического катода вблизи его поверхности могут покидать эту поверхность, обладая высокой кинетической энергией за счёт нагревания – явление термоэлектронной эмиссии. Свободные электроны, покинувшие поверхность катода, попадают в зону действия электрического поля между анодом и катодом. Линии напряжённости этого поля направлены от анода к катоду. Электроны, будучи отрицательно заряженными частицами, движутся от катода к аноду – против линии напряжённости поля. Так в трубке возникает электрический ток, направленный от анода к катоду. Если использовать анод, покрытый специальным материалом, который светится при попадании на него заряжённых частиц, можно пронаблюдать место попадания электронов по световому пятну. Именно так и работает электронно-лучевая трубка. При подаче напряжения на анод и катод мы видим небольшое зелёное пятно на аноде – это место бомбардировки экрана электронами.
4. Опыты с осциллографом
Если воспользоваться осциллографом (рис.6), то будет показано не световое пятно, а светящаяся линия. Когда одним из полюсов подводят к горизонтальной линии, находящейся на осциллографе – она отклоняется от своего первоначального значения в направлении перпендикулярном направлению скорости и направлению линий магнитного поля, поскольку магнитное поле направлено от северного полюса к южному. Это на качественном уровне подтверждает гипотезу.
Попытаемся получить не только качественные, но и количественные результаты. Для этого будем проверять зависимость силы действующей со стороны магнитного поля от различных факторов. В частности от скорости движения электронов. Каким образом можно поменять скорость движения электронов в осциллографе? При помощи регулировки яркости линии на осциллографе можно изменить скорость движения электронов в осциллографе. Чем ярче линия – тем быстрее движется электроны внутри трубки. Если поднести магнит к осциллографу северным полюсом и менять скорость движения электронов – то по мере уменьшения яркости – искажение лини также будет уменьшаться. Это означает, что сила, действующая со стороны магнитного поля на электроны, при уменьшении скорости электронов тоже уменьшается. Более точные измерения дадут нам прямую пропорциональность между силой, действующей со стороны магнитного поля на движущиеся заряды и скоростью этих зарядов. Сила, действующая на заряды со стороны магнитного поля, пропорциональна индукции – если поднести несколько магнитов к осциллографу, то искажение будет гораздо сильнее. Величина силы действующей со стороны магнитного поля на движущийся заряд зависит от взаимного направления вектора магнитной индукции и вектора скорости движения частиц – при поднесении магнитов к осциллографу южным полюсом – линия будет искажаться в противоположном направлении.

Рис. 6. Осциллограф (Источник)
5. Электромагниты
Обобщим выводы из проделанных экспериментов. На движущийся в магнитном поле заряд (q) со стороны магнитного поля действует сила (F), направление которой зависит от взаимного направления вектора скорости движения ( 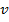 ) заряда и вектора магнитной индукции поля (В). Величина силы пропорциональна скорости движения заряда и модулю магнитной индукции. Направление силы определяется по правилу «Левой руки» (рис. 4).
) заряда и вектора магнитной индукции поля (В). Величина силы пропорциональна скорости движения заряда и модулю магнитной индукции. Направление силы определяется по правилу «Левой руки» (рис. 4).
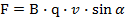 (1.7)
(1.7)
Таким образом, полученное ранее выражение для силы, описывает взаимодействие магнитного поля с движущимся в этом поле электрическим зарядом. Открытие силы действия магнитного поля на движущийся в нём заряд стало возможным только благодаря улучшению представлений о строении вещества, электрическом токе в металлах, движении заряженных частиц. И огромную роль во всех этих задачах сыграл Лоренц, поэтому открытая сила и получила название – сила Лоренца.
6. Выводы
Сделаем ещё несколько замечаний.
1. Вектор силы Лоренца перпендикулярен вектору скорости
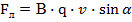 (1.8)
(1.8)
 (1.9)
(1.9)
 (1.10)
(1.10)
2. Если сила перпендикулярна вектору скорости, то такая сила называется центростремительной. И тогда под её действием – тело движется по окружности. Следовательно, сила Лоренца – центростремительная сила:
 (1.11)
(1.11)
3. Из-за того, что под действием силы Лоренца заряд движется по дуге окружности, следовательно, он обладает центростремительным ускорением. Центростремительное ускорение может быть рассчитано как квадрат скорости движения, делённый на радиус окружности, который описывает тело:
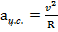 (1.12)
(1.12)
4. Так, согласно второму закону Ньютона сила может быть определена как произведение массы тела на приобретаемое им ускорение:
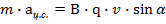 (1.13)
(1.13)
После подстановки уравнения 1.12 в 1.13 получим:
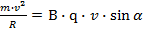 (1.14)
(1.14)
После сокращения скорости получим следующие соотношения:
 (1.15)
(1.15)
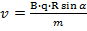 (1.16)
(1.16)
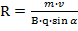 (1.17.)
(1.17.)
Действие магнитного поля на движущийся заряд. Сила Лоренца
Электрический ток – это совокупность упорядоченно движущихся заряженных частиц. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца.
Модуль силы Лоренца равен отношению модуля силы Ампера, действующей на участок проводника, к числу заряженных частиц в этом участке проводника:
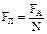
Сила Ампера равна 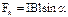 , сила тока равна
, сила тока равна 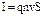 (см. стр. 12). Подставив эти выражения в формулу для силы Лоренца, получим:
(см. стр. 12). Подставив эти выражения в формулу для силы Лоренца, получим:
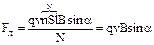
где  — угол между векторами скорости и магнитной индукции.
— угол между векторами скорости и магнитной индукции.
Направление силы Лоренца определяют для положительного заряда по правилу левой руки. (Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону).
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. А, согласно теореме о кинетической энергии, это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.
Закон Ампера
Поместим в магнитное поле проводник длинной l, по которому течет ток I. На проводник действует сила, прямо пропорциональная силе тока, текущего по проводнику, индукции магнитного поля, длине проводника, и зависящая от ориентации проводника в магнитном поле. |F|=IBlsina, где a — угол между направлением тока в проводнике и направлением вектора магнитной индукции B, Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, что магнитные силовые линии входят в ладонь, четыре вытянутых пальца направить по току, то отогнутый большой палец укажет направление силы. Очевидно, что сила Ампера равна нулю, если проводник расположен вдоль силовых линий поля и максимальна, если проводник перпендикулярен силовым линиям. Движение заряженных частиц в магнитном поле. На проводник с током в магнитном поле действует сила Ампера FА IBlsina.Ток, в свою очередь, это направленное движение заряженных частиц. Сила тока равна I=qnvS, где q – заряд частицы, n-концентрация движущихся заряженных частиц, v-средняя скорость их направленного движения, S-площадь поперечного сечения проводника. Подставив I в выражение для FА, получим FА= qnvSBlsina, где nsl=N – общее число частиц, создающих ток. Тогда сила, действующая на отдельный движущийся заряд – сила Лоренца, равна Fл=qvBsina. где a — угол между векторами скорости и магнитной индукции. Направление силы Лоренца определяется для положительно заряженной частицы по правилу левой руки.
Закон Ампера
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Экспериментальное изучение магнитного взаимодействия показывает, что модуль силы Ампера пропорционален длине проводника с током, силе тока и зависит от ориентации проводника в магнитном поле.
Опыт показывает, что магнитное поле, вектор индукции которого направлен вдоль проводника с током, не оказывает влияния на ток. Поэтому модуль силы зависит лишь от модуля составляющей вектора магнитной индукции, перпендикулярной проводнику.
Закон Ампера заключается в следующем. Сила Ампера равна произведению магнитной индукции поля на силу тока, длину участка проводника и на синус угла между магнитной индукцией и участком проводника:
Направление силы ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая магнитной индукции входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 большой палец покажет направление силы, действующей на отрезок проводника.
Магнитное взаимодействие проводников с током используется в Международной системе для определения единицы сила тока –ампера.
Ампер –сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывал бы между этими проводниками силу магнитного взаимодействия, равную Н на каждый метр длины.
Сила, действующая на заряд, движущийся в магнитном поле — Студопедия
Каждуй проводник с током создает в окружающем пространстве магнитное поле. Электрический ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что любой движущийся в вакууме или среде заряд создает вокруг себя магнитное поле. В результате обобщения опытных данных был установлен закон, определяющий поле 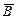 точечного заряда
точечного заряда 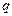 , свободно движущегося (т.е. с постоянной скоростью
, свободно движущегося (т.е. с постоянной скоростью  ):
):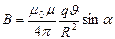 , где
, где 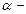 угол между
угол между  и радиус-вектором
и радиус-вектором  , проведенным от заряда к точке наблюдения. Получаем, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока:
, проведенным от заряда к точке наблюдения. Получаем, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока: 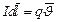 .
.
Данные закономерности справедливы лишь при малых скоростях 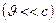 движущихся зарядов, когда электрическое поле свободно движущегося заряда можно считать электростатическим, т.е. создаваемым неподвижным зарядом, находящимся в той точке, где в данный момент времени расположен движущийся заряд.
движущихся зарядов, когда электрическое поле свободно движущегося заряда можно считать электростатическим, т.е. создаваемым неподвижным зарядом, находящимся в той точке, где в данный момент времени расположен движущийся заряд.
Из закона Ампера легко получить одно из фундаментальных физических соотношений: выражение для силы, действующей на движущуюся в магнитном поле заряженную частицу, — силы Лоренца. Пусти частицы с зарядом 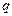 каждая движутся со скоростью
каждая движутся со скоростью  внутри провода сечением
внутри провода сечением 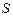 и длиной
и длиной 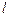 . Если
. Если 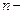 число свободных электронов в единице объема проводника (концентрация частиц), то сила тока
число свободных электронов в единице объема проводника (концентрация частиц), то сила тока 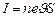 .
.
Сила Ампера 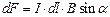 Для однородного прямолинейного проводника
Для однородного прямолинейного проводника 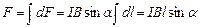 . С учетом того, что
. С учетом того, что  объем проводника, а
объем проводника, а 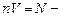 общее число зарядов, создающих ток, то
общее число зарядов, создающих ток, то 
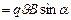 .
.
 Сила
Сила (сила Лоренца), действующая на заряд
(сила Лоренца), действующая на заряд 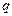 , движущийся со скоростью
, движущийся со скоростью 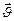 в магнитном поле с индукцией
в магнитном поле с индукцией 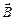 :
: 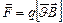 или
или  , где
, где 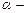 угол, образованный вектором скорости
угол, образованный вектором скорости  движения частицы и вектором
движения частицы и вектором 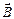 индукции магнитного поля.
индукции магнитного поля.

Впервые это выражение вывел нидерландский физик Хендрик Антон Лоренц. Формула замечательна тем, что ее нельзя объяснить без введения принципиально нового, невещественного объекта – поля. Ведь любая упругая среда передает возмущения от источника (магнита) к приемнику (заряженной частице) радиально. И действующая на приемник сила не может быть направлена столь странным для механики образом. Сила Лоренца направлена перпендикулярно векторам индукции магнитного поля и скорости частицы. В поле магнита, поднесенного к электронно-лучевой трубке, поток электронов смещается вниз.
Сила Лоренца изменяет только направление скорости, не изменяя ее модуля, т.е. работы не совершает и кинетическая энергия заряженной частицы при движении в магнитном поле не изменяется.
Задача 4. Электрон, ускоренный разностью потенциалов 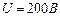 , движется параллельно прямолинейному длинному проводу на расстоянии
, движется параллельно прямолинейному длинному проводу на расстоянии  от него. Какая сила действует на электрон, если по проводнику пустить ток
от него. Какая сила действует на электрон, если по проводнику пустить ток  ?
?
Дано: Решение:
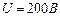


 ,
,
Индукция магнитного поля проводника с током равна 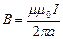 , получаем
, получаем 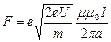 .
.
Ответ:
Задача 5. Электрон, ускоренный разностью потенциалов 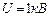 , влетел в однородное магнитное поле с индукцией
, влетел в однородное магнитное поле с индукцией 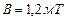 перпендикулярно к направлению линий поля. Определить радиус R, период вращения Т и момент импульса электрона.
перпендикулярно к направлению линий поля. Определить радиус R, период вращения Т и момент импульса электрона.
Дано: Решение:
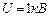
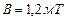
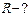 ,
, 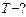 ,
,

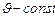 . Из механики известно, что постоянная сила, перпендикулярная к скорости, вызывает движение по окружности. Ускорение
. Из механики известно, что постоянная сила, перпендикулярная к скорости, вызывает движение по окружности. Ускорение  , где
, где 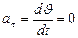 ,
, 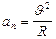 . Электрон будет двигаться с постоянным по модулю ускорением
. Электрон будет двигаться с постоянным по модулю ускорением  которое перпендикулярно скорости. Радиус кривизны траектории
которое перпендикулярно скорости. Радиус кривизны траектории 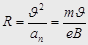 . Период обращения электрона не зависит от скорости:
. Период обращения электрона не зависит от скорости: 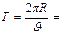
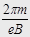 , Момент импульса электрона
, Момент импульса электрона  , но т.к. векторы
, но т.к. векторы 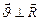 , то
, то 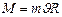 .
.
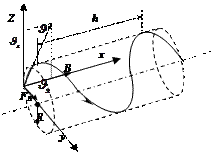
Задача 6. Электрон, обладающий скоростью 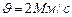 ., влетел в однородное магнитное поле с индукцией
., влетел в однородное магнитное поле с индукцией 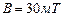 под углом
под углом 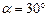 к направлению линий поля. Определить радиус R, период вращения Т и шаг h винтовой линии, по которой будет двигаться электрон.
к направлению линий поля. Определить радиус R, период вращения Т и шаг h винтовой линии, по которой будет двигаться электрон.
|
Дано: Решение:
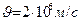
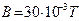
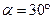
 ,
, 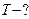 ,
,
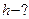
будет двигаться и вдоль поля со скоростью  :
: 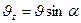 ,
, 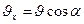 . В результате одновременного движения по окружности и по прямой электрон будет двигаться по винтовой линии. Т.к. сила Лоренца вызывает движение по окружности, то она является центростремительной силой
. В результате одновременного движения по окружности и по прямой электрон будет двигаться по винтовой линии. Т.к. сила Лоренца вызывает движение по окружности, то она является центростремительной силой 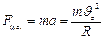
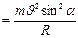 . Отсюда получаем
. Отсюда получаем 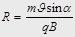 ,
,  . Период обращения электрона
. Период обращения электрона 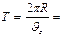
 ,
, 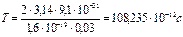 т.о. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду
т.о. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду  и магнитной индукцией поля, но не зависит от ее скорости (при
и магнитной индукцией поля, но не зависит от ее скорости (при 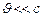 ). Шаг винтовой линии будет равен пути, пройденному электроном вдоль поля со скоростью
). Шаг винтовой линии будет равен пути, пройденному электроном вдоль поля со скоростью  за время, которое понадобится электрону для того, чтобы совершить один оборот:
за время, которое понадобится электрону для того, чтобы совершить один оборот: 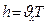
 .
. 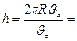
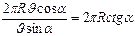
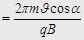 .
. 
Ответ:  ,
, 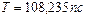 ,
,  .
.
Если на движущийся электрический заряд помимо магнитного поля с индукцией 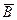 действует и электрическое поле с напряженностью
действует и электрическое поле с напряженностью 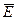 , то результирующая сила
, то результирующая сила 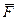 , приложенная к заряду, равна векторной сумме сил:
, приложенная к заряду, равна векторной сумме сил: 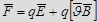 — формула Ленца.
— формула Ленца.
Разность потенциалов 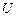 на концах проводника длиной
на концах проводника длиной 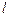 , движущегося в однородном магнитном поле со скоростью
, движущегося в однородном магнитном поле со скоростью 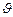 :
: 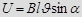 , где
, где 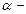 угол между направлением вектора скорости и вектора магнитной индукции.
угол между направлением вектора скорости и вектора магнитной индукции.
Эффект Холла: возникновение в металле (или полупроводнике) с током плотностью 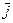 , помещенном в магнитное поле
, помещенном в магнитное поле 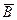 , электрического поля в направлении, перпендикулярном
, электрического поля в направлении, перпендикулярном 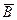 и
и 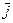 .
.

Это явление было обнаружено Холлом в 1879 г. и называется эффектом Холла или гальваномагнитнымявлением. Поместим металлическую пластину с током плотностью 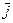 в магнитное поле
в магнитное поле 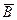 , перпендикулярное
, перпендикулярное 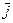 . Скорость носителей тока – электронов – направлена противоположно
. Скорость носителей тока – электронов – направлена противоположно 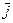 . Электроны испытывают действие силы Лоренца, которая направлена в данном случае вверх. У верхнего края пластинки возникнет повышенная концентрация электронов, а у нижнего – их недостаток. В результате между краями пластинки возникнет дополнительное поперечное электрическое поле, направленное снизу вверх. Когда напряженность
. Электроны испытывают действие силы Лоренца, которая направлена в данном случае вверх. У верхнего края пластинки возникнет повышенная концентрация электронов, а у нижнего – их недостаток. В результате между краями пластинки возникнет дополнительное поперечное электрическое поле, направленное снизу вверх. Когда напряженность  этого поперечного поля достигнет такой величины, что его действие на заряды будет уравновешивать силу Лоренца, то установится стационарное распределение зарядов в поперечном направлении. Тогда
этого поперечного поля достигнет такой величины, что его действие на заряды будет уравновешивать силу Лоренца, то установится стационарное распределение зарядов в поперечном направлении. Тогда 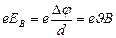 или
или 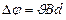 , где
, где 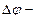 поперечная (холловская) разность потенциалов,
поперечная (холловская) разность потенциалов, 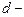 ширина пластинки. Т.к.
ширина пластинки. Т.к. 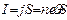 и
и 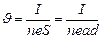 , т.е.
, т.е. 
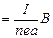 . Получаем, что поперечная разность потенциалов
. Получаем, что поперечная разность потенциалов 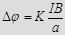 , где
, где 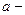 толщина пластины,
толщина пластины,  постоянная Холла, зависящая от вещества. Зная постоянную Холла и удельную проводимость материала
постоянная Холла, зависящая от вещества. Зная постоянную Холла и удельную проводимость материала  , можно найти подвижность носителей тока
, можно найти подвижность носителей тока 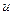 , определить концентрацию носителей тока, судить о природе проводимости полупроводников, т.к. знак постоянной Холла совпадает со знаком заряда носителей тока. Эффект Холла – наиболее эффективный метод изучения энергетического спектра носителей тока в металлах и полупроводниках. Он применяется так же для умножения постоянных токов в аналоговых вычислительных машинах, в измерительной технике (датчики Холла) и т.д.
, определить концентрацию носителей тока, судить о природе проводимости полупроводников, т.к. знак постоянной Холла совпадает со знаком заряда носителей тока. Эффект Холла – наиболее эффективный метод изучения энергетического спектра носителей тока в металлах и полупроводниках. Он применяется так же для умножения постоянных токов в аналоговых вычислительных машинах, в измерительной технике (датчики Холла) и т.д.
Закон полного тока.
Аналогично циркуляции вектора напряженности электростатического поля введем циркуляцию вектора магнитной индукции. Циркуляция вектора 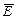 электростатического поля всегда равна нулю – электростатическое поле является потенциальным. Циркуляция вектора
электростатического поля всегда равна нулю – электростатическое поле является потенциальным. Циркуляция вектора 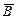 магнитного поля не равна нулю – вихревое поле, и зависит от выбора контура.
магнитного поля не равна нулю – вихревое поле, и зависит от выбора контура.
Рассмотрим магнитное поле бесконечного прямолинейного проводника с током  , находящегося в вакууме (см.рис.). Линии магнитной индукции представляют собой окружности, плоскости которых перпендикулярны проводнику, а центры лежат на его оси. Найдем циркуляцию вектора
, находящегося в вакууме (см.рис.). Линии магнитной индукции представляют собой окружности, плоскости которых перпендикулярны проводнику, а центры лежат на его оси. Найдем циркуляцию вектора 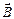 вдоль произвольной линии магнитной индукции – окружности радиуса
вдоль произвольной линии магнитной индукции – окружности радиуса 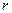 .
.

Опр. Циркуляцией вектора 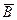 по заданному замкнутому контуру называется интеграл
по заданному замкнутому контуру называется интеграл 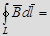

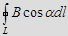 , где
, где 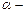 угол между
угол между 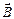 и
и 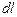 . Во всех точках линии индукции вектор
. Во всех точках линии индукции вектор 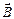 равен по модулю
равен по модулю 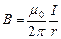 и направлен по касательной к этой линии, т.е.
и направлен по касательной к этой линии, т.е. 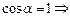
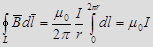 .
.
Получаем, что циркуляция вектора 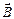 поля прямолинейного тока в вакууме одинакова вдоль всех линий магнитной индукции.
поля прямолинейного тока в вакууме одинакова вдоль всех линий магнитной индукции.
 Данная формула справедлива для замкнутого контура произвольной формы, охватывающего бесконечно длинный проводник с током
Данная формула справедлива для замкнутого контура произвольной формы, охватывающего бесконечно длинный проводник с током  . Доказать!
. Доказать!
Циркуляция вектора магнитной индукции поля прямолинейного проводника с током вдоль замкнутого контура, не охватывающего этот проводник, равна нулю. 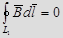 Доказать!
Доказать!
Соотношения (1) и (2) в вакууме универсальны. Они справедливы для магнитного поля проводника с током любой формы и размеров, а не только для поля бесконечного прямолинейного проводника с током. Доказать!
|
В общем случае магнитное поле может создавать целая система из 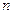 проводников с токами
проводников с токами 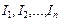 . Обозначим
. Обозначим 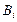 индукцию магнитного поля в вакууме одного
индукцию магнитного поля в вакууме одного  го проводника с током
го проводника с током 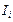 . Индукция результирующего магнитного поля, согласно принципу суперпозиции,
. Индукция результирующего магнитного поля, согласно принципу суперпозиции, 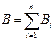 . Циркуляция вектора
. Циркуляция вектора  вдоль произвольного замкнутого контура
вдоль произвольного замкнутого контура  , проведенного в поле, равна
, проведенного в поле, равна 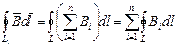 . Исходя из формул (1) и(2) получим:
. Исходя из формул (1) и(2) получим:  , следовательно,
, следовательно, 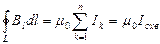 . В сумму входят только те токи, которые охватываются контуром
. В сумму входят только те токи, которые охватываются контуром  .
.
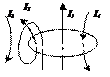
Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора 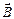 ):
): 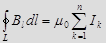 , где
, где  число проводников с токами, охватываемых контуром
число проводников с токами, охватываемых контуром  произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Закон справедлив только для поля в вакууме, т.к. для поля в веществе необходимо учитывать молекулярные токи.
произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Закон справедлив только для поля в вакууме, т.к. для поля в веществе необходимо учитывать молекулярные токи.
Напр., для системы токов, изображенной на рисунке: 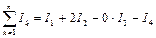 .
.
Теорема о циркуляции позволяет находить индукцию поля без применения закона Био – Савара – Лапласа.
Циркуляция вектора напряженности Н магнитного поля вдоль замкнутого контура, охватывающего ток I: 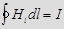 , где
, где 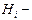 проекция вектора напряженности Н на направление касательной к контуру, содержащей элемент
проекция вектора напряженности Н на направление касательной к контуру, содержащей элемент 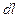 . Если контур охватывает n токов:
. Если контур охватывает n токов: 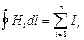 , где сумма – алгебраическая сумма токов, охватываемых контуром.
, где сумма – алгебраическая сумма токов, охватываемых контуром.
Замечание. Применение теоремы о циркуляции вектора магнитной индукции значительно упрощает расчеты симметричных магнитных полей. При этом важно, чтобы через точку, в которой требуется определить вектор 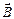 , можно было провести такой замкнутый контур
, можно было провести такой замкнутый контур  , совпадающий с линией индукции поля, для всех точек которого выполнялось соотношение
, совпадающий с линией индукции поля, для всех точек которого выполнялось соотношение 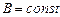 . В этом случае для всех элементов контура
. В этом случае для всех элементов контура 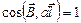 и уравнение приобретает простой вид:
и уравнение приобретает простой вид:  .
.
Магнитное поле соленоида и тороида.
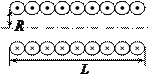
Соленоид – цилиндрическая катушка, состоящая из большого числа витков проволоки, образующих винтовую линию. Если витки расположены вплотную или очень близко друг к другу, то соленоид можно рассматривать как систему последовательно соединенных круговых токов одинакового радиуса с общей осью.
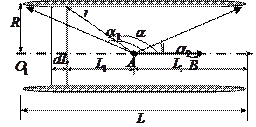
На рис. показано сечение соленоида радиуса 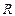 и длины
и длины  с током
с током  . Число витков соленоида
. Число витков соленоида  . Экспериментальное изучение магнитного поля соленоида показывает, что внутри соленоида поле является однородным, вне соленоида – неоднородным и очень слабым. Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь.
. Экспериментальное изучение магнитного поля соленоида показывает, что внутри соленоида поле является однородным, вне соленоида – неоднородным и очень слабым. Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь.
Магнитная индукция поля соленоида равна геометрической сумме магнитных индукций  полей всех витков этого соленоида. В произвольной точке А, лежащей на оси соленоида
полей всех витков этого соленоида. В произвольной точке А, лежащей на оси соленоида 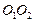 , все векторы
, все векторы  и результирующий вектор
и результирующий вектор  направлены по оси
направлены по оси 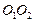 в ту сторону, куда перемещается буравчик с правой резьбой при вращении его рукояти в направлении электрического тока в витках соленоида. На малый участок соленоида длиной
в ту сторону, куда перемещается буравчик с правой резьбой при вращении его рукояти в направлении электрического тока в витках соленоида. На малый участок соленоида длиной 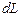 вдоль оси приходится
вдоль оси приходится 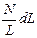 витков. Если
витков. Если 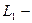 расстояние вдоль оси от этих витков до точки А, то магнитная индукция поля этих витков
расстояние вдоль оси от этих витков до точки А, то магнитная индукция поля этих витков 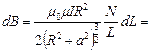
 , т.к.
, т.к. 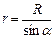 ,
, 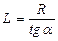 , то
, то 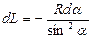 и
и 

 . В пределах соленоида угол
. В пределах соленоида угол 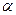 изменяется от
изменяется от 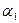 до
до 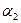 , поэтому
, поэтому 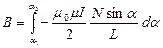
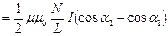 , где
, где  ,
,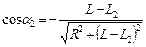 . В максимально, если
. В максимально, если 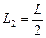 .
.
Магнитное поле длинного соленоида 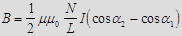 , где
, где  число витков на единицу длины соленоида,
число витков на единицу длины соленоида, и
и 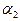 — углы, под которыми из точки А видны концы соленоида
— углы, под которыми из точки А видны концы соленоида 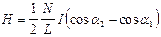 .
.
на оси в точке, удаленной от концов:  ,
, 
в точках оси, совпадающих с ее концами: 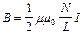 ,
, 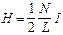 .
.
Для бесконечно длинного соленоида 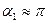
 , т.е.
, т.е. 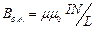
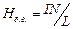
Магнитный момент соленоида равен геометрической сумме магнитных моментов всех его витков: 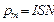 .
.
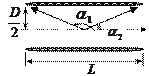
Задача 7. Каким должно быть отношение длины катушки к ее диаметру, чтобы магнитное поле в центре катушки можно было рассматривать как поле бесконечно длинного соленоида. Ошибка при таком допущении не должна превышать  . Указание:
. Указание: 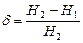 , где
, где 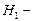 напряженность поля внутри катушки конечной длины и
напряженность поля внутри катушки конечной длины и 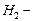 напряженность поля внутри бесконечно длинной катушки.
напряженность поля внутри бесконечно длинной катушки.
§ 4 учебника К.Ю. Богданова для 11 класса
§ 4. Действие магнитного поля на движущуюся заряженную частицу. Сила лоренца
На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца, равная произведению его индукции, заряда частицы, ее скорости и синуса угла между направлением скорости и вектором индукции.
Электрический ток представляет собой упорядоченное направленное движение заряженных частиц. Поэтому действие магнитного поля на проводник с током (сила Ампера) является результатом того, что это поле действует на движущиеся внутри проводника заряженные частицы. Силу, действующую на заряженную частицу в магнитном поле, называют силой Лоренца в честь голландского физика Х. Лоренца.
Найдём направление и модуль силы Лоренца FЛ с помощью закона Ампера (3.1). Пусть на прямолинейный участок проводника длиной L при силе тока в нем I, находящийся в однородном магнитном поле с индукцией В (рис.4а), действует сила Ампера FА. Если N – число заряженных частиц, упорядоченно движущихся на этом участке проводника, то, очевидно, что сила Лоренца, FЛ равна:
Найдём N, исходя из того, что сила тока I равна произведению заряда частицы q, их концентрации n, скорости их упорядоченного движения v и площади поперечного сечения проводника S:
I = qnvS. (4.2)
Так как , то из (4.2) получаем следующее выражение для N:
подставляя которое в (4.1) и учитывая формулу (3.1), получим формулу для FЛ:
Если заряд положительный, то для определения направления силы Лоренца можно пользоваться правилом левой руки (рис. 4б). На движущуюся отрицательно заряженную частицу сила Лоренца действует в противоположном направлении. Сила Лоренца не совершает работы, так как её вектор перпендикулярен вектору скорости движения частицы.
Сила Лоренца используется в электронно-лучевых трубках (ЭЛТ) телевизоров и мониторов, где магнитное поле позволяет отклонять электроны, летящие к экрану ЭЛТ.
Заряженная частица, влетая в однородном магнитном поле, направленное перпендикулярно вектору ее скорости, начинает равномерно двигаться по окружности радиуса r, а сила Лоренца в этом случае является центростремительной силой (рис. 4в). Радиус окружности движения частиц в магнитном поле можно узнать из соотношения:
где m – масса заряженной частицы. Как следует из (4.5), r зависит от массы частицы, и это используется в масс-спектрометрах – устройствах, где анализ движения заряженных частиц в магнитном поле позволяет измерять их массы. Частицы разных знаков, влетая в магнитное поле, поворачивают в разные стороны, что даёт возможность определить знак заряда частиц.
Если заряженная частица движется в магнитном поле так, что вектор скорости v составляет с вектором магнитной индукции B угол , то траекторией движения частицы является винтовая линия (рис. 4г). Поэтому заряженная частица, влетая в магнитное поле, продолжает свое движение вдоль линий индукции этого поля. Таким же образом магнитное поле Земли защищает нас и всё живое от потоков заряженных частиц космического пространства.
Вопросы для повторения:
· Как найти направление и модуль силы Лоренца?
· Как действует сила Лоренца на модуль скорости заряженной частицы?
· Опишите движение заряженной частицы в однородном магнитном поле, если её начальная скорость перпендикулярна линиям магнитной индукции.
Рис. 4. (а) – к вычислению силы Лоренца; (б) – определение направления силы Лоренца с помощью правила левой руки; движение по окружности (в) и винтовой линии (г) заряженной частицы в магнитном поле.
Сила Лоренца — Студопедия
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B,
может быть выражена через силы, действующие на отдельные носители заряда.
Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение nqυS, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику:
Выражение для силы Ампера можно записать в виде:
Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно nSΔl, то сила, действующая на одну заряженную частицу, равна
Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью 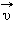 и вектором магнитной индукции
и вектором магнитной индукции 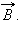 Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов
Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов 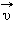 ,
, 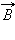 и
и 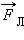 для положительно заряженной частицы показано на рис. 4.18.1.
для положительно заряженной частицы показано на рис. 4.18.1.
Сила Лоренца направлена перпендикулярно векторам 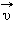 и
и 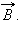
При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость 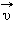 лежит в плоскости, перпендикулярной вектору
лежит в плоскости, перпендикулярной вектору 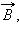 то частица будет двигаться по окружности радиуса
то частица будет двигаться по окружности радиуса
|
Сила Лоренца в этом случае играет роль центростремительной силы (рис. 4.18.2).

|
| Рисунок 4.18.2. Круговое движение заряженной частицы в однородном магнитном поле. |
Период обращения частицы в однородном магнитном поле равен
|
Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории R.
Угловая скорость движения заряженной частицы по круговой траектории
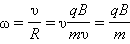
|
называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рис. 4.18.3.
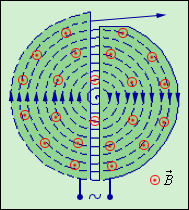
|
| Рисунок 4.18.3. Движение заряженных частиц в вакуумной камере циклотрона. |
Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное электрическое напряжение, частота которого равна циклотронной частоте. Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.
Однородные магнитные поля используются во многих приборах и, в частности, в масс-спектрометрах – устройствах, с помощью которых можно измерять массы заряженных частиц – ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов, то есть ядер атомов с одинаковым зарядом, но разными массами (например, 20Ne и 22Ne). Простейший масс-спектрометр показан на рис. 4.18.4. Ионы, вылетающие из источника S, проходят через несколько небольших отверстий, формирующих узкий пучок. Затем они попадают в селектор скоростей, в котором частицы движутся в скрещенных однородных электрическом и магнитном полях. Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Начальная скорость 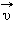 заряженных частиц направлена перпендикулярно векторам
заряженных частиц направлена перпендикулярно векторам 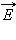 и
и 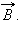
На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила 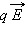 и магнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.
и магнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.
Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле 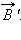 Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = mυ / qB’. Измеряя радиусы траекторий при известных значениях υ и B’ можно определить отношение q / m. В случае изотопов (q1 = q2) масс-спектрометр позволяет разделить частицы с разными массами.
Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = mυ / qB’. Измеряя радиусы траекторий при известных значениях υ и B’ можно определить отношение q / m. В случае изотопов (q1 = q2) масс-спектрометр позволяет разделить частицы с разными массами.
Современные масс-спектрометры позволяют измерять массы заряженных частиц с точностью выше 10–4.

|
| Рисунок 4.18.4. Селектор скоростей и масс-спектрометр. |
Если скорость частицы 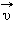 имеет составляющую
имеет составляющую 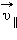 вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ┴ вектора
вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ┴ вектора 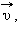 а шаг спирали p – от модуля продольной составляющей υ|| (рис. 4.18.5).
а шаг спирали p – от модуля продольной составляющей υ|| (рис. 4.18.5).
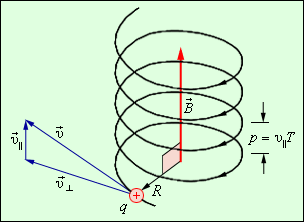
|
| Рисунок 4.18.5. Движение заряженной частицы по спирали в однородном магнитном поле. |
Таким образом, траектория заряженной частицы как бы навивается на линии магнитной индукции. Это явление используется в технике для магнитной термоизоляции высокотемпературной плазмы, то есть полностью ионизированного газа при температуре порядка 106 K. Вещество в таком состоянии получают в установках типа «Токамак» при изучении управляемых термоядерных реакций. Плазма не должна соприкасаться со стенками камеры. Термоизоляция достигается путем создания магнитного поля специальной конфиругации. В качестве примера на рис. 4.18.6 изображена траектория движения заряженной частицы в магнитной «бутылке»(или ловушке).

|
| Рисунок 4.18.6. Магнитная «бутылка». Заряженные частицы не выходят за пределы «бутылки». Магнитное поле «бутылки» может быть создано с помощью двух круглых катушек с током. |
Аналогичное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Быстрые заряженные частицы из космоса (главным образом от Солнца) «захватываются» магнитным полем Земли и образуют так называемые радиационные пояса (рис. 4.18.7), в которых частицы, как в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка 500 км до десятков земных радиусов. Следует вспомнить, что южный магнитный полюс Земли находится вблизи северного географического полюса (на северо-западе Гренландии). Природа земного магнетизма до сих пор не изучена.

|
| Рисунок 4.18.7. Радиационные пояса Земли. Быстрые заряженные частицы от Солнца (в основном электроны и протоны) попадают в магнитные ловушки радиационных поясов. Частицы могут покидать пояса в полярных областях и вторгаться в верхние слои атмосферы, вызывая полярные сияния. |
Движение заряженной частицы в магнитном поле — Формула и типы
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 11-12
- КОНКУРСНЫЙ ЭКЗАМЕН
- BNAT 000 NC
- 000 NC Книги
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- Книги NCERT для класса 11
- Книги NCERT для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT 9000 9000
- NCERT Exemplar Class
- Решения RS Aggarwal, класс 12
- Решения RS Aggarwal, класс 11
- Решения RS Aggarwal, класс 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- RD Sharma Class 6 Решения
- Решения RD Sharma Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- 000 NC Книги
- PHYSICS
- Механика
- Оптика
- Термодинамика Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора 0004
- 000300030004
- Простые числа
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Деление фракций
- BNAT 000 NC
- 000
- 000
- 000
- 000
- 000
- 000 Microology
- 000
- 000 Microology
- 000 BIOG3000
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 0003000 PBS4000
- 000300030002 Примеры калькуляторов химии Класс 6
- Образцы бумаги CBSE для класса 7
- Образцы бумаги CBSE для класса 8
- Образцы бумаги CBSE для класса 9
- Образцы бумаги CBSE для класса 10
- Образцы бумаги CBSE для класса 11
- Образцы бумаги CBSE чел для класса 12
- Классы
- CBSE Контрольный документ за предыдущий год
- CBSE Контрольный документ за предыдущий год Класс 10
- Контрольный документ за предыдущий год CBSE, класс 12
- HC Verma Solutions
- HC Verma Solutions Class 11 Physics
- Решения HC Verma, класс 12, физика
- Решения Лакмира Сингха
- Решения Лакмира Сингха, класс 9
- Решения Лакмира Сингха, класс 10
- Решения Лакмира Сингха, класс 8
- Заметки CBSE
- CBSE Notes
- Примечания CBSE класса 7
- Примечания CBSE класса 8
- Примечания CBSE класса 9
- Примечания CBSE класса 10
- Примечания CBSE класса 11
- Примечания CBSE класса 12
- Примечания к редакции
- CBSE Class
- Примечания к редакции класса 10 CBSE
- Примечания к редакции класса 11 CBSE 9000 4
- Примечания к редакции класса 12 CBSE
- Дополнительные вопросы CBSE
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке класса 9 CBSE
Дополнительные вопросы по математике для класса 10
- CBSE Class
- Дополнительные вопросы по науке, класс 10 по CBSE
- , класс 3
- , класс 4
- , класс 5
- , класс 6
- , класс 7
- , класс 8
- , класс 9 Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия Решения для биологии класса 11
- Решения NCERT для математики класса 11 9 0003 NCERT Solutions Class 11 Accountancy
- NCERT Solutions For Класс 12 по физике
- Решения NCERT для химии класса 12
- Решения NCERT для класса 12 по биологии
- Решения NCERT для класса 12 по математике
- Решения NCERT Класс 12 Бухгалтерия
- Решения NCERT, класс 12, бизнес-исследования
- Решения NCERT, класс 12 Экономика
- NCERT Solutions Class 12 Accountancy Part 1
- NCERT Solutions Class 12 Accountancy Part 2
- NCERT Solutions Class 12 Micro-Economics
- NCERT Solutions Class 12 Commerce
- NCERT Solutions Class 12 Macro-Economics
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для математики класса 6
- Решения NCERT для науки класса 6
- Решения NCERT для социальных наук класса 6
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для класса 7 Наука
- Решения NCERT для класса 7 по социальным наукам
- Решения NCERT для класса 7 Английский
- Решения NCERT для класса 8 Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для социальных наук 8 класса
- Решение NCERT ns для класса 8 Английский
- Решения NCERT для социальных наук класса 9
- Решения NCERT для математики класса 9 Глава 1
- Решения NCERT для Математика класса 9 Глава 2
- Решения NCERT для математики класса 9 Глава 3
- Решения NCERT для математики класса 9 Глава 4 Решения NCERT
- для математики класса 9 Глава 5
- Решения NCERT для математики класса 9 Глава 6
- Решения NCERT для Математика класса 9 Глава 7
- Решения NCERT для математики класса 9 Глава 8 Решения NCERT
- для математики класса 9 Глава 9 Решения NCERT
- для математики класса 9 Глава 10
- Решения NCERT для математики класса 9 Глава 11
- Решения NCERT для Математика класса 9 Глава 12
- Решения NCERT для математики класса 9 Глава 13 Решения
- NCERT для математики класса 9 Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки класса 9 Глава 1
- Решения NCERT для науки класса 9 Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для Науки Класса 9 Глава 4
- Решения NCERT для Науки Класса 9 Глава 5
- Решения NCERT для Науки Класса 9 Глава 6
- Решения NCERT для Науки Класса 9 Глава 7
- Решения NCERT для Класса 9 Наука Глава 8
- Решения NCERT для Науки Класса 9 Глава 9
- Решения NCERT для Науки Класса 9 Глава 10
- Решения NCERT для Науки Класса 9 Глава 12
- Решения NCERT для Науки Класса 9 Глава 11
- Решения NCERT для Класса 9 Наука Глава 13
- Решения NCERT для класса 9 Наука Глава 14
- Решения NCERT для класса 9 по науке Глава 15
- Решения NCERT для класса 10 по социальным наукам
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- Решения NCERT для математики класса 10 Глава 3
- Решения NCERT для математики класса 10 Глава 4
- Решения NCERT для математики класса 10 Глава 5
- Решения NCERT для математики класса 10 Глава 6
- Решения NCERT для математики класса 10 Глава 7
- Решения NCERT для математики класса 10 Глава 8
- Решения NCERT для математики класса 10 Глава 9 Решения NCERT
- для математики класса 10 Глава 10 Решения
- NCERT для математики класса 10 Глава 11
- Решения NCERT для математики класса 10 Глава 12
- Решения NCERT для математики класса 10 Глава 13
- NCERT Sol Решения NCERT для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки класса 10 Глава 1
- Решения NCERT для науки класса 10 Глава 2
- Решения NCERT для науки класса 10, глава 3
- Решения NCERT для науки класса 10, глава 4
- Решения NCERT для науки класса 10, глава 5
- Решения NCERT для науки класса 10, глава 6
- Решения NCERT для науки класса 10, глава 7
- Решения NCERT для науки 10 класса, глава 8
- Решения NCERT для науки класса 10 Глава 9
- Решения NCERT для науки класса 10 Глава 10
- Решения NCERT для науки класса 10 Глава 11
- Решения NCERT для науки класса 10 Глава 12
- Решения NCERT для науки 10 класса Глава 13
- Решения NCERT для науки 10 класса Глава 14
- Решения NCERT для науки 10 класса Глава 15
- Решения NCERT для науки 10 класса Глава 16
- Class 11 Commerce Syllabus
- ancy Account
- Программа бизнес-исследований 11 класса
- Учебная программа по экономике 11 класса
- Учебная программа по коммерции 12 класса
- Учебная программа по бухгалтерии 12 класса
- Учебная программа по бизнесу 12 класса
- Учебная программа по экономике
- 9000 9000
- Образцы документов по коммерции класса 11
- Образцы документов по коммерции класса 12
- TS Grewal Solutions
- TS Grewal Solutions Class 12 Accountancy
- TS Grewal Solutions Class 11 Accountancy
- Отчет о движении денежных средств
- Что такое Entry eurship
- Защита прав потребителей
- Что такое основной актив
- Что такое баланс
- Формат баланса
- Что такое акции
- Разница между продажами и маркетингом
- ICSE
- Документы
- ICSE
- Вопросы ICSE
- ML Aggarwal Solutions
- ML Aggarwal Solutions Class 10 Maths
- ML Aggarwal Solutions Class 9 Maths
- ML Aggarwal Solutions Class 8 Maths
- ML Aggarwal Solutions Class 7 Maths
- ML 6 Maths
- ML 6 Maths
- Selina Solutions
- Selina Solutions для класса 8
- Selina Solutions для Class 10
- Selina Solutions для Class 9
- Frank Solutions
- Frank Solutions для математики класса 10
- Frank Solutions для математики класса 9
- Класс ICSE 9000 2
- ICSE Class 6
- ICSE Class 7
- ICSE Class 8
- ICSE Class 9
- ICSE Class 10
- ISC Class 11
- ISC Class 12
- Exam
- IAS
- Civil
- Сервисный экзамен
- Программа UPSC
- Бесплатная подготовка к IAS
- Текущие события
- Список статей IAS
- Пробный тест IAS 2019
- Пробный тест IAS 2019 1
- Пробный тест IAS 2019 2
- Экзамен KPSC KAS
- Экзамен UPPSC PCS
- Экзамен MPSC
- Экзамен RPSC RAS
- TNPSC Group 1
- APPSC Group 1
- Экзамен BPSC
- WBPS3000 Экзамен 9000 MPC 9000 9000 MPC4000 Jam
- Ключ ответов UPSC 2019
- IA S Coaching Бангалор
- IAS Coaching Дели
- IAS Coaching Ченнаи
- IAS Coaching Хайдарабад
- IAS Coaching Мумбаи
- BYJU’SEE
- 9000 JEE 9000 Основной документ JEE 9000 JEE 9000
- Вопросник JEE
- Биномиальная теорема
- Статьи JEE
- Квадратичное уравнение
- Программа BYJU NEET
- NEET 2020
- NEET Приемлемость 9000 Критерии 9000 NEET4 9000 Пример 9000 NEET 9000 9000 NEET
- Поддержка
- Разрешение жалоб
- Служба поддержки клиентов
- Центр поддержки
- GSEB
- GSEB Syllabus
- GSEB4
- GSEB3 Образец статьи 004
- MSBSHSE
- MSBSHSE Syllabus
- MSBSHSE Учебники
- Образцы статей MSBSHSE
- Вопросники MSBSHSE
- AP Board
- APSCERT
- APS4
- Syll
- AP
- Syll 9000SC4
- Syll
- AP 9000S4 9000 Syll
- Syll
- MP Board
- MP Board Syllabus
- MP Board Образцы документов
- Учебники MP Board
- Assam Board
- Assam Board Syllabus
- Assam Board Учебники 9000 9000 Board4
- Assam Board Учебники 9000 Board4 BSEB
- Bihar Board Syllabus
- Bihar Board Учебники
- Bihar Board Question Papers
- Bihar Board Model Papers
- BSE Odisha
- Odisha Board Syllabus
- Odisha Board Syllabus
- Программа PSEB
- Учебники PSEB
- Вопросы PSEB
- RBSE
- Rajasthan Board Syllabus
- RBSE Учебники
- RBSE Question Papers
- HPBOSE
- HPBOSE 000 Syllab HPBOSE
000 HPBOSE - JKBOSE
- Программа JKBOSE
- Образцы документов JKBOSE
- Шаблон экзамена JKBOSE
- TN Board
- TN Board Syllabus
- TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 Paper 9000 Paper JAC
- Программа JAC
- Учебники JAC
- Вопросники JAC
- Telangana Board
- Telangana Board Syllabus
- Telangana Board Учебники
- Papers Telangana Board Учебники
- KSEEB Syllabus
- Типовые вопросы KSEEB
- KBPE
- KBPE Syllabus
- Учебники KBPE
- KBPE Вопросы
- 9000 UPMSP Board 9000 UPMSP Board2
- Совет по Западной Бенгалии
- Учебный план Совета по Западной Бенгалии
- Учебники по Совету по Западной Бенгалии
- Вопросы для Совета по Западной Бенгалии
- UBSE
- TBSE
- Гоа Совет
- 000
- NBSE000
- Mega Board
- Manipur Board
- Haryana Board
- Банковские экзамены
- Экзамены SBI
- Экзамены IBPS
- Экзамены RBI
- IBPS
03
- Экзамены SSC
9SC2 - SSC GD
- SSC CPO 900 04
- SSC CHSL
- SSC CGL
- Экзамены RRB
- RRB JE
- RRB NTPC
- RRB ALP
- O Экзамены на страхование
- LIC4
- LIC4
- UPSC CAPF
- Список статей государственных экзаменов
- Класс 1
- Класс 2
- Класс 3
- Вопросы по физике
- Вопросы по химии
- Вопросы по химии
- Вопросы
- Вопросы по науке
- Вопросы GK
магнетизм | Определение, примеры, физика и факты
Магнетизм , явление, связанное с магнитными полями, возникающими в результате движения электрических зарядов. Это движение может принимать разные формы. Это может быть электрический ток в проводнике или заряженные частицы, движущиеся в пространстве, или это может быть движение электрона по атомной орбитали. Магнетизм также связан с элементарными частицами, такими как электрон, которые обладают свойством, называемым спином.
Основы
В основе магнетизма лежат магнитные поля и их влияние на материю, как, например, отклонение движущихся зарядов и крутящих моментов на другие магнитные объекты.Свидетельством наличия магнитного поля является магнитная сила, действующая на заряды, движущиеся в этом поле; сила направлена под прямым углом как к полю, так и к скорости заряда. Эта сила отклоняет частицы, не меняя их скорости. Отклонение можно наблюдать в крутящем моменте стрелки компаса, который выравнивает стрелку с магнитным полем Земли. Игла представляет собой тонкий кусок железа, намагниченный, то есть небольшой стержневой магнит. Один конец магнита называется северным полюсом, а другой — южным.Сила между северным и южным полюсами притягательна, тогда как сила между такими же полюсами отталкивает. Магнитное поле иногда называют магнитной индукцией или плотностью магнитного потока; он всегда обозначается B . Магнитные поля измеряются в единицах тесла (Тл). (Другой единицей измерения, обычно используемой для B , является гаусс, хотя он больше не считается стандартной единицей измерения. Один гаусс равен 10 −4 тесла.)
Основным свойством магнитного поля является то, что его поток через любую замкнутую поверхность равен нулю.(Замкнутая поверхность — это поверхность, которая полностью окружает объем.) Математически это выражается как div B = 0 и может быть понято физически в терминах линий поля, представляющих B . Эти линии всегда замыкаются сами по себе, поэтому, если они входят в определенный объем в какой-то момент, они также должны покинуть этот объем. В этом отношении магнитное поле сильно отличается от электрического поля. Силовые линии электрического поля могут начинаться и заканчиваться на заряде, но, несмотря на многочисленные поиски так называемых магнитных монополей, не было найдено эквивалентного магнитного заряда.
Наиболее распространенным источником магнитных полей является электрическая петля. Это может быть электрический ток в круглом проводнике или движение вращающегося электрона в атоме. С обоими этими типами токовых петель связан магнитный дипольный момент, значение которого составляет i A , произведение тока i и площади контура A . Кроме того, электроны, протоны и нейтроны в атомах имеют магнитный дипольный момент, связанный с их собственным спином; такие магнитные дипольные моменты представляют собой еще один важный источник магнитных полей.Частицу с магнитным дипольным моментом часто называют магнитным диполем. (Магнитный диполь можно представить как крошечный стержневой магнит. Он имеет такое же магнитное поле, что и такой магнит, и ведет себя таким же образом во внешних магнитных полях.) При помещении во внешнее магнитное поле магнитный диполь может подвергаться воздействию крутящий момент, который стремится выровнять его с полем; если внешнее поле неоднородно, на диполь также может действовать сила.
Britannica Premium: удовлетворение растущих потребностей искателей знаний.Получите 30% подписки сегодня. Подпишись сейчасВсе вещества в той или иной степени проявляют магнитные свойства. При помещении в неоднородное поле материя либо притягивается, либо отталкивается в направлении градиента поля. Это свойство описывается магнитной восприимчивостью вещества и зависит от степени намагниченности вещества в поле. Намагниченность зависит от размера дипольных моментов атомов в веществе и степени выравнивания дипольных моментов относительно друг друга.Определенные материалы, такие как железо, демонстрируют очень сильные магнитные свойства из-за выравнивания магнитных моментов их атомов в определенных небольших областях, называемых доменами. В нормальных условиях различные домены имеют компенсирующие поля, но их можно выровнять друг с другом для создания чрезвычайно сильных магнитных полей. Различные сплавы, такие как NdFeB (сплав неодима, железа и бора), поддерживают выравнивание своих доменов и используются для изготовления постоянных магнитов. Сильное магнитное поле, создаваемое типичным магнитом из этого материала толщиной три миллиметра, сравнимо с электромагнитом, сделанным из медной петли, по которой проходит ток в несколько тысяч ампер.Для сравнения, ток в обычной лампочке составляет 0,5 ампера. Поскольку выравнивание доменов материала создает магнит, нарушение упорядоченного выравнивания разрушает магнитные свойства материала. Тепловое перемешивание, возникающее в результате нагрева магнита до высокой температуры, разрушает его магнитные свойства.
Магнитные поля сильно различаются по силе. Некоторые типичные значения приведены в таблице.
| Типичные магнитные поля | |
|---|---|
| внутри атомных ядер | 10 11 т |
| в сверхпроводящих соленоидах | 20 т |
| в циклотроне со сверхпроводящей катушкой | 5 т |
| возле небольшого керамического магнита | 0.1 т |
| Поле Земли на экваторе | 4 (10 −5 ) т |
| в межзвездном пространстве | 2 (10 −10 ) т |
Электромагнитная сила — Energy Education
Электромагнитная сила , также называемая силой Лоренца , объясняет, как взаимодействуют движущиеся и неподвижные заряженные частицы. Это называется электромагнитной силой, потому что она включает ранее отличавшуюся электрическую силу и магнитную силу; магнитные силы и электрические силы — это действительно одна и та же фундаментальная сила. [1] Электромагнитная сила — одна из четырех фундаментальных сил.
Электрическая сила действует между всеми заряженными частицами, независимо от того, движутся они или нет. [1] Магнитная сила действует между движущимися заряженными частицами. Это означает, что каждая заряженная частица излучает электрическое поле, независимо от того, движется она или нет. Движущиеся заряженные частицы (например, частицы электрического тока) излучают магнитные поля. Эйнштейн разработал свою теорию относительности, исходя из того, что если наблюдатель движется вместе с заряженными частицами, магнитные поля трансформируются в электрические и наоборот! Одним из частных случаев электромагнитной силы, когда все заряды являются точечными (или могут быть разбиты на точечные заряды), является закон Кулона.
Поскольку вычисление силы каждого отдельного заряда на каждый другой отдельный заряд смехотворно сложно, физики разработали инструменты для упрощения этих расчетов. Эти упрощенные вычисления превращаются в макроскопические повседневные явления, перечисленные ниже:
- повседневные силы нравятся
- большая часть химии
- удерживает атомы вместе
- химические связи между атомами с образованием молекул, как при горении
- сохраняет твердые частицы определенной формы
- Клейкие предметы, такие как клейкая лента или смола, прилипающие к поверхности
- Магниты для приклеивания картин к холодильнику
- Сила, действующая на электроны в проволочной петле вблизи изменяющегося магнитного поля.Электромагнитная сила очень тесно связана с электродвижущей силой, которая заставляет электрический ток течь.
Современная физика объединила электромагнитные и слабые взаимодействия в электрослабую силу. Полное понимание электромагнитной силы и всех последствий электромагнетизма требует многих лет изучения. Некоторые хорошие места для получения дополнительной информации об электромагнетизме включают гиперфизику.
Ниже представлены серии Scishow по фундаментальным силам, часть 4a (электричество) и 4b (магнетизм):
А вот и часть 2.
В других видео рассматривается сильное ядерное взаимодействие, слабое ядерное взаимодействие и гравитация. Посетите их канал на YouTube, чтобы увидеть больше подобных видео! (прекрасный ресурс для любопытных).
Для дальнейшего чтения
Для получения дополнительной информации см. Соответствующие страницы ниже:
Список литературы
- ↑ 1.0 1.1 Р. Д. Найт, «Закон силы Лоренца» в книге Физика для ученых и инженеров: стратегический подход, 3-е изд.Сан-Франциско, США: Pearson Addison-Wesley, 2008, глава 35, раздел 5, стр. 1096-1097.


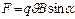 . Т.к. сила Лоренца всегда перпендикулярна к скорости, то величина скорости не будет изменяться под действием этой силы. Но при постоянной скорости величина силы тоже будет постоянной. Из механики известно, что постоянная сила, перпендикулярная к скорости, вызывает движение по окружности. Следовательно, электрон, влетевший в магнитное поле, будет двигаться по окружности в плоскости, перпендикулярной полю, со скоростью, равной поперечной составляющей
. Т.к. сила Лоренца всегда перпендикулярна к скорости, то величина скорости не будет изменяться под действием этой силы. Но при постоянной скорости величина силы тоже будет постоянной. Из механики известно, что постоянная сила, перпендикулярная к скорости, вызывает движение по окружности. Следовательно, электрон, влетевший в магнитное поле, будет двигаться по окружности в плоскости, перпендикулярной полю, со скоростью, равной поперечной составляющей  скорости; одновременно он
скорости; одновременно он  охватывает ток
охватывает ток 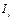 ) (
) (