Действие магнитного поля на движущийся электрический заряд 11 класс онлайн-подготовка на Ростелеком Лицей
«Модели эфиров»
Если бы Андре Мари Ампер (рис. 1) знал о действии электрического тока, то продвинулся бы гораздо дальше в своих открытиях.
Рис. 1. Андри Мари Ампер (Источник)
Как и многие ученые того периода, Ампер придерживался «модели эфира»: электрический ток – эфир, некая жидкость, которая протекает по проводникам. Именно отсюда и сам термин «электрический ток» – то, что течет. Только в самом конце XIX века – начале ХХ модели эфиров стали отходить, а на смену им стали появляться новые модели, адекватнее отражающие наблюдаемые явления. В частности, были открыты катодные лучи, была выявлена радиоактивность, проведены исследования Фарадея по электролизу – все это наводило на мысль о существовании заряженных частиц, которые как-то движутся.
Электронная модель Хендрика Лоренца
Ученый Хендрик Лоренц (рис. 2) предложил так называемую «электронную модель» металлов.
2) предложил так называемую «электронную модель» металлов.
Рис. 2. Хендрик Лоренц (Источник)
При образовании кристаллической решетки металлов от каждого атома металла отрывается по одному внешнему электрону, таким образом, в узлах кристаллической решетки находятся положительные ионы, а в объеме этой решетки почти свободно могут двигаться электроны (рис. 3).
Рис. 3. Кристаллическая решетка
Модель, предложенная Лоренцом, была хороша хотя бы тем, что достаточно легко объясняла возникновение электрического тока в металлах. При обычных условиях эти электроны находятся в беспорядочном движении вокруг кристаллической решетки. И только при подаче разности потенциалов на конце проводника, когда внутри проводника появляется электрическое поле, кроме этой хаотической составляющей появляется другая – упорядоченная составляющая, или направленное движение. Именно это движение, согласно модели Лоренца, представляет собой электрический ток.
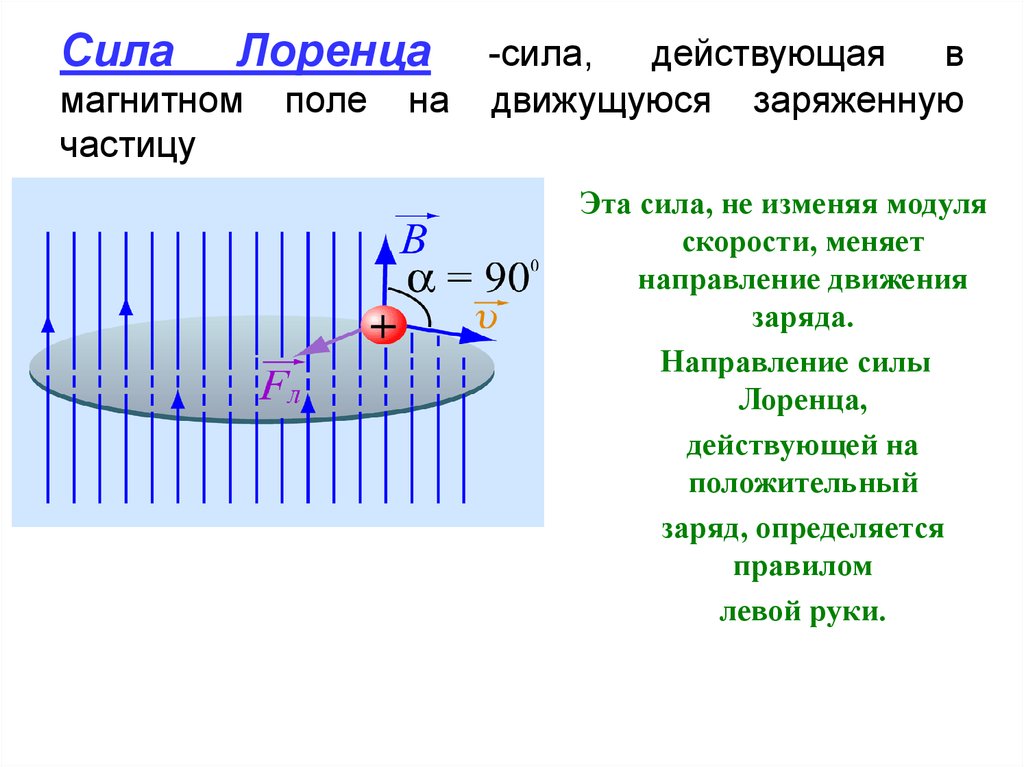
Вы знаете, что стороны магнитного поля (B) на проводник с током (I) действует сила Ампера (F), перпендикулярная направлению тока и направлению линий магнитного поля (рис. 4).
4).
Рис. 4. Направление силы Ампера
«Если электрический ток представляет собой направленное движение зарядов, то не будет ли со стороны магнитного поля действовать такая же сила на сами заряды?» – примерно так рассуждал Лоренц. В выражение для силы Ампера вместо силы тока подставим определение силы тока – отношение перенесенного заряда в проводнике ко времени, за которое было осуществлено данное перенесение:
Также заметим, что отношение элемента длины проводника к интервалу времени – скорость движения заряда:
Тогда выражение принимает вид:
Модуль силы равен произведению величины магнитной индукции поля на количество переносимого через проводник заряда на скорость частиц, которые переносят заряд и на синус угла между направлением движения заряда и направлением вектора магнитной индукции.
Учтем, что носителями электрического тока в проводнике являются электроны, величина зарядов которых одинакова. Поэтому можно записать, что совокупный заряд, переносимый через поперечное сечение проводника, – произведение заряда электрона q на количество электронов N, переносимых через поперечное сечение проводника.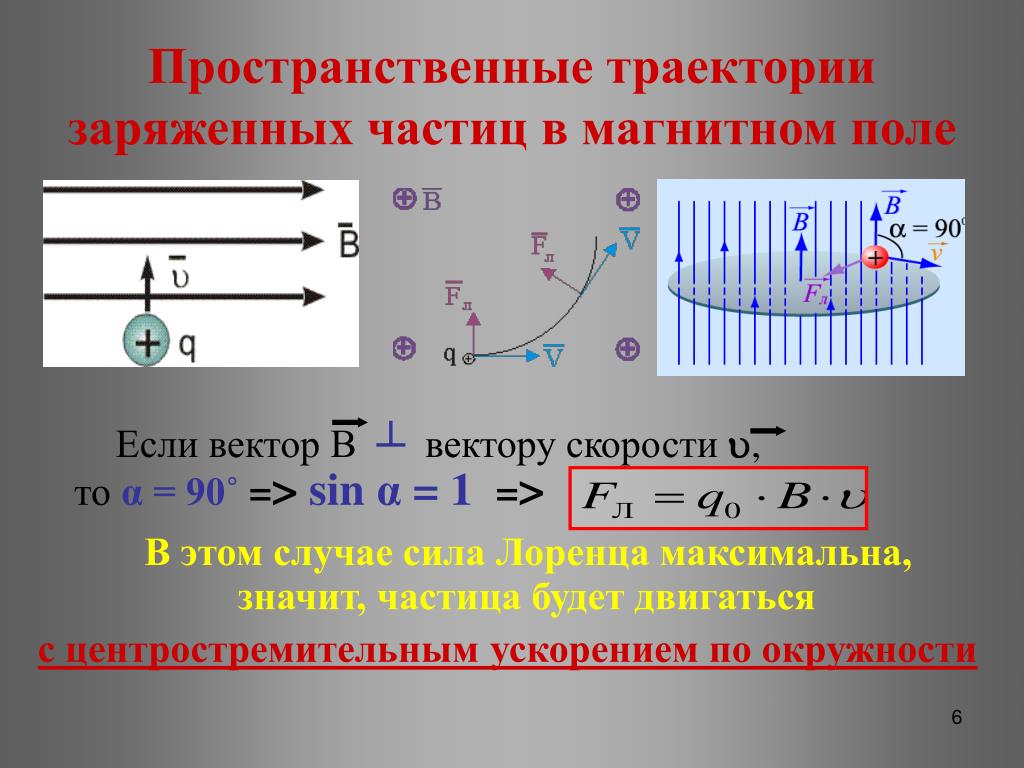
Тогда:
Вывод приведенной формулы был сугубо формальным, однако даже такой вывод позволял предположить, что не только на проводник с током, но и на отдельный заряд в магнитном поле будет действовать сила со стороны этого поля. Предположим, что число зарядов равно единице и этот заряд движется не внутри кристаллической решетки, а в свободном пространстве. Возникает вопрос: что произойдет с этим зарядом, если он войдет в область, где существует однородное магнитное поле? Согласно нашей гипотезе, на частицу, движущуюся в однородном магнитном поле, должна действовать сила, которая перпендикулярна скорости этой частицы (поскольку именно так будет направлен электрический ток, связанный с движением этих частиц) и перпендикулярна линиям магнитного поля (рис. 5).
Рис. 5. Направление действия силы на движущийся заряд
Величина этой силы будет определяться так:
Проверка гипотезы Лоренца. Принцип работы электронно-лучевой трубки
Открытие катодных лучей, а также радиоактивности позволили проверить экспериментально гипотезу Лоренца. Воспользуемся электронно-лучевой трубкой.
Воспользуемся электронно-лучевой трубкой.
В вакуумной трубке размещены две пластины: анод и катод. На катод подается отрицательный потенциал, на анод – положительный. Для того чтобы в трубке возникли свободные электроны, катод нагревается нитью накала. Свободные электроны металлического катода вблизи его поверхности могут покидать эту поверхность, обладая высокой кинетической энергией за счет нагревания – явление термоэлектронной эмиссии. Свободные электроны, покинувшие поверхность катода, попадают в зону действия электрического поля между анодом и катодом. Линии напряженности этого поля направлены от анода к катоду (изображены белыми стрелками). Электроны, будучи отрицательно заряженными частицами, движутся от катода к аноду – против линии напряженности поля (направление движения изображено красными стрелками). Так, в трубке возникает электрический ток, направленный от анода к катоду (рис. 6).
Рис. 6. Электронно-лучевая трубка
Если использовать экран, покрытый специальным материалом, который светится при попадании на него заряженных частиц, можно пронаблюдать место попадания электронов по световому пятну.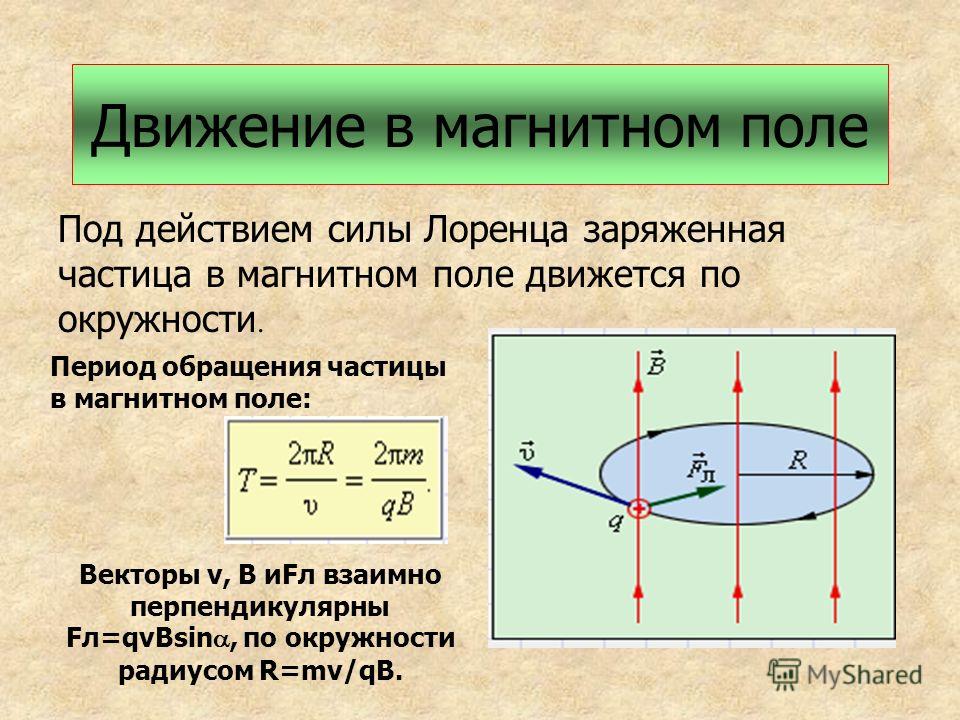 Именно так и работает электронно-лучевая трубка. При подаче напряжения на анод и катод мы видим небольшое зеленое пятно на экране – это место бомбардировки экрана электронами (рис. 7).
Именно так и работает электронно-лучевая трубка. При подаче напряжения на анод и катод мы видим небольшое зеленое пятно на экране – это место бомбардировки экрана электронами (рис. 7).
Рис. 7. Работа электронно-лучевой трубки
Опыты с осциллографом
Воспользуемся осциллографом. Для удобства будем следить не за световым пятном, а за светящейся линией (рис. 8).
Рис. 8. Светящаяся линия на экране осциллографа
Когда одним из полюсов подводят к горизонтальной линии, находящейся на осциллографе, она отклоняется от своего первоначального значения в направлении, перпендикулярном направлению скорости и направлению линий магнитного поля, поскольку магнитное поле направлено от северного полюса к южному. Это на качественном уровне подтверждает гипотезу (рис. 9).
Рис. 9. Отклонения электронов в электронно-лучевой трубке
Попытаемся получить не только качественные, но и количественные результаты. Для этого будем проверять зависимость силы, действующей со стороны магнитного поля, от различных факторов. В частности, от скорости движения электронов. Каким образом можно поменять скорость движения электронов в осциллографе? При помощи регулировки яркости линии на осциллографе можно изменить скорость движения электронов в осциллографе. Чем ярче линия, тем быстрее движутся электроны внутри трубки. Если поднести магнит к осциллографу северным полюсом и менять скорость движения электронов, то по мере уменьшения яркости искажение линии также будет уменьшаться (рис. 10). Это означает, что сила, действующая со стороны магнитного поля на электроны, при уменьшении скорости электронов тоже уменьшается. Более точные измерения дадут нам прямую пропорциональность между силой, действующей со стороны магнитного поля на движущиеся заряды, и скоростью этих зарядов.
Для этого будем проверять зависимость силы, действующей со стороны магнитного поля, от различных факторов. В частности, от скорости движения электронов. Каким образом можно поменять скорость движения электронов в осциллографе? При помощи регулировки яркости линии на осциллографе можно изменить скорость движения электронов в осциллографе. Чем ярче линия, тем быстрее движутся электроны внутри трубки. Если поднести магнит к осциллографу северным полюсом и менять скорость движения электронов, то по мере уменьшения яркости искажение линии также будет уменьшаться (рис. 10). Это означает, что сила, действующая со стороны магнитного поля на электроны, при уменьшении скорости электронов тоже уменьшается. Более точные измерения дадут нам прямую пропорциональность между силой, действующей со стороны магнитного поля на движущиеся заряды, и скоростью этих зарядов.
Рис. 10. При уменьшении яркости искажение линии уменьшается
Сила, действующая на заряды со стороны магнитного поля, пропорциональна индукции – если поднести несколько магнитов к осциллографу, то искажение будет гораздо сильнее.
Рис. 11. При усилении магнитного поля искажение линии увеличивается
Величина силы действующей со стороны магнитного поля на движущийся заряд зависит от взаимного направления вектора магнитной индукции и вектора скорости движения частиц. При поднесении магнитов к осциллографу южным полюсом линия будет искажаться в противоположном направлении.
Рис. 12. При поднесении магнитов южным полюсом линия искажается в противоположном направлении
Сила Лоренца
Обобщим выводы из проделанных экспериментов. На движущийся в магнитном поле заряд (q) со стороны магнитного поля действует сила (F), направление которой зависит от взаимного направления вектора скорости движения (v) заряда и вектора магнитной индукции поля (В). Величина силы пропорциональна скорости движения заряда и модулю магнитной индукции. Направление силы определяется по правилу «левой руки».
Таким образом, полученное ранее выражение для силы описывает взаимодействие магнитного поля с движущимся в этом поле электрическим зарядом. Открытие силы действия магнитного поля на движущийся в нем заряд стало возможным только благодаря улучшению представлений о строении вещества, электрическом токе в металлах, движении заряженных частиц. И огромную роль во всех этих задачах сыграл Лоренц, поэтому открытая сила и получила название сила Лоренца.
Открытие силы действия магнитного поля на движущийся в нем заряд стало возможным только благодаря улучшению представлений о строении вещества, электрическом токе в металлах, движении заряженных частиц. И огромную роль во всех этих задачах сыграл Лоренц, поэтому открытая сила и получила название сила Лоренца.
Формулы, описывающие движение заряженной частицы в магнитном поле
Сделаем еще несколько замечаний.
1. Вектор силы Лоренца перпендикулярен вектору скорости:
2. Если сила перпендикулярна вектору скорости, то она называется центростремительной. Под ее действием тело движется по окружности. Следовательно, сила Лоренца – центростремительная сила.
3. Под действием силы Лоренца заряд движется по дуге окружности, следовательно, он обладает центростремительным ускорением. Центростремительное ускорение может быть рассчитано как квадрат скорости движения, деленный на радиус окружности, который описывает тело:
4. Согласно второму закону Ньютона, сила может быть определена как произведение массы тела на приобретаемое им ускорение:
Согласно второму закону Ньютона, сила может быть определена как произведение массы тела на приобретаемое им ускорение:
Подставив выражения для силы Лоренца, получим:
Подставим выражение для центростремительного ускорения:
(1.14)
После сокращения скорости получим следующие соотношения:
Список литературы
- Касьянов В. А. Физика 11 кл.: Учебн. для общеобразоват. учреждений. 4-е изд., стереотип. – М.: Дрофа, 2004. – 416 с.: ил., 8 л. цв. вкл.
- Степанова Г. Н. Физика 11. – М.: Русское слово.
- Пурышева Н. С., Важеевская Н. Е., Исаев Д. А., Чаругин В. М. Физика 11. – М.: Дрофа.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «fizika.in» (Источник)
- Интернет-портал «Классная физика» (Источник)
- Интернет-портал «balancer.ru» (Источник)
Домашнее задание
- Касьянов В.
 А. Физика 11 кл.: Учебн. для общеобразоват. учреждений. 4-е изд., стереотип. – М.: Дрофа, 2004. – 416с.: ил., 8 л. цв. вкл., ст. 85, в. 5, з. 2–4.
А. Физика 11 кл.: Учебн. для общеобразоват. учреждений. 4-е изд., стереотип. – М.: Дрофа, 2004. – 416с.: ил., 8 л. цв. вкл., ст. 85, в. 5, з. 2–4. - Какая сила действует на протон, который движется со скоростью 2 ∙ 106 м/с в однородном магнитном поле с индукцией 0,1 Тл? Протон движется под углом 60° по отношению к линиям магнитной индукции поля.
- На рис. 13 и 14 схематически показаны разные случаи взаимодействия заряженной частицы, которая движется, и магнитного поля. Сформулируйте задачу в каждом случае и решите ее.
| Рис. 13 | Рис. 14 |
4. * Электрон, который влетел в однородное магнитное поле под углом 60° по отношению к линиям магнитной индукции, двигается по винтовой линии радиусом 2 см, делая один оборот за 30 нс. Определите магнитную индукцию поля и шаг винтовой линии.
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.
 1 Электростатика
1 Электростатика - 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 4.
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.

- 6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см.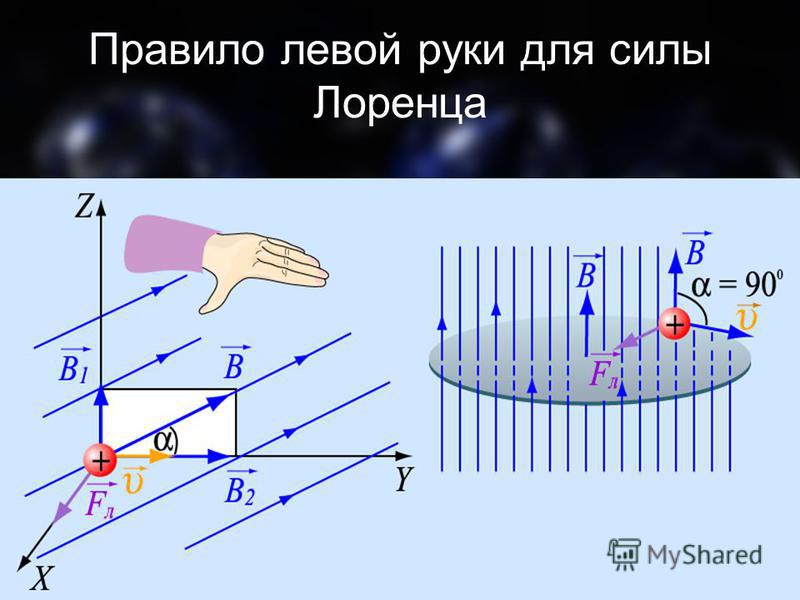 справку), обсуждать уже созданные.
справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Действие магнитного поля на движущийся заряд. Сила Лоренца.
Урок 4. Действие магнитного поля на движущийся заряд. Сила Лоренца.
Цель урока: изучить новое физическое явление – действие магнитного поля на движущийся заряд, вывести формулу и ввести мнемоническое правило для определения модуля и направления силы Лоренца, показать возможность применения знаний для расчёта периода обращения частицы в магнитном поле, познакомить учащихся с практическим применением действия силы Лоренца в ускорителях.
Задачи:
Образовательные: изучить поведение движущихся электрических зарядов в магнитном поле;
вывести формулу и правило для определения модуля и направления силы Лоренца.
Развивающие: развитие практических навыков рассчитывать силу Лоренца, определять ее направление.
Воспитательные: привитие наблюдательности, внимания.
Тип урока: комбинированный урок
План:
1) Организационный момент. Актуализация знаний.
2) Изучение нового материала.
3) Закрепление изученного. Итог урока.
Ход урока:
1)Организационный момент.
Объявление темы и цели урока.
Вопросы для повторения:
1. Почему магнитные силы, действующие на проводники катушки прибора, не зависят от угла поворота катушки?
2. Что удерживает рамку от вращения в магнитном поле?
3. Чем амперметр отличается от вольтметра?
4. Укажите направление вектора магнитной индукции, электрического тока и силы Ампера на схеме громкоговорителя (см. рис. 1.22).
Укажите направление вектора магнитной индукции, электрического тока и силы Ампера на схеме громкоговорителя (см. рис. 1.22).
2)Изучение нового материала
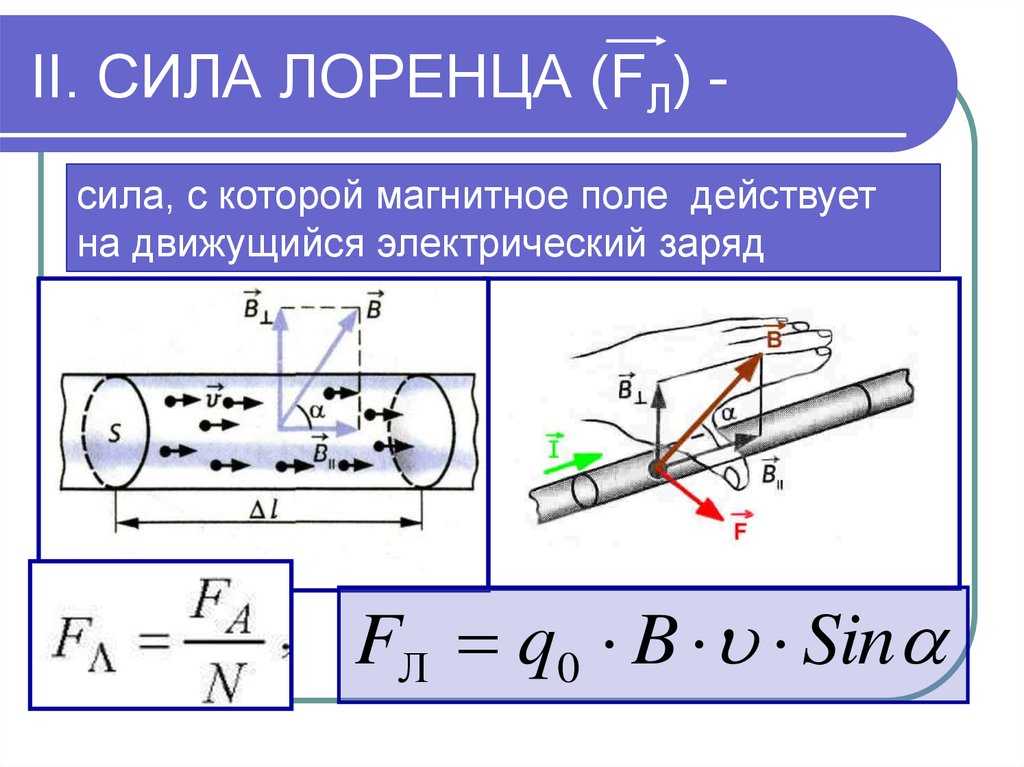
Электрический ток — это упорядоченно движущиеся заряженные частицы. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника. Найдем силу, действующую на одну частицу.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика X. Лоренца (1853— 1928) — основателя электронной теории строения вещества. Силу Лоренца можно найти с помощью закона Ампера.
Модуль силы Лоренца
Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:
Рассмотрим отрезок тонкого прямого проводника с током (рис. 1.23). Пусть длина отрезка δl и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля можно считать одинаковым в пределах этого отрезка проводника. Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения υ следующей формулой:
1.23). Пусть длина отрезка δl и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля можно считать одинаковым в пределах этого отрезка проводника. Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения υ следующей формулой:
I = qnυS. (1.4)
Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен:
F = |I| BΔl sin α.
Подставляя в эту формулу выражение (1.4) для силы тока, получаем:
F = |q| nυS&ΔlB sin α = υ|q| NB sin α,
где N = nSΔl — число заряженных частиц в рассматриваемом объеме. Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:
где α — угол между вектором скорости и вектором магнитной индукции.
Сила Лоренца перпендикулярна векторам и . Ее направление определяется с помощью того же правила левой руки, что и направление силы Ампера: если левую руку расположить так, чтобы составляющая магнитной индукции , перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° большой палец укажет направление действующей на заряд силы Лоренца Fл (рис. 1.24).
Электрическое поле действует на заряд q с силой Fэл = q . Следовательно, если есть и электрическое поле, и магнитное поле, то суммарная сила , действующая на заряд, равна:
= ал + л
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работы. Согласно теореме о кинетической энергии (см. учебник физики для 10 класса) это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.
Под действием силы Лоренца меняется лишь направление скорости частицы.
Движение заряженной частицы в однородном магнитном поле. Рассмотрим движение частицы с зарядом q в однородном магнитном поле , направленном перпендикулярно к начальной скорости частицы (рис. 1.25).
Сила Лоренца зависит от модулей векторов скорости частицы и индукции магнитного поля. Так как магнитное поле не меняет модуль скорости движущейся частицы, то остается неизменным и модуль силы Лоренца. Эта сила перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы. Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что частица равномерно движется по окружности радиусом r. Определим этот радиус.
Согласно второму закону Ньютона (см. рис. 1.25)
Время, за которое частица делает полный оборот (период обращения), равно:
Использование действия магнитного поля на движущийся заряд
Действие магнитного поля на движущийся заряд широко используют в современной технике.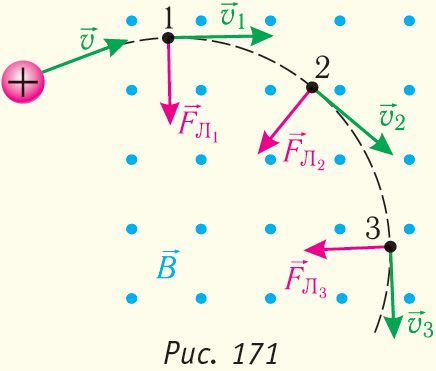 Достаточно упомянуть телевизионные трубки (кинескопы), в которых летящие к экрану электроны отклоняются с помощью магнитного поля, создаваемого особыми катушками.
Достаточно упомянуть телевизионные трубки (кинескопы), в которых летящие к экрану электроны отклоняются с помощью магнитного поля, создаваемого особыми катушками.
Сила Лоренца используется в ускорителе заряженных частиц (циклотрон) для получения частиц с большими энергиями. Циклотрон состоит из двух полых полуцилиндров (дуантов) 3, находящихся в однородном магнитном поле (рис. 1.26). Между дуантами создается переменное электрическое поле. Согласно формуле (1.6) при увеличении скорости частицы 1 радиус окружности (траектории 2), по которой движется частица, увеличивается. Период обращения частицы не зависит от скорости (см. формулу (1.7)), и, следовательно, через полпериода, вследствие изменения направления электрического поля, частица снова оказывается в ускоряющем ее поле и т. д. На последнем витке частица вылетает из циклотрона.
На действии магнитного поля основано также и устройство приборов, позволяющих разделять заряженные частицы по их удельным зарядам, т. е. по отношению заряда частицы к ее массе, и по полученным результатам точно определять массы частиц. Такие приборы получили название масс-спектрографов.
е. по отношению заряда частицы к ее массе, и по полученным результатам точно определять массы частиц. Такие приборы получили название масс-спектрографов.
На рисунке 1.27 изображена принципиальная схема простейшего масс-спектрографа. Вакуумная камера прибора помещена в магнитное поле (вектор индукции перпендикулярен рисунку). Ускоренные электрическим полем заряженные частицы (электроны или ионы), описав дугу, попадают на фотопластинку, где оставляют след, позволяющий с высокой точностью измерить радиус траектории r. По этому радиусу определяется удельный заряд иона. Зная заряд иона, легко вычислить его массу.
На движущуюся заряженную частицу со стороны магнитного поля действует сила Лоренца. Эта сила перпендикулярна скорости и не совершает работы.
3) Закрепление изученного. Итог урока.
Домашнее задание. §6 вопросы
1. Чему равен модуль силы Лоренца?
2. Как движется заряженная частица в однородном магнитном поле, если начальная скорость частицы перпендикулярна линиям магнитной индукции?
3. Как определить направление силы Лоренца?
Как определить направление силы Лоренца?
Движение заряженных частиц в магнитном поле. Сила Лоренца. Школьный курс физики
Главная | Физика 11 класс | Движение заряженных частиц в магнитном поле
Сила Лоренца.
Значительный интерес представляет движение заряженных частиц в области пространства, где одновременно имеются электрическое и магнитное поля. Для этого случая Лоренц получил выражение для силы, которую в честь него называют силой Лоренца. Она представляет собой сумму сил, действующих на заряженную частицу, которая движется в электрическом и магнитном полях.
Пусть заряженная частица с зарядом q движется со скоростью в однородном магнитном поле с индукцией и в однородном электрическом поле с напряжённостью . Электрическое поле действует на заряд
q с силой, модуль которой равен Fэ = qE.
Её модуль можно найти с помощью закона Ампера. Предположим, что проводник с током находится в однородном магнитном поле. Вдоль проводника движутся заряженные частицы. Рассмотрим отрезок проводника длиной Δl и площадью поперечного сечения S (рис. 3.38).
Рис. 3.38
На него со стороны магнитного поля действует сила Ампера. В § 1 «Условия существования электрического тока. Электрический ток в проводниках»
I = qnυS.
Подставив это выражение в формулу для модуля силы Ампера FA = BIΔlsin α, получим
FA = BqnvSΔlsin α,
где N = nSΔl — число заряженных частиц в рассматриваемом объёме SΔl. Магнитная составляющая силы Лоренца равна по модулю
Магнитная составляющая силы Лоренца равна по модулю
где α — угол между векторами и .
Магнитная составляющая силы Лоренца всегда перпендикулярна плоскости, в которой располагаются вектор скорости заряженной частицы и вектор индукции магнитного поля.
В силу того что данная сила перпендикулярна скорости частицы, она не совершает работы.
Следовательно, если есть и электрическое поле, и магнитное, то полная сила , действующая на движущуюся частицу, равна
= э + л.
Для определения направления магнитной составляющей силы Лоренца используют правило левой руки.
Если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца показывали направление скорости движения положительно заряженной частицы, то отогнутый (в плоскости ладони) на 90° большой палец покажет направление действующей на заряженную частицу магнитной составляющей силы Лоренца.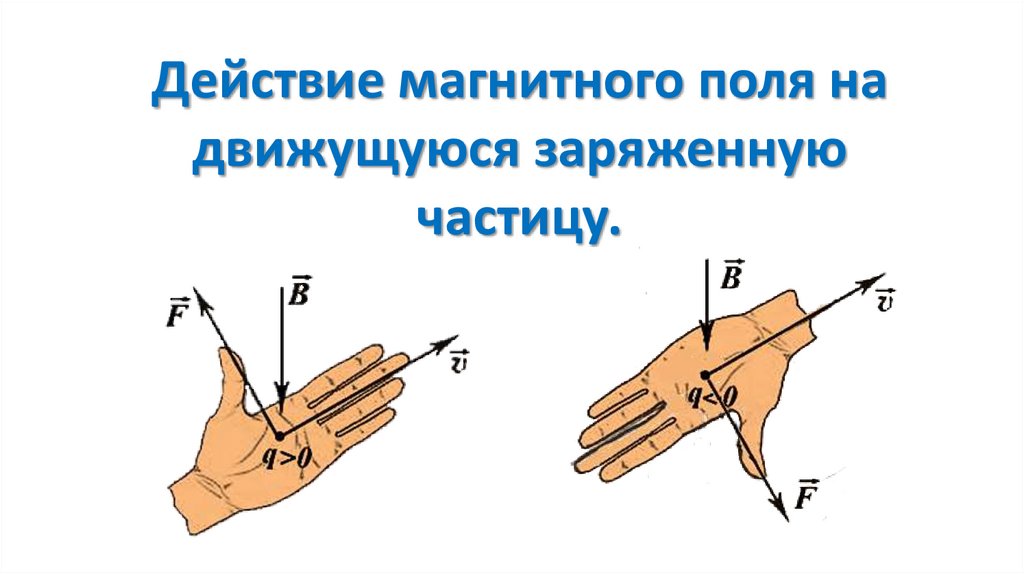
Если в магнитном поле движутся отрицательно заряженные частицы, то пальцы левой руки следует располагать противоположно направлению вектора скорости. Для иллюстрации применения правила левой руки приведём рисунок 3.39.
Рис. 3.39
На нём штриховыми линиями указаны траектории движения зарядов (на рис. 3.39, а — положительного заряда, на рис. 3.39, б — отрицательного заряда).
Движение заряженной частицы в однородном магнитном поле.
Рассмотрим наиболее простой случай движения заряженной частицы в магнитном поле — это движение в однородном магнитном поле с индукцией, перпендикулярной начальной скорости частицы (рис. 3.40).
Рис. 3.40
Так как магнитное поле не изменяет модуля скорости заряженной частицы, то остаётся неизменным и модуль магнитной составляющей силы Лоренца. Поскольку эта сила перпендикулярна скорости, то частица движется с центростремительным ускорением. Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что радиус кривизны R траектории частицы постоянен. Частица движется равномерно по окружности радиусом R. Согласно второму закону Ньютона,
Частица движется равномерно по окружности радиусом R. Согласно второму закону Ньютона,
Следовательно, измерив R при известных υ и В, мы можем определить удельный заряд различных частиц.
Масс-спектрограф.
C помощью магнитного поля можно разделять заряженные частицы по их удельным зарядам и точно определять массы частиц. Разделение частиц осуществляется в масс-спектрографах 1.
1 Масс-спектрограф был впервые сконструирован в 1919 г. учеником Дж. Дж. Томсона — Франсисом Астоном (1877—1945). C помощью этого прибора он произвёл точные измерения масс и дефектов масс ряда изотопов.
Рис. 3.41
На рисунке 3.41, а изображена схема простейшего масс-спектрографа, а на рисунке 3.41, б — внешний вид современного прибора. Вакуумная камера масс-спектрографа помещена в магнитное поле (вектор магнитной индукции перпендикулярен рисунку). Ускоренные электрическим полем заряженные частицы (электроны или ионы), описав дугу, попадают на фотопластинку, где оставляют след, позволяющий с большой точностью измерить радиус траектории R. По этому радиусу можно определить удельный заряд иона и, следовательно, его массу.
Вакуумная камера масс-спектрографа помещена в магнитное поле (вектор магнитной индукции перпендикулярен рисунку). Ускоренные электрическим полем заряженные частицы (электроны или ионы), описав дугу, попадают на фотопластинку, где оставляют след, позволяющий с большой точностью измерить радиус траектории R. По этому радиусу можно определить удельный заряд иона и, следовательно, его массу.
Циклотрон.
Используя формулу для радиуса траектории, найдём время прохождения заряженной частицей полуокружности:
т. е. Δt зависит только от свойств частицы и индукции магнитного поля.
Этот факт был использован американским физиком Эрнестом Лоуренсом (1901 — 1958), который в 1931 г. создал циклотрон. Это устройство позволяет ускорять заряженные частицы сравнительно небольшим электрическим полем в течение ряда циклов.
Рассмотрим устройство циклотрона (рис. 3.42).
Рис. 3.42
Два электрода специальной формы — дуанты находятся в камере, где поддерживается вакуум (рис. 3.43).
3.43).
Рис. 3.43
Дуанты помещают между полюсами сильного магнита, и к ним подводится переменная разность потенциалов. В центре камеры между дуантами располагают источник заряженных частиц. В тот момент, когда между дуантами существует высокая разность потенциалов, электрическое поле в промежутке между ними ускоряет заряженные частицы.
Ускоренные частицы влетают во внутреннюю часть дуанта, где электрическое поле практически отсутствует. Двигаясь под действием магнитной составляющей силы Лоренца по окружности, заряженные частицы через половину оборота снова появляются в щели между дуантами.
Те из частиц, которые двигались с подходящей скоростью, пройдут через щель как раз в тот момент (через половину периода изменения приложенного к дуантам напряжения), когда там электрическое поле успеет сменить своё направление на противоположное. Такие частицы снова ускоряются, описывают внутри другого дуанта полуокружность ещё большего радиуса и снова в необходимый момент подходят к ускоряющему промежутку (время прохождения частицами полуокружности остаётся неизменным, так как оно не зависит от скорости частицы) и т.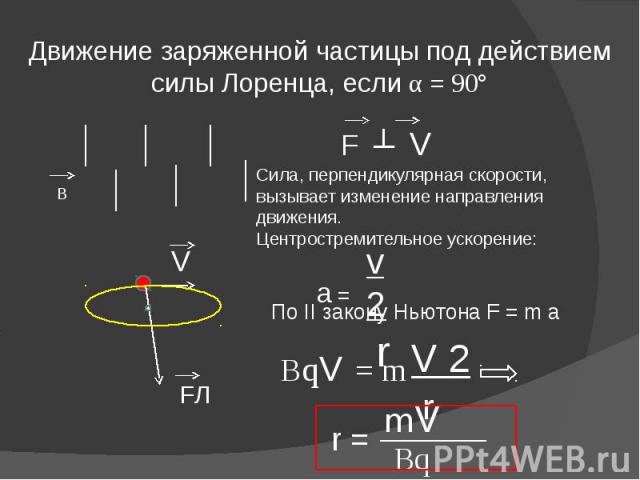 д. Остальные частицы ускоряются незначительно или совсем не ускоряются.
д. Остальные частицы ускоряются незначительно или совсем не ускоряются.
Циклотроны и другие более мощные ускорители заряженных частиц (например, фазотроны, синхротроны, синхрофазотроны) находят широкое применение в ядерной физике и физике элементарных частиц. Изучая столкновения ускоренных частиц с частицами мишени, физики получают возможность исследовать строение микрочастиц, действующие между ними силы, взаимные превращения элементарных частиц.
Магнитный щит земли.
Магнитное поле Земли оказывает существенное влияние на поток заряженных частиц из космоса (космические лучи). Оно образует третий «защитный пояс» наряду с атмосферой и ионосферой, защищающий живые организмы на Земле от губительного действия космических лучей.
На большой высоте магнитное поле Земли невелико, но захватывает громадные области пространства. Действуя на заряженную частицу длительное время, оно существенно изменяет её траекторию. Вместо прямой линии получается спираль, навивающаяся на линии индукции магнитного поля (рис. 3.44).
3.44).
Рис. 3.44
На летящую вдоль линии магнитной индукции частицу сила Лоренца не действует. Вот почему частицы свободно могут приближаться к полюсам, откуда веером расходятся линии магнитной индукции.
Кроме того, магнитное поле Земли удерживает на большой высоте заряженные частицы не слишком больших энергий. Эти области с повышенной концентрацией заряженных частиц, окружающих земной шар, называют радиационными поясами. Большинство частиц внешнего радиационного пояса Земли составляют электроны, а её внутреннего радиационного пояса — протоны (рис. 3.45).
Рис. 3.45
Протоны задерживаются более сильным магнитным полем во внутреннем радиационном поясе. В радиационных поясах заряженные частицы движутся от одного полюса к другому, оставаясь в «магнитной ловушке».
Вопросы:
1. Что называют:
а) электрической составляющей силы Лоренца;
б) магнитной составляющей силы Лоренца?
2. В каком случае магнитная составляющая силы Лоренца будет максимальной?
В каком случае магнитная составляющая силы Лоренца будет максимальной?
3. Как можно определить направление магнитной составляющей силы Лоренца, действующей:
а) на положительно заряженную частицу;
б) на отрицательно заряженную частицу?
4. Для чего используют:
а) масс-спектрограф;
б) циклотрон?
5. Как влияет магнитное поле Земли на потоки космических лучей?
Вопросы для обсуждения:
1. Действует ли магнитная составляющая силы Лоренца:
а) на незаряженную частицу в однородном магнитном поле;
б) на заряженную частицу, покоящуюся в магнитном поле;
в) на заряженную частицу, движущуюся вдоль линий магнитного поля?
2. Как будет двигаться положительно заряженная частица в параллельных электрическом и магнитном полях, если её начальная скорость направлена под некоторым углом к и к ?
Пример решения задачи
Электрон влетает в однородное магнитное поле с индукцией 10 -3 Тл перпендикулярно линиям магнитной индукции и под углом α = π/4 к границе поля (рис. 3.46, а).
3.46, а).
Рис. 3.46
Модуль скорости электрона равен 106 м/с. В направлении осей X и Y магнитное поле безгранично. На каком расстоянии от точки влёта электрон вылетит из поля? Отношение заряда электрона к его массе e/m = 1,76 ∙ 1011 Кл/кг.
В магнитном поле под действием магнитной составляющей силы Лоренца электрон опишет дугу окружности. Найдём её радиус R. Запишем второй закон Ньютона:
m = л .
Ответ: l = 8 мм.
Упражнения:
1. Протон в магнитном поле с индукцией 0,01 Тл описал окружность радиусом 10 см. Чему равна скорость протона?
2. Найдите ускорение протона, который движется со скоростью 2 м/с в магнитном поле с индукцией 3 мТл перпендикулярно линиям магнитной индукции.
3. Определите кинетическую энергию электрона, движущегося по окружности радиусом 1 см в однородном магнитном поле с индукцией 0,03 Тл. Приведите ответ в Дж и в эВ.
Приведите ответ в Дж и в эВ.
4. Протон с энергией 600 эВ влетает в однородное магнитное поле с индукцией 0,33 Тл перпендикулярно линиям магнитной индукции. Найдите радиус траектории протона. Будет ли изменяться кинетическая энергия протона при движении в этом магнитном поле?
5. Электрон влетает в однородное магнитное поле с индукцией 9,4 мТл так, что вектор его скорости составляет угол 30° с направлением линий магнитной индукции (рис. 3.47).
Рис. 3.47
Определите радиус витков траектории электрона и расстояние, пройденное им вдоль линии магнитной индукции за три витка. Скорость электрона равна 2,5 ∙ 106 м/с.
6. Электрон, влетающий в однородное магнит ное поле под углом 60° к линиям магнитной индукции, движется по спирали диаметром 10 см с периодом обращения 6 ∙ 10 -5 с. Определите скорость электрона, индукцию магнитного поля и шаг спирали.
Предыдущая страницаСледующая страница
2.
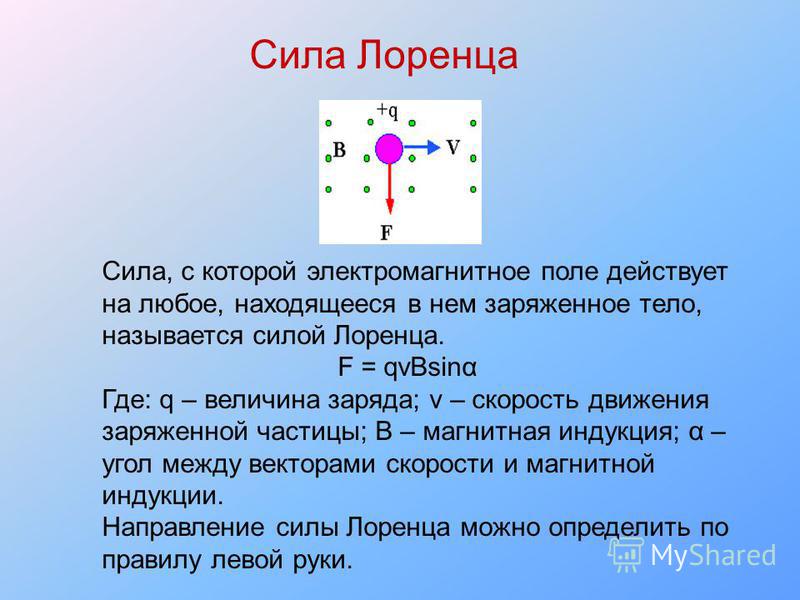 1. Сила Лоренца. Движение заряженной частицы в однородном постоянном магнитном поле
1. Сила Лоренца. Движение заряженной частицы в однородном постоянном магнитном полеОсновные формулы
Сила, действующая на электрический заряд , движущийся со скоростью в магнитном поле
, (18)
где – вектор магнитной индукции поля.
Модуль силы, действующей на заряженную частицу, движущуюся в магнитном поле
, (19)
где – модуль заряда частицы; – модуль вектора скорости; – модуль вектора индукции магнитного поля, – угол между векторами и .
Направление силы определяется по правилу левой руки:
если
ладонь левой руки расположить так, чтобы
в нее входил вектор магнитной индукции ,
а четыре вытянутых пальца направить
вдоль скорости движения положительного
заряда (против направления движения
отрицательного заряда), то отогнутый
на 90° большой палец покажет направление
силы, действующей на заряд.
Если заряд движется в области, где существуют одновременно электрическое и магнитное поля, то на него действует полная сила
, (20)
формула (20) называется формулой Лоренца.
Методические рекомендации
1. Полная электромагнитная сила (сила Лоренца), действующая на заряд, определяется формулой (20). Данная формула справедлива как для постоянных, так и для переменных электрических и магнитных полей.
Эту силу разделяют на электрическую и магнитную составляющие. Если заряженная частица находится только в магнитном поле, то силу, определяемую выражением (18), обычно и называют силой Лоренца.
Важная
особенность силы Лоренца – она всегда
перпендикулярна вектору скорости заряда
и поэтому не совершает над зарядом
работы. Следовательно, в постоянном
магнитном поле энергия движущейся
заряженной частицы всегда постоянна.
Разделение полной электромагнитной силы на электрическую и магнитную зависит от выбора системы отсчета, так как магнитная составляющая силы Лоренца меняется при переходе от одной системы отсчета к другой, а значит, меняется и электрическая составляющая.
2. Под действием силы Лоренца заряженные частицы движутся в магнитном поле по криволинейным траекториям. Характер движения частицы в магнитном поле зависит от угла между первоначальным направлением скорости движения частицы и направлением линий индукции магнитного поля.
Если скорость частицы перпендикулярна линиям магнитной индуции, то частица движется по круговой траектории (рис. 23).
Радиус окружности траектории
;
Рис. 23
период вращения частицы по окружности:
,
где
–
масса частицы;
–
модуль скорости частицы;
–
модуль вектора индукции магнитного
поля;
–
модуль электрического заряда.
Если заряженная частица движется вдоль линий магнитной индукции, сила Лоренца на нее не действует и характер ее движения не меняется.
Если угол между первоначальным направлением скорости частицы и линиями магнитной индукции не равен ни 0°, ни 90°, ни 180°, траектория движения частицы представляет собой винтовую линию, накручивающуюся на линии магнитной индукции (рис. 24).
Рис. 24
– тангенциальная составляющая скорости ; ;
– нормальная составляющая скорости; ;
– шаг винтовой линии; .
3.
При движении заряженной частицы в
области пространства, занятой одновременно
и электрическим и магнитным полями
характер ее движения зависит от
направления этих полей и величины сил,
действующих с их стороны, а также от
скорости частицы.
► Векторы и взаимно-перпендикулярны и скорость положительно заряженной частицы перпендикулярна силовым линиям этих полей. В этом случае на частицу действуют две силы: электрическая и магнитная , которые могут быть как сонаправлены, так и противоположно направлены. Если силы противоположно направлены и равны по модулю ( ), то частица будет двигаться равномерно и прямолинейно, согласно первому закону Ньютона.
В случае если силы не уравновешивают друг друга, то движение частицы будет сложным: она будет двигаться с ускорением вдоль линии напряженности электрического поля и совершать вращательное движение вокруг линии индукции магнитного поля.
Если силы, действующие на движущуюся заряженную частицу сонаправлены, то движение частицы также будет представлять суперпозицию двух движений: прямолинейного с ускорением вдоль линий вектора и вращательного вокруг линий вектора .
► Частица
влетает в область пространства параллельно
векторам
и
. В этом случае на нее действует только
электрическая сила (сила
Лоренца ,
так как и ).
Под действием этой силы частица
движется прямолинейно с ускорением .
В этом случае на нее действует только
электрическая сила (сила
Лоренца ,
так как и ).
Под действием этой силы частица
движется прямолинейно с ускорением .
Примеры решения задач
Пример 1. Протон влетает в однородное магнитное поле с индукцией 20 мкТл перпендикулярно линиям индукции магнитного поля. Сколько оборотов в секунду будет делать протон в магнитном поле?
Решение
На заряженную частицу в магнитном поле действует сила
, (а)
где – заряд частицы, – индукция магнитного поля, – скорость частицы, – угол между векторами и .
В данной задаче , значит протон будет двигаться в магнитном поле по окружности радиуса с центростремительным (нормальным) ускорением
(б)
По второму закону Ньютона
, (в)
где
–
масса частицы.
Приравнивая правые части выражений (б) и (в), с учетом формулы (а), получаем
, (г)
так как , то после небольшого преобразования получаем
. (д)
С другой стороны,
, (е)
где – угловая скорость.
Получаем
. (ж)
Приравняем правые части уравнений (д) и (л), получим
,
откуда выразим – частоту вращения, т. е. число оборотов в секунду,
. (и)
Размерность: .
Подставляем числовые значения в формулу (и):
.
Вычисления дают .
Пример 2. Электрон, имеющий скорость 8·106 м/с, влетает в однородное магнитное поле с индукцией 31,4 мТл под углом 30° к его направлению. Определите радиус и шаг винтовой линии, по которой будет двигаться электрон (рис. 24).
Решение
Скорость разложим на две составляющие: тангенциальную , параллельную линиям индукции магнитного поля и нормальную , перпендикулярную им,
; (а)
. (б)
На электрон действует магнитная сила (благодаря нормальной составляющей скорости)
. (в)
Под действием этой силы электрон будет двигаться по окружности радиуса , который можно найти из условия:
, (г)
так
как сила Лоренца является центростремительной
силой.
Из формулы (г) получаем
, (д)
где – модуль заряда электрона; – масса электрона; – индукция магнитного поля.
Вдоль силовых линий поля магнитная сила не действует, поэтому частица движется прямолинейно с постоянной скоростью .
В результате суперпозиции двух движений электрон будет двигаться по винтовой линии радиусом и шагом винта :
, (е)
где – период движения по окружности,
. (ж)
С учетом формул (б), (д) и (ж), уравнение (е) принимает вид:
. (и)
Размерность: .
Подставляем числовые данные в выражение (и):
.
Вычисления дают:
.
Пример 3. Перпендикулярно магнитному полю с индукцией 0,1 Тл возбуждено электрическое поле напряженностью 1·105 В/м. Перпендикулярно обоим полям, не отклоняясь от прямолинейной траектории, движется заряженная частица. Найти скорость этой частицы (рис. 25). Решение Согласно условию задачи, частица движется равномерно и прямолинейно ( ). По первому закону Ньютона геометрическая сумма сил, действующих на частицу, равна нулю. В данном случае на частицу действует сила Лоренца , где – электрическая составляющая силы Лоренца, – её магнитная составляющая (рис. 25). |
|
Следовательно, ,
т. е. электрическая и магнитная силы
равны по модулю и противоположно
направлены:
е. электрическая и магнитная силы
равны по модулю и противоположно
направлены:
откуда скорость частицы равна:
Согласно условию ( ), поэтому
.
Размерность:
.
Подставляем числовые данные: .
Получаем при вычислении: .
Пример 4. Электрон влетает со скоростью 600 м/с в область пространства, где имеются сонаправленные однородные электрическое и магнитное поля, под углом 60° к силовым линиям полей. Напряженность электрического поля 0,2 кВ/м, индукция магнитного поля 20 мТл. С каким ускорением станет двигаться электрон в этой области пространства? (рис. 26). Решение Согласно второму закону Ньютона, ускорение электрона имеет вид: , где
–
сила Лоренца, действующая на электрон
со стороны электрического и магнитного
полей;
–
масса электрона. Сила Лоренца определяется по формуле |
|
,
где – электрическая составляющая силы Лоренца; – её магнитная составляющая (рис. 26).
Вектор направлен противоположно вектору , так как заряд электрона отрицательный. Вектор магнитной силы перпендикулярен вектору магнитной индукции. Следовательно, векторы и взаимно-перпендикулярны.
Модуль силы находится по теореме Пифагора:
,
где – модуль заряда электрона (элементарный заряд).
Ускорение
.
Направление совпадает с направлением вектора , определяемом по правилу сложения векторов.
Подставим числовые значения:
=
600 м/с;
=
60°; =
0,2 кВ/м = 200 В/м;
=
20 мТл = 2·10-2 Тл;
=
1,6 ·10-19 Кл;
=
9,11·10-31 кг.
Вычисления дают: = 3,5 ·1013 м/с2.
Пример 5. Шарик массой , заряженный положительным зарядом и подвешенный на нити длиной , движется по окружности в вертикальном однородном магнитном поле с индукцией. Определите кинетическую энергию шарика, если во время движения нить образует угол с вертикалью.
Решение
Выберем систему отсчета x0y, начало которой поместим в ту точку пространства, где находится шарик в начальный момент времени. Предположим, что нить – невесома, нерастяжима и неэлектропроводна. Заряженный шарик примем за материальную точку. Заряд шарика будем считать точечным.
На шарик действуют сила тяжести , сила натяжения нити и сила со стороны магнитного поля (рис. 27).
|
|
По второму закону Ньютона
.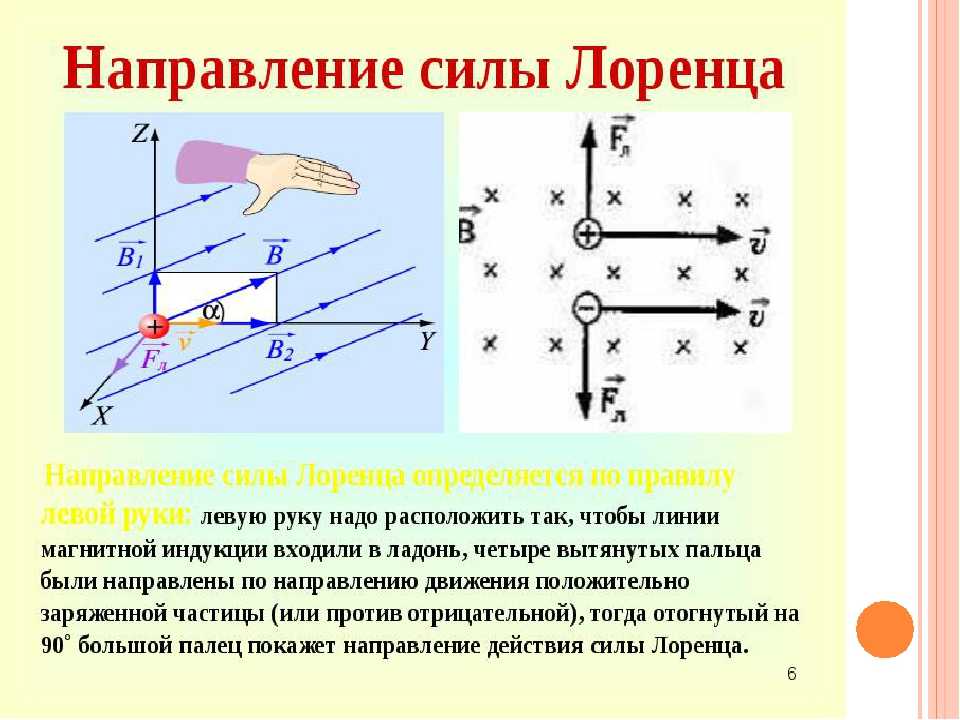 (а)
(а)
Направление всех сил указано на рис. 27 в предположении, что вектор магнитной индукции направлен вверх, а шарик движется по часовой стрелке.
Запишем уравнение (а) в проекциях на выбранные оси координат
; (б)
. (в)
После преобразования, получаем
; (г)
. (д)
Разделим (г) на (д), получим
. (и)
Шарик движется с нормальным ускорением , (к)
где – линейная скорость шарика по окружности, – радиус окружности.
Из чертежа следует:
. (л)
(л)
Сила Лоренца определяется выражением
, (м)
где = 90° (по условию задачи),
С учетом выражений (к)–(м) уравнение (и) принимает вид:
,
или
.
Решаем квадратное уравнение относительно переменной :
,
получаем
.
Так как модуль скорости > 0, то из последнего выражения следует:
.
Кинетическая энергия определяется соотношением:
.
Задачи для самостоятельного решения
1.
Пучок
электронов движется в вакууме в магнитном
поле с напряженностью 5,56·103 А/м по окружности радиусом 3 см.
Определите скорость и энергию электронов,
период обращения и момент импульса.
(Ответ: = 36,3·106 м/с; = 33·10-23 Дж; = 5·10-9 с; = 99·10-26 (кг·м2)/с).
2. В однородном магнитном поле с индукцией 0,1 Тл по окружности движется электрон. Найти величину эквивалентного кругового тока, созданного движением электрона.
(Ответ: = 4,5·10-10 А).
3. Однозарядный ион натрия прошел ускоряющую разность потенциалов 1 кВ и влетел в однородное магнитное поле с индукцией 0,5 Тл перпендикулярно силовым линиям поля. Определите относительную массу иона, если он описал окружность радиусом 4,37 см.
(Ответ: 23 а.е.м.).
4.
Протон,
прошедший ускоряющую разность потенциалов
600 В, влетел в однородное магнитное поле
с напряженностью 2,4·104 А/м перпендикулярно линиям магнитной
индукции. Найти радиус описанной протоном
окружности, его импульс и частоту
вращения протона в магнитном поле.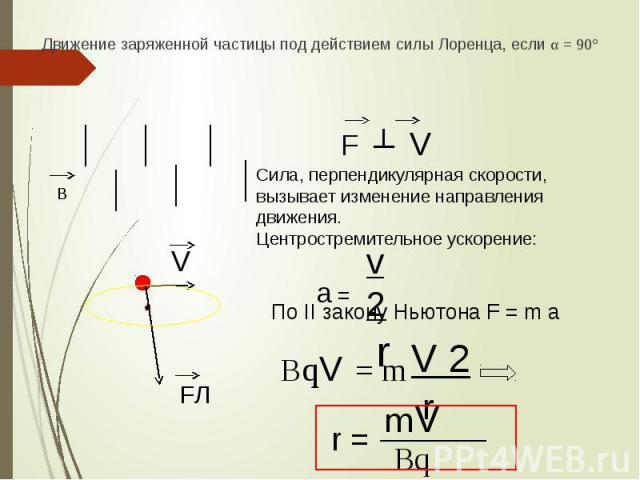
(Ответ: = 0,33 м; = 18·10-21 Н·с; = 3·103с-1).
5. Два иона, имеющие одинаковый заряд и прошедшие одинаковую ускоряющую разность потенциалов, влетели в однородное магнитное поле. Первый ион движется по дуге окружности радиусом 5 см, второй – по дуге окружности радиусом 2,5 см. Определите отношение масс ионов.
(Ответ: ).
6. Электрон влетает в область магнитного поля ширины . Скорость электрона перпендикулярна как индукции поля, так и границам области. Под каким углом к границам области электрон вылетит из магнитного поля?
(Ответ: , если ; рад, если ).
7. Предполагая, что электрон в атоме водорода движется по круговой орбите радиусом 53 пм, определите период обращения электрона вокруг ядра и индукцию магнитного поля, создаваемого движущимся электроном в центре его орбиты.
(Ответ:
=
1,5·10-16 с;
=
12,45 Тл).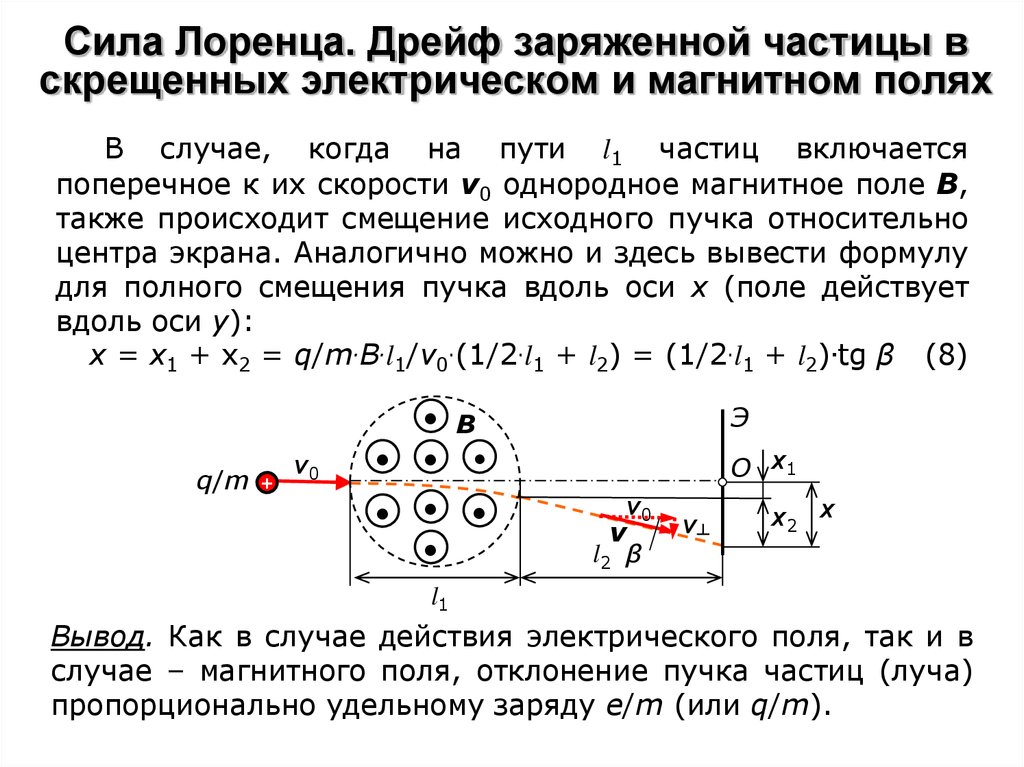
8. Частица, имеющая элементарный заряд, влетает в однородное магнитное поле под углом 45° к линиям индукции и движется по винтовой линии с шагом 2 см. Определите импульс частицы, если индукция поля равна 10-2 Тл.
(Ответ: = 7,2·10-24 кг·м/с).
9. Электрон, кинетическая энергия которого 1,5 МэВ, движется по окружности в однородном магнитном поле с индукцией 20 мТл. Определите период обращения электрона.
(Ответ: = 7 нс).
10. Электрон в однородном магнитном поле движется по винтовой линии радиусом 5 см и шагом 20 см. Определить скорость электрона, если индукция магнитного поля 0,1 Тл.
(Ответ: = 1,04 Мм/с).
11.
Протон,
находящийся в магнитном поле с индукцией
20 мТл описывает окружность радиусом 40
см. Найти импульс протона и его кинетическую
энергию.
Найти импульс протона и его кинетическую
энергию.
(Ответ: = 1,3·10-21 кг·м/с; = 5·10-16 Дж).
12. Протон и альфа-частица влетают в однородное магнитное поле перпендикулярно его силовым линиям. Во сколько раз различаются радиусы окружностей, по которым движутся эти частицы, если у них одинаковы: а) скорость; б) кинетическая энергия? Заряд альфа-частицы в два раза больше заряда протона, а масса альфа-частицы в четыре раза больше массы протона.
(Ответ: (а) ; б) ).
13. В масс-спектрографе заряженная частица, пролетев без начальной скорости ускоряющую разность потенциалов , влетает в однородное магнитное поле индукцией перпендикулярно магнитным линиям. Удельный заряд частицы . Определить диаметр окружности , по которой стала двигаться частица.
(Ответ: ).
14. В вертикальном направлении создано однородное магнитное поле индукцией . Шарик массой и зарядом , подвешенный на нити длиной , движется по окружности так, что нить составляет угол с вертикалью. Найти угловую скорость движения шарика.
(Ответ: ).
15. Однозарядные ионы гелия и водорода, ускоренные из состояния покоя в электрическом поле напряжением 2 кВ, влетают вместе в магнитное поле индукцией 100 мТл перпендикулярно магнитным линиям. Описав полуокружность, они попадают на фотопластинку. Найти расстояние между следами этих ионов на фотопластинке.
(Ответ: = 1,3 см).
16. Электрон с кинетической энергией 1 кэВ попал в однородное магнитное поле с индукцией 21 мТл и стал двигаться по окружности. Определить магнитный момент эквивалентного кругового тока.
(Ответ: = 7,6·10-15 А·м2).
17.
Электрон,
ускоренный разностью потенциалов 300 В,
движется параллельно прямолинейному
длинному проводу на расстоянии 4 мм от
него.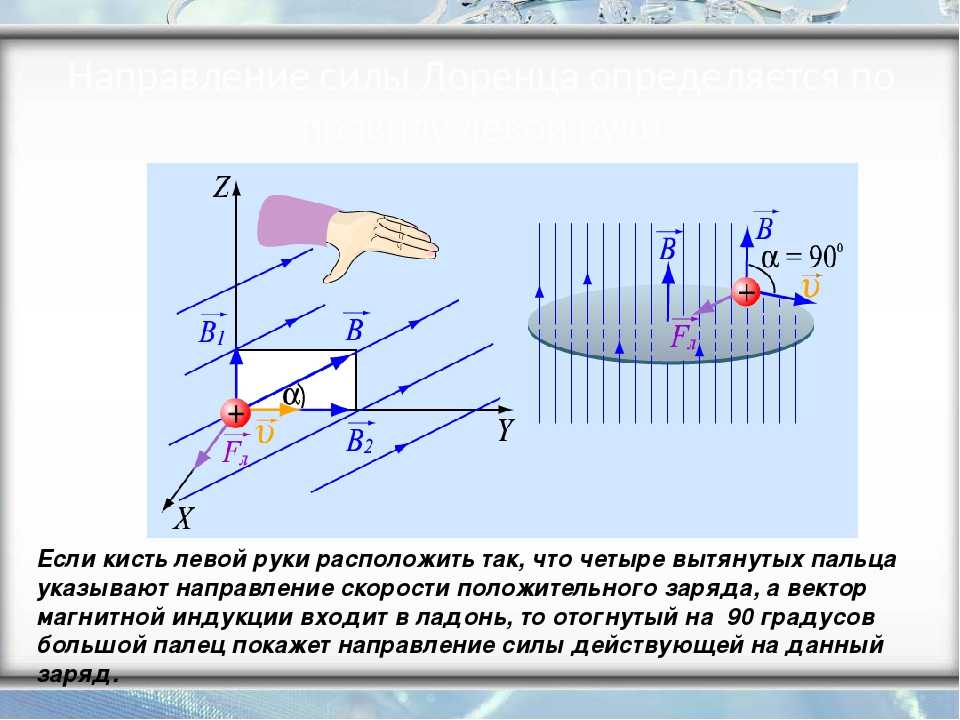 Какая сила действует на электрон,
если по проводнику пропустить ток силой
5
А?
Какая сила действует на электрон,
если по проводнику пропустить ток силой
5
А?
(Ответ: = 4·10-16 Н).
18. Электрон влетает в однородное магнитное поле, направление которого перпендикулярно к направлению его движения. Скорость электрона 4·107 м/с. Индукция магнитного поля 1 мТл. Найти тангенциальное и нормальное ускорения электрона в магнитном поле. (Ответ: = 0; = 7·1015 м/с2). 19.
Пучок
электронов, ускоренных разностью
потенциалов 300 В, влетает в однородное
магнитное поле, направленное от чертежа
«к нам»
(рис. 28). Ширина
поля
=
2,5 см. В отсутствие магнитного поля
пучок электронов дает пятно в точке
А флуоресцирующего экрана, расположенного
на расстоянии
=
5 см от края полюсов магнита. |
|
(Ответ: x = 4,9 см).
20. В
установке для разделения изотопов
U235 и U238 пучок однократно ионизованных
ускоренных ионов с энергией 5 кэВ
попадает от источника через щель S
(рис. 29) в однородное магнитное поле,
перпендикулярное к плоскости рисунка.
В магнитном поле ионы разных масс
движутся по различным окружностям и,
совершив полуоборот, попадают в
приемники. Конструкция последних
должна быть такова, чтобы расстояние
между пучками изотопов на выходе было
не меньше
=
5 мм. (Ответ: 4000 Гс). |
|
21. В конденсаторе, электроды которого составляют часть коаксиальных цилиндрических поверхностей радиусами 5 и 6 см, вдоль оси цилиндров действует однородное магнитное поле с индукцией 0,2 Тл (рис. 30). Через узкую щель в диафрагме АА в конденсатор влетает α-частица с энергией 1 кэВ. Какую разность потенциалов следует создать между электродами конденсатора, чтобы α-частица прошла посередине между электродами? (Внешний электрод имеет отрицательный потенциал).
(Ответ: = 38,5 В).
22.
В
магнетроне анод представляет металлический
цилиндр радиусом
=1
см, а катод – металлическую нить радиусом ,
расположенную по оси цилиндра (рис. 31).
Постепенно увеличивая индукцию магнитного
поля, направленного вдоль оси цилиндра,
добились того, что при анодном напряжении
100 В и индукции 6,7·10-3 Тл анодный ток стал равен нулю. Какое
значение удельного заряда получается
по результатам этого опыта?
Какое
значение удельного заряда получается
по результатам этого опыта?
(Ответ: = 1,76·1011 Кл/кг).
Рис. 30 Рис. 31
23. Магнитное поле напряженностью 8 кА/м и электрическое поле напряженностью 1 кВ/м направлены одинаково. Электрон влетает в электромагнитное поле со скоростью 105 м/с. Найти нормальное, тангенциальное и полное ускорение электрона. Задачу решить для случая, когда скорость электрона направлена параллельно силовым линиям полей.
(Ответ: = 0; = 1,76·1014 м/с2).
24.
Магнитное
поле напряженностью 8 кА/м и электрическое
поле напряженностью 1 кВ/м направлены
одинаково. Электрон влетает в
электромагнитное поле со скоростью 105 м/с. Найти нормальное, тангенциальное
и полное ускорение электрона. Задачу
решить для случая, когда скорость
электрона направлена перпендикулярно
силовым линиям полей.
Электрон влетает в
электромагнитное поле со скоростью 105 м/с. Найти нормальное, тангенциальное
и полное ускорение электрона. Задачу
решить для случая, когда скорость
электрона направлена перпендикулярно
силовым линиям полей.
(Ответ: = 0; = 2,5·1014 м/с2).
25. Магнитное поле с индукцией 0,5 мТл направлено перпендикулярно электрическому полю напряженностью 1 кВ/м. Электрон влетает в электромагнитное поле перпендикулярно к плоскости, в которой лежат векторы и . Найти скорость электронов, если при одновременном действии обоих полей пучок не испытывает отклонения. Каким будет радиус траектории движения электронов при условии включения одного магнитного поля?
(Ответ: = 2·106 м/с; = 2,3 см)
26.
Электрон
влетает в плоский горизонтальный
конденсатор параллельно его пластинам
со скоростью 107 м/с. Длина конденсатора 5 см. Напряженность
электрического поля конденсатора 10
кВ/м. При вылете из конденсатора электрон
попадает в магнитное поле, перпендикулярное
к электрическому. Индукция магнитного
поля 10 мТл. Найти радиус и шаг винтовой
траектории электрона в магнитном
поле.
Длина конденсатора 5 см. Напряженность
электрического поля конденсатора 10
кВ/м. При вылете из конденсатора электрон
попадает в магнитное поле, перпендикулярное
к электрическому. Индукция магнитного
поля 10 мТл. Найти радиус и шаг винтовой
траектории электрона в магнитном
поле.
(Ответ: = 5 мм; = 3,6 см).
27. Протон влетел в скрещенные под углом 120° магнитное и электрическое поля. Определить ускорение протона, если его скорость 4·105 м/с перпендикулярна векторам и , напряженность электрического поля 20 кВ/м, индукция магнитного поля 50 мТл.
(Ответ: = 3,3·1012 м/с2)
28.
Через
сечение алюминиевой
пластинки (
– толщина,
–
высота) пропускается ток
=
5 А. Пластинка помещена в магнитное поле,
перпендикулярное к ребру
и
направлению тока. Найти возникающую
при этом поперечную разность потенциалов.
Индукция магнитного поля
=
0,5 Тл. Толщина пластинки
=
0,1 мм. Концентрацию электронов проводимости
считать равной концентрации атомов.
Концентрацию электронов проводимости
считать равной концентрации атомов.
(Ответ: = 2,7 мкВ).
29. Через сечение медной пластинки ( – толщина, – высота) пропускается ток = 20 А. При помещении пластинки в магнитное поле, перпендикулярное к ребру и направлению тока, возникает поперечная разность потенциалов = 3,1 мкВ. Индукция магнитного поля = 1 Тл. Найти концентрацию электронов проводимости в меди и их скорость при этих условиях.
(Ответ: = 8,1 ·1028 м-3; = 0,31 мм/с).
30.
Заряженная
частица, двигаясь перпендикулярно
скрещенным под прямым углом электрическому
(
= 400 кВ/м) и магнитному (
= 0,25 Тл) полям,
не испытывает отклонений от своей
траектории при определенной скорости.
Определить эту скорость и возможные
отклонения от нее, если значения индукции
магнитного и напряженности электрического
полей могут быть обеспечены с точностью,
не превышающей 0,2 %.
(Ответ: = 1,6·106 м/с; = 6,4 ·103 м/с).
Действие магнитного поля на движущуюся заряженную частицу. Сила Лоренца презентация, доклад, проект
Действие магнитного поля на движущуюся заряженную частицу. Сила Лоренца.
План урока:
Выполните тест «магнитное поле-3».
Изучите новый материал и сделайте конспект (его нужно будет сфотографировать и прислать на проверку).
Прорешайте задачи, поставив презентацию на воспроизведение (сначала попробуйте дать ответ, а затем смотрите решение).
Если какие-то вопросы остались непонятными, сообщите заранее (для подготовки видеообзора).
Сила Лоренца.
Сила Лоренца – сила, действующая со стороны магнитного поля на движущийся заряд.
Сила Лоренца равна произведению модуля заряда на скорость движения частицы, магнитную индукцию и синус угла между вектором скорости и вектором магнитной индукции.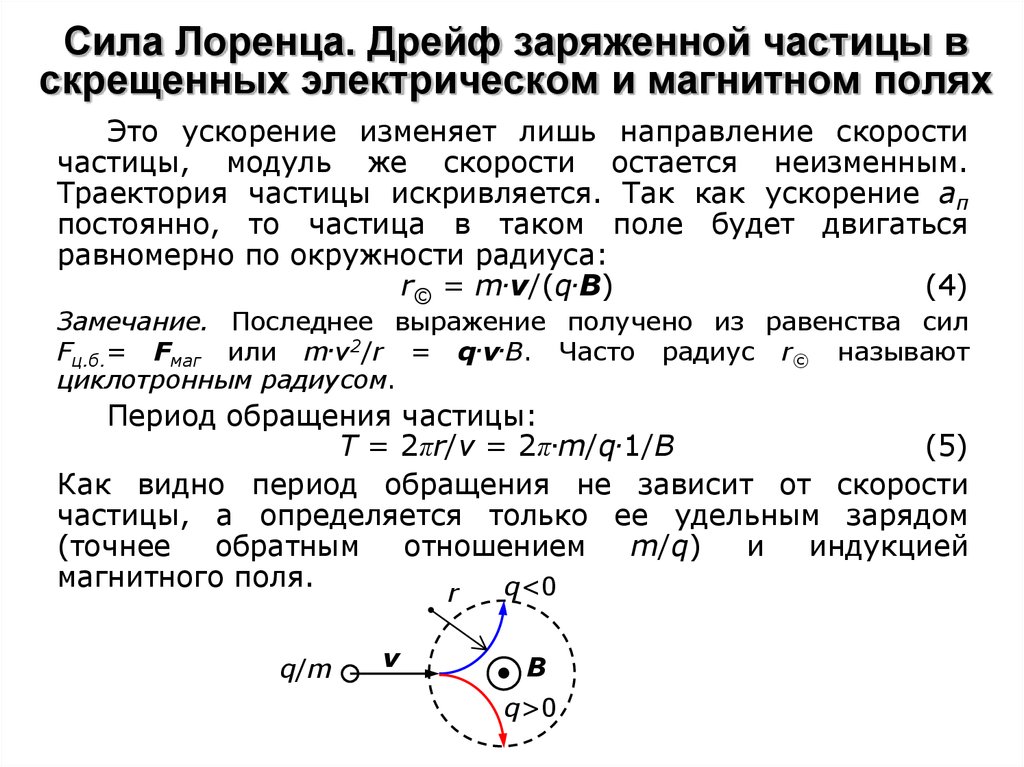
F=|q|∙V∙B∙sinα
Вывод формулы силы Лоренца
Направление силы Лоренца.
Правило левой руки.
Правило левой руки:
4 пальца левой руки направлены по движению положительного заряда;
Вертикальная составляющая вектора магнитной индукции входит в ладонь;
Большой палец отогнутый на угол 90˚ покажет направление силы Лоренца.
Движение заряженной частицы в однородном магнитном поле.
(случай первый).
Вектор магнитной индукции поля перпендикулярен вектору скорости частицы.
Как направлена сила Лоренца?
Магнитное поле не меняет модуля скорости частицы – меняет только направление движения частицы.
Выведем формулы, характеризующие движение частицы в магнитном поле.
Вывод формул, характеризующих движение частицы в магнитном поле.
Второй закон Ньютона: (1)
Сила Лоренца: (2)
Центростремительное ускорение: (3)
Из формул (1), (2), (3):
После сокращения: (4)
Радиус кривизны траектории и период обращения частицы в магнитном поле
Из формулы получим формулу радиуса кривизны траектории частицы:
Найдем период (время одного оборота) обращения частицы в магнитном поле:
Таким образом:
Траектория частицы в однородном магнитном поле (вид сверху)
Частица влетает в магнитное поле перпендикулярно силовым линиям.
Решение задач.
Задача 18.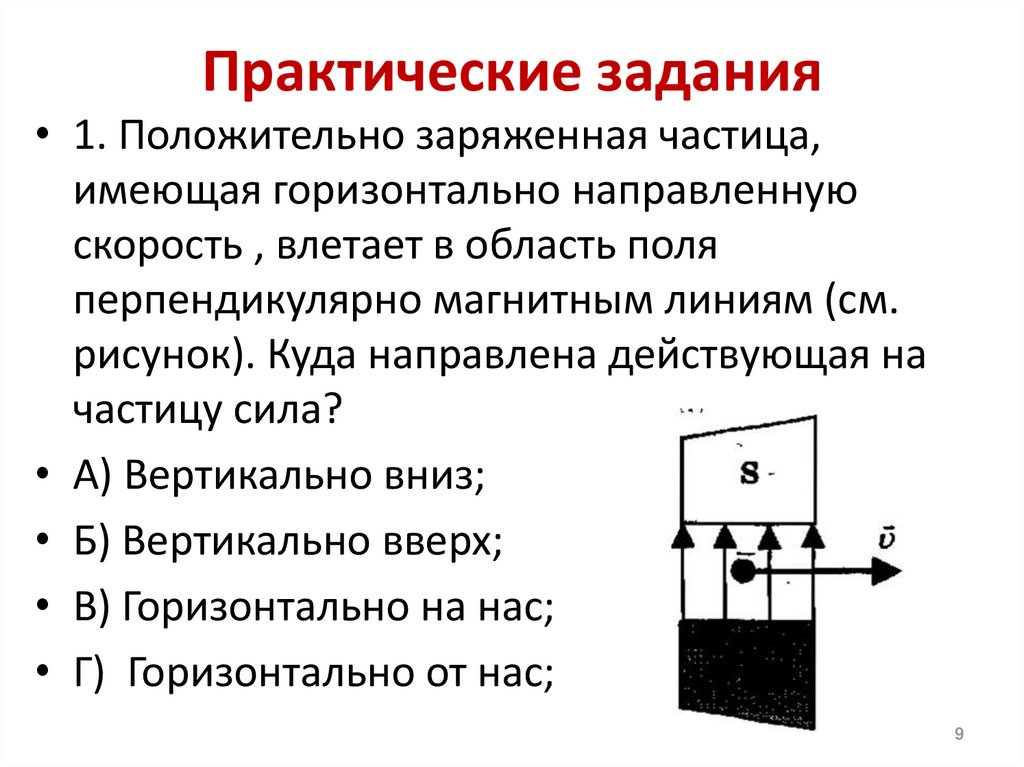
Протон влетевший в зазор между полюсами электромагнита, имеет горизонтальную скорость, перпендикулярную вектору магнитной индукции, направленного вертикально. Куда направлена действующая на него сила Лоренца?
По правилу
левой руки:
4 пальца
направляются
по вектору
скорости
частицы;
вектор магнитной индукции входит в ладонь; большой палец покажет направление силы Ампера.
Сила Ампера направлена горизонтально к нам.
Задача 19.
Электрон, влетевший в зазор между полюсами электромагнита, имеет горизонтально направленную скорость, перпендикулярную вектору индукции. Куда направлена действующая на него сила Лоренца?
Используя правило левой руки…
Сила Лоренца направлена вертикально вверх.
Задача 20.
Как изменится период обращения заряженной частицы в однородном магнитном поле при увеличении ее скорости в 5 раз? Рассматривается нерелятивистский случай.
Период обращения частицы в магнитном поле определяется формулой: T=2πR/V=2πm/|q|∙B
Из этой формулы видно, что период обращения частицы не зависит от ее скорости в магнитном поле.
Задача 21.
Нейтрон и протон влетают в однородное магнитное поле перпендикулярно вектору магнитной индукции с одинаковыми скоростями. Чему равно отношение модуля силы, действующей на нейтрон к модулю силы, действующей на протон
В магнитном поле действует сила Лоренца: F=|q|∙V∙B∙sinα
Но сила Лоренца действует только на протон, т.к. нейтрон не имеет заряда.
Отношение сил равно нулю.
Задача 22.
Электрон и протон влетают в однородное магнитное поле перпендикулярно вектору магнитной индукции с одинаковыми скоростями. Чему равно отношение модулей сил, действующих на них со стороны магнитного поля?
На электрон и протон действует сила Лоренца.
F=|q|∙V∙B∙sinα
Следовательно, сила, действующая на частицы зависит от величины заряда частиц.
Заряды электрона и протона равны, значит, равны и силы, действующие на них.
Ответ: отношение сил
равно 1.
Задача 23.
Электрон и α-частица влетают в однородное магнитное поле перпендикулярно вектору магнитной индукции с одинаковыми скоростями. Чему равно отношение модуля силы, действующей со стороны магнитного поля на электрон к модулю силы, действующей на α-частицу.
На электрон и α-частицу действует сила Лоренца.
F=|q|∙V∙B∙sinα
Следовательно, сила, действующая на частицы зависит от величины заряда частиц.
Заряд электрона в 2 раза меньше заряда α-частицы.
Ответ: отношение сил
равно 1:2.
Задача 24.
Два первоначально покоившихся электрона ускоряются в электрическом поле: первый проходит разность потенциалов U, второй 2U.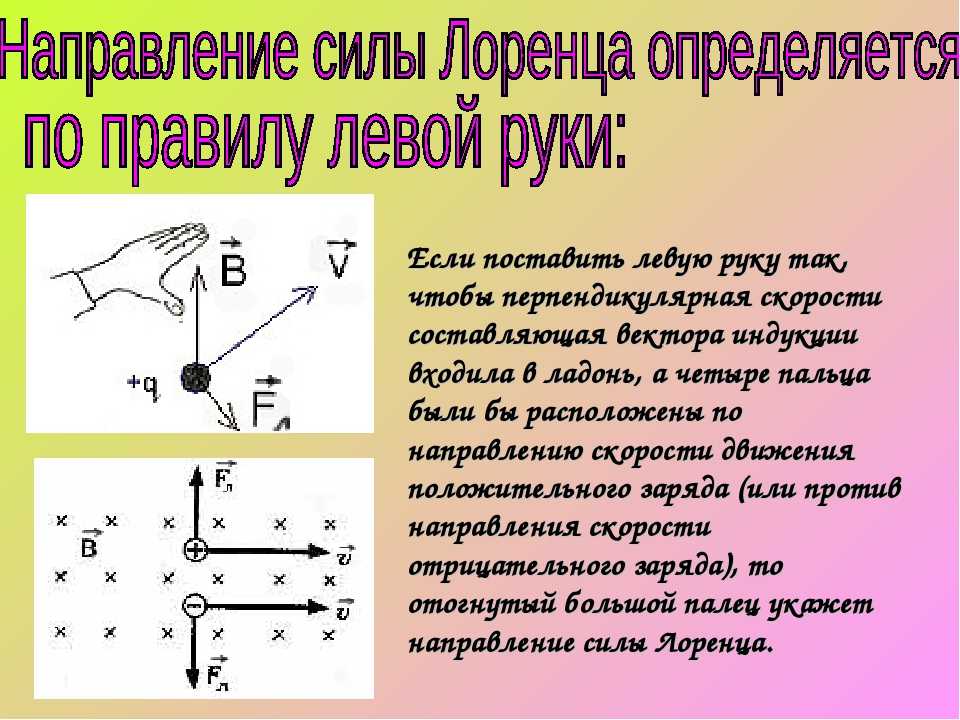 Ускорившиеся электроны влетают в магнитное поле перпендикулярно линиям магнитной индукции. Чему равно отношение радиусов кривизны траекторий первого и второго электронов?
Ускорившиеся электроны влетают в магнитное поле перпендикулярно линиям магнитной индукции. Чему равно отношение радиусов кривизны траекторий первого и второго электронов?
В электрическом поле кинетическая энергия электронов приобретается за счет энергии поля: (mV2/2=eU) =>
V=√2eU/m; V₁~√U, V₂~√2U ; V₁/V₂=1/√2
Радиус кривизны: r=m∙V/|q|∙B; r~V => r₁/r₂= V₁/V₂=1/√2.
Ответ: 1/√2 или √2/2.
Домашнее задание.
Тест «Магнитное поле-3»
§ 6 (11кл).
конспект.
Скачать презентацию
21.4: Движение заряженной частицы в магнитном поле
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 15649
цели обучения
- Сравнить влияние электрического и магнитного полей на заряженную частицу
Электрические и магнитные силы
Сила, обусловленная как электрическими, так и магнитными силами, будет влиять на движение заряженных частиц. Однако результирующее изменение траектории частиц будет качественно различаться между двумя силами. Ниже мы кратко рассмотрим два типа сил, а также сравним и сопоставим их воздействие на заряженную частицу.
Однако результирующее изменение траектории частиц будет качественно различаться между двумя силами. Ниже мы кратко рассмотрим два типа сил, а также сравним и сопоставим их воздействие на заряженную частицу.
Сила электростатического и магнитного поля, действующая на заряженную частицу
Напомним, что в статическом неизменном электрическом поле E сила, действующая на частицу с зарядом q, будет равна:
\[\mathrm { F } = \mathrm { qE }\]
Где F — вектор силы, q — заряд, а E — вектор электрического поля. Обратите внимание, что направление F идентично E в случае позитивистского заряда q и противоположное направление в случае отрицательно заряженной частицы. Это электрическое поле может быть создано большим зарядом Q, действующим на меньший заряд q на расстоянии 9{ 2 } }\]
Следует подчеркнуть, что электрическая сила F действует параллельно электрическому полю E . Ротор электрической силы равен нулю, т.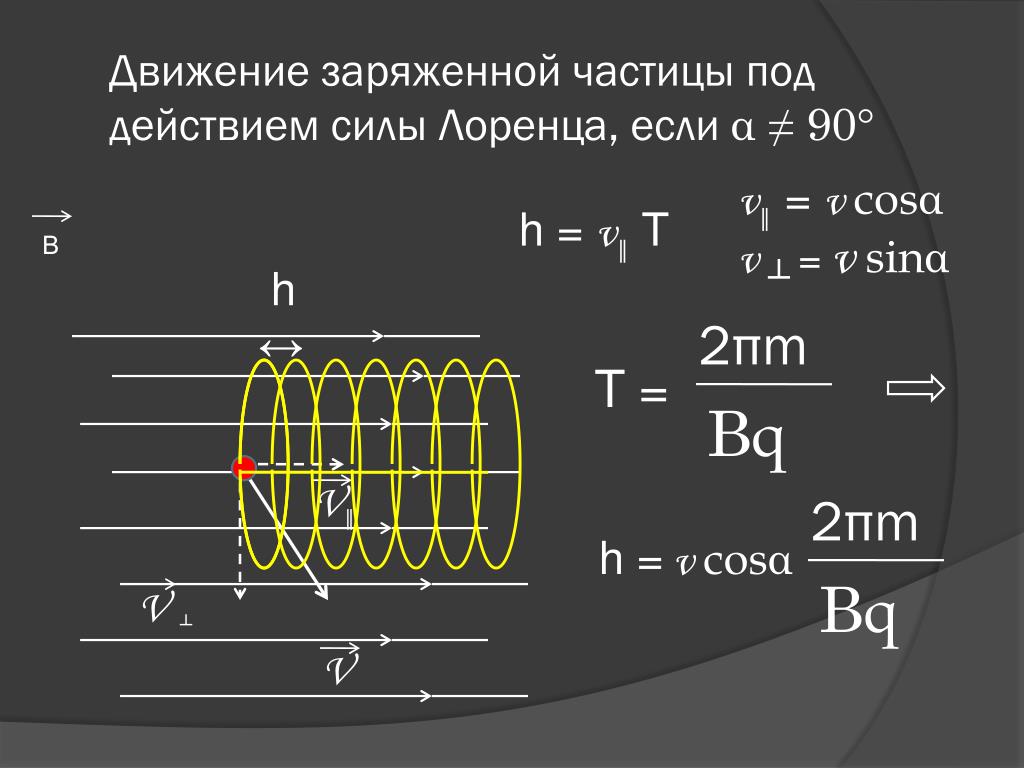 е. будет следовать по касательной к линии электрического поля .
е. будет следовать по касательной к линии электрического поля .
Напротив, вспомните, что магнитная сила, действующая на заряженную частицу, ортогональна магнитному полю, так что:
\[\mathrm { F } = \mathrm { qv } \times \mathrm { B } = \mathrm { q } \mathrm { vB } \sin \theta\]
где B вектор магнитного поля , v — скорость частицы, а θ — угол между магнитным полем и скоростью частицы. Направление F можно легко определить с помощью правила правой руки.
Правило правой руки : Магнитные поля воздействуют на движущиеся заряды. Эта сила является одной из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B, и следует правилу правой руки-1 (RHR-1), как показано. Величина силы пропорциональна q, v, B и синусу угла между v и B.
Если скорость частицы параллельна магнитному полю или равна нулю, магнитная сила будет равна нулю. Это отличается от случая электрического поля, где скорость частицы не имеет никакого отношения в любой данный момент к величине или направлению электрической силы.
Угловая зависимость магнитного поля также заставляет заряженные частицы двигаться перпендикулярно силовым линиям магнитного поля по окружности или спирали, в то время как частица в электрическом поле будет двигаться по прямой линии вдоль линии электрического поля.
Еще одно различие между магнитными и электрическими силами заключается в том, что магнитные поля не связаны между собой, поскольку движение частиц является круговым и, следовательно, заканчивается в одном и том же месте. Мы выражаем это математически как:
\[\mathrm { W } = \oint \mathrm { B } \cdot \mathrm { dr } = 0\]
Сила Лоренца
Сила Лоренца представляет собой объединенную силу, действующую на заряженный частица из-за электрического и магнитного полей, которые часто рассматриваются вместе для практических приложений. Если частица с зарядом q движется со скоростью v в присутствии электрического поля E и магнитного поля B , то на него будет действовать сила:
\[\mathrm { F } = \mathrm { q } [ \mathrm { E } + \mathrm { vB } \sin \theta ]\]
Линии электрического и магнитного поля
Выше мы кратко упоминали, что движение заряженных частиц относительно силовых линий различается в зависимости от того, имеет ли дело с электрические или магнитные поля. Есть некоторые заметные различия между тем, как концептуализируются силовые линии электрического и магнитного поля. Линии электрического поля от положительного изолированного заряда представляют собой просто последовательность равномерно расположенных радиально направленных линий, направленных наружу от заряда. В случае отрицательного заряда направление поля меняется на противоположное. Электрическое поле направлено по касательной к силовым линиям. Конечно, мы воображаем, что силовые линии тем плотнее упакованы, чем больше заряды. Можно ясно видеть, что ротор электрической силы равен нулю.
Есть некоторые заметные различия между тем, как концептуализируются силовые линии электрического и магнитного поля. Линии электрического поля от положительного изолированного заряда представляют собой просто последовательность равномерно расположенных радиально направленных линий, направленных наружу от заряда. В случае отрицательного заряда направление поля меняется на противоположное. Электрическое поле направлено по касательной к силовым линиям. Конечно, мы воображаем, что силовые линии тем плотнее упакованы, чем больше заряды. Можно ясно видеть, что ротор электрической силы равен нулю.
Электрическое поле, создаваемое точечными зарядами : Электрическое поле, окружающее три различных точечных заряда: (a) положительный заряд; б) отрицательный заряд равной величины; в) больший отрицательный заряд.
Если задействовано несколько зарядов, линии поля генерируются на положительных зарядах и заканчиваются на отрицательных.
В случае магнитов силовые линии возникают на северном полюсе (+) и заканчиваются на южном полюсе (-) – см. рисунок ниже. Однако магнитные «заряды» всегда идут парами — нет магнитных монополей (изолированных северных или южных полюсов). Следовательно, ротор магнитного поля, создаваемого обычным магнитом, всегда отличен от нуля. Заряженные частицы будут вращаться вокруг этих силовых линий до тех пор, пока у частиц есть некоторая ненулевая составляющая скорости, направленная перпендикулярно силовым линиям.
рисунок ниже. Однако магнитные «заряды» всегда идут парами — нет магнитных монополей (изолированных северных или южных полюсов). Следовательно, ротор магнитного поля, создаваемого обычным магнитом, всегда отличен от нуля. Заряженные частицы будут вращаться вокруг этих силовых линий до тех пор, пока у частиц есть некоторая ненулевая составляющая скорости, направленная перпендикулярно силовым линиям.
Модель магнитного полюса : Модель магнитного полюса: два противоположных полюса, северный (+) и южный (-), разделенные расстоянием d, создают H-поле (линии).
Магнитное поле также может быть создано током с силовыми линиями, представленными в виде концентрических окружностей вокруг провода с током. Магнитная сила в любой точке в этом случае может быть определена с помощью правила правой руки и будет перпендикулярна как ток, так и магнитное поле.
Постоянная скорость образует прямую линию
Если скорость заряженной частицы параллельна магнитному полю, результирующая сила отсутствует и частица движется прямолинейно.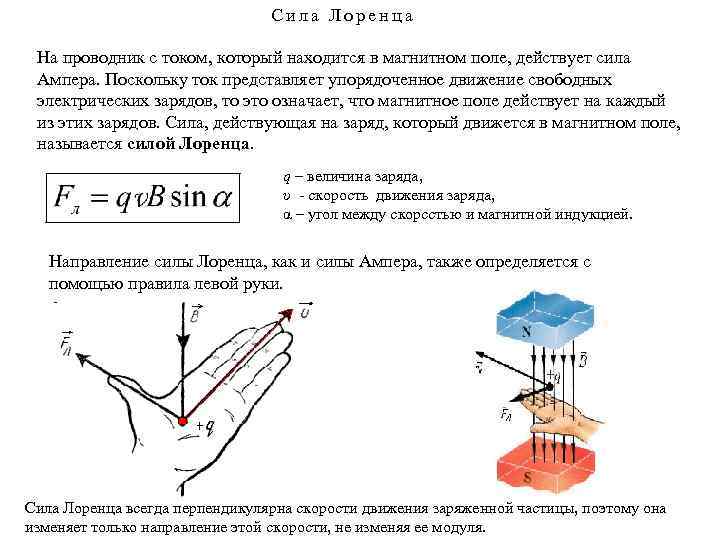
цели обучения
- Определить условия, необходимые для того, чтобы частица двигалась прямолинейно в магнитном поле
Постоянная скорость создает прямолинейное движение
Вспомните первый закон движения Ньютона. Если на объект не действует результирующая сила, то его скорость постоянна: объект либо покоится (если его скорость равна нулю), либо движется по прямой линии с постоянной скоростью (если его скорость отлична от нуля).
Во многих случаях на частицу может не действовать результирующая сила. Частица могла существовать в вакууме вдали от любых массивных тел (которые проявляют гравитационные силы) и электромагнитных полей. Или на частицу могут действовать две или более сил, которые уравновешены так, что результирующая сила равна нулю. Так обстоит дело, скажем, с частицей, подвешенной в электрическом поле, где электрическая сила точно уравновешивает гравитацию.
Если результирующая сила, действующая на частицу, равна нулю, то ускорение обязательно равно нулю по второму закону Ньютона: F=ma. Если ускорение равно нулю, любая скорость, которую имеет частица, будет поддерживаться бесконечно (или до тех пор, пока результирующая сила больше не будет равна нулю). Поскольку скорость является вектором, направление остается неизменным вместе со скоростью, поэтому частица движется в одном направлении, например, по прямой линии.
Если ускорение равно нулю, любая скорость, которую имеет частица, будет поддерживаться бесконечно (или до тех пор, пока результирующая сила больше не будет равна нулю). Поскольку скорость является вектором, направление остается неизменным вместе со скоростью, поэтому частица движется в одном направлении, например, по прямой линии.
Заряженные частицы, движущиеся параллельно магнитным полям
Сила, которую заряженная частица «чувствует» благодаря магнитному полю, зависит от угла между вектором скорости и вектором магнитного поля B . Напомним, что магнитная сила равна:
Нулевая сила, когда скорость параллельна магнитному полю : В приведенном выше случае магнитная сила равна нулю, потому что скорость параллельна линиям магнитного поля.
\[\mathrm {F} = \mathrm {q} \mathrm {v} \mathrm {B} \sin \theta\]
Если магнитное поле и скорость параллельны (или антипараллельны), то sinθ равен нулю и силы нет. В этом случае заряженная частица может продолжать прямолинейное движение даже в сильном магнитном поле.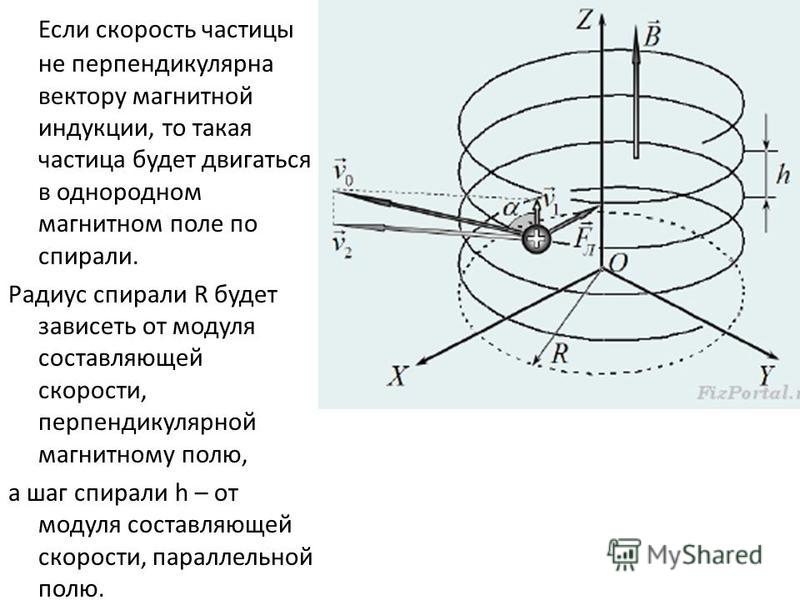 Если находится в диапазоне от 0 до 90 градусов, то составляющая v , параллельная B , остается неизменной.
Если находится в диапазоне от 0 до 90 градусов, то составляющая v , параллельная B , остается неизменной.
Круговое движение
Поскольку магнитная сила всегда перпендикулярна скорости заряженной частицы, частица будет совершать круговое движение.
цели обучения
- Описать условия, которые приводят к круговому движению заряженной частицы в магнитном поле
Круговое движение заряженной частицы в магнитном поле
Магнитные силы могут заставить заряженные частицы двигаться по кругу или по спирали. Ускорители частиц удерживают протоны по круговым траекториям с магнитной силой. Космические лучи будут двигаться по спирали при столкновении с магнитным полем астрофизических объектов или планет (одним из примеров является магнитное поле Земли). Фотография пузырьковой камеры на рисунке ниже показывает заряженные частицы, движущиеся по таким изогнутым траекториям. Искривленные траектории заряженных частиц в магнитных полях лежат в основе ряда явлений и даже могут использоваться аналитически, например, в масс-спектрометре. показывает путь, пройденный частицами в пузырьковой камере.
показывает путь, пройденный частицами в пузырьковой камере.
Пузырьковая камера : Следы пузырьков образуются заряженными частицами высокой энергии, движущимися через перегретый жидкий водород в этом художественном исполнении пузырьковой камеры. Существует сильное магнитное поле, перпендикулярное странице, что приводит к искривлению траекторий частиц. Радиус пути можно использовать для определения массы, заряда и энергии частицы.
Итак, магнитная сила вызывает круговое движение? Магнитная сила всегда перпендикулярна скорости, поэтому на заряженную частицу она не действует. Таким образом, кинетическая энергия и скорость частицы остаются постоянными. Направление движения влияет, но не скорость. Это характерно для равномерного кругового движения. Простейший случай имеет место, когда заряженная частица движется перпендикулярно однородному В-полю, как показано на рис. (Если это происходит в вакууме, магнитное поле является доминирующим фактором, определяющим движение. { 2 } } { \ mathrm { r } } \] 9{ 2 } } { \mathrm { r } }\]
{ 2 } } { \ mathrm { r } } \] 9{ 2 } } { \mathrm { r } }\]
решение для r дает
\[\mathrm { r } = \dfrac { \mathrm { m } \mathrm { v } } { \mathrm { qB } } \]
Здесь r , называемый гирорадиусом или циклотронным радиусом, представляет собой радиус кривизны пути заряженной частицы с массой m и зарядом q , движущейся со скоростью v перпендикулярно магнитное поле напряженностью B . Другими словами, это радиус кругового движения заряженной частицы в присутствии однородного магнитного поля. Если скорость не перпендикулярна магнитному полю, то v — составляющая скорости, перпендикулярная полю. Составляющая скорости, параллельная полю, не изменяется, так как магнитная сила равна нулю при движении параллельно полю. Мы рассмотрим последствия этого случая в следующем разделе, посвященном спиральному движению.
Частица, совершающая круговое движение из-за однородного магнитного поля, называется находящейся в циклотронном резонансе . Этот термин происходит от названия циклического ускорителя частиц, называемого циклотроном, показанного на рис.0036 v выше и заменив частоту циркуляции так, что
Этот термин происходит от названия циклического ускорителя частиц, называемого циклотроном, показанного на рис.0036 v выше и заменив частоту циркуляции так, что
Циклотрон : Французский циклотрон, произведенный в Цюрихе, Швейцария, в 1937 году
\[\mathrm { f } = \dfrac { \mathrm { v } } { 2 \pi \mathrm { r } }\]
становится
\[\mathrm{ f } = \dfrac { \mathrm { qB } } { 2 \pi \mathrm { m } } \]
Циклотрон частота тривиально задается в радианах в секунду как
\[\omega = \dfrac { \mathrm{q} \mathrm { B } } { \mathrm { m } }\]
Винтовое движение
Винтовое движение возникает, когда вектор скорости не перпендикулярен вектору магнитного поля.
цели обучения
- Описать условия, которые приводят к винтовому движению заряженной частицы в магнитном поле
Винтовое движение
В разделе о круговом движении мы описали движение заряженной частицы с вектором магнитного поля, направленным перпендикулярно скорости частицы.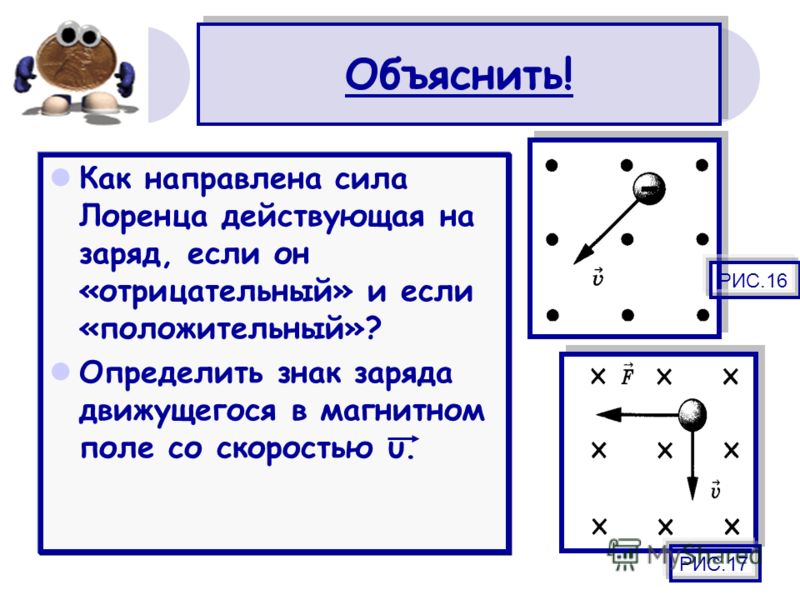 В этом случае магнитная сила также перпендикулярна скорости (и, конечно, вектору магнитного поля) в любой момент времени, что приводит к круговому движению. Скорость и кинетическая энергия частицы остаются постоянными, но направление изменяется в каждый момент перпендикулярной магнитной силой. быстро просматривается эта ситуация в случае отрицательно заряженной частицы в магнитном поле, направленном внутрь страницы.
В этом случае магнитная сила также перпендикулярна скорости (и, конечно, вектору магнитного поля) в любой момент времени, что приводит к круговому движению. Скорость и кинетическая энергия частицы остаются постоянными, но направление изменяется в каждый момент перпендикулярной магнитной силой. быстро просматривается эта ситуация в случае отрицательно заряженной частицы в магнитном поле, направленном внутрь страницы.
Круговое движение заряженной частицы в магнитном поле : Отрицательно заряженная частица движется в плоскости страницы в области, где магнитное поле перпендикулярно странице (представлено маленькими кружками с крестиком — как хвосты стрелок). Магнитная сила перпендикулярна скорости, поэтому скорость изменяется по направлению, но не по величине. Результат равномерного кругового движения.
Что делать, если скорость не перпендикулярна магнитному полю? Тогда мы рассматриваем только 9{ 2 } } { \ mathrm { r } } \]
\[\ mathrm { F } = \ mathrm { q } \ mathrm { vB } \ sin \ theta = \ mathrm { qv } _ { \ perp } \ mathrm { B }\]
Составляющая скорости, параллельная полю, не изменяется, так как магнитная сила равна нулю при движении параллельно полю. Это производит спиральное движение (то есть спиральное движение), а не круговое движение.
Это производит спиральное движение (то есть спиральное движение), а не круговое движение.
показывает, как электроны, не движущиеся перпендикулярно силовым линиям магнитного поля, следуют за силовыми линиями. Составляющая скорости, параллельная линиям, не изменяется, поэтому заряды закручиваются вдоль силовых линий. Если напряженность поля увеличивается в направлении движения, поле будет оказывать силу, чтобы замедлить заряды (и даже изменить их направление), образуя своего рода магнитное зеркало.
Винтовое движение и магнитные зеркала : Когда заряженная частица движется вдоль линии магнитного поля в область, где поле становится сильнее, на частицу действует сила, уменьшающая составляющую скорости, параллельную полю. Эта сила замедляет движение вдоль силовой линии и здесь меняет его направление, образуя «магнитное зеркало». “
Движение заряженных частиц в магнитных полях связано с такими разными вещами, как Aurora Borealis или Aurora Australis (северное и южное сияние) и ускорителями частиц. Заряженные частицы, приближающиеся к силовым линиям магнитного поля, могут захватываться спиральными орбитами вокруг линий, а не пересекать их , как показано выше. Некоторые космические лучи, например, следуют линиям магнитного поля Земли, проникая в атмосферу вблизи магнитных полюсов и вызывая южное или северное сияние за счет ионизации молекул в атмосфере. Те частицы, которые приближаются к средним широтам, должны пересекать силовые линии магнитного поля, и многие из них не могут проникнуть в атмосферу. Космические лучи являются компонентом фонового излучения; следовательно, они дают более высокую дозу радиации на полюсах, чем на экваторе.
Заряженные частицы, приближающиеся к силовым линиям магнитного поля, могут захватываться спиральными орбитами вокруг линий, а не пересекать их , как показано выше. Некоторые космические лучи, например, следуют линиям магнитного поля Земли, проникая в атмосферу вблизи магнитных полюсов и вызывая южное или северное сияние за счет ионизации молекул в атмосфере. Те частицы, которые приближаются к средним широтам, должны пересекать силовые линии магнитного поля, и многие из них не могут проникнуть в атмосферу. Космические лучи являются компонентом фонового излучения; следовательно, они дают более высокую дозу радиации на полюсах, чем на экваторе.
Заряженные частицы движутся по спирали вдоль силовых линий магнитного поля Земли : Энергичные электроны и протоны, составляющие космические лучи, исходящие от Солнца и глубокого космоса, часто следуют силовым линиям магнитного поля Земли, а не пересекают их. (Напомним, что северный магнитный полюс Земли на самом деле является южным полюсом с точки зрения стержневого магнита. )
)
Примеры и приложения
Циклотроны, магнетроны и масс-спектрометры представляют собой практическое технологическое применение электромагнитных полей.
цели обучения
- Обсудить применение масс-спектрометров, движение заряженных частиц в циклотроне и то, как микроволны генерируются в резонаторном магнетроне
Примеры и приложения – Движение заряженной частицы в магнитном поле
Обзор
Напомним, что заряженные частицы в магнитном поле будут двигаться по круговой или спиральной траектории в зависимости от того, совмещен ли вектор их скорости с магнитным полем. вектор. Последствия такого движения могут иметь глубокое практическое применение. Многие технологии основаны на движении заряженных частиц в электромагнитных полях. Мы рассмотрим некоторые из них, в том числе циклотрон и синхротрон, резонаторный магнетрон и масс-спектрометр.
Циклотроны и синхротроны
Циклотрон — это тип ускорителя частиц, в котором заряженные частицы ускоряются наружу от центра по спиральной траектории. Частицы удерживаются на спиральной траектории постоянным магнитным полем и ускоряются быстро меняющимся (радиочастотным) электрическим полем.
Частицы удерживаются на спиральной траектории постоянным магнитным полем и ускоряются быстро меняющимся (радиочастотным) электрическим полем.
Эскиз циклотрона : Эскиз частицы, ускоряемой в циклотроне и выбрасываемой через луч.
Циклотроны ускоряют пучки заряженных частиц с помощью высокочастотного переменного напряжения, которое подается между двумя D-образными электродами (также называемыми «ди»). Дополнительное статическое магнитное поле прикладывается в направлении, перпендикулярном плоскости электрода, что позволяет частицам повторно сталкиваться с ускоряющим напряжением много раз в одной и той же фазе. Для этого частота напряжения должна соответствовать частоте циклотронного резонанса частицы
\[\mathrm { f } = \dfrac { \mathrm { qB } } { 2 \pi \mathrm { m } }\]
с релятивистской массой m и зарядом q . Эта частота определяется равенством центростремительной силы и магнитной силы Лоренца. Частицы, инжектированные вблизи центра магнитного поля, увеличивают свою кинетическую энергию только при рециркуляции через зазор между электродами; таким образом, они движутся наружу по спиральному пути. Их радиус будет увеличиваться до тех пор, пока частицы не попадут в цель по периметру вакуумной камеры или не покинут циклотрон с помощью лучевой трубки, что позволит их использовать. Частицы, ускоренные циклотроном, можно использовать в терапии частицами для лечения некоторых видов рака. Кроме того, циклотроны являются хорошим источником высокоэнергетических пучков для ядерно-физических экспериментов.
Их радиус будет увеличиваться до тех пор, пока частицы не попадут в цель по периметру вакуумной камеры или не покинут циклотрон с помощью лучевой трубки, что позволит их использовать. Частицы, ускоренные циклотроном, можно использовать в терапии частицами для лечения некоторых видов рака. Кроме того, циклотроны являются хорошим источником высокоэнергетических пучков для ядерно-физических экспериментов.
Синхротрон представляет собой усовершенствование циклотрона, в котором направляющее магнитное поле (изгибающее частицы по замкнутому пути) зависит от времени и синхронизировано с пучком частиц с возрастающей кинетической энергией. Синхротрон — одна из первых концепций ускорителя, которая позволяет создавать крупномасштабные установки, поскольку изгибание, фокусировку луча и ускорение можно разделить на разные компоненты.
Резонаторный магнетрон
Резонаторный магнетрон представляет собой мощную вакуумную лампу, генерирующую микроволны за счет взаимодействия потока электронов с магнитным полем. Все резонаторные магнетроны состоят из горячего катода с высоким (постоянным или импульсным) отрицательным потенциалом, создаваемым высоковольтным источником питания постоянного тока. Катод встроен в центр вакуумированной лопастной круглой камеры. Магнитное поле, параллельное нити накала, создается постоянным магнитом. Магнитное поле заставляет электроны, притянутые к (относительно) положительной внешней части камеры, двигаться по спирали наружу по круговой траектории, что является следствием силы Лоренца. По краю камеры расположены цилиндрические полости. Полости открыты по своей длине и соединяют общее полостное пространство. Когда электроны проносятся мимо этих отверстий, они индуцируют в полости резонансное высокочастотное радиополе, которое, в свою очередь, заставляет электроны группироваться в группы.
Все резонаторные магнетроны состоят из горячего катода с высоким (постоянным или импульсным) отрицательным потенциалом, создаваемым высоковольтным источником питания постоянного тока. Катод встроен в центр вакуумированной лопастной круглой камеры. Магнитное поле, параллельное нити накала, создается постоянным магнитом. Магнитное поле заставляет электроны, притянутые к (относительно) положительной внешней части камеры, двигаться по спирали наружу по круговой траектории, что является следствием силы Лоренца. По краю камеры расположены цилиндрические полости. Полости открыты по своей длине и соединяют общее полостное пространство. Когда электроны проносятся мимо этих отверстий, они индуцируют в полости резонансное высокочастотное радиополе, которое, в свою очередь, заставляет электроны группироваться в группы.
Схема резонаторного магнетрона : Схема поперечного сечения резонаторного магнетрона. Магнитные силовые линии параллельны геометрической оси этой структуры.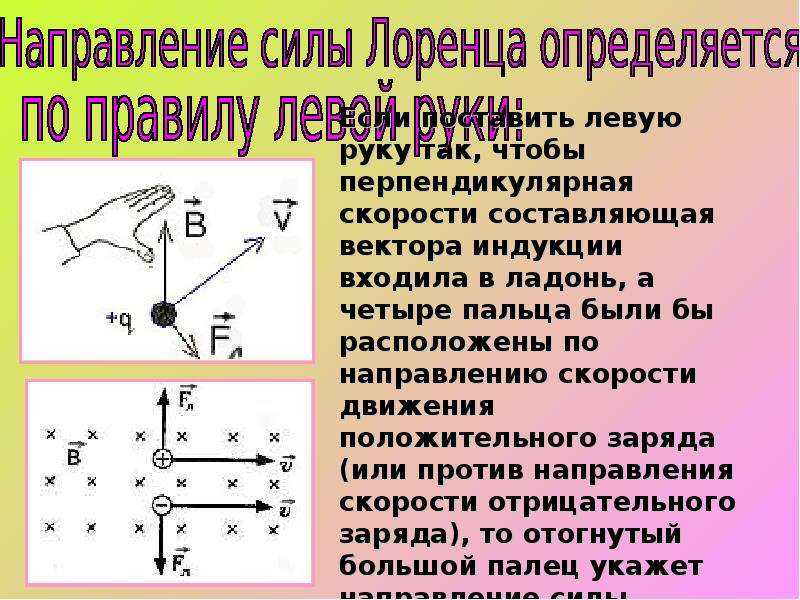
Размеры полостей определяют резонансную частоту и, следовательно, частоту излучаемых микроволн. Магнетрон представляет собой автоколебательное устройство, не требующее никаких внешних элементов, кроме источника питания. Магнетрон имеет практическое применение в радиолокации, нагреве (как основной компонент микроволновой печи) и освещении.
Масс-спектрометрия
Масс-спектрометрия — это аналитический метод, который измеряет отношение массы заряженных частиц к заряду. Он используется для определения массы частиц и определения элементного состава образца или молекулы.
Масс-анализаторы разделяют ионы в соответствии с отношением их массы к заряду. Следующие два закона управляют динамикой заряженных частиц в электрическом и магнитном полях в вакууме: { B } ) \text{ (сила Лоренца)}\]
\[\mathrm { F } = \mathrm { ma }\]
Приравнивая приведенные выше выражения для силы, приложенной к иону, получаем:
\[( \mathrm { m } / \mathrm { Q } ) \ mathrm { a } = \mathrm { E } + \mathrm { v } \times \mathrm { B }\]
Это дифференциальное уравнение вместе с начальными условиями полностью определяет движение заряженной частицы в терминах m/Q. Существует много типов масс-анализаторов, использующих статические или динамические поля, магнитные или электрические поля, но все они работают в соответствии с приведенным выше дифференциальным уравнением.
Существует много типов масс-анализаторов, использующих статические или динамические поля, магнитные или электрические поля, но все они работают в соответствии с приведенным выше дифференциальным уравнением.
На следующем рисунке показан один тип масс-спектрометра. Отклонения частиц зависят от отношения массы к заряду. В случае изотопного диоксида углерода все молекулы имеют одинаковый заряд, но разные массы. Масс-спектрометр будет разделять частицы в пространстве, позволяя детектору измерять отношение массы к заряду каждой частицы. Поскольку заряд известен, абсолютную массу можно определить тривиально. Относительное содержание можно определить, подсчитав количество частиц каждой заданной массы.
Масс-спектрометрия : Схема простого масс-спектрометра с масс-анализатором секторного типа. Это для измерения соотношения изотопов углекислого газа (IRMS), как в дыхательном тесте с мочевиной на углерод-13.
Ключевые моменты
- Сила, действующая на заряженную частицу из-за электрического поля, направлена параллельно вектору электрического поля в случае положительного заряда и антипараллельно в случае отрицательного заряда.
 Она не зависит от скорости частицы.
Она не зависит от скорости частицы. - Напротив, магнитная сила, действующая на заряженную частицу, ортогональна вектору магнитного поля и зависит от скорости частицы. Для определения направления силы можно использовать правило правой руки.
- Электрическое поле может совершать работу над заряженной частицей, тогда как магнитное поле не совершает работы.
- Сила Лоренца представляет собой комбинацию электрической и магнитной сил, которые часто рассматриваются вместе для практических приложений.
- Линии электрического поля генерируются на положительных зарядах и заканчиваются на отрицательных. Силовые линии изолированного заряда направлены прямо радиально наружу. Электрическое поле касается этих линий.
- Линии магнитного поля в случае магнита генерируются на северном полюсе и заканчиваются на южном полюсе. Магнитные полюса не существуют изолированно. Как и в случае силовых линий электрического поля, магнитное поле касается силовых линий.
 Заряженные частицы будут вращаться вокруг этих силовых линий.
Заряженные частицы будут вращаться вокруг этих силовых линий. - Первый закон движения Ньютона гласит, что если на объект не действует результирующая сила, то его скорость постоянна.
- Частица с постоянной скоростью будет двигаться по прямой через пространство.
- Если скорость заряженной частицы полностью параллельна магнитному полю, магнитное поле не будет воздействовать на частицу, и поэтому скорость останется постоянной.
- В случае, когда вектор скорости не параллелен и не перпендикулярен магнитному полю, составляющая скорости, параллельная полю, останется постоянной. 9{ 2 } } { \mathrm { r } }\).
- Решение для r выше дает гриорадиус, или радиус кривизны траектории частицы с зарядом q и массой m, движущейся в магнитном поле напряженностью B. Тогда гриорадиус определяется выражением \(\mathrm{ \Gamma = \ frac { m v } { q B }} \).
- Циклотронная частота (или, что то же самое, гирочастота) – это количество циклов, совершаемых частицей по кругу за каждую секунду, и определяется выражением \(\mathrm { f } = \frac { \mathrm { q } \mathrm { B } } { 2 \pi \mathrm { m } }\).

- Ранее мы видели, что круговое движение возникает, когда скорость заряженной частицы перпендикулярна магнитному полю. Скорость и кинетическая энергия частицы остаются постоянными, но направление изменяется в каждый момент перпендикулярной магнитной силой.
- Если скорость не перпендикулярна магнитному полю, при расчетах мы учитываем только ту составляющую v, которая перпендикулярна полю.
- Составляющая скорости, параллельная полю, не изменяется, так как магнитная сила равна нулю при движении параллельно полю. Это приводит к винтовому движению.
- Заряды могут двигаться по спирали вдоль силовых линий. Если сила магнитного поля увеличивается в направлении движения, поле будет оказывать силу, чтобы замедлить заряды и даже изменить их направление. Это известно как магнитное зеркало.
- Циклотрон — это тип ускорителя частиц, в котором заряженные частицы ускоряются наружу от центра по спиральной траектории. Частицы удерживаются на спиральной траектории постоянным магнитным полем и ускоряются быстро меняющимся электрическим полем.

- Резонаторный магнетрон представляет собой мощную вакуумную лампу, генерирующую микроволны за счет взаимодействия потока электронов с магнитным полем. Магнетрон применяется в радиолокации, отоплении и освещении.
- Масс-спектрометры измеряют отношение массы к заряду заряженных частиц с помощью электромагнитных полей для разделения частиц с разными массами и/или зарядами. Его можно использовать для определения элементного состава молекулы или образца.
Ключевые термины
- ортогональный : Из двух объектов под прямым углом; перпендикулярны друг другу.
- прямолинейное движение : движение в одном направлении.
- гирорадиус : Радиус кругового движения заряженной частицы в присутствии однородного магнитного поля.
- циклотронная частота : Частота заряженной частицы, движущейся перпендикулярно направлению однородного магнитного поля B (постоянная величина и направление).
 Дано равенством центростремительной силы и магнитной силы Лоренца.
Дано равенством центростремительной силы и магнитной силы Лоренца. - спиральное движение : Движение, возникающее, когда одна составляющая скорости постоянна по величине и направлению (т. е. прямолинейное движение), а другая составляющая имеет постоянную скорость, но равномерно изменяется по направлению (т. е. круговое движение) . Это суперпозиция прямолинейного и кругового движения.
- магнитное зеркало : Конфигурация магнитного поля, при которой напряженность поля изменяется при движении вдоль силовой линии. Зеркальный эффект приводит к стремлению заряженных частиц отскакивать от области сильного поля.
- циклотрон : Ускоритель первых частиц, в котором заряженные частицы генерировались в центральном источнике и ускорялись по спирали наружу посредством фиксированного магнитного и переменного электрического полей.
- масс-спектрометр : Устройство, используемое в масс-спектрометрии для определения массового состава данного вещества.

- магнетрон : устройство, в котором электроны заставляют резонировать в камере особой формы и, таким образом, производить микроволновое излучение; используется в радарах и в микроволновых печах.
ЛИЦЕНЗИИ И АВТОРСТВО
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, ПРЕДОСТАВЛЕННОЕ РАНЕЕ
- Курирование и пересмотр. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, КОНКРЕТНОЕ АВТОРСТВО
- OpenStax College, College Physics. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 18 сентября 2013 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Колледж OpenStax, Колледж физики. 18 сентября 2013 г. Предоставлено : OpenStaxCNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42308/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Электрическая сила. Предоставлено : Википедия. Расположен по адресу : en.
 Wikipedia.org/wiki/Electric_force . Лицензия : CC BY-SA: Attribution-ShareAlike
Wikipedia.org/wiki/Electric_force . Лицензия : CC BY-SA: Attribution-ShareAlike - Электрическое поле. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Electric_field . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42310/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Линии магнитного поля. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_field_lines%23Magnetic_field_lines .
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - Колледж OpenStax, Колледж физики. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42370/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Магнитная сила. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_force%23History . Лицензия : CC BY-SA: Attribution-ShareAlike
- ортогональный. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/orthogonal . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики.
 10 декабря 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
10 декабря 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Линии магнитного поля. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_field_lines%23Magnetic_field_lines . Лицензия : Общественное достояние: Авторские права неизвестны
- Колледж OpenStax, Колледж физики. 14 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики.
 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Законы Ньютона. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Newton’s_laws . Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/straight-line-motion . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 10 декабря 2012 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : http://cnx.org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Линии магнитного поля. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_field_lines%23Magnetic_field_lines . Лицензия : Общественное достояние: Нет данных Авторские права
- Колледж OpenStax, Колледж физики. 14 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 28 ноября 2012 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Циклотронный резонанс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Cyclotron_resonance . Лицензия : CC BY-SA: Attribution-ShareAlike
- Циклотрон. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Cyclotron . Лицензия : CC BY-SA: Attribution-ShareAlike
- Гирорадиус. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Gyroradius . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики.
 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - гирорадиус. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/gyroradius . Лицензия : CC BY-SA: Attribution-ShareAlike
- циклотронная частота. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/cyclotron%20frequency . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 10 декабря 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Линии магнитного поля. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_field_lines%23Magnetic_field_lines . Лицензия : Общественное достояние: Авторские права неизвестны
- Колледж OpenStax, Колледж физики. 14 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 28 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Колледж OpenStax, Колледж физики. 16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 26 ноября 2012 г. Предоставлено : OpenStaxCNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Циклотрон. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Cyclotron .
 Лицензия : Общественное достояние: Нет данных Авторские права
Лицензия : Общественное достояние: Нет данных Авторские права - Магнитное зеркало. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_mirror . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/helical-motion . Лицензия : CC BY-SA: Attribution-ShareAlike
- магнитное зеркало.
 Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic%20mirror . Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic%20mirror . Лицензия : CC BY-SA: Attribution-ShareAlike - Колледж OpenStax, Колледж физики. 10 декабря 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Линии магнитного поля. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_field_lines%23Magnetic_field_lines . Лицензия : Общественное достояние: Нет данных Авторские права
- Колледж OpenStax, Колледж физики. 14 ноября 2012 г.
 Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Колледж OpenStax, Колледж физики. 28 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 26 ноября 2012 г.
 Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Циклотрон. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Cyclotron . Лицензия : Общественное достояние: Нет данных Авторские права
- Колледж OpenStax, Колледж физики. 27 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 26 ноября 2012 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Колледж OpenStax, Колледж физики. 27 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Атрибуция
- Масс-спектрометры. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Mass_spectrometers . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Магнетрон. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetron . Лицензия : CC BY-SA: Attribution-ShareAlike
- Синхротрон. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Synchrotron . Лицензия : CC BY-SA: Attribution-ShareAlike
- Циклотрон. Предоставлено : Википедия. Расположен по адресу : http://en.Wikipedia.org/wiki/Cyclotron . Лицензия : CC BY-SA: Attribution-ShareAlike Циклотрон
- .
 Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/cyclotron . Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/cyclotron . Лицензия : CC BY-SA: Attribution-ShareAlike - магнетрон. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/magnetron . Лицензия : CC BY-SA: Attribution-ShareAlike Масс-спектрометр
- . Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/mass_spectrometer . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 10 декабря 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Линии магнитного поля. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic_field_lines%23Magnetic_field_lines . Лицензия : Общественное достояние: Нет данных Авторские права
- Колледж OpenStax, Колледж физики. 14 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 28 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Колледж OpenStax, Колледж физики. 16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 26 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Циклотрон. Предоставлено : Википедия. Расположен по адресу : http://en.Wikipedia.org/wiki/Циклотрон .
 Лицензия : Общественное достояние: Нет данных Авторские права
Лицензия : Общественное достояние: Нет данных Авторские права - Колледж OpenStax, Колледж физики. 27 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 26 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 27 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.
 7 . Лицензия : CC BY: Атрибуция
7 . Лицензия : CC BY: Атрибуция - Масс-спектрометры. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Mass_spectrometers . Лицензия : Общественное достояние: Нет данных Авторские права
- Магнетрон. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetron . Лицензия : Общественное достояние: неизвестно Авторские права
- Циклотрон. Предоставлено : Википедия. Расположен по адресу : http://en.Wikipedia.org/wiki/Cyclotron . Лицензия : Общественное достояние: Нет данных Авторские права
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Показать оглавление
- нет
- Теги
- Циклотрон
- циклотронная частота
- гирорадиус
- спиральное движение
- магнитное зеркало
- магнетрон
- Масс-спектрометр
- ортогональный
- source@https://ocw.
 mit.edu/courses/electrical-engineering-and-computer-science/6-013-electromagnetics-and-applications-spring-2009
mit.edu/courses/electrical-engineering-and-computer-science/6-013-electromagnetics-and-applications-spring-2009 - прямолинейное движение
Сила, действующая на движущийся заряд в однородном магнитном и электрическом поле
Сила Лоренца (или электромагнитная сила) действительно является результатом воздействия электромагнитных полей на точечный заряд электрическими и магнитными силами. В электрическом поле E и магнитном поле B на частицу с зарядом q, движущуюся со скоростью v, действует сила . Электромагнитная сила, действующая на заряд q, описывается как комбинация силы, направленной в направлении электрического поля Е, пропорциональной величине поля и количеству заряда, а также силы, направленной под прямым углом к магнитному полю В и скорость заряда v, пропорциональная величине поля, заряда и скорости. Магнитная сила, действующая на провод с током (часто называемая силой Лапласа), электродвижущая сила в стерильной петле, движущейся через магнитное поле, а также сила, действующая на движущуюся заряженную частицу, описываются вариациями этой основной формулы.
Электромагнитная сила F, действующая на пробный заряд в заданном месте и в заданное время, является функцией его заряда q и скорости v, что можно количественно выразить в функциональной форме ровно двумя векторами E и B:
Присоединяйтесь к программе регулярных занятий Infinity Learn!
Загрузите БЕСПЛАТНО PDF-файлы, решенные вопросы, работы за предыдущий год, викторины и головоломки!
+91
Подтвердить OTP-код (обязательно)
Класс
— Класс 6Класс 7Класс 8Класс 9Класс 10Класс 11Класс 12
Курс
—CBSEIIT-JEENEET
Школа/колледж4 Chaan Chaan?
НетДа
Я согласен с условиями и политикой конфиденциальности.
F = q (E + v * B)
Даже для частиц со скоростью, близкой к скорости света (т. е. с величиной v, |v| c), это верно. В результате два векторных поля E и B определены в пространстве и времени и называются «электрическим полем» и «магнитным полем» соответственно. Независимо от того, доступен ли заряд для испытания силы, поля определяются везде в пространстве и времени с точки зрения того, какую силу может воспринять пробный заряд.
Независимо от того, доступен ли заряд для испытания силы, поля определяются везде в пространстве и времени с точки зрения того, какую силу может воспринять пробный заряд.
Поскольку реальная частица (в отличие от гипотетического «пробного заряда» с бесконечно малой массой и зарядом) будет создавать свои собственные конечные поля E и B, изменяя электромагнитную силу, которую она испытывает, сила Лоренца — это просто теоретическое определение.
Важные понятия Что вызывает магнитное поле с точки зрения силы?Магнитные поля могут воздействовать только на движущийся электрический заряд, поскольку движущийся заряд создает магнитное поле. С увеличением заряда и силы магнитного поля эта сила возрастает. Кроме того, когда заряды имеют более высокие скорости, сила больше.
Однако магнитная сила всегда поперечна скорости. В результате эта сила никогда не могла производить вещество на заряде или передавать ему кинетическую энергию. Магнитное поле определяется как
Fm = q v × B
Q = заряд
V = скорость
B = магнитное поле
4 всегда перпендикулярна скорости и магнитному полю. В результате он всегда действует вне плоскости и не дает никакого вклада в работу заряда. Он может только изменить направление скорости; он не может изменить величину. Используя правило правой руки Флеминга, вы можете быстро вычислить направление силы.
В результате он всегда действует вне плоскости и не дает никакого вклада в работу заряда. Он может только изменить направление скорости; он не может изменить величину. Используя правило правой руки Флеминга, вы можете быстро вычислить направление силы.
Параллельно оси электрического поля Если равно 0, частица не имеет магнитной силы и будет продолжать течь вдоль силовых линий без отклонения. Когда v и B расположены под прямым углом, ускорители заряженных частиц, такие как циклотроны, используют тот факт, что частицы движутся по круговой орбите. Идеально синхронизированное электрическое поле обеспечивает частицы большей кинетической энергией с каждым раундом, заставляя их двигаться по все более крупным кругам. Когда частицы достигают необходимой энергии, их собирают и используют для различных целей, начиная от исследования субатомных частиц и заканчивая лечением рака.
Символ носителей заряда в проводнике раскрывается магнитной силой на движущийся заряд. Носители положительного заряда, движущиеся справа налево, носители отрицательного заряда, движущиеся с левой стороны на правую сторону, или их сочетание могут вызвать течение тока в проводнике справа налево.
Сила электрического поля, действующая на заряд, включена в его определение. Он всегда функционирует либо параллельно, либо антипараллельно электрическому полю, независимо от скорости заряда. Это свидетельствует о том, что он может работать и обеспечивать энергией заряд.
F e = q E
Магнитная сила вдоль обоих типов экситонов имеет одинаковое направление, когда проводник помещен в поле B, перпендикулярное току. Эта сила вызывает крошечную разность потенциалов между сторонами проводника. Когда электрическое поле согласовано с направлением магнитной силы, это явление известно как эффект Холла. Эффект Холла показывает, что электроны преобладают в проводимости меди. С другой стороны, проводимость в цинке определяется движением переносчиков положительного заряда. Когда электроны в цинке стимулируются из валентной зоны, они оставляют дырки, которые действуют как носители положительного заряда. Большая часть электропроводности цинка обусловлена подвижностью этих дырок.
Большая часть электропроводности цинка обусловлена подвижностью этих дырок.
Темы NEET предназначены для разъяснения и предоставления наиболее вероятных вопросов, которые будут заданы на экзамене. Наблюдения компетентных ученых в этой области, опубликованные на бесплатном веб-сайте Infinity Learn, можно использовать для их объяснения простыми словами. Если учащиеся хорошо понимают темы, затронутые в ходе программы, вопросы с несколькими вариантами ответов легко практиковать.
Текущая страница о силе Лоренца охватывает все аспекты силы, действующей на движущийся заряд в однородных магнитном и электрическом полях. Внимательно изучите подробные примечания, чтобы убедиться, что вы понимаете эту тему, поскольку это улучшит вашу подготовку к экзамену NEET. Можно также сделать некоторые заметки об упругой энергии для дальнейшего рассмотрения.
Сила Лоренца обрисовывает в общих чертах математические уравнения, а также физическое значение нагрузок, действующих на заряженные частицы, путешествующие в пространстве с электрическими и магнитными полями. Вот почему сила Лоренца так важна.
Сила Лоренца используется в следующих случаях:
- Сила Лоренца используется в циклотронах, а также в других ускорителях частиц.
- Сила Лоренца используется в пузырьковой камере для создания графика, используемого для расчета траекторий заряженных частиц.
- Сила Лоренца используется в телевизорах с электронно-лучевой трубкой, чтобы отклонять электроны по прямой линии, чтобы они попадали в определенные области экрана.
Читайте также: Важная тема физики: Принцип суперпозиции
Часто задаваемые вопросы (Часто задаваемые вопросы)Вопрос 1: Что такое сила Лоренца и как она действует?
Ответ : Сила Лоренца относится к силе, действующей на заряженную частицу электрическим и магнитным полями.
Вопрос 2: Какова формула расчета силы Лоренца?
Ответ : F=q (E +v ∗ B)
Вопрос 3: В честь кого названа сила Лоренца?
Ответ : Хендрик Лоренц — это имя силы Лоренца.
Вопрос 4: Скольким гауссам равен один тесла?
Ответ : Гаусс Теслы равен 10 000.
Вопрос 5: Какой закон используется для расчета магнитной силы?
Ответ : Правило правши.
Вопрос 6: Каковы характеристики электрических и магнитных сил с точки зрения полей?
Ответ : Магнитные силы всегда были перпендикулярны полю, но электрические силы всегда коллинеарны.
Вопрос 7: Что такое сила Лоренца и как она работает?
Ответ : При наличии полей E и B полезно определить направление движущегося заряда.
Сопутствующее содержание
Магнитная сила | bartleby
Что такое магнитная сила?
Магнитная сила возникает, когда заряженная частица или проводник с током помещаются в магнитное поле. Он создается из-за движения заряженных частиц.
Он создается из-за движения заряженных частиц.
Рассмотрим электрический провод с заряженными частицами, движущимися со скоростью (v) в магнитном поле (B). Магнитная сила относится к взаимодействию между магнитным полем, создаваемым движущимися частицами, и приложенным магнитным полем. Здесь заряд (q) испытывает магнитную силу. Суммарная сила, действующая на электрический провод, равна
F⇀=Fe⇀+Fm⇀
Где
Fe⇀ — сила электрического поля
Fm⇀ — сила магнитного поля
Что такое магнит?
Магнит представляет собой материал или вещество, которое используется для создания магнитного поля в области, окружающей материал. Магнит имеет два полюса, северный полюс и южный полюс. Однополюсные отталкиваются, а разноименные притягиваются.
Магнит притягивает ферромагнитные материалы, такие как железо (Fe), никель (Ni) и кобальт (Co). Такие материалы, как дерево, хлопок и пластик, не имеют магнитного поля.
Как найти магнитную силу
Возьмем двухточечный заряд, который имеет величины магнитной силы, соединяющей частицы. Магнитная сила зависит от количества зарядов и движений в каждом из двух точечных зарядов и от того, насколько они удалены друг от друга. Направление силы зависит от относительного движения заряда.
Магнитная сила зависит от количества зарядов и движений в каждом из двух точечных зарядов и от того, насколько они удалены друг от друга. Направление силы зависит от относительного движения заряда.
Здесь положительный заряд (q) движется с неизменным магнитным полем (B) со скоростью ( v ). Угол между магнитным полем и скоростью равен θ. Таким образом, магнитная сила, наблюдаемая заряженной частицей, зависит от следующих факторов.
1. Величина силы, наблюдаемой зарядом, прямо пропорциональна его величине.
F α q
2. Величина силы F прямо пропорциональна ее скорости v, которая действует на перпендикулярные направления магнитного поля.
F α vsinθ
3. Величина силы прямо пропорциональна величине приложенной магнитной силы.
F α B
Сравнивая уравнения (1), (2) и (3), получаем,
Fα qvBsinθ
Теперь перепишем вышеприведенное уравнение:
F=kqvBsinθ
Где
k — константа пропорциональности (k=1).
Теперь уравнение можно переписать как
F=qvBsinθ
В векторном выражении
F→=q(v→×B→)
Здесь v=1, q=1 и sin θ =1,
then,
F=B
Приведенное выше выражение описывает, что индукция магнитного поля в точке на магнитном поле равна силе, наблюдаемой его единичным зарядом, движущимся с единичной скоростью, которая перпендикулярна направлениям магнитного поля.
Сила Лоренца
Сила Лоренца описывает сочетание электрического поля и магнитного поля на точечных зарядах магнитной силы. Сила, приложенная к заряженной частице (q), заставляет ее двигаться со скоростью (v) через магнитное поле (B) и электрическое поле (E). Вся электромагнитная сила (F), действующая на заряженные частицы, называется силой Лоренца.
Сила Лоренца может быть описана как
F→=q(E→+v→ × B→)
Где
F — сила, действующая на заряженную частицу.
q — заряд частицы.
v — скорость частицы.
E — электрическое поле.
B — магнитное поле.
Правило левой руки Флеминга
Правило левой руки Флеминга описывает некоторые особые случаи, когда заряд наблюдает максимальные силы. Если растянуть большой, средний и указательный пальцы левой руки так, чтобы получился угол 90 градусов, то они лягут перпендикулярно друг другу. Эти пальцы представляют направление магнитного поля и скорость.
- Указательный или указательный палец показывает направление магнитного поля.
- Средний палец показывает направления движения электрического заряда.
- Большой палец показывает силу, наблюдаемую заряженной частицей.
Если скорость v→ лежит на оси x, магнитное поле B→ лежит на оси y, а магнитная сила F→ лежит на оси z.
Сила магнитного поля на проводе с током
Возьмем проводник или провод с током. Сила, заключенная в проводнике или проводе, обусловлена его магнитным полем. Когда заряженные частицы движутся ниже магнитного поля, существуют некоторые силы, перпендикулярные движению заряженных частиц. Длина провода или проводника равна l, а площадь поперечного сечения равна A. В проводнике или проводе с током число движущихся электронов принимается равным 9.0036 и .
Длина провода или проводника равна l, а площадь поперечного сечения равна A. В проводнике или проводе с током число движущихся электронов принимается равным 9.0036 и .
В дальнейшем общее количество заряженных частиц описывается как nAI, где I — стабильный ток, протекающий в проводнике или проводе. Скорость дрейфа каждого движущегося электрона представлена vd. Проводник с током находится в магнитном поле B. Таким образом, магнитная сила, приложенная к движущимся электронам, может быть выражена как
F=(nAI)qvd× B
носители заряда или электроны.
Использование магнитной силы
Масс-спектрометр
Масс-спектрометры широко используются для определения состава, свойств и химической структуры различных материалов с помощью магнитного поля (или магнетизма) и электрического поля.
Электронно-лучевая трубка (ЭЛТ)
Электронные лучи ЭЛТ генерируются электронной пушкой, расположенной в катоде. Две пары магнитных катушек используются для направления электронов в вертикальном направлении, а другая — в горизонтальном направлении для достижения цели. Эти ЭЛТ-трубки используются во многих старых телевизорах, осциллографах и компьютерных мониторах.
Эти ЭЛТ-трубки используются во многих старых телевизорах, осциллографах и компьютерных мониторах.
Магнитно-резонансная томография (МРТ)
Магнитно-резонансная томография является важным методом, используемым в медицине. Он используется для изображения внутренних органов и тканей из-за их магнетизма.
Ферромагнетизм
Ферромагнитные материалы играют жизненно важную роль в современных технологиях. Благодаря высокому магнитному свойству эти ферромагнитные материалы используются в датчиках, жестких дисках, магнитофонах, трансформаторах, динамиках и т. д.
Компас
Компас — это инструмент или устройство для определения направления в результате действия магнитного поля. Штифтовая магнитная стрелка, помещенная на компасе, свободно перемещается лицом в направлении севера или юга.
Электродвигатель
В нашей повседневной жизни мы используем фены, триммеры и электрические бритвы, все из которых работают с помощью магнитной силы. Здесь электродвигатели преобразуют электрическую энергию в магнитные поля с помощью катушки. Магнитное поле создает магнитную силу, которая позволяет двигателю работать.
Здесь электродвигатели преобразуют электрическую энергию в магнитные поля с помощью катушки. Магнитное поле создает магнитную силу, которая позволяет двигателю работать.
Формулы
Уравнение силы Лоренца определяется как,
F→=q(E→+v→ × B→)
Величина магнитной силы определяется как,
F=qvBsinθ
Контекст и приложения
Эта тема является одним из важнейших приложений во всех формах классической механики и важна как для бакалавриата, так и для аспирантов, особенно для:
- Бакалавров естественных наук (физика)
- Магистр наук (физика)
Практические задачи
1. Заряженная частица (q) движется в постоянном магнитном поле (B) со скоростью 3×103 м/с. Угол между магнитным полем и скоростью равен 25º. Найдите магнитную силу, действующую на заряженные частицы. Здесь q=3 мкКл и B=100 Гс.
а. 3,8×10-4N
б. 4,3×10-4Н
в. 6×10-3N
6×10-3N
d. 3×104N
Answer: a
Given data :
q=3 µC
B=100 G
v=3×103 m/s
θ=25°
Explanation:
Величина магнитной силы, действующей на подвижный носитель, рассчитывается по следующей формуле:
F=qvBsinθ =(3×10-4)×(3×103)×100×sin(25°)=3,8×10- 4 Н
Магнитная сила, действующая на подвижный носитель, равна 3,8×10-4 Н.
2. Когда заряды с током движутся в одном направлении в двух проводниках, сила равна __________.
а. Отталкивающий
б. Привлекательный
c. Противостояние
d. Втягивание
Ответ: b
Пояснение: Если два проводника имеют заряженные частицы, движущиеся в одном направлении, то силы двух проводников будут направлены друг к другу.
3. Пространство вокруг проводника с током, в котором может ощущаться его магнитное действие, называется ________.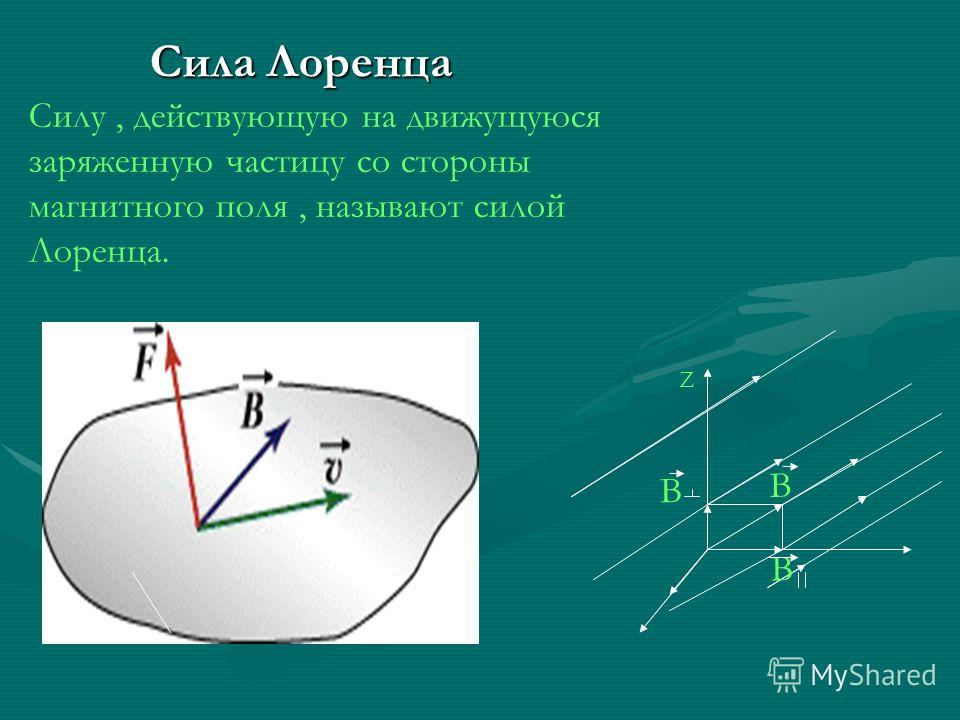
а. Электрический столб
б. Электрическое поле
c. Магнитный столб
d. Магнитное поле
Ответ: d
Пояснение: Когда ток проходит через проводник, он изменяет пространство вокруг проводника и образует магнитное поле.
4. С какой силой действует неподвижный заряд, помещенный в магнитное поле?
а. Максимум
б. Ноль
в. Минимум
д. Ничего из вышеперечисленного
Ответ: b
Объяснение: Неподвижный заряд не создает никакого магнитного поля и не взаимодействует с внешним магнитным полем. Следовательно, приложенная сила равна нулю.
5. Найти магнитную силу, действующую на заряд 2,5 Кл с магнитной индукцией 3 единицы, имеющий скорость 2 м/с.
а. 20 шт.
б. 15 шт.
гр. 28 ед.
д. 30 ед.
Ответ: b
Приведенные данные :
Заряд (q) = 2,5 Кл
Плотность потока (B) =3 ед.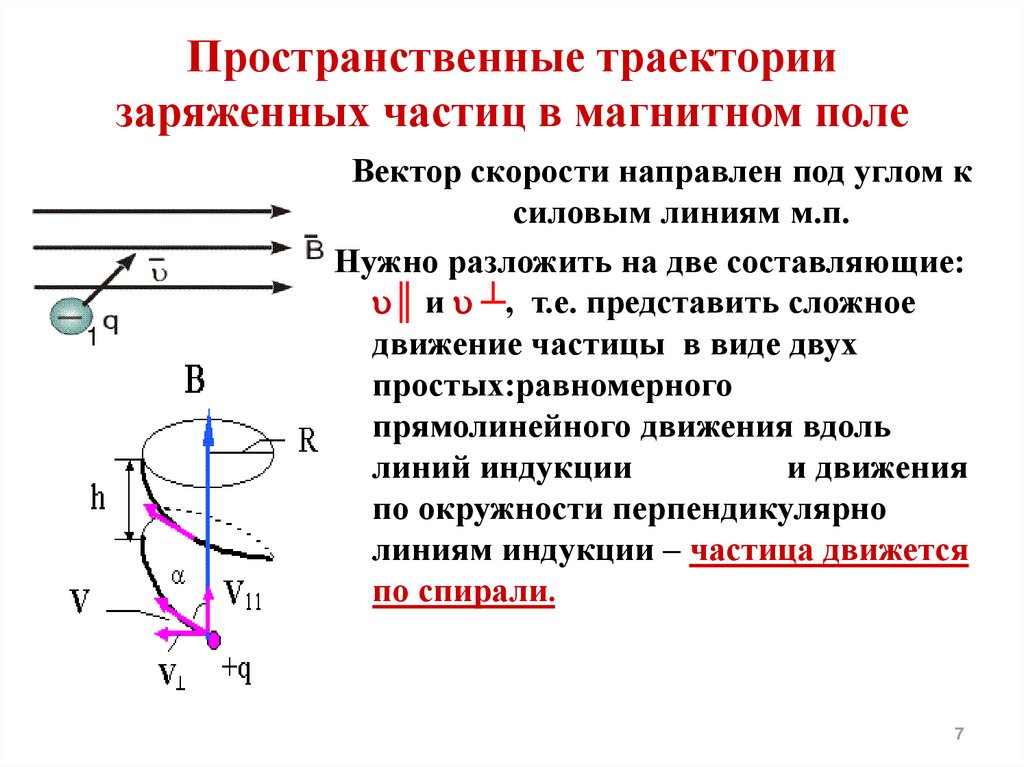
Скорость (v) = 902 м/с4
Объяснение:
Величина магнитной силы определяется формулой0023 Магнитная сила составляет 15 единиц.
Напряженность магнитного поля: сила, действующая на движущийся заряд в магнитном поле | Физика |
Цели обучения
К концу этого раздела вы сможете:
- Описывать влияние магнитных полей на движущиеся заряды.
- Используйте правило правой руки 1, чтобы определить скорость заряда, направление магнитного поля и направление магнитной силы, действующей на движущийся заряд.
- Рассчитайте магнитную силу, действующую на движущийся заряд.
Каков механизм воздействия одного магнита на другой? Ответ связан с тем фактом, что весь магнетизм вызван током, потоком заряда. Магнитные поля воздействуют на движущиеся заряды , и поэтому они воздействуют на другие магниты, все из которых имеют движущиеся заряды.
Правило правой руки 1
Магнитная сила, действующая на движущийся заряд, является одной из самых фундаментальных известных. Магнитная сила так же важна, как электростатическая или кулоновская сила. И все же магнитная сила более сложна как по количеству воздействующих на нее факторов, так и по своему направлению, чем относительно простая кулоновская сила. Величина Магнитная сила F на зарядке Q Перемещение на скорости V в магнитном поле прочности B дается
F = QVB SIN θ , QVB SIN θ , . QVB SIN .
где θ — угол между направлениями v и B. Эту силу часто называют силой Лоренца . Фактически именно так мы определяем напряженность магнитного поля B — через силу, действующую на заряженную частицу, движущуюся в магнитном поле. Единица СИ для напряженности магнитного поля B называется тесла (T) в честь эксцентричного, но гениального изобретателя Николы Теслы (1856–1943).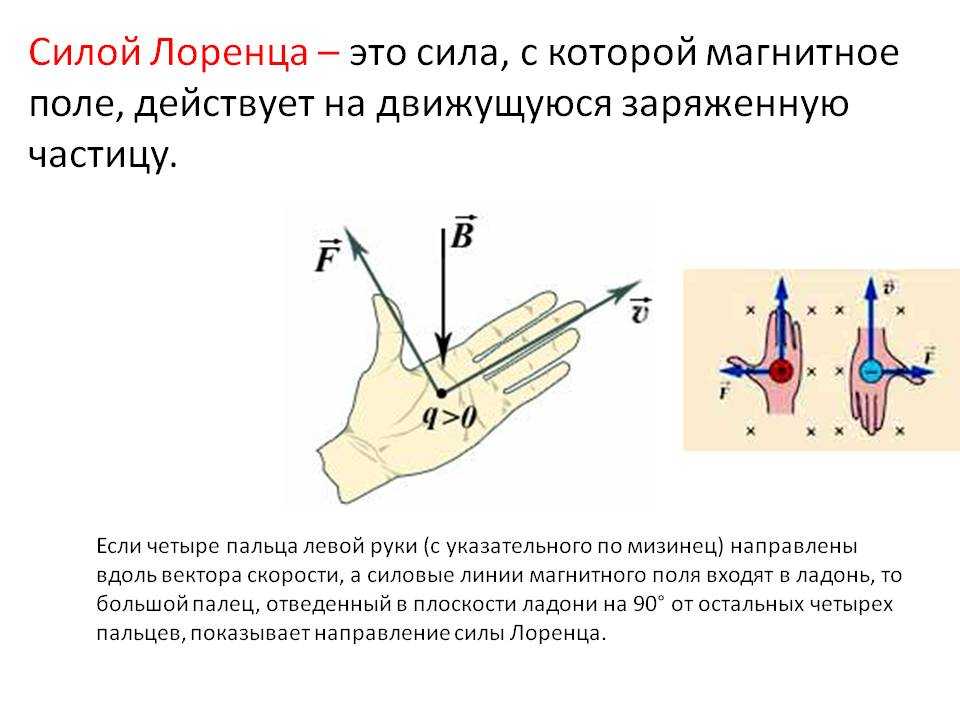 Чтобы определить, как тесла соотносится с другими единицами СИ, мы решаем F = qvB sin θ для B .
Чтобы определить, как тесла соотносится с другими единицами СИ, мы решаем F = qvB sin θ для B .
B=FqvsinθB=\frac{F}{qv \sin\theta}\\B=qvsinθF
Поскольку sin θ безразмерно, тесла равен
1 T=1 N C⋅ м/с=1 NA⋅ м1\text{ T}=\frac{1\text{ N}}{\text{ C} \cdot\text{ м/с}}=\frac{1\text{ N}}{\text{A}\cdot\text{ м}}\\1 T= C⋅ м/с1 N=A⋅ м1 N
(обратите внимание, что C/s = A). Иногда используется другая меньшая единица, называемая гаусс (G), где 1 G = 10 −4 Тл. Самые сильные постоянные магниты имеют поля около 2 Тл; сверхпроводящие электромагниты могут достигать 10 Тл и более. Магнитное поле Земли на ее поверхности составляет всего около 5 × 10 −5 Тл, или 0,5 Гс.
, как определено правило правой руки 1 (или RHR-1 ), которое показано на рисунке 1. RHR-1 утверждает, что для определения направления магнитной силы на положительный движущийся заряд вы указываете большим пальцем правой руки в направлении v , пальцы в направлении B , а перпендикуляр к ладони указывает в направлении F . Один из способов запомнить это состоит в том, что существует одна скорость, и поэтому ее представляет большой палец. Есть много линий поля, поэтому пальцы представляют их. Сила направлена в том направлении, куда вы бы толкнули ладонью. Сила, действующая на отрицательный заряд, направлена прямо противоположно силе на положительном заряде.
Один из способов запомнить это состоит в том, что существует одна скорость, и поэтому ее представляет большой палец. Есть много линий поля, поэтому пальцы представляют их. Сила направлена в том направлении, куда вы бы толкнули ладонью. Сила, действующая на отрицательный заряд, направлена прямо противоположно силе на положительном заряде.
Рис. 1. Магнитные поля воздействуют на движущиеся заряды. Эта сила является одной из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B, и следует правилу правой руки-1 (RHR-1), как показано. Величина силы пропорциональна q, v, B и синусу угла между v и B.
Соединения: заряды и магниты На статические заряды не действует магнитная сила. Однако на движущиеся заряды действует магнитная сила. Когда заряды неподвижны, их электрические поля не действуют на магниты. Но когда заряды движутся, они создают магнитные поля, которые воздействуют на другие магниты. При относительном движении возникает связь между электрическим и магнитным полями — одно влияет на другое.
При относительном движении возникает связь между электрическим и магнитным полями — одно влияет на другое.
Пример 1. Расчет магнитной силы: магнитное поле Земли на заряженном стеклянном стержне
За исключением компаса, вы редко видите или лично испытываете силы, связанные с небольшим магнитным полем Земли. Чтобы проиллюстрировать это, предположим, что в физической лаборатории вы натираете стеклянную палочку шелком, помещая на нее положительный заряд в 20 нКл. Вычислите силу, действующую на стержень со стороны магнитного поля Земли, если бросить его с горизонтальной скоростью 10 м/с строго на запад в месте, где поле Земли направлено строго на север параллельно земле. (Направление силы определяется правилом правой руки 1, как показано на рисунке 2.)
Рис. 2. Положительно заряженный объект, движущийся строго на запад в области, где магнитное поле Земли направлено строго на север, подвергается воздействию силы, направленной прямо вниз, как показано на рисунке. Отрицательный заряд, движущийся в том же направлении, почувствовал бы силу прямо вверх.
Отрицательный заряд, движущийся в том же направлении, почувствовал бы силу прямо вверх.
Нам дан заряд, его скорость, напряженность и направление магнитного поля. Таким образом, мы можем использовать уравнение F = qvB sin θ , чтобы найти силу.
9{-11}\text{ N}\end{массив}\\F==(20×10−9 C)(10 м/с)(5×10−5 T)1×10−11(C ⋅ м/с)( C⋅ м/сN)=1×10−11 N.
Обсуждение Этой силой можно пренебречь на любом макроскопическом объекте, что согласуется с опытом. (Оно вычисляется только с точностью до одной цифры, поскольку поле Земли меняется в зависимости от местоположения и выражается только одной цифрой.) Однако магнитное поле Земли оказывает очень важное воздействие, особенно на субмикроскопические частицы. Некоторые из них исследуются в книге «Сила движущегося заряда в магнитном поле: примеры и приложения».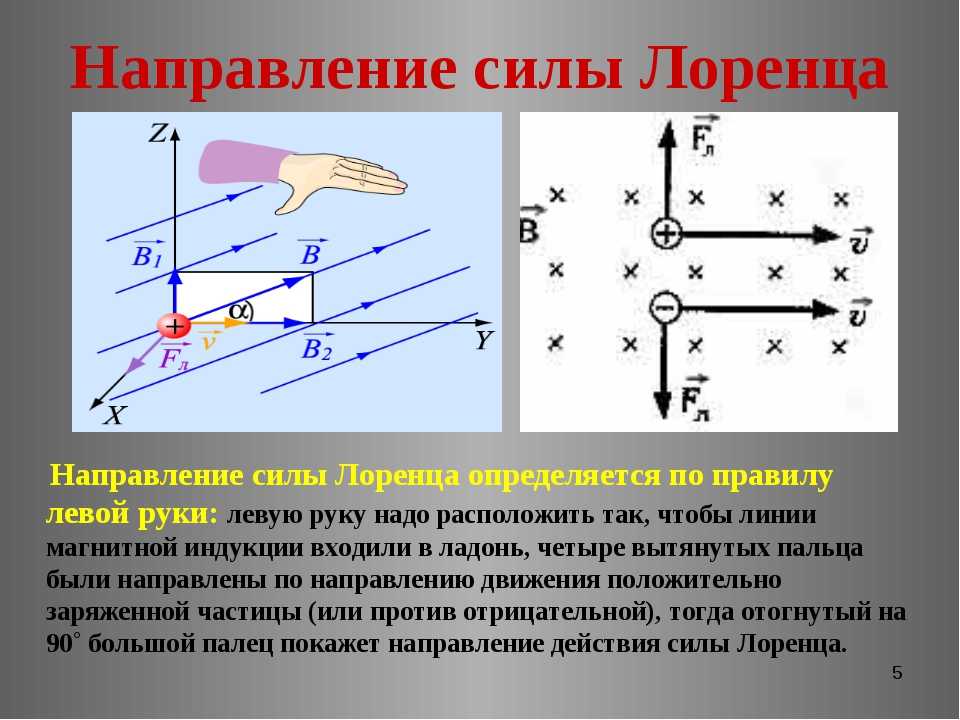
Резюме раздела
Концептуальные вопросы
1. Если заряженная частица движется прямолинейно через некоторую область пространства, можете ли вы сказать, что магнитное поле в этой области обязательно равно нулю?
Задачи и упражнения
1. Каково направление магнитной силы, действующей на положительный заряд, который движется так, как показано в каждом из шести случаев, показанных на рис. 3?
Рис. 3.
2. Повторите упражнение 1 для отрицательного заряда.
3. Каково направление скорости отрицательного заряда, на который действует магнитная сила, показанная в каждом из трех случаев на рис. 4, если предположить, что он движется перпендикулярно B ?
Рис. 4.
4.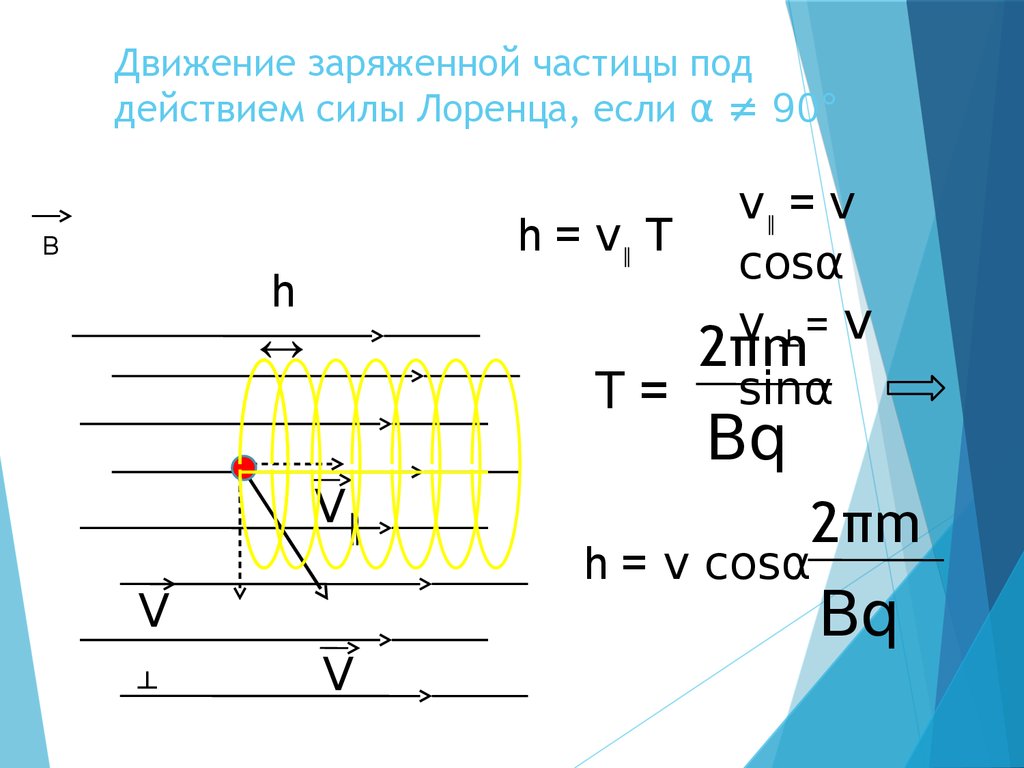 Повторите рисунок 4 для положительного заряда.
Повторите рисунок 4 для положительного заряда.
5. Каково направление магнитного поля, которое создает магнитную силу на положительном заряде, как показано в каждом из трех случаев на рисунке ниже, при условии, что B перпендикулярно против ?
Рис. 5.
6. Повторите упражнение 5 для отрицательного заряда.
7. Какова максимальная сила на алюминиевом стержне с зарядом 0,100 мкКл, которую вы передаете между полюсами постоянного магнита 1,50 Тл со скоростью 5,00 м/с? В каком направлении сила?
8. (a) Самолеты иногда приобретают небольшие статические заряды. Предположим, что сверхзвуковая струя имеет заряд 0,500 мкКл и летит строго на запад со скоростью 660 м/с над южным магнитным полюсом Земли, где 8,00 × 10 −5 -T магнитное поле направлено прямо вверх. Каковы направление и величина магнитной силы на плоскости? (b) Обсудите, подразумевает ли значение, полученное в части (а), это значительный или незначительный эффект.
Каковы направление и величина магнитной силы на плоскости? (b) Обсудите, подразумевает ли значение, полученное в части (а), это значительный или незначительный эффект.
9. (a) Протон космического луча, движущийся к Земле со скоростью 5,00 × 10 7 , испытывает магнитную силу 1,70 × 10 −16 Н. Какова напряженность магнитного поля, если между ними существует угол 45º а скорость протона? (b) Соответствует ли значение, полученное в части (а), известной напряженности магнитного поля Земли на ее поверхности? Обсуждать.
10. На электрон, движущийся со скоростью 4,00 × 10 3 м/с в магнитном поле силой 1,25 Тл, действует магнитная сила 1,40 × 10 −16 Н. Какой угол составляет скорость электрона с магнитным полем? Есть два ответа.
11. (a) Физик, выполняющий чувствительные измерения, хочет ограничить магнитную силу, действующую на движущийся заряд в ее оборудовании, величиной менее 1,00 × 10 92 349 −12 92 350 Н. Каким наибольшим может быть заряд, если он движется с максимальной скорость 30,0 м/с в поле Земли? (b) Обсудите, будет ли трудно ограничить заряд меньше значения, найденного в (а), сравнив его с типичным статическим электричеством и отметив, что статическое электричество часто отсутствует.
Каким наибольшим может быть заряд, если он движется с максимальной скорость 30,0 м/с в поле Земли? (b) Обсудите, будет ли трудно ограничить заряд меньше значения, найденного в (а), сравнив его с типичным статическим электричеством и отметив, что статическое электричество часто отсутствует.
Глоссарий
- Правило правой руки 1 (RHR-1):
- правило для определения направления магнитной силы на положительный движущийся заряд: когда большой палец правой руки указывает направление скорости заряда v и пальцы указывают в направлении магнитного поля B , тогда сила на заряде перпендикулярна и направлена от ладони; сила отрицательного заряда перпендикулярна ладони
- сила Лоренца:
- сила, действующая на заряд, движущийся в магнитном поле
- тесла:
- Тл, единица СИ напряженности магнитного поля;
1 T=1 N A⋅ m1\text{ T}=\frac{1 \text{ N}}{\text{ A}\cdot \text{ m}}\\1 T= A⋅ m1 N
- магнитная сила:
- сила, действующая на заряд при его движении через магнитное поле; сила Лоренца
- гаусс:
- Гс, единица напряженности магнитного поля; 1 г = 10 –4 T
Избранные решения задач и упражнений
1. (a) Влево (Запад) (b) На страницу (c) Вверх (Север) (d) Без силы (e) Вправо (Восток) (f) Вниз (Юг)
(a) Влево (Запад) (b) На страницу (c) Вверх (Север) (d) Без силы (e) Вправо (Восток) (f) Вниз (Юг)
3. (a) Восток ( справа) (b) На страницу (c) Юг (вниз)
5. (a) На страницу (b) Запад (слева) (c) За пределы страницы
7. 7,50 × 10 −7 N перпендикулярно как силовые линии магнитного поля, так и скорость
9. (а) 3,01 × 10 −5 Тл (б) Это немного меньше напряженности магнитного поля 5 × 10 −5 Тл на поверхности Земли, поэтому оно соответствует.
10. (a) 6,67 × 10 −10 C (считая поле Земли равным 5,00 × 10 −5 Tл) (b) Менее типичного статического, поэтому сложно
Лицензии и ссылки
Контент по лицензии CC, совместно используемый ранее
- College Physics. Автор: : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units.
 Лицензия : CC BY: Attribution . Условия лицензии : Находится в лицензии
Лицензия : CC BY: Attribution . Условия лицензии : Находится в лицензии
Магнитный эффект текущих банкнот
Магнитный эффект текущих банкнот ТЕМА: Магнитное действие тока
Движение заряженной частицы в комбинированном электрическом и магнитном поле
Когда на движущуюся заряженную частицу одновременно воздействуют и электрическое поле, и магнитное поле B, на движущуюся заряженную частицу будут действовать электрическая сила Fe = qE и магнитная сила Fm = q(v × B), поэтому результирующая сила, действующая на него, будет равна
F = q[ E + (v × B)], которое называется уравнением силы Лоренца:
Случай (I), когда все три v, B и E коллинеарны
поле, магнитная сила на него будет равна нулю и будет действовать только электрическая сила, поэтому
Следовательно, частица будет двигаться прямолинейно с изменяющейся скоростью и, следовательно, кинетической энергией, импульс также изменится
Случай (II) v, E и B взаимно перпендикулярны
v, Е и В взаимно перпендикулярны.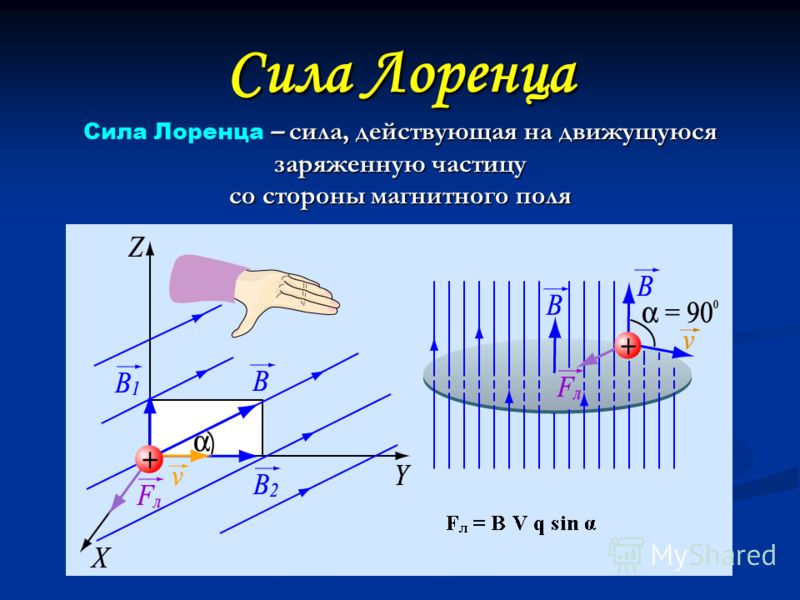
В случае, если положение E и B таково, что
F = Fe + Fm = 0
Тогда a = 0, частица будет двигаться в исходном состоянии без изменения скорости в этом положении
qE = qvB
или v = E/B
Этот принцип используется в селекторе скорости для получения заряженного пучка с определенной скоростью
РЕШЕННАЯ ЗАДАЧА
Q) Частица массой 1×10-26 кг и зарядом +1,6×10-19 Кл, движущаяся со скоростью 1,28×106 м /s в направлении +x входит в область, в которой присутствуют однородное электрическое поле E и однородное магнитное поле b, такие что Ex = Ey = 0; Ez = 102,4 кВ/м
и Bx = Bz = 0, Bz = 8×10-2 вт/м2. Частица входит в область в начале координат в момент времени t = 0.
Найдите положение (x, y, z) частицы в момент времени t = 5×10-6 с
Решение:
Из уравнения Лоренца
F =q[ E +(v × B)]
F=q[102,4 × 103 i + (1,28 × 106 i × 8×10-2 k )]
F=q[102,4 × 103 i + ( -102,4 × 103 i )]
F =0
Следовательно, частица будет двигаться вдоль оси + x с постоянной скоростью 1,28 × 106 м/с
X=vt = 6,40 м
Местоположение: (6. 4, 0, 0)
4, 0, 0)
Циклотрон
Циклотрон — это устройство, используемое для ускорения заряженных частиц до высоких энергий. Он был разработан Лоуренсом.
Принцип
Циклотрон работает по принципу, согласно которому заряженная частица, движущаяся перпендикулярно магнитному полю, испытывает магнитную силу Лоренца, благодаря которой частица движется по круговой траектории.
Конструкция
Состоит из полого металлического цилиндра, разделенного на две секции D1 и D2, называемые Dees, заключенными в вакуумированную камеру. Ди держат отдельно, а источник ионов помещают в центр в промежутке между Ди. Они размещены между полюсом
штук сильного электромагнита. Магнитное поле действует перпендикулярно плоскости Ди. Dees подключены к высокочастотному генератору. Вся сборка вакуумирована, чтобы свести к минимуму столкновения между ионами и молекулами воздуха. На ДЭ подается переменное напряжение высокой частоты. В схеме, показанной на рис., положительные ионы или положительно заряженные частицы (например, протоны) испускаются в центре P.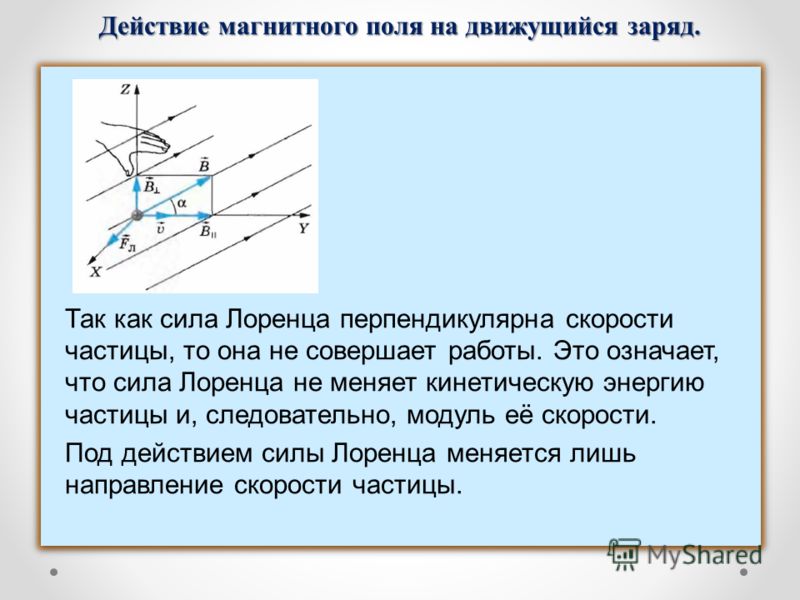
Рабочий
Когда положительный ион заряда q и массы m вылетает из источника, он ускоряется в направлении Ди, имеющий отрицательный потенциал в этот момент времени. Из-за нормального магнитного поля ион испытывает магнитную силу Лоренца и движется по круговой траектории. К тому времени, когда ион достигает промежутка между Ди, полярность Ди меняется на противоположную. Следовательно, частица еще раз ускоряется и движется в другой Ди с большей скоростью по окружности большего радиуса. Таким образом, частица движется по спирали с увеличивающимся радиусом и, подходя к краю, выносится с помощью
пластина дефлектора (D.P). Частица с высокой энергией теперь может поразить цель. Когда частица движется по окружности радиуса r со скоростью v, магнитная сила Лоренца обеспечивает необходимую центростремительную силу. Они движутся по полукругу в одном из дуанов и достигают промежутка между дуантами через интервал времени T/2; где Т, период обращения
г.
Время, необходимое для описания окружности
Из уравнения видно, что время, необходимое иону для описания окружности, не зависит от
(i) радиуса (r) пути и (ii) скорости (v) частица
Итак, в однородном магнитном поле ион проходит все окружности точно за одно и то же время.
Если высокочастотный осциллятор настроен на получение колебаний с частотой, указанной в уравнении, возникает резонанс. Циклотрон используется для ускорения протонов, дейтронов и
α — частицы.
Ограничения
(i) Поддержание однородного магнитного поля на большой площади Dees затруднено.
(ii) При больших скоростях релятивистское изменение массы частицы нарушает условие резонанса.
(iii) На высоких частотах заметно релятивистское изменение массы электрона и, следовательно, электроны не могут быть ускорены циклотроном.
Решенный числовой
В) Частица с зарядом 2C проходит через магнитное поле напряженностью 4 кТл и некоторое однородное электрическое поле со скоростью 25 и . Если сила Лоренца, действующая на него, равна 400 i Н, найти электрическое поле в этой области
Решение
Сила Лоренца
F =q[ E +(v ×B)]
400 i = 2 [E + 25(4 ) ( j × k )]
400 i = 2E + 200 i E = 100 i В/м
Все содержимое © Copyright 2013 www.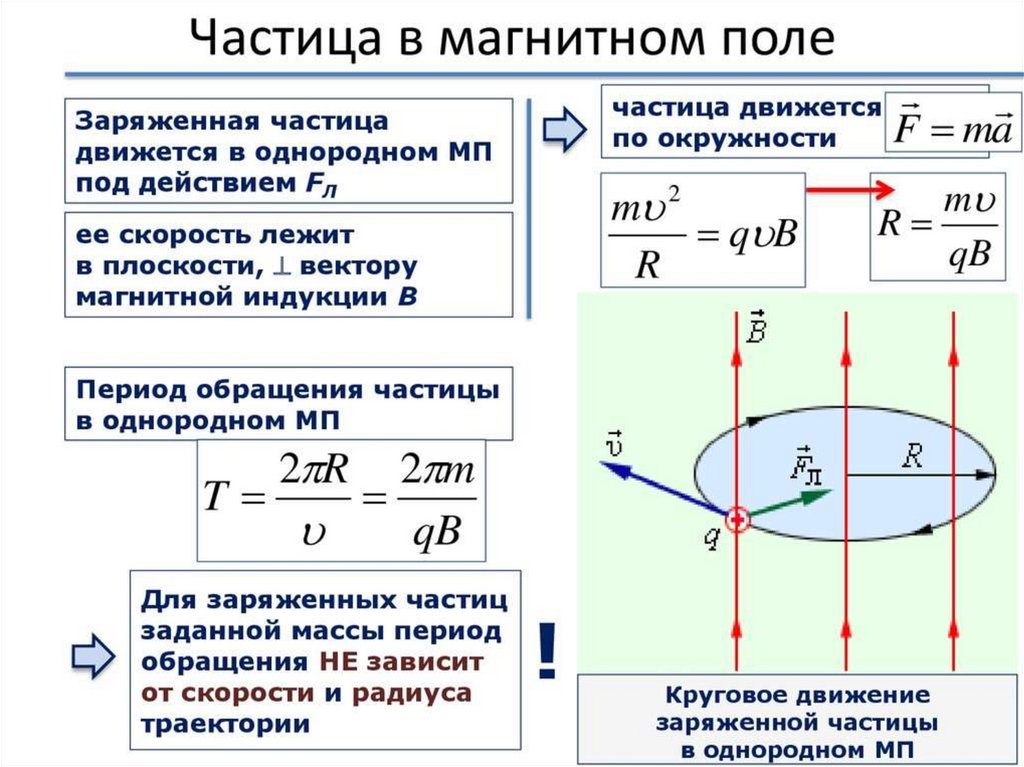 gneet.com
gneet.com
Дизайн сайта © 2013 Все права защищены Gore Coaching Classes
Сила, действующая на движущийся заряд в магнитном поле, называется магнитной силой Лоренца. — Сартакс eConnect
← Предыдущий вопрос Следующий вопрос →
1 ответ
+1 голос
ответил по сони02 (27,1 тыс. баллов)выбрано от Раджу Кумар
Лучший ответ
1. \(\overrightarrow F=q(\overrightarrow V\times \overrightarrow B)\)
2. Рассмотрим стержень однородного поперечного сечения A и длины I . Пусть n будет числом электронов в единице объема (численная плотность). ‘v d ’ – дрейфовая скорость электронов для постоянного тока ‘I’.
Общее количество электронов во всем объеме стержня = nAI
Заряд всех электронов = nA I . e ‘e’ – это заряд одного электрона.
e ‘e’ – это заряд одного электрона.
Сила Лоренца, действующая на электрон,
\(\overrightarrow F = nAle(\overrightarrow V_d\times \overrightarrow B)\)
\(\overrightarrow F=nAV_de(\overrightarrow l\times \overrightarrow B)\)
\(\overrightarrow F=I(\overrightarrow l\times \overrightarrow B)\) \( (I = neAV_d)\)
3. Да, когда электрон движется в магнитном поле под углом θ, электрон совершает спиральное движение. Скорость электрона имеет две составляющие: usinθ и ucosθ.
Компонент usinθ создает круговое движение, а ucosθ — поступательное движение. Комбинированный эффект кругового движения и поступательного движения будет спиральным движением.
← Предыдущий вопрос Следующий вопрос →
Похожие вопросы
Электрический заряд испытывает силу в однородном электрическом поле. Аналогично подвижный заряд
спросил
19 фев. 2021 г.
в движущихся зарядах и магнетизме
по
Раджу Кумар
(27,4 тыс. баллов)
баллов)
- движущиеся заряды и магнетизм 9-27 кг с положительным зарядом, равным удвоенному заряду электрона, движется с
спросил 19 фев. 2021 г. в движущихся зарядах и магнетизме по Раджу Кумар (27,4 тыс. баллов)
- движущиеся заряды и магнетизм
- класс-12
Направление движения блока положительного пробного заряда дает направление электрического поля.
спросил 18 фев. 2021 г. в движущихся зарядах и магнетизме по сони02 (27,1 тыс. баллов)
- движущиеся заряды и магнетизм
- класс-12
В комплект входят гальванометр, резистор и несколько соединительных проводов.
спросил 19 фев. 2021 г. в движущихся зарядах и магнетизме по Раджу Кумар (27,4 тыс. баллов)
- движущиеся заряды и магнетизм
- класс-12
Электрон, вращающийся вокруг ядра, действует как магнитный диполь.

спросил 19 фев. 2021 г. в движущихся зарядах и магнетизме по Раджу Кумар (27,4 тыс. баллов)
- движущиеся заряды и магнетизм
- класс-12
Категории
- Все категории
- JEE (28,1к)
- NEET (8,5к)
- Наука (740к)
- Математика (240к)
- Статистика (2,8к)
- Наука об окружающей среде (3,6к)
- Биотехнология (536)
- коммерция (62,1к)
- Электроника (3,7к)
- Компьютер (15,6к)
- Искусственный интеллект (ИИ) (1,4к)
- Информационные технологии (13,2к)
- Программирование (8.6к)
- Политическая наука (6,4к)
- Домашняя наука (4.0k)
- Психология (3,3к)
- Социология (5,5к)
- Английский (57,6к)
- хинди (20,3к)
- Способность (23,7к)
- Рассуждение (14,6к)
- ГК (25,7к)
- Олимпиада (527)
- Советы по навыкам (72)
- CBSE (710)
- РБСЭ (49,1к)
- Общий (56,9к)
- МСБШСЭ (1,8к)
- Совет Тамилнаду (59,3к)
- Совет Кералы
(24,5к)
- 12 класс
(10,6к)
- Математика (616)
- Физика
(462)
- Электрические заряды и поля (32)
- Электрический потенциал и емкость (42)
- Текущее электричество (51)
- Движущиеся заряды и магнетизм (42)
- Магнетизм и материя (19)
- Электромагнитная индукция (13)
- Переменный ток (24)
- Электромагнитные волны (16)
- Лучевая оптика и оптические приборы (38)
- Волновая оптика (31)
- Двойственная природа излучения и материи (41)
- Атомы (12)
- ядра (32)
- Полупроводниковая электроника: материалы, устройства и простые схемы (48)
- Системы связи (21)
- Химия
(1.

- 12 класс
(10,6к)


 А. Физика 11 кл.: Учебн. для общеобразоват. учреждений. 4-е изд., стереотип. – М.: Дрофа, 2004. – 416с.: ил., 8 л. цв. вкл., ст. 85, в. 5, з. 2–4.
А. Физика 11 кл.: Учебн. для общеобразоват. учреждений. 4-е изд., стереотип. – М.: Дрофа, 2004. – 416с.: ил., 8 л. цв. вкл., ст. 85, в. 5, з. 2–4.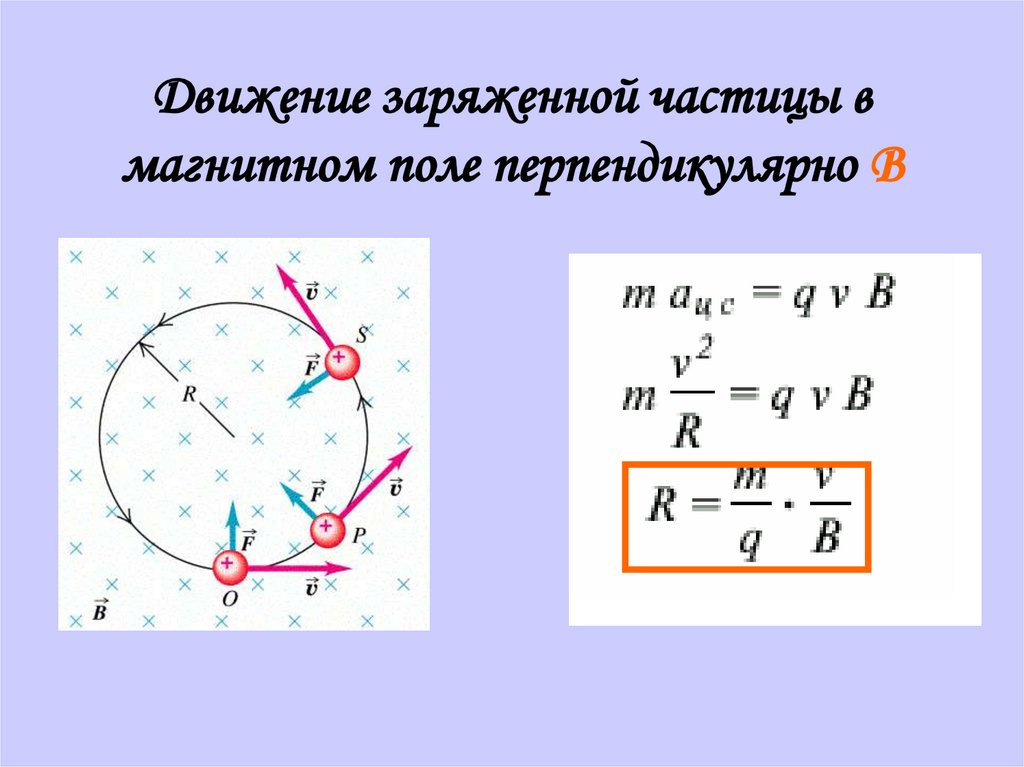 1 Электростатика
1 Электростатика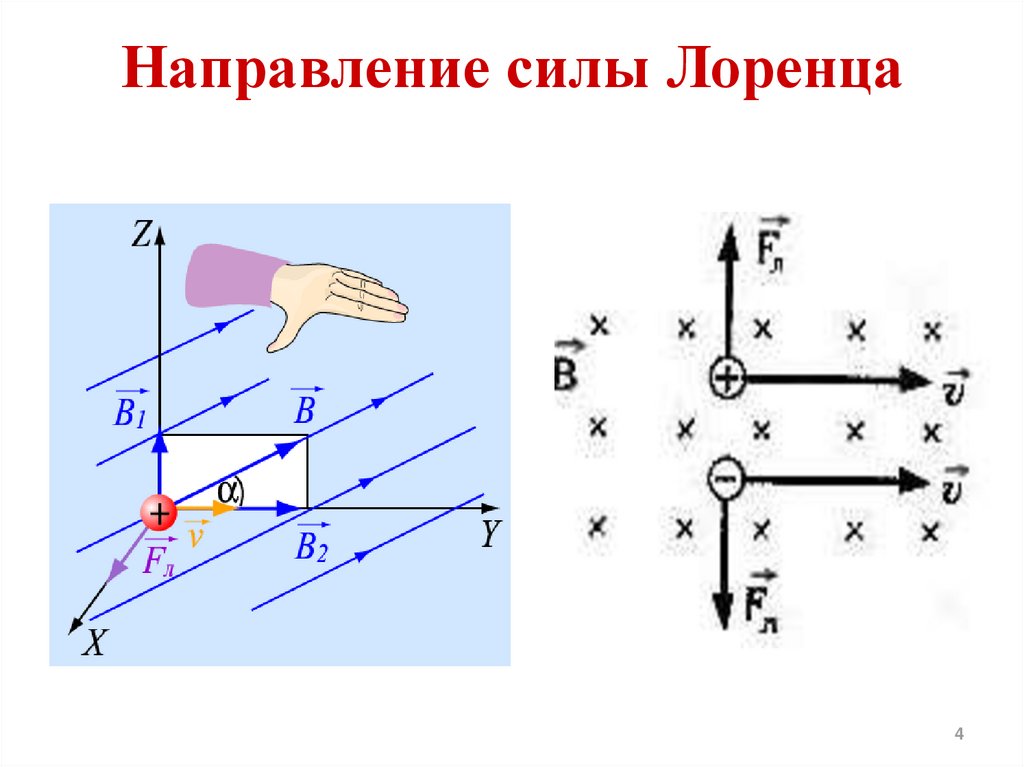

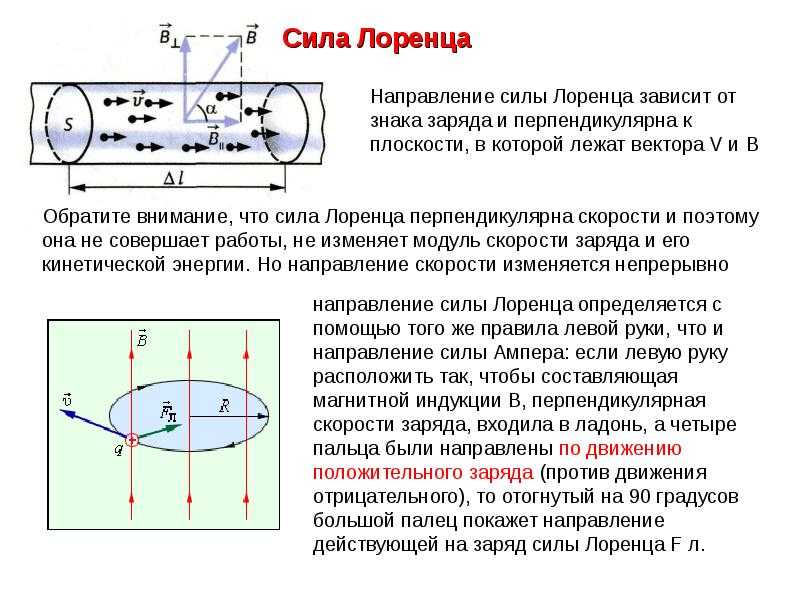 При
включении магнитного поля пятно
смещается в точку В. Найти смещение x
= АВ пучка электронов, если известно,
что индукция магнитного поля 14,6 мкТл.
При
включении магнитного поля пятно
смещается в точку В. Найти смещение x
= АВ пучка электронов, если известно,
что индукция магнитного поля 14,6 мкТл. Каково должно быть магнитное
поле, удовлетворяющее этому
условию?
Каково должно быть магнитное
поле, удовлетворяющее этому
условию? 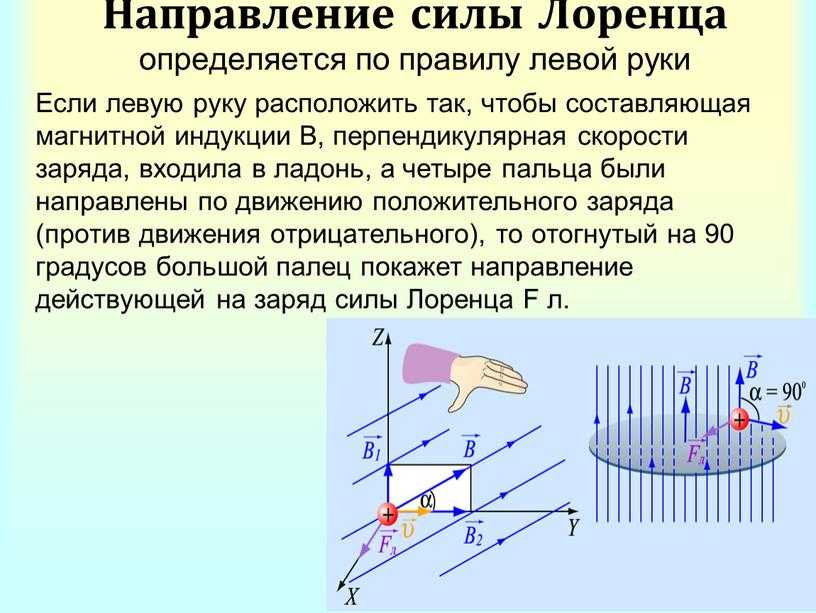 Она не зависит от скорости частицы.
Она не зависит от скорости частицы. Заряженные частицы будут вращаться вокруг этих силовых линий.
Заряженные частицы будут вращаться вокруг этих силовых линий.
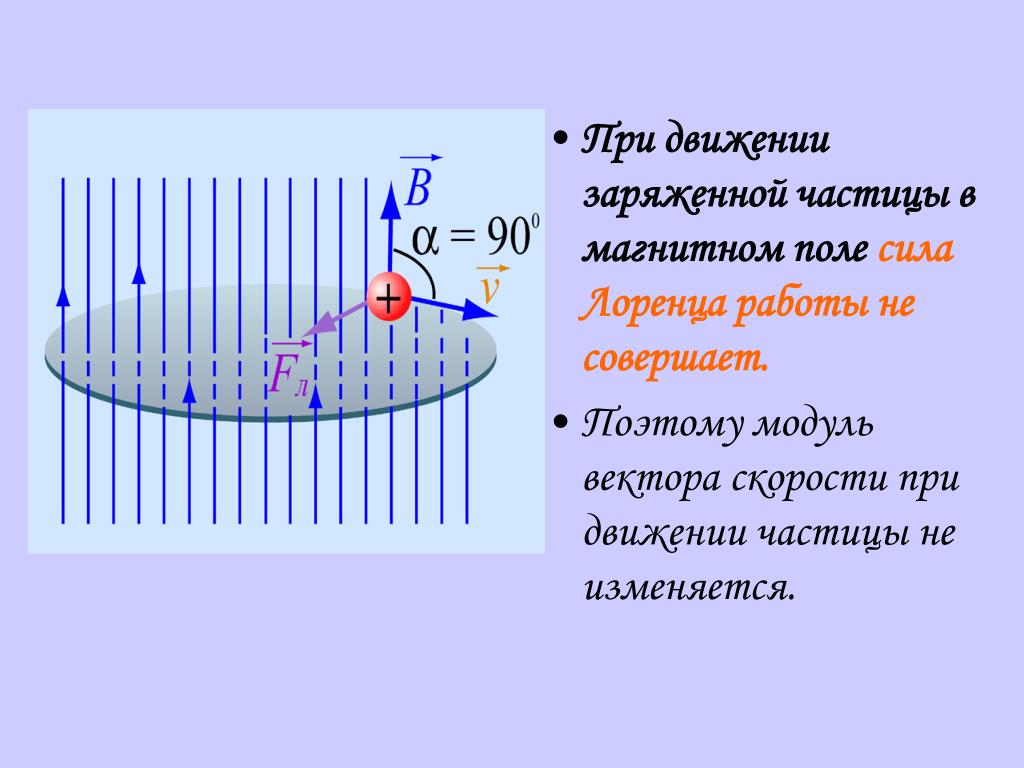
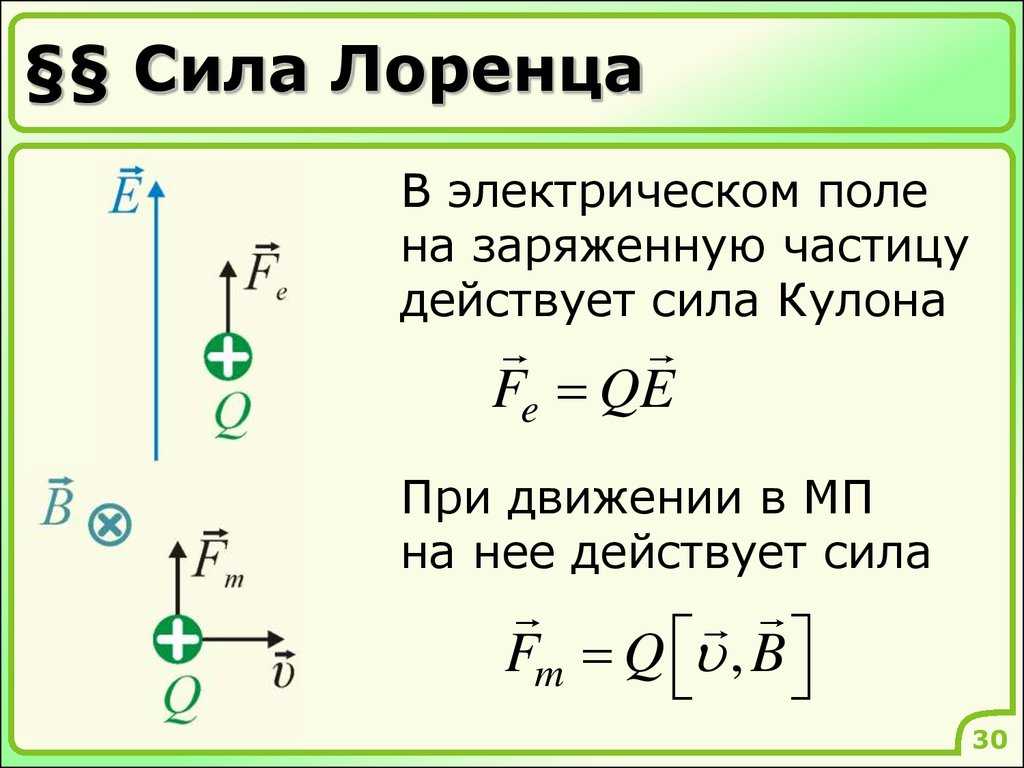 Дано равенством центростремительной силы и магнитной силы Лоренца.
Дано равенством центростремительной силы и магнитной силы Лоренца.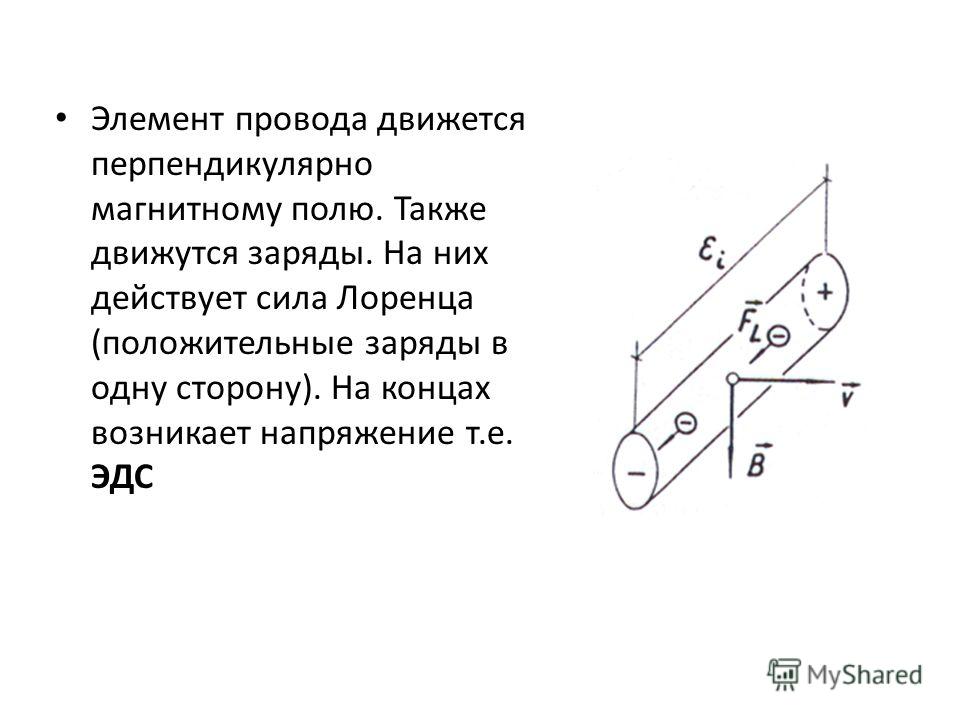
 Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution 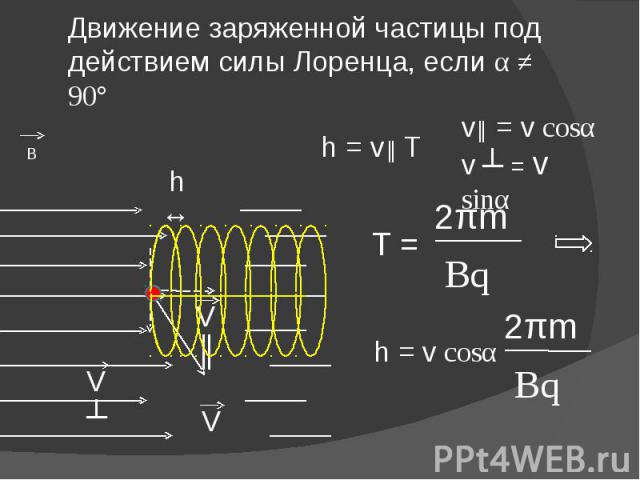 Wikipedia.org/wiki/Electric_force . Лицензия : CC BY-SA: Attribution-ShareAlike
Wikipedia.org/wiki/Electric_force . Лицензия : CC BY-SA: Attribution-ShareAlike  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  10 декабря 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
10 декабря 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution  17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution 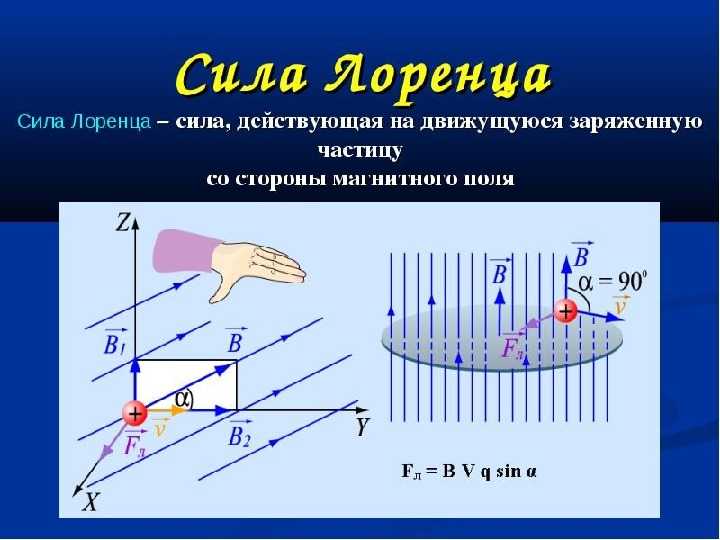 Расположен по адресу : http://cnx.org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution 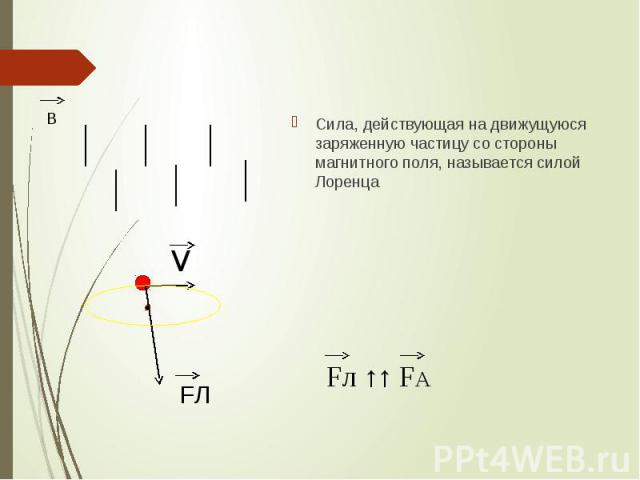 Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution  17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution 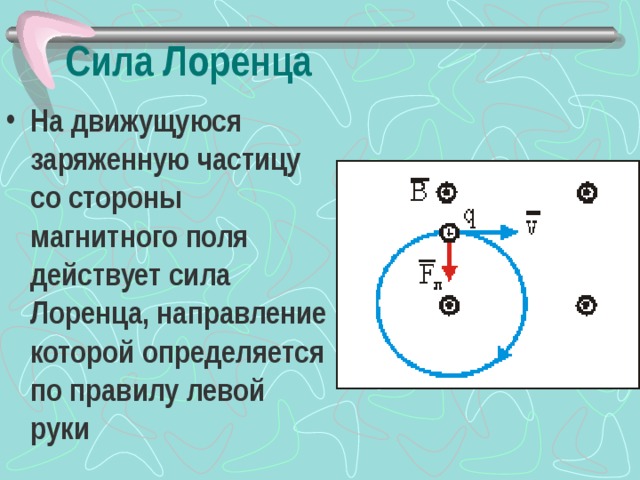 org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution 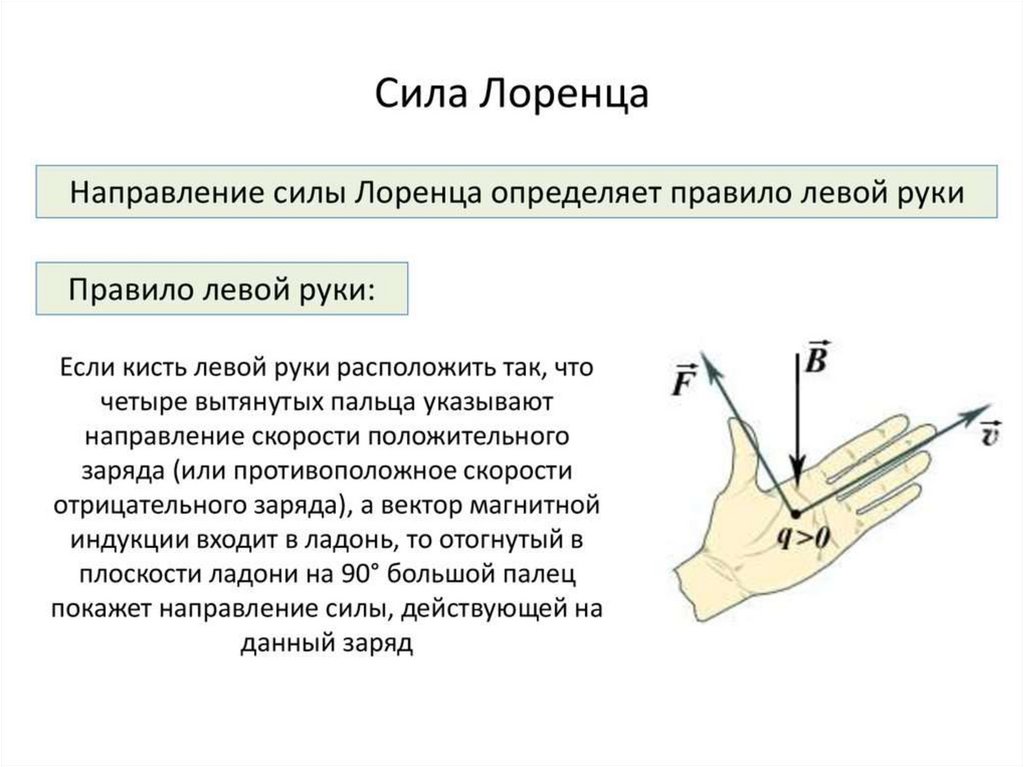 org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution 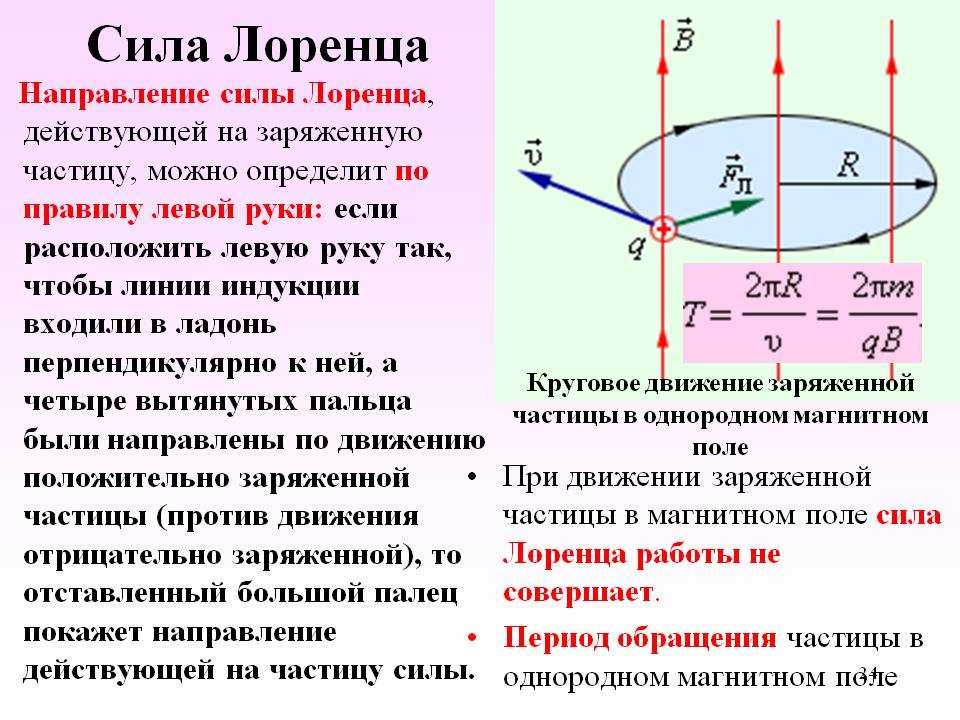 Лицензия : Общественное достояние: Нет данных Авторские права
Лицензия : Общественное достояние: Нет данных Авторские права  Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic%20mirror . Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Magnetic%20mirror . Лицензия : CC BY-SA: Attribution-ShareAlike  Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution  Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution  Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution 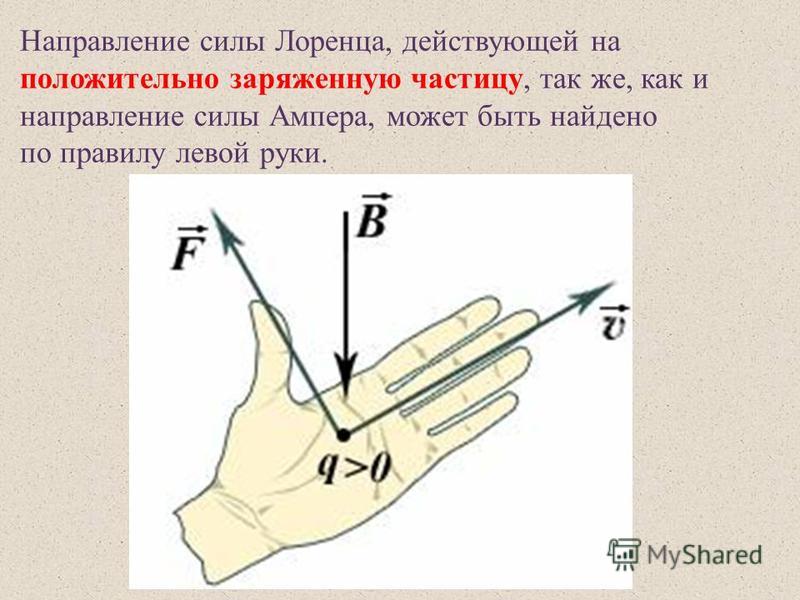 org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
org/content/m42375/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution  Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/cyclotron . Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/cyclotron . Лицензия : CC BY-SA: Attribution-ShareAlike  org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
org/content/m42312/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution  org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
org/content/m42372/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution  Лицензия : Общественное достояние: Нет данных Авторские права
Лицензия : Общественное достояние: Нет данных Авторские права 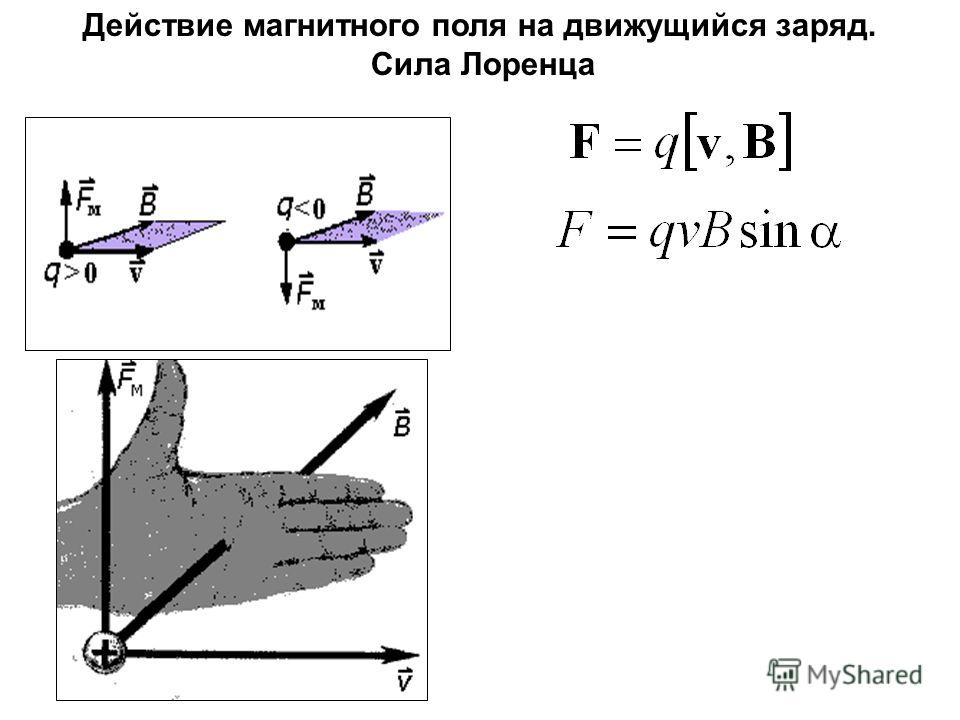 7 . Лицензия : CC BY: Атрибуция
7 . Лицензия : CC BY: Атрибуция 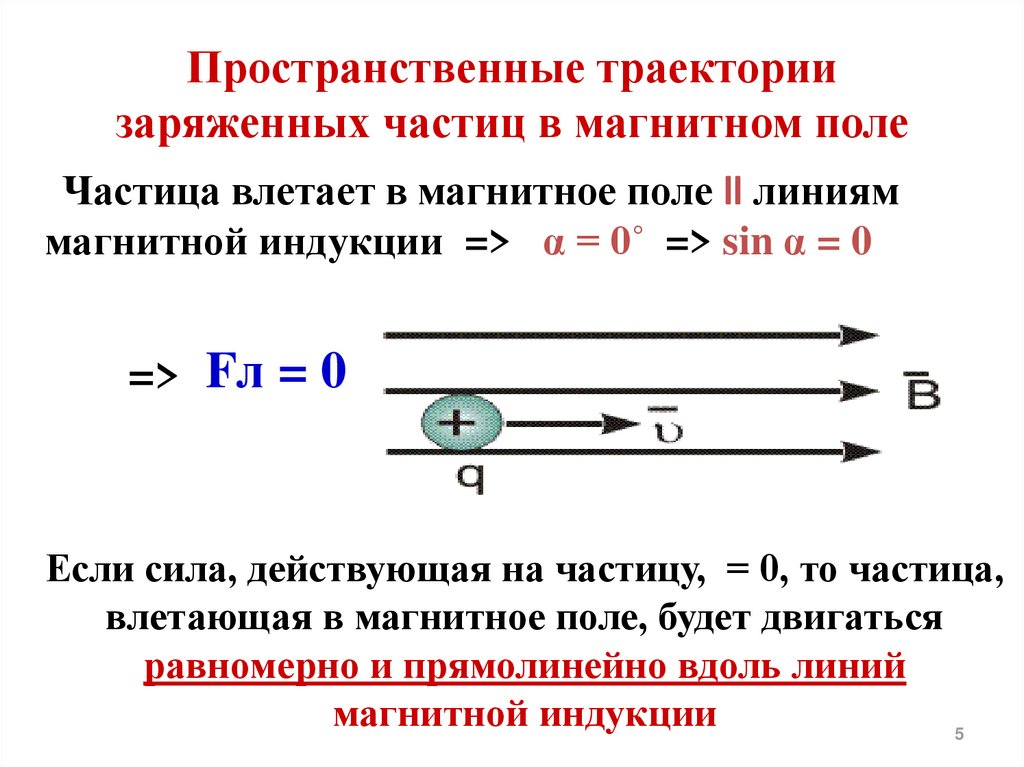 mit.edu/courses/electrical-engineering-and-computer-science/6-013-electromagnetics-and-applications-spring-2009
mit.edu/courses/electrical-engineering-and-computer-science/6-013-electromagnetics-and-applications-spring-2009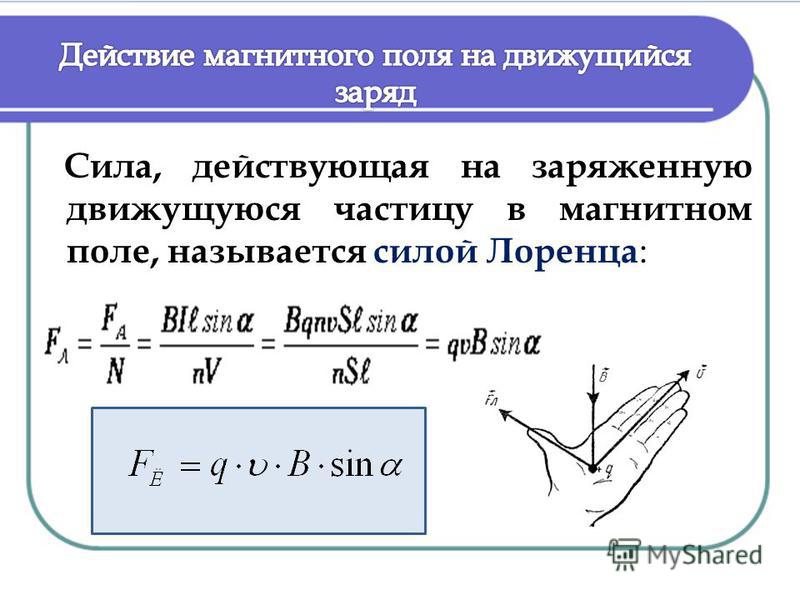 Лицензия : CC BY: Attribution . Условия лицензии : Находится в лицензии
Лицензия : CC BY: Attribution . Условия лицензии : Находится в лицензии