Электростатика — Википедия

Электростатика (от др.-греч. ἤλεκτρον, «янтарь», и лат. staticus, «неподвижный») — раздел учения об электричестве, изучающий взаимодействие неподвижных электрических зарядов.

Издавна известно, что некоторые материалы, например янтарь, притягивают легкие предметы (пушинки, пылинки, кусочки бумаги). Электростатические явления возникают вследствие взаимодействия электрических зарядов друг с другом. Сила этого взаимодействия описывается законом Кулона. Несмотря на то, что электростатические силы могут показаться довольно слабыми, некоторые из них, например сила взаимодействия протона и электрона в атоме водорода, на 36 порядков больше, чем действующая между ними гравитационная сила.

Существует множество примеров электростатических явлений, начиная простым притяжением воздушного шарика к шерстяному свитеру, притяжение бумаги и тонера в лазерных принтерах, заканчивая спонтанным возгоранием зернохранилища вследствие электризации зерна.

Закон Кулона утверждает, что:

«Сила взаимодействия двух точечных зарядов в вакууме пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними.»

Эта сила направлена вдоль прямой, соединяющей эти заряды. Если заряды имеют одинаковый знак — они отталкиваются, если разный — притягиваются. Пусть r{\displaystyle r}— расстояние (в метрах) между двумя зарядами Q{\displaystyle Q} и q{\displaystyle q}, тогда абсолютная величина силы взаимодействия F{\displaystyle F}(в ньютонах) между ними будет равна:

F=14πε0qQr2=k0qQr2,{\displaystyle F={\frac {1}{4\pi \varepsilon _{0}}}{\frac {qQ}{r^{2}}}=k_{0}{\frac {qQ}{r^{2}}},}

где ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная вакуума, равная:

ε0≈10−936π≈8.854187817×10−12{\displaystyle \varepsilon _{0}\approx {10^{-9} \over 36\pi }\approx 8.854187817\times 10^{-12}}Ф/м.

Постоянная Кулона равна:

k0≈14πε0≈8.987551787×109{\displaystyle k_{0}\approx {\frac {1}{4\pi \varepsilon _{0}}}\approx 8.987551787\times 10^{9}} Н·м²·Кл⁻².

Использование ε₀ вместо k₀ в выражении закона Кулона связано с тем, что сила обратно пропорциональна площади поверхности сферы с радиусом, равным расстоянию между двумя зарядами.

Протон имеет заряд e, электрон имеет заряд −e. Величина е называется элементарный заряд и равна:

e≈1.602 176 565×10−19.{\displaystyle e\approx 1.602\ 176\ 565\times 10^{-19}.}

Физические константы (ε₀, k₀, e) в настоящее время определены так, что ε₀ и k₀ точно рассчитаны, а e — измеренная величина.

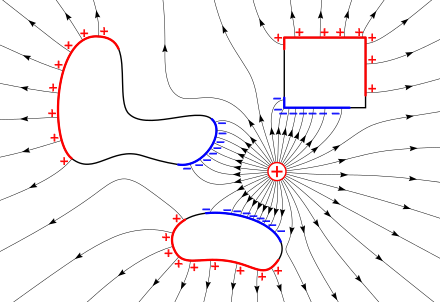Электрическое поле (линии со стрелками) положительного заряда (+) разделяет свободные заряды в проводниках. Явление разделения зарядов под действием электрического поля называется электростатическая индукция. Отрицательные заряды (синий) притягиваются и впоследствии перемещаются на поверхность проводника, обращенную к внешнему заряду. Положительные заряды (красный) отталкиваются и перемещаются на обратную сторону. Разделенные заряды равны и противоположны по знаку, поэтому электрические поля, созданные ими, компенсируют друг друга. Поэтому электрическое поле внутри проводников равно нулю, а потенциал — постоянная величина.

Электрическое поле — векторное поле, которое может быть определено в любой точке пространства вокруг заряда, исключая точку, в которой находится заряд (где поле равно бесконечности). Основной силовой характеристикой электрического поля является его напряженность E→{\displaystyle {\vec {E}}\,}. Она равна отношению силы F→{\displaystyle {\vec {F}}\,}, с которой поле действует на пробный точечный заряд, к величине этого заряда q{\displaystyle q\,}:

E→=F→q.{\displaystyle {\vec {E}}={{\vec {F}} \over q}.}

Визуализировать электрическое поле удобно с помощью силовых (полевых) линий. Силовые линии начинаются на положительном заряде и заканчиваются на отрицательном. Векторы напряженности поля являются касательными к линиям напряженности, а плотность линий является мерой величины поля, то есть чем гуще силовые линии, тем сильнее поле в данной области пространства.

Принцип суперпозиции полей[править | править код]

Если поле создается несколькими точечными зарядами, то на пробный заряд q{\displaystyle q} действует со стороны заряда Qi{\displaystyle Q_{i}} такая сила F→i{\displaystyle {\vec {F}}_{i}}, как если бы других зарядов не было. Результирующая сила определится выражением:

F→=∑i14πε0qQiri2ri→|ri|=∑iFi→,{\displaystyle {\vec {F}}=\sum \limits _{i}{\frac {1}{4\pi \varepsilon _{0}}}{\frac {qQ_{i}}{r_{i}^{2}}}{\frac {\vec {r_{i}}}{|r_{i}|}}=\sum \limits _{i}{\vec {F_{i}}},}

где ri{\displaystyle r_{i}}— расстояние между зарядами q{\displaystyle q} и Qi,{\displaystyle Q_{i},} а r→i|ri|{\displaystyle {\frac {{\vec {r}}_{i}}{|r_{i}|}}}- единичный вектор, характеризующий направление поля. Так как F→=qE→,{\displaystyle {\vec {F}}=q{\vec {E}},} то E→{\displaystyle {\vec {E}}} — результирующая напряженность поля в точке, где расположен пробный заряд q{\displaystyle q}, так же подчиняется принципу суперпозиции:

E→=E1→+E2→+…=∑iEi→.{\displaystyle {\vec {E}}={\vec {E_{1}}}+{\vec {E_{2}}}+…=\sum \limits _{i}{\vec {E_{i}}}.}

Теорема Гаусса[править | править код]

Теорема Гаусса утверждает, что поток вектора электрической индукции D→{\displaystyle {\vec {D}}} через любую замкнутую поверхность S{\displaystyle S} пропорционален суммарному свободному электрическому заряду, заключённому внутри этой поверхности^[1]. Утверждение можно записать в виде уравнения:

∮S⁡D→⋅ds→=∫Vρdv,{\displaystyle \oint \limits _{S}{\vec {D}}\cdot d{\vec {s}}=\int \limits _{V}\rho dv,}

где ds→{\displaystyle d{\vec {s}}} — элемент поверхности S{\displaystyle S}, ρ{\displaystyle \rho } — объёмная плотность свободного заряда, dv=dx dy dz{\displaystyle dv=dx\ dy\ dz} — элемент объёма. Используя формулу Гаусса — Остроградского, можно записать данное уравнение в дифференциальной форме:

∇→⋅D→=ε0∇→⋅εE→=ρ.{\displaystyle {\vec {\nabla }}\cdot {\vec {D}}=\varepsilon _{0}{\vec {\nabla }}\cdot \varepsilon {\vec {E}}=\rho .}

Уравнения Пуассона и Лапласа[править | править код]

Определение электростатического потенциала в сочетании с дифференциальной формой закона Гаусса (выше) дает зависимость между потенциалом ϕ{\displaystyle \phi } и плотностью заряда ρ{\displaystyle \rho }:

∇2ϕ=−ρεε0.{\displaystyle {\nabla }^{2}\phi =-{\rho \over \varepsilon \varepsilon _{0}}.}

Это соотношение является формой уравнения Пуассона. При отсутствии свободного электрического заряда (когда объемная плотность равна нулю) уравнение становится уравнением Лапласа:

∇2ϕ=0.{\displaystyle {\nabla }^{2}\phi =0.}

Работа и потенциал электростатического поля[править | править код]

В основе электростатики лежит допущение того, что электростатическое поле E→{\displaystyle {\vec {E}}} является потенциальным (безвихревым):

∇→×E→=0.{\displaystyle {\vec {\nabla }}\times {\vec {E}}=0.}

Из этого допущения следует полное отсутствие изменяющихся во времени магнитных полей:

∂B→∂t=0.{\displaystyle {\frac {\partial {\vec {B}}}{\partial t}}=0.}

Однако, электростатика не требует отсутствия магнитных полей или электрических токов. Скорее, если магнитные поля или электрические токи существуют, то они не должны изменяться во времени, или, в худшем случае, они должны изменяться очень медленно.

Работа электрического поля[править | править код]

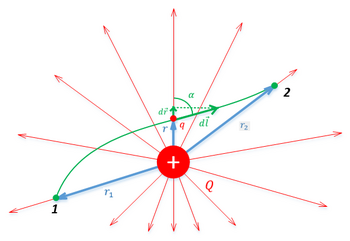Работа кулоновских сил при перемещении заряда q{\displaystyle q} зависит только от расстояний r1{\displaystyle r_{1}} и r2{\displaystyle r_{2}} начальной и конечной точек траектории.

Из механики известно определение элементарной работы:

dA=F→dℓ→.{\displaystyle dA={\vec {F}}d{\vec {\ell }}.}

Тогда, с учётом закона Кулона, работа, совершаемая полем заряда Q{\displaystyle Q}, при перемещении пробного заряда q{\displaystyle q} равна:

dA=Fdℓcos⁡α=14πε0qQr2dℓcos⁡α.{\displaystyle dA={F}d{\ell }\cos \alpha ={\frac {1}{4\pi \varepsilon _{0}}}{\frac {qQ}{r^{2}}}d\ell \cos \alpha .}

Так как dr=dℓcos⁡α{\displaystyle dr=d\ell \cos \alpha }, то интегрируя элементарную работу по dr{\displaystyle dr} получают:

A=∫r1r214πε0qQr2dℓcos⁡α=qQ4πε0∫r1r2drr2=qQ4πε0(1r1−1r2).{\displaystyle A=\int \limits _{r_{1}}^{r_{2}}{\frac {1}{4\pi \varepsilon _{0}}}{\frac {qQ}{r^{2}}}d\ell \cos \alpha ={\frac {qQ}{4\pi \varepsilon _{0}}}\int \limits _{r_{1}}^{r_{2}}{\frac {dr}{r^{2}}}={\frac {qQ}{4\pi \varepsilon _{0}}}\left({{\frac {1}{r_{1}}}-{\frac {1}{r_{2}}}}\right).}

Потенциал[править | править код]

Электростатическое поле потенциально, кулоновские силы — консервативные, а работа консервативных сил может быть представлена как убыль потенциальной энергии, то есть:

A=W1−W2=−ΔW.{\displaystyle A=W_{1}-W_{2}=-\Delta W.}

Таким образом, потенциальная энергия точечного заряда q{\displaystyle q} в поле, созданном зарядом Q{\displaystyle Q}, определяется как

W=k0qQr.{\displaystyle W=k_{0}{\frac {qQ}{r}}.}

Если исследовать электростатическое поле заряда Q{\displaystyle Q} различными пробными зарядами q0{\displaystyle q_{0}}, отношение

Wq0=k0Qr{\displaystyle {\frac {W}{q_{0}}}=k_{0}{\frac {Q}{r}}}

будет одинаковым для различных пробных зарядов, и это отношение называется потенциал. Потенциал является энергетической характеристикой электростатического поля, характеризующей потенциальную энергию W{\displaystyle W}, которой обладает единичный положительный пробный заряд q0{\displaystyle q_{0}}, помещённый в данную точку поля:

ϕ=Wq0.{\displaystyle \phi ={\frac {W}{q_{0}}}.}

Поскольку предполагается, что поле E→{\displaystyle {\vec {E}}} является безвихревым, его можно описать с помощью градиента потенциала. Электрическое поле направлено из области с высоким электрическим потенциалом в области с более низким. Математически это можно записать как

E→=−∇→ϕ.{\displaystyle {\vec {E}}=-{\vec {\nabla }}\phi .}

Используя формулу Гаусса—Остроградского можно показать, что разность потенциалов, так же известная как напряжение, представляет собой работу, совершаемую полем, при перемещении единичного заряда из точки a{\displaystyle a} в точку b{\displaystyle b}:

∫abE→⋅dℓ→=ϕ(a)−ϕ(b)=U.{\displaystyle \int \limits _{a}^{b}{{\vec {E}}\cdot \mathrm {d} {\vec {\ell }}}=\phi (a)-\phi (b)=U.}

Трибоэлектрический эффект представляет собой тип контактной электризации, при котором некоторые материалы приобретают заряд, когда они приводятся в контакт с другими материалами и затем разделяются. Один из материалов заряжается положительно, а другой приобретает отрицательный заряд. Полярность и величина создаваемых зарядов различаются в зависимости от материала, шероховатости поверхности, температуры, деформации и других свойств. Например, янтарь можно положительно зарядить при трении о шерсть. Это свойство, впервые описанное Фалесом Милетским, было первым электрическим явлением, исследованным людьми. Другие примеры материалов, которые могут получить заряд при трении включают стекло, потертое о шёлк, и твердый каучук, потертый о мех.

Как уже упомянуто выше, Максвелл явился истолкователем идей Фарадея. Он облек эти идеи в математическую форму. Основание теории Максвелла заключается не в законе Кулона, а в принятии гипотезы, которая выражается в следующем равенстве:

∬KFcos⁡εdS=4πQ.(13){\displaystyle \iint {KF\cos \varepsilon dS}=4\pi Q.\qquad (13)}

Здесь интеграл распространяется по какой угодно замкнутой поверхности S, F обозначает величину электрической силы, которую испытывает единица электричества в центре элемента этой поверхности dS, ε обозначает угол, образуемый этой силой с внешней нормалью к элементу поверхности dS, К обозначает диэлектрический коэффициент среды, прилегающей к элементу dS, и Q обозначает алгебраическую сумму количеств электричества, заключающихся внутри поверхности S. Следствиями выражения (13) являются нижеследующие уравнения:

∇K∇V+4πρ=0,(14){\displaystyle \nabla K\nabla V+4\pi \rho =0,\qquad (14)}

K1dVdn1+K2dVdn2+4πσ=0.(15){\displaystyle K_{1}{\frac {dV}{dn_{1}}}+K_{2}{\frac {dV}{dn_{2}}}+4\pi \sigma =0.\qquad (15)}

Эти уравнения более общи, чем уравнения (5) и (7). Они относятся к случаю каких угодно изотропных изолирующих сред. Функция V, являющаяся общим интегралом уравнения (14) и удовлетворяющая вместе с этим уравнению (15) для всякой поверхности, которая отделяет собой две диэлектрические среды с диэлектрическими коэффициентами K

1 и K₂, а также условию V = пост. для каждого, находящегося в рассматриваемом электрическом поле проводника, представляет собой потенциал в точке (x, у, z). Из выражения (13) также следует, что кажущееся взаимодействие двух зарядов q и q₁, находящихся в двух точках, расположенных в однородной изотропной диэлектрической среде на расстоянии r друг от друга, может быть представлено формулой

f=qq1Kr2,(16){\displaystyle f={\frac {qq_{1}}{Kr^{2}}},\qquad (16)}

то есть это взаимодействие обратно пропорционально квадрату расстояния, как это должно быть согласно закону Кулона.

Из уравнения (15) мы получаем для проводника:

σ=K4πdVdn,(17){\displaystyle \sigma ={\frac {K}{4\pi }}{\frac {dV}{dn}},\qquad (17)}

Fn=4πσK,(18){\displaystyle F_{n}={\frac {4\pi \sigma }{K}},\qquad (18)}

P=2πσ2K.(19){\displaystyle P={\frac {2\pi \sigma ^{2}}{K}}.\qquad (19)}

Формулы эти более общие, чем вышеприведенные (9), (10) и (12).

KFcos⁡εdS{\displaystyle KF\cos \varepsilon dS} представляет собой выражение потока электрической индукции через элемент dS. Проведя через все точки контура элемента dS линии, совпадающие с направлениями F в этих точках, мы получаем (для изотропной диэлектрической среды) трубку индукции. Для всех сечений такой трубки индукции, не заключающей внутри себя электричества, должно быть, как это следует из уравнения (14),

KFcos⁡εdS=const.{\displaystyle KF\cos \varepsilon dS=const.}

Не трудно доказать, что если в какой-либо системе тел электрические заряды находятся в равновесии, когда плотности электричества соответственно суть σ₁ и ρ₁ или σ₂ и ρ₂, то заряды будут в равновесии и тогда, когда плотности будут σ = σ₁ + σ₂ и ρ = ρ₁ + ρ₂  (принцип сложения зарядов, находящихся в равновесии). Равным образом легко доказать, что при данных условиях может быть только одно распределение электричества в телах, составляющих собой какую-либо систему.

Весьма важным оказывается свойство проводящей замкнутой поверхности, находящейся в соединении с землёй. Такая замкнутая поверхность является экраном, защитой для всего пространства, заключённого внутри неё, от влияния каких угодно электрических зарядов, расположенных с внешней стороны поверхности. Вследствие этого электрометры и другие измерительные электрические приборы окружаются обыкновенно металлическими футлярами, соединяемыми с землёй. Опыты показывают, что для таких электрических экранов нет надобности употреблять сплошной металл, вполне достаточно эти экраны устраивать из металлических сеток или даже металлических решёток.

Система наэлектризованных тел обладает энергией, то есть обладает способностью совершить определённую работу при полной потере своего электрического состояния. B электростатике выводится следующее выражение для энергии системы наэлектризованных тел:

W=12ΣVQ.(20){\displaystyle W={\frac {1}{2}}\Sigma VQ.\qquad (20)}

В этой формуле Q и V обозначают соответственно какое-либо количество электричества в данной системе и потенциал в том месте, где находится это количество; знак ∑ указывает, что надо взять сумму произведений VQ для всех количеств Q данной системы. Если система тел представляет собой систему проводников, то для каждого такого проводника потенциал имеет одну и ту же величину во всех точках этого проводника, а потому в данном случае выражение для энергии получает вид:

W=12(V1q1+V2q2+…+Vnqn).(21){\displaystyle W={\frac {1}{2}}\left(V_{1}q_{1}+V_{2}q_{2}+…+V_{n}q_{n}\right).\qquad (21)}

Здесь 1, 2.. n суть значки разных проводников, входящих в состав системы. Это выражение может быть заменено другими, а именно, электрическая энергия системы проводящих тел может быть представлена или в зависимости от зарядов этих тел, или же в зависимости от потенциалов их, то есть для этой энергии могут быть применены выражения:

WQ=12α11Q12+α12Q1Q2+α13Q1Q3+…+12α22Q22+α23Q2Q3+…+12αnnQn2,(22){\displaystyle W_{Q}={\frac {1}{2}}\alpha _{11}Q_{1}^{2}+\alpha _{12}Q_{1}Q_{2}+\alpha _{13}Q_{1}Q_{3}+…+{\frac {1}{2}}\alpha _{22}Q_{2}^{2}+\alpha _{23}Q_{2}Q_{3}+…+{\frac {1}{2}}\alpha _{nn}Q_{n}^{2},\qquad (22)}

WV=12β11V12+β12V1V2+β13V1V3+…+12β22V22+β23V2V3+…+12βnnVn2.(23){\displaystyle W_{V}={\frac {1}{2}}\beta _{11}V_{1}^{2}+\beta _{12}V_{1}V_{2}+\beta _{13}V_{1}V_{3}+…+{\frac {1}{2}}\beta _{22}V_{2}^{2}+\beta _{23}V_{2}V_{3}+…+{\frac {1}{2}}\beta _{nn}V_{n}^{2}.\qquad (23)}

В этих выражениях различные коэффициенты α и β зависят от параметров, определяющих собой положения проводящих тел в данной системе, а также формы и размеры их. При этом коэффициенты β с двумя одинаковыми значками, как то β₁₁, β₂₂, β₃₃ и т. д. представляют собой электроемкости (см. Электрическая ёмкость) тел, отмеченных этими значками, коэффициенты β с двумя различными значками, как то β₁₂, β₂₃, β₂₄, и т. д., представляют собой коэффициенты взаимной индукции двух тел, значки которых стоят у данного коэффициента.

Имея выражение электрической энергии, мы получаем выражение для силы, какую испытывает какое-либо тело, значок которого i, и от действия которой параметр s_i, служащий для определения положения этого тела, получает приращение. Выражение этой силы Fsi{\displaystyle F_{s_{i}}} будет

Fsi=−∂Wq∂si,(24){\displaystyle F_{s_{i}}=-{\frac {\partial W_{q}}{\partial s_{i}}},\qquad (24)}

или

fsi=−∂Wv∂si.(25){\displaystyle f_{s_{i}}=-{\frac {\partial W_{v}}{\partial s_{i}}}.\qquad (25)}

Электрическая энергия может быть представлена ещё иначе, а именно, через

W=18π∭KF2dxdydz.(26){\displaystyle W={\frac {1}{8\pi }}\iiint {KF^{2}dxdydz}.\qquad (26)}

В этой формуле интегрирование распространяется по всему беспредельному пространству, F обозначает величину электрической силы, испытываемой единицей положительного электричества в точке (x, у, z), то есть напряжённость электрического поля в этой точке, а K обозначает диэлектрический коэффициент в этой же точке. При таком выражении электрической энергии системы проводящих тел эту энергию можно рассматривать распределенной только в изолирующих средах, причём на долю элемента dxdyds диэлектрика приходится энергий K8πF2dxdydz{\displaystyle {\frac {K}{8\pi }}F^{2}dxdydz}. Выражение (26) вполне соответствует взглядам на электрические процессы, которые были развиты Фарадеем и Максвеллом.

Чрезвычайно важной формулой в электростатике является формула Грина, а именно:

∭UΔVdxdydz+∬UdVdndS=∭VΔUdxdydz+∬VdUdndS.(27){\displaystyle \iiint {U\Delta Vdxdydz}+\iint {U{\frac {dV}{dn}}dS}=\iiint {V\Delta Udxdydz}+\iint {V{\frac {dU}{dn}}dS}.\qquad (27)}

В этой формуле оба тройные интеграла распространяются на весь объём какого-либо пространства А, двойные — на все поверхности, ограничивающие это пространство, ∆V и ∆U обозначают суммы вторых производных от функций V

электростатическое поле — это… Что такое электростатическое поле?

электрическое поле неподвижных электрических зарядов.

ЭЛЕКТРОСТАТИ́ЧЕСКОЕ ПО́ЛЕ, электрическое поле неподвижных и не меняющихся со временем электрических зарядов, осуществляющее взаимодействие между ними.
Электростатическое поле характеризуется напряженностью электрического поля (см. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ) Е, которая является его силовой характеристикой: Напряженность электростатического поля показывает, с какой силой электростатическое поле действует на единичный положительный электрический заряд (см. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД), помещенный в данную точку поля. Направление вектора напряженности совпадает с направлением силы, действующей на положительный заряд, и противоположно направлению силы, действующий на отрицательный заряд.
Электростатическое поле является стационарным (постоянным), если его напряженность не изменяется с течением времени. Стационарные электростатические поля создаются неподвижными электрическими зарядами.
Электростатическое поле однородно, если вектор его напряженности одинаков во всех точках поля, если вектор напряженности в различных точках различается, поле неоднородно. Однородными электростатическими полями являются, например, электростатические поля равномерно заряженной конечной плоскости и плоского конденсатора (см. КОНДЕНСАТОР (электрический)) вдали от краев его обкладок.
Одно из фундаментальных свойств электростатического поля заключается в том, что работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от траектории движения, а определяется только положением начальной и конечной точек и величиной заряда. Следовательно, работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Силовые поля, обладающие этим свойством, называют потенциальными или консервативными. То есть электростатическое поле — это потенциальное поле, энергетической характеристикой которого является электростатический потенциал (см. ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКИЙ) , связанным с вектором напряженности Е соотношением:
Е = -gradj.
Для графического изображения электростатического поля используют силовые линии (см. СИЛОВЫЕ ЛИНИИ) (линии напряженности) — воображаемые линии, касательные к которым совпадают с направлением вектора напряженности в каждой точке поля.
Для электростатических полей соблюдается принцип суперпозиции (см. СУПЕРПОЗИЦИИ ПРИНЦИП). Каждый электрический заряд создает в пространстве электрическое поле независимо от наличия других электрических зарядов. Напряженность результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженности полей, создаваемых в данной точке каждым из зарядов в отдельности.
Всякий заряд в окружающем его пространстве создает электростатическое поле. Чтобы обнаружить поле в какой-либо точке, надо поместить в точку наблюдения точечный пробный заряд — заряд, который не искажает исследуемое поле (не вызывает перераспределения зарядов, создающих поле).
Поле, создаваемое уединенным точечным зарядом q, является сферически симметричным. Модуль напряженности уединенного точечного заряда в вакууме с помощью закона Кулона (см. КУЛОНА ЗАКОН) можно представить в виде:
Е = q/4pe_оr².
Где e_о — электрическая постоянная, = 8,85^.10^-12Ф/м.
Закон Кулона, установленный при помощи созданных им крутильных весов (см. Кулона весы (см. КУЛОНА ВЕСЫ)), — один из основных законов, описывающих электростатическое поле. Он устанавливает зависимость между силой взаимодействия зарядов и расстоянием между ними: сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
Эту силу называют кулоновской, а поле — кулоновским. В кулоновском поле направление вектора зависит от знака заряда Q: если Q > 0, то вектор направлен по радиусу от заряда, если Q ( см. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ) среды) меньше, чем в вакууме.
Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда. Электрическое поле можно характеризовать значением потока вектора напряженности электрического поля, который можно рассчитать в соответствии с теоремой Гаусса (см. ГАУССА ТЕОРЕМА). Теорема Гаусса устанавливает связь между потоком напряженности электрического поля через замкнутую поверхность и зарядом внутри этой поверхности. Поток напряженности зависит от распределения поля по поверхности той или иной площади и пропорционален электрическому заряду внутри этой поверхности.
Если изолированный проводник поместить в электрическое поле, то на свободные заряды q в проводнике будет действовать сила. В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, компенсирует полностью внешнее поле, т. е. установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в ноль: во всех точках внутри проводника Е = 0, то есть поле отсутствует. Силовые линии электростатического поля вне проводника в непосредственной близости к его поверхности перпендикулярны поверхности. Если бы это было не так, то имелась бы составляющая напряженности поля, вдоль поверхности провод­ника и по поверхности протекал бы ток. Заряды располагаются только на поверхности проводника, при этом все точки поверхности проводника имеют одно и то же значение потенциала. Поверхность проводника является эквипотенциальной поверхностью (

см. ЭКВИПОТЕНЦИАЛЬНАЯ ПОВЕРХНОСТЬ). Если в проводнике есть полость, то электрическое поле в ней также равно нулю; на этом основана электростатическая защита электрических приборов.
Если в электростатическое поле поместить диэлектрик, то в нем происходит процесс поляризации — процесс ориентации диполей ( см. ДИПОЛЬ) или появление под воздействием электрического поля ориентированных по полю диполей. В однородном диэлектрике электростатическое поле вследствие поляризации (см. Поляризация диэлектриков) убывает в ? раз.

Электростатическое поле

№1

суммарный заряд электрически изолированной системы не может изменятся. Система называется эл. изолированной, если через ограничивающую её поверхность не могут проникать заряженные частицы. Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями от этого тела до других тел, несущих эл.заряд.

Закон Кулона: сила взаимодействия двух неподвижных, точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними.

где k – коэффициент пропорциональности, е₁₂ – единичный вектор имеющий направление от заряда q₁ к заряду q₂

поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии

электрических токов).

• Напряженность электростатического поля

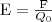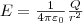есть физическая величина, определяемая силой, которая действует на пробный единичный положительный заряд, помещенный в эту точку поля: (1) Как следует из формулы (1) и закона Кулона, напряженность поля точечного заряда в вакууме или (2)

• Силовая линия

это кривая, касательная к которой в любой точке совпадает по направлению с вектором, характеризующим данное поле в этой точке. (Силовые линии

электростатического поля всегда незамкнуты: они начинаются на положительных зарядах и оканчиваются на отрицательных)

№2

• Принцип суперпозиции.

Напряжённость поля системы зарядов равна векторной сумме напряжённостей полей, которые создавал бы каждый из зарядов системы в отдельности.

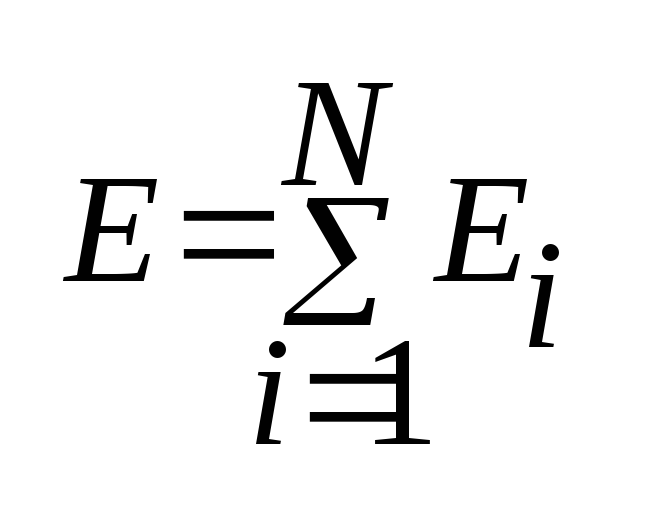
Выделим малую площадку площадью ΔS, ориентация которой задается единичным вектором нормали 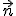(рис. 157).

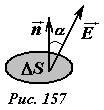
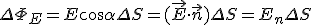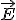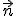В пределах малой площадки электрическое поле можно считать однородным, тогда поток вектора напряженности ΔФ_E определяется как произведение площади площадки на нормальную составляющую вектора напряженности где — скалярное произведение векторов и ; E_n — нормальная к площадке компонента вектора напряженности.

№3

• Теорема Гаусса , и ее применение к расчету полей заряженной плоскости, цилиндра, шара.

Поток вектора напряжённости электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгеброической сумме заключенных внутри этой поверхности зарядов делённой на ₀ .

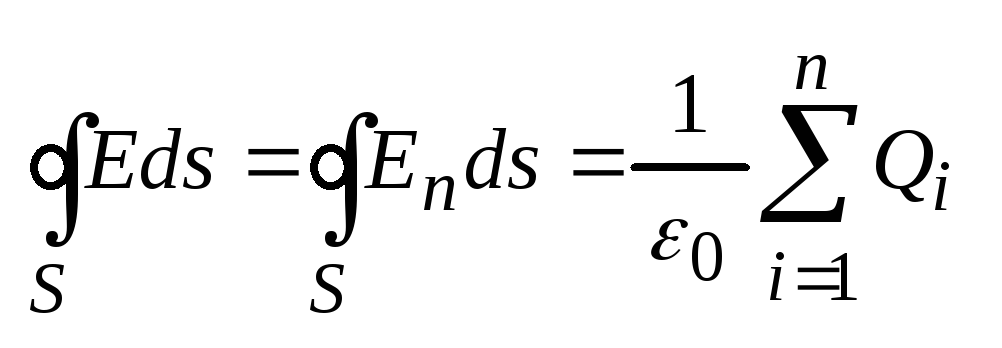
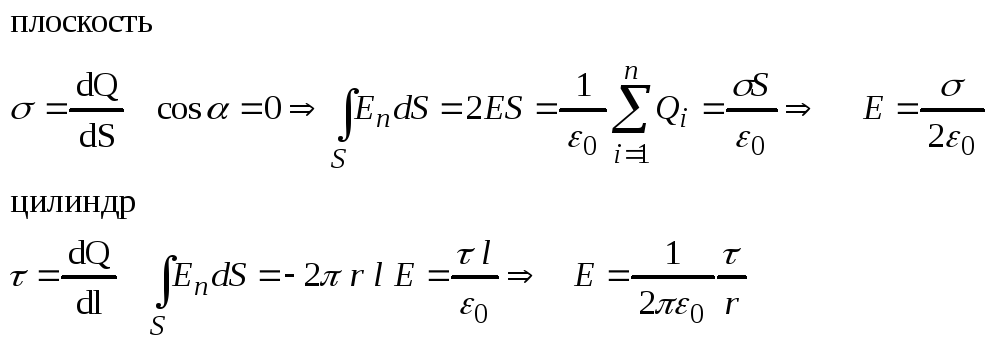
№4

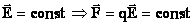в каждой точке поля. 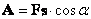   Следовательно: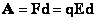

Т.к. если вектор перемещения перпендикулярен вектору силы (напряженности поля), работа поля равна нулю, то работа электростатического поля по перемещению заряда по любой траектории определяется разностью координат этих точек: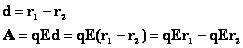

Работа по перемещению заряда по замкнутому контуру равна 0.

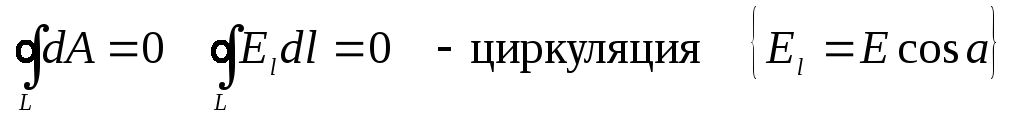
№5

Работа по перемещению единичного положительного заряда вдоль оси Х равна 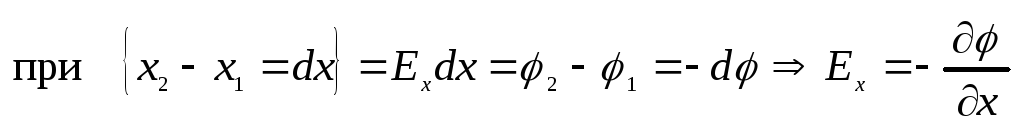повторив это для осейy,z получим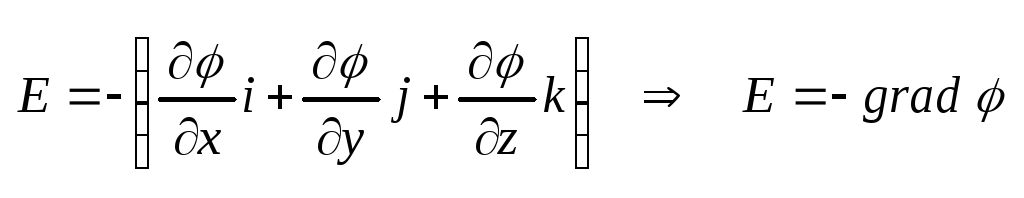

Эквипотенциальная поверхность – поверхность во всех точках которой потенциал имеет одно и тоже значение.

• Уравнение Пуассона

— эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает электростатическое поле. Это уравнение имеет вид: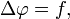

где —оператор Лапласа или лапласиан, а 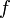—вещественная или комплексная функция на некотором многообразии.

В трёхмерной декартовой системе координат уравнение принимает форму: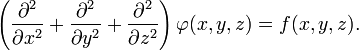

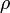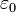где — электростатический потенциал (ввольтах), — объёмнаяплотность заряда, а —диэлектрическая проницаемость вакуума .

№9

• Энергия системы неподвижных зарядов

Потенциальная энергия W_p неподвижной системы зарядов представляет собой работу, необходимую для создания этой системы из отдельных частей, т.е. энергию, запасенную в созданной системе. Это — скалярная величина, являющаяся свойством системы в целом.

Как создать электростатическое поле. Электростатическое поле и единичный заряд

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Нижегородский Государственный Технический Университет

Выксунский филиал

Кафедра общеобразовательных и общепрофессиональных дисциплин

Лабораторная работа № 2-2.

(методическое пособие)

Составили: А.М. Кривенко, В.П.Маслов, И.И.Рожков, Р.В.Щербаков.

Свойства электростатического поля: Лаб. Работа № 2-20 по общей физике для студентов всех специальностей ВФ НГТУ;

Приведены основные сведения по теории электростатического поля. Дана методика исследования электростатического поля методом электролитической ванны. При составлении пособия использованы описания лабораторных работ НГТУ, МАИ, МИФИ, СФТИ и др. вузов.

Научный редактор: Радионов А.А

Цель работы. Исследование свойств электростатического поля при простейших распределениях зарядов. Экспериментальное определение по­тенциала и напряженности электрического поля, построение силовых и эк­випотенциальных линий поля между электродами определенной формы и вблизи проводников.

Теоретическая часть

Электростатическое, то есть не меняющееся во времени, поле соз­дается неподвижными в данной системе координат электрическими заряда­ми.

Основные характеристики: напряженность электрического поля (векторная величина) — силовая характеристика и потенциал поля (скалярная величина) — энергетическая характеристика.

Напряженностью электрического поля в данной точке пространства называется отношение силы () действующей на точечный заряд q поме­щенный в эту точку, к величине заряда:

(1)

где — напряженность электрического поля; — сила, действующая на заряд q

Потенциал электрического поля () в некоторой точкеравен от­ношению потенциальной энергииW() положительного точечного зарядаq помещенного в эту точку, к величине заряда:

(2)

где W () — потенциальная энергия; () — потенциал поля.

Потенциал электрического поля измеряется работой, которую совершают силы поля, перемещая положительный единичный зарядиз данной точки в бесконечность (или другую точку, потенциал которой условно принят рав­ным нулю).

Работа сил поля определяется по формуле: A 12 = q ( 1 — 2 ).

В электростатическом поле работа при перемещении заряда не зависит от пути, по которому движется заряд, а определяется лишь начальным (1-м) и конечным (2-м) положениями заряда. Поле, отвечающее этому условию, принято называть потенциальным.

Работа, совершаемая силами поля над зарядом q при перемещении его из 1-й точки во 2-ю, может быть вычислена также по формуле:

где d- элементарное перемещение заряда q.

Единицы измерений в СИ:

Напряженность и потенциал не являются независимыми характе­ристиками электрического поля. Они связаны друг с другом соотношением

Напряженность поля равна со знаком минус градиенту потенциала . Знак называется оператором «набла», его математическое выражение зависит от выбранной системы координат. В декартовой системе его пони­мают следующим образом:

(4)

где – орты (единичные векторы)осей декартовой системы координат,

и т.д. — соответствующие частные производные.

Градиент потенциала характеризует быстроту возрастания потенциала в направлении нормали к эквипотенциальной поверхности, т.е. вдоль силовой линии.

Связь между и можно представить в форме

(5)

где — проекция вектора Ена направление интегрирования 1, которая согласно (4) равна

(6)

Графическое представление электрического поля

Электрическое поле можно наглядно представить с помощью линий напряженности (или силовых линий) и эквипотенциальных поверхностей.

Линии напряженности — это направленные линии, касательные к кото­рым в каждой точке совпадают по направлению с вектором напряженности в этой точке, а густота линий (число линий, пронизывавших единичную пло­щадку, перпендикулярную к линиям в этой точке) пропорциональна модулю вектора. Силовые линии начинаются на положительных и заканчиваются на отрицательных зарядах (свободных и связанных) и нигде не пересекаются.

Эквипотенциальные поверхности – это поверхности равного потенциа­ла .

Уравнение такой поверхности задается условием:

(x,y,z,) — const.

Числовое значение const определяет величину постоянного потенциала. В каждой, точке на эквипотенциальной поверхности вектор перпендикулярен поверхности и направлен в сторону уменьшения потенциала. Это следует из формулы (6).

При изображении электростатического поля с помощью силовых линий и эквипотенциальных поверхностей последние обычно проводятся так, чтобы разность потенциалов между двумя соседними поверхностями была всюду одинаковой. В этом случае по густоте эквипотенциальных поверхностей и силовых линий можно судить о численном значении напряженности поля в каких-либо его точках.

Основное математические понятия

ТЕОРИЯ ПОЛЯ

Теория поля есть учение об электрических и магнитных явлениях, о теоретических положениях и законах, которым подчиняются эти явления и о вытекающих из них методах расчета.

Электромагнитное поле является особым видом материи, оно является носителем энергии и обладает специфическими (присущими только ему) электрическими и магнитными свойствами. Изложение основных свойств и методов расчета полей произведем в порядке перехода от более простых к более сложным. В соответствии с этим в начале рассмотрим поля, неизменные во времени, и только после этого изучим переменное электромагнитное поле. Изучение всех видов полей расширяет физические представления о поле, известные и курса физики, способствует более глубокому пониманию процессов, происходящих в электротехнических устройствах, важно с прикладной точки зрения, т.к. дает возможность решать многие задачи, имеющие существенное значение не только для теории электрических цепей, но и более общих задач (излучение и канализация электрической энергии и др.).

Мы будем изучать только поля в однородных (одинаковых во всех точках поля) и изотропных (со свойствами, н

Электростатическое поле — Мегаэнциклопедия Кирилла и Мефодия — статья

Электростати́ческое по́ле, электрическое поле неподвижных и не меняющихся со временем электрических зарядов, осуществляющее взаимодействие между ними.

Электростатическое поле характеризуется напряженностью электрического поляЕ, которая является его силовой характеристикой: Напряженность электростатического поля показывает, с какой силой электростатическое поле действует на единичный положительный электрический заряд, помещенный в данную точку поля. Направление вектора напряженности совпадает с направлением силы, действующей на положительный заряд, и противоположно направлению силы, действующий на отрицательный заряд.

Электростатическое поле является стационарным (постоянным), если его напряженность не изменяется с течением времени. Стационарные электростатические поля создаются неподвижными электрическими зарядами.

Электростатическое поле однородно, если вектор его напряженности одинаков во всех точках поля, если вектор напряженности в различных точках различается, поле неоднородно. Однородными электростатическими полями являются, например, электростатические поля равномерно заряженной конечной плоскости и плоского конденсатора вдали от краев его обкладок.Одно из фундаментальных свойств электростатического поля заключается в том, что работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от траектории движения, а определяется только положением начальной и конечной точек и величиной заряда. Следовательно, работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Силовые поля, обладающие этим свойством, называют потенциальными или консервативными. То есть электростатическое поле — это потенциальное поле, энергетической характеристикой которого является электростатический потенциал, связанным с вектором напряженности Е соотношением:

Е = -gradj.

Для графического изображения электростатического поля используют силовые линии (линии напряженности) — воображаемые линии, касательные к которым совпадают с направлением вектора напряженности в каждой точке поля.Для электростатических полей соблюдается принцип суперпозиции. Каждый электрический заряд создает в пространстве электрическое поле независимо от наличия других электрических зарядов. Напряженность результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженности полей, создаваемых в данной точке каждым из зарядов в отдельности.

Всякий заряд в окружающем его пространстве создает электростатическое поле. Чтобы обнаружить поле в какой-либо точке, надо поместить в точку наблюдения точечный пробный заряд — заряд, который не искажает исследуемое поле (не вызывает перераспределения зарядов, создающих поле).

Поле, создаваемое уединенным точечным зарядом q, является сферически симметричным. Модуль напряженности уединенного точечного заряда в вакууме с помощью закона Кулона можно представить в виде:

Е = q/4pe_оr².

Где e_о — электрическая постоянная, = 8, 85^.10^-12Ф/м.

Закон Кулона, установленный при помощи созданных им крутильных весов (см. Кулона весы), — один из основных законов, описывающих электростатическое поле. Он устанавливает зависимость между силой взаимодействия зарядов и расстоянием между ними: сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.Эту силу называют кулоновской, а поле — кулоновским. В кулоновском поле направление вектора зависит от знака заряда Q: если Q > 0, то вектор направлен по радиусу от заряда, если Q ? раз (? — диэлектрическая проницаемость среды) меньше, чем в вакууме.Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда. Электрическое поле можно характеризовать значением потока вектора напряженности электрического поля, который можно рассчитать в соответствии с теоремой Гаусса. Теорема Гаусса устанавливает связь между потоком напряженности электрического поля через замкнутую поверхность и зарядом внутри этой поверхности. Поток напряженности зависит от распределения поля по поверхности той или иной площади и пропорционален электрическому заряду внутри этой поверхности.Если изолированный проводник поместить в электрическое поле, то на свободные заряды q в проводнике будет действовать сила. В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, компенсирует полностью внешнее поле, т. е. установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в ноль: во всех точках внутри проводника Е = 0, то есть поле отсутствует. Силовые линии электростатического поля вне проводника в непосредственной близости к его поверхности перпендикулярны поверхности. Если бы это было не так, то имелась бы составляющая напряженности поля, вдоль поверхности провод­ника и по поверхности протекал бы ток. Заряды располагаются только на поверхности проводника, при этом все точки поверхности проводника имеют одно и то же значение потенциала. Поверхность проводника является эквипотенциальной поверхностью. Если в проводнике есть полость, то электрическое поле в ней также равно нулю; на этом основана электростатическая защита электрических приборов.Если в электростатическое поле поместить диэлектрик, то в нем происходит процесс поляризации — процесс ориентации диполей или появление под воздействием электрического поля ориентированных по полю диполей. В однородном диэлектрике электростатическое поле вследствие поляризации (см. Поляризация диэлектриков) убывает в ? раз.

Электростатическое поле, напряженность и электростатический диполь

Электрическое поле, которое окружает заряд, это реальность, независящая от нашего желания что-либо изменить и как-то повлиять на это. Отсюда можно сделать вывод, что электрическое поле является одной из форм существования материи, так же как и вещество.

Электрическое поле зарядов, находящихся в состоянии покоя, называют электростатическим. Чтобы обнаружить электростатическое поле определенного заряда нужно внести в его поле другой заряд, на который будет действовать определенная сила в соответствии с законом Кулона. Однако без наличия второго заряда электростатическое поле первого заряда существует, но никак себя не проявляет.

Напряженностью Е характеризуют электростатическое поле. Напряженность в некоторой точке электрического поля – физическая величина, которая равна силе, действующей на помещенный в определенную точку поля единичный положительный покоящийся заряд, и направленная в сторону действия силы.

Если в электрическое поле, создаваемое  зарядом q, внести «пробный» положительный точечный заряд q_пр, то по закону Кулона на него будет действовать сила:

Если в одну точку поля помещать различные пробные заряды q^/_пр,  q^//_пр и так далее, то на каждый из них будут действовать различные силы, пропорциональные величине заряда. Отношение F/q_пр для всех зарядов, вносимых в поле, будет идентичным, а также будет зависеть лишь от q и r, определяющих электрическое поле в данной точке. Данную величину можно выразить формулой:

Если предположить, что q_пр = 1, то E = F. Отсюда делаем вывод, что напряженность электрического поля является его силовой характеристикой. Из формулы (2) с учетом выражения кулоновской силы (1) следует:

Из формулы (2) видно, что за единицу напряженности принимается напряженность в определенной точке поля, где на единицу заряда будет действовать единица силы. Поэтому в системе СГС единицей напряженности является дин/СГС_q, а в системе СИ будет Н/Кл. Соотношение между приведенными единицами называют абсолютной электростатической единицей напряженности (СГС_Е):

Вектор напряженности направлен от заряда вдоль радиуса при образующем поле положительном заряде q+, а при отрицательном – q – по направлению к заряду вдоль радиуса.

Если электрическое поле образовано несколькими зарядами, то силы, которые будут действовать на пробный заряд, складываются по правилу сложения векторов. Поэтому напряженность системы, состоящей из нескольких зарядов, в данной точке поля будет равна векторной сумме напряженностей каждого заряда в отдельности:

Данное явление носит название принцип суперпозиции (наложения) электрических полей.

Напряженность в любой точке электрического поля двух точечных зарядов – q₂ и +q₁ можно найти использовав принцип суперпозиции:

По правилу параллелограмма будет происходить сложение векторов Е₁ и Е₂. Направление результирующего вектора Е определяется построением, а его абсолютная величина может быть вычислена с использованием формулы ниже:

Где α – угол между векторами Е₁ и Е₂.

Давайте рассмотрим электрическое поле, которое создает диполь. Электрический диполь – это система равных по величине (q = q₁ = q₂), но противоположных по знаку зарядов, расстояние между которыми очень мало, если сравнивать с расстоянием до рассматриваемых точек электрического поля.

Электрический дипольный момент p, являющийся основной характеристикой диполя и определяемый как вектор, направленный от отрицательного заряда к положительному, и равный произведению плеча диполя l на заряд q:

Также вектором является плечо диполя l, направленным от отрицательного заряда к положительному, и определяет расстояние между зарядами. Линия, которая проходит через оба заряда, носит название – ось диполя.

Давайте определим напряженность электрического поля в точке, которая лежит на оси диполя по середине (рисунок ниже а)):

В точке В напряженность Е будет равна векторной сумме напряженностей Е^/ и Е^//, которые создаются положительными и отрицательными зарядами но отдельности. Между зарядами –q и +q векторы напряженностей Е^/ и Е^// направлены в одну сторону, поэтому по абсолютной величине результирующая напряженность Е будет равна их сумме.

Если же нам необходимо найти Е в точке A, лежащей на продолжении оси диполя, то в разные стороны будут направлены вектора Е^/ и Е^//, соответственно по абсолютной величине результирующая напряженность будет равна их разности:

Где r – расстояние между точкой, которая лежит на оси диполя и в которой происходит определение напряженности, и средней точкой диполя.

В случае r>>l, величиной (l/2) в знаменателе можно пренебречь, тогда получим следующее соотношение:

Где p – момент электрический диполя.

Данная формула в системе СГС примет вид:

Теперь нужно вычислить напряженность электрического поля в точке С (рисунок выше б)), лежащей на перпендикуляре, восстановленном из средней точки диполя.

Так как r₁ = r₂, то будет иметь место равенство:

В точке С вектор результирующей напряженности по абсолютной величине будет равен:

Так как r>>l, то можно считать r₁ ≈ r, тогда представленную выше формулу можно записать в другом виде:

Напряженность диполя в произвольной точке можно определить по формуле:

Где α – угол между плечом диполя l и радиус-вектором r, r – расстояние от точки, в которой определяется напряженность поля, до центра диполя, р – электрический момент диполя.

Пример

На расстоянии R = 0,06 м друг от друга находятся два одинаковых точечных заряда q₁ = q₂ = 10^-6 Кл (рисунок ниже):

Необходимо определить напряженность электрического поля в точке А, которая расположена на перпендикуляре, восстановленном в центре отрезка, который соединяет заряды, на расстоянии h = 4 см от этого отрезка. Также нужно определить напряженность и в точке В, находящейся на середине отрезка,  который соединяет заряды.

Решение

По принципу суперпозиции (наложением полей) определяется напряженность поля Е. Таким образом, векторной (геометрической) суммой определяется Е, создаваемых каждым зарядом в отдельности: Е = Е₁ + Е₂.

Напряженность электрического поля первого точечного заряда равна:

Где q₁ и q₂ – заряды, образующие электрическое поле; r – расстояние от точки, в которой вычисляется напряженность, до заряда; ε₀ – электрическая постоянная; ε – относительная диэлектрическая проницаемость среды.

Для определения напряженности в точке В сначала нужно построить векторы напряженности электрических полей от каждого заряда. Поскольку заряды положительны, то векторы Е^/ и Е^// будут направлены от точки В в разные стороны. По условию q₁ = q₂:

Это значит, что в средине отрезка напряженность поля равна нулю.

В точке А необходимо произвести геометрическое сложение векторов Е₁ и Е₂. В точке А напряженность будет равна:

 

Электростатическое поле

Электростатическое поле также как и электрическое поле является особой формой материи, которая окружает тела, имеющие электрический заряд. Но в отличие от последнего, электростатическое поле создается только вокруг неподвижных заряженных тел, то есть, когда нет условий для создания электрического тока.

Свойства электростатического поля

Электростатическое поле характеризуется свойствами, которые отличают его от других видов полей, образующихся в электрических цепях.

Основное его отличие заключается в том, что его силовые линии никогда не пересекаются и не касаются друг друга. Если электростатическое поле создано положительным зарядом, то его силовые линии начинаются с заряда и заканчиваются где-то в бесконечности. Если мы имеем дело с отрицательным зарядом, то силовые линии его электростатического поля наоборот начинаются где-то в бесконечности, а заканчиваются на самом заряде. То есть они направлены от положительного заряда или к отрицательному.

Кстати чем больше заряд, тем более сильное поле он создает и тем большая густота его силовых линий. Правда силовые линии поля – это скорее графическое (воображаемое) его изображение, принятое в физике и электронике. На самом деле четких отчерченных линий ни одно из полей не создает.

Основная характеристика, по которой судят о электрических и физических свойствах электростатического поля – это его напряженность. Она показывает, с какой силой поле действует на электрические заряды.

Кстати, если поместить в электростатическое поле диэлектрик, можно наблюдать процесс его поляризации.

< Предыдущая		Следующая >