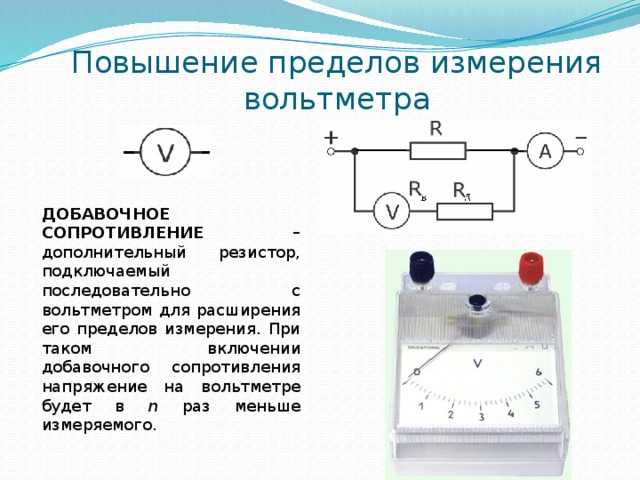
13. Почему с помощью вольтметра нельзя точно измерить эдс источника.
Потому что вольтметр имеет хоть и большое, но не бесконечное сопротивление, и оно в любом случае будет влиять на результаты измерений.
Если к источнику тока подключить вольтметр, то измерительный ток создаст падение напряжения на самом вольтметре и на внутреннем сопротивлении источника тока. По закону Ома для полной цепи: ε=U+Ir(1)Отсюда показания вольтметра будет равно: U=ε –Ir(2)Из формулы (2) видно, что показание вольтметра отличается от ЭДС на величину падения напряжения внутри источника тока. Чем больше измерительный ток, тем больше ошибка, а без измерительного тока вольтметр не работает.
14 Какие существуют потери мощности в катушке с магнитопроводом при питании постоянными и переменными токами?
На
постоянном токе — только омические — на
сопротивлении катушки. На переменном
— омические (никуда не деваются)
реактивные, на излучение и в сердечнике
на перемагничивание.
15. Какой из амперметров электродинамический или магнитоэлектрический имеет большую чувствительность и почему?
Магнитоэлектрические амперметры по сравнению с электродинамическим имеют большую чувствительность и точность, т.е. в магнитоэлектрическом амперметре более легкий и тонкий провод, который пропускает меньший ток.
16. Что произойдёт если амперметр и вольтметр при измерении мощности случайно поменять местами?
стрелка
и амперметра и вольтметра отклоняются
на угол пропорциональный силе тока
текущему через них. у амперметра очень
маленькое собственное сопротивление,
поэтому он зашунтирует участок цепи
на котором подключен параллельно,
сопротивление цепи заметно уменьшится,
сила тока возрастет и он весь потечет
через амперметр, поэтому он зашкалит
или сгорит. у вольтметра, наоборот очень
большое собственное сопротивление и
он увеличит сопротивление цепи куда
он подключен последовательно. тогда
сила тока заметно уменьшится стрелка
вольтметра отклонится только чуть чуть
или вовсе останется неподвижной.
17. Можно ли с помощью вольтметра определить ток в цепи?
можно. Но для этого его нужно превратить в амперметр. Достаточно пропустить ток через сопротивление, на нём возникнет напряжение, которое и измерим вольтметром. Сопротивление вольтметра должно быть максимально большим (в идеале — бесконечным). Чем больше сопротивления вольтметра, тем меньше его подключение меняет параметры измеряемой цепи (вольтметр подключается параллельно).
Непосредственно — нельзя. Но можно измерить падение напряжения на резисторе с очень маленьким сопротивлением (чем меньше сопротивление, тем меньше влияние на измеряемый параметр) и таким образом вычислить ток. Так как измеряемое напряжение прямо пропорционально силе тока, то легко находим её по закону Ома. (I=U/R).
18.
Как получают суммарную характеристику
нелинейных элементов при их последовательном
и параллельном соединении Нелинейным элементом электрической
цепи постоянного тока является такой,
у которого отсутствует линейная связь
между током и напряжением и поэтому он
определяется ВАХ, которая связывает
ток и напряжение данного элемента. Нелинейной считается цепь, содержащая
хотя бы один нелинейный элемент.
НЭ:конденсаторы, индуктивности,
резисторы. Как и в случае линейных
электрических цепей, задача расчета
нелинейной резистивной цепи заключается
в общем случае в определении токов
ветвей и напряжений на элементах цепи
при заданных параметрах независимых
источников энергии. Для нелинейных
цепей справедливы законы Кирхгофа.
Особенность нелинейных цепей в
уравнениях, составленных по законам
Кирхгофа, отражается зависимостью
коэффициентов уравнений от воздействий
и реакций (напряжений и токов).
Следовательно, процессы в нелинейной
электрической цепи описываются
нелинейными уравнениями, т.е. уравнениями,
в которых хотя бы один из коэффициентов
зависит от переменной. При анализе
нелинейных цепей нельзя пользоваться
принципом суперпозиции.
Нелинейной считается цепь, содержащая
хотя бы один нелинейный элемент.
НЭ:конденсаторы, индуктивности,
резисторы. Как и в случае линейных
электрических цепей, задача расчета
нелинейной резистивной цепи заключается
в общем случае в определении токов
ветвей и напряжений на элементах цепи
при заданных параметрах независимых
источников энергии. Для нелинейных
цепей справедливы законы Кирхгофа.
Особенность нелинейных цепей в
уравнениях, составленных по законам
Кирхгофа, отражается зависимостью
коэффициентов уравнений от воздействий
и реакций (напряжений и токов).
Следовательно, процессы в нелинейной
электрической цепи описываются
нелинейными уравнениями, т.е. уравнениями,
в которых хотя бы один из коэффициентов
зависит от переменной. При анализе
нелинейных цепей нельзя пользоваться
принципом суперпозиции.
1.При
последовательном соединении НЭ (рис.
1) характеристики складываются при
одинаковом токе: U(I) = U1(I)+U2(I). Так как
нелинейные элементы соединены
последовательно, то по ним протекает
один и тот же ток. Для решения сначала
находим суммарную ВАХ этих сопротивлений
методом выбранных значений токов далее
проектируем заданное напряжение до
пересечения с суммарной характеристикой
это точка даёт искомое решение.
Для решения сначала
находим суммарную ВАХ этих сопротивлений
методом выбранных значений токов далее
проектируем заданное напряжение до
пересечения с суммарной характеристикой
это точка даёт искомое решение.
2.При параллельном соединении НЭ (рис. 2) характеристики складываются при одинаковом напряжении: I (U) = I1(U)+ I2(U). Так как нелинейные элементы соединены паралельно то к ним приложено одно и тоже напряжение. Для решения сначала находи суммарную ВАХ. Далее проектируем заданное напряжение до пересечения с суммарной характеристикой. Эта точка даёт искомое решение.
Лабораторная работа №2. Измерение ЭДС и внутреннего сопротивления источника тока. Школьный курс физики
Главная | Физика 11 класс | Измерение ЭДС и внутреннего сопротивления источника тока
Цель работы
Освоить метод измерения ЭДС и внутреннего сопротивления источника тока с помощью амперметра и вольтметра.
Оборудование
Выпрямитель лабораторный, амперметр, вольтметр, ключ, резистор сопротивлением 5 Ом на подставке, соединительные провода.
Необходимые сведения
В качестве источника тока, характеристики которого определяют, используется лабораторный выпрямитель. Схема электрической цепи представлена на рисунке 3.
Рис. 3
Напряжение на резисторе U зависит от ЭДС источника , его внутреннего сопротивления r и сопротивления резистора R:
Выражение (1) следует из законов Ома для участка цепи и полной (замкнутой) цепи.
Из формулы (1) видно, что если R = ∞ (ключ разомкнут), то U = ,т. е. ЭДС можно измерить вольтметром, подключив его к выводам источника тока без нагрузки. Затем к источнику подключают нагрузку (резистор R), и по цепи пойдёт ток. Сила тока I =
Следовательно, значение внутреннего сопротивления можно определить, измерив ЭДС источника тока, напряжение на резисторе и силу тока в цепи.
Подготовка к работе
1. Определите приборные погрешности амперметра и вольтметра.
2. Запишите формулы для определения абсолютных погрешностей измерения Δ и ∆r. Не забудьте, что эти величины получаются в результате косвенных измерений.
3. Подготовьте таблицу для записи результатов измерений и вычислений.
| ,В | ∆,В | U,В | ∆U,В | I,А | ∆I,А | r,Ом | ∆r,Ом |
Порядок выполнения работы
1. Соберите электрическую цепь (см. рис. 3).
2.
3. Измерьте ЭДС выпрямителя.
4. Замкните ключ и измерьте напряжение U на резисторе и силу тока I в цепи.
5. Оцените абсолютные погрешности измерения I и U с учётом класса точности приборов (амперметра и вольтметра).
6. Вычислите значение внутреннего сопротивления r выпрямителя.
7. Найдите абсолютные погрешности измерения ∆r и Δ.
8. Запишите значения и r с учётом абсолютных погрешностей измерения:
Предыдущая страницаСледующая страница
напряжение — Вольтметр для измерения электродвижущей силы аккумулятора
спросил
Изменено 6 лет, 3 месяца назад
Просмотрено 5к раз
\$\начало группы\$
Известно, что подключение вольтметра непосредственно к клеммам (без какой-либо другой нагрузки) батареи покажет вам значение ЭДС батареи. Однако я не очень понимаю, как это происходит. Электродвижущая сила равна :E=U+u(E=ЭДС,u=внутреннее падение напряжения,U=внешнее падение напряжения). Напряжение, которое выдает батарея, равно U. Мой вопрос: как вольтметр измеряет ЭДС батареи и почему это не так? показать значение U при подключении напрямую к аккумулятору?
Однако я не очень понимаю, как это происходит. Электродвижущая сила равна :E=U+u(E=ЭДС,u=внутреннее падение напряжения,U=внешнее падение напряжения). Напряжение, которое выдает батарея, равно U. Мой вопрос: как вольтметр измеряет ЭДС батареи и почему это не так? показать значение U при подключении напрямую к аккумулятору?
- напряжение
- измерение напряжения
- вольтметр
\$\конечная группа\$
2
\$\начало группы\$
В вашей модели батарея представляет собой источник напряжения с последовательно включенным сопротивлением. Когда батарея не отдает ток, через это внутреннее сопротивление нет тока, и, следовательно, падающее напряжение равно 0. Таким образом, напряжение холостого хода батареи такое же, как и ее внутреннее напряжение. Когда вы кладете нагрузку на батарею, течет ток, внутреннее сопротивление падает на некоторое напряжение, а внешнее напряжение становится меньше внутреннего напряжения.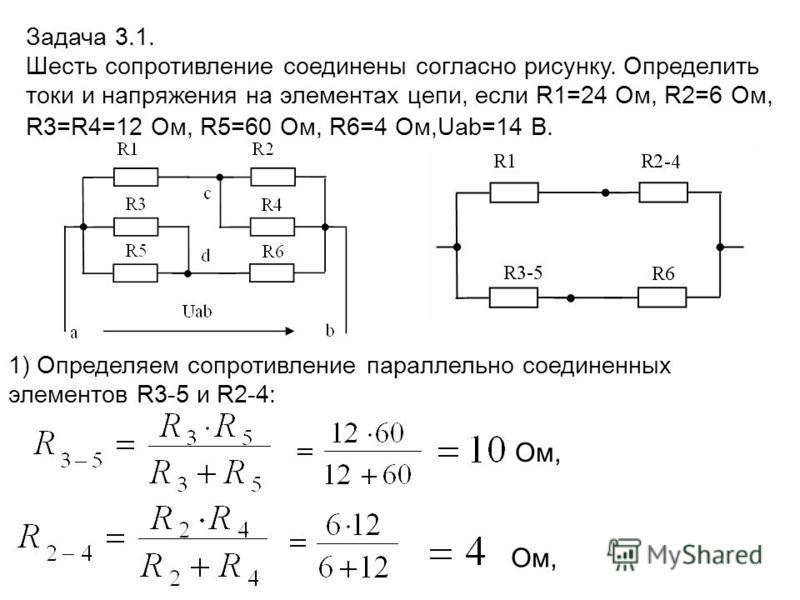
Вольтметры имеют высокое полное сопротивление. Они создают настолько маленькую нагрузку на батарею, что мы можем игнорировать ее в практических целях. Таким образом, внутреннее и внешнее напряжения батареи для практических целей одинаковы при измерении вольтметром. Иными словами, измерение батареи только с помощью вольтметра означает ее измерение в условиях разомкнутой цепи.
Я имею в виду внутреннее напряжение, которое вырабатывается непосредственно ячейкой, а внешнее напряжение — это минус то, что падает на неизбежное и неизбежное внутреннее сопротивление батареи.
\$\конечная группа\$
4
\$\начало группы\$
Чтобы измерить фактическую ЭДС, вы измеряете U, когда ток, подаваемый от батареи, точно равен 0.
Для этого традиционно используется не вольтметр, а амперметр… и прибор для измерения потенциала — то есть потенциометр.
Этот «потенциометр» питается от некоторого более высокого (неизвестного) напряжения и регулируется до тех пор, пока ток, потребляемый от батареи, не станет равным нулю и даст отношение двух сопротивлений.
Само по себе это не очень полезно, пока вы также не измерите ЭДС стандартного элемента (ячейки Дэниела или Уэстона), используя тот же метод, который позволяет вам откалибровать неизвестное управляющее напряжение, и, наконец, ЭДС элемента, который вы используете. повторное тестирование.
На практике, конечно, ток, потребляемый обычным вольтметром, достаточно мал, чтобы u было достаточно близко к 0, чтобы не иметь значения, а U = ЭДС.
\$\конечная группа\$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
законов Кирхгофа — Могут ли два вольтметра, подключенных к одним и тем же клеммам, показывать разные значения? Цепь с ЭДС индукции
ДА , два вольтметра, подключенные к одной и той же паре клемм, могут одновременно показывать два разных значения. Причина в том, что, поскольку цепь контура охватывает область переменного магнитного потока, «теоретическая разность потенциалов» между точками D и A не определена (однозначно).
На самом деле, это все, что нужно .
Поскольку, если ваша схема находится в области с переменным магнитным полем, то все пути между узлами находятся в диапазоне дБ/дт, и, поскольку линейный интеграл электрического поля вдоль любого замкнутого пути не всегда будет равен нулю (это основное физика), невозможно определить потенциальную функцию так, чтобы линейный интеграл от E от D до A зависел только от значений в D и A .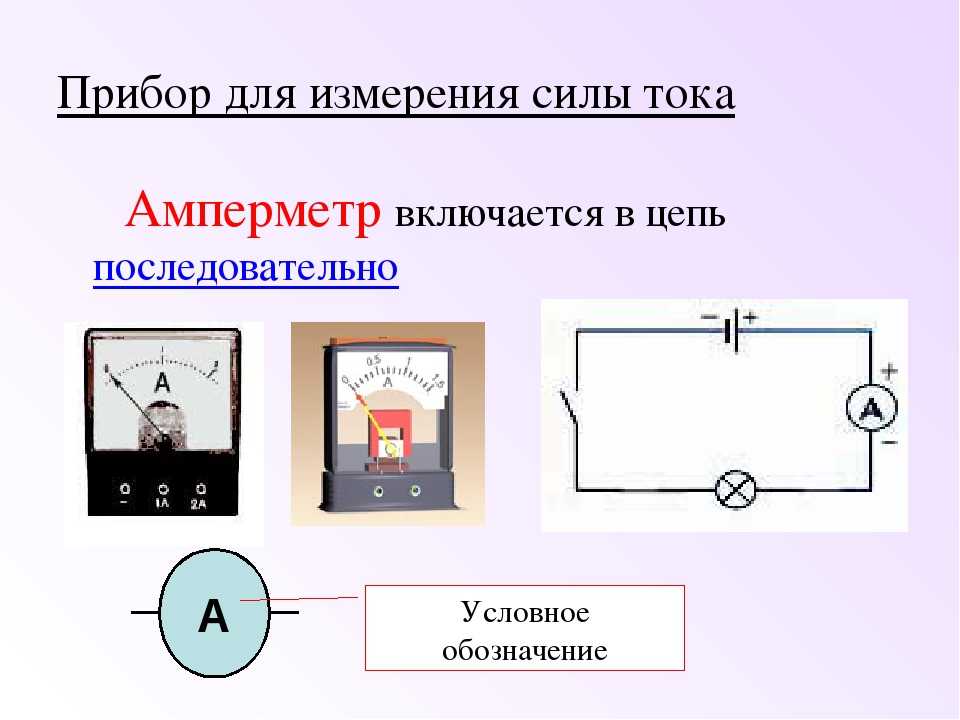 Это будет зависеть от пути.
(Это основное исчисление)
Это будет зависеть от пути.
(Это основное исчисление)
Так как это понятие обычно сталкивается с определенным сопротивлением, чтобы быть принятым, стоит глубже взглянуть на то, откуда оно взялось и что оно влечет за собой в деталях. Чтобы ответить на все сомнения, возникшие в результате многочисленных взаимодействий в Интернете после того, как Уолтер Левин сделал свое «супердемо» доступным для масс, требуется много места. Для людей, занимающихся TL;DR, остальная часть этого поста структурирована следующим образом:
- Определение разности потенциалов
Где мы определяем, что обычно подразумевается под напряжением в теории цепей и почему его можно свести к разности потенциалов (подсказка: безвихревость электрического поля делает напряжение функцией только конечных точек ) - Теория сосредоточенных цепей I: Кирхгоф рулез
Где мы видим, какие физические условия позволяют иметь безвихревое поле E и использовать концепцию напряжения как разности потенциалов. (Подсказка: это отсутствие переменного магнитного потока: закон Кирхгофа о напряжении — это всего лишь закон Фарадея, когда dphi/dt = 0)
(Подсказка: это отсутствие переменного магнитного потока: закон Кирхгофа о напряжении — это всего лишь закон Фарадея, когда dphi/dt = 0) - Теория сосредоточенных цепей II: Ограниченные области неконсервативности вне пути цепи
Где мы пытаемся спасти КВЛ, скрывая ограниченные области переменного магнитного потока внутри магнитных компонентов (примечание: это то, что Левин называет вонючим физика «взятия правой стороны на левую сторону» и того, что я называю «новым КВЛ» или «исправленным КВЛ»: если путь цепи не охватывает переменное магнитное поле, мы можем притворяться существует уникальное напряжение, которое можно выразить как разность потенциалов, просто не заглядывая внутрь магнитных компонентов) - Кольцо Ромера-Левина, или: несочетаемая цепь
Где мы видим, что когда цепь окружает переменный магнитный поток, KVL больше не подлежит восстановлению, и напряжение в вашей цепи становится зависимым от пути (что означает: оно больше невозможно выразить как разность потенциалов) - Скалярный и векторный потенциалы
Где мы рассмотрим альтернативное определение напряжения, допускающее скалярный потенциал. (подсказка: это то, что я называю маневром Макдональда, и он влечет за собой разделение полного электрического поля на две составляющие части, одну консервативную, вызванную кулоновским взаимодействием, и одну вращательную, вызванную магнитной индукцией)
(подсказка: это то, что я называю маневром Макдональда, и он влечет за собой разделение полного электрического поля на две составляющие части, одну консервативную, вызванную кулоновским взаимодействием, и одну вращательную, вызванную магнитной индукцией) - Роль поверхностных зарядов
Где мы рассмотрим, что делает общее поле в проводнике и резисторах таким, какое оно есть. - Понятие частичной индуктивности
Здесь мы рассмотрим, как попытка моделирования наведенного напряжения с частичными сосредоточенными «вторичными» катушками соответствует другой физической ситуации и как можно использовать частичную индуктивность (с должной осторожностью) в качестве инструмента в области электромагнитной совместимости
.
Когда вы определяете напряжение как разность потенциалов между двумя точками
VBA = VB — VA = Vab (переход от a к b)
, вы неявно предполагаете, что — кроме аддитивной константы — функция потенциала определена однозначно, то есть (отрицательный) интеграл по путям электрического поля от a до b
не зависит от конкретного выбранного пути интеграции. Эта ситуация требует, чтобы электрическое поле Е было консервативным или, как говорит само это название, безвихревым .
Эта ситуация требует, чтобы электрическое поле Е было консервативным или, как говорит само это название, безвихревым .
Если электрическое поле сделать вращательным, как это происходит при наличии переменного магнитного поля, то можно получить сразу разные результаты для Vab, в зависимости от того, какой путь вы выберете для вычисления интеграла: вы идете по пути который проходит через R1, вы получаете 0,9В; вы идете по пути, который проходит через R2, вы получаете -0,1 В; вы идете по произвольному пути, который следует профилю Snoopy внутри и вне проводника и резисторов, вы получаете 0,741 В, что угодно. (Обратите внимание, что я вообще не упоминаю пробники.) Одних конечных точек уже недостаточно для однозначного определения напряжения.
Вот устранение неоднозначности между двумя соглашениями, которые я собираюсь использовать. Поскольку было бы слишком много использовать разные буквы для обозначения напряжения, зависящего от пути, и напряжения, не зависящего от пути, я буду использовать V для обоих, оставив мелкий текст, чтобы отличить их друг от друга.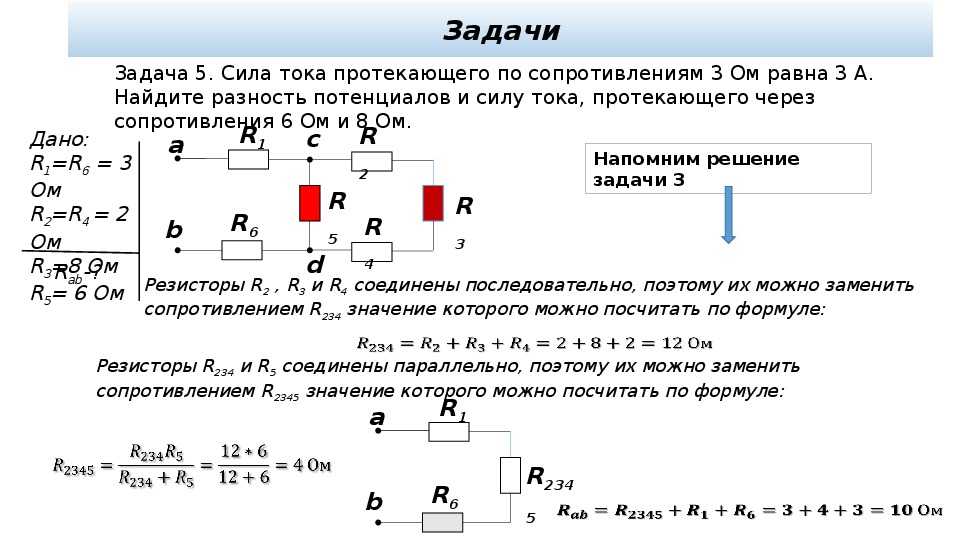 Итак, Ваб означает
Итак, Ваб означает
и это энергия на единицу заряда, необходимая для перехода из точки A в точку B по пути гамма (a->b). l будет обозначать это, как правило, зависящее от пути напряжение с Vab, строчными буквами от начальной точки до конечной точки. Когда электрическое поле безвихревое, существует потенциальная функция V такая, что
так, что линейный интеграл становится независимым от пути , и необходимо указывать только конечные точки A и B, а не гамма-пути, соединяющую их. (подойдет любой путь).
Я буду называть это напряжение «разностью потенциалов» и обозначать его с помощью VBA, с заглавными буквами, упорядоченными от конечной точки к начальной точке. Примечание: конечная точка идет первой, так как я принимаю соглашение VBA = VB — VA (графически представлено стрелкой, идущей от A к B). Это также поможет различать их.
Небольшое отступление
На самом деле нет ничего странного в том, что линейные интегралы зависят от пути, на самом деле это консервативные поля, которые почти магически особенные. В реальном мире нормально считать, что функция, вычисляемая путем интегрирования вдоль пути, зависит от самого конкретного пути, а не только от его конечных точек.
В реальном мире нормально считать, что функция, вычисляемая путем интегрирования вдоль пути, зависит от самого конкретного пути, а не только от его конечных точек.
Рассмотрим энергию, потраченную на то, чтобы добраться до вершины горы на автомобиле с той же парковки, и давайте измерим ее в галлонах бензина: если вы выберете прямой путь, вам потребуется 10 галлонов, если вы выберете свободную спираль, вам потребуется 20 галлон, свободная спираль против ветра и это 25 галлонов, но если по ветру это 18 галлонов; шаткий путь с назад и вперед, и это 35 галлонов. (Заметьте, это очень высокая гора). Не покажется ли вам странным, если ответ на вопрос «Каков теоретический расход бензина для поездки из пункта А в пункт Б?» было «это зависит»? Конечно, нет, вы бы удивились, если бы узнали обратное. (И все же вы могли бы подумать о минимальном потреблении, которое можно было бы считать «уникальным», я вернусь к этому позже, когда буду вводить векторный потенциал).
Кроме того, вы ожидаете, что ваш бензобак наполнится сам, просто спустившись на стоянку? Я полагаю, что вы были бы очень удивлены, если бы это произошло.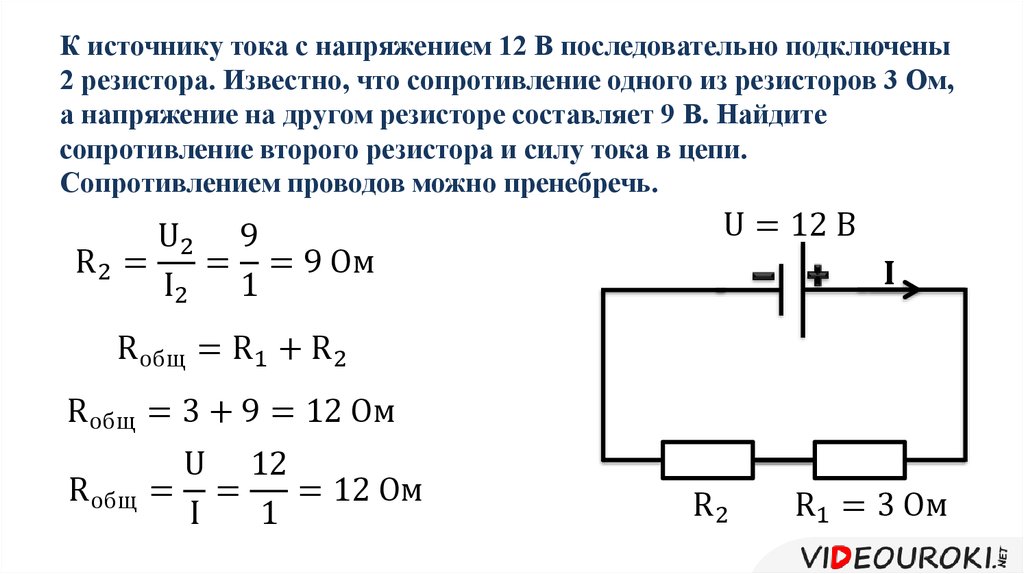 И тем не менее, это то, что происходит с консервативными полями: прохождение полного круга даст вам нулевой линейный интеграл. Они нелогичны, а не наоборот.
И тем не менее, это то, что происходит с консервативными полями: прохождение полного круга даст вам нулевой линейный интеграл. Они нелогичны, а не наоборот.
Теория цепей с сосредоточенными параметрами настолько проста, потому что она основана на этом особом, почти волшебном поле. Теория настолько проста и красива, что многие инженеры не могут от нее отказаться и пытаются использовать даже тогда, когда она неприменима. Фундаментальное предположение теории схем с сосредоточенными параметрами состоит в том, что вы должны иметь возможность определять напряжение между двумя точками независимо от пути. Учитывая определение напряжения, данное выше, это означает, что
и, в частности, если выбрать замкнутый путь интегрирования, т. е. a=b, то циркуляция Е должна быть равна нулю
необходимое и достаточное условие существования потенциальной функции. Теперь, поскольку один из фундаментальных законов физики, закон Фарадея, гласит, что
, из этого следует, что если мы хотим иметь возможность выражать напряжение как независимую от пути разность потенциалов, мы должны избегать областей с изменяющимся магнитным потоком. Фейнман очень ясно говорит об этом в своих лекциях: том II, гл. 22, «Цепи переменного тока» (выделено мной)
Фейнман очень ясно говорит об этом в своих лекциях: том II, гл. 22, «Цепи переменного тока» (выделено мной)
Предположим, у нас есть схема, состоящая из генератора и нескольких импедансы, соединенные вместе, как показано на рис. 22–9. Согласно нашему приближения магнитное поле отсутствует в области за пределами отдельные элементы схемы .
Таким образом, линейный интеграл E вокруг любой кривой, которая не проходит через любой из элементов равен нулю. Рассмотрим затем кривую Γ, показанную ломаной линией, которая проходит по всему контуру в Рис. 22–9. Линейный интеграл от E вокруг этой кривой состоит из несколько штук. Каждая часть представляет собой линейный интеграл от одной клеммы элемент цепи к другому. Этот линейный интеграл мы назвали падение напряжения на элементе цепи. Полный линейный интеграл равен то просто сумма падений напряжения на всех элементах в цепь:
Поскольку линейный интеграл равен нулю, мы имеем, что сумма потенциалов разности вокруг полного цикла цепи равны нулю:
Этот результат следует из одного из уравнений Максвелла — что в области где нет магнитных полей, линейный интеграл от E вокруг любого полный цикл равен нулю.

Итак, КВЛ — это всего лишь частный частный случай закона Фарадея, когда электрическое поле ведет себя тем волшебным образом, что пополнит ваш бензобак, когда вы пойдете с вершины горы обратно на стоянку. Если путь вашей цепи охватывает переменное магнитное поле, то вам не повезло: напряжения в вашей цепи не будут иметь уникальных значений для одних и тех же конечных точек, но также будут зависеть от конкретного пути, вдоль которого вы вычисляете линейный интеграл. Но обратите внимание, что Фейнман говорит:
«Согласно нашим предположениям, магнитное поле отсутствует в области вне отдельных элементов схемы .»
Итак, кажется, есть место для безумия магнитного поля. Ну в пределах разумного.
Если бы мы полностью избегали областей переменного магнитного (и смещения) поля, мы застряли бы с простыми резистивными цепями. Давайте посмотрим, сможем ли мы разработать решение, которое позволит включить в картину динамические элементы, такие как катушки индуктивности (и конденсаторы), не отказываясь от простых инструментов, представленных KVL (и KCL). Оказывается, мы можем, если мы добавим дополнительную оговорку, что все сумасшествие переменного поля останется за пределами пути схемы, ограничивая его внутри сосредоточенных компонентов.
Оказывается, мы можем, если мы добавим дополнительную оговорку, что все сумасшествие переменного поля останется за пределами пути схемы, ограничивая его внутри сосредоточенных компонентов.
Оставив переменную магнитную область за пределами пути цепи , мы сможем определить напряжения в цепи уникальным образом и использовать законы Кирхгофа для вычисления напряжений и токов, как мы это делали с резистивными цепями. Скрывая сложность переменных магнитных (и электрических полей) внутри динамических компонентов, мы можем представить , что напряжение на них и ток через них по-прежнему подчиняются правилам Кирхгофа, тогда как на самом деле глубоко внутри они определяются более общие законы Фарадея-Неймана и Ампера-Максвелла.
Рассмотрим следующую схему с генератором, резистором, катушкой индуктивности и конденсатором на пути, который соединяет все их клеммы вместе: магнитный элемент. Замкнутый путь можно разбить на следующие сегменты:
Теперь, если — как это происходит на этом рисунке — путь цепи не охватывает область переменного магнитного поля, мы можем записать интеграл по пути электрического поля через замкнутый цикл a-b-c-d-a и будьте уверены, что он равен нулю. Это условие необходимо для того, чтобы считать напряжения функцией только конечных точек, и для работы КВЛ (сумма напряжений по замкнутой цепи равна нулю).
KVL работает, потому что, не заключая какое-либо переменное магнитное поле в нашу цепь Gamma, все напряжения можно считать независимыми от пути, и не имеет значения, как мы интегрируем от одного вывода к другому.
Это условие необходимо для того, чтобы считать напряжения функцией только конечных точек, и для работы КВЛ (сумма напряжений по замкнутой цепи равна нулю).
KVL работает, потому что, не заключая какое-либо переменное магнитное поле в нашу цепь Gamma, все напряжения можно считать независимыми от пути, и не имеет значения, как мы интегрируем от одного вывода к другому.
Но действительно ли все напряжения в этой цепи независимы от пути? Ну, нет . Мы просто притворяемся, что они есть, закрывая глаза на тех, кто ими не является.
Оказывается, когда мы сталкиваемся с магнитной составляющей, мы можем выбирать пути, идущие от одного терминала к другому, входя или огибая область переменного магнитного потока. Напряжение, вычисляемое как линейный интеграл вдоль этих путей, в общем случае будет зависеть от пути.
Не все пути, идущие от одного терминала к другому, дают одинаковый результат, если мы заходим внутрь компонента
У нас могут быть пути из C в D, пересекающие область переменного магнитного поля, так что есть замкнутые петли, проходящие из C и D, линейный интеграл которых не равен нулю. Это означает, что у нас может быть несколько значений напряжения между C и D. В частности, существуют разные значения линейного интеграла, идущего от точки C к точке D в пространстве между терминалом (скажем, напряжение V) и другое, отличное значение для линейного интеграла по пути, который следует за катушкой внутри проводника (и это значение равно нулю).
Это означает, что у нас может быть несколько значений напряжения между C и D. В частности, существуют разные значения линейного интеграла, идущего от точки C к точке D в пространстве между терминалом (скажем, напряжение V) и другое, отличное значение для линейного интеграла по пути, который следует за катушкой внутри проводника (и это значение равно нулю).
Однако надежда есть. Среди бесконечного числа путей на выбор те, которые не проходят внутри или вокруг запрещенной области (например, обозначенные \$\gamma_1\$, \$\gamma_2\$ и \$\gamma_3\$), все дают один и тот же результат (на самом деле, выбирая их, мы всегда получаем общий путь цепи, который не будет охватывать область магнитных переменных). область переменного магнитного потока, путь нашей цепи будет чист, и — если мы сможем обмануть себя, что напряжение катушки зависит только от конечных точек (а это не так!) — мы сможем использовать макетную версию KVL (во многом так же, как при перемычке на клеммах конденсатора мы можем использовать макет KCL)
Теперь проблема состоит в том, чтобы найти то одно значение интеграла пути вдоль любого «безопасного» пути, который идет от одного терминала к другому, не заходя внутрь или вокруг запрещенной зоны магнитного элемента. Оказывается, мы можем легко вычислить его, используя, как вы уже догадались, закон Фарадея.
Оказывается, мы можем легко вычислить его, используя, как вы уже догадались, закон Фарадея.
Поддельная «разность потенциалов» на катушке
Мы собираемся рассмотреть эту часть схемы, где значение \$B(t)\$ или \$\Phi(t)\$ определяется эффекты ядерного взрыва, падающего магнита, другой катушки или даже эльфийской магии (но обратите внимание, что я не рассматриваю случай движущейся катушки — это означает, что мы находимся в системе отсчета, где катушка CD находится в покое)
Нас интересует линейный интеграл вдоль одного из «безопасных» путей из C в D, который мы назовем \$\gamma_{term}\$. Мы можем легко вычислить его, рассматривая его как часть замкнутого контура, который окружает область переменного магнитного потока, проходя через медь (так что электрическое поле имеет известную или легко вычисляемую величину и направление)
Мы можем разделить замкнутый контур петлевая линия, объединенная в составные части, т. е. путь, соединяющий клеммы от C к D (\$\gamma_{term}\$), и путь, проходящий через медь от D к C (\$\gamma_{copper}\ $):
нас интересует первый интеграл в правой части, который соответствует макету «разности потенциалов» на выводах катушки. Мы можем найти его сразу, учитывая, что циркуляция электрического поля по замкнутому контуру имеет значение, определяемое законом Фарадея, и что линейный интеграл, проходящий через медь, равен нулю, поскольку электрическое поле внутри неподвижного идеального проводника — даже при эффект индукции — равен нулю:
Мы можем найти его сразу, учитывая, что циркуляция электрического поля по замкнутому контуру имеет значение, определяемое законом Фарадея, и что линейный интеграл, проходящий через медь, равен нулю, поскольку электрическое поле внутри неподвижного идеального проводника — даже при эффект индукции — равен нулю:
и вот результат для нашего макета «разность потенциалов»:
Я взял «VDC» в кавычки, потому что это не реальная разность потенциалов, так как вообще это напряжение зависит от пути, а не только от конечные точки C и D. Но если мы сможем удостовериться, что относим его к путям, которые не попадают внутрь или вокруг внутренностей индуктора, мы можем притвориться, что оно однозначно.
Напряжение, которое вы видите на клеммах катушки индуктивности, является производной магнитного потока фи по времени. Знак напряжения зависит от ориентации магнитного поля и от того, как оно изменяется (убывает, увеличивается) Если хотите, добавьте, что \$\Phi = L * i\$ (и в таком случае, поскольку магнитный поток создается током в самой петле, знак напряжения будет следовать из закона Ленца) или \$\Phi = M*i\$ (здесь еще и знак зависит от того, как вы сориентируете витки) и вы получите ну известные соотношения для собственной и взаимной индуктивности. Но этот результат справедлив и для изменений магнитного поля, вызванных падением магнита или ядерным взрывом.
Но этот результат справедлив и для изменений магнитного поля, вызванных падением магнита или ядерным взрывом.
Нулевое поле в проводнике означает отсутствие нарастания напряжения внутри катушки. состоит из нуля. Нет, так сказать, «добавочного нарастания напряжения». Все напряжение появляется на клеммах. Вот как это выразили Рамо, Уиннери и Ван-Дюзер (стр. 171 во 2-м издании, выделено мной)
«Напряжение на клеммах магнитного элемента поступает от скорость изменения магнитного потока внутри индуктора, показанная на фигура как катушка. Предположим сначала, что сопротивление проводника катушка пренебрежимо мала, возьмем замкнутый линейный интеграл электрического поле вдоль проводника катушки, возвращаясь по пути поперек клеммы, рис. 4.2б. С вклад по части путь, который следует за проводником, равен нулю , появляется все напряжение через терминалы.»
Как возможно, чтобы интеграл по траектории (полного, см. далее расширение) электрического поля E был равен нулю внутри проводника катушки, когда мы можем измерить напряжение на его клеммах? Ну, как и в случае с электростатической индукцией, заряд, который создает поле снаружи меди, является тем же самым зарядом, который делает его равным нулю внутри меди. В электростатическом случае интеграл по пути равен нулю как внутри, так и вне проводника; в квазистатическом случае индукции в неподвижном проводнике интеграл по путям равен нулю внутри, но не равен нулю снаружи.
В электростатическом случае интеграл по пути равен нулю как внутри, так и вне проводника; в квазистатическом случае индукции в неподвижном проводнике интеграл по путям равен нулю внутри, но не равен нулю снаружи.
Если вычислить линейный интеграл электрического поля, перескакивающего по безопасному пути от одной клеммы к другой, вы получите ненулевые значения (соответствующие напряжению, которое определяется производной магнитного потока по времени), потому что существует общее неконсервативное электрическое поле в пространстве между клеммами, но если вы вычислите линейный интеграл от тех же двух концов, зайдя внутрь проводника, вы получите нуль, потому что внутри идеального проводника в этих квазистатических условиях нет электрического поля. поле.
Итак, вот оно: несколько значений напряжения между одними и теми же двумя точками во всех ваших цепях с любой формой катушки индуктивности.
Уловка, которую мы используем в теории цепей, состоит в том, чтобы просто притвориться, что не видим бесконечно много значений, которые может иметь линейный интеграл, если мы выбираем пути внутри запрещенной области компонента, и смотрим только на хорошие пути за ее пределами, которые постоянно дают одно и то же стоимость. Забыв, что это лишь одно из многих значений, мы называем это напряжение «разностью потенциалов» 9 .0085, даже если нет потенциальной функции .
Забыв, что это лишь одно из многих значений, мы называем это напряжение «разностью потенциалов» 9 .0085, даже если нет потенциальной функции .
Теперь, если бы вы произвели измерения напряжения в своей цепи, вы бы получили стабильные результаты, независимо от того, какой путь вы выберете , до тех пор, пока вы остаетесь снаружи и не обходите запрещенную область внутри магнитного компонента . Именно с этой оговоркой мы можем сделать вид, что все еще можем говорить о независимых от пути напряжениях и разностях потенциалов. Работа вашей схемы основана на этом иллюзорном «уникальном» напряжении на клеммах катушки индуктивности. Но если вы поместите свои зонды вокруг или внутри магнитного компонента, вы совершите ошибку зондирования, потому что вмешательство в запретную область разрушит эту иллюзию.
Предварительный просмотр: Почему «измененный KVL» не работает в кольце Ромера-Левина?
Кольцо Ромера-Левина имеет некоторые общие черты с описанной выше схемой с сосредоточенными параметрами, но также и некоторые существенные отличия. Как и в схеме с индуктором, внутри проводника нет полного электрического поля, и все поле E оказывается между выводами резисторов (или немагнитных компонентов).
Действительно большая разница в том, что теперь это путь цепи , который окружает область с переменным магнитным потоком, следовательно, мы всегда находимся внутри «запретной зоны», где КВЛ не работает и мы не можем «остаться» за ее пределами, как это было в случае с изолированным магнитным компонентом. Поскольку в общем случае линейный интеграл полного электрического поля вдоль любого замкнутого контура будет не равен нулю, а будет равен минус производная по времени от магнитного потока, охватываемого путем, мы не можем иметь потенциальную функцию. Напряжения в цепи, как правило, будут зависеть от пути , и мы должны ожидать множественных значений напряжения между двумя точками.
Как и в схеме с индуктором, внутри проводника нет полного электрического поля, и все поле E оказывается между выводами резисторов (или немагнитных компонентов).
Действительно большая разница в том, что теперь это путь цепи , который окружает область с переменным магнитным потоком, следовательно, мы всегда находимся внутри «запретной зоны», где КВЛ не работает и мы не можем «остаться» за ее пределами, как это было в случае с изолированным магнитным компонентом. Поскольку в общем случае линейный интеграл полного электрического поля вдоль любого замкнутого контура будет не равен нулю, а будет равен минус производная по времени от магнитного потока, охватываемого путем, мы не можем иметь потенциальную функцию. Напряжения в цепи, как правило, будут зависеть от пути , и мы должны ожидать множественных значений напряжения между двумя точками.
Эта многозначность напряжения не является результатом погрешности измерения, это просто следствие того, что вся цепь сидит (опоясывает) в запретной зоне, а значит и КВЛ, даже не «исправленная», не может там работать. Вы не можете вынуть две клеммы и поместить их в «безопасную» цепь . Траектория не обходит запрещенную зону, как мы сделали для индуктора с сосредоточенными параметрами в предыдущей схеме.
Более того, если бы вы вычли эффекты индукции, думая, что это и есть хорошее зондирование, вы совершили бы зондирующую ошибку. В конечном итоге вы измерите напряжение, которое не соответствует фактической конфигурации электрического поля в цепи, а вместо этого соответствует только его части (это показано в части 5, где индуцированное поле вычитается из общего поля).
Вы не можете вынуть две клеммы и поместить их в «безопасную» цепь . Траектория не обходит запрещенную зону, как мы сделали для индуктора с сосредоточенными параметрами в предыдущей схеме.
Более того, если бы вы вычли эффекты индукции, думая, что это и есть хорошее зондирование, вы совершили бы зондирующую ошибку. В конечном итоге вы измерите напряжение, которое не соответствует фактической конфигурации электрического поля в цепи, а вместо этого соответствует только его части (это показано в части 5, где индуцированное поле вычитается из общего поля).
Что такое «5 + 3 = 8 не 5 + 3 — 8 = 0»?
Если бы мы выбрали переход от одного вывода катушки индуктивности к другому, следуя за проводником, нам пришлось бы отказаться от КВЛ и прибегнуть к более общему закону Фарадея, потому что новая общая цепь замыкала бы переменное магнитное поле:
И это правильный способ решения проблем с изменением магнитного потока: 5 + 3 = 8. Он не претендует на независимость напряжения от пути (это не так) и делает вклад магнитного потока явным в правой части уравнения.
Но если мы отчаянно хотим снова увидеть наш любимый KVL, мы можем перенести член из правой части в левую часть, и мы получим 5 + 3 — 8 = 0, «исправленную версию» KVL, где макетное напряжение катушки индуктивности представляет собой производную магнитного потока по времени.
Это удобно, потому что мы можем делать вид, что KVL все еще работает, но это также вводит в заблуждение, потому что создается впечатление, что напряжение не зависит от пути, хотя на самом деле это не так.
В кольце Ромера-Левина два (сосредоточенных) резистора помещаются внутрь катушки, охватывающей область переменного магнитного потока, так что путь цепи охватывает область дБ/dt. Фейнман непреклонен: вы не можете использовать теорию схем с сосредоточенными параметрами. Левин также непреклонен: вы не можете использовать закон Кирхгофа (он для птиц!), поэтому нам нужно вернуться к более общему соотношению: закону Фарадея.
Если принять, что переменное поле B будет генерировать вращательное поле E, то все можно объяснить, посмотрев на то, как заряды в цепи реагируют на индуцированное поле, изменяют свою конфигурацию и создают другое результирующее электрическое поле внутри и вблизи кольца. .
.
Если бы магическим образом заставить кольцо из медного проводника и два резистора оказаться внутри этого циркулирующего поля, заряды внутри и на поверхности его частей почти мгновенно перераспределились бы таким образом, чтобы подчиняться закону Ома.
Мы можем получить представление о том, что движет перераспределением заряда, рассмотрев уравнение непрерывности. Смещение заряда — градиенты плотности заряда \$\rho\$ — происходит на поверхности и в продольном направлении, везде, где есть градиенты значений проводимости и магнитной проницаемости. Если предположить, что \$\frac{\partial \rho}{\partial t}=0\$, то уравнение неразрывности принимает вид div j = 0, и, добавляя соответствие закону Ома, мы получаем
, если \$\sigma \$ зависит от координат, мы можем расширить вышеуказанное до
Плотность заряда связана с электрическим смещением, и в среде с относительной проницаемостью \$\epsilon_r\$ мы можем выразить это через электрическое поле как
Избавимся от div E = -1/sigma . град сигма
град сигма
А теперь выразим E через \$j = \sigma E\$. Мы находим, что плотность заряда в цепи составляет
, и мы видим, что плотность заряда при заданной плотности тока изменяется в соответствии с градиентами проводимости и проницаемости.
Удачи в решении этой проблемы.
Но когда вы это сделаете, вы увидите, что заряд будет смещен, создав дополнительное электрическое поле, которое почти полностью нейтрализует тангенциальную часть электрического поля в проводнике. В идеальном проводнике с бесконечной проводимостью тангенциальное поле внутри него было бы равно нулю. При конечном значении сигмы мы получаем результирующее тангенциальное поле E, совместимое с определяющим уравнением \$j = \sigma E\$. (Малое поле в меди, большое поле в резистивных материалах.)
Заряды будут распределяться по проводнику, чтобы создать очень небольшое, обычно незначительное электрическое поле, направленное в осевом направлении вдоль медного проводника, и они также будут накапливаться на разрывах проводимости на крайних точках резисторов, в основном создавая напряжение, которое согласуется с законом Ома для результирующего тока.
Резюмируя: если считать плотность тока j одинаковой по всей цепи (взяв проводник и резистор одинакового диаметра, различающихся только материалом), мы увидим очень малое электрическое поле внутри высокопроводящего медь (отсюда отсутствие распределения воображаемых парциальных напряжений катушек внутри проводника), большое электрическое поле внутри маленького резистора (отвечающего за «напряжение» 0,1 В на пути, проходящем через него, знак зависит от направления) и сильное большее электрическое поле внутри большего резистора (отвечающего за 0,9V «напряжение» на пути, проходящем через него). Сумма всех напряжений в петле (обратите внимание, что они имеют определенные значения, потому что я указываю путь) равна , а не нулю , а составляет 1 В, как и предсказывает закон Фарадея.
Обратите внимание, что на рисунке выше нет датчиков .
Все показанные напряжения являются однозначными, потому что мы вычисляем их, задавая путь вдоль цепи (опять же, мы должны указать путь, потому что в неконсервативных полях такие интегралы зависят от пути).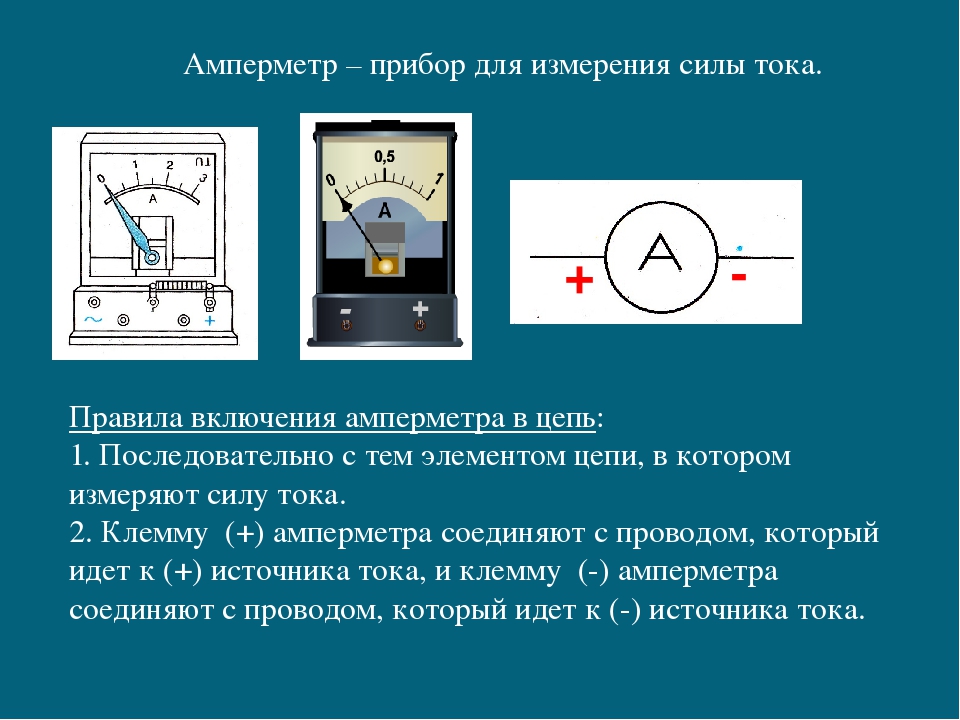


 (Подсказка: это отсутствие переменного магнитного потока: закон Кирхгофа о напряжении — это всего лишь закон Фарадея, когда dphi/dt = 0)
(Подсказка: это отсутствие переменного магнитного потока: закон Кирхгофа о напряжении — это всего лишь закон Фарадея, когда dphi/dt = 0)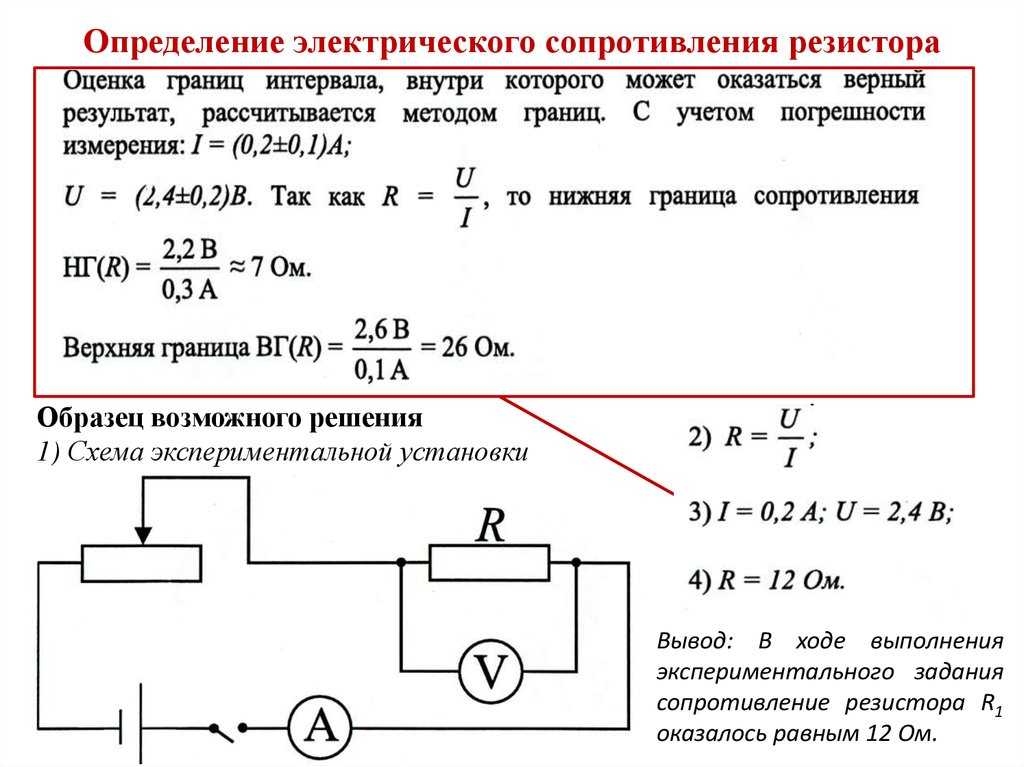 (подсказка: это то, что я называю маневром Макдональда, и он влечет за собой разделение полного электрического поля на две составляющие части, одну консервативную, вызванную кулоновским взаимодействием, и одну вращательную, вызванную магнитной индукцией)
(подсказка: это то, что я называю маневром Макдональда, и он влечет за собой разделение полного электрического поля на две составляющие части, одну консервативную, вызванную кулоновским взаимодействием, и одну вращательную, вызванную магнитной индукцией)