1.2. Осевые моменты инерции Jx ; Jy
Осевой момент инерции равен сумме произведений элементарных площадок на квадрат расстояния до соответствующей оси.
(7)
(8)
Единица измерения [см4], [мм4].
Знак всегда «+».
Не бывает равным 0.
Свойство:Принимает минимальное значение, когда точка пересечения координатных осей совпадает с центром тяжести сечения.
Чем дальше площадь удалена от центральной оси, тем осевой момент инерции сечения больше. Жесткость конструкции повышается.
Осевой момент инерции сечения применяют при расчетах на прочность, жесткость и устойчивость.
1.3. Полярный момент инерции сечения Jρ
Рис. 3
(9)
Взаимосвязь полярного и осевого моментов инерции:
(10)
(11)
Полярный момент инерции сечения равен сумме осевых моментов.
Свойство:
при
повороте осей в любую сторону, один из
осевых моментов инерции возрастает, а
другой убывает (и наоборот).
1.4. Центробежный момент инерции сечения Jxy
Центробежный момент инерции сечения равен сумме произведений элементарных площадок на расстояния до обеих осей
(12)
Единица измерения [см4], [мм4].
Знак «+» или «-».
, если координатные оси являются осями симметрии (пример – двутавр, прямоугольник, круг), или одна из координатных осей совпадает с осью симметрии (пример – швеллер).
Таким образом для симметричных фигур центробежный момент инерции равен 0.
Координатные оси uиv, проходящие через центр тяжести сечения, относительно которых центробежный момент равен нулю, называютсяглавными центральными осями инерции сечения.
У
сечений, не обладающих симметрией
относительно осей xилиy, например у
уголка,не будет равен нулю.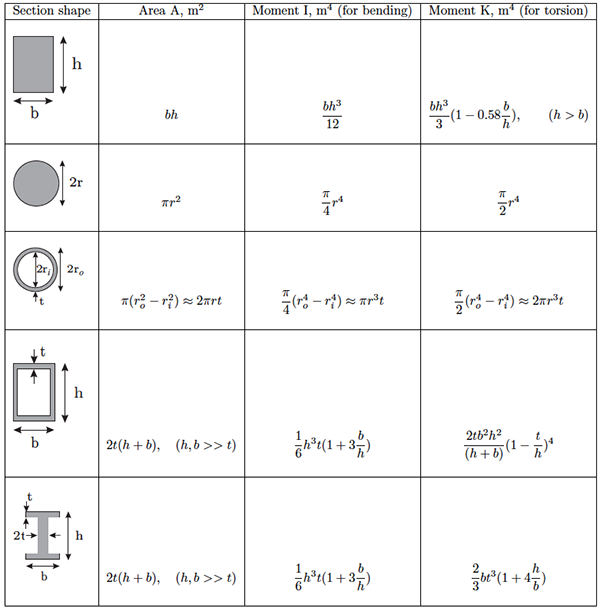
Для этих сечений
определяют положение осейuиvс помощью
вычисления угла поворота осейxиy
(13)
Центробежный момент относительно осей uиv—
Формула для определения осевых моментов инерции относительно главных центральных осей
(14)
где — осевые моменты инерции относительно центральных осей,
— центробежный момент инерции относительно центральных осей.
1.5. Момент инерции относительно оси, параллельной центральной (теорема Штейнера)
Теорема Штейнера:
Момент инерции относительно оси, параллельной центральной, равен центральному осевому моменту инерции плюс произведение площади всей фигуры на квадрат расстояния между осями.
(15)
Рис. 4
Доказательство теоремы Штейнера.
Согласно рис. 5 расстояние удо элементарной площадкиdF
Рис. 5
Подставляя значение ув формулу, получим:
Слагаемое
,
так как точка С является центром тяжести
сечения (см.
Для прямоугольника высотой h и шириной b :
Осевой момент инерции:
Момент сопротивления изгибу:
момент сопротивления изгибу равен отношению момента инерции к расстоянию наиболее удаленного волокна от нейтральной линии:
т.к. , то
Для круга:
Полярный момент инерции:
Осевой момент инерции:
Момент сопротивления кручению:
Т.к. , то
Момент сопротивления изгибу:
Пример 2. Определить момент инерции прямоугольного сечения относительно центральной оси Сx.
Рис. 6
Решение.
Разобьём площадь прямоугольника на
элементарные прямоугольники с размерами b(ширина) иdy(высота). Тогда площадь такого прямоугольника
(на рис. 6 заштрихована) равна dF=bdy.
Вычислим значение осевого момента
инерции Jx
По аналогии запишем
— осевой момент инерции сечения относительно центральной
оси у
Центробежный момент инерции
, так как оси Сxи Сyявляются осями симметрии.
Пример 3. Определить полярный момент инерции круглого сечения.
Рис. 7
Решение. Разобьём круг на бесконечно тонкие кольца толщиной радиусом, площадь такого кольца. Подставляя значениев выражение для полярного момента инерции интегрируя, получим
Учитывая равенство осевых моментов круглого сечения и
, получаем
Осевые моменты инерции для кольца равны
с – отношение диаметра выреза к наружному диаметру вала.
Лекция №2 «Главные оси и
Рассмотрим, как изменяются моменты
инерции при повороте координатных осей.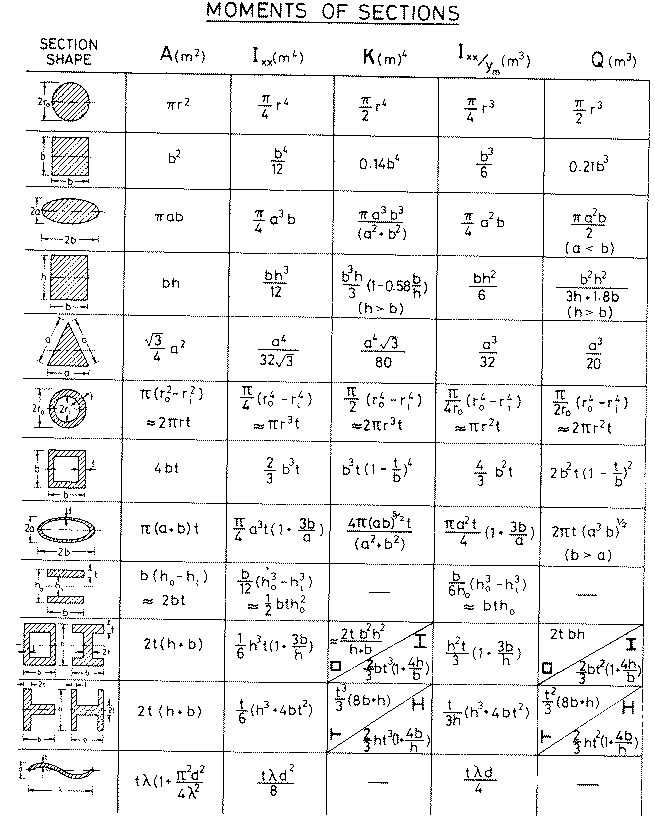
Положим, даны моменты инерции некоторого
сечения относительно осей 0х, 0у(не обязательно центральных)- ,-
осевые моменты инерции сечения. Требуется
определить,-
осевые моменты относительно осейu,v, повёрнутых
относительно первой системы на угол(рис. 8)
Рис. 8
Так как проекция ломаной линии ОАВС равна проекции замыкающей, находим:
(15)
Исключим uиvв выражениях моментов инерции:
Тогда
Откуда
(16)
(17)
(18)
Рассмотрим два первых уравнения. Складывая их почленно, получим
Таким образом, сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей не зависит от угла и при повороте осей остается постоянной. Заметим при этом, что
Где — расстояние от начала координат до элементарной площадки (см. рис.5). Таким образом
Где — уже знакомый нам полярный момент инерции:
Определим
осевой момент инерции круга относительно
диаметра.
Так как в силу симметрии но, как известно,
Следовательно, для круга
С изменением угла поворота осей значения моментов именяются, но сумма остается неизменной. Следовательно существует такое значение, при котором один из моментов инерции достигает своего максимального значения, в то время как другой момент принимает минимальное значение. Дифференцируя выражениепо углуи приравнивая производную к нулю, находим
(19)
При этом значении угла один из осевых моментов будет наибольшим, а другой — наименьшим. Одновременно центробежный момент инерции
Оси,
относительно которых центробежный
момент инерции равен нулю, а осевые
моменты принимают экстремальные
значения, называются главнымиосями.Если они к тому же являются центральными
(точка начала координат совпадает с
центром тяжести сечения), то тогда они
называютсяглавными центральными
осями (u; v).
Осевые моменты инерции относительно
главных осей называются
И их значение определяется по следующей формуле:
(20)
Знак плюс соответствует максимальному моменту инерции, знак минус — минимальному.
Существует ещё одна геометрическая характеристика – радиус инерциисечения.Эта величина часто используется в теоретических выводах и практических расчётах.
Радиусом инерции сечения относительно некоторой оси, например 0x,называется величина ,определяемая из равенства
(21)
F– площадь поперечного сечения,
— осевой момент инерции сечения,
Из определения следует, что радиус инерции равен расстоянию от оси 0
(22)
Радиусы инерции, соответствующие главным осям, называютсяглавными радиусами инерциии определяются по формулам
(23)
Лекция
3.
Кручение стержней круглого поперечного
сечения.
Техническая система — единица — Большая Энциклопедия Нефти и Газа, статья, страница 3
Cтраница 3
Здесь и далее — принята техническая система единиц
Естественно, что такое определение технической системы единиц для практика дает так же мало, как, например, указание, что 1 м равен одной сорокамиллионной части земного меридиана. Систему единиц нужно укрепить путем точного определения некоторых легко воспроизводимых величин. Так, в результате интернационального соглашения установлены единицы сопротивления и электрического тока. Так называемый — международный ом есть сопротивление ртутного столба с поперечным сеченяем в 1 мм2 и длиной 106 3 см при 0; международный ампер есть ток, который в течение секунды выделяет 1 118 мг серебра. Международный вольт лрогоняет по проводнику с сопротивлением в 1 ом ток в 1 ампер. [32]
Естественно, что такое определение технической системы единиц для практика дает так же мало, как, например, указание, что 1 м равен одной сорокамиллионной части земного меридиану.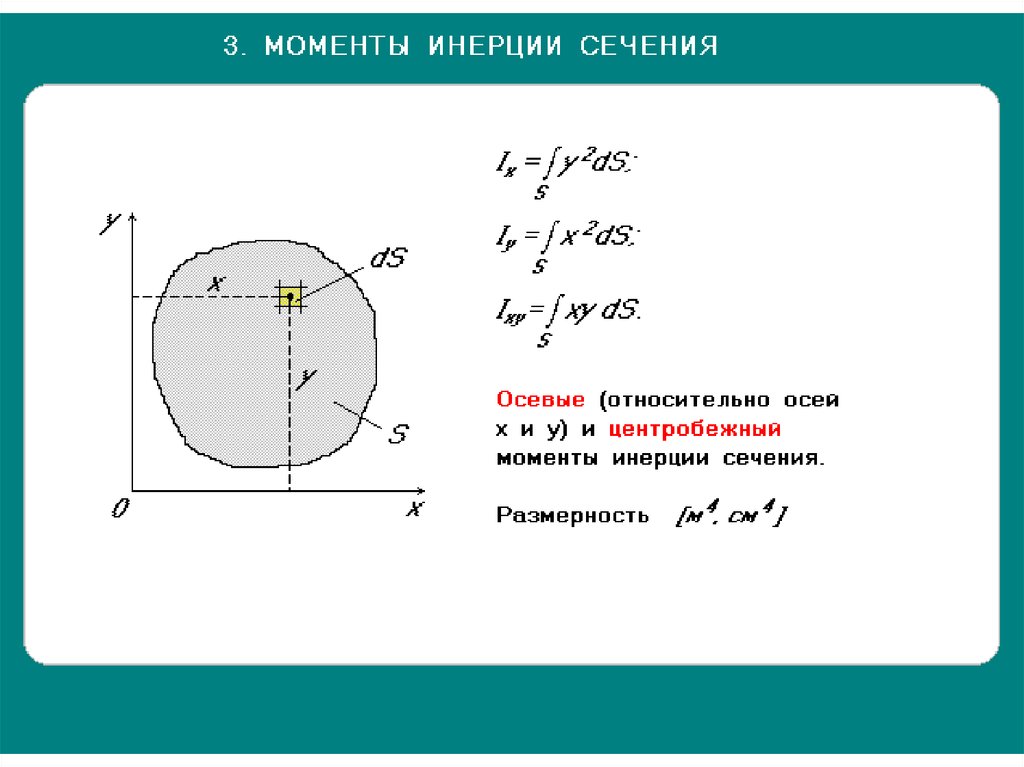
Систему единиц нужно укрепить путем точного определения некоторых легко воспроизводимых величин. Так, в результате интернационального соглашения установлены единицы сопротивления и электрического тока. Так называемый международный ом есть сопротивление ртутного столба с поперечным сечением в 1 лш2и длиной 106 3 см при 0; международный ампер есть ток, который в течение секунды выделяет 1 118 мг серебра. Международный вольт дрогоняет по проводнику с сопротивлением в 1 ом ток в 1 ампер.
[33]
Приведенные выше формулы справедливы для технической системы единиц измерения. Это означает, что проницаемость должна быть выражена в дарси, время — в секундах, длина — в сантиметрах, а давление — в атмосферах. [34]
В технике применяют так называемую техническую систему единиц, основными единицами которой являются: единицей длины — метр, единицей силы — ки-лограмм-сила и единицей времени — секунда. Техническая система имеет обозначение МкГС пли MK1S, где кГ и Kf — символы килограмм-силы.
[35]
Момент силы относительно оси в технической системе единиц выражается в килограммометрах. [36]
Единицей измерения моментов инерции в технической системе единиц является момент инерции материальной точки, имеющей массу, равную одной технической единице массы, и находящейся на расстоянии одного метра от данной оси или от данной точки. [37]
Момент силы относительно оси в технической системе единиц выражается в килограммометрах. [38]
Единицей измерения моментов инерции в технической системе единиц является момент инерции материальной точки, имеющей массу, равную одной технической единице массы, и находящейся на расстоянии одного метра от данной оси или от данной точки. [39]
Момент силы относительно оси в технической системе единиц выражается в килограммометрах. [40]
Единицей измерения моментов инерции в технической системе единиц является момент инерции материальной точки, имеющей массу, равную одной технической единице массы, и находящейся на расстоянии одного метра от данной оси или от данной точки.
Следовательно, единицей измерения моментов инерции служит 1 кгмсекг.
[41]
Касательное напряжение т имеет в технической системе единиц ( килограмм-сила, метр, секунда)) размерность KL-2, а градиент скорости du / dy — размерность Т 1, где К есть символ силы, L — символ длины, а Т — символ времени. [42]
Система единиц измерения МКГСС является технической системой единиц. [43]
В ГОСТ 356 — 59 принята техническая система единиц. [44]
Комплекс цСр / Х ( в технической системе единиц gpcp / ty является безразмерной величиной. [45]
Страницы: 1 2 3 4
Калькулятор момента сопротивления | Рассчитать момент сопротивления
✖Модуль упругости Юнга — это мера способности материала выдерживать изменения длины при продольном растяжении или сжатии. ТехническийАттопаскальБарБарьеСантиметр ртутного столба (0 °C)Сантиметр водяного столба (4 °C)СантипаскальДекапаскальДеципаскальДин на квадратный сантиметрЭксапаскальФемтопаскальФут морской воды (15 °C)ФемтопаскальВода фута (60 °F)ГигапаскальГрамм-сила на квадратный сантиметрГектопаскальДюйм ртутного столба (32 °F) )Дюйм ртутного столба (60 °F)Дюйм водяного столба (4 °C)Дюйм водяного столба (60 °F)Килограмм-сила на квадратный сантиметрКилограмм-сила на квадратный метрКилограмм-сила на квадратный миллиметрКилоньютон на квадратный метрКилопаскальКилофунт на квадратный дюймКип-сила на квадратный дюймМегапаскальМорской Водяной метр Вода (4 °C)МикробарМикропаскальМиллибарМиллиметр ртутного столба (0 °C)Миллиметр водяного столба (4 °C)МиллипаскальНанопаскальНьютон на квадратный сантиметрНьютон на квадрат e МетрНьютон на квадратный миллиметрПаскальПетапаскальПикопаскальПьезфунт на квадратный дюймФунт на квадратный футФунт-сила на квадратный футФунт-сила на квадратный дюймФунт на квадратный футСтандартная атмосфераТерапаскальтонна-сила (длинная) на квадратный футтонна-сила (длинная) на квадратный дюймтонна-сила (короткая) на квадратный фут-тонна- Сила (короткая) на квадратный дюйм торр | +10% -10% | ||
Circular ] | сантиметрал. | +10% -10% | |
✖ Радиус нейтрального уровня является любым из сегментов линейки от своего центра до его периметра, и в более современном. использования, это также их длина.ⓘ Радиус нейтрального слоя [R] | AlnAngstromArpentАстрономическая единица Аттометр AU длиныЯчменьМиллиард световых летБор РадиусКабель (Международный)Кабель (Великобритания)Кабель (США)КалибрСантиметрЦепьКубит (Греческий)Кубит (Длинный)Кубит (Великобритания)ДекаметрДециметр Радиус РадиусРасстояние от Земли до Луны (ClassiusEarthPearthРасстояние от СолнцаЗемля) EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedReed (Long )RodRoman ActusВеревкаРусский АрчинПролет (Ткань)Радиус СолнцаТераметрTwipVara CastellanaVara ConuqueraVara De TareaЯрдYOctometerYottameterZeptometerZettamete р | +10% -10% |
Millimeter⁴ ✖Момент сопротивления определяется как пара, создаваемая внутренними силами в балке, подвергаемой изгибу при максимально допустимом напряжении. | Дин-метр Дин-миллиметрГрам-сила-сантиметрГрам-сила-метрГрам-сила-миллиметрКилограмм-метрКилограмм-сила-сантиметрКилограмм-сила-метрКилограмм-сила-миллиметрКилоньютон-метрНьютон-сантиметрНьютон-метрНьютон-миллиметрУнция-сила-футУнция-сила-футФунт-сила-футФунт-сила-дюйм | ⎘ Копировать |
ⓘ Момент сопротивления [M сопротивление ]👎
Формула
Перезагрузить
👍
Момент сопротивления Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Модуль пучка Юнга: 14 мегапаскалей —> 14000000 паскалей (проверьте преобразование здесь)
M.
I площади круглого сечения: 1154 миллиметра⁴ —> 1,154E-09 метра⁴ (проверьте преобразование здесь)
Радиус нейтрального слоя: 2 миллиметра —> 0,002 метра (проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: преобразование результата в единицы измерения
8,078 ньютон-метр —> 8078 ньютон-миллиметр (проверьте преобразование здесь)
< 10+ Калькуляторы изменения напряженияМомент инерции площади сечения при заданном модуле Юнга балки
MI площади круглого сечения = (момент сопротивления * радиус нейтрального слоя) / модуль Юнга пучка Идти
Радиус нейтральной оси с использованием момента сопротивления
Радиус нейтрального слоя = (модуль Юнга луча * M.I площади круглого сечения) / момент сопротивления Идти
Расстояние между нейтральным и рассматриваемым слоем с использованием момента сопротивления
Расстояние от нейтрального слоя = (Напряжение в слое * M.
I площади круглого сечения) / Момент сопротивления
Идти
Момент инерции площади сечения балки при напряжении в слое
MI площади круглого сечения = (момент сопротивления * расстояние от нейтрального слоя)/напряжение в слое Идти
Момент сопротивления с использованием напряжения в слое балки
Момент сопротивления = (напряжение в слое * M.I площади круглого сечения) / расстояние от нейтрального слоя Идти
Напряжение в слое балки с учетом момента сопротивления
Напряжение в слое = (момент сопротивления * расстояние от нейтрального слоя)/M.I площади круглого сечения Идти
Напряжение в слое, если считается, что балка подвергается простому изгибу
Напряжение в слое = (модуль пучка Юнга * расстояние от нейтрального слоя)/радиус нейтрального слоя Идти
Расстояние между нейтральным и рассматриваемым слоями в лучах
Расстояние от нейтрального слоя = (напряжение в слое * радиус нейтрального слоя) / модуль Юнга пучка Идти
Модуль Юнга пучка
Модуль Юнга пучка = (Напряжение в слое * Радиус нейтрального слоя) / Расстояние от нейтрального слоя Идти
Радиус нейтрального слоя
Радиус нейтрального слоя = (модуль пучка Юнга*расстояние от нейтрального слоя)/напряжение в слое Идти
Формула момента сопротивления
Момент сопротивления = (модуль Юнга луча * M.
I площади круглого сечения) / радиус нейтрального слоя
M сопротивление = (E*I круговое )/R
Что понимают под напряжением изгиба?
Напряжение изгиба — это нормальное напряжение, с которым сталкивается объект, когда он подвергается большой нагрузке в определенной точке, которая заставляет объект изгибаться и утомляться. Напряжение изгиба возникает при эксплуатации промышленного оборудования, а также в бетонных и металлических конструкциях при воздействии на них растягивающей нагрузки.
Как рассчитать момент сопротивления?
Калькулятор момента сопротивления использует Момент сопротивления = (Модуль Юнга луча * M.I площади круглого сечения) / Радиус нейтрального слоя для расчета момента сопротивления. Формула момента сопротивления определяется как пара, создаваемая внутренним силы в балке, подвергаемой изгибу при максимально допустимом напряжении.
Момент сопротивления обозначается цифрой M сопротивление символ.
Как рассчитать момент сопротивления с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для момента сопротивления, введите модуль Юнга балки (E) , MI площади кругового сечения (I круговой ) и радиус нейтрального слоя (R) и нажмите кнопку расчета . Вот как можно объяснить расчет момента сопротивления с заданными входными значениями -> 8,078 = (14000000*1,154E-09)/0,002 .
Часто задаваемые вопросы
Что такое момент сопротивления?
Формула момента сопротивления определяется как пара, создаваемая внутренними силами в балке, подвергаемой изгибу при максимально допустимом напряжении, и представляется как Момент сопротивления = (Модуль Юнга луча * M.I площади круглого сечения) / Радиус нейтрального слоя . Модуль Юнга пучка является мерой способности материала выдерживать изменения длины при растяжении или сжатии в продольном направлении, MI площади кругового сечения представляет собой второй момент площади сечения относительно нейтральной оси и радиуса нейтральной слой — это любой отрезок линии от его центра до периметра, а в более современном использовании — это также их длина.
Как рассчитать момент сопротивления?
Формула момента сопротивления определяется как пара, создаваемая внутренними силами в балке, подвергаемой изгибу при максимально допустимом напряжении, рассчитывается с использованием Момент сопротивления = (Модуль Юнга луча * M.I площади круглого сечения) / Радиус нейтрального слоя . Чтобы рассчитать момент сопротивления, вам потребуются модуль Юнга балки (E) , MI площади кругового сечения (I круговой ) и радиус нейтрального слоя (R) . С помощью нашего инструмента вам нужно ввести соответствующие значения для модуля Юнга пучка, MI площади круглого сечения и радиуса нейтрального слоя и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Сколько существует способов расчета момента сопротивления?
В этой формуле момент сопротивления использует модуль Юнга пучка, MI площади кругового сечения и радиус нейтрального слоя. Мы можем использовать 1 другой способ (способы) для расчета того же самого, который выглядит следующим образом:
- Момент сопротивления = (Напряжение в слое * M.I площади кругового сечения) / Расстояние от нейтрального слоя
Доля
Скопировано!
Измерение деформации с помощью тензодатчиков
Что такое деформация
При механических испытаниях и измерениях необходимо понимать, как объект реагирует на различные силы. Величина деформации, которую испытывает материал из-за приложенной силы, называется деформацией. Деформация определяется как отношение изменения длины материала к исходной длине без изменений, как показано на рисунке 1. Деформация может быть положительной (растяжение) из-за удлинения или отрицательной (сжатие) из-за сжатия. Когда материал сжимается в одном направлении, тенденция к расширению в двух других направлениях, перпендикулярных этой силе, известна как эффект Пуассона. Коэффициент Пуассона (v) является мерой этого эффекта и определяется как отрицательное отношение деформации в поперечном направлении к деформации в осевом направлении. Несмотря на безразмерность, деформация иногда выражается в таких единицах, как дюйм/дюйм. или мм/мм. На практике величина измеряемой деформации очень мала, поэтому ее часто выражают как микродеформацию (µε), которая составляет ε x 10 -6 .
Четыре различных типа деформации: осевая, изгибная, сдвиговая и крутильная. Наиболее распространены осевая и изгибающая деформации (см. рис. 2). Осевая деформация измеряет, как материал растягивается или сжимается в результате действия линейной силы в горизонтальном направлении. Деформация изгиба измеряет растяжение на одной стороне материала и сжатие на противоположной стороне из-за линейной силы, приложенной в вертикальном направлении. Деформация сдвига измеряет величину деформации, которая возникает из-за линейной силы с компонентами как в горизонтальном, так и в вертикальном направлениях. Деформация кручения измеряет круговую силу с компонентами как в вертикальном, так и в горизонтальном направлениях.
Рис. 2. Осевая деформация показывает, как материал растягивается или разрывается. Деформация при изгибе измеряет растяжение с одной стороны и сжатие с другой.
Измерение деформации
Вы можете измерить деформацию несколькими способами, но наиболее распространенным является тензодатчик. Электрическое сопротивление тензорезистора изменяется пропорционально величине напряжения в устройстве. Наиболее широко используемым тензорезистором является металлический тензорезистор. Металлический тензорезистор состоит из очень тонкой проволоки или, чаще, из металлической фольги, расположенной в виде сетки. Решетка максимизирует количество металлической проволоки или фольги, подвергающихся деформации в параллельном направлении. Сетка приклеивается к тонкой подложке, называемой держателем, которая прикрепляется непосредственно к испытуемому образцу. Следовательно, деформация, испытываемая испытуемым образцом, передается непосредственно на тензорезистор, который реагирует линейным изменением электрического сопротивления.
Рис. 3. Электрическое сопротивление металлической сетки изменяется пропорционально величине деформации, испытываемой испытуемым образцом.
Основным параметром тензорезистора является его чувствительность к деформации, выражаемая количественно как коэффициент тензорезистора (GF). GF представляет собой отношение относительного изменения электрического сопротивления к относительному изменению длины или деформации:
GF для металлических тензорезисторов обычно составляет около 2. Фактическое GF конкретного тензорезистора можно узнать у поставщика датчика или в документации на датчик.
На практике измерения деформации редко включают величины, превышающие несколько миллидеформаций (например, 10 -3 ). Следовательно, чтобы измерить деформацию, вы должны точно измерить очень малые изменения сопротивления. Например, предположим, что испытуемый образец подвергается деформации в 500 мкс. Тензорезистор с GF, равным 2, показывает изменение электрического сопротивления всего в 2 (500×10 -6 ) = 0,1%. Для датчика на 120 Ом это изменение составляет всего 0,12 Ом.
Для измерения таких небольших изменений сопротивления конфигурации тензорезисторов основаны на концепции моста Уитстона. Общий мост Уитстона, показанный на рис. 4, представляет собой сеть из четырех резистивных плеч с напряжением возбуждения VEX, которое прикладывается к мосту.
Рис. 4. Тензодатчики конфигурируются в схемах моста Уитстона для обнаружения небольших изменений сопротивления.
Мост Уитстона представляет собой электрический эквивалент двух параллельных цепей делителя напряжения. R 1 и R 2 составляют одну цепь делителя напряжения, а R 4 и R 3 составляют вторую цепь делителя напряжения. Выход моста Уитстона Vo измеряется между средними узлами двух делителей напряжения.
Из этого уравнения видно, что когда R 1 /R 2 = R 4 /R 3 , выходное напряжение V O равно нулю. В этих условиях говорят, что мост разбалансирован. Любое изменение сопротивления в любом плече моста приводит к ненулевому выходному напряжению. Следовательно, если вы замените R 4 на рис. 4 активным тензорезистором, любые изменения сопротивления тензорезистора разбалансируют мост и создадут ненулевое выходное напряжение, которое является функцией деформации.
Правильный выбор тензодатчика
Типы тензодатчиков
Три типа конфигураций тензорезисторов: четверть-, полу- и мостовая, определяются количеством активных элементов в мосте Уитстона, ориентацией деформации датчики и тип измеряемой деформации.
Четвертьмостовой тензодатчик
Конфигурация Тип I
7 902 Измерения осевых деформаций или изгибов
Рис. 5. Конфигурации четвертьмостового тензометра .
Тип конфигурации II
В идеале сопротивление тензорезистора должно изменяться только в зависимости от приложенной деформации. Однако материал тензорезистора, а также материал образца, на который наносится тензорезистор, также реагируют на изменения температуры. Конфигурация четвертьмостового тензодатчика типа II помогает еще больше минимизировать влияние температуры за счет использования двух тензорезисторов в мосту. Как показано на рисунке 6, обычно один тензорезистор (R4) является активным, а второй тензорезистор (R3) устанавливается в тесном тепловом контакте, но не приклеивается к образцу и размещается поперек главной оси деформации. Таким образом, деформация мало влияет на этот макет манометра, но любые изменения температуры одинаково влияют на оба манометра. Поскольку изменения температуры в двух тензодатчиках идентичны, соотношение их сопротивлений не меняется, выходное напряжение (Vo) не меняется, а влияние температуры сведено к минимуму.
Рис. 6. Манекены тензодатчиков устраняют влияние температуры на измерение деформации.
Полумостовой тензодатчик
Вы можете удвоить чувствительность моста к деформации, активировав оба тензорезистора в полумостовой конфигурации.
Тип конфигурации I
- Измерение осевой деформации или деформации изгиба
- Требуются согласующие резисторы полумоста для завершения моста Уитстона
- R4 — активный тензодатчик для измерения деформации растяжения (+ε)
- R3 — активный тензодатчик, компенсирующий эффект Пуассона (-νε)
Эту конфигурацию обычно путают с четвертьмостовой конфигурацией типа II, но тип I имеет активный элемент R3, прикрепленный к деформируемому образцу.
Тип конфигурации II
Измеряет только деформацию изгиба
Требуются резисторы завершения полумоста для завершения моста Уитстона
R4 — активный тензодатчик для измерения деформации растяжения (+ε)
R3 — активный тензодатчик для измерения деформации сжатия (-ε)
Рис. 7. Полумостовые тензорезисторы в два раза более чувствительны, чем четвертьмостовые.
Мостовой тензорезистор
Мостовой тензорезистор включает четыре активных тензорезистора и доступен в трех различных типах. Типы I и II измеряют деформацию изгиба, а тип III измеряет осевую деформацию. Только типы II и III компенсируют эффект Пуассона, но все три типа минимизируют влияние температуры.
Тип конфигурации I: только деформация изгиба
Конфигурация типа II
Измеряет только деформацию изгиба
Требуются резисторы завершения полумоста для завершения моста Уитстона
R4 — активный тензодатчик для измерения деформации растяжения (+ε)
R3 — активный тензодатчик для измерения деформации сжатия (-ε)
R4 — активный тензодатчик для измерения деформации растяжения (+e)
Тип конфигурации III: только осевая деформация
Измеряет осевую деформацию
R1 и R3 — активные тензодатчики, измеряющие сжимающий эффект Пуассона (–νe)
R2 и R4 — активные тензодатчики для измерения деформации растяжения (+e)
Рис. 8. Конфигурации тензорезисторов с полным мостом
Технические характеристики тензорезисторов, которые следует учитывать
После того как вы определились с типом деформации, которую собираетесь измерять (осевая или изгибная), необходимо учитывать другие факторы, включая чувствительность, стоимость и условия эксплуатации. Для одного и того же тензорезистора изменение конфигурации моста может повысить его чувствительность к деформации. Например, конфигурация типа I с полным мостом в четыре раза более чувствительна, чем конфигурация с четвертью моста типа I. Однако для полномостового типа I требуется на три тензодатчика больше, чем для четвертьмостового типа I. Он также требует доступа к обеим сторонам конструкции с датчиками. Кроме того, полномостовые тензодатчики значительно дороже, чем полумостовые и четвертьмостовые. Сводную информацию о различных типах тензорезисторов см. в следующей таблице.
Ширина сетки
Использование более широкой сетки, если она не ограничена местом установки, улучшает рассеивание тепла и повышает стабильность тензорезистора. Однако, если испытуемый образец имеет серьезные градиенты деформации, перпендикулярные основной оси деформации, рассмотрите возможность использования узкой сетки, чтобы свести к минимуму ошибку из-за влияния деформации сдвига и деформации Пуассона.
Номинальное сопротивление
Номинальное тензометрическое сопротивление — это сопротивление тензодатчика в ненагруженном положении. Вы можете получить номинальное сопротивление конкретного датчика у поставщика датчика или в документации датчика. Наиболее распространенные номинальные значения сопротивления коммерческих тензорезисторов составляют 120 Ом, 350 Ом и 1000 Ом. Рассмотрите более высокое номинальное сопротивление, чтобы уменьшить количество тепла, выделяемого напряжением возбуждения. Более высокое номинальное сопротивление также помогает уменьшить вариации сигнала, вызванные изменениями сопротивления проводов из-за колебаний температуры.
Температурная компенсация
В идеале сопротивление тензорезистора должно изменяться только в ответ на деформацию. Однако удельное сопротивление и чувствительность тензорезистора также изменяются с изменением температуры, что приводит к ошибкам измерения. Производители тензорезисторов пытаются свести к минимуму чувствительность к температуре, обрабатывая материал тензорезистора, чтобы компенсировать тепловое расширение материала образца, для которого предназначен тензорезистор. Эти конфигурации моста с температурной компенсацией более устойчивы к температурным воздействиям. Также рассмотрите возможность использования типа конфигурации, который помогает компенсировать влияние колебаний температуры.
Установка
Установка тензорезисторов может занять значительное количество времени и ресурсов, и эта сумма сильно зависит от конфигурации моста. Количество приклеенных датчиков, количество проводов и место установки — все это может повлиять на уровень усилий, необходимых для установки. В некоторых конфигурациях моста даже требуется установка манометра на противоположных сторонах конструкции, что может быть затруднительно или даже невозможно. Четвертьмостовой тип I является самым простым, поскольку требует установки только одного датчика и двух или трех проводов.
| Тип конфигурации I | Конфигурация типа II: только деформация изгиба |
| |
| Тип конфигурации I | Тип конфигурации II |
Эту конфигурацию обычно путают с четвертьмостовой конфигурацией типа II, но тип I имеет активный элемент R3, прикрепленный к деформируемому образцу. |
|
| Тип конфигурации I: только деформация изгиба | Конфигурация типа II: только деформация при изгибе | Конфигурация типа III: только осевая деформация | |
| |||
| Тип конфигурации I | Тип конфигурации II | Тип конфигурации III | |
|
|
Тип измерения | Квартальный мост | Полумост | Полный мост | ||||
Тип I | Тип II | Тип I | Тип II | Тип I | Тип II | Тип III | |
| Осевая деформация | Да | Да | Да | № | № | № | Да |
| Деформация изгиба | Да | Да | Да | Да | Да | Да | № |
| Компенсация |
|
|
|
|
|
|
|
| Поперечная чувствительность | № | № | Да | № | № | Да | Да |
| Температура | № | Да | Да | Да | Да | Да | Да |
| Чувствительность |
|
|
|
|
|
|
|
| Чувствительность при 1000 мкс | ~0,5 мВ/В | ~0,5 мВ/В | ~0,65 мВ/В | ~1,0 мВ/В | ~2,0 мВ/В | ~1,3 мВ/В | ~1,3 мВ/В |
| Установка |
|
|
|
|
|
|
|
| Количество приклеенных датчиков | 1 | 1* | 2 | 2 | 4 | 4 | 4 |
| Место установки | Односторонняя | Односторонняя | Односторонняя | Противоположные стороны | Противоположные стороны | Противоположные стороны | Противоположные стороны |
| Количество проводов | 2 или 3 | 3 | 3 | 3 | 4 | 4 | 4 |
| Завершающие резисторы моста | 3 | 2 | 2 | 2 | 0 | 0 | 0 |
| *Второй тензорезистор размещается в тесном тепловом контакте со структурой, но не приклеивается. | |||||||
Преобразование сигнала для тензодатчиков
Измерения тензодатчиков сложны, и несколько факторов могут повлиять на их эффективность. Следовательно, вам необходимо правильно выбрать и использовать мост, преобразование сигнала, проводку и компоненты сбора данных для обеспечения надежных измерений. Например, допуски сопротивления и деформация, вызванная приложением манометра, создают некоторое начальное напряжение смещения, когда деформация не применяется. Точно так же длинные отводящие провода могут увеличить сопротивление плеча моста, что добавляет ошибку смещения и снижает чувствительность выходного сигнала моста. Для точных измерений деформации подумайте, нужны ли вам следующие вещи:
- Завершение моста для завершения необходимой схемы четверть- и полумостовых тензорезисторов
- Возбуждение для питания схемы моста Уитстона
- Дистанционное измерение для компенсации ошибок в напряжении возбуждения из-за длинных проводов
- Усиление для увеличения разрешения измерения и улучшения отношения сигнал/шум
- Фильтрация для удаления внешнего высокочастотного шума
- Обнуление смещения для балансировки моста до выходного напряжения 0 В при отсутствии напряжения
- Калибровка шунта для проверки выхода моста на известное ожидаемое значение
Чтобы узнать, как компенсировать эти ошибки, и ознакомиться с другими соображениями относительно аппаратного обеспечения для измерения деформации, загрузите Руководство инженера по точным измерениям датчиков .
