Техническая механика. Теоретическая механика | ПроСопромат.ру
Часто в прикладных задачах механики приходится определять моменты сил, приложенных к телу, относительно его оси. Покажем, что в сечениях тела под действием внешних сил всегда возникают внутренние силы.
Рассмотрим устройство для подъема грузов, состоящее из вала ABC, на который насажены барабан АВ с радиусом r и зубчатое колесо С с радиусом R.
Вал приводится во вращение от электродвигателя D через зубчатую передачу. Вес поднимаемого груза Q передается через трос на обод барабана, а от шестерни K, насаженной на вал электродвигателя, передается движущая

При равномерном подъеме груза моменты внешних сил, приложенных к валу, должны уравновешиваться, т. е.
Реакции опор А и В не войдут в уравнение моментов, так как они пересекают ось z и, следовательно, не создают относительно этой оси моментов.
Из составленного уравнения равновесия следует, что PR = Qr или Мz (Р) = Мz (Q), т. е. на концы участка вала, расположенного между сечением приложения груза
Участок вала между сечениями приложения вращающих моментов, как уже отмечалось, находится в равновесии.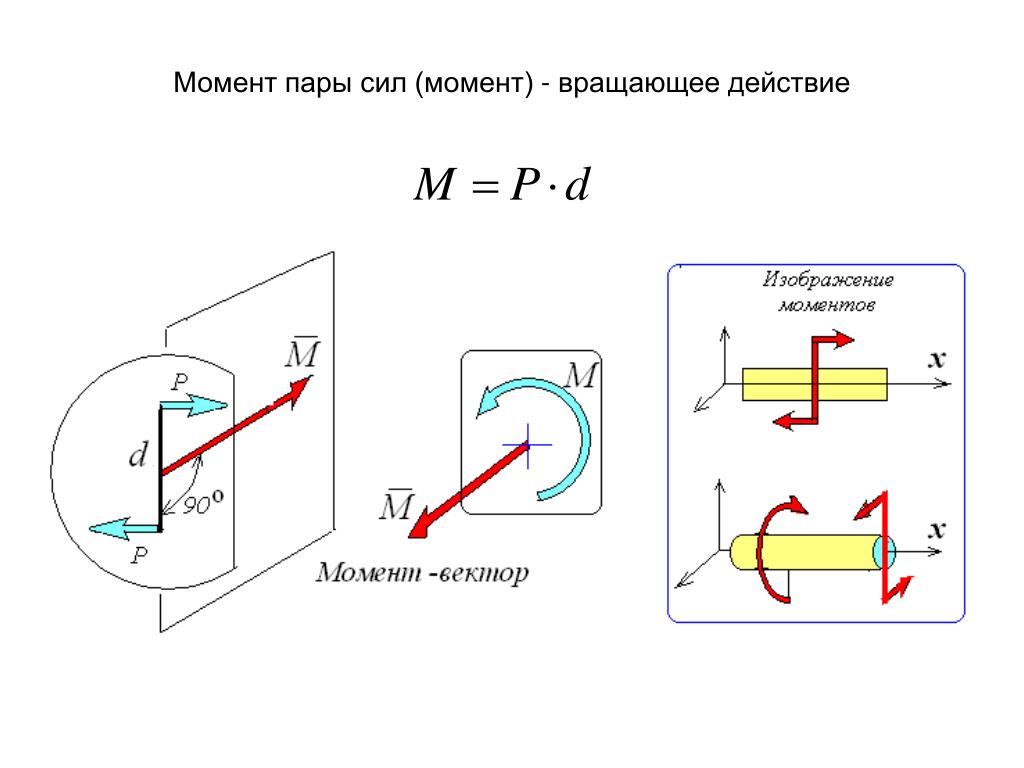 Естественно, что любая часть, мысленно отсеченная от этого вала, также должна быть в равновесии. На рисунке внизу проведено сечение Е.
Естественно, что любая часть, мысленно отсеченная от этого вала, также должна быть в равновесии. На рисунке внизу проведено сечение Е.
Чтобы отсеченная часть
Использованный здесь метод установления внутренних сил в сечении вала называется методом сечений (более подробно о методе сечений — см. здесь).
Момент внутренних
 е. вращающих моментов, приложенных к отсеченной части вала:
е. вращающих моментов, приложенных к отсеченной части вала:,
где n — число вращающих моментов, приложенных к отсеченной части рассматриваемого вала.
Знак крутящего момента в поперечном сечении вала можно установить, исходя из направления внешних вращающих моментов. 
При возрастании веса поднимаемого груза соответственно увеличиваются вращающие моменты. Будут возрастать также крутящие моменты в сечениях вала. Очевидно, что при данных размерах вала нельзя допускать безграничного возрастания вращающего, а следовательно, и крутящего моментов, так как вал может разрушиться или сильно деформироваться. Поэтому определение крутящих моментов имеет очень большое практическое значение для расчетов на прочность.
Запись опубликована автором admin в рубрике Пара сил и моменты сил.Рычаг обладает способностью вращаться вокруг оси закрепления (рис. а).
а).
Равновесие рычага будет обеспечено только в том случае, когда алгебраическая сумма моментов всех действующих на рычаг сил относительно его неподвижной
Неподвижной точкой рычага, относительно которой мы будем составлять уравнение моментов, является точка пересечения оси вращения рычага с плоскостью чертежа (рис.а)
или
Рычаг можно использовать для подъема грузов, для создания больших давлений с помощью небольшого усилия и т. п. Рычаги двух видов показаны на рис.б и в.
Запись опубликована автором admin в рубрике Пара сил и моменты сил. 42).
42).На рисунке показаны две составляющие силы Р — это силы Р1 и Р2 . Составляющая Р2 параллельна оси Оz, поэтому ее момент относительно этой оси равен нулю. Составляющая Р1 даст момент относительно оси
Таким образом,
Запись опубликована автором admin в рубрике Задачи по механике.Когда момент силы относительно оси равен нулю?
Момент силы относительно оси равен нулю, когда сила и ось расположены в одной плоскости.
1) сила параллельна оси;
2) линия действия силы пересекает ось.
И в том, и в другом случае момент силы относительно оси равен нулю.
Запись опубликована автором admin в рубрике Вопросы по механике.Рассмотрим, как определяется момент силы относительно оси. Стремление силы вращать тело вокруг неподвижной оси зависит от величины силы, ее наклона и расстояния от оси
Из опыта известно, что силы, проходящие через ось, и силы, параллельные оси, НЕ МОГУТ ВЫЗВАТЬ ВРАЩЕНИЯ ТЕЛА вокруг этой оси. Посмотрим на рисунок.
Ни сила Р1, линия действия которой пересекает ось Oz, ни сила Р2, параллельная оси, не смогут повернуть тело вокруг этой оси.
Для вращательного эффекта силы относительно закрепленной оси вводится понятие
Пусть на тело в какой-то точке действует произвольная сила Р, не параллельная оси вращения Oz и не пересекающая эту ось. Проведем плоскость H, перпендикулярную оси Oz и проходящую через начало вектора силы. Разложим заданную силу Р на две составляющие: Р1, расположенную в плоскости H, и Р2, параллельную оси Oz.
Составляющая Р2, параллельная оси Oz момента относительно этой оси не создает. Составляющая Р1, действующая в плоскости H, создает момент относительно оси Oz или, что то же самое, относительно точки О. Момент силы Р1 измеряется произведением модуля самой силы на длину а перпендикуляра, опущенного из точки О на направление этой силы, т. е.
Составляющая Р1, действующая в плоскости H, создает момент относительно оси Oz или, что то же самое, относительно точки О. Момент силы Р1 измеряется произведением модуля самой силы на длину а перпендикуляра, опущенного из точки О на направление этой силы, т. е.
В выражение момента силы относительно оси входит не вся сила, а только ее составляющая, лежащая в плоскости, перпендикулярной оси вращения.
Знак момента по общему правилу определяется направлением вращения тела: (+) при движении по часовой стрелке, (—) при движении против часовой стрелки (правило условно). При определении знака момента наблюдатель должен непременно находиться со стороны положительного направления оси. На рисунке вверху момент силы Р относительно оси Oz положителен, так как для наблюдателя, смотрящего со стороны положительного направления оси (сверху), тело под действием заданной силы представляется вращающимся вокруг оси по ходу часовой стрелки.
На рисунке вверху момент силы Р относительно оси Oz положителен, так как для наблюдателя, смотрящего со стороны положительного направления оси (сверху), тело под действием заданной силы представляется вращающимся вокруг оси по ходу часовой стрелки.
На рисунке внизу момент силы Р относительно оси Oz — величина отрицательная.
Рассмотрим частный случай.
В частном случае момент силы Р, расположенной в плоскости H, относительно оси Oz, перпендикулярной этой плоскости, определится произведением полной величины силы Р на ее плечо l относительно точки пересечения оси Oz и плоскости H
Итак, для определения момента силы относительно оси нужно спроектировать силу на плоскость, перпендикулярную оси, и найти момент проекции силы на плоскость относительно точки пересечения оси с этой плоскостью.
Зависят ли величина и направление момента силы относительно точки от взаимного расположения этой точки и линии действия силы?
Зависят. Момент силы относительно относительно точки определяется произведением модуля силы на плечо, поэтому величина и направление (знак) момента силы зависят от положения точки, относительно которой определяется момент.
Запись опубликована автором admin в рубрике Вопросы по механике.Какой из отрезков — ОВ, ОА или ОН — является плечом силы Р относительно точки О?
Плечом является отрезок ОН, так как плечо силы относительно точки- это длина перпендикуляра, опущенного из точки на линию действия силы.
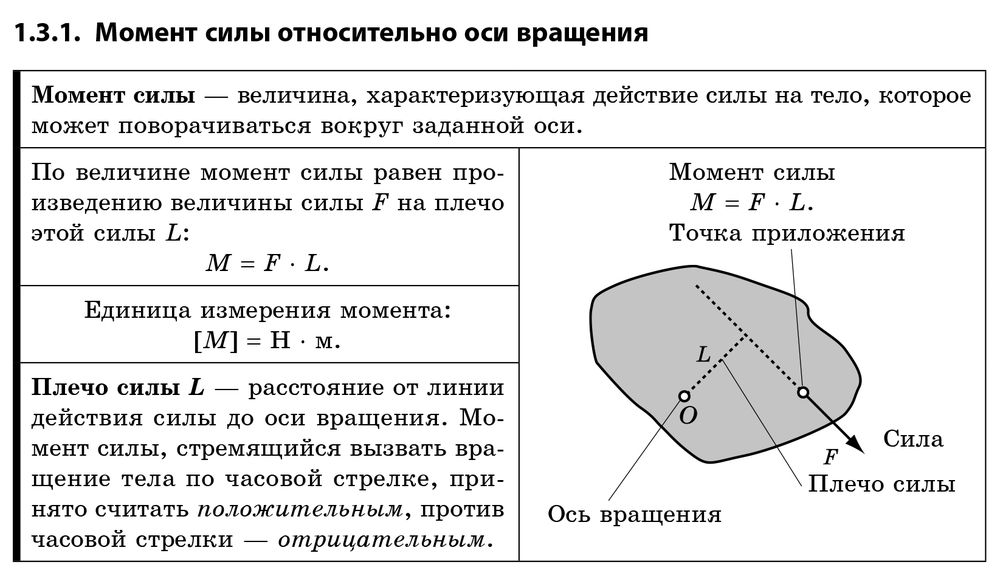
Моментом силы относительно точки называется произведение величины силы на длину перпендикуляра, опущенного из точки на линию действия силы (рис. а).
Если бы тело было закреплено в точке О, то сила Р стремилась бы вращать тело вокруг этой точки. Точка О, относительно которой берется момент, называется центром
момента, а перпендикуляр а называется плечом силы относительно центра момента.
Таким образом,
М = сила×плечо.
Момент силы Р относительно О обозначается
М0(Р) = Ра.
Моменты сил измеряют в ньютонометрах (Нм) или килограммометрах (кГм) или в соответствующих кратных и дольных единицах, как и моменты пар.
Принято считать момент положительным, если сила стремится вращать тело по часовой стрелке (рис. а), и отрицательным — против часовой стрелки (рис. б).
Установленное правило знаков для моментов сил, как и для моментов пар, условно.
Когда линия действия силы проходит через данную точку, ее момент относительно этой точки равен нулю, так как в рассматриваемом случае плечо равно нулю а = 0 (рис. в).
Между моментом пары и моментом силы есть одно существенное различие. У момента пары сил величина и направление не зависят от положения этой пары в пространстве. У момента силы величина и направление (знак) момента силы зависят от положения точки, относительно которой определяется момент.
У момента силы величина и направление (знак) момента силы зависят от положения точки, относительно которой определяется момент.
К телу приложены две пары, лежащие в параллельных плоскостях. Первая пара образована силами по 4 кн, имеет плечо 0,5 м и ее момёнт вращает по часовой стрелке. Вторая пара образована силами 6 кн, имеет плечо 0,4 м и ее момент вращает против часовой стрелки. Определить величину и направление момента пары сил, которой можно уравновесить эти пары.
Определим сначала моменты каждой из пар сил. Момент первой пары М1 = 4· 0,5 =2 кН·м;
момент второй пары М2 = — 6· 0,4 = -2, 4 кН·м.
Таким образом, алгебраическая сумма моментов пар сил равна М=М1+М2= -0,4 кН·м.
Следовательно, величина и направление момента пары сил, которой можно уравновесить эти пары будет равна +0,4 кН·м.
Запись опубликована автором admin в рубрике Вопросы по механике.Будет ли тело находиться в равновесии, если на него действуют три пары сил, приложенных в одной плоскости, и моменты этих пар имеют следующие значения:
М1 = —600 Н·м; М2 = 320 Н·м и М3 = 280 Н· м.
Для того чтобы узнать — будет ли тело находиться в равновесии, следует определить алгебраическую сумму моментов пар сил. Если данная сумма будет равна нулю, то система пар уравновешена, и тело будет находиться в равновесии.
Определим алгебраическую сумму моментов пар сил
М = —600 + 320 + 280 =0.
Следовательно, тело будет находиться в равновесии.
Запись опубликована автором admin в рубрике Вопросы по механике.Теоретическая механика
Лекция (1-5). Введение. Момент силы.
Лекция (6-10). Аксиомы
Лекция (11). Аксиома отвердевания
Лекция (12). Системы сил
Лекция (13). Сила — скользящий вектор
Лекция (14-15). Элементарные операции
Лекция (16). Приведение к 2-м силам
Лекция (17). Пара сил
Лекция (20). Теорема Пуансо
Лекция (21). Условие равновесия
Лекция (22). Варианты систем уравнений равновесия плоской системы
Лекция (23).
 Условие равновесия плоской системы
Условие равновесия плоской системыЛекция (24). Формула Пуансо
Лекция (25-26). Динама
Лекция (27). Случаи приведения
Лекция (28). Трение скольжения
Лекция (29). Трение качения
Лекция (30). Ферма
Лекция (30) eng. Truss
Лекция eng. Constraints and Their Reactions
Задача. Фигура из стержней
Задача. Самолет
Задача. Плоская фигура. Способ 1 (разбиение)
Задача. Плоская фигура. Способ 2 (метод отрицательных площадей)
Задача. Плоская фигура. Способ 4 (формула Грина)
Задача. Плоская фигура. Способ 5 (эксперимент)
Лекция. Сложение параллельных сил. Свойство пары.Лекция в Н202. 9.2.2016
Лекция. Часть 1. Приведение системы сил к центру.
 Изменение центра приведения.
Изменение центра приведения.Лекция. Часть 2. Скалярный инвариант.
Лекция. Часть 3. Уравнение центральной винтовой оси. Динама.
Лекция. Часть 4. Минимальный момент приведения.
Лекция. Часть 5. Уравнение центральной винтовой оси. Пример.
Решение задачи на равновесие одного тела (2015)
Решение задачи на равновесии рамы (2016). Три реакции. ТФ-04-15
Рама. Одно тело, скользящая заделка, подвижная опора (1A)
Рама. Одно тело, скользящая заделка, подвижная опора (1B)
Рама. Одно тело, скользящая заделка, подвижная опора (1С)
Рама. Составная конструкция (2)
Рама. Составная конструкция (2a). Заделка-шарнир-подвижный шарнир. Анимация и графика П.Горшкова.
Составная трехшарнирная конструкция.
Рама.
 Составная конструкция (2b). Два шарнира и скользящая заделка. Анимация и графика П.Горшкова.
Составная конструкция (2b). Два шарнира и скользящая заделка. Анимация и графика П.Горшкова.Цепь . Определяем положение равновесия. Анимация и графика П.Горшкова.
Задача на теорему о трех силах. . Определяем реакции опор. Анимация и графика П.Горшкова.
Составная конструкция (3 тела, шарнир) . Определяем реакции опор. Анимация и графика П.Горшкова.
Составная конструкция (3 тела, шарнир, стержень) . Определяем реакции опор. Анимация и графика П.Горшкова.
Рама. Составная конструкция (3)
Рама. Составная конструкция. (4)
Рама. Составная конструкция. Три тела (5)
Рама. Составная конструкция. Три тела (6)
Плоская стержневая система (6 стержней). Вырезание узлов. Анимация Петра Горшкова. Задача из Решебника (с.15)
Составная конструкция. Решение задачи в системе Maple.
Составная конструкция.
 Линейно распределенная нагрузка. (1-я часть)
Линейно распределенная нагрузка. (1-я часть)Составная конструкция. Линейно распределенная нагрузка. Maple (2-я часть)
Составная конструкция. Распределенная нагрузка.
Составная конструкция. Линейно распределенная нагрузка. Съемка на практических занятиях в гр. ТФ-06-13
Составная конструкция. Нагрузка, распределенная по дуге. + решение в Maple
Составная конструкция.Нагрузка, распределенная по дуге. ТФ-05-13, 21.2.2014.
Составная конструкция с цилиндром и нитями. + решение в Maple
Составная конструкция. Две пластины. + решение в Maxima
Две пластины.
Составная конструкция.Пластина и уголок
Ферма. Программа
Диаграмма Максвелла-Кремоны
Ферма/Диаграмма-Максвелла-Кремоны
Ферма (8)
Трение качения (7)
Трение качения.
 Механизм
МеханизмЗадача на трение качения (3 тела) . Определяем условие равновесия системы. Анимация и графика П.Горшкова.
Задача на трение скольжения. Определяем условие равновесия рамы. Анимация и графика П.Горшкова.
Задача на трение скольжения . Определяем условие равновесия рамы + некоторые рассуждения на общие темы…
Пространственная стержневая система (6 стержней). Вырезание узлов. Анимация Петра Горшкова. Задача из Решебника (с.86)
Полка (9)
Инварианты (10)
Плита на 6 стержнях
Текст программы для MaximaОдносторонняя связь в раме
Центр тяжести
СТАТИКА
Плоская система сил. Задачи
Ферма
Трение
Пространственная система сил. Задачи
Полярные координаты. Лекция.
Радиус кривизны. ТФ-05-13.
Многозвенный механизм.
 Метод кинематических графов. МЦС. Все в общем виде.
Метод кинематических графов. МЦС. Все в общем виде.Многозвенный механизм. Скорости и ускорения. МЦС. МЦУ.
Пятизвенник. Уравнение трех угловых скоростей и ускорений
Метод кинематических графов. Многозвенный механизм. Угловые скорости. Решение в Maple
Многозвенный механизм. МЦС
Четырехзвенник. Уравнение трех угловых скоростей (1)
Четырехзвенник. Уравнение трех угловых скоростей (2)
Четырехзвенник. Теорема трапеции
План скоростей.
Ускорение точки тела при плоском движении.
Ускорения. Механизм
Планетарный механизм. Метод графов и метод МЦС
Планетарный механизм (1). Метод Виллиса и метод МЦС
Планетарный механизм (2). Метод Виллиса и метод МЦС
Угловые скорости многозвенного механизма. Эффективное решение с помощью уравнения трех угловых скоростей
Сложное движениеСложное движение точки.
 Ускорение Кориолиса. Вывод формулы
Ускорение Кориолиса. Вывод формулыСложное движение точки. Ускорение Кориолиса. Правило Жуковского
Сложное движение точки. Ускорение Кориолиса. Пример
Сложное движение точки. Абсолютное ускорение. Задача
Сложное движение точки. Задача о муфте (К13,1)
Сложное движение точки. Задача о муфте/Ускорение (ТФ-05-13)
Сложное движение точки. Задача о муфте (К13,2)
Сложное движение точки. Задача о качающейся муфте (К13,3). Программа для Maple
Сферическое движение. Кинематические уравнения Эйлера в проекции на подвижные оси
3D кинематика. Решение задачи о треугольнике
3D кинематика. Параллелепипед с шарнирной крышкой
3D кинематика. Передача вращений
Редуктор (на занятиях ЭР-16-11)
Формула поворота Родрига (на лекции)
КИНЕМАТИКА
ТочкаПлоское движение
-
ДИНАМИКА
Кинетическая энергия.
 Решение задачи Д2 (приведенные массы)
Решение задачи Д2 (приведенные массы)Решение задачи на теорему об изменении кинетической энергии. Maple
Решение задачи на теорему о движении центра масс. Maple
Решение задачи на теорему о движении центра масс. ТФ-05-13, практические занятия в МЭИ
Теорема Эйлера о движении жидкости . Лекция 1.4.2014
Решение задачи динамики для механизма с двумя степенями свободы (D11) (Уравнение Лагранжа 2-го рода)
Задача о механизме с двумя степенями свободы. Уравнение Лагранжа. Лекция 22.4.2014
Динамика кулисы. Лекция 15.12.2014
Maple-программа к лекции, Текст задачи из лекции.Потенциальное силовое поле (Лекция в МЭИ, 22.4.2014)
Решение задачи с помощью принципа возможных перемещений(Определение реакций опор)
Решение задачи с помощью принципа возможных перемещений(Определение условия равновесия механизма, Р-16-11, 24 марта)
Три способа решения простой задачи динамики (Катушка на нити, определяем ускорение)
Динамика механизма с неизвестным параметром (Д7)
Вывод уравнения Лагранжа 2-го рода
Кинетическая энергия тела в пространстве
Кинетическая энергия тела в простейших случаях движения
Кинетическая энергия системы (стержни, блок).
 Приведенная масса
Приведенная массаЗадачи на принцип возможных перемещений
Регулярная прецессия гироскопа.
Задачи о гироскопе. Гироскопический момент
Динамические уравнения Эйлера.
Теорема Карно
Прямой удар. Точка. Коэффициент восстановления
Косой удар.
Центр удара.
Удар по пластине
Удар в зубчатой передаче. (Лекция 15 мая 2015 г. ИТАЭ, МЭИ)
Два груза на балке Лекция 11.9.2015 в гр. С-12-11
Стабильность Лекция 5 мая 2015 в гр. ЭР-16-12
Момент инерции тела относительно произвольной оси.
Несвободное движение точки. Уравнение Лагранжа
Динамическая балансировка
Уравнение Лагранжа в форме Лагранжа
Устойчивость по Ляпунову
Уравнение Мещерского.
 Формула Циолковского
Формула ЦиолковскогоСиловое поле. Условие потенциальности
Колебания механической системы
Колебания системы с 2 степенями свободы. Задача 1.
Колебания системы с 2 степенями свободы. Задача 2.
Колебания узла фермы
Предельные частоты и предельные массы
Колебания точки
Задача о двойном маятнике (лекция 27 мая 2014, МЭИ)
Законы Кеплера
Теория удара
Колебания, устойчивость и др.
1. Два цилиндра, пластина, стержни.
2. Брусок, цилиндр сверху, шток и стержень. Простая задача.
3. Используем теорему о сложении скоростей.
4.
 Задача с муфтой. Используем метод прямого дифференцирования.
Задача с муфтой. Используем метод прямого дифференцирования.5. Задача с линейной обобщенной координатой. Цилиндр, клин и муфта.
6. Задача с параллелограммом.
7. Кривошип, два цилиндра, наклонный стержень, муфта
8. Цилиндр, закрепленный шарнирно на ободе, брусок и пластина между ними
9. Цилиндр, наклонная плоскость, пресс и пластина между ними. Линейная обобщенная координата
10. Невесомый прямоугольный уголок, скользящий по ребрам неподвижного бруска.
11. Блок из колес с неподвижной осью, груз на наклонной плоскости. Повернутые оси координат. Линейная обобщенная координата.
12. Блок из колес с неподвижной осью и цилиндр с подвижной осью.
 Линейная обобщенная координата.
Линейная обобщенная координата.13. Два цилиндра и груз. Один цилиндр катится по неподвижной поверхности, другой закреплен на ободе первого и катится по грузу.
14. Два цилиндра и соединяющий их стержень
15. Два цилиндра, сверху балка и вертикальный шток
Экзаменационная задача в МЭИ. Решение задачи на составление уравнения Лагранжа 2-го рода
|
19.09.2017 18:55
Полное введение в силы и моменты с примерами.
Опубликовано: 21 июня 2022 г.
|
Учебник
Добро пожаловать в серию руководств по фундаментальной инженерной механике. Это первая часть серии, состоящей из нескольких частей, предназначенной для всех, кто только начинает изучать инженерное дело; Студенты первого курса технических специальностей должны найти эту серию особенно полезной. Каждый пост основан на одной теме и будет содержать лекционное видео и несколько видеороликов с примерами работы, а также ссылки на существующие соответствующие ресурсы DegreeTutors. Вы можете получить доступ ко всем видео из этой серии (по мере публикации каждой новой части), а также к загружаемым версиям заметок, присоединившись к сопровождающему курсу ниже. В этом уроке мы сосредоточимся на силах, моменте силы и на том, как оценивать системы сил и моментов.
Вы можете получить доступ ко всем видео из этой серии (по мере публикации каждой новой части), а также к загружаемым версиям заметок, присоединившись к сопровождающему курсу ниже. В этом уроке мы сосредоточимся на силах, моменте силы и на том, как оценивать системы сил и моментов.
1.0 Силы, момент силы и силовые системы
Будучи инженерами, мы тратим много времени на анализ сил и их влияние на конструкции, которые мы проектируем. Поэтому на данном этапе было бы неплохо точно определить, что такое сила. Проще говоря, сила — это произведение массы и ускорения.
(1)
Здесь, на Земле, вся масса испытывает ускорение примерно . Итак, масса испытывает гравитационную силу
Единицы силы более условно выражаются в Ньютонах (Н) в честь сэра Исаака Ньютона. Таким образом, равно . Важно понимать различие между массой и силой, т.е. масса, опирающаяся на балку, воздействует на балку не силой, а силой. Точно так же вы можете весить , но вы прикладываете силу примерно .
Таким образом, равно . Важно понимать различие между массой и силой, т.е. масса, опирающаяся на балку, воздействует на балку не силой, а силой. Точно так же вы можете весить , но вы прикладываете силу примерно .
Сила является векторной величиной. Это означает, что она имеет как величину, так и направление. Это в отличие от скейлерных величин, таких как масса, объем, высота и т. д., которые могут быть полностью описаны величиной. Поскольку сила является векторной величиной, к силам можно применить все обычные правила и методы анализа, связанные с векторами.
Все силы, которые мы будем обсуждать в этом уроке, занимают двумерную плоскость. Это означает, что они могут быть полностью описаны двумя ортогональными (под прямым углом друг к другу) компонентами x и y в двумерной системе координат. Это представляет собой сокращение от полного трехмерного евклидова пространства. Как только вы поймете основные концепции двухмерных силовых систем, расширение до трехмерных не составит труда.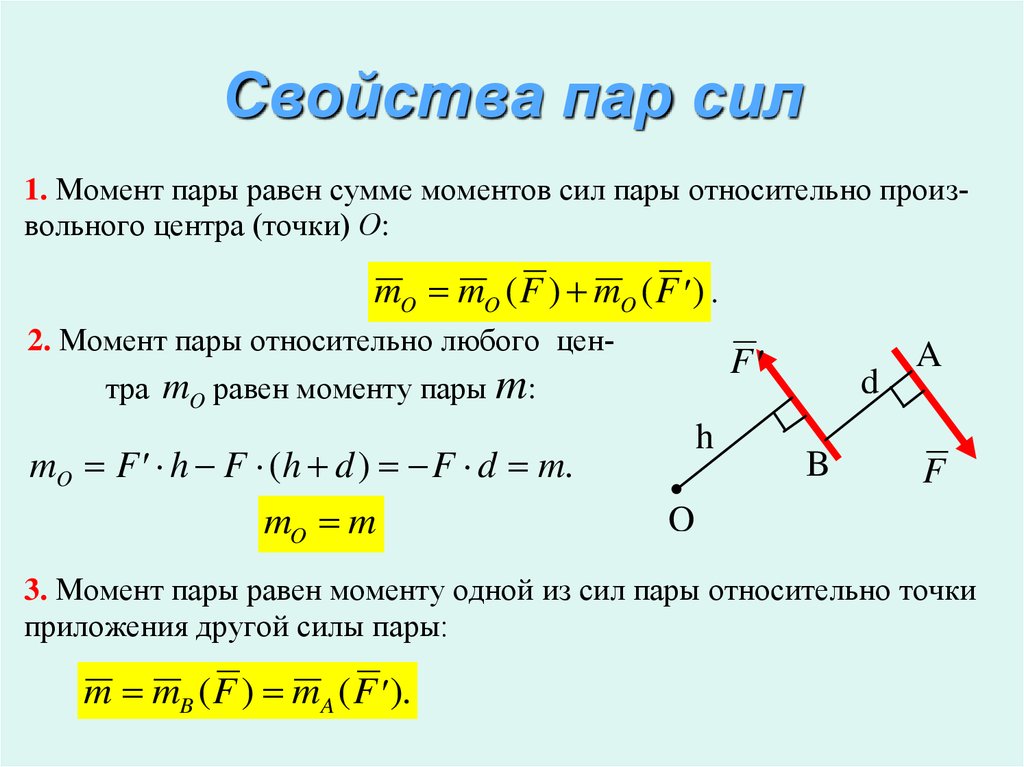
Поскольку двумерные силы могут быть представлены в виде двумерных векторов, мы можем представить любую силу как комбинацию двух ортогональных компонентов. Точно так же любое количество сил может быть представлено как единая равнодействующая силы с определенной величиной и направлением. Большая часть того, что мы будем делать в оставшейся части этого урока, будет включать в себя:
- Разрушающие силы на их ортогональные составляющие
- объединение нескольких сил для определения их результирующей силы
Рассмотрим силу 100 Н, показанную ниже. Обратите внимание, что мы определили силу в пределах двумерной плоскости, определяемой осями x и y. Сила приложена в месте . Он имеет звездную величину . Его направление можно указать, заявив, что сила составляет угол (против часовой стрелки) относительно положительной оси x.
Рис. 1. Вектор силы ориентирован под углом против часовой стрелки от положительной оси x и его ортогональные компоненты, и .
Эту силу можно разложить на 2 ортогональные составляющие, обозначенные выше и . Обратите внимание, что на самом деле это могут быть любые два ортогональных вектора силы. Для удобства мы выбрали две ортогональные компоненты, параллельные осям x и y. Для определения величин и можно использовать простую геометрию.
Мы можем рассчитать числовые значения и с помощью некоторого основного Python (или любого другого калькулятора, который вы предпочитаете).
1 2 3 4 5 6 7 8 10 110005 12 13 14 200955 |
#Определить константы F_mag = 100 # (Н) Величина силы theta_deg = 30 # (град) Угол силы с положительной осью x theta = theta_deg*math.pi/180 # (rads) Угловая сила составляет с положительной осью x
#Рассчитать величину ортогональных составляющих Fx_100 = F_mag*math. Fy_100 = F_mag*math.sin(theta)
round(Fx_100,1)} N в положительном направлении x (вправо)») print(f»Fy is {round(Fy_100,1)} N в положительном направлении y (вверх)»)
|
Fx составляет 86,6 Н в положительном направлении x (вправо)
Fy составляет 50,0 Н в положительном направлении y (вверх)
Таким же образом можно оценить комбинированное влияние нескольких сил, разбив каждую из них на ортогональные компоненты и объединив эти компоненты в единую равнодействующую силы. Рассмотрим две силы, показанные ниже. Сила та же самая сила, оцененная выше. Теперь нам нужно определить компоненты силы.
Рис. 2. Два вектора силы, представленные на двухмерной плоскости x-y.1 2 3 4 5 6 7 8 9 10 11 12 13 14 05 |
#Определить константы F_mag = 60 # (Н) Величина силы theta_deg = 40 # (град) Угол силы с отрицательной осью x theta = theta_deg*math.
# Расчет величины ортогональных составляющих Fx_60 = F_mag*math.cos(theta) Fy_60 = F_mag*math.sin(theta)
#Вывод на печать print(f»Fx is {round(Fx_60,1)} N в отрицательном направлении x (влево)») print(f»Fy is {round(Fy_60,1)} N в положительном направлении оси Y (вверх)»)
|
Fx составляет 46,0 Н в отрицательном направлении оси x (влево)
Fy составляет 38,6 Н в положительном направлении оси y (вверх)
Полная горизонтальная сила получается как алгебраическая сумма горизонтальных составляющих и силы. Отметив, что горизонтальная составляющая силы действует в направлении, противоположном горизонтальной составляющей силы, .
Fx_total = Fx_100 — Fx_60 print(f»Fx_total равно {round(Fx_total,1)} N»)
|
Fx_total составляет 40,6 Н
и представляет собой две ортогональные составляющие силы, поэтому они могут быть представлены одним вектором силы, величина и ориентация которого (измеренные относительно положительной оси x) теперь могут быть легко оценены .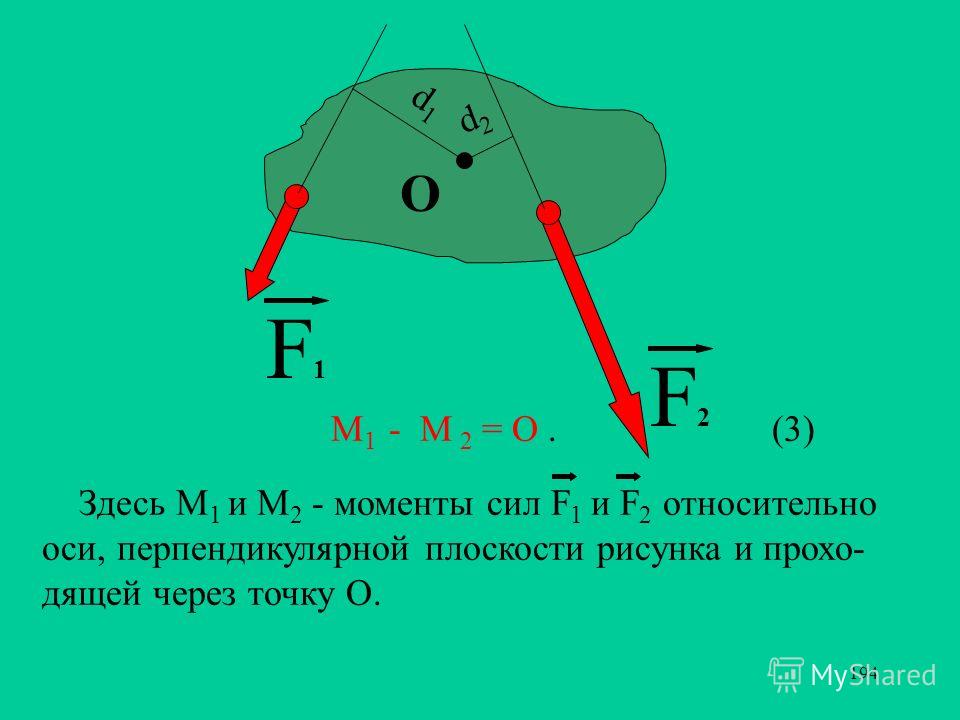
(2)
(3)
Числовая оценка,
1 2 3 4 5 6 7 |
#Magnitude mag = math.sqrt(Fx_total**2 + Fy_total**2) alpha = math.atan(Fy_total/Fx_total) alpha_deg = alpha.4090/math*180 (f»F_res a имеет величину {round(mag,1)} N и ориентацию {round(ori_deg,1)} градусов относительно положительной оси x»)
|
F_res a имеет величину 97,4 Н и ориентацию 65,4 градуса относительно положительной оси x результирующая сила в правой системе координат. Мы рассмотрим эту концепцию эквивалентных систем ниже. Две системы сил, показанные ниже, эквивалентны с точки зрения силы. Однако это еще не все . Чтобы получить две полностью эквивалентные системы, нам необходимо также учитывать момент или крутящий момент каждой силы.
Рис. 3. Система сил с двумя силами (слева) и единственной результирующей силой, представляющей их совместное влияние (справа).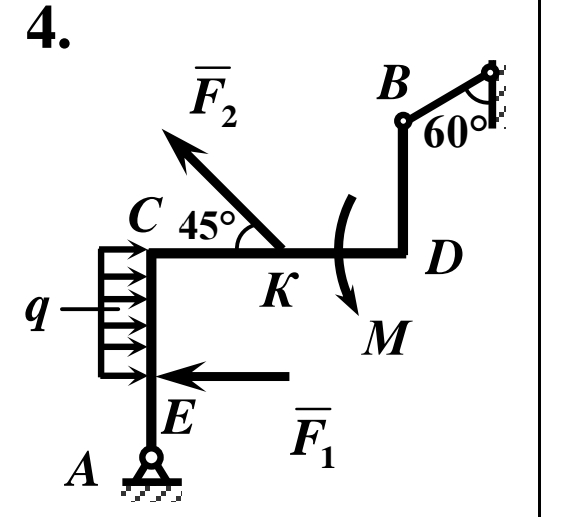
2.0 Момент силы
Момент силы — это крутящий эффект или крутящий момент, который сила создает или создает относительно точки . Более конкретно, момент силы равен произведению величины силы на плечо рычага расстояние. Плечо рычага — это перпендикулярное расстояние между линией действия силы и точкой, вокруг которой происходит вращение (или вычисляется крутящий момент).
Держите тяжелую коробку обеими руками на вытянутых руках; это требует гораздо больше усилий, чем если бы вы держали коробку близко к груди. Это связано с тем, что когда ваши руки вытянуты, сила, создаваемая тяжелым ящиком, создает больший момент относительно точки вращения (вашего плеча), чем когда вы держите ящик близко к груди.
Например, рассмотрим силу, показанную на рис. 4 ниже, приложенную к точке на плоскости x-y с координатами . Сила образует угол с положительной осью x. Продолжив вектор силы, мы получим линию действия этой силы.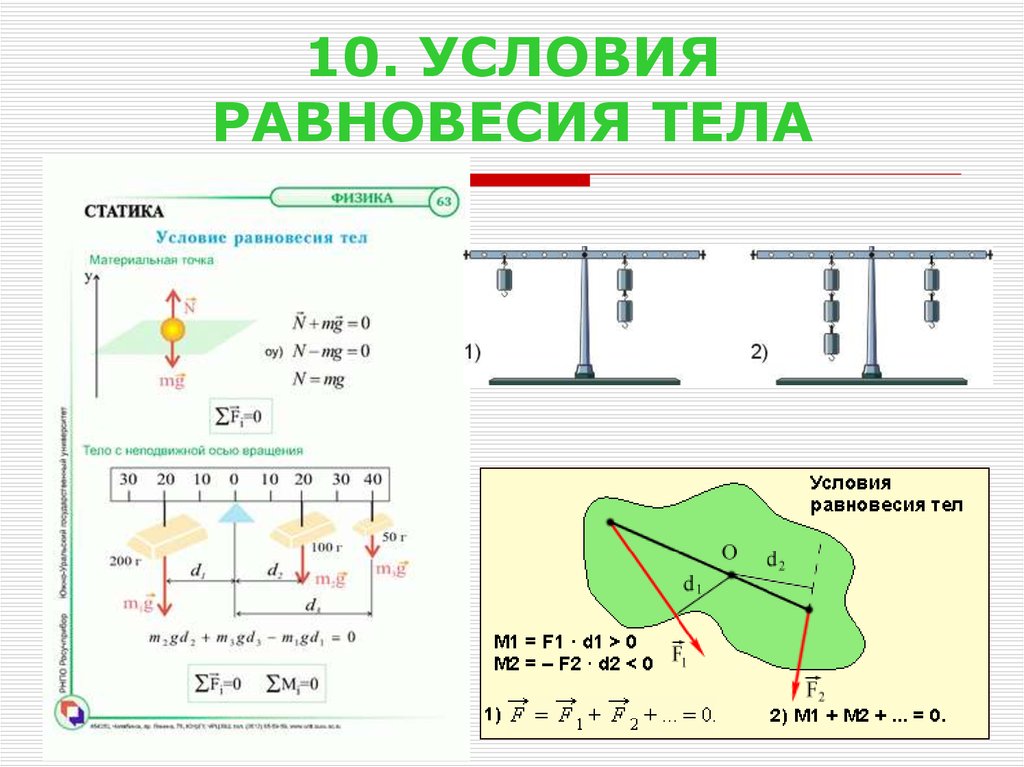 Проецируя перпендикулярно линии действия к началу координат, мы получаем плечо рычага для силы относительно начала координат. Следовательно, эта сила создает крутящий момент или момент относительно начала координат.
Проецируя перпендикулярно линии действия к началу координат, мы получаем плечо рычага для силы относительно начала координат. Следовательно, эта сила создает крутящий момент или момент относительно начала координат.
Мы можем интуитивно понять направление вращения по часовой стрелке. Другими словами, сила будет стремиться вызвать вращение по часовой стрелке вокруг начала координат. Если у вас возникли проблемы с определением направления вращения, нарисуйте исходную точку и надавите на лист бумаги так, чтобы бумага удерживалась булавкой или иглой через исходную точку. Используйте свой палец, чтобы применить силу F, и вы увидите, что бумага имеет тенденцию вращаться по часовой стрелке вокруг булавки. Вам нужно будет сделать это только один или два раза, прежде чем вы сможете визуализировать чувство вращения, которое сила вызывает вокруг точки. Сила будет вращать бумагу либо по часовой стрелке, либо против часовой стрелки, и это будет зависеть от положения и ориентации силы относительно точки, относительно которой вычисляются моменты.
Теперь, чтобы рассчитать момент, мы можем использовать умную геометрию для определения . Однако есть более простой способ рассчитать момент, создаваемый . Мы можем просто рассмотреть момент, создаваемый его ортогональными компонентами. Горизонтальные и вертикальные компоненты и получаются как
1 2 3 4 5 6 |
F_x = 50*math.cos(20*math.pi/180) F_y = 50*math.sin(20*math.pi/180) print(f»Fx = {округление(F_x,1)} N») print(f»Fy = {округление(F_y,1) )} Н»)
|
Fx = 47,0 Н
Fy = 17,1 Н
Теперь мы можем игнорировать исходную силу и работать только с ее ортогональными составляющими, и . Мы можем довольно легко увидеть, что имеет плечо рычага в то время как имеет плечо рычага (см. рис. 4). Мы также можем распознать, что это будет генерировать вращение по часовой стрелке, в то время как будет генерировать вращение против часовой стрелки (не забудьте использовать трюк с вращением бумаги, если вы этого не видите).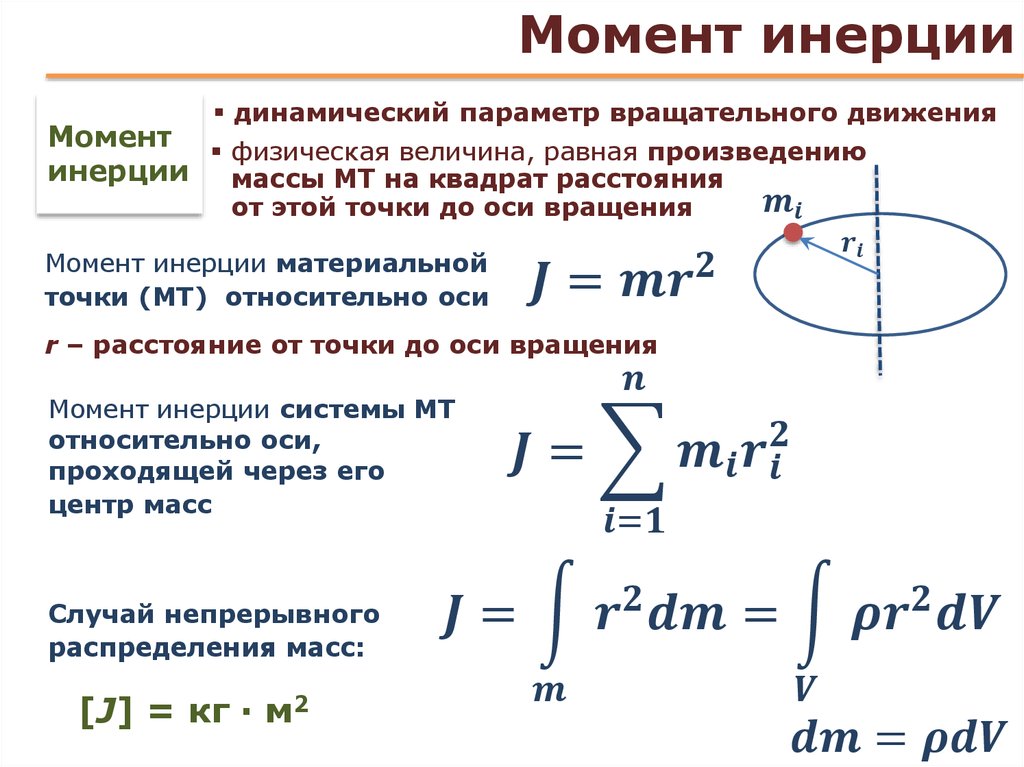 Таким образом, мы можем оценить момент, создаваемый с учетом моментов относительно происхождения следующим образом,
Таким образом, мы можем оценить момент, создаваемый с учетом моментов относительно происхождения следующим образом,
(4)
1 2 3 4 5 6 |
la_fx = 6 #плечо горизонтальной составляющей силы Fx la_fy = 3 #плечо рычага вертикальной составляющей силы Fy M = (F_x * la_fx) — (F_y * la_fy) print(f «M = {раунд(M,1)} Нм»)
|
М = 230,6 Н·м
Помните, что момент связан с вращением, в отличие от сил, связанных с линейным перемещением. Таким образом, мы определяем момент как наличие направления вращения по часовой стрелке или против часовой стрелки. Обратите внимание, что в приведенном выше уравнении мы неявно предположили, что моменты по часовой стрелке положительны, а против часовой стрелки отрицательны. Поэтому тот факт, что момент оценивается как положительное число, указывает на то, что результирующий момент имеет направление вращения по часовой стрелке. Если бы получилось отрицательное число, мы бы знали, что согласно нашему соглашению о знаках, момент имеет вращение против часовой стрелки.
Если бы получилось отрицательное число, мы бы знали, что согласно нашему соглашению о знаках, момент имеет вращение против часовой стрелки.
Следуя той же самой логике, мы можем оценить суммарный крутящий момент, создаваемый несколькими силами относительно точки, вычислив сумму моментов для каждой силы по очереди. Мы обсудим это ниже.
2.1 Пары силГоворят, что две силы образуют пару когда:
- они имеют одинаковую величину
- имеют параллельные линии действия
- действовать в противоположных направлениях
Например, если предположить, что и ниже имеют одинаковую величину, они образуют пару.
Рис. 5. Две силы и образующие пару моментовПара сил создает момент, равный величине одной силы, умноженной на перпендикулярное расстояние между их линиями действия. Таким образом, пара, созданная и равна
(5)
. По направлениям стрелок видно, что изображенная пара создает момент по часовой стрелке. Если бы направления стрелок были изменены на противоположные, создаваемый момент был бы направлен против часовой стрелки. Если у вас возникли проблемы с визуализацией этого, представьте точку вращения на полпути вдоль красной пунктирной линии и спросите себя, как эти две силы заставят бумагу вращаться вокруг этой точки.
Если бы направления стрелок были изменены на противоположные, создаваемый момент был бы направлен против часовой стрелки. Если у вас возникли проблемы с визуализацией этого, представьте точку вращения на полпути вдоль красной пунктирной линии и спросите себя, как эти две силы заставят бумагу вращаться вокруг этой точки.
Пары сил часто встречаются в технике. Вы обнаружите, что регулярно оцениваете эффект момента силовых пар. Сейчас мы просто хотим определить концепцию.
3.0 Системы эквивалентных сил и моментов
До сих пор мы рассматривали векторные свойства сил (компоненты и равнодействующие). Мы также обсудили концепцию крутящего момента или моментов, создаваемых силой относительно определенной точки на плоскости. Теперь мы объединим эти идеи, чтобы оценить системы сил и моментов и определить их равнодействующие или эквивалентные системы.
Две системы двумерных сил и моментов считаются эквивалентными, если выполняются три условия:
1. Сумма всех сил в направлении x одинакова в обеих системах
(6)
2. сумма всех сил в направлении y одинакова в обеих системах
сумма всех сил в направлении y одинакова в обеих системах
(7)
Обратите внимание, что выбор направлений x и y произволен. Можно оценить равенство сил вдоль любых двух ортогональных направлений. Направления x и y обычно выбираются для удобства, поскольку они также являются направлениями осей системы.
3. Сумма моментов, создаваемых всеми силами и моментами в системе A, равна сумме моментов, создаваемых всеми силами и моментами в системе B
(8)
Практическая ценность идентификации эквивалентных систем что это позволяет нам представлять несколько сил одной равнодействующей силой, которая создает одно и то же воздействие силы и момента.
Снова рассмотрим систему сил, которую мы обсуждали ранее,
Рис. 6. Двухмерная система сил A.В дополнение к оценке равнодействующей силы (завершено выше), теперь нам нужно определить результирующий момент. Оценивая сумму моментов относительно начала координат (снова предполагая, что моменты по часовой стрелке положительны),
(9)
M = 86,6*2 — 50*2 — 46*8 — 38,6*10 print(f»Результирующий момент относительно начала координат равен {round(M,1)} Нм»)
|
Результирующий момент относительно начала координат составляет -680,8 Нм
Знак минус здесь указывает, что результирующий момент направлен против часовой стрелки в соответствии с нашим соглашением о знаках. Поэтому, обращаясь к диаграмме ниже, мы можем сказать, что система сил в системе A эквивалентна одиночной силе и моменту в системе B. Другими словами, система A имеет точно такое же действие силы и момента, что и система B.
Поэтому, обращаясь к диаграмме ниже, мы можем сказать, что система сил в системе A эквивалентна одиночной силе и моменту в системе B. Другими словами, система A имеет точно такое же действие силы и момента, что и система B.
Это в значительной степени охватывает теорию по данной теме. На этом этапе вы должны попытаться проработать приведенные ниже примеры вопросов. В каждом случае попробуйте сначала решить вопрос самостоятельно, прежде чем смотреть видео с отработанным решением.
Пример
Замените силы и моменты, показанные в системе A, эквивалентной системой, состоящей из одной силы (в начале координат) и момента (относительно начала координат).
(Подсказка: моменты не учитываются в уравнении суммирования сил, но они учитывают в уравнении суммирования моментов.)
Рис. 8. Пример 1 системы сил. Решение Видеорешение этого вопроса показано в конце основного видео-лекции в верхней части этого поста.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# Рассчитать величины горизонтальной и вертикальной составляющей силы #(направление пока не учитывается, только величина) F_Ax = 100 F_Ay = 0 F_Bx = 0 F_By = 90 F_Cx = 40*math*0math.cos. F_Cy = 40*math.sin(45*math.pi/180) F_Dx = 50*math.cos(35*math.pi/180) F_Dy = 50*math.sin(35*math. pi/180)
#Величина момента (без учета направления вращения) M_E = 150
#Возьмите моменты относительно начала координат (предположим, что моменты по часовой стрелке положительны) M_o = F_Ax*2 — F_By*9 + F_Cx*6 + F_Cy*5 + F_Dx*6 — F_Dy*1 + M_E print(f»Результирующий момент равен {round(M_o,1)} Нм»)
#Оценить сумму горизонтальных сил Fx = F_Ax + F_Cx + F_Dx print(f»Результирующая горизонтальная сила равна {round(Fx,1)} Н»)
#Оценить сумма вертикальных сил Fy = F_By — F_Cy + F_Dy print(f»Результирующая вертикальная сила {round(Fy,1)} Н»)
# Оценить результирующую величину F_res = math. print(f»Результирующая величина силы равна {round(F_res,1)} Н») #Оценить результирующую ориентацию alpha = math.atan(Fy/Fx)*180/math.pi print(f»Результирующая сила образует угол {round(alpha,1)} градусов с положительной ось x»)
|
Результирующий момент 68,2 Нм
Результирующая горизонтальная сила 169.2 Н
Результирующая вертикальная сила равна 90,4 Н
Результирующая сила равна 191,9 Н
Результирующая сила образует угол 28,1 градуса с положительной осью абсцисс
Рабочий пример 1 и силы ниже, замените силы и моменты, показанные в системе А, эквивалентной системой, состоящей из одной силы.
(Подсказка: подумайте, где бы вы хотели разместить свою единственную силу в системе замещения.)
Рис. 9. Пример 2 силовой системы. Решение 1 youtube.com/embed/KRorO-Uh2Ko?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Рабочий пример 2
Со ссылкой на приведенную ниже систему моментов и сил определите величину силы , при которой результирующие момент и сила для системы равны нулю.
Рис. 10. Пример 3 силовой системы. Раствор 2Рабочий пример 3
Со ссылкой на систему моментов и сил ниже; эта система должна быть заменена одной силой, расположенной вдоль вертикальной линии в точке . Определите местоположение, величину и ориентацию замещающей силы.
Вот и все для этого урока. Теперь вы должны хорошо понимать, как оценивать системы сил и моментов. В следующем уроке этой серии мы применим то, что вы здесь узнали, и начнем анализировать устойчивость простых структур. Не забудьте присоединиться к курсу, который сопровождает эту серию руководств, чтобы получить доступ ко всем заметкам и видео в одном месте. Курс будет расширяться по мере публикации новых руководств из этой серии.
Линкедин Твиттер YouTube
Автор
Д-р Шон Кэрролл
Бакалавр технических наук (с отличием), MSc, PhD, CEng MIEI, FHEA
Привет, я Шон, основатель DegreeTutors. com. Я надеюсь, что вы нашли этот урок полезным. Проработав 10 лет в качестве преподавателя в университете по проектированию конструкций, я создала DegreeTutors.com, чтобы помочь большему количеству людей понять инженерное дело и получить от его изучения такое же удовольствие, как и я. Не стесняйтесь связаться или подписаться на DegreeTutors в любой из социальных сетей.
com. Я надеюсь, что вы нашли этот урок полезным. Проработав 10 лет в качестве преподавателя в университете по проектированию конструкций, я создала DegreeTutors.com, чтобы помочь большему количеству людей понять инженерное дело и получить от его изучения такое же удовольствие, как и я. Не стесняйтесь связаться или подписаться на DegreeTutors в любой из социальных сетей.
Если вам нужен полный доступ ко всей библиотеке курсов DegreeTutors (и коду!) за небольшую ежегодную плату, рассмотрите возможность подписки на Полный доступ к DegreeTutors . Вы можете прочитать больше о преимуществах членства здесь или просмотреть заголовки и подписаться непосредственно ниже. Если вы учитесь в колледже или университете, станьте участником программы DegreeTutors, чтобы совершенно бесплатно получить доступ к ряду премиальных курсов.
Доступ ко всем курсам и инструментам
$ 279 / Год
(меньше кофе в неделю ☕ ☕)
Гарантия цен — избегайте будущего повышения цен, когда мы выращиваем
. Неограниченный доступ к инструментам онлайн-анализа. 🛠️
Неограниченный доступ к инструментам онлайн-анализа. 🛠️
Упакованный план разработки курсов и инструментов 🏗️
Доступ к хабу участника DegreeTutors:Labs 🧪
Неограниченная потоковая передача всех текущих и будущих курсов
Ранний доступ к новым курсам
Доступ ко всем загрузкам, руководствам в формате pdf и кодам Python
Сертификаты об окончании курса
Приоритетная поддержка вопросов и ответов
Подпишитесь на обновления учебников и курсов
© 2023 DegreeTutors & Mind Map Media Ltd. Все права защищены
ПРИКЛАДНАЯ МЕХАНИКА — Момент — УЧЕБНЫЕ МАТЕРИАЛЫ
МОМЕНТ:
Стремление сил состоит не только в перемещении тела, но и во вращении тела. Эта вращательная тенденция силы известна как МОМЕНТ.
МОМЕНТ – вращательное действие силы, действующей на тело вокруг шарнирной точки.
Произведение силы на перпендикулярное расстояние от точки до линии действия силы называется моментом силы относительно этой точки. Таким образом, момент силы зависит от следующего:
Таким образом, момент силы зависит от следующего:
- Величина силы.
- Перпендикулярное расстояние от шарнирной точки до линии действия силы.
Рассмотрим тело, прибитое гвоздем в точке O и действующее под действием силы F. Эта сила F стремится повернуть тело вокруг точки O. Это вращательное действие силы F называется моментом силы. Однако если сила такова, что она проходит через точку О, то она не будет стремиться вращать тело, а будет стремиться сдвинуть тело по прямой линии.
Величина момента в точке O, M o = F x d
, где d — расстояние по перпендикуляру от точки O до линии действия силы.
Момент силы является векторной величиной
Направление M o будет получено с помощью правила правой руки. Для этого пальцы правой руки складывают таким образом, чтобы они следовали направлению вращения. Затем большой палец указывает вдоль оси момента, которая дает направление и ощущение момента.
Затем большой палец указывает вдоль оси момента, которая дает направление и ощущение момента.
ЕДИНИЦЫ МОМЕНТА:
В единицах МКС = кг-м
В единицах СИ = Н-м точка или линия, моменты классифицируются как моменты по часовой стрелке и против часовой стрелки.
МОМЕНТ ПО ЧАСОВОЙ СТРЕЛКЕ
Если сила, действующая на тело, стремится повернуть тело по часовой стрелке, то момент, возникающий при этом, называется МОМЕНТ ПО ЧАСОВОЙ СТРЕЛКЕ .
Момент в точке поворота = F x d (по часовой стрелке)
МОМЕНТ ПРОТИВ ЧАСОВОЙ СТРЕЛКИ .
Момент в точке опоры = F x d (против часовой стрелки)
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ МОМЕНТА:
Рассмотрим силу F, действующую на тело и представленную вектором AB. Пусть О — точка, относительно которой нужно вычислить момент силы. Опустите ОС перпендикулярно АВ. Присоединяйтесь к ОА и ОБ.
Момент силы около O, Mo = F x OC
Mo = AB x OC
Mo = 2 x (1/2 x AB x OC)
Mo = 2 x Площадь △OAB
Следовательно, момент силы относительно точки равен удвоенной площади треугольника, образованного таким образом, если взять точку за вершину треугольника и прямую за основание треугольника.
ПРИНЦИП МОМЕНТА:
Если тело находится в равновесии под действием ряда сил, одновременно действующих на тело, то алгебраическая сумма моментов всех сил относительно точки в их плоскости равна нулю.
или
Если тело находится в равновесии под действием ряда сил, одновременно действующих на тело, то алгебраическая сумма моментов сил относительно точки по часовой стрелке равна сумме моментов сил относительно точки против часовой стрелки. та же самая точка.
Рассмотрим четыре компланарные силы F1, F2, F3 и F4, действующие на тело, и тело находится в равновесии.
Пусть О — точка, вокруг которой может вращаться тело. Пусть d1, d2, d3 и d4 — перпендикулярное расстояние точки O, образующей линию действия сил F1, F2, F3 и F4 соответственно. Момент сил F1, F2, F3 и F4 относительно точки О равен:
Пусть d1, d2, d3 и d4 — перпендикулярное расстояние точки O, образующей линию действия сил F1, F2, F3 и F4 соответственно. Момент сил F1, F2, F3 и F4 относительно точки О равен:
Момент силы F1 = F1 x d1 (против часовой стрелки)
Момент силы F2 = F2 x d2 (против часовой стрелки)
Момент силы F3 = F3 x d3 (по часовой стрелке)
Момент силы F4 = F4 x d4 (по часовой стрелке)
Равнодействующая этих моментов будет равна алгебраической сумме всех моментов относительно O.
Результирующий момент ∑M = F1d1 + F2d2 – F3d3 – F4d4
Так как тело находится во вращательном равновесии, согласно принципу моментов , результирующий момент, т.е. алгебраическая сумма всех моментов, должен быть равен нулю.
∑m = 0
F1D1 + F2D2 — F3D3 — F4D4
F1D1 + F2D2 = F3D3 + F4D4
Сумма против часовой стрелки =
Моменты по часовой стрелке
VarignOn’s The ORMENS:
. на тело действуют силы, то алгебраическая сумма их моментов относительно точки равна моменту их равнодействующей относительно этой же точки.
Пусть F1 и F2 — две силы, действующие на тело, равнодействующая которых равна F, тогда
Mo = r x F1 + r x F2
Mo = r(F1 + F2)
Mo = r x F
Пусть F1 и F2 — две силы, представленные линиями AB и AD. Пусть O будет точкой, относительно которой нужно взять момент. Из O проведите линию OC, параллельную AB, с пересечением AD в точке D. Соедините BC, чтобы завершить параллелограмм. Теперь соедините диагональ AC, которая дает результирующую R двух сил. Присоединяйтесь к ОА и ОБ.
Из рисунка
площадь △ ABC = площадь △ ADC = площадь △ AOB
(∵ Эти треугольники лежат на одном основании и между двумя одинаковыми параллельными прямыми)
Теперь,
Момент силы F1 относительно O = 2 x площадь △OAB
Момент силы F2 относительно O = 2 x площадь △OAD
Момент равнодействующей силы R относительно O = 2 x площадь △OAC
Сумма моментов двух сил относительно O = 2 x площадь △OAB + 2 x площадь △OAD
= 2 x площадь △ADC + 2 x площадь △OAD
= 2 x (площадь △OAB + площадь △ OAD)
= 2 x площадь △OAC
= момент равнодействующей силы R о O


 Условие равновесия плоской системы
Условие равновесия плоской системы Изменение центра приведения.
Изменение центра приведения.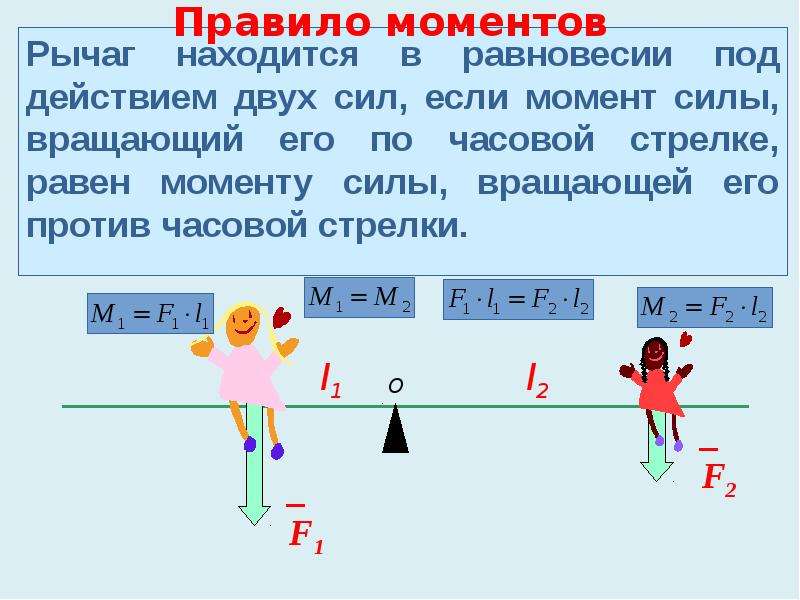 Составная конструкция (2b). Два шарнира и скользящая заделка. Анимация и графика П.Горшкова.
Составная конструкция (2b). Два шарнира и скользящая заделка. Анимация и графика П.Горшкова.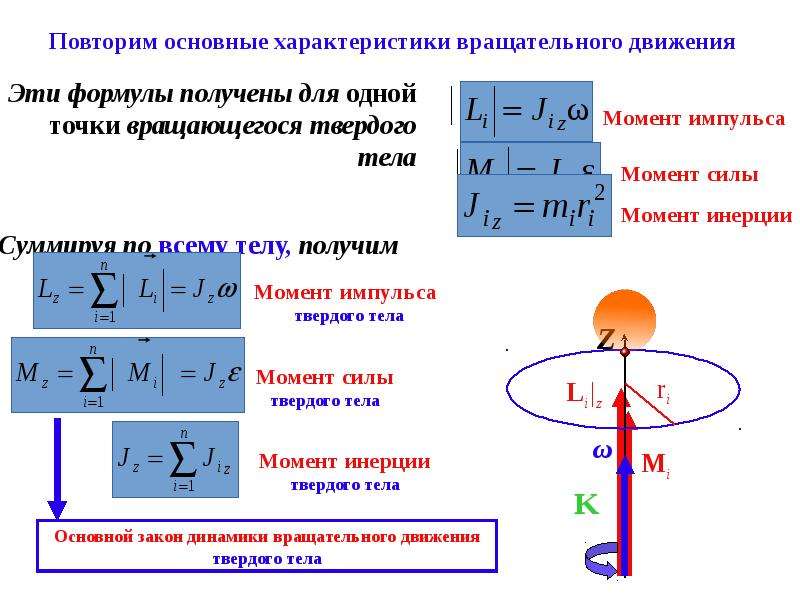 Линейно распределенная нагрузка. (1-я часть)
Линейно распределенная нагрузка. (1-я часть) Механизм
Механизм Метод кинематических графов. МЦС. Все в общем виде.
Метод кинематических графов. МЦС. Все в общем виде. Ускорение Кориолиса. Вывод формулы
Ускорение Кориолиса. Вывод формулы Решение задачи Д2 (приведенные массы)
Решение задачи Д2 (приведенные массы) Приведенная масса
Приведенная масса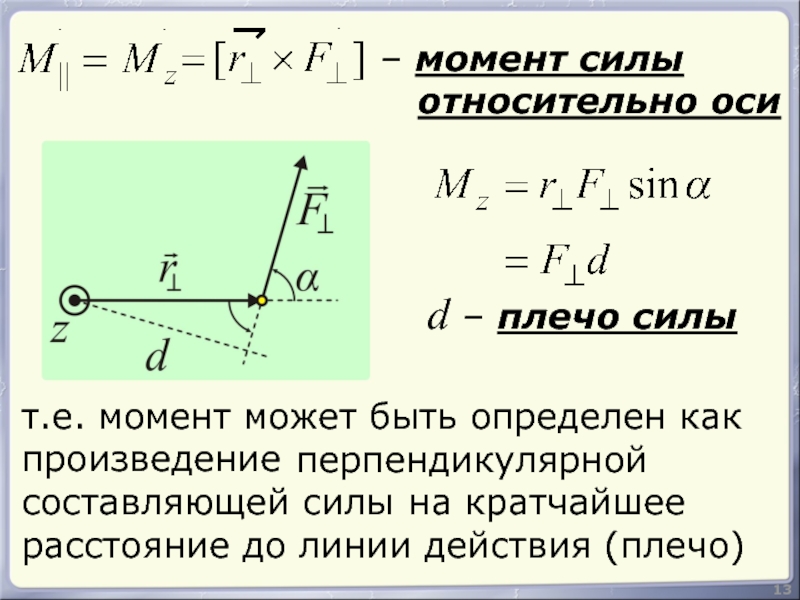 Формула Циолковского
Формула Циолковского Задача с муфтой. Используем метод прямого дифференцирования.
Задача с муфтой. Используем метод прямого дифференцирования. Линейная обобщенная координата.
Линейная обобщенная координата. cos(theta)
cos(theta)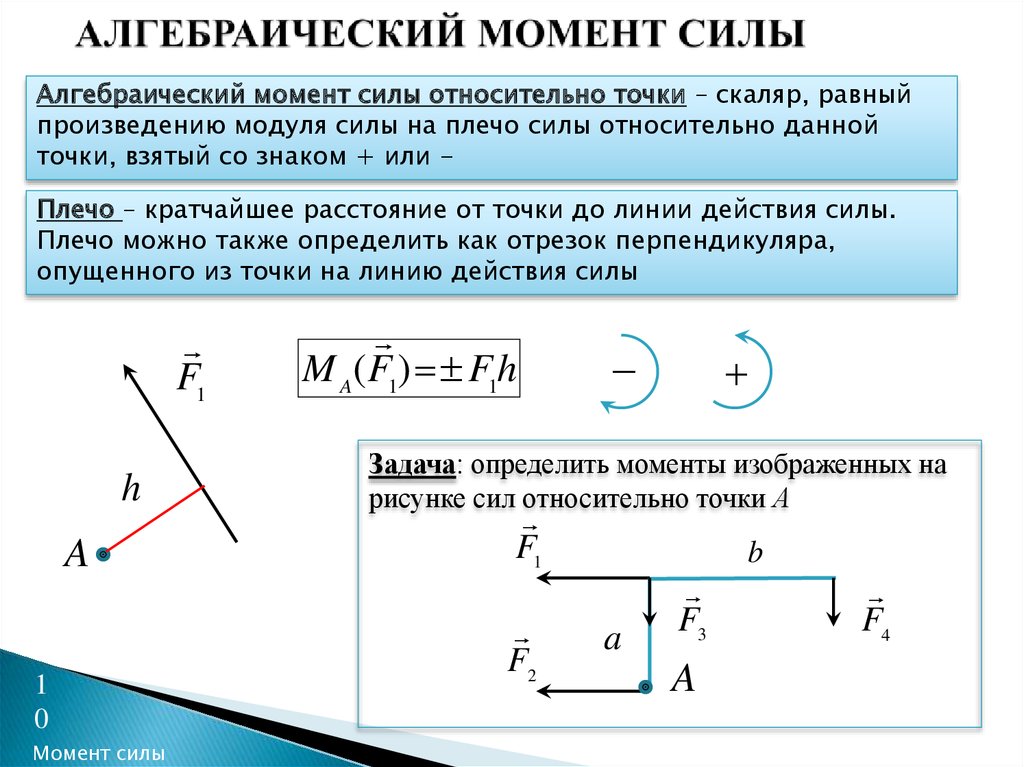 pi/180 # (rads) Угловая сила действует с отрицательной осью x
pi/180 # (rads) Угловая сила действует с отрицательной осью x sqrt(Fx**2 + Fy**2)
sqrt(Fx**2 + Fy**2)