Условия равновесия рычага — формула, правило

Покажем, как применять знание физики в жизни

Начать учиться

Палящее солнце освещает пустыню, но она отнюдь не безлюдна. Миллионы людей строят великую пирамиду Хеопса! Работа изнуряющая, тяжелая, но есть необычный механизм, который позволяет выполнить строительство в срок. Рабочие говорят, что это — подарок богов, который ниспослан им для священного дела: это устройство способно поднять огромный каменный столб усилиями всего пяти строителей.

Представили эту картину? Впечатляюще, правда? Как вы думаете, механизм, о котором идет речь, действительно волшебный или же его действие основано на физических законах?

Сегодня мы разгадаем эту загадку, а еще узнаем:

• какие механизмы использовали древние строители;

• что такое рычаг и где он применяется;

• что такое плечо рычага и момент силы;

• закон равновесия рычага и золотое правило механики.

Будет интересно, мы обещаем!

Простые механизмы

Строительство домов, памятников, дворцов и фонтанов — дело не из простых, поэтому еще в древние времена люди изобрели механизмы, которые позволяли упростить процесс.

Простые механизмы — это устройства, которые позволяют изменить величину или направление приложенных к ним сил.

В общем случае простой механизм позволяет затратить меньше усилий для выполнения работы, приложить меньшую силу, получив при этом значительный результат.

К простым механизмам относятся рычаги (на основе которых были созданы блоки и ворот), а также наклонная плоскость, принцип действия которой был заложен в работу клина и винтов.

Обычно простые механизмы — это элементы более сложных устройств, которые используются в быту и промышленности. Без них выполнять такую работу, как поднятие тяжелых предметов на высоту, было бы невозможно.

Полезные подарки для родителей

В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!

Рычаг в физике

Рычаг — это твердое тело, которое может вращаться вокруг неподвижной опоры.

Самый простой пример рычага вы могли видеть в мультфильмах или фильмах: герой подставляет большую доску под камень, опирает ее на бочку или ведро, прикладывает силу к краю доски и… поднимает камень! С помощью такой конструкции можно приподнять любой предмет, весь секрет только в расположении опоры (оси вращения) и правильном распределении усилия.

На рисунке представлен демонстрационный рычаг.  — точка опоры, слева и справа от которой подвешены грузы. Заметим, что количество грузов неравное, но рычаг остается в положении равновесия.

Но главное назначение рычага — не быть в равновесии, а давать выигрыш в силе. Каким образом? Все дело в том, что на рычаг могут действовать разные по величине силы, и точки приложения этих сил располагаются на разном расстоянии от точки опоры. Правильно распределив силы и подобрав расстояние до опоры, можно поднять груз, вес которого намного больше, чем сила, приложенная для его подъёма.

Плечо силы рычага

Плечо силы рычага — это кратчайшее расстояние от точки опоры до точки приложения силы.

На рисунке, который мы рассмотрели, отрезки  и  являются плечом сил  и  соответственно.

Чтобы найти плечо, необходимо из точки опоры опустить перпендикуляр на линию действия силы, длина этого перпендикуляра является плечом данной силы.

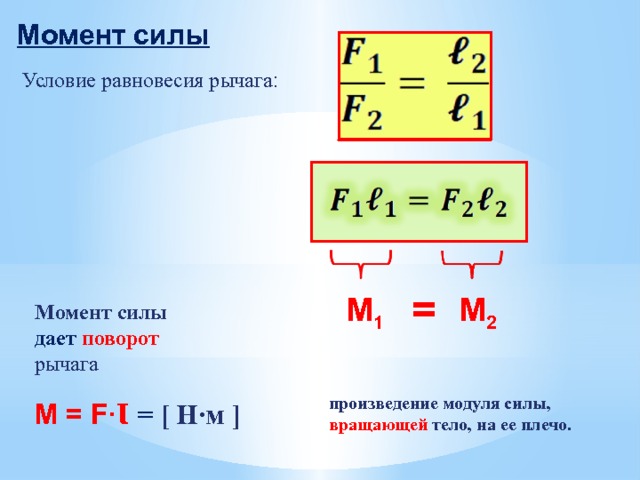
Условие равновесия рычага

В каком случае рычаг находится в равновесии? Как необходимо расположить точки приложения сил, чтобы достигнуть этого состояния? Это условие было сформулировано еще много столетий назад.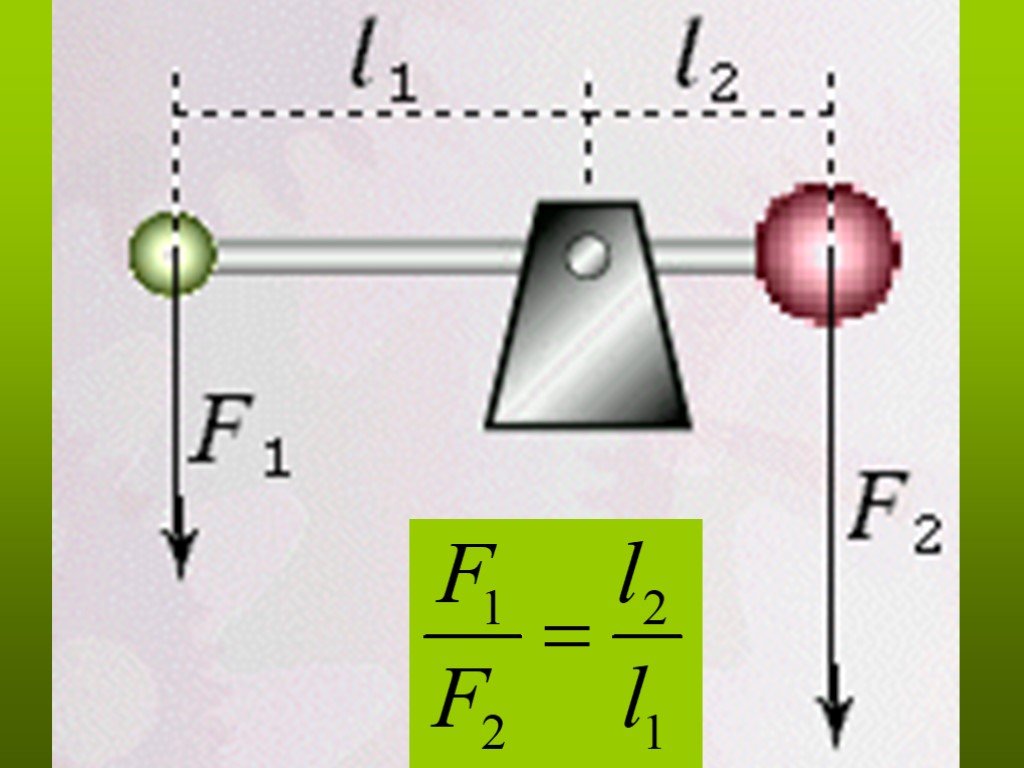

Рычаг будет находится в равновесии, если силы, действующие на него, обратно пропорциональны плечам этих сил:

, где  и  — приложенные к рычагу силы,  и  — плечи сил  и  соответственно.

Давайте еще раз рассмотрим рисунок:

Предположим, вес одного груза — , а единичный отрезок равен 1 м. Тогда м, м:

Момент силы и рычаги

Правило равновесия рычагов можно переписать, используя понятие «момент силы». Но что это такое?

Момент силы — это произведение величины силы на ее плечо.

В теме 7 класса «Рычаги в физике» вы также можете встретить и другое определение.

Момент силы — физическая величина, характеризующая действие силы на объект, которое вызывает его вращательное движение.

Простыми словами, момент силы — это величина, которая дает характеристику вращательному усилию.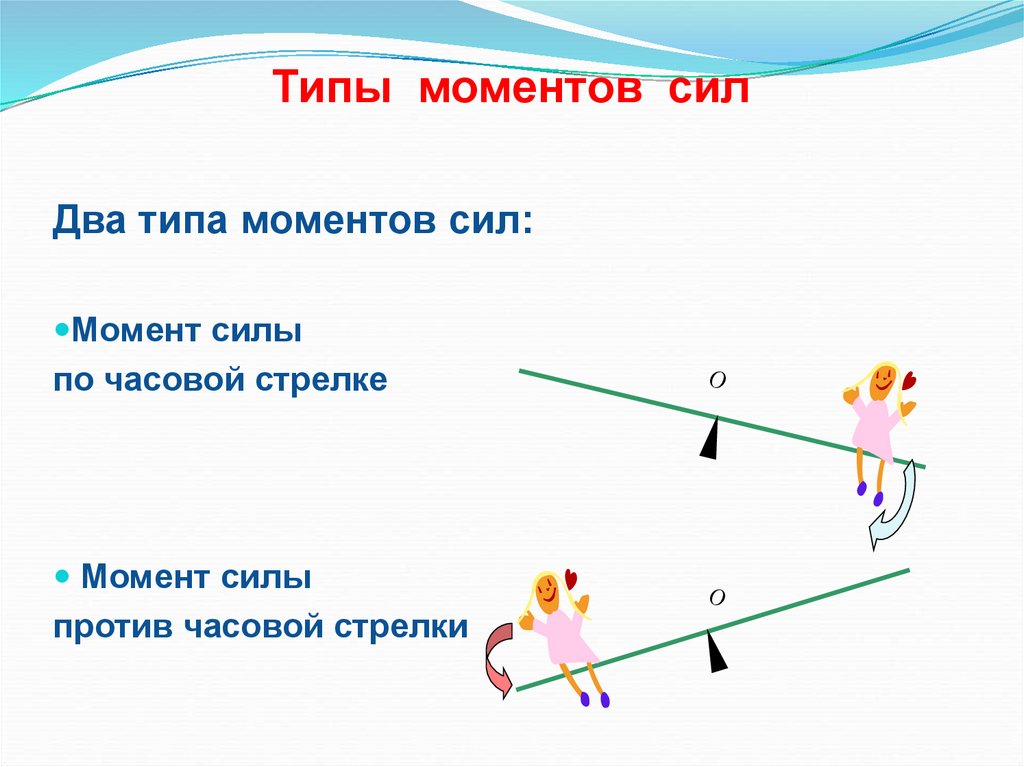 Представьте, что вам необходимо закрутить гайку с помощью гаечного ключа. Вы берете ключ, причем автоматически перемещаете руки на его крайнюю часть — так выполнять действие намного проще. Говоря физическим языком, вы увеличиваете плечо силы, чтобы не прикладывать много усилий для закручивания гайки. А еще таким образом вы увеличиваете величину момента вращения.

В физике момент силы обозначается буквой а измеряется в Формула момента силы:

Преобразуем условие равновесия рычагов, умножив накрест по основному свойству пропорции:

а так как то

А значит, сформулировать условие равновесия рычага можно так: рычаг будет находиться в равновесии, когда моменты сил, приложенных к его разным концам, равны.

Задачи

Закрепим пройденный материал, решив парочку задач.

Задача 1

Длина меньшего плеча рычага — 0,05 м, большего — 0,8 м. На меньшее плечо действует 16 H.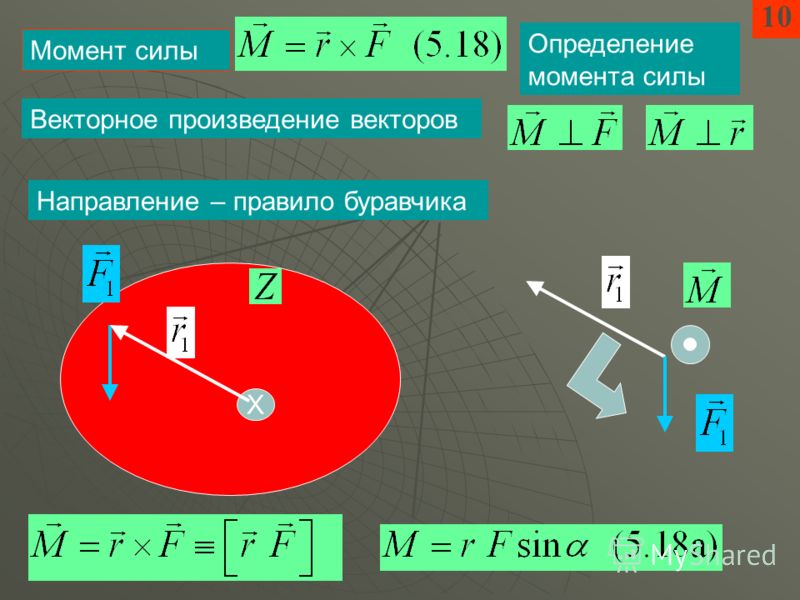 Какую силу нужно приложить к большему плечу, чтобы уравновесить рычаг (весом рычага можно пренебречь)?

Дано:	Решение: Запишем формулу равновесия рычага и преобразуем ее, выразив : Подставим исходные значения и найдем большую силу:
Найти: — ?

Ответ: 1H

Задача 2

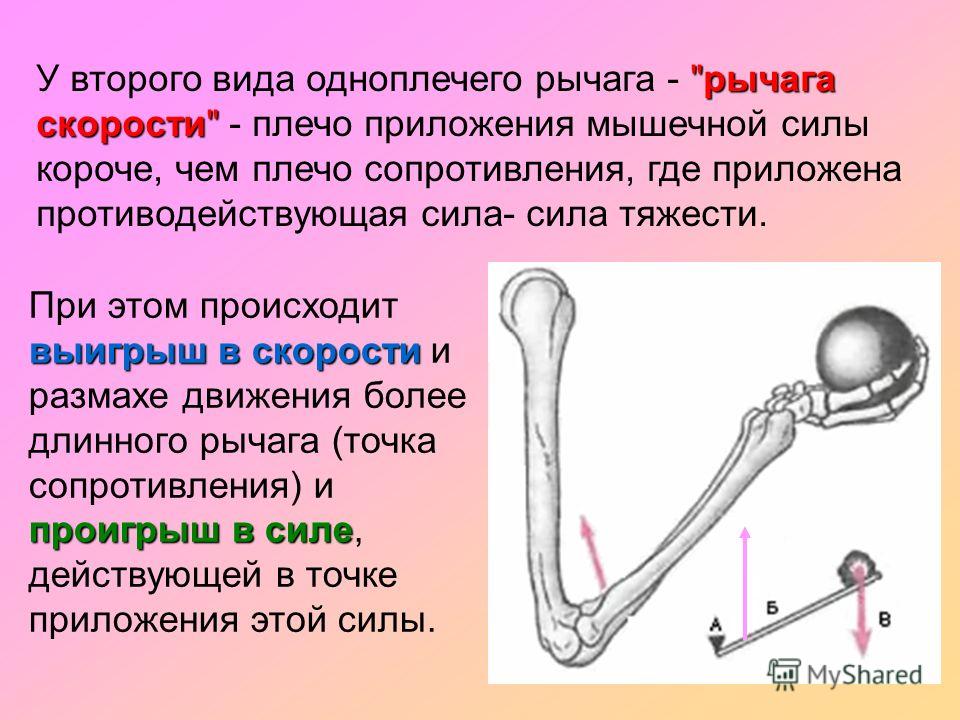На концах невесомого рычага действуют силы 50 и 250 Н. Расстояние от точки опоры до меньшей силы равно 0,06 м. Определи длину плеча большей силы, если рычаг находится в равновесии.

Дано:	Решение: Запишем условие равновесия рычага и преобразуем его, выразив : Подставим исходные значения и найдем длину плеча большей силы:
Найти: — ?

Ответ: 0,012 м.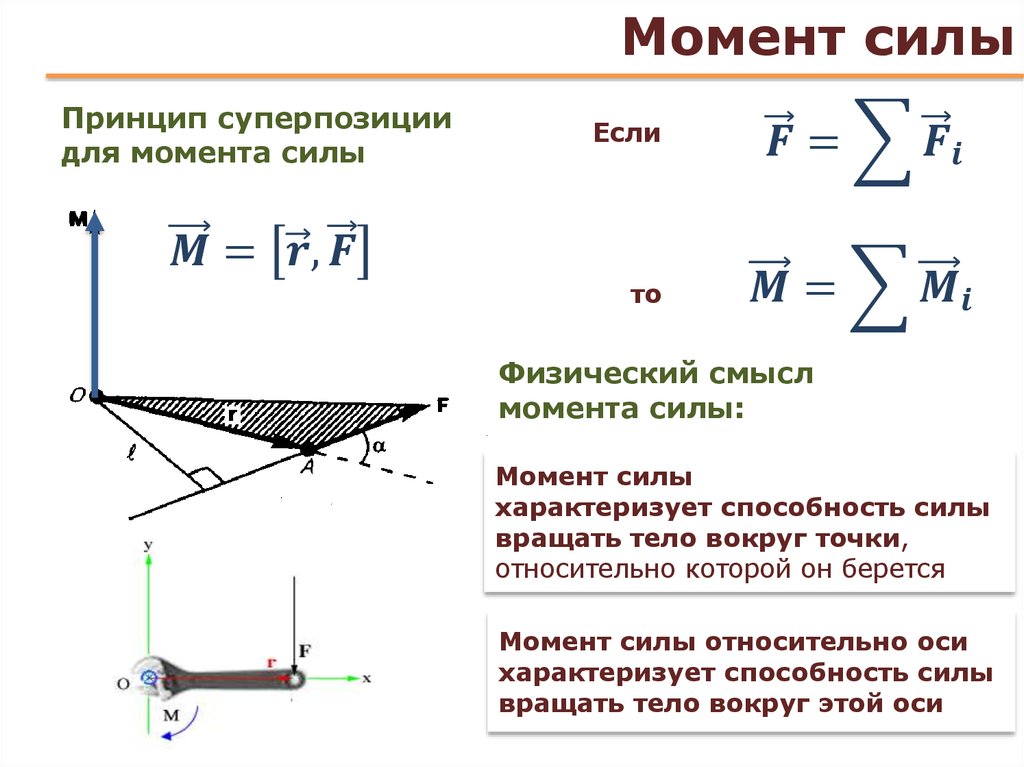

Золотое правило механики

Как мы видим, рычаги могут дать значительный выигрыш в силе. Этим свойством пользовались древние строители, когда возводили монументальные сооружения. Но помимо выгоды, есть и достаточно плохая новость: чем больший выигрыш в силе нам нужно получить, тем значительнее должны отличаться плечи сил.

Представьте, что вам необходимо поднять камень в тонну при вашей массе 50 кг. Силы отличаются в 200 раз! А значит, и плечи сил должны отличаться во столько же. Если между камнем и точкой опоры будет 0,5 метра, то расстояние от вас до точки опоры должно быть не менее 100 метров. Придется очень потрудиться, чтобы найти доску такой длины.

Золотое правило механики гласит: во сколько раз мы выигрываем в силе, во столько же раз проигрываем в расстоянии.

Применение рычагов

Рычаги встречаются нам ежедневно в обычной жизни, просто до изучения этой темы вы могли их не замечать. Так, ножницы, щипцы для раскалывания орехов, пинцет, механические весы и весло в лодке являются типичными рычагами: у них есть явная точка опоры и плечи сил.

В теле человека тоже есть система рычагов. К ним можно отнести кости рук, ног, пальцев и даже челюсть и череп. Мышцы руки, такие как бицепс и трицепс, тоже можно назвать рычагами: они участвуют во многих движениях, поочередно растягиваясь и сжимаясь.

Виды рычагов

Рычаги делятся на три вида по своему строению. Рассмотрим каждый из них.

В рычаге первого типа точки приложения сил лежат по разные стороны от точки опоры, силы направлены в одну сторону. Одна из сил стремится повернуть рычаг по часовой стрелке, другая — против часовой стрелки.

Примеры: лом, пила, ножницы, плоскогубцы, детские качели.

В рычаге второго рода обе точки приложения сил лежат по одну сторону от точки опоры, причем одна из сил имеет меньшее плечо. Примером такого рычага является обычная садовая тачка: чтобы поднять груз, находящийся в ней, необходимо направить нашу силу вверх, чуть приподнимая тачку.

Еще к рычагам второго типа можно отнести щипцы для колки орехов, ключ для открывания бутылок.

В рычаге третьего типа обе точки приложения сил лежат по одну сторону от точки опоры, но тело, которое необходимо поднять, имеет большее плечо силы. Чтобы поднять такое тело, нам необходимо приложить силу, во много раз превышающую вес груза. К таким рычагам можно отнести ложку, метлу, заднюю дверь багажника и капот легковых автомобилей.

Великий греческий ученый Архимед как-то сказал: «Дайте мне точку опоры, и я сдвину (переверну) Землю!». Имел ли он в виду, что может действительно создать такой масштабный рычаг, сейчас никто не подтвердит. Но мы точно знаем: уверенность в своих силах и знаниях позволит вам справиться с любым сложным делом. Именно такую уверенность дают онлайн-курсы физики в школе Skysmart. Записывайтесь на уроки, и тогда все вам будет нипочем: и школьные уроки физики, и лабораторные работы, и даже олимпиады. И тогда вы, как и Архимед, сможете сказать про себя: я могу сдвинуть даже Землю!💪

Дарья Вишнякова

К предыдущей статье

Как подготовиться к ОГЭ по физике

К следующей статье

Как подготовиться к ЕГЭ по физике

Получите индивидуальный план обучения физике на бесплатном вводном уроке

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Момент силы, условия равновесия рычага, правило, применение рычагов

1. Устройство и виды рычагов
2. Момент силы
3. Правило моментов для двух сил
4. Правило моментов для нескольких сил
5. Применение рычагов в быту и технике
6. Задачи
7. Лабораторная работа №9. Проверка условия равновесия рычага

п.1. Устройство и виды рычагов

Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры. Рычаг состоит из перекладины и опоры. Точка опоры делит перекладину рычага на два плеча рычага. Назначение рычага – получить выигрыш в силе или расстоянии. Если к плечу рычага достаточно приложить меньшую силу, то переместить конец рычага придётся на бóльшее расстояние: выигрыш в силе оборачивается проигрышем в расстоянии. И наоборот, если удаётся сократить перемещение конца рычага, придётся приложить бóльшую силу: выигрыш в расстоянии оборачивается проигрышем в силе.

В зависимости от взаимного расположения точки опоры и нагрузки различают три вида рычагов.

Рычаг 1-го рода Опора располагается между точками приложения сил Даёт выигрыш в силе	Рычаг 2-го рода Точки приложения сил располагаются по одну сторону от опоры, нагрузка приложена между точкой опоры и точкой приложения силы Даёт выигрыш в силе
Рычаг 3-го рода Точки приложения сил располагаются по одну сторону от опоры, усилие приложено между точкой опоры и нагрузкой. 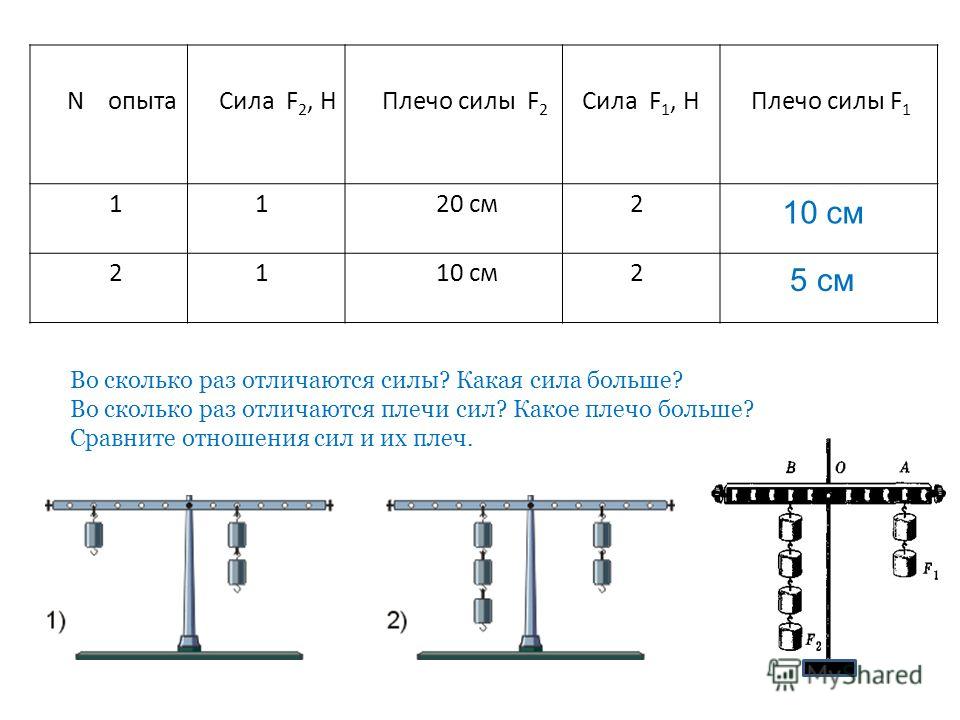Проигрыш в силе – выигрыш в расстоянии

п.2. Момент силы

Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.

Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.

На рисунке \(l_1\) – плечо силы \(F_1,\ l_2\) — плечо силы \(F_2\).

Силы вращают рычаг вокруг точки опоры – по часовой или против часовой стрелки.

Ось вращения проходит через точку опоры перпендикулярно плоскости вращения.

На рисунке сила \(F_1\) вращает рычаг против часовой стрелки, а сила \(F_2\) — по часовой стрелке.

Момент силы – это произведение силы, вращающей тело, на её плечо. $$ M=Fl $$ В системе СИ единица измерения момента силы — Н·м.

Момент силы определяется не для всего тела, а для некоторой его точки, удалённой от центра (оси) вращения. Эта величина имеет смысл только для вращающихся тел.

п.3. Правило моментов для двух сил

Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.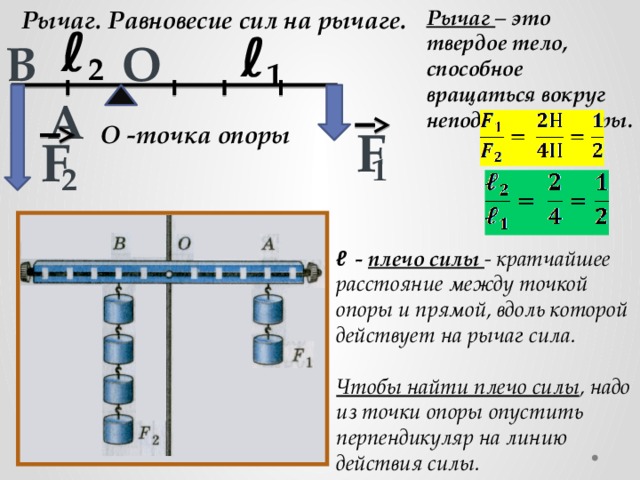

$$ F_1l_1=F_2l_2 $$

п.4. Правило моментов для нескольких сил

Правило моментов для нескольких сил
Рычаг находится в равновесии, если сумма моментов всех сил, вращающих его по ходу часовой стрелки, равен сумме моментов всех сил, вращающих его против хода часовой стрелки.

Например:

Силы \(F_1,\ F_2,\ F_3\) вращают рычаг против часовой стрелки, а сила \(F_4\) — по часовой стрелке. Поэтому: $$ F_1l_1+F_2l_2+F_3l_3=F_4l_4 $$

п.5. Применение рычагов в быту и технике

Рычаги первого рода

Весы Предмет, вес которого нужно измерить, — это нагрузка, а гиря создает усилие. Они равны, так как находятся на одном расстоянии от точки опоры.	Рычажные весы Точка опоры смещена относительно центра. Грузило передвигается по основанию, пока не уравновесит взвешиваемый объект.
Гвоздодёр Усилие ручки увеличивается плечом и вытаскивает гвоздь. Нагрузкой здесь является сопротивление гвоздя.	Ручная тележка Небольшое усилие, прикладываемое к ручкам тележки, позволяет поднимать тяжелый груз.
Плоскогубцы Составной рычаг, пара простых рычагов, соединенных в точке опоры. Нагрузка — сопротивление предмета захвату инструментом.	Ножницы Составной рычаг первого рода, развивают мощное режущее действие очень близко к месту крепления. Нагрузка — сопротивление материала лезвиям.

Рычаги второго рода

Тачка Небольшое усилие, приложенное к ручкам тачки, поднимает тяжелый груз, расположенный ближе к колесу.

Открывалка Давление на ручку преодолевает сопротивление крышки бутылки.

Щипцы для орехов Составной рычаг второго рода. Нагрузка — сопротивление скорлупы.

Рычаги третьего рода

Молоток Точка опоры — плечевой сустав (рука — продолжение рукоятки), а нагрузка — сопротивление дерева. Во время удара по гвоздю головка молотка двигается быстрее, чем рука с рукояткой.	Удочка Одна рука прикладывает усилие для движения удочки, вторая становится точкой опоры. Нагрузка — это вес рыбы, который поднимается на большую высоту легким движением руки.
Пинцет Составной рычаг третьего рода. На кончиках пинцета усилие меньше, чем со стороны пальцев, так что можно захватывать хрупкие предметы. Нагрузка — сопротивление предмета.

п.6. Задачи

Задача 1. Для каждого положения тела укажите плечо силы.

При необходимости достраиваем линию действия силы и опускаем на неё перпендикуляр из точки опоры. Этот перпендикуляр и есть искомое плечо.

Задача 2. Грузы уравновешены на рычаге.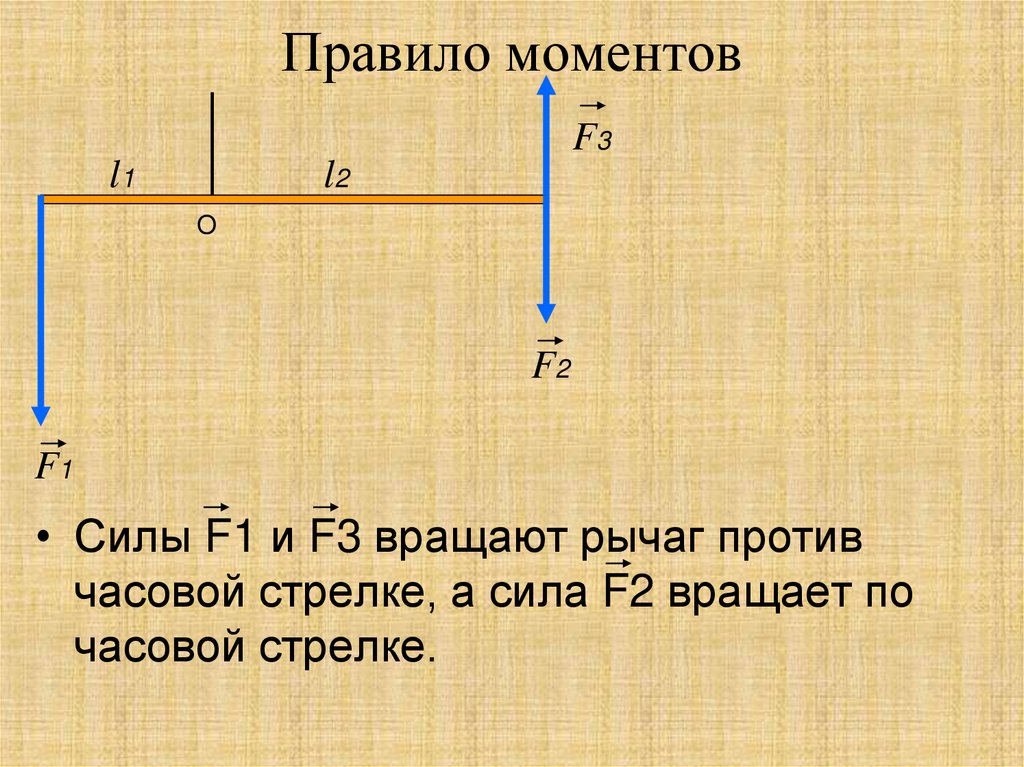 Отношение плеч рычага 1:5. Масса большего груза 2,5 кг. Найдите массу меньшего груза.

Дано:
\(\frac{l_1}{l_2}=\frac 15\)
\(m_1=2,5\ \text{кг}\)
__________________
\(m_2-?\)

По правилу моментов \begin{gather*} F_1l_1=F_2l_2 \end{gather*} На обоих концах рычага действуют силы тяжести: $$ F_1=m_1g,\ \ F_2=m_2g $$ Получаем: \begin{gather*} m_1gl_1=m_2gl_2\\[7pt] m_2=\frac{m_1l_1}{l_2} \end{gather*} Подставляем: $$ m_2=2,5\cdot \frac 15=0,5\ (\text{кг}) $$ Ответ: 0,5 кг

Задача 3. На концах рычага действуют силы 15 Н и 60 Н, направленные вниз. Рычаг находится в равновесии. Расстояние между точками приложения сил 1 м. Где расположена точка опоры?

Дано:
\(F_1=15\ \text{Н}\)
\(F_2=60\ \text{Н}\)
\(l_1+l_2=1\ \text{м}\)
__________________
\(l_1,\ l_2-?\)

По правилу моментов \begin{gather*} F_1l_1=F_2l_2. \end{gather*} Получаем систему уравнений \begin{gather*} \left\{ \begin{array}{l l} 15l_1=60l_2 \\ l_1+l_2=1 \end{array} \right.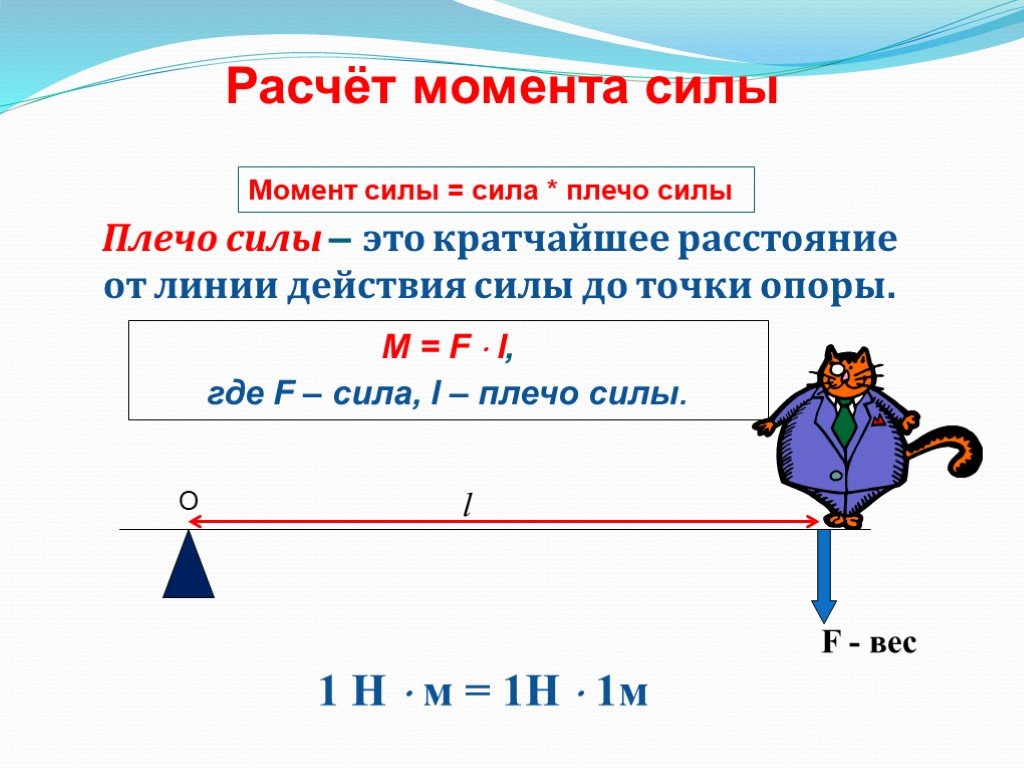 2\)
\(OB=4OA\)
__________________
\(F_A,\ F_B-?\)

Сила тяжести \(F_{\text{т}}=mg\), направленная вниз, уравновешивается силами реакции опор \(F_A\) и \(F_B\), направленными вверх. \begin{gather*} F_A+F_B=mg \end{gather*} По правилу моментов при равновесии \begin{gather*} F_A\cdot OA=F_B\cdot OB=F_B\cdot 4OA\Rightarrow F_A=4F_B \\[7pt] F_A+F_B=5F_B=mg\Rightarrow F_B=\frac{mg}{5} \end{gather*} Получаем: \begin{gather*} F_B=\frac{500\cdot 10}{5}=1000\ \text{Н}=1\ \text{кН},\ \ F_A=4\cdot 100=4000\ \text{Н}=4\ \text{кН} \end{gather*} Ответ: 4 кН и 1 кН

п.7. Лабораторная работа №9. Проверка условия равновесия рычага

Цель работы
Исследовать условия равновесия рычага под действием двух параллельных сил.

Теоретические сведения

Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.

В работе используется рычаг 1-го рода, в котором опора располагается между точками приложения сил.

Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг. Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.

Момент силы – это произведение силы, вращающей тело, на её плечо: \(M=Fl\).

Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.

\begin{gather*} M_1=M_2\\[7pt] F_1l_1=F_2l_2 \end{gather*}

В работе используется лабораторный рычаг с отверстиями диаметром 4 мм, находящимися на расстоянии 5 см друг от друга. Отверстий нечетное количество; центральное отверстие (центр тяжести) используется для подвеса рычага на штативе в положении равновесия. Абсолютную погрешность определения плеча на данном рычаге принимаем равной половине диаметра отверстия $$ \Delta l=\frac D2=2\ \text{мм} $$

Для измерения веса груза используется динамометр с ценой деления $$ d=0,1\ \text{Н}. $$

Абсолютная погрешность определения веса $$ \Delta_F=\frac d2=0,05\ \text{Н}. $$

Относительные погрешности измерений: $$ \delta_l=\frac{\Delta_l}{l},\ \ \delta_F=\frac{\Delta_F}{F},\ \ \delta_M=\delta_l+\delta_F $$

Абсолютная погрешность определения момента силы $$ \Delta_M=M\cdot \delta_M $$

Погрешности определения отношений сил и плечей: \begin{gather*} r_F=\frac{F_1}{F_2},\ \ \delta_{rF}=\frac{\Delta_F}{F_1}+\frac{\Delta_F}{F_2},\ \ \Delta_{rF}=\frac{F_1}{F_2}\cdot \delta_{rF}\\[7pt] r_l=\frac{l_2}{l_1},\ \ \delta_{rF}=\delta_{rl}\frac{\Delta_l}{l_1}+\frac{\Delta_l}{l_2},\ \ \Delta_{rl}=\frac{l_2}{l_1}\cdot \delta_{rl} \end{gather*}

Приборы и материалы
Лабораторный рычаг, штатив, стержень, динамометр, набор грузов.

Ход работы

1. Закрепите стержень в штативе, наденьте на него рычаг. Если стержень проходит через центральное отверстие рычага, он находится в равновесии.
2. Подвесьте три груза на динамометре, запишите их вес \(F_1\).
3. Подвесьте грузы слева от оси вращения рычага на расстоянии 5 см.
4. С помощью динамометра определите, какую силу нужно приложить на расстоянии 15 см справа от оси вращения, чтобы удерживать рычаг в равновесии.
5. Как направлены в этом случае силы, действующие на рычаг? Запишите длину плеч этих сил.
6. Найдите моменты сил \(M_1\) и \(M_2\), их относительные и абсолютные погрешности.
7. Вычислите отношение сил \(\frac{F_1}{F_2}\) и плеч \(\frac{l_2}{l_1}\) для этого случая, погрешности их определения.
8. Сделайте выводы.

Результаты измерений и вычислений

\(F_1,\ \text{Н}\)	\(l_1,\ \text{см}\)	\(F_2,\ \text{Н}\)	\(l_2,\ \text{см}\)	\(F_1/F_2\)	\(l_2/l_1\)
2,9	5	1,0	15	2,9	3,0

Погрешности прямых измерений: $$ \Delta_l=2\ \text{мм}=0,2\ \text{см},\ \ \Delta_F=0,05\ \text{Н} $$ Найдем моменты сил и погрешности вычислений: \begin{gather*} M_1=F_1\cdot l_1=2,9\cdot 5=14,5\ (\text{Н}\cdot \text{м})\\[7pt] \delta_{M1}=\frac{\Delta_l}{l_1}+\frac{\Delta_F}{F_1}=\frac{0,2}{5}+\frac{0,05}{2,9}\approx 0,04+0,017=0,057=5,7\text{%} \\[7pt] \Delta_{M1}=M_1\cdot \delta_{M1}=14,5\cdot 0,057\approx 0,8\ (\text{Н}\cdot \text{м})\\[7pt] M_1=(14,5\pm 0,8)\ \text{Н}\cdot \text{м}\\[7pt] \\[7pt] M_2=F_2\cdot l_2=1,0\cdot 15=15,0\ (\text{Н}\cdot \text{м})\\[7pt] \delta_{M2}=\frac{\Delta_l}{l_2}+\frac{\Delta_F}{F_2}=\frac{0,2}{15}+\frac{0,05}{1,0}\approx 0,013+0,05=0,063=6,3 \text{%} \\[7pt] \Delta_{M2}=M_2\cdot \delta_{M2}=15,0\cdot 0,063\approx 0,9\ (\text{Н}\cdot \text{м})\\[7pt] M_2=(15,0\pm 0,9)\ \text{Н}\cdot \text{м} \end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ M_1=M_2 $$

Погрешность вычислений для \(\frac{F_1}{F_2}\) \begin{gather*} \delta_{rF}=\frac{\Delta_F}{F_1}+\frac{\Delta_F}{F_2}=\frac{0,05}{2,9}+\frac{0,05}{1,0}\approx 0,017+0,05=0,067=6,7\text{%}\\[7pt] \Delta_{rF}=\frac{F_1}{F_2}\cdot \delta_{rF}=2,9\cdot 0,067\approx 0,2\\[7pt] \frac{F_1}{F_2}=2,9\pm 0,2 \end{gather*}

Погрешность вычислений для \(\frac{l_2}{l_1}\) \begin{gather*} \delta_{rl}=\frac{\Delta_l}{l_1}+\frac{\Delta_l}{l_2}=\frac{0,2}{5}+\frac{0,2}{15}\approx 0,04+0,013=0,053=5,3\text{%}\\[7pt] \Delta_{rl}=\frac{l_2}{l_1}\cdot \delta_{rl}=3,0\cdot 0,053\approx 0,2\\[7pt] \frac{l_2}{l_1}=3,0\pm 0,2 \end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ \frac{F_2}{F_2}=\frac{l_2}{l_1} $$

Выводы
На основании проделанной работы можно сделать следующие выводы.

Моменты сил, приложенных слева и справа от оси вращения рычага, равны $$ M_1=(14,5\pm 0,8)\ \text{Н}\cdot \text{м},\ \ M_2=(15,0\pm 0,9)\ \text{Н}\cdot \text{м} $$ Таким образом, с учетом вычисленных погрешностей, \(M_1=M_2\) — правило моментов выполняется.

Отношения сил и плечей равны \begin{gather*} \frac{F_1}{F_2}=2,9\pm 0,2,\ \ \frac{l_2}{l_1}=3,0\pm 0,2 \end{gather*}

Таким образом, с учетом вычисленных погрешностей \(\frac{F_1}{F_2}=\frac{l_2}{l_1}\) — правило отношений выполняется.

Эксперименты подтвердили условие равновесия рычага.

Рейтинг пользователей

за неделю

• за неделю
• один месяц
• три месяца

Помогай другим

Отвечай на вопросы и получай ценные призы каждую неделю

См. подробности

моментов, рычаги и шестерни: принцип и пример | StudySmarter

Моменты очень часто встречаются в повседневной жизни. Возможно, у вас уже есть интуитивное представление о моментах, и вы можете использовать его в своих интересах, даже если вы не знакомы с его физической теорией. Например, мы применяем понятие момента, когда играем на качелях на детской площадке и измеряем массу с помощью неравноплечевых весов. При правильном использовании моменты могут помочь нам использовать нашу силу и тяжелые предметы, которые мы не можем переместить в одиночку. Знаменитый греческий математик и философ Архимед так увлекся таким способом применения моментов, что сказал: «Дайте мне точку опоры, и я переверну мир!» Возможно, вы видели, как люди уравновешивают предметы так, что кажется, будто они бросают вызов гравитации, например, те наклонные держатели для бутылок. Да, это еще одно применение понятия моментов! Продолжайте читать, чтобы узнать больше о значении, принципе и причинах Моменты, выбывшие и шестеренки.

Бутылка балансируется без усилий благодаря продуманному использованию моментов в конструкции держателя бутылки, StudySmarter Originals

Что означает момент в физике?

Когда мы прикладываем силу к объекту в определенном направлении, мы можем заставить его вращаться. Точка, вокруг которой происходит вращение, называется точкой разворота . Моменты посвящены пониманию и количественной оценке эффективности силы, заставляющей объект поворачиваться.

Момент — это название, которое мы даем в физике вращательному действию силы, заставляющей объект вращаться вокруг оси.

Чтобы определить момент силы M, мы умножаем приложенную силу F на перпендикулярное расстояние линии действия силы от точки вращения d.

M=Fd

момент силы = сила × расстояние

Поскольку единицами силы являются ньютоны (Н), а единицами расстояния являются метры, мы измеряем момент в ньютон-метрах (Нм).

На следующем рисунке показано, как создать момент в гайке с помощью разводного ключа, прикладывая усилие в правильном направлении. В этом случае центр гайки является точкой поворота.

Сила, приложенная к гаечному ключу, вызывает момент, заставляющий гайку вращаться вокруг своего центра, StudySmarter Originals

В качестве эксперимента попробуйте открыть дверь, толкая ее на разном расстоянии от петли. Вы обнаружите, что чем дальше от петли вы нажимаете, тем легче будет сдвинуть дверь. Вам нужно меньше силы, когда вы находитесь дальше от шарнира, потому что вы увеличиваете перпендикулярное расстояние от линии действия силы — вашего толчка — до оси вращения — шарнира. Таким образом, момент становится больше, что делает поворотное воздействие на дверь более эффективным.

Набор грузов общим весом 8 шекелей размещен на балке, уравновешенной в точке опоры, как показано на диаграмме ниже. Этот комплект размещается на расстоянии 2 м от оси. Чему равен момент, обусловленный набором масс?


Набор грузов на балке над точкой опоры создает момент. GCSE

Для этого вопроса нам нужно использовать приведенное выше уравнение для момента:

M=Fd

Приложенная сила — это вес набора, 8 Н. Поскольку груз действует вниз, заданное расстояние перпендикулярно линии действия груза, равной 2 м. Обе величины уже указаны в единицах СИ, поэтому мы можем напрямую использовать уравнение, чтобы найти момент.

M=FdM=8N×2mM=16Nm

Момент, создаваемый набором масс, равен 16Nm.

Причины моментов

Из приведенного выше определения мы знаем, что сила вызывает момент. Но не всякой силы! Например, обратите внимание, что если линия действия силы проходит через точку опоры, момента не будет, так как перпендикулярное расстояние равно нулю. Следовательно, в таком случае нет вращения.

Линия действия силы проходит через точку вращения. В этом случае ключ не заставляет гайку проворачиваться, так как момент отсутствует. StudySmarter Originals

Используя эту идею, мы можем балансировать объекты так, чтобы они не падали. Нам просто нужно убедиться, что их вес, направленный вниз, действует в направлении, которое проходит через точку опоры конструкции, которую мы пытаемся уравновесить, — точку опоры. Вы помните определение центра масс?

центр масс — это точка, в которой мы можем считать, что сосредоточена вся масса объекта. Его расположение зависит от распределения массы объекта.

Сбалансировать объект легко, если мы знаем, где находится центр масс. Рассмотрим бутылку, показанную в начале. Если бутылка наклонена, ее центр масс не совпадает с точкой опоры. Поэтому его вес будет действовать на некотором перпендикулярном расстоянии от оси вращения, создавая момент. В этот момент бутылка поворачивается к поверхности, на которой она стоит, и падает.

Вес бутылки создает момент, потому что центр масс не совмещен с точкой вращения. StudySmarter Originals

Однако наклонный держатель для бутылок сконструирован таким образом, что центр масс системы держатель для бутылок и бутылок находится непосредственно над точкой опоры. Таким образом, вес системы не создает момента.

Центр масс системы бутылкодержатель-бутылка совмещен с точкой поворота. Следовательно, система не подвержена никакому моменту из-за своего веса. StudySmarter Originals

Вы можете попробовать это дома. Если у вас есть две одинаковые вилки, две зубочистки и солонка, вы можете сбалансировать вилки удивительным образом.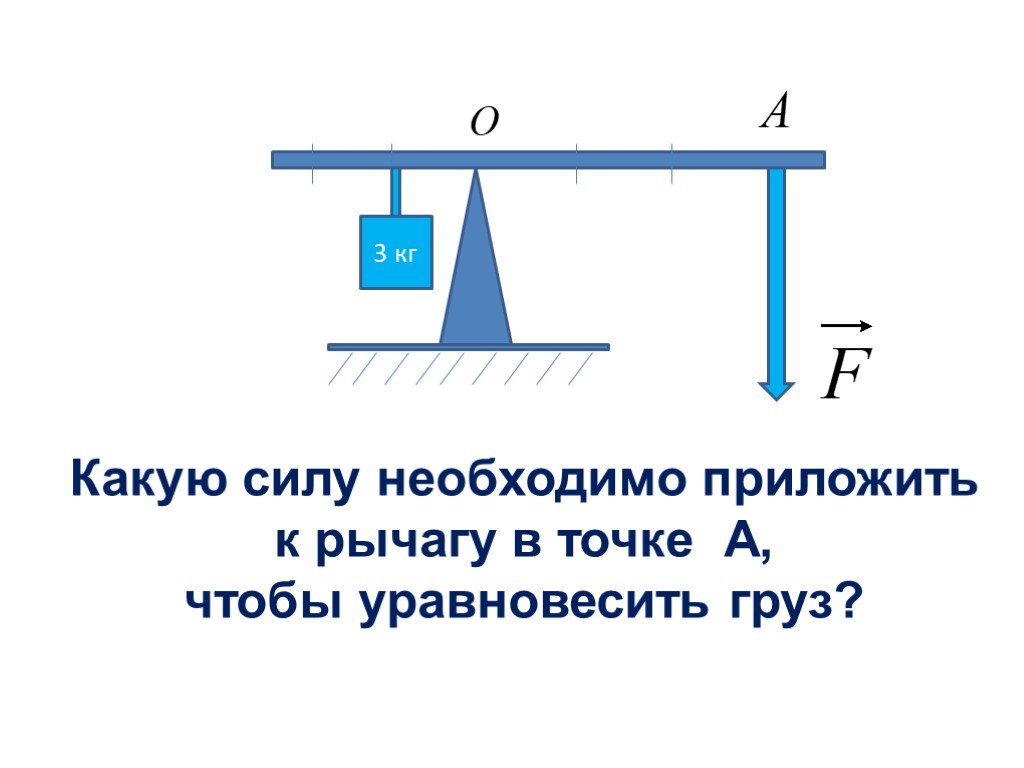 Сначала заблокируйте зубцы вил, как показано на рисунке ниже.

Блокировка зубцов вил, StudySmarter Originals

Теперь вставьте зубочистку в один из прорезей в блокируемых вилках, пока она не затвердеет. Если все сделано правильно, у вас получится конструкция с центром масс, расположенным на вертикальной линии, проходящей через невставленный конец зубочистки. Из-за этого вы должны быть в состоянии сбалансировать всю конструкцию на одном из ваших пальцев от невставленного конца зубочистки.

Конструкция легко балансируется с невставленного конца зубочистки, поскольку расположение центра масс находится прямо под ним. StudySmarter Originals

Но мы можем сделать лучше! Закрепите вторую зубочистку в одном из отверстий солонки. Аккуратно сбалансируйте структуру вилки-зубочистки на второй зубочистке вместо пальца. Эта установка будет работать и сбалансирована, потому что центр масс системы вилок выровнен с вертикальной зубочисткой, не создавая момента, чтобы заставить вилки упасть.

Поскольку вес конструкции действует по линии, проходящей через точку вращения — второй конец зубочистки, — нет момента, чтобы заставить вилки упасть.

Принцип моментов

Теперь мы знаем, что моменты могут вызывать вращение объекта, но, как и в предыдущих примерах, иногда мы можем предпочесть, чтобы наша система оставалась статической. Рассмотрим конструкции, поднятые во время строительства. Очень важно, чтобы эти конструкции не раскачивались, потому что это было бы слишком опасно. Однако мы не всегда можем сбалансировать объекты, используя их центр масс. В таких случаях нам нужно сбалансировать моменты , и принцип моментов может помочь нам с этим .

Принцип моментов утверждает, что система сбалансирована , если сумма моментов по часовой стрелке равна сумме моментов против часовой стрелки.

Объект будет вращаться, только если существует дисбаланс моментов по часовой стрелке и против часовой стрелки. Следовательно, мы можем предотвратить нежелательный момент, вызывающий вращение по часовой стрелке, уравновешивая его, используя момент против часовой стрелки той же величины.

Когда система находится в равновесии, говорят, что она находится в равновесии. Примером этого может служить ситуация, когда два человека одинаковой массы сидят по обе стороны от качелей. Поскольку их веса равны, равны и расстояния от центра вращения до обеих сил. Генерируемые моменты равны из-за равных сил — одинаковых весов — и перпендикулярных расстояний до оси вращения. Следовательно, эффекты поворота от двух сил компенсируют друг друга, и качели не вращаются. Обратите внимание, что в точке поворота также действует сила реакции (обозначенная буквой Fpin на диаграмме ниже). Однако это не вызывает никакого момента, потому что перпендикулярное расстояние для него равно нулю.

Моменты, возникающие у каждого ребенка на качелях, зависят от их массы и расстояния от оси вращения, philschatz

Двое детей сидят по обе стороны от качелей. Система находится в равновесии и не движется. Момент, прикладываемый к качелю ребенком с левой стороны, составляет 600 Нм. Масса ребенка справа 30 кг. Какова общая длина качелей?

Можно предположить, что качели расположены горизонтально, а силы, действующие от веса детей, перпендикулярны ему, так как направлены вниз. Уравнение момента, вызванного силой, имеет вид:

M=Fd,

, где F — сила в ньютонах (Н), а — расстояние по перпендикуляру линии действия силы от оси вращения в метрах (м). Мы можем изменить это выражение, чтобы изолировать расстояние от точки разворота:

d=MF.

Нам нужно рассчитать вес ребенка справа, так как система находится в равновесии, поэтому она вызовет тот же момент, что и ребенок слева. Сила веса ребенка составляет:

Вт=мг,

принимая g за 10 мс2:

Вт=30 кг × 10 м2=300 кг мс2=300 Н

Теперь мы можем подставить этот результат в уравнение для расстояния.

d=MF=MW=600Н м300Н=2м.

Однако мы должны быть осторожны. Вопрос касается длины качелей. Эта длина равна , удвоенной по , на расстоянии от точки вращения до любого из дочерних элементов, поэтому она равна 4 м.

Другие примеры и применение моментов: рычаги и шестерни

С рассмотренными примерами вы, возможно, уже начали понимать, как часто моменты присутствуют в повседневной жизни. Некоторые другие приложения моментов включают ножницы и кусачки, которые мы можем использовать, чтобы разрезать даже металл силой наших рук. Другой пример — удаление гвоздя с помощью головки молотка и нажатия или вытягивания рукоятки молотка. Пример молотка и гвоздя показан ниже. Помните, что мы должны учитывать перпендикулярное расстояние от оси вращения до линии действия силы, а не расстояние от точки вращения до места приложения силы.

Молоток, удаляющий гвоздь, представляет собой приложение моментов, StudySmarter Originals

Все эти конкретные приложения моментов известны как рычаги . Давайте посмотрим, как они работают более подробно.

Что такое рычаг и как он работает?

Рычаг состоит из жесткого стержня или балки, опирающейся на шарнир (также называемый точкой опоры).

Мы можем использовать рычаги, чтобы легче поднимать тяжести. Рычаги работают по принципу, что мы можем создать больший момент (и, следовательно, больший вращательный эффект), применяя меньшую силу на большем расстоянии от оси вращения. Идея состоит в том, чтобы точка опоры находилась ближе к грузу — весу, который мы хотим поднять, — чем к точке приложения силы или усилия. Посмотрите на картинку ниже. В данном случае груз представляет собой большой камень. Вес камня создает момент в системе рычагов. Однако мы можем создать момент, равный или больший, используя меньшую силу, потому что расстояние, на котором прикладывается усилие, больше.

Рычаг использует моменты для подъема тяжелого веса. Поднимаемый груз вызывает момент. Однако мы можем вызвать больший момент, приложив меньшую силу, чем вес груза, если приложим ее на большем расстоянии от точки опоры.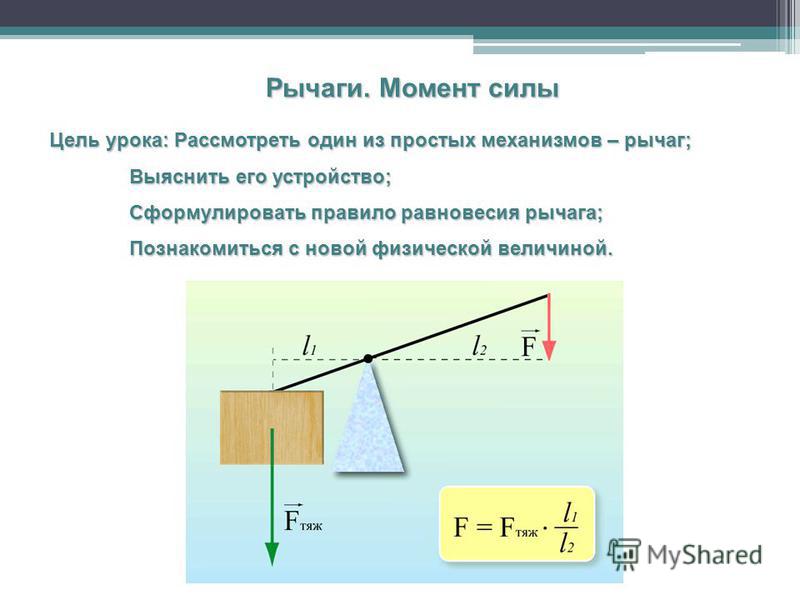 StudySmarter Originals

Тачка — еще один пример применения рычагов. Грузы, которые слишком тяжелы для прямой перевозки, вместо этого можно перевозить с помощью тачек. Груз размещается внизу над колесом, а к нему подходят два руля. Эти рули можно поднимать с меньшим усилием, чем сам груз, поскольку усилие прикладывается дальше от оси вращения, чем груз.

P представляет собой тяговое усилие или «усилие», прилагаемое человеком, а R представляет собой сопротивление нагрузки из-за его веса. Шарнир расположен в центре колеса, tec.amordediocadiz

На приведенной выше диаграмме показаны силы, действующие в этой ситуации. Обе силы действуют слева от оси системы, которая находится в центре колеса. Однако эти силы действуют в противоположных направлениях. Вес груза вызывает момент против часовой стрелки. С другой стороны, сила, которую человек прикладывает, дергая за руль, — усилие — создает момент по часовой стрелке.

Мы видим, что рычаги очень полезны, но это не единственное применение моментов.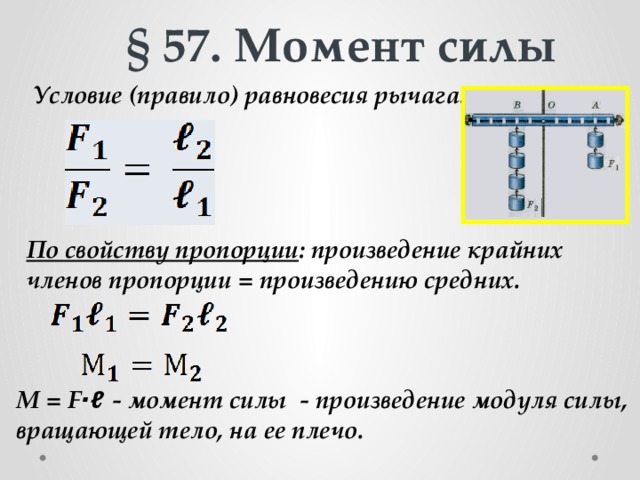 Мы также применяем эту концепцию при использовании передач.

Что такое шестерня и как она работает?

Шестерни представляют собой зубчатые колеса (они имеют небольшие выступы по краям), которые могут сцепляться друг с другом.

Возможно, вы видели шестерни в разных местах, например, на велосипедах и шкивах. Шестерни, хотя и простые, могут быть очень полезными, поскольку они имеют разные применения. Например, когда шестерни соединены друг с другом, они могут вращаться с разной скоростью, потому что для того, чтобы большая шестерня могла совершить один оборот, меньшей шестерне необходимо совершить больше оборотов. Точное количество оборотов зависит от размеров шестерен. Обратите внимание, что если одна шестерня вращается против часовой стрелки, это заставляет подсоединенную шестерню вращаться по часовой стрелке. Следовательно, мы можем использовать их для изменения направления вращения объекта.

Если одна шестерня вращается в одном направлении, это приведет к тому, что другая повернется в противоположном направлении, Wikimedia commons

Но как именно здесь применяется понятие момента? В месте контакта зубьев шестерен действуют силы, равные и противоположные друг другу.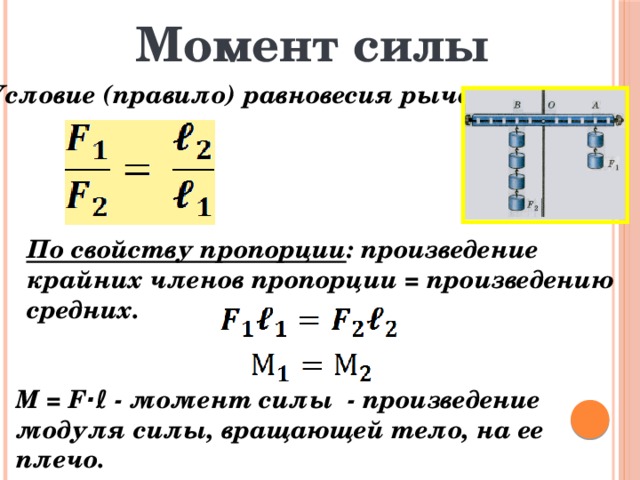 Однако, поскольку их радиусы различны, моменты, действующие на каждую шестерню, также различны. Приложение силы к меньшей шестерне вызовет больший момент на большей шестерне, потому что сила, приложенная к ней, будет такой же, но ее радиус больше.

Ключевые выводы

• Момент — это вращательный эффект силы, которая заставляет объект вращаться вокруг оси.

• Мы вычисляем момент силы, умножая приложенную силу на расстояние по перпендикуляру от оси вращения до линии действия силы.

• Принцип моментов гласит, что когда система находится в равновесии, сумма моментов по часовой стрелке равна сумме моментов против часовой стрелки относительно оси вращения.

• Сила, действующая непосредственно через стержень системы, не создает момента относительно стержня.

• Рычаги выгодно используют моменты и могут использоваться для увеличения момента, чтобы что-то повернуть или поднять тяжелый предмет.

• Шестерни различных размеров могут быть соединены для увеличения или уменьшения величины момента.

Рычаги

Рычаг — это механизм, который можно использовать для приложения большой силы на небольшом расстоянии к одному концу рычага путем приложения небольшой силы на большом расстоянии к другому концу.

The moment action on both sides of the lever is equal and can be expressed as

F _e d _e = F _l d _l                               (1)

где

F _e = сила усилия (Н, фунты)

F _l = сила нагрузки (Н, фунты) (обратите внимание, что вес является силой) расстояние от силы нагрузки до точки опоры (м, фут)

D _E = Расстояние от силы усилий до точки зрения (M, FT)

Сила усилия может быть рассчитана путем модификации (1) до

F _E = F _{L L L L L L L L L L L L L L L L L L L D L / D E}

= M A _G DL / DE (1B)

, где

MARSLARS 2920217 MARSLERS MARSLINGS MARSLINGS MARSLINGS 9028

. 0218 г = ускорение свободного падения (9,81 м/с ² , 32,17 фут/с ² )

Калькулятор рычага

Этот калькулятор можно использовать для расчета силы усилия рычага. Его можно использовать как для метрических, так и для имперских единиц, если использование единиц согласовано.

F _l — сила нагрузки (Н, кг, фунт)

d _l — расстояние от силы нагрузки до точки опоры (м, фут)

9 усилие — d 90 усилие до точки опоры (м, фут ⁾

• Обратите внимание, что кг – это единица измерения массы в системе СИ. Подробнее о массе и весе (силе)

Пример – самодельный автомобильный подъемник как показано на рисунке выше. При расстоянии нагрузки до точки опоры

0,2 м , расстоянии силы усилия до точки опоры 2 м и нагрузке на рычаг — половине веса автомобиля 2000 кг — силу усилия можно рассчитать

F _E = (0,5 2000 кг) (9,81 м / с ² ) (0,2 м) / (2 м)

= 981 N

≈ 100 KG

9013 Рычаги

Рычаги первого порядка

• точка опоры расположена между усилием и нагрузкой
• усилие меньше нагрузки
• усилие перемещается дальше нагрузки
• рычаг можно рассматривать как усилитель силы

Рычаги второго порядка

• усилие и нагрузка расположены по одну сторону от точки опоры, но приложены в противоположных направлениях
• нагрузка расположена между усилием и точкой опоры
• усилие меньше нагрузки
усилие перемещается дальше груза
• рычаг можно рассматривать как усилитель силы

рычаги третьего порядка

• усилие лежит между грузом и точкой опоры
• усилие больше, чем груз
• груз перемещается дальше, чем усилие
• рычаг можно рассматривать как увеличитель расстояния рычаг на расстоянии 1 фут от точки опоры

  Сила усилия на расстоянии 2 фута от точки опоры может быть рассчитана как

  F _e = (1 фунт) (1 фут) / (2 футов)

      = 0,5 (фунт)

  Формула (1) может быть изменена, чтобы выразить требуемую нагрузку, если известно усилие, или требуемое расстояние от точки опоры, если известны нагрузка и усилие, и так далее.

  Уровень выше, где точка опоры расположена между нагрузкой и усилием, часто характеризуется как первоклассный механизм уровня .

  Уровень, на котором нагрузка и усилие расположены на одной стороне точки опоры, часто характеризуется как механизм уровня второго класса .

  Пример — Рычаг второго класса (порядок)

  Сила (вес) 1 фунт действует на расстоянии 1 фут от точки опоры.

  Сила усилия на расстоянии 2 фута от точки опоры может быть рассчитана как фунты)

  Пример — расчет рычага в единицах СИ — вес

  1 кг действующая масса 1 м от точки опоры

  Сила усилия на расстоянии 2 м от точки опоры может быть рассчитана как 1 м) / (2 м)

      = 4,9 Н

  Рычажный механизм, в котором входное усилие выше, чем выходная нагрузка, часто характеризуется как рычажный механизм третьего класса.

  Пример — Рычаг третьего класса (порядка)

  Сила (вес) 1 фунт действует на расстоянии 2 фута от точки опоры.

  The effort force at a distance of 1 ft from the fulcrum can be calculated as

  F _e = F _l d _l / d _e

      = ( 1 фунт) (2 фута) / (1 фут)

      = 2 (фунта)

  Одна или несколько сил, действующих на рычаг

  Рычаг с двумя действующими силами нагрузки и одним усилием показан на рисунке ниже:

  Общее уравнение для одного усилия с одним или несколькими действующими усилиями нагрузки может быть выражено как

  F _e = (F _LA D _LA + F _LB D _LB + _{.. + F LN D LN ) / D E (2). три действующие нагрузки ниже.}

  Пример. Рычаг с тремя действующими нагрузками и одной силой усилия

  Груз A из 1 фунт действует на расстоянии 1 фут от точки опоры.