Правило рычага. Формулировка и формула
Рычаг представляет собой один из простых механизмов, который служил и продолжает служить людям для облегчения их физического труда. В статье рассмотрим, что такое рычаг, какие виды его бывают и где они применяются, а также поясним, в чем заключается правило рычага.
Рычаг в физике
Несмотря на то что речь идет о простом механизме, он все же имеет свои составные части. Во-первых, это балка или доска, которая предназначена для воздействия на нее двух противоположных сил. Во-вторых, это опора, которая, с геометрической точки зрения, представляет собой ось вращения, вокруг которой может двигаться балка. В зависимости от расположения опоры под балкой различают три типа рычага, которые будут рассмотрены ниже.
Еще одним важным понятием для любого рычага является «плечо». Под ним понимают часть балки, которая находится между ее концом и опорой при условии, что воздействующие силы приложены к концам балки. Длина плеча играет важную роль при определении условий равновесия рычага.
Рычаг предназначен для преобразования силы в перемещение или, наоборот, перемещения в силу. Другими словами, рассматриваемый простой механизм, используется для перераспределения работы, которую следует выполнить, в пользу приложенной силы или в пользу осуществляемого перемещения. Рисунок ниже показывает пример рычага первого рода.

Когда человечество начало использовать рычаг?
Ответить уверенно на этот вопрос нельзя. Известно, что рычаги с древнейших времен использовались в Месопотамии и Древнем Египте для подъема тар с водой из колодцев и рек.

Единственным письменным свидетельством, которое сохранилось до наших дней, свидетельствующим об использовании рассматриваемого механизма, является всем известный рычаг Архимеда. В работе Плутарха «Параллельные жизни» (100 год до н. э.) говорится, что Архимед в одиночку смог поднять корабль с грузом и пассажирами над поверхностью воды. При этом философ использовал систему блоков и рычагов.
Если подойти к поставленному в названии пункта вопросу более строго, то можно сказать, что человек пользуется рычагом с момента собственного появления в этом мире, ведь наши предплечья и плечи работают по принципу этого простого механизма.
Понятие о моменте силы
Прежде чем переходить к формулировке правила равновесия рычага, рассмотрим понятие крутящего момента или момента силы. В физике под ним понимают величину, равную произведению плеча силы на саму силу. Математически это записывается так:
M = d*F.
Где, F — воздействующая сила, d — плечо силы, которое соответствует расстоянию от точки приложения F до оси вращения. Последний элемент системы, то есть ось вращения, играет принципиальную роль при определении момента M. Без наличия оси вращения нет никакого смысла говорить о действующем моменте силы.
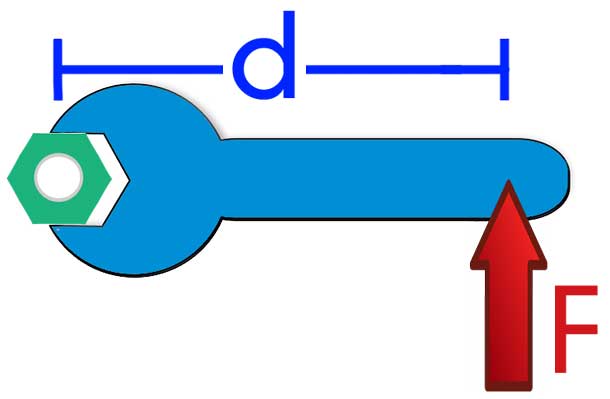
Физический смысл величины M заключается в отражении способности силы F совершить поворот системы вокруг оси. На практике эту способность можно ощутить, если попытаться открутить гайку не гаечным ключом, а руками, или же если постараться открыть дверь не за ручку, а толкая ее вблизи навесных петель.
Во время решения задач момент силы M может приводить как к вращению системы по часовой стрелке, так и против ее хода. В первой случае момент считают отрицательным, во втором — положительным.
Рассмотрим классический рычаг с двумя плечами, когда опора находится вдали от концов балки. Пример такого механизма изображен ниже.
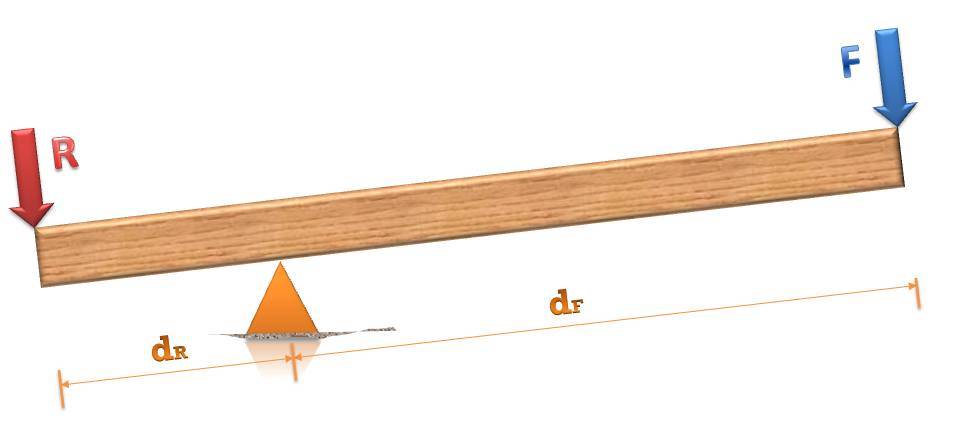
Мы видим, что когда этот рычаг применяют для совершения физической работы, то на него действует две силы:
- внешняя сила F, которую прикладывают для выполнения полезной работы;
- сила R, которая оказывает сопротивление силе F (она выполняет отрицательную работу).
В большинстве случаев сила F создается усилием человека, а сила R представляет собой вес некоторого груза.
Рассматриваемый рычаг будет находиться в равновесии, и перестанет испытывать вращение только тогда, когда сумма действующих на него моментов будет равна нулю. Используя обозначения рисунка выше, и применяя формулу для M, запишем правило равновесия рычага:
R*dR — F*dF = 0.
Заметим, что момент силы F записан со знаком минус, поскольку он стремится повернуть плечо рычага по часовой стрелке. Остается перенести второй член в правую часть равенства, чтобы записать правило рычага:
R*dR = F*dF.
Таким образом, равенство моментов силы действия F и силы противодействия R является достаточным условием равновесия рассматриваемого простого механизма.
Кто установил правило равновесия рычага? Этот вопрос отчасти пересекается с рассмотренным выше историческим. Поскольку сохранились только письменные свидетельства научной деятельности Архимеда, связанной с этим механизмом, то именно он в настоящее время считается тем философом, кто установил правило рычага.
Равновесие рассматриваемой системы обеспечивается не только равенством нулю суммы моментов, но также равенством нулю всех действующих сил. Выше были названы лишь две силы (F и R). На самом же деле существует еще сила реакции опоры, направленная против сил F и R. Реакцию опоры момента силы не создает ввиду нулевой длины ее плеча.
Выигрыш и проигрыш в использовании рычага
Следует четко понимать, что при использовании рычага сохраняется полная энергия системы. Чтобы поднять груз на некоторую высоту, необходимо совершить определенную работу. Поскольку в формуле правила рычага стоит произведение силы на длину плеча, то отмеченную работу можно выполнить как с помощью большей силы, так и с помощью меньшей. Однако в первом случае необходимо будет переместить плечо рычага в вертикальном направлении на малую величину, во втором же случае — на большую величину. Это и есть выигрыш и проигрыш в использовании рычага.
Заметим, что в формуле правила рычага стоят значения моментов. Никакого отношения к работе они не имеют. Момент силы выполняет работу только тогда, когда система за счет его действия поворачивается вокруг оси на некоторый угол.
Виды рычагов
Выше уже упоминалось, что все рычаги относятся к одному из трех типов. В основе классификации лежит относительное расположение сил R, F и опоры. Охарактеризуем все три типа:
- Рычаг 1-го типа, или рода, был показан выше. Опора расположена в нем между силами R и F. В зависимости от длины плеч dR и dF его можно использовать как для выигрыша в пути, так и для выигрыша в силе. Примером этого типа рычага являются ножницы, весы, гвоздодер.
- Рычаг 2-го рода предполагает, что сила R приложена между опорой и силой F. В таком случае получается выигрыш только в силе. Примерами таких рычагов в быту являются орехокол или ручная тачка.
- Рычаг 3-го рода предполагает, что сила F расположена между опорой и грузом R. В этом случае выигрыш возможен только в пути. Использование лопаты, циркуля или удочки для рыбалки — это яркие примеры рычага 3-го рода в работе.

Простой механизм блок
Рассматривая правила рычага, полезно сказать несколько слов о еще одном простом механизме — блоке. Представляет он собой обычный цилиндр с осью вращения, который имеет углубление по периметру своей боковой поверхности. Пример использования неподвижного блока показан ниже.
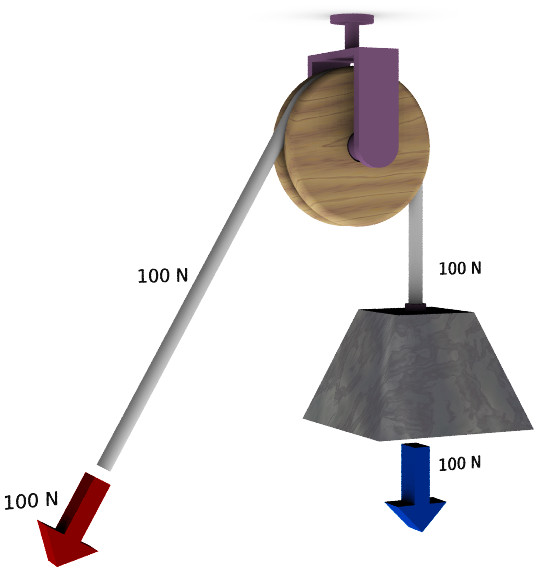
Как видно, выигрыша в силе и пути не происходит, однако неподвижный блок позволяет изменить направление воздействующей силы F.
Применение правила равновесия рычага к блоку производят, когда требуется рассчитать выигрыш в силе при использовании подвижных блоков. Один такой блок позволяет выиграть в 2 раза в силе и во столько же раз проиграть в пути.
Решение задачи
Ручная тачка сделана таким образом, что центр массы груза в ней находится на расстоянии 1/3*l от колеса, где l — длина тачки. Какой массы груз может переместить с помощью тачки человек, если известно, что он может приложить максимальную вертикальную силу F = 200 Н.
Воспользуемся правилом рычага, получим:
F*l = R*1/3*l
F = m*g/3
m = 3*F/g = 3*200/9,81 ≈ 61 кг.
Отметим, что сила F = 200 Н равна весу тела массой всего 20,4 кг. Таким образом, данная ручная тачка позволяет выиграть в 3 раза в силе.
Момент силы. 7 класс — Класс!ная физика
Момент силы. 7 класс
- Подробности
- Просмотров: 128
Правило равновесия рычага:
можно преобразовать:
1. Что называется моментом силы?
Произведение модуля силы, вращающей тело, на ее плечо называется моментом силы и обозначается буквой М.
2. В чем состоит правило моментов?
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.
Правило моментов:
Например:
Если силы, действующие на рычаг: 2 Н и 4 Н.
Их плечи соответственно составляют 4 и 2 деления рычага.
То моменты этих сил при равновесии рычага равны.
Момент силы может быть измерен.
За единицу момента силы принимается момент силы в 1 Н, плечо которой равно 1 м.
Единица момента силы в системе СИ называется ньютон-метр (Н м).
Что показывает момент силы?
Момент силы характеризует действие силы и показывает, что оно зависит одновременно и от модуля силы, и от ее плеча.
Например:
Действие силы на дверь зависит и от модуля силы, и от того, где приложена сила.
Дверь тем легче повернуть, чем дальше от оси вращения приложена действующая на нее сила.
Гайку легче отвернуть длинным гаечным ключом, чем коротким.
Ведро тем легче поднять из колодца, чем длиннее ручка ворота.
Следующая страница — смотреть
Назад в «Оглавление» — смотреть
Конспект «Золотое правило механики» — УчительPRO
«Простые механизмы. Золотое правило механики»
Код ОГЭ 1.19. Простые механизмы. «Золотое правило механики». Рычаг. Момент силы. Условие равновесия рычага. Подвижный и неподвижный блоки. КПД простых механизмов.
Простыми механизмами называются устройства, позволяющие совершить работу без применения источников немеханической энергии. С их помощью можно получить выигрыш в силе или изменить направление её действия.
Золотое правило механики: При отсутствии трения выигрыш в силе равен проигрышу в расстоянии (простые механизмы не дают выигрыша в работе).
Коэффициент полезного действия (КПД, ɳ) – физическая величина, равная отношению полезной работы (мощности, энергии) ко всей затраченной работе (мощности, энергии), выраженному в процентах: .
.
Виды простых механизмов
- Рычаг – твёрдое тело, имеющее закрёпленную ось вращения.
Условие равновесия рычага: Суммарный момент сил, вращающих рычаг по часовой стрелке, равен суммарному моменту сил, вращающих рычаг против часовой стрелки.
Момент силы
Плечо силы (l или d) относительно указанной точки – кратчайшее расстояние от точки до линии действия силы, то есть длина перпендикуляра, опущенного из точки на линию действия силы.

Линия действия силы – прямая линия, на которой лежит вектор силы.
Выигрыш в силе:  Работа полезная: Ап = F1
Работа полезная: Ап = F1
- Неподвижный блок (частный случай рычага).
Выигрыш в силе: – выигрыша в силе нет, но меняется направление её действия.
– выигрыша в силе нет, но меняется направление её действия.
Работа полезная: Ап = F1s1. Работа затраченная: Аз = F2s2.
- Подвижный блок (частный случай рычага).
Выигрыш в силе: – выигрыш в силе в 2 раза.
– выигрыш в силе в 2 раза.

- Наклонная плоскость.
Выигрыш в силе: .
.
Работа полезная: Ап = mgh. Работа затраченная: Аз = Fl.
Конспект урока по физике в 9 классе «Простые механизмы. Золотое правило механики».
Дополнительные материалы по физике в 7 классе: 1) Простые механизмы. Блоки. 2) Рычаг. Равновесие рычага. Момент силы. 3) ЗАДАЧИ на простые механизмы с решениями. 4) ЗАДАЧИ на КПД простых механизмов.
Следующая тема: «Давление твердого тела, газа и жидкости» (код ОГЭ 1.20)
С самых давних пор человек применяет различные вспомогательные приспособления для облегчения своего труда. Как часто, когда нам надо сдвинуть с места очень тяжелый предмет, мы берем себе в помощники палку или шест. Это пример простого механизма – рычага.
Применение простых механизмов
Видов простых механизмов очень много. Это и рычаг, и блок, и клин, и многие другие. Простыми механизмами в физике называют приспособления, служащие для преобразования силы. Наклонная плоскость, которая помогает вкатывать или втаскивать тяжелые предметы наверх – это тоже простой механизм. Применение простых механизмов очень распространено как в производстве, так и в быту. Чаще всего простые механизмы применяют для того, чтобы получить выигрыш в силе, то есть увеличить в несколько раз силу, действующую на тело.
Рычаг в физике — простой механизм
Один из самых простых и распространенных механизмов, который изучают в физике еще в седьмом классе – рычаг. Рычагом в физике называют твердое тело, способное вращаться вокруг неподвижной опоры.
Различают два вида рычагов. У рычага первого рода (рис. а) точка опоры находится между линиями действия приложенных сил. У рычага второго рода (рис. б) точка опоры расположена по одну сторону от них. То есть, если мы пытаемся при помощи лома сдвинуть с места тяжелый предмет, то рычаг первого рода – это ситуация, когда мы подкладываем брусок под лом, надавливая на свободный конец лома вниз. Неподвижной опорой у нас в данном случае будет являться брусок, а приложенные силы располагаются по обе стороны от него. А рычаг второго рода – это когда мы, подсунув край лома под тяжесть, тянем лом вверх, пытаясь таким образом перевернуть предмет. Здесь точка опоры находится в месте упора лома о землю, а приложенные силы расположены по одну сторону от точки опоры.
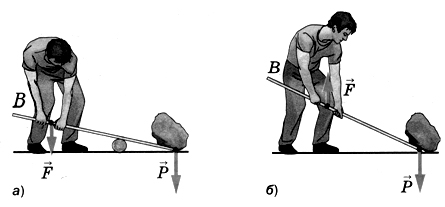
Закон равновесия сил на рычаге
Используя рычаг, мы можем получить выигрыш в силе и поднять неподъемный голыми руками груз. Расстояние от точки опоры до точки приложения силы называют плечом силы. Причем, можно рассчитать равновесие сил на рычаге по следующей формуле:
F1 / F2 = l2 / l1,
где F1 и F2 – силы, действующие на рычаг,
а l2 и l1 – плечи этих сил.
Это и есть закон равновесия рычага, который гласит: рычаг находится в равновесии тогда, когда действующие на него силы обратно пропорциональны плечам этих сил. Этот закон был установлен Архимедом еще в третьем веке до нашей эры. Из него следует, что меньшей силой можно уравновесить большую. Для этого необходимо, чтобы плечо меньшей силы было больше плеча большей силы. А выигрыш в силе, получаемый с помощью рычага, определяется отношением плеч приложенных сил.
Начав использоваться с глубокой древности, рычаг повсеместно применяется и в наши дни, как на производстве, например, подъемные краны, так и в быту, например, ножницы, весы и так далее.
Упражнения.
Задача 1. На одном конце линейки длиной 100 см подвешена гиря массой 500 г. Посередине линейки снизу находится опора, относительно которой линейка может свободно поворачиваться. Где надо подвесить второй груз массой 750 г, чтобы линейка находилась в равновесии?

Задача 2. На концах легкого стержня длиной 32 см подвешены грузы массами 40 г и 120 г. Где нужно подпереть стержень, чтобы он находился в равновесии?

Решите самостоятельно:
Решить задачи в тетради.
Задача №1.
С помощью рычага рабочий поднимает плиту массой 120 кг. Какую силу он прикладывает к большему плечу рычага, равному 2,4 м, если меньшее плечо 0,8 м?
Задача №2.
На концах рычага действуют силы 20 Н и 120 Н. Расстояние от точки опоры до большей силы равно 2 см. Определите длину рычага, если рычаг находится в равновесии.
Дата публикации — 18.04.2020
| 1. | Момент силы | 1 вид — рецептивный | лёгкое | 1 Б. | |
| 2. | Рычаг, вычисление веса противовеса | 1 вид — рецептивный | лёгкое | 2 Б. | Вычисление веса противовеса, при котором рычаг находится в состоянии равновесия. |
| 3. | Наклонная плоскость, определение экономии силы | 1 вид — рецептивный | лёгкое | 2 Б. | Определение экономии силы, которую даёт наклонная плоскость. |
| 4. | Соответствие распределения нагрузки типу конструкции моста | 2 вид — интерпретация | лёгкое | 1 Б. | Необходимо определить, соответствует ли заданное распределение нагрузки заданной конструкции моста. |
| 5. | Распределение нагрузки в различных конструкциях мостов | лёгкое | 1 Б. | Необходимо определить, является ли правильным изображение распределения указанной нагрузки в данной конструкции моста. | |
| 6. | Рычаг, определение массы противовеса для равновесия | 2 вид — интерпретация | среднее | 3 Б. | Необходимо подобрать массу противовеса, чтобы рычаг оказался в состоянии равновесия. |
| 7. | Рычаг | 1 вид — рецептивный | среднее | 3 Б. | Расчёт сил на рычаговых качелях. |
| 8. | Качели | 2 вид — интерпретация | среднее | 1 Б. | Определение местоположения брата по отношению к оси качелей, если известны массы брата и сестры, а также длина качелей. |
| 9. | Сила поднятия балки | 2 вид — интерпретация | среднее | 2 Б. | Вычисление силы, которую надо приложить, чтобы приподнять балку, если известны длина балки и её масса. |
| 10. | Наклонная плоскость, определение наибольшей экономии силы | 1 вид — рецептивный | среднее | 2 Б. | Необходимо определить, какая из наклонных плоскостей даёт наибольшую экономию силы. |
| 11. | Рычаг, показание динамометра при равновесии | 3 вид — анализ | среднее | 3 Б. | Необходимо определить показание динамометра, когда рычаг находится в равновесии. |
| 12. | Рычаг, расчёт силы, создаваемой в плоскогубцах | 2 вид — интерпретация | среднее | 3 Б. | Расчёт силы, создаваемой в плоскогубцах. |
| 13. | Рычаг, условие равновесия для многоуровневого рычага | 3 вид — анализ | сложное | 8 Б. | Необходимо вычислить массу противовеса, при которой многоуровневый рычаг находится в состоянии равновесия. |
Цели урока
Образовательная:
- ввести понятие «простой механизм»;
- изучить устройство и принцип действия рычага;
- выяснить условие равновесия рычага;
- исследовать использование простых механизмов в природе и технике.
Развивающие:
- способствовать развитию умения анализировать, выдвигать гипотезы, предположения, строить прогнозы, наблюдать и экспериментировать;
- способствовать развитию логического мышления;
- развитие учебно-коммуникативных умений (задавать вопросы, объяснять и доказывать свою точку зрения).
Воспитательные:
- способствование расширению политехнического кругозора учащихся;
- пробуждение познавательного интереса к предмету и окружающим явлениям.
Планируемые результаты
Ученики приобретут знания о
- простых механизмах;
- видах простых механизмов;
- плече силы;
- условии равновесия рычага;
- практическом применении рычага.
Ученики приобретут умения:
- измерять плечо силы;
- экспериментально определять соотношение сил и плеч для равновесия рычага.
Ученики закрепят навыки и умения:
- планировать эксперимент;
- выбирать главное из текста;
- анализировать информацию;
- делать выводы.
Тип урока: урок открытия нового знания
Вид урока: урок – исследование
Оборудование: штатив, набор грузов, рычаги, динамометр, ножницы, гаечный ключ, щипцы.
План урока
- Организационный момент (1 мин)
- Мотивационный момент (3 мин)
- Освоение нового материала (20 мин)
- Первичная проверка усвоения знаний (10 мин)
- Первичное закрепление знаний (7 мин)
- Подведение итогов урока (рефлексия) (3 мин)
- Домашнее задание (1 мин)
Ход урока
1. Организационный момент. Психологический настрой
2. Мотивация учащихся.
Учитель: Здравствуйте, ребята. Сегодня у нас необычный урок: урок-исследование.
Для начала решим задачу:

Штангист держит штангу весом 2 кН на высоте 2,5 м. Какую работу при этом он совершает? (А = mgh = 2ּ 103Н ּ 2,5м = 5ּ 103 = 5кДж).
А, если это будет более тяжелый предмет, например, шкаф. Как его приподнять? Зачастую человеческой силы для этого недостаточно. Что делать? Ученики: Можно подсунуть под край шкафа крепкую палку или, например, клюшку.
Учитель: Верно. А, чтобы разрезать ткань, например, используют ножницы. Чтобы открутить гайку используют гаечный ключ.

Все эти приспособления с точки зрения физики называются одинаково – рычаг. Как вы думаете, для чего нужен рычаг?
Ученики: Для того чтобы увеличить силу, прикладываемую человеком.
3. Освоение нового материала
Учитель: Приспособления, служащие для преобразования силы, называют механизмами. Рычаг – один из первых простейших механизмов, изобретенных человеком. Рычаг – это любое твердое тело, способное вращаться вокруг какой — либо неподвижной опоры. (Учащиеся записывают тему урока и определение рычага).
Чтобы поднять тяжелый груз на некоторую высоту, его вкатывают по наклонной плоскости или поднимают с помощью блоков. Таким образом, наклонная плоскость и блок – это тоже простые механизмы. Приведите примеры простых механизмов, которые вам встречались в быту, технике.
Ученики: качели, весло, щипцы, плоскогубцы, весы, подъемный кран.
Учитель: Различают два вида рычагов:
У рычага 1 рода (рис. а) точка опоры располагается между линиями действия приложенных сил, а у рычага 2 рода (рис. б) она располагается по одну сторону от них.

Создание проблемной ситуации
Учитель: Почему качели находятся в равновесии?

Ученики выдвигают гипотезы: Кот и ежик сидят на разных расстояниях от оси вращения (точки опоры) и имеют разный вес.
Учитель: Меньшей силой уравновешена большая сила. Какой можно сделать вывод?
Ученики: Чтобы меньшей силой уравновесить большую, нужно увеличить расстояние от точки опоры до линии действия меньшей силы.
Учитель: Будут ли в равновесии эти рычаги? Как уравновесить эти рычаги?

Учитель: У вас на столах рычаг на штативе, грузы и динамометр. На левую часть рычага подвесьте два груза. Опытным путем установите, на каком расстоянии вправо от оси вращения надо подвесить: а) один груз: б) два груза; в) три груза, чтобы рычаг пришел в равновесие.

Сделайте вывод о соотношении сил и расстояний от точки опоры до линии действия сил.
Ученики: Если силы (вес грузов) отличаются в 2 раза, то и расстояния, на которых подвешены грузы также отличаются в 2 раза. Причем большая сила должна быть приложена на меньшем расстоянии от точки опоры.
Учитель: Кратчайшее расстояние от линии действия силы до точки опоры называется плечом силы. Найдите в учебнике правило нахождения плеча силы. (Работают с учебником).
Учащиеся записывают определение плеча силы.
Ученик зачитывает: Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.
Учитель: Рычаг позволяет получить выигрыш в силе — это отношение сил F1/ F2.
Условие равновесия рычага:
Вывод: рычаг находится в равновесии, если отношение сил обратно пропорционально отношению расстояний.
Учащиеся записывают в тетрадь условие равновесия рычага.
4. Первичная проверка усвоения знаний
Учитель предлагает указать на рисунках плечи сил:
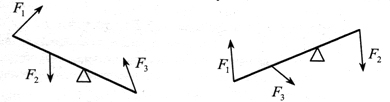
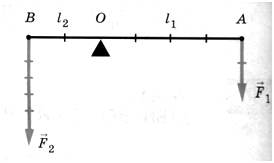
Учитель предлагает решить расчетную задачу: Длина одного плеча рычага 12 см, другого – 24 см. На меньшем плече подвешен груз массой 50 кг. Какая сила должна действовать на другое плечо рычага, чтобы он находился в равновесии?
Учитель предлагает проделать экспериментальное задание: Возьмите спичку и разломите ее пополам, получившиеся части снова разломите пополам, и так продолжайте ломать спичку на все более маленькие кусочки. Почему маленькие кусочки труднее разламывать, чем большие?
Учащиеся проделывают задание и отвечают на вопрос.
Физминутка: Встаньте, сначала повращайте одной рукой, затем — другой. Теперь приподнимитесь на носочках. Вы знаете, стопы ног, руки – это тоже рычаги.
5. Первичное закрепление знаний
Класс делится на 3 группы, каждая группа получает задание:
Задание 1 группе
Оборудование: ножницы разных видов, кусачки, гаечный ключ, линейка.
Измерьте с помощью линейки плечи рычагов. Определите выигрыш в силе данных простых механизмов.
Задание 2 группе
Сконструировать из подручного материала один из простых механизмов и продемонстрировать его в действии.

Задание 3 группе
Составить ребусы, кроссворд на тему: Простые механизмы в природе.
6. Подведение итогов урока (рефлексия)
- Что называется простыми механизмами?
- Какие виды простых механизмов вы знаете?
- Что такое рычаг?
- Что называется плечом силы?
- Каково правило равновесия рычага?
- Где применяется в нашей жизни рычаг?
- Какое значение имеют простые механизмы в жизни человека?
Учащиеся отвечают на вопросы.
7. Домашнее задание
§ 57, 58, 60; задачи № 736, 742, 747.
Домашние опыты:
- Положите под середину линейки карандаш так, чтобы линейка находилась в равновесии. Не изменяя взаимного расположения линейки и карандаша, уравновесьте на полученном рычаге одну монету с одной стороны и стопку из трех таких же монет с другой стороны. Измерьте плечи приложенных (со стороны монет) сил и проверьте правило рычага.
- Определите массу линейки. У вас имеются измерительная линейка, карандаш и монета. Масса монеты считать известной, равной m.
Учитель: Желаю Вам найти свою точку опоры и всегда оставаться в равновесии! Спасибо за урок!
Тест. Момент силы
© 2020, ООО КОМПЭДУ, http://compedu.ru При поддержке проекта http://videouroki.net
Будьте внимательны! У Вас есть 10 минут на прохождение теста. Система оценивания — 5 балльная. Разбалловка теста — 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!Список вопросов теста
Вопрос 1
Как называется произведение силы на ее плечо?
Варианты ответов
- работа силы
- мощность
- момент силы
- среди ответов нет правильного
Вопрос 2
Что характеризует момент силы?
Варианты ответов
- свойство рычага
- результат действия силы
- точку приложения силы
Рычаги
Рычаг — это механизм, который может быть использован для приложения большого усилия на небольшое расстояние на одном конце рычага путем приложения небольшого усилия на большее расстояние на другом конце.
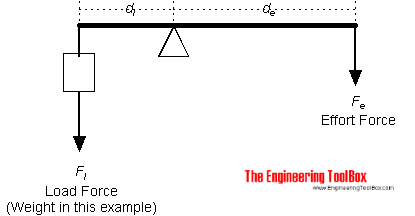
Моментное действие с обеих сторон рычага одинаково и может быть выражено как
F e d e = F l d l (1)
, где
F e = сила усилия (Н, фунт)
F l = сила нагрузки (Н, фунт) (обратите внимание, что вес является силой)
d л = расстояние от силы нагрузки до точки опоры (м, футы)
d e = расстояние от силы усилия до точки опоры (м, футы)
Усилие усилия можно рассчитать, изменив (1) на
F e = F l d l / d e
= ma г дл / де (1b)
, где
м = масса (кг, слизняки)
a г = ускорение свободного падения (9.81 м / с 2 , 32,17 фут / с 2 )
Калькулятор рычага
Этот калькулятор можно использовать для расчета силы усилия рычага. Его можно использовать как в метрических, так и в имперских единицах, если использование единиц соответствует.
Пример — импровизированный автомобильный лифт
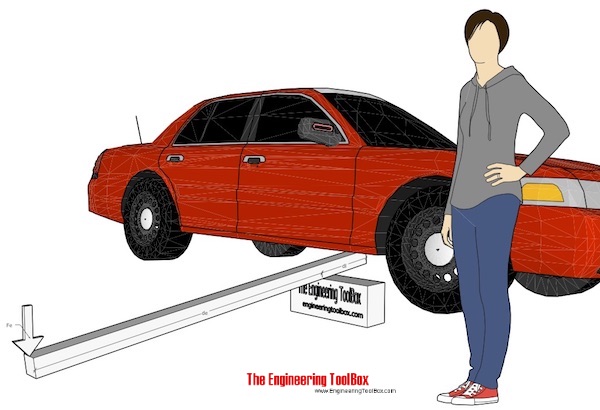
Импровизированный автомобильный лифт может быть изготовлен из пиломатериала, как показано на рисунке выше. С расстоянием нагрузки на точку опоры 0,2 м , силой усилия на расстояние до точки опоры 2 м и нагрузкой на рычаг — вдвое меньше веса автомобиля 2000 кг — сила усилия может быть рассчитана
F e = (0.5 2000 кг) (9,81 м / с 2 ) (0,2 м) / (2 м)
= 981 N
≈ 100 кг
Приказы о рычагах
Рычаги первого порядка
- точка опоры расположена между усилием и нагрузкой
- усилие меньше, чем нагрузка
- усилие перемещается дальше, чем нагрузка
- рычаг можно рассматривать как увеличитель силы
Рычаги второго порядка
- усилие и нагрузка расположены на одной и той же стороне опоры, но прикладываются в противоположных направлениях
- нагрузка лежит между усилием и опорой
- усилие меньше, чем нагрузка
- усилие движется дальше, чем нагрузка
- рычаг можно рассматривать как увеличитель силы
Рычаги третьего порядка
- усилие лежит между грузом и опорой
- усилие больше, т При нагрузке
- нагрузка перемещается дальше, чем усилие
- Рычаг может рассматриваться как увеличитель расстояния
Пример — Рычаг первого класса (Заказ) — Усилие (вес) 1 фунт действует на конец рычага на расстоянии 1 фут от точки опоры
Усилие усилия на расстоянии 2 фута от точки опоры можно рассчитать как
F e = (1 фунт) (1 фут) / (2 фута)
= 0.5 (фунт)
Формула (1) может быть изменена, чтобы выразить требуемую нагрузку, если вы знаете усилие, или требуемое расстояние от точки опоры, если известны нагрузка и усилия усилия и так далее.
Уровень выше, где точка опоры, расположенная между нагрузкой и усилием усилия, часто характеризуется как первоклассный механизм уровня .
Уровень, на котором нагрузка и сила усилия расположены на одной и той же точке опоры, часто характеризуется как механизм уровня второго класса .
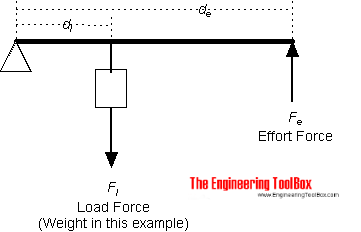
Пример — Рычаг второго класса (Заказ)
Усилие (вес) в 1 фунт действует на расстоянии 1 фут от точки опоры.
Усилие усилия на расстоянии 2 фута от точки опоры можно рассчитать как
F e = (1 фунт) (1 (фут) / (2 фута)
= 0,5 ( lb)
Пример — расчет рычага с единицами СИ — вес 1 кг масса, действующая 1 м от точки опоры
Усилие усилия на расстоянии 2 м от точки опоры можно рассчитать как
F e = (1 кг) (9.81 м / с 2 ) (1 м) / (2 м)
= 4,9 N
Рычажный механизм, в котором входное усилие выше, чем выходная нагрузка, часто характеризуется как третье- рычажный механизм класса
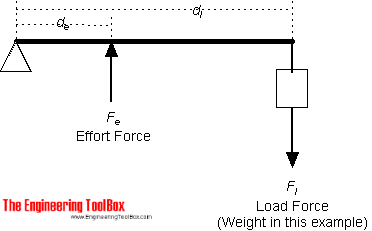
Пример — Рычаг третьего класса (Заказ)
Сила (вес) в 1 фунт действует на расстоянии 2 фута от точки опоры.
Усилие усилия на расстоянии 1 фут от точки опоры можно рассчитать как
F e = F l d l / d e
= ( 1 фунт) (2 фута) / (1 фут)
= 2 (фунт)
Одна или несколько сил, действующих на рычаг
Рычаг с двумя действующими усилиями нагрузки и одной силой усилия указан на рисунок ниже:
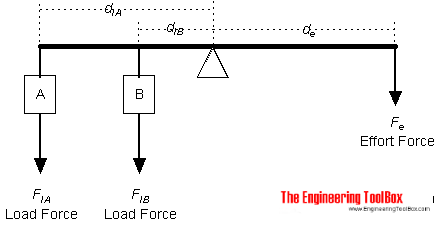
Общее уравнение для одной силы усилия с одной или несколькими действующими нагрузками может быть выражено как
F e = (F lA d lA + F фунтов d фунтов + ., + F lN d lN ) / d e (2)
Это уравнение изменено для трех действующих нагрузок ниже.
Пример — Рычаг с тремя действующими нагрузками и одной силой усилия
Вес А 1 фунт прилагается на расстоянии 1 фут от точки опоры. Вес B 2 фунта оказывается на расстоянии 2 фута от точки опоры, а вес C 3 фунта действует на расстоянии 3 фута от точки опоры.
Усилие на расстоянии 2 фута от точки опоры можно рассчитать как
.F e = (F lA d lA + F lB d lB + F l C d lC ) / d e
= ((1 фунт) (1 фут) + (2 фунта) (2 фута) + (3 фунта) (3 фута) ) / (2 фута)
= 7 (фунт)
Что такое момент?
Что такое момент?
Что такое момент?
Момент силы мера его склонности заставлять тело вращаться вокруг определенной точка или ось. Это отличается от тенденции тела двигаться или перевести, в направлении силы. Для того, чтобы на мгновение развиваться, сила должна воздействовать на тело таким образом, чтобы тело начало крутить Это происходит каждый раз, когда применяется сила, чтобы она не пройти через центр тяжести тела.Момент из-за силы, не имеющей равная и противоположная сила непосредственно вдоль линии его действия.
Представьте, что два человека толкают дверь у дверной ручки с противоположных сторон.
Если оба они толкают с равной силой, то есть состояние
равновесие. Если один из них внезапно отпрыгнет от двери,
толчок другого человека больше не будет иметь никакого сопротивления и дверь
будет качаться прочь Человек, который все еще толкал дверь, создал
момент.
Элементы Момента
Величина момента силы, действующей вокруг точки или оси, равна
прямо пропорционально расстоянию силы от точки или оси.Он определяется как произведение силы (F) и момента (d). моментного рычага или рычажного рычага представляет собой перпендикулярное расстояние между
линия действия силы и центр моментов.
Момент = Сила х Расстояние или М = (F) (d)
Центр Моментов может быть фактической точкой, о которой сила вызывает вращение. Это также может быть опорная точка или ось, относительно которой сила может рассматриваться как вызывающая вращение.Это не имеет значения, как долго в качестве конкретной точки всегда принимается в качестве контрольной точки. Последний случай Гораздо более распространенная ситуация в задачах структурного проектирования.
Момент выражается в единицах фут-фунтов, кип-футов,
Ньютон-метры или килоньютон-метры. Момент также имеет смысл; По часовой стрелке
вращение вокруг центра моментов будет считаться положительным моментом;
в то время как вращение против часовой стрелки относительно центра моментов будет рассмотрено
отрицательный. Самый распространенный способ выразить момент — это
Пример показывает, как гаечный ключ прикладывается к гайке.100 фунтов силы применяется к нему в точке С, центр гайки. Сила применяется при х-расстояние 12 дюймов от гайки. Центр моментов может быть точка C, но также может быть точки A или B или D.
Момент около C
Моментное плечо для расчета момента вокруг точки C составляет 12 дюймов.
величина момента около точки C равна 12 дюймам, умноженным на силу
100 фунтов, чтобы дать общий момент 1200 дюймов-фунтов (или 100 фунтов-фунтов).
моментный рычаг (d) = 12 дюймов
Величина (F) = 100 фунтов
Момент = M = 100 фунтов х 12 дюймов= 1200 фунтов-фунтов
Точно так же мы можем найти моменты о любой точке пространства.
| Момент @ | A | B | D |
| Рука Момента | 8 дюймов | 2 дюйма | 0 дюймов |
| Величина F | 100 фунтов | 100 фунтов | 100 фунтов |
| Общий момент | 800 фунтов | 200 фунтов | 0 фунтов |
Момент вызывает вращение вокруг точки или оси.Если момент для принять за точку из-за силы F, то для того, чтобы на мгновение развиваться, линия действия не может пройти через эту точку. Если линия действий проходит через эту точку, момент равен нулю, потому что величина момент рука ноль. Так было в случае точки D в предыдущем гаечном ключе poblem. Общий момент был равен нулю, потому что момент рука тоже был равен нулю.
В качестве другого примера, давайте предположим, что сила 200 фунтов применяется к
гаечный ключ, как указано.Момент силы 200 фунтов, приложенной к С, равен нулю.
потому что:
M = F x d = 200 фунтов x 0 in = 0 дюймов-фунтов
Другими словами, нет никакого 200-фунтового усилия, чтобы вызвать гаечный ключ для вращения гайки. Можно увеличить величину силы пока болт наконец не сломался (отказ сдвига).
Момент о точках X, Y и Z также будет нулевым, потому что они также
лежать на линии действий.
Момент можно также считать результатом отклонения сил от
прямая линия, проведенная между точкой загрузки системы и ее опорами.В этом случае синяя сила является эксцентрической силой. Для того, чтобы достичь
Основание колонны, оно должно сделать объезд через луч. Чем больше
объезд, тем больше момент. Самые эффективные структурные системы
иметь как можно меньше объездов. Это будет обсуждаться в более
подробно в лекции 37 и
последующие курсы.
Есть случаи, когда легче вычислить моменты Компоненты силы вокруг определенной точки, чем для расчета момент самой силы.Возможно, что определение перпендикулярного Расстояние силы сложнее, чем определить перпендикуляр расстояние составляющих силы. Момент нескольких сил о точка — это просто алгебраическая сумма составляющих их моментов та же точка. При добавлении моментов составных частей нужно стараться быть последовательным с чувством каждого момента. Это часто разумно отметить смысл рядом с моментом, когда предпринимаются такие проблемы.
Комбинированный
Моменты
Моменты
на Луч
Распространенные ошибки
При добавлении моментов компонентов, нужно быть очень осторожным, чтобы быть последовательным со смыслом каждого момента.Часто целесообразно отметить смысл следующего до момента, когда предпринимаются такие проблемы.
Часто задаваемые вопросы
Любая трудность с вычислением момента обычно может быть связана с одним из
следующее:
- Центр моментов не был установлен правильно или четко понят.
- Предполагаемый момент плеча не является ПЕРПЕНДИКУЛЯРНЫМ расстоянием между линия действия силы и центр моментов.
- Направление или смысл вращения был проигнорирован или неправильно понят.
Вопросы для размышления
Что такое момент о точке B и о точке D для обоих случаев
показано на примере гаечного ключа выше? Как можно добавить расширение к
конец гаечного ключа поможет повернуть ржавый болт? Какие структурные системы
будет иметь наименьшее количество «объездов»?
Задачи
Связанные чтения
Shaeffer, R.E. Элементарные структуры для архитекторов и строителей. С. 33-39.
Copyright © 1995, 1996 Chris H. Luebkeman and Дональд Петинг
Copyright © 1996, 1997, 1998 Chris H. Luebkeman ,
Сил Штанги: Рычаги, Моменты и Крутящий Момент
Джордан Фейгенбаум MS, CSCS, HFS, USAW Клубный тренер
DFM Директор по силе и кондиционированию
Ну, может, нет, пока ты не стошнишь … Я не хочу этого видеть.Эта статья посвящена силе и ее отношению к телу во время приседа. Хотя вы можете и не задумываться о том, какие силы происходят, когда вы садитесь на корточки (или должны сидеть на корточках), понимание того, как сила воздействует на ваши суставы, а также как максимизировать вашу эффективность в качестве атлета, является частью повышения вашего мастерства в железная игра.К концу этой статьи вам будет удобно обсуждать векторы, рычаги, моментные рычаги и крутящий момент при применении приседания. Это должно радовать ваших друзей по физической терапии и хиропрактики, если они скажут, что приседания вредны для вашего _________.
Моментальный рычаг — это горизонтальное расстояние между тем, где груз воздействует на кинетическую цепь (плечи в приседе или руки под лопаткой в становой тяге) до точки вращения, сустава, также известного как точка опоры в физике.Силы, действующие на штангу и тело во время тренировки со штангой, включают сжатие, растяжение, момент силы (или крутящий момент) и, возможно, импульс. Например, в приседе нагрузка ложится на плечи, что вызывает сжатие всех скелетных компонентов атлета, поскольку сила тяжести воздействует на штангу вертикально вниз. Кроме того, мышцы атлета создают напряжение, когда вес прошел из стойки, чтобы держать скелет более или менее в вертикальном положении.Недостаток напряжения, достаточного для мышц спортсмена, приведет к быстрому падению на пол спортсмена и штангу в случае приседания. Последняя сила, которую нужно обсудить, — это сила момента. Сила, создаваемая гравитацией на штанге, является векторной силой с величиной и направлением. В случае приседания этот вектор указывает прямо вниз. Каждый раз, когда существует горизонтальное расстояние между этим вертикальным вектором и точкой вращения или соединения, создается моментный рычаг.Импульс может также присутствовать во время тренировки со штангой, если она движется очень быстро. Атлет, который слишком быстро падает в нижнюю часть приседания, фактически добавляет усилие к верхней части груза штанги, и это может привести к пропуску подъема из-за увеличения эффективной нагрузки, которую атлет пытается поднять.
[youtube = http: //www.youtube.com/watch? V = XRcc2oo3Ymk]
В полностью вертикальном положении приседа (сверху) силы момента минимальны, если таковые имеются, поскольку нет горизонтального расстояния между нагрузкой и возможными точками вращения в спине, бедрах и коленях (точки опоры) ,В этом вертикальном положении штанга идеально сбалансирована относительно середины стопы спортсмена, что исключает возможность присутствия в любой момент рук, пока атлет полностью находится в вертикальном положении и скелетные компоненты выровнены. Кроме того, отсутствие моментных рычагов приводит к отсутствию крутящего момента на этих соединениях. Всякий раз, когда между этими суставами и вектором штанги создается горизонтальное расстояние, рычаги приводят как к позвоночнику / спине, так и к бедренным сегментам.
После начала приседания, когда бедра и колени входят в сгибание, в последующем развиваются рычаги, моментальные руки и силы вдоль спины / позвоночника и бедра.Теперь мы обсудим три соответствующих рычага, моментные руки и моментные силы, которые развиваются во время спуска (эксцентричная часть) приседа.
Вертикальная линия, висящая отвесом от штанги, создает моментальные руки между всеми суставами в кинетической цепи, прежде всего между поясницей и бедрами, бедрами и проксимальным отделом бедра, а также дистальным бедром и коленным суставом.Рычаг спины / позвоночника — это расстояние от места переноса штанги (возможно, в нижнем положении — ниже позвоночника лопатки) до точки вращения, в которой поясничные позвонки сочленяются с крестцом и друг с другом.Теперь есть горизонтальное расстояние между вектором штанги и поясничным отделом позвоночника, что дает мгновенную руку. Плечо момента определяется как это горизонтальное расстояние, а рычаг — это фактический позвоночный столб, который находится между нагрузкой и бедрами. Сила, действующая на моментное плечо, является моментной силой, которая представляет собой крутящий момент, эквивалентный весу штанги, умноженному на моментный рычаг (горизонтальное расстояние). В правильно выполненном низком приседе с откидной спинкой туловище спортсмена сместится к горизонтали, в какой степени определяется антропометрией спортсмена, и этот рычаг должен оставаться жестким, чтобы сила не рассеивалась через разблокированный позвоночник.Вот почему изометрическая функция эректоров так важна в приседе. Эти мышцы должны зафиксировать позвоночник в его нормальном анатомическом положении, которое является нейтральным лордозом в поясничной области и грудным отростком , , и удерживать его там, чтобы предотвратить рассеивание силы, которая будет создаваться атлетом. Убедившись в том, что этот рычаг является жестким, мы можем быть уверены, что сила, которую атлет прикладывает к штанге, будет эффективно передаваться вдоль этого сегмента к нагрузке для ее подъема вверх во время концентрической части приседа.
Расположение планки определяет углы остальной части сегмента тела. Приседание спереди требует, чтобы колени двигались дальше вперед (больше моментальной руки и крутящего момента на коленях), в то время как приседание назад с низкой штангой требует большего горизонтального угла спины (больше моментальной руки и крутящего момента на бедрах).По мере того, как спуск продолжается вниз к низу приседания, длина рычага, а затем моментная рука увеличивается, когда центр штанги перемещается дальше от точки опоры поясничных позвонков, крестца и бедер.Это происходит, когда во время приседа штанга должна оставаться сбалансированной относительно середины ноги спортсмена. В случае, если штанга отклоняется вперед или назад от этой средней ступни, возникает другая мгновенная рука между средней ногой спортсмена и вектором штанги. Это, скорее всего, приведет к тому, что неудачный представитель упадет вперед или назад или снизит уровень эффективности в системе для приложения силы к штанге со стороны спортсмена. Во время концентрического сокращения мышц, ответственных за разгибание бедра и колена, прикладывают усилие вверх к нижнему концу спинного рычага.Поскольку длина рычага максимально увеличена относительно положения стержня над серединой стопы, эта сила увеличивается и эффективнее, чем та же сила, действующая на более короткий рычаг.
Эд Коан приседает 961 как 220-фунтовый атлет, конечно, низкий бар…Следующий интересующий нас рычаг — это проксимальный отдел бедра. Во время опускания приседа вектор штанги пересекает бедро где-то вдоль его диафиза и, таким образом, создает рычаг от точки, в которой он пересекает бедро, до места, где бедро сочленяется в вертлужной впадине бедра.Результирующий момент плеча — это горизонтальное расстояние от точки, в которой вектор штанги пересекает бедренную кость, до вертикальной линии, продолжающейся вниз от середины тазобедренного сустава. Тогда момент силы или крутящий момент — это вес штанги, умноженный на длину (расстояние) рычага момента. Важно отметить, что в приседе с низкой штангой проксимальный бедренный рычаг больше на расстоянии относительно дистального бедренного рычага. Это передает больший процент нагрузки на бедра, а не на колени.В переднем приседе, который имеет более короткий проксимальный бедренный сегмент и более длинный дистальный бедренный сегмент, большая часть нагрузки передается на коленный сустав, когда рычаг, моментальный рычаг и результирующий крутящий момент больше.
Клоков тоже не сутулый, несмотря на слабые рычаги приседания на передних сиденьях. Здесь он восстанавливается после 234 кг (514,8 фунтов) чистой.Опять же, во время спуска на корточках вектор штанги должен оставаться в равновесии с серединой ноги спортсмена. Чтобы максимизировать нагрузку на мышцы, действующие на границу бедра и бедра, длина этого сегмента должна увеличиваться во время эксцентрической фазы (вниз) приседания.В правильно выполненном низком приседе со спиной длина проксимального бедренного рычага увеличивается с увеличением расстояния между вектором штанги и центром сочленения бедра с увеличением бедра. Этот более длинный рычаг позволяет увеличить усилие, которое должно быть приложено к бедрам, благодаря этому увеличенному расстоянию. Как сказал Архимед: «Дайте мне место, чтобы я встал, и я буду двигать Землю рычагом». Опять же, крутящий момент является количественно произведением длины рычага и силы, действующей на него. Учитывая определенное усилие, более длинный рычаг увеличивает крутящий момент и, таким образом, позволяет перемещать более тяжелые грузы.
Чем больше длина рычага (чем дальше от точки опоры), тем больше усилие. Крутящий момент — это сила х расстояние от момента руки.Как обсуждалось ранее, третий важный рычаг — это дистальный отдел бедренной кости. От точки, в которой вектор штанги пересекает стержень бедренной кости до центра коленного сустава, указывается длина этого дистального бедренного рычага. Тогда моментное плечо — это горизонтальное расстояние между вектором штанги (прямо вниз) и центром коленного сустава.Наконец, сила момента или крутящий момент, действующий на этот сегмент, может быть рассчитана путем умножения длины плеча момента на нагрузку штанги.
Подобно другим обсуждаемым рычагам, длина рычага дистальной бедренной кости увеличивается во время спуска приседания, при условии, что во время приседания выполняется правильная форма. Во время спуска коленный сустав движется немного вперед по линии ступней к точке, которая определяется антропометрией спортсмена. По мере того как атлет опускается в нижнюю часть приседания, горизонтальное расстояние между вектором штанги и центром коленного сустава увеличивается, что делает этот более длинный рычаг доступным.Внизу приседания мышцы четырехглавой мышцы действуют, чтобы создать силу для разгибания колена, и этот немного более длинный рычаг способствует увеличению силы так же, как обсуждалось ранее.
Во время подъема на корточки три вышеупомянутые длины рычага начинают уменьшаться, поскольку спина становится более вертикальной от разгибания бедра, угол бедра увеличивается из-за разгибания бедра, и угол колена также увеличивается из-за разгибания колена. Несмотря на уменьшенную длину рычагов и, следовательно, меньший крутящий момент, приложенный к суставам, мышцы теперь имеют лучшую длину для максимальной сократимости из-за соотношения силы и длины мышц и повышенной распространенности сшивания актин-миозина это может произойти на этих конкретных длинах.Кроме того, импульс веса, перемещаемого вверх, помогает в успешном завершении повторения.
-thefitcoach
,

 – выигрыша в силе нет, но меняется направление её действия.
– выигрыша в силе нет, но меняется направление её действия. – выигрыш в силе в 2 раза.
– выигрыш в силе в 2 раза. .
.