Момент силы относительно оси
Момент силы относительно оси – это характеристика вращательного действия силы на тело, закрепленное на оси, т.е. алгебраический момент проекции этой силы на плоскость, перпендикулярную к оси, относительно точки пересечения оси с этой плоскостью (рисунок 2).
Момент силы относительно, например, оси Oz (рисунок 1), равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси (F’) относительно точки пересечения оси с плоскостью, т.е.
Mz(F) = MO(F’) = F’∙ h’. (1.9)
Момент силы относительно оси – скалярная величина.
Рисунок 1
Моменты силы относительно координатных осей можно получить, расписав векторное произведение
Величины, стоящие в скобках, представляют собой моменты силы F относительно соответствующих осей.
Рисунок 2
Наш короткий видеоурок про момент силы с примерами:
Другие видео
Правило знаков
Момент считается положительным, если проекция силы на плоскость, перпендикулярную к оси, стремится вращать тело вокруг положительного направления оси против движения часовой стрелки, и отрицательным, если она стремится вращать тело по движению часовой стрелки:
Mz(F) = MО(FП) = ± h FП,
где FП – вектор проекции силы F на плоскость П, перпендикулярную к оси Oz, точка O – точка пересечения оси Oz с плоскостью П, h — плечо силы.
Это значит, что момент считается положительным, если мы смотрим навстречу оси и видим проекцию силы, стремящуюся повернуть плоскость чертежа в направлении против хода часовой стрелки.
Момент силы относительно оси равен нулю, если линия действия силы пересекает ось, т.е. h=0 (например Mz(P)), или сила параллельна оси, т.е. ее проекция на плоскость равна нулю, например, Mz(Q).
Свойства момента силы относительно оси
Момент силы относительно оси обладает следующими свойствами:
- момент равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси;
- момент равен нулю, если линия действия силы пересекается с осью. В этом случае равно нулю плечо силы.
Другими словами, момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.
Примеры решения задач >
Связь момента силы относительно оси с векторным моментом силы относительно точки >
Пара сил >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
На нашем сайте можно бесплатно скачать:
— Рамки A4 для учебных работ
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Сохранить или поделиться с друзьями
Помощь с решением
ВЫБЕРИТЕ РАЗДЕЛ МЕХАНИКИ
- Техническая механика (техмех)
- Теоретическая механика (теормех)
- Сопротивление материалов (сопромат)
- Строительная механика (строймех)
- Теория механизмов и машин (ТММ)
- Детали машин и ОК (ДМ)
Момент силы относительно оси
Моментом силы относительно оси называется алгебраическая величина, равная произведению проекции этой силы на перпендикулярную к оси плоскость на кратчайшее расстояние от линии действия проекции до оси, т.е.
.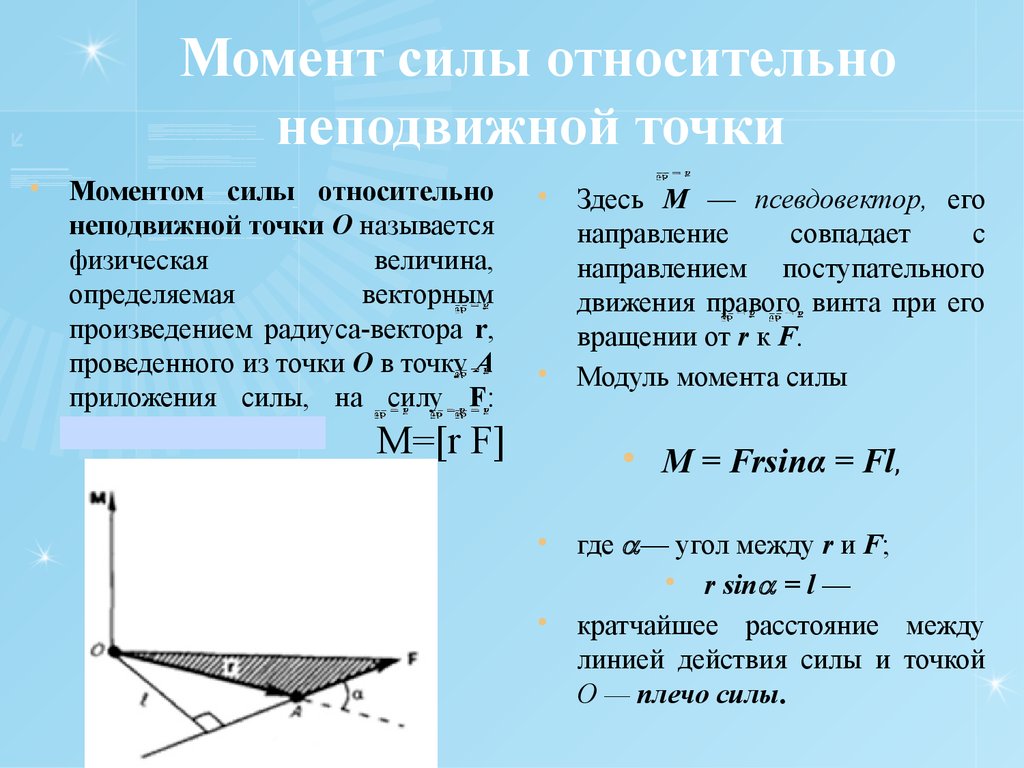 (2)
(2)
Знак «+» ставится тогда, когда сила стремится повернуть тело против часовой стрелки, «–» – когда – по часовой стрелке (смотреть на силу с положительного конца оси).
Таким образом, чтобы найти момент силы относительно оси, необходимо:
спроектировать силу на перпендикулярную к оси плоскость, т.е. найти ; т.е. определить кратчайшее расстояние от линии действия проекции силы до оси, и составить затем алгебраическое произведение. Из определения следует, что если сила параллельна оси или ее линия действия пересекает ось, то момент силы относительно оси равен нулю. |
Примечание. Иногда момент силы относительно оси
(точки) проще вычислить следующим
образом. Сначала силу раскладывают на
составляющие, а затем определяют моменты
каждой составляющей (теорема Вариньона).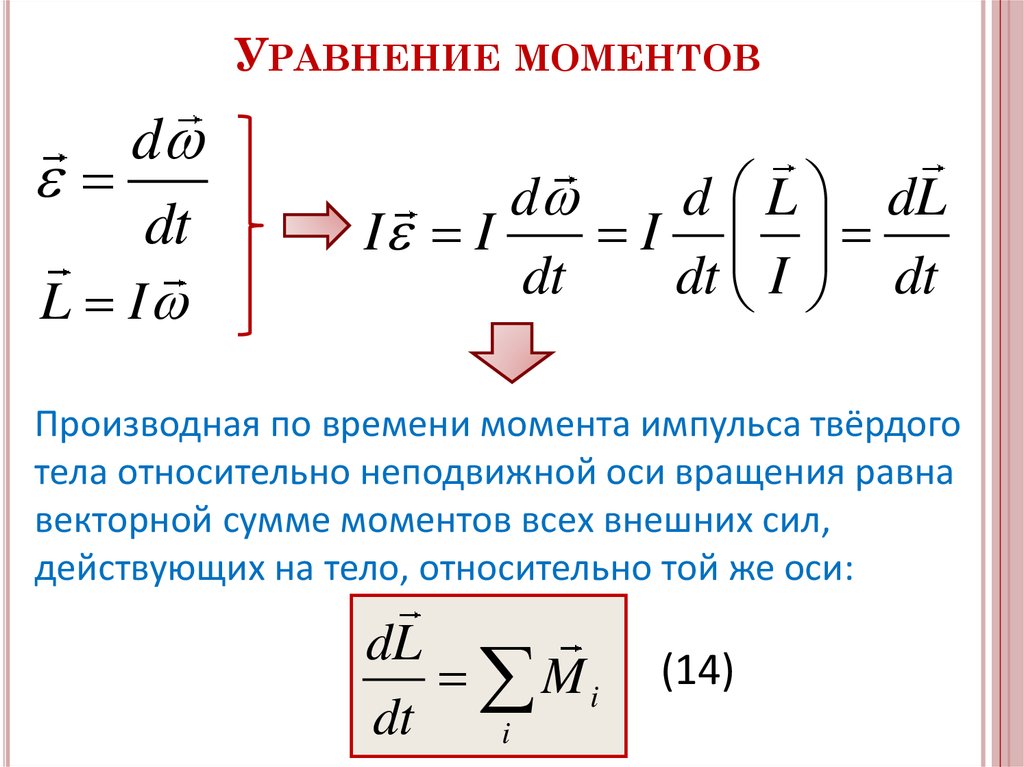
Момент силы относительно оси (точки)
. (3)
Все тела можно разделить на две группы свободные и несвободные.
Тело называют свободным, если оно может получать перемещение в любом направлении (свободно падающий камень).
Тело называют несвободным, если оно не может получать перемещения хотя бы в одном направлении (шарик на нити не может удалиться от точки подвеса).
Физические тела, ограничивающие свободу других тел, называют механическими связями, или просто связями.
Сила,
с которой связь действует на рассматриваемый
объект, называется
В
подавляющем большинстве тела являются
несвободными. Это значит, что связей
имеется бесчисленное множество. Однако
их можно объединить в группы (типы) по
различным признакам.
Однако
их можно объединить в группы (типы) по
различным признакам.
1. Гладкая поверхность. Связь ограничивает перемещение тела лишь в одном направлении. Ее реакция совпадает с нормалью к поверхности связи в точке касания (см. ). Если в точке касания к связи нельзя провести нормаль (край стены, острие), то реакцию направляют по нормали к поверхности касающегося тела (см.). |
2. Негладкая (шероховатая) поверхность. В этом случае кроме нормальной реакции имеется также составляющая в касательной плоскости (силы трения). |
3. Гибкая
связь (трос,
канат, ремень, цепь, нить). Такая связь
считается невесомой, нерастяжимой,
гибкой.
4. Невесомый стержень. Такой стержень является промежуточным звеном между телом и опорой. Он соединен с ними посредством шарниров без трения, и его реакция всегда направлена вдоль прямой, соединяющей шарниры (см. и). |
5. Шарнирные опоры. Различают три случая таких опор.
Тело
соединено цилиндрическим шарниром с
неподвижной опорой (шарнирно-неподвижная
опора).
Соединение позволяет телу поворачиваться
вокруг оси шарнира. Реакция в шарнире
перпендикулярна к его оси и при решении
задач раскладывается обычно на две
перпендикулярные составляющие. | ||
Тело соединено цилиндрическим шарниром с опорой, которая может перемещаться по другой опорной поверхности (шарнирно-подвижная опора). Если эта поверхность – гладкая, то реакция направлена по нормали к опорной поверхности. | ||
Тело соединено сферическим шарниром с неподвижной опорой. Соединение позволяет телу поворачиваться вокруг центра шарнира. Реакция в шарнире может иметь любое направление и при решении задач обычно раскладывается на три перпендикулярные составляющие.
а) | б) |
Жесткая
заделка. |
такой связи состоит из силы и пары. Силу раскладывают на две перпендикулярные составляющие, а пару сил прикладывают к защемленному концу, направляя ее по ходу или против хода стрелки часов (для плоской системы сил). Или на три перпендикулярные составляющие и на три пары сил вокруг трех перпендикулярных осей (для пространственной системы сил).
Скользящая
заделка. Связь
ограничивает линейное перемещение
тела в одном направлении и не позволяет
телу поворачиваться вокруг опоры. Ее
реакция раскладывается на силу
,
которая направлена по нормали к заделке
и на пару сил приложенных к телу с
моментом. | |
Двойная скользящая заделка. Связь препятствует повороту тела. Ее реакция представляет собой пару сил приложенных к телу с моментом . Следует помнить, что рассмотренные выше связи во многом идеализированы (гладкая поверхность, невесомые стержни, шарниры без трения и прочее). |
Кроме того, в инженерных или даже в учебных задачах по теоретической механике часто не оговариваются типы связей, действующие на тело. В этих условиях необходимо самому проанализировать свойства связей и отнести их к тому или иному типу.
Правильно определить типы связей и показать направление их реакций – третье необходимое условие умения решать задачи статики.
Полное введение в силы и моменты с примерами.
Опубликовано: 21 июня 2022 г.
|
Учебник
Добро пожаловать в серию руководств по фундаментальной инженерной механике. Это первая часть серии, состоящей из нескольких частей, предназначенной для всех, кто только начинает изучать инженерное дело; Студенты первого курса технических специальностей должны найти эту серию особенно полезной. Каждый пост основан на одной теме и будет содержать лекционное видео и несколько видеороликов с примерами работы, а также ссылки на существующие соответствующие ресурсы DegreeTutors. Вы можете получить доступ ко всем видео из этой серии (по мере публикации каждой новой части), а также к загружаемым версиям заметок, присоединившись к сопровождающему курсу ниже. В этом уроке мы сосредоточимся на силах, моменте силы и на том, как оценивать системы сил и моментов.
1.0 Силы, момент силы и силовые системы
Будучи инженерами, мы тратим много времени на анализ сил и их влияние на конструкции, которые мы проектируем. Поэтому на данном этапе было бы неплохо точно определить, что такое сила. Проще говоря, сила — это произведение массы и ускорения.
Поэтому на данном этапе было бы неплохо точно определить, что такое сила. Проще говоря, сила — это произведение массы и ускорения.
(1)
Здесь, на Земле, вся масса испытывает ускорение приблизительно
. Итак, масса испытывает гравитационную силу,
Единицы силы более условно выражаются в ньютонах (Н) в честь сэра Исаака Ньютона. Таким образом,
равно . Важно понимать различие между массой и силой, т.е. масса, опирающаяся на балку, воздействует на балку не силой, а силой. Точно так же вы можете весить , но вы прикладываете силу примерно .
1.1 Компоненты силы и равнодействующие Сила является векторной величиной. Это означает, что она имеет как величину, так и направление. Это в отличие от скейлерных величин, таких как масса, объем, высота и т. д., которые могут быть полностью описаны величиной. Поскольку сила является векторной величиной, к силам можно применить все обычные правила и методы анализа, связанные с векторами.
Все силы, которые мы будем обсуждать в этом уроке, занимают двумерную плоскость. Это означает, что они могут быть полностью описаны двумя ортогональными (под прямым углом друг к другу) компонентами x и y в двумерной системе координат. Это представляет собой сокращение от полного трехмерного евклидова пространства. Как только вы поймете основные концепции двухмерных силовых систем, расширение до трехмерных не составит труда.
Поскольку двумерные силы могут быть представлены в виде двумерных векторов, мы можем представить любую силу как комбинацию двух ортогональных компонентов. Точно так же любое количество сил может быть представлено как единая равнодействующая силы с определенной величиной и направлением. Большая часть того, что мы будем делать в оставшейся части этого урока, будет включать в себя:
- Разрушающие силы на их ортогональных составляющих
- объединение нескольких сил для определения их равнодействующей силы
Рассмотрим силу 100 Н, показанную ниже. Обратите внимание, что мы определили силу в пределах двумерной плоскости, определяемой осями x и y. Сила приложена к местоположению
Обратите внимание, что мы определили силу в пределах двумерной плоскости, определяемой осями x и y. Сила приложена к местоположению
. Он имеет звездную величину . Его направление можно указать, заявив, что сила составляет угол (против часовой стрелки) относительно положительной оси x.
Рис. 1. Вектор силы ориентирован под углом против часовой стрелки от положительной оси x и его ортогональные компоненты, и .Эта сила может быть разделена на 2 ортогональные составляющие, обозначенные выше как
и . Обратите внимание, что на самом деле это могут быть любые два ортогональных вектора силы. Для удобства мы выбрали две ортогональные компоненты, параллельные осям x и y. Для определения величин и можно использовать простую геометрию.
Мы можем вычислить числовые значения
и с помощью базового Python (или любого другого калькулятора, который вы предпочитаете).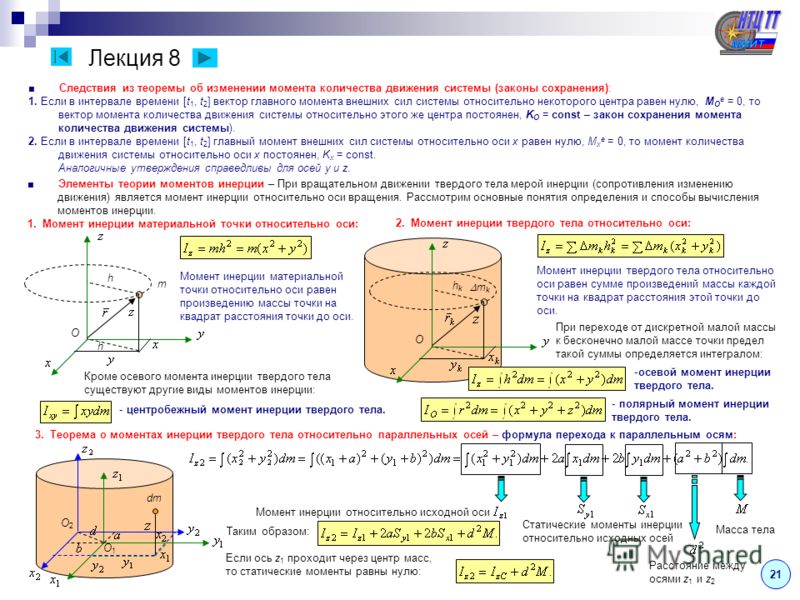
1 2 3 4 5 6 7 8 10 110005 12 13 14 |
# Определить константы F_mag = 100 # (Н) Величина силы theta_deg = 30 # (градус) Угловая сила действует с положительной осью x theta = theta_deg*math.pi/180 # (рад) Угловая сила действует с положительной осью X *math.sin(theta)
#Вывод на печать print(f»Fx is {round(Fx_100,1)} N в положительном направлении x (вправо)») print(f» Fy равно {round(Fy_100,1)} N в положительном направлении оси Y (вверх)»)
|
Fx составляет 86,6 Н в положительном направлении x (вправо)
Fy составляет 50,0 Н в положительном направлении y (вверх)
Таким же образом мы можем оценить комбинированное влияние нескольких сил, разбивая каждую на его ортогональные компоненты и рекомбинацию этих компонентов в единую результирующую силу. Рассмотрим две силы, показанные ниже. Сила
Рассмотрим две силы, показанные ниже. Сила
— это та же самая сила, оцененная выше. Теперь нам нужно определить компоненты силы.
Рис. 2. Два вектора силы, представленные на двухмерной плоскости x-y.1 2 3 4 5 6 7 8 10 110005 12 13 14 |
# Определить константы F_mag = 60 # (Н) Величина силы theta_deg = 40 # (градус) Угловая сила с отрицательной осью x theta = theta_deg*math.pi/180 # (rads) Угловая сила делает с отрицательной осью x
#Рассчитать величину ортогональных компонент Fx_60 = F_mag*math.cos(theta) Fy_60 = F_mag*math.sin(theta)
5 print is(0f) round(Fx_60,1)} N в отрицательном направлении x (влево)») print(f»Fy is {round(Fy_60,1)} N в положительном направлении y (вверх)»)
|
Fx составляет 46,0 Н в отрицательном направлении оси x (влево)
Fy составляет 38,6 Н в положительном направлении оси Y (вверх)
Суммарная горизонтальная сила получается как алгебраическая сумма горизонтальных составляющих
и сил.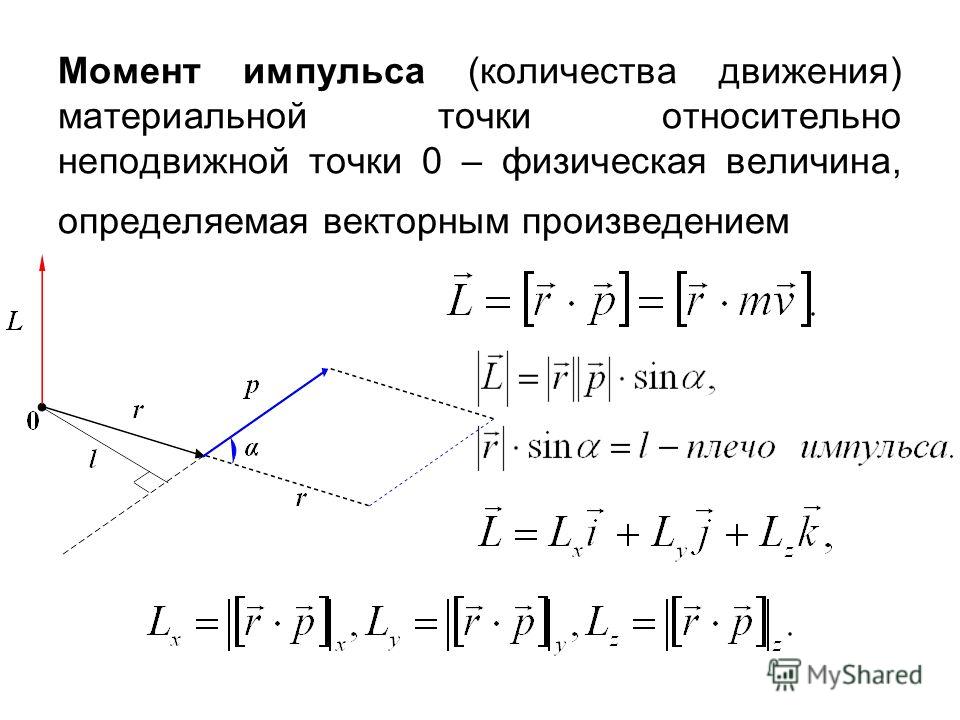 Отметив, что горизонтальная составляющая силы действует в направлении, противоположном горизонтальной составляющей силы, .
Отметив, что горизонтальная составляющая силы действует в направлении, противоположном горизонтальной составляющей силы, .
Fx_total = Fx_100 — Fx_60 print(f»Fx_total равно {round(Fx_total,1)} N»)
|
Fx_total равен 40,6 N
и представляют собой два ортогональных компонента силы, и как таковые они могут быть представлены одним вектором силы, величина и ориентация которого (измеренные относительно положительной оси x) теперь могут быть легко оценены.
(2)
(3)
Числовая оценка:
1 2 3 4 5 6 7 |
#величина mag = math.sqrt(Fx_total**2 + Fy_total**2) alpha = math.atan(Fy_total/Fx_total) alpha_deg = alpha*180/math.pi print(f»F_res a имеет величину {round(mag,1)} N и ориентация {round(ori_deg,1)} градусов относительно положительной оси x»)
|
F_res a имеет величину 97,4 Н и ориентацию 65,4 градуса относительно положительной оси x. результирующая сила в правой системе координат. Мы рассмотрим эту концепцию эквивалентных систем ниже. Две системы сил, показанные ниже, эквивалентны с точки зрения силы. Однако это еще не все. . Чтобы получить две полностью эквивалентные системы, нам необходимо также учитывать момент или крутящий момент каждой силы.
результирующая сила в правой системе координат. Мы рассмотрим эту концепцию эквивалентных систем ниже. Две системы сил, показанные ниже, эквивалентны с точки зрения силы. Однако это еще не все. . Чтобы получить две полностью эквивалентные системы, нам необходимо также учитывать момент или крутящий момент каждой силы.
2.0 Момент силы
Момент силы — это крутящий эффект или крутящий момент, который сила прикладывает или создает относительно точки . Более конкретно, момент силы равен произведению величины силы на плечо рычага расстояние. Плечо рычага — это перпендикулярное расстояние между линией действия силы и точкой, вокруг которой происходит вращение (или вычисляется крутящий момент).
Держите тяжелую коробку обеими руками на вытянутых руках; это требует гораздо больше усилий, чем если бы вы держали коробку близко к груди. Это связано с тем, что когда ваши руки вытянуты, сила, создаваемая тяжелым ящиком, создает больший момент относительно точки вращения (вашего плеча), чем когда вы держите ящик близко к груди.
Это связано с тем, что когда ваши руки вытянуты, сила, создаваемая тяжелым ящиком, создает больший момент относительно точки вращения (вашего плеча), чем когда вы держите ящик близко к груди.
Например, рассмотрим силу
, показанную на рис. 4 ниже, приложенную к точке на плоскости x-y с координатами . Сила образует угол с положительной осью x. Продолжив вектор силы, мы получим линию действия этой силы. Проецируя перпендикулярно линии действия к началу координат, мы получаем плечо рычага для силы относительно начала координат. Следовательно, эта сила создает крутящий момент или момент относительно начала координат.
Рис. 4. Сила, создающая крутящий момент или момент относительно начала координат.Мы можем интуитивно понять направление вращения по часовой стрелке. Другими словами, сила
будет стремиться вызвать вращение вокруг начала координат по часовой стрелке. Если у вас возникли проблемы с определением направления вращения, нарисуйте исходную точку и надавите на лист бумаги так, чтобы бумага удерживалась булавкой или иглой через исходную точку. Используйте свой палец, чтобы применить силу F, и вы увидите, что бумага имеет тенденцию вращаться по часовой стрелке вокруг булавки. Вам нужно будет сделать это только один или два раза, прежде чем вы сможете визуализировать чувство вращения, которое сила вызывает вокруг точки. Сила будет вращать бумагу либо по часовой стрелке, либо против часовой стрелки, и это будет зависеть от положения и ориентации силы относительно точки, относительно которой вычисляются моменты.
Если у вас возникли проблемы с определением направления вращения, нарисуйте исходную точку и надавите на лист бумаги так, чтобы бумага удерживалась булавкой или иглой через исходную точку. Используйте свой палец, чтобы применить силу F, и вы увидите, что бумага имеет тенденцию вращаться по часовой стрелке вокруг булавки. Вам нужно будет сделать это только один или два раза, прежде чем вы сможете визуализировать чувство вращения, которое сила вызывает вокруг точки. Сила будет вращать бумагу либо по часовой стрелке, либо против часовой стрелки, и это будет зависеть от положения и ориентации силы относительно точки, относительно которой вычисляются моменты.
Теперь, чтобы рассчитать момент, мы можем использовать умную геометрию, чтобы идентифицировать
. Однако есть более простой способ рассчитать момент, создаваемый . Мы можем просто рассмотреть момент, создаваемый его ортогональными компонентами. Горизонтальная и вертикальная составляющие и получаются как
1 2 3 4 5 6 |
F_x = 50*math. F_y = 50*math.sin(20*math.pi/180) print(f»Fx = {округление(F_x,1)} N») print(f»Fy = {округление(F_y, 1)} Н»)
|
Fx = 47,0 Н
Fy = 17,1 Н
Теперь мы можем игнорировать исходную силу
и работать только с ее ортогональными составляющими, и . Мы можем довольно легко увидеть, что имеет плечо рычага в то время как имеет плечо рычага (см. рис. 4). Мы также можем распознать, что это будет генерировать вращение по часовой стрелке, в то время как будет генерировать вращение против часовой стрелки (не забудьте использовать трюк с вращением бумаги, если вы этого не видите). Таким образом, мы можем оценить момент, создаваемый используя моменты о происхождении следующим образом,
(4)
1 2 3 4 5 6 |
la_fx = 6 # рычаг для горизонтальной составляющей силы Fx la_fy = 3 # рычаг для вертикальной составляющей силы Fy M = (F_x * la_fx) — (F_y * la_fy) print(f «M = {раунд(M,1)} Нм»)
|
М = 230,6 Н·м
Помните, что момент связан с вращением, в отличие от сил, связанных с линейным перемещением. Таким образом, мы определяем момент как наличие направления вращения по часовой стрелке или против часовой стрелки. Обратите внимание, что в приведенном выше уравнении мы неявно предположили, что моменты по часовой стрелке положительны, а против часовой стрелки отрицательны. Следовательно, тот факт, что момент оценивается как положительное число, указывает на то, что результирующий момент
Таким образом, мы определяем момент как наличие направления вращения по часовой стрелке или против часовой стрелки. Обратите внимание, что в приведенном выше уравнении мы неявно предположили, что моменты по часовой стрелке положительны, а против часовой стрелки отрицательны. Следовательно, тот факт, что момент оценивается как положительное число, указывает на то, что результирующий момент
имеет направление вращения по часовой стрелке. Если бы получилось отрицательное число, мы бы знали, что согласно нашему соглашению о знаках, момент имеет вращение против часовой стрелки.
Следуя той же самой логике, мы можем оценить суммарный крутящий момент, создаваемый несколькими силами относительно точки, вычислив сумму моментов для каждой силы по очереди. Мы обсудим это ниже.
2.1 Пары силГоворят, что две силы образуют пару когда:
- они имеют одинаковую величину
- имеют параллельные линии действия
- действовать в противоположных направлениях
Например, предположим, что
и ниже имеют одинаковую величину, они образуют пару.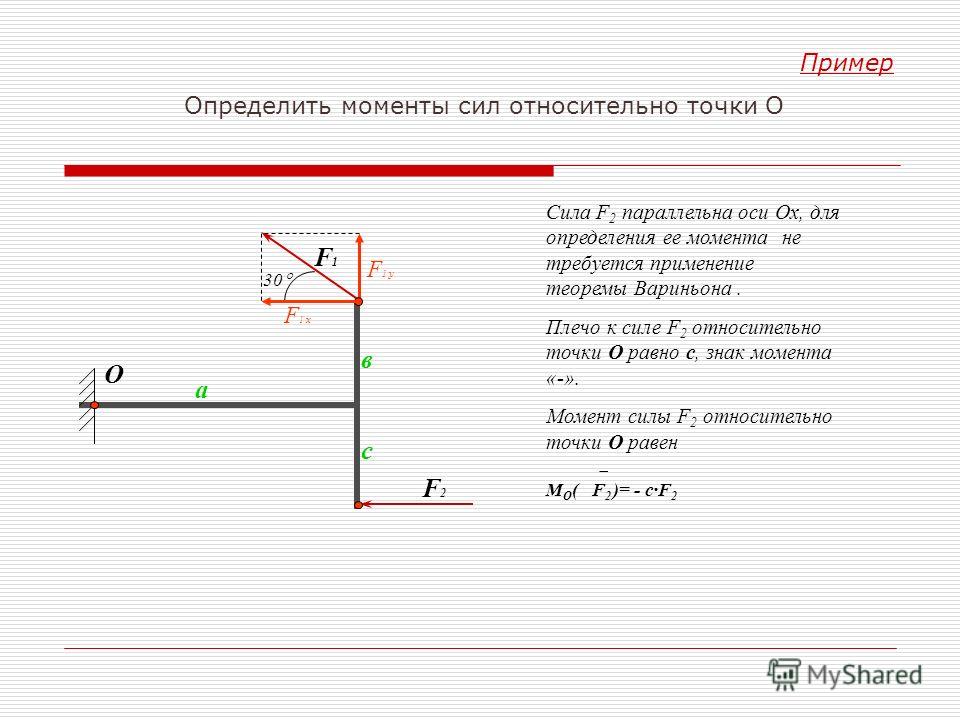
Пара сил создает момент, равный величине одной силы, умноженной на перпендикулярное расстояние между их линиями действия. Итак, пара, сгенерированная
и есть,
(5)
По направлениям стрелок видно, что изображенная пара создает момент по часовой стрелке. Если бы направления стрелок были изменены на противоположные, создаваемый момент был бы направлен против часовой стрелки. Если у вас возникли проблемы с визуализацией этого, представьте точку вращения на полпути вдоль красной пунктирной линии и спросите себя, как эти две силы заставят бумагу вращаться вокруг этой точки.
Пары сил часто встречаются в технике. Вы обнаружите, что регулярно оцениваете эффект момента силовых пар. Сейчас мы просто хотим определить концепцию.
3.0 Системы эквивалентных сил и моментов
До сих пор мы рассматривали векторные свойства сил (компоненты и равнодействующие). Мы также обсудили концепцию крутящего момента или моментов, создаваемых силой относительно определенной точки на плоскости. Теперь мы объединим эти идеи, чтобы оценить системы сил и моментов и определить их равнодействующие или эквивалентные системы.
Теперь мы объединим эти идеи, чтобы оценить системы сил и моментов и определить их равнодействующие или эквивалентные системы.
Две системы двумерных сил и моментов,
и считаются эквивалентными, если выполняются три условия:
1. Сумма всех сил в направлении x одинакова в обеих системах
(6)
2. Сумма всех сил в направлении y одинакова в обеих системах
(7)
Обратите внимание, что выбор направлений x и y является произвольным. Можно оценить равенство сил вдоль любых двух ортогональных направлений. Направления x и y обычно выбираются для удобства, поскольку они также являются направлениями осей системы.
3. Сумма моментов, создаваемых всеми силами и моментами в системе А, равна сумме моментов, создаваемых всеми силами и моментами в системе В
(8)
Практическая ценность идентификации эквивалентных систем что это позволяет нам представлять несколько сил одной равнодействующей силой, которая создает одно и то же воздействие силы и момента.
Снова рассмотрим систему сил, которую мы обсуждали ранее,
Рис. 6. Двухмерная система сил A.В дополнение к оценке равнодействующей силы (завершено выше), теперь нам нужно определить результирующий момент. Оценивая сумму моментов относительно начала координат (снова предполагая, что моменты по часовой стрелке положительны),
(9)
M = 86,6*2 — 50*2 — 46*8 — 38,6*10 print(f»Результирующий момент относительно начала координат равен {round(M,1)} Нм»)
|
Результирующий момент относительно начала координат составляет -680,8 Нм
Знак минус здесь указывает, что результирующий момент направлен против часовой стрелки в соответствии с нашим соглашением о знаках. Поэтому, обращаясь к диаграмме ниже, мы можем сказать, что система сил в системе A эквивалентна одиночной силе и моменту в системе B. Другими словами, система A имеет точно такое же действие силы и момента, что и система B.
Это в значительной степени охватывает теорию по данной теме. На этом этапе вы должны попытаться проработать приведенные ниже примеры вопросов. В каждом случае попробуйте сначала решить вопрос самостоятельно, прежде чем смотреть видео с отработанным решением.
Пример
Замените силы и моменты, показанные в системе А, эквивалентной системой, состоящей из одной силы (в начале координат) и момента (относительно начала координат).
(Подсказка: моменты не учитываются в уравнении суммирования сил, но они учитывают в уравнении суммирования моментов.)
Рис. 8. Пример 1 системы сил. РешениеВидеорешение этого вопроса показано в конце основного видео-лекции вверху этого поста.
Кодированный раствор1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# Расчет модулей горизонтальной и вертикальной составляющих силы #(направление пока не учитывается, только величина) F_Ax = 100 F_Ay = 0 F_Bx = 0 F_By = 90 F_Cx = 40*math*0math. F_Cy = 40*math.sin(45*math.pi/180) F_Dx = 50*math.cos(35*math.pi/180) F_Dy = 50*math.sin(35*math. pi/180)
#Величина момента (без учета направления вращения) M_E = 150
#Возьмите моменты относительно начала координат (предположим, что моменты по часовой стрелке положительны) M_o = F_Ax*2 — F_By*9 + F_Cx*6 + F_Cy*5 + F_Dx*6 — F_Dy*1 + M_E print(f»Результирующий момент равен {round(M_o,1)} Нм»)
#Оценить сумму горизонтальных сил Fx = F_Ax + F_Cx + F_Dx print(f»Результирующая горизонтальная сила равна {round(Fx,1)} Н»)
#Оценить сумма вертикальных сил Fy = F_By — F_Cy + F_Dy print(f»Результирующая вертикальная сила {round(Fy,1)} Н»)
# Оценить результирующую величину F_res = math.sqrt(Fx**2 + Fy**2) print(f»Результирующая величина силы равна {round(F_res,1)} Н») #Оценить результирующую ориентацию alpha = math. print(f»Результирующая сила образует угол {round(alpha,1)} градусов с положительной ось x»)
|
Результирующий момент 68,2 Нм
Результирующая горизонтальная сила 169.2 Н
Результирующая вертикальная сила равна 90,4 Н
Результирующая сила составляет 191,9 Н
Результирующая сила образует угол 28,1 градуса с положительной осью абсцисс
Рабочий пример 1 и силы ниже, замените силы и моменты, показанные в системе А, эквивалентной системой, состоящей из одной силы.
(Подсказка: подумайте, где бы вы хотели разместить свою единственную силу в системе замещения.)
Рис. 9. Пример 2 силовой системы. Решение 1Рабочий пример 2
Со ссылкой на приведенную ниже систему моментов и сил определите величину силы , при которой результирующие момент и сила для системы равны нулю.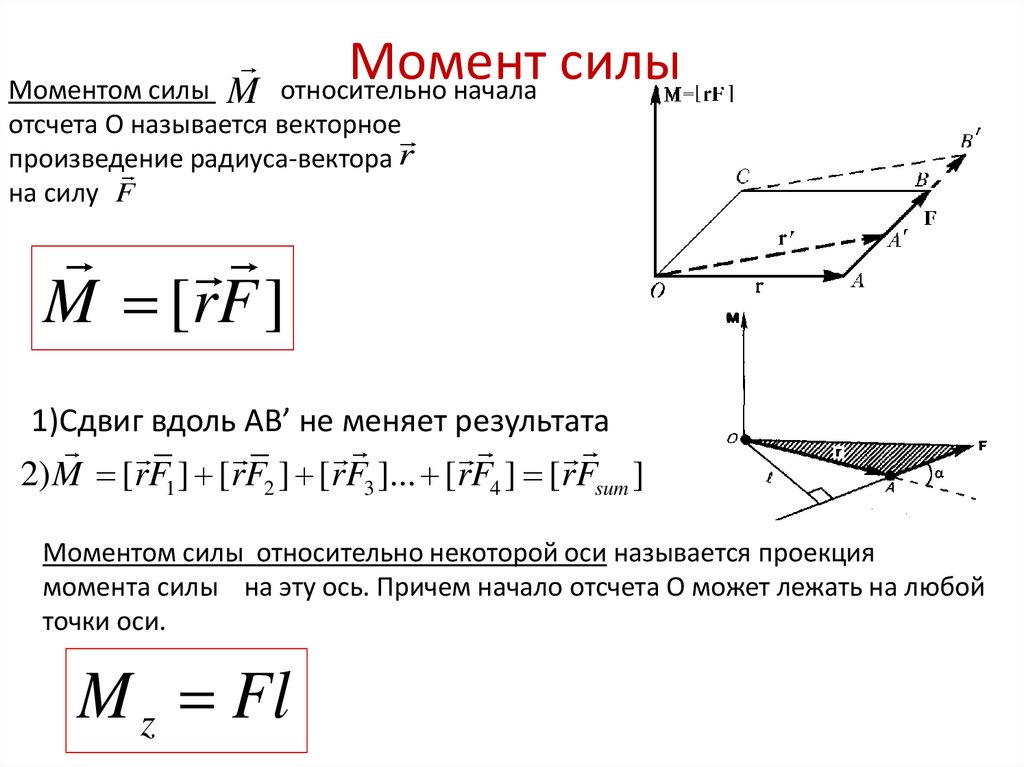
Рабочий пример 3
Со ссылкой на систему моментов и сил ниже; эта система должна быть заменена одной силой, расположенной вдоль вертикальной линии в точке . Определите местоположение, величину и ориентацию замещающей силы.
Рис. 11. Пример 4 силовой системы. Решение 3 Вот и все для этого урока. Теперь вы должны хорошо понимать, как оценивать системы сил и моментов. В следующем уроке этой серии мы применим то, что вы здесь узнали, и начнем анализировать устойчивость простых структур. Не забудьте присоединиться к курсу, который сопровождает эту серию руководств, чтобы получить доступ ко всем заметкам и видео в одном месте. Курс будет расширяться по мере публикации новых руководств из этой серии.
Теперь вы должны хорошо понимать, как оценивать системы сил и моментов. В следующем уроке этой серии мы применим то, что вы здесь узнали, и начнем анализировать устойчивость простых структур. Не забудьте присоединиться к курсу, который сопровождает эту серию руководств, чтобы получить доступ ко всем заметкам и видео в одном месте. Курс будет расширяться по мере публикации новых руководств из этой серии.
Линкедин Твиттер YouTube
Автор
Доктор Шон Кэрролл
Бакалавр искусств (с отличием), MSc, PhD, CEng MIEI, FHEA
Привет, я Шон, основатель DegreeTutors.com. Я надеюсь, что вы нашли этот урок полезным. Проведя 10 лет в качестве преподавателя в университете по проектированию конструкций, я запустила DegreeTutors.com, чтобы помочь большему количеству людей понять инженерию и получить такое же удовольствие от ее изучения, как и я. Не стесняйтесь связаться или подписаться на DegreeTutors в любой из социальных сетей.
Если вам нужен полный доступ ко всей библиотеке курсов DegreeTutors (и коду!) за небольшую годовую плату, рассмотрите возможность подписки на Полный доступ к DegreeTutors . Вы можете прочитать больше о преимуществах членства здесь или просмотреть заголовки и подписаться непосредственно ниже. Если вы учитесь в колледже или университете, станьте участником программы DegreeTutors, чтобы совершенно бесплатно получить доступ к ряду премиальных курсов.
Вы можете прочитать больше о преимуществах членства здесь или просмотреть заголовки и подписаться непосредственно ниже. Если вы учитесь в колледже или университете, станьте участником программы DegreeTutors, чтобы совершенно бесплатно получить доступ к ряду премиальных курсов.
Доступ ко всем курсам и инструментам
$ 279 / Год
(меньше кофе в неделю ☕ ☕)
Гарантия цен — избегайте будущего повышения цен, когда мы выращиваем
. Среди 740 лекций и более 140 часов видео контента
740. Неограниченный доступ к инструментам онлайн-анализа. 🛠️
Упакованный план разработки курсов и инструментов 🏗️
Доступ к хабу участника DegreeTutors:Labs 🧪
Неограниченная потоковая передача всех текущих и будущих курсов
Ранний доступ к новым курсам
Доступ ко всем загрузкам, руководствам в формате pdf и кодам Python
Сертификаты об окончании курса
Приоритетная поддержка вопросов и ответов
Подпишитесь на обновления учебников и курсов
© 2022 DegreeTutors & Mind Map Media Ltd. Все права защищены
Все права защищены
векторов — Момент силы относительно данной оси
спросил
Изменено 5 лет, 11 месяцев назад
Просмотрено 2к раз
$\begingroup$
На уроке я научился находить момент силы F относительно точки A по формуле
М = г × Ж
где r — вектор, направленный из точки А в исходную точку F
Задача из учебника требует, чтобы я нашел момент силы относительно оси. Я просмотрел https://en.wikipedia.org/wiki/Bending_moment#Computing_the_moment_of_force и нашел другую формулу:
М = e · ( r × F )
Правда, теперь я не могу понять, что r брать в этой формуле.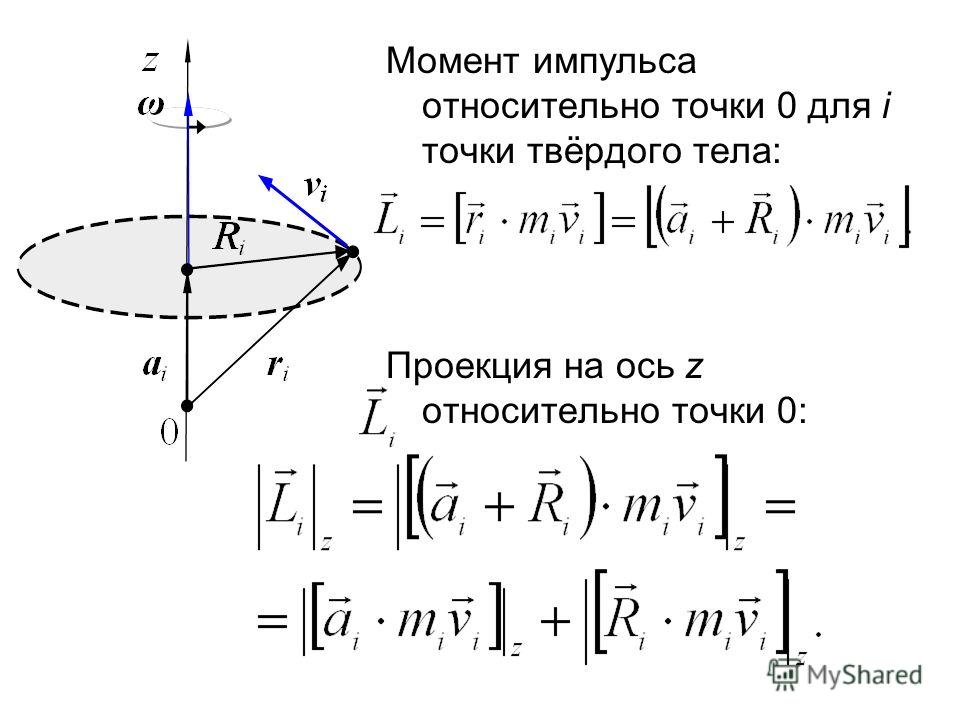



 Если тело со связью соединено жестко
(не допускаются никакие перемещения),
то такое соединение называют жесткой
заделкой, или защемлением (конец балки в кирпичной или бетонной
кладке, конец столба в земле). Реакция
Если тело со связью соединено жестко
(не допускаются никакие перемещения),
то такое соединение называют жесткой
заделкой, или защемлением (конец балки в кирпичной или бетонной
кладке, конец столба в земле). Реакция
 cos(20*math.pi/180)
cos(20*math.pi/180) cos.
cos. atan(Fy/Fx)*180/math.pi
atan(Fy/Fx)*180/math.pi