Определение момента силы относительно неподвижной оси вращения.
Моментом силы относительно неподвижной
оси z называется скалярная величина Mz,
равная проекции на эту ось вектора 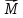 момента силы, определенного относительно
произвольной точки О данной оси z.
Значение момента Мz не зависит от выбора
положения точки О на оси z. Если ось z
совпадает с направлением вектора М, то
момент силы представляется в виде
вектора, совпадающего с осью:
момента силы, определенного относительно
произвольной точки О данной оси z.
Значение момента Мz не зависит от выбора
положения точки О на оси z. Если ось z
совпадает с направлением вектора М, то
момент силы представляется в виде
вектора, совпадающего с осью: 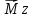 =[
=[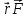 ]z.
]z.
Определение момента силы относительно точки.
Моментом силы относительно неподвижной
точки О называется физическая величина
М, определяемая векторным произведением
радиус-вектора r, проведенного из точки
О в точку приложения силы, на силу F: 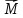
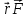 ],
где
],
где 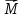 – псевдовектор, его направление совпадает
с направлением поступательного движения
правого винта при его вращении от
– псевдовектор, его направление совпадает
с направлением поступательного движения
правого винта при его вращении от 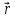 к
к 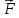 .
.Модуль момента силы M=Frsinα=Fl, где α – угол между r и F, а l – кратчайшее расстояние между точкой О и линией действия силы – плечо силы.
Выведите формулу момента инерции диска.
Диск – плоский однородный цилиндр
высотой h и радиусом R. Разобьем диск на
отдельные кольца бесконечно малой
толщины dr с внутренним радиусом r и
внешним r+dr. Момент инерции каждого
кольца dJ=r2dm, объем
кольца 2πrhdr. Если ρ –
плотность материала, то dm=2πrhρdr
и dJ=2πhρr3dr.
Тогда момент инерции всего диска J=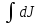 =
=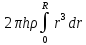 = 1/2πhρR4. Но масса
диска m=πhρR2, тогда
момент инерции диска J=1/2mR
= 1/2πhρR4. Но масса
диска m=πhρR2, тогда
момент инерции диска J=1/2mR
Формулировка теоремы Штейнера. Поясните величины, входящие в формулу Штейнера.
Момент инерции тела относительно произвольной оси (Jz) равен сумме момента инерции относительно параллельной оси, проходящей через центр масс тела (Jc) и произведения массы тела на квадрат расстояния между осями: Jz=Jc+md2
Jz – момент инерции относительно произвольной оси
Jc – момент инерции относительно оси, проходящей через центр масс
d – расстояние между осями
m – масса тела
Определение момента импульса материальной точки и твердого тела относительно неподвижной оси вращения.
Моментом импульса относительно
неподвижной оси z называется скалярная
величина Lz, равная проекции на эту ось
вектора момента импульса 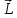
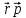 ]=[
]=[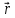 ,
m
,
m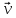 ],
определенного относительно произвольной
точки О данной оси. Момент импульса Lz
не зависит от положения точки О на оси
z.
],
определенного относительно произвольной
точки О данной оси. Момент импульса Lz
не зависит от положения точки О на оси
z. При вращении абсолютно твердого тела
вокруг неподвижной оси z каждая точка
тела движется по окружности постоянного
радиуса ri с некоторой
скоростью vi. Скорость
viи импульс
m
Момент импульса твердого тела относительно
оси есть сумма моментов импульса
отдельных частиц: Lz= 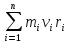 =
=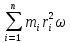 =ω
=ω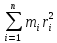 =Jzω
=Jzω
Напишите таблицу аналогий для поступательного и вращательного движений и поясните соответствующие величины.
Масса m – момент инерции J
Скорость v=dr/dt – угловая скорость ω=dϕ/dt
Ускорение a=dv/dt – угловое ускорение ε=dω/dt
Сила F – Момент силы Mz или M
Импульс p=mv – момент импульса Lz=Jzω
Основное уравнение динамики: F=ma – Mz=Jzε
Работа: dA=Fsds – dA=Mzdϕ
Кинетическая энергия: mv2/2 — Jzω2/2
4.3. Момент силы. Уравнение динамики вращательного движения твердого тела
Моментом силы  относительно неподвижной точки
относительно неподвижной точки
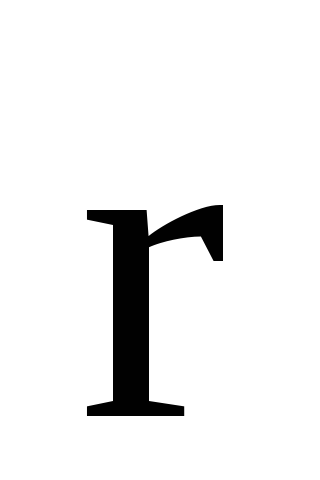 ,
проведенного из точки О в точку А
приложения cилы, на силу
,
проведенного из точки О в точку А
приложения cилы, на силу (рис.22): М=[
(рис.22): М=[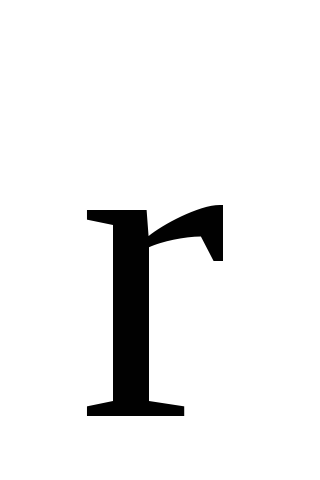
 ]
.
]
. Моментом силы относительно
неподвижной оси является скалярная величина Mz,
равная проекции на эту ось вектора 
Если ось z
совпадает с направлением вектора  ,
то момент, силы представляется в виде
вектора, совпадающего с осью: Мz=[
,
то момент, силы представляется в виде
вектора, совпадающего с осью: Мz=[
 ]z.
]z.
Найдем выражение для работы
при вращении тела (рис. 24). Пусть сила  приложена в точке В, находящейся от оси
вращения на расстоянии r,
– угол между направлением силы и
радиусом-вектором
приложена в точке В, находящейся от оси
вращения на расстоянии r,
– угол между направлением силы и
радиусом-вектором  .
Так как тело абсолютно твердое, то работа
этой силы равна работе, затраченной
на поворот всего тела.
.
Так как тело абсолютно твердое, то работа
этой силы равна работе, затраченной
на поворот всего тела.
При повороте тела на бесконечно малый угол d точка приложения В проходит путь ds=rd, и работа равна произведению проекции силы на направление смещения на величину смещения:
dA=Fsinrd.(4.4)
Так как Frsin=Fl=Mz – момент силы относительно оси Z, то можно записать, что dA=Mzd. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота.
Работа при вращении тела
идет на увеличение его кинетической
энергии: dA=dT,
но 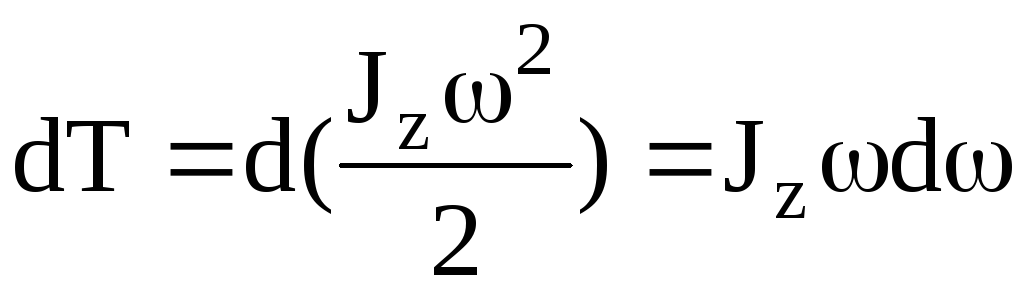 ,
поэтому
,
поэтому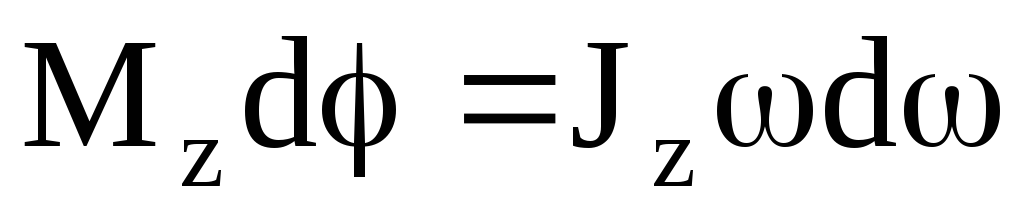 или
или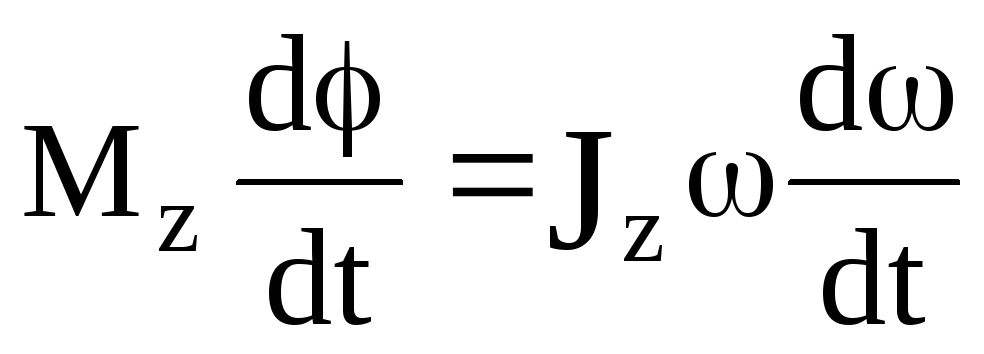
Учитывая, что 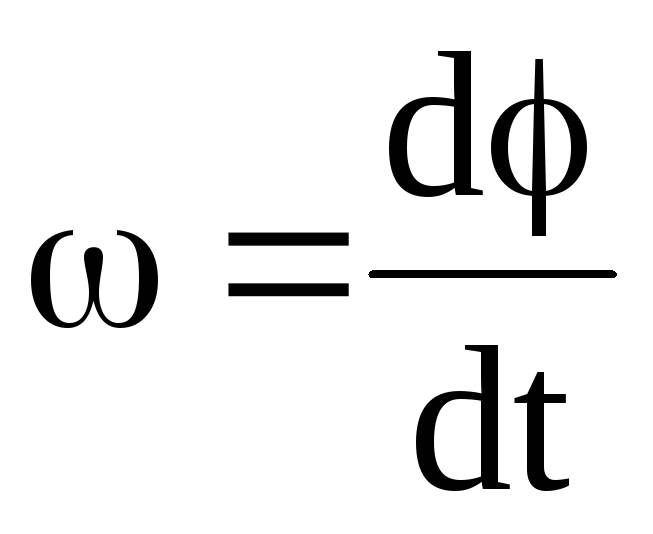 ,
получим
,
получим
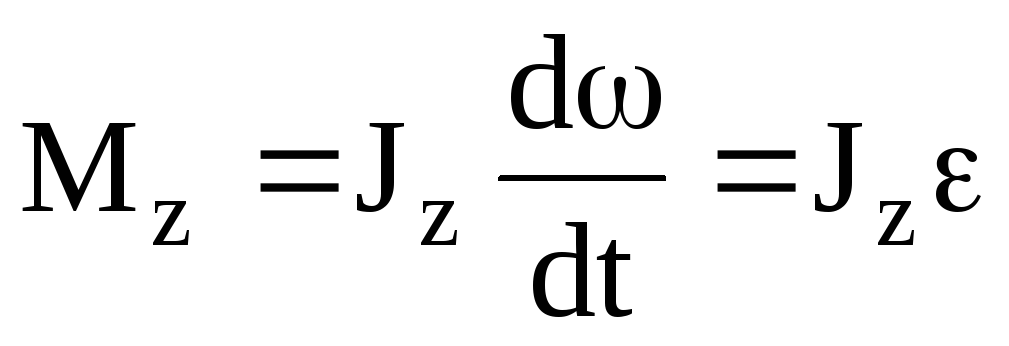 .
(4.5)
.
(4.5)
Уравнение (4.5) представляет собой уравнение динамики вращательного движения твердого телаотносительно неподвижной оси. Можно показать, что если ось вращения совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство
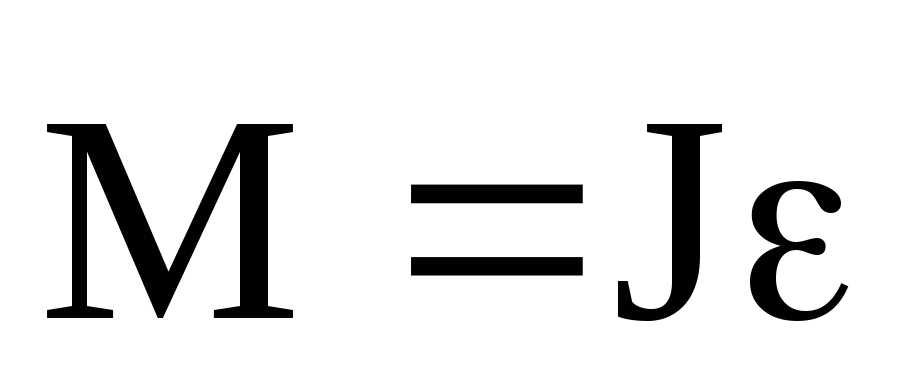 ,
,
где J — главный момент инерции тела (момент инерции относительно главной оси).
4.4. Момент импульса и закон его сохранения
При сравнении законов поступательного и вращательного движений просматривается аналогия между ними, только во вращательном движении вместо силы «выступает» ее момент, роль массы играет момент инерции. Какая же величина будет аналогом импульса тела? Ею является момент импульса тела относительно оси.
Моментом импульса (количество движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
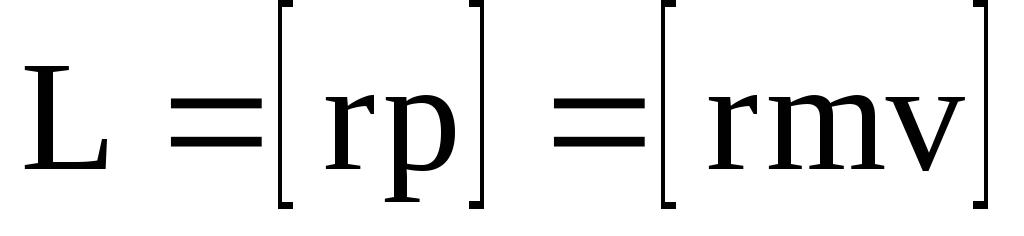 ,
,
где –псевдовектор, его направление совпадает с
 к
к ;
;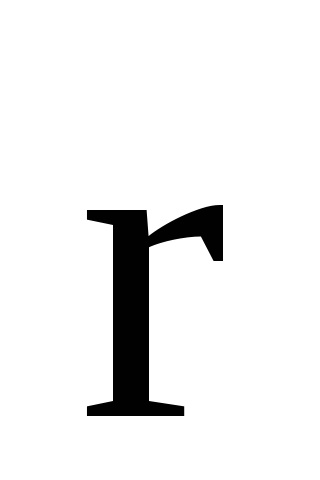 — радиус-вектор, проведенный из точки О
в точку А ;
— радиус-вектор, проведенный из точки О
в точку А ;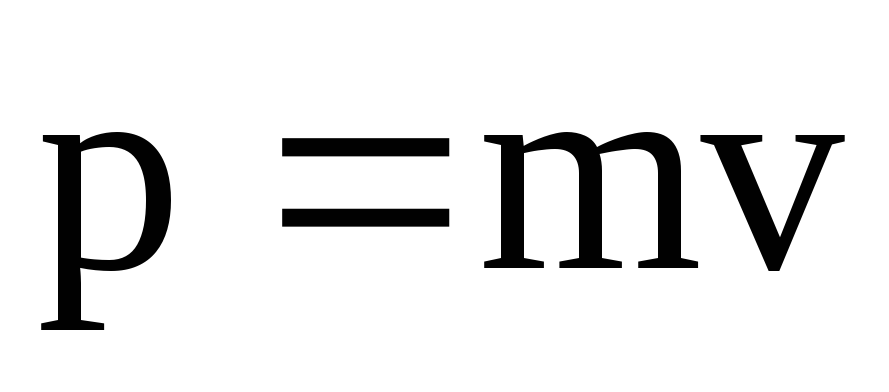 —
импульс материальной точки (рис.22) .
—
импульс материальной точки (рис.22) .Модуль вектора момента импульса:
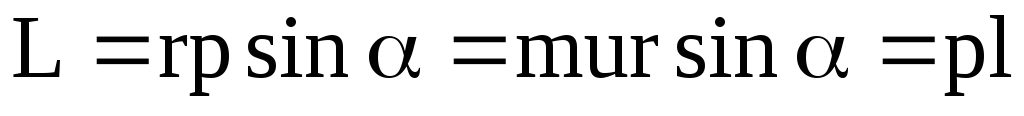 ,
,
где -
угол между векторами 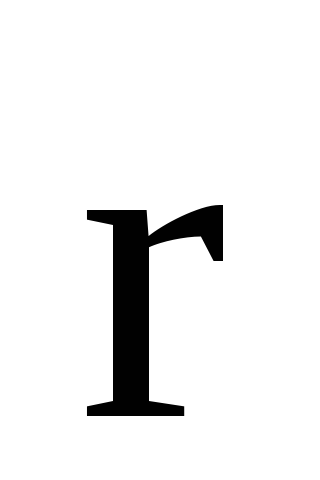 и
и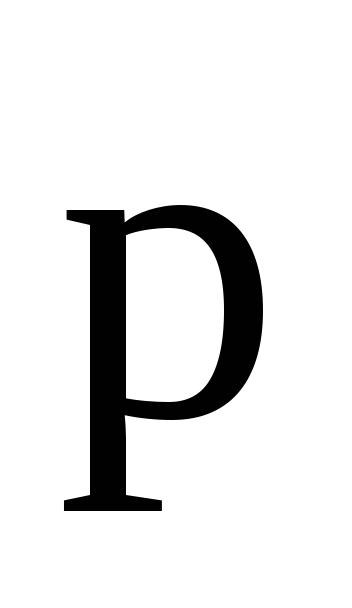 ,
1 — плечо вектора
,
1 — плечо вектора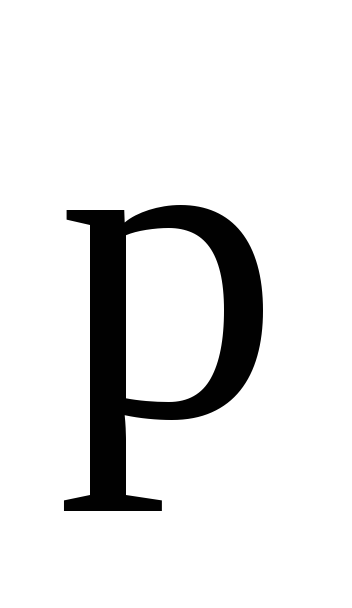 относительно точки О.
относительно точки О.
Моментом импульса относительно неподвижной оси Z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно точки О данной оси. Значение момента импульса Lz не зависит от положения точки О на оси z.
При вращении абсолютно
твердого тела вокруг неподвижной оси
z
каждая отдельная точка тела движется
по окружности постоянного радиуса r
с некоторой скоростью  .
Скорость
.
Скорость и импульс
и импульс 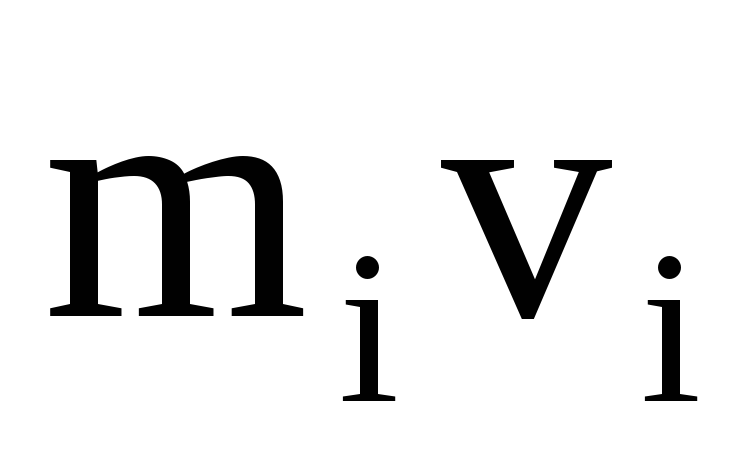 перпендикулярны этому радиусу, т.е.
радиус является плечом вектора
перпендикулярны этому радиусу, т.е.
радиус является плечом вектора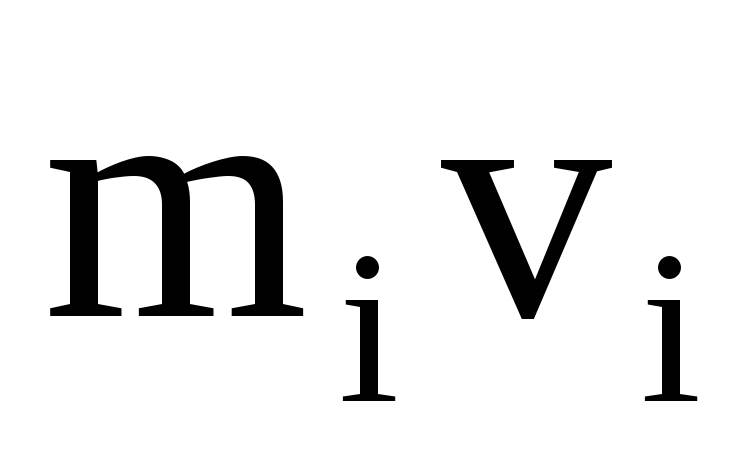 .
Поэтому можем записать, что момент
импульса отдельной частицы.
.
Поэтому можем записать, что момент
импульса отдельной частицы.
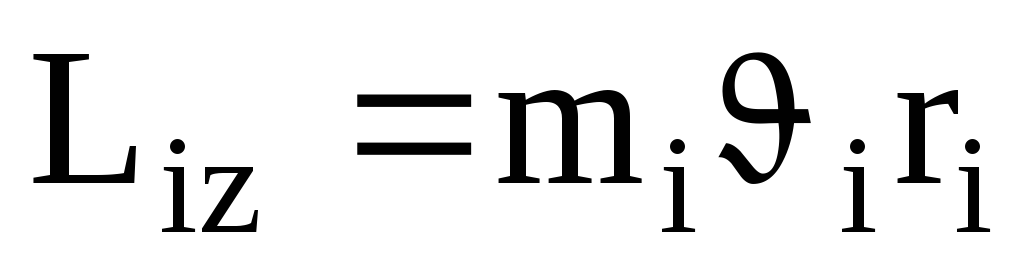 (4.6)
(4.6)
и направлен по оси в сторону, определяемую правилом правого винта.
Момент импульса твердого телаотносительно оси есть сумма моментов импульса отдельных частиц:
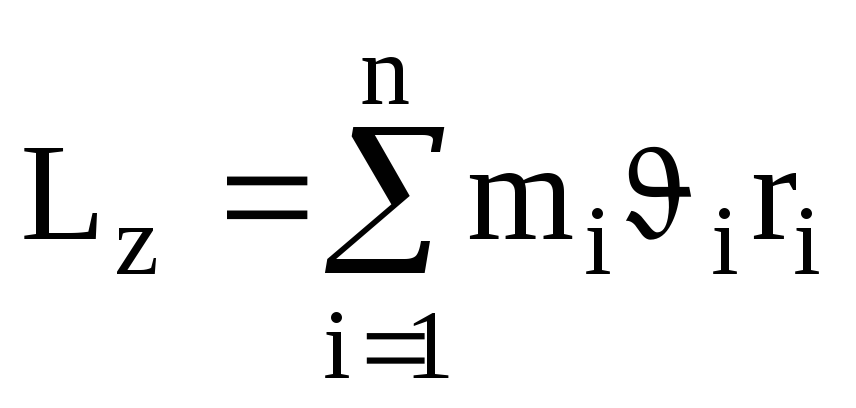 .
.
Используя формулу 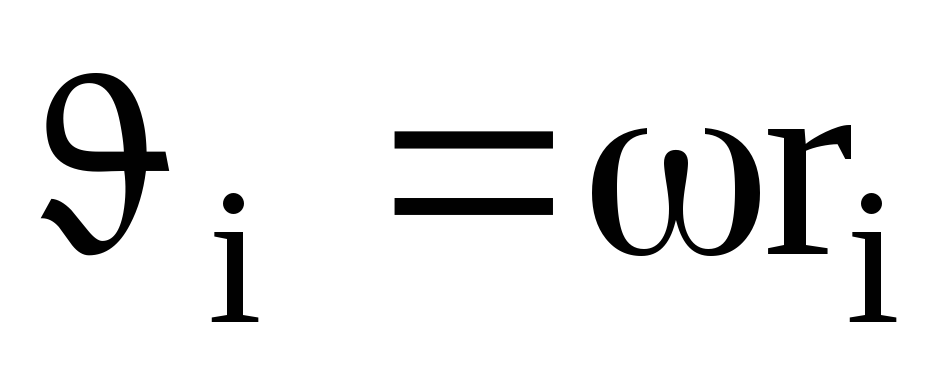 ,
получим
,
получим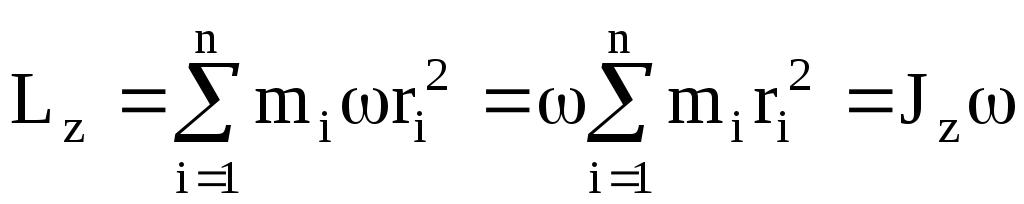 ,
,
т.е. 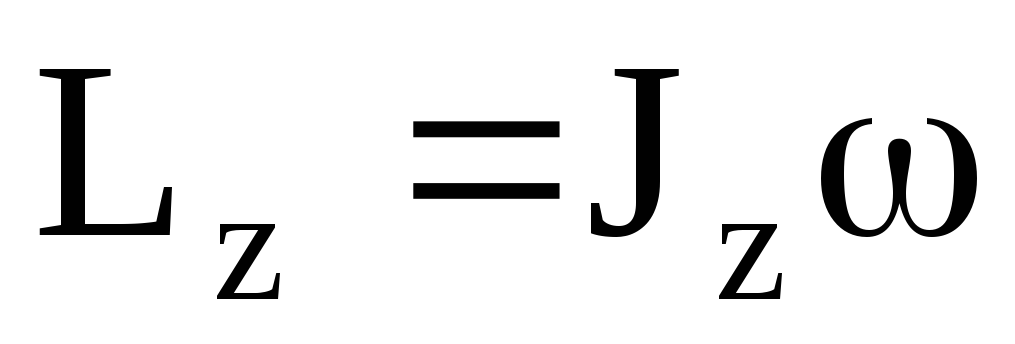 .(4.7) Таким образом, момент импульса
твердого тела относительно оси равен
произведению момента инерции тела
относительно той же оси на угловую
скорость.
.(4.7) Таким образом, момент импульса
твердого тела относительно оси равен
произведению момента инерции тела
относительно той же оси на угловую
скорость.
Продифференцируем уравнение (4.7) по времени:
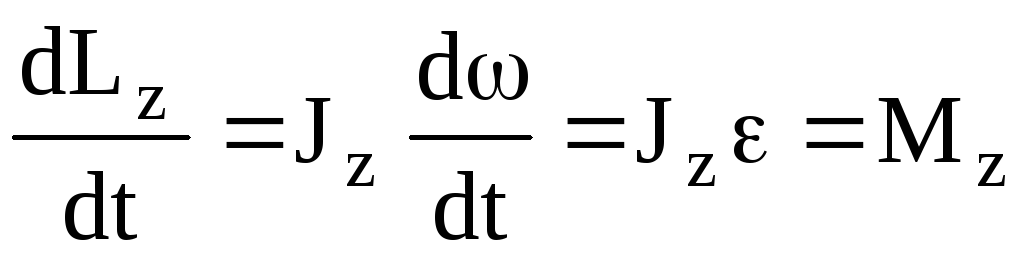 ,
,
т.е.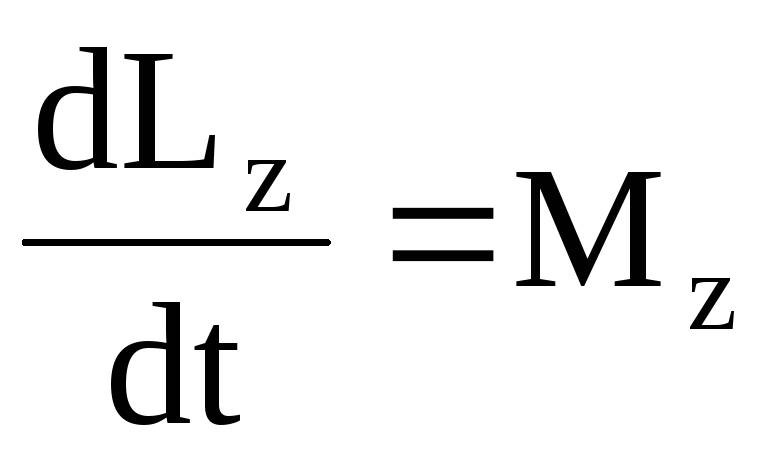 .
.
Это выражение – еще одна форма уравнения (закона) динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси. Можно показать, что имеет место векторное равенство
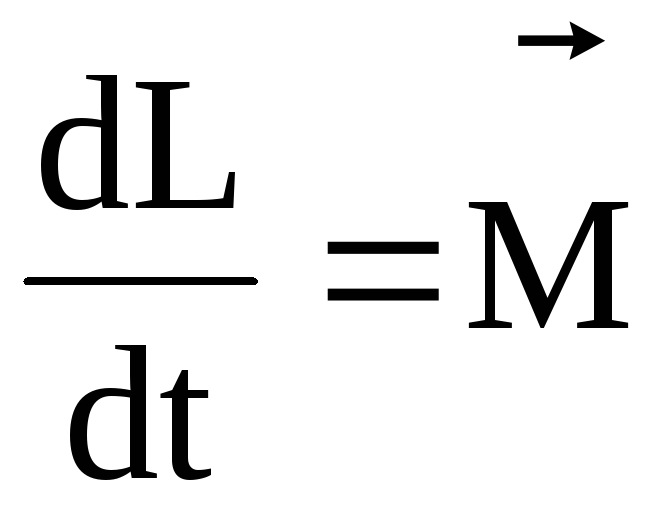 .
(4.8)
.
(4.8)
В замкнутой системе момент
внешних сил 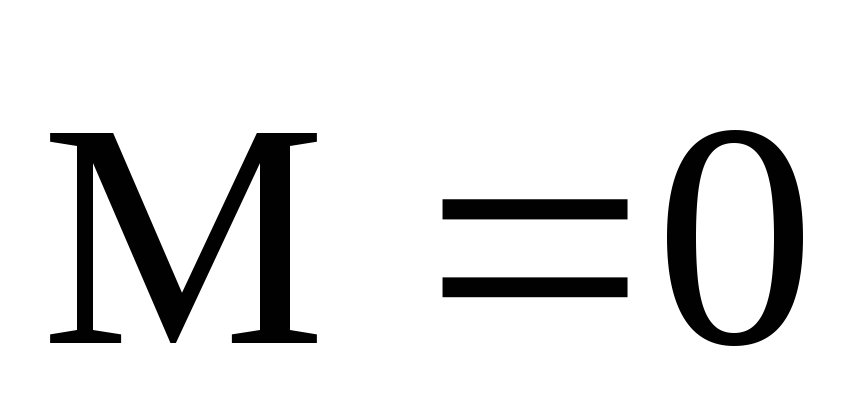 и
и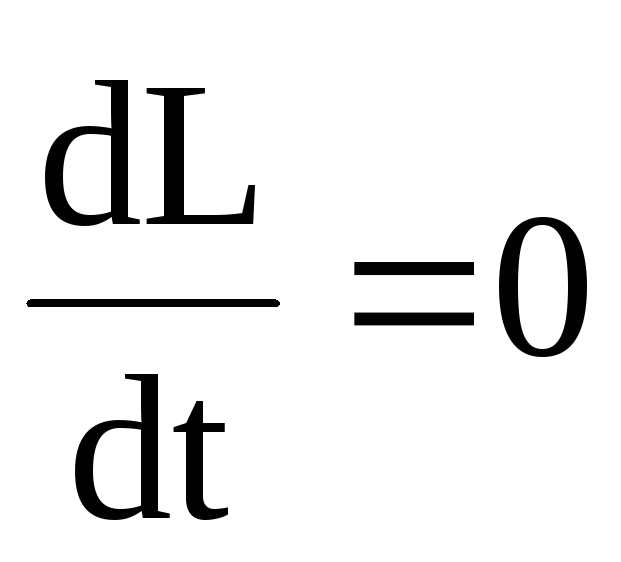 ,откуда
,откуда
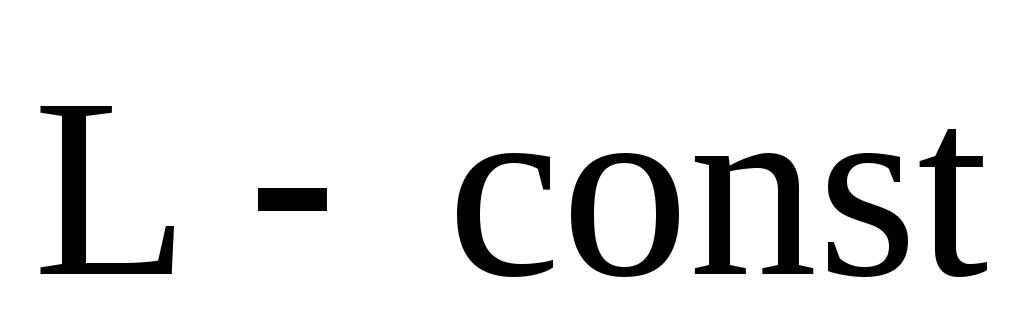 .(4.9)
.(4.9)
Выражение (4.9) представляет собой закон сохранения момента импуль-са: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени.
Закон сохранения момента импульса – фундаментальный закон природы. Он связан со свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).
Продемонстрировать закон сохранения момента импульса можно с помощью скамьи Жуковского. Пусть человек, сидящий на скамье, которая без трения вращается вокруг вертикальной оси, и держащий в вытянутых руках гантели .приведен во вращение с угловой скоростью .
Если человек прижмет гантели к себе, то момент инерции системы уменьшится. Поскольку момент внешних сил равен нулю, момент импульса системы сохраняется, и угловая скорость вращения 2 возрастает. Гимнаст во время прыжка через голову поджимает к туловищу руки и ноги, чтобы уменьшить свой момент инерции и увеличить тем самым угловую скорость вращения.
 .
.
Момент силы относительно неподвижной точки О и неподвижной оси Z. Уравнение динамики вращательного движения твердого тела
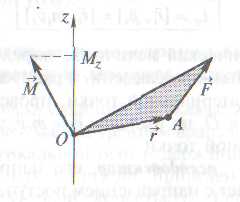
Момент силы относительно неподвижной точки О. 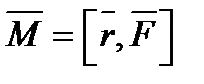 —это физическая величина, определяемая векторным произведением радиуса-вектора
—это физическая величина, определяемая векторным произведением радиуса-вектора 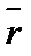 , проведенного из точки О в точку А приложения силы, на силу
, проведенного из точки О в точку А приложения силы, на силу 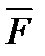 .
.
Момент силы – это векторная величина, его направление определяется следующим образом: если сила 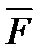 стремится повернуть тело вокруг точки О против хода часовой стрелки, то вектор перпендикулярен плоскости действия силы и направлен вверх. Модуль вектора момента силы: из центра точки О надо восстановить перпендикуляр на линию действия силы, тогда
стремится повернуть тело вокруг точки О против хода часовой стрелки, то вектор перпендикулярен плоскости действия силы и направлен вверх. Модуль вектора момента силы: из центра точки О надо восстановить перпендикуляр на линию действия силы, тогда 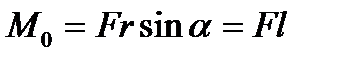 (
( 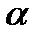 — угол между
— угол между 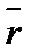 и
и 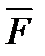 ;
; 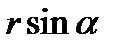 =
= 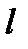 — кратчайшее расстояние между линией действия силы и точкой О — плечо силы).
— кратчайшее расстояние между линией действия силы и точкой О — плечо силы).
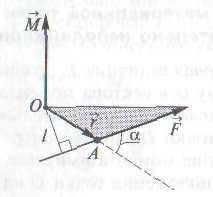 |
Момент силы относительно неподвижной оси Z
Это скалярная величина 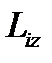 , равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси Z. Значение момента импульса
, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси Z. Значение момента импульса 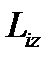 не зависит от выбора положения точки О на оси Z.
не зависит от выбора положения точки О на оси Z.
 |
Если ось z совпадает с направлением вектора 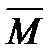 , то момент силы представляется в виде вектора, совпадающего с осью.
, то момент силы представляется в виде вектора, совпадающего с осью.
Дата добавления: 2016-12-16; просмотров: 6236;
Похожие статьи:
§ 4.2. Момент импульса и момент сил относительно
неподвижной оси
Векторное уравнение (4.4.) эквивалентно трем скалярным уравнениям:
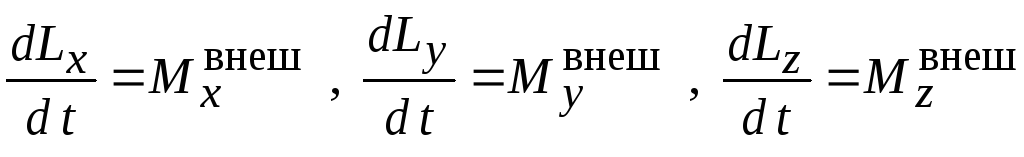 ,
(4.5)
,
(4.5)
которые получаются из уравнения (4.4.) путем проектирования на неподвижные оси декартовой системы координат. Индекс «внеш.», указывающий на то, что при вычислении момента сил внутренние силы могут не приниматься во внимание, в дальнейшем обычно будет опускаться. Таким образом, под М в уравнении моментов всегда будет подразумеваться момент внешних сил. Величины Lx и Мхназываются соответственно моментами импульса и сил относительно оси Х. Аналогично говорят о моментах импульса и сил относительно координатных осей Y и Z.
Вообще, моментами Lx и Мх импульса и сил относительно произвольной оси Х называют проекции векторов L и М на эту ось в предположении, что начало О лежит на рассматриваемой оси.
Уравнение
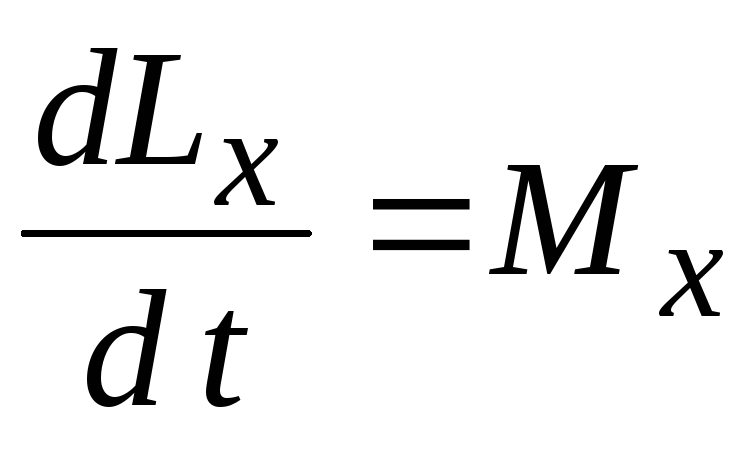 (4.6.)
(4.6.)
называется уравнением моментов относительно неподвижной оси Х.
Когда момент внешних сил относительно какой-либо неподвижной оси равен нулю, то момент импульса системы относительно той же оси остается постоянным. Это – закон сохранения момента импульса относительно неподвижной оси.
§ 4.3. Уравнение момента импульса для вращения вокруг неподвижной оси. Момент инерции
Применим уравнение моментов относительно оси к рассмотрению вращательного движения. За неподвижную ось моментов удобно выбрать ось вращения.
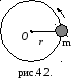
| Если материальная точка вращается по окружности радиуса r (см. рис.4.2.), то момент ее импульса относительно оси вращения О равен L = mVr. Пусть угловая скорость вращения, тогда V = r и, следовательно, L = mr2. |
Если
вокруг оси О вращается система материальных точек
с одной и той же угловой скоростью ω,
то L = 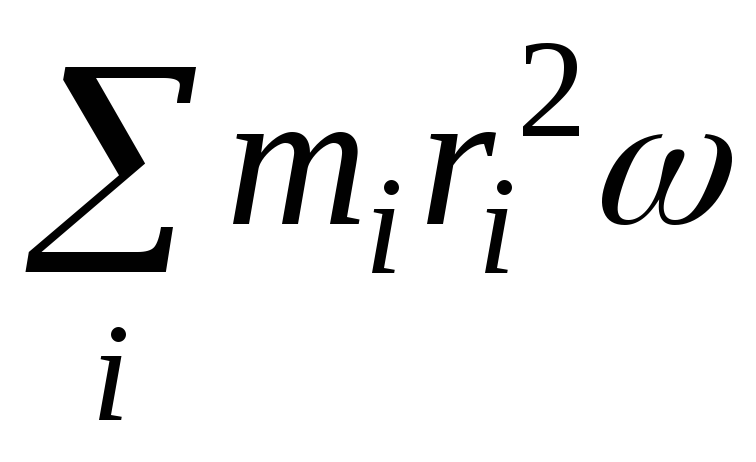 , где
суммирование производится по всем
материальным точкам системы. Величину как одинаковую для всех материальных
точек можно вынести из-под знака суммы.
Тогда получится
, где
суммирование производится по всем
материальным точкам системы. Величину как одинаковую для всех материальных
точек можно вынести из-под знака суммы.
Тогда получится
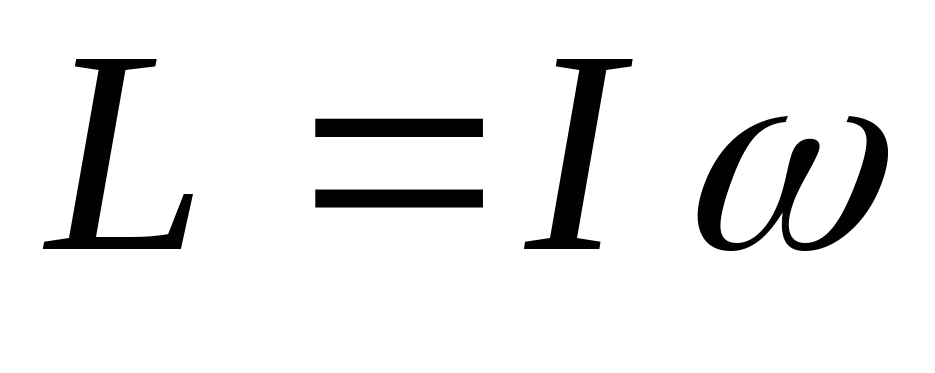 ,
(4.7)
,
(4.7)
где
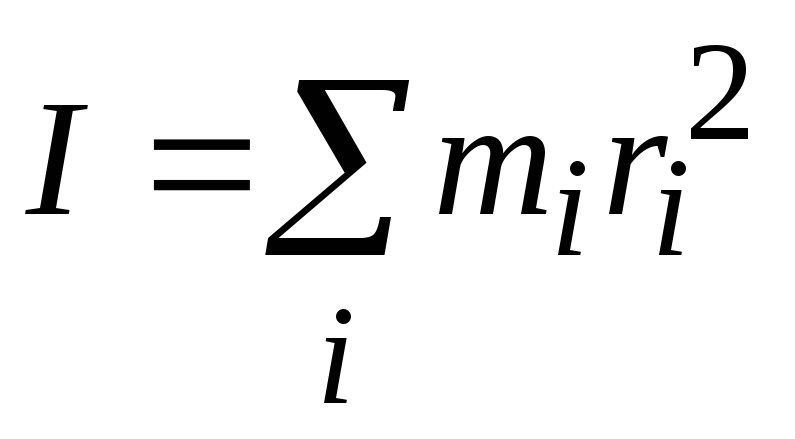 . (4.8)
. (4.8)
Величина I, равная сумме произведений масс материальных точек на квадраты расстояний их до оси вращения, называется моментом инерции системы относительно этой оси. Уравнение (4.7) показывает, что при вращении системы момент ее импульса относительно оси вращения равен произведению момента инерции относительно той же оси на угловую скорость.
Если на вращательное движение системы материальных точек накладывается еще радиальное движение их, а также движение параллельно оси, то наличие таких движений не отразится на справедливости формулы (4.7). Это следует из того, что момент импульса материальной точки зависит от ее скорости V линейно. Когда же скорость V направлена по радиусу или параллельно оси вращение, то момент импульса относительно этой оси равен нулю. Поэтому такие движения непосредственно не сказываются на виде связи между моментом импульса системы относительно оси вращения и ее угловой скоростью. Их влияние косвенное и состоит в том, что момент инерции I перестает быть постоянной величиной, а меняется во времени в соответствии с изменением мгновенной конфигурации системы. В этом случае уравнение (4.8) принимает вид
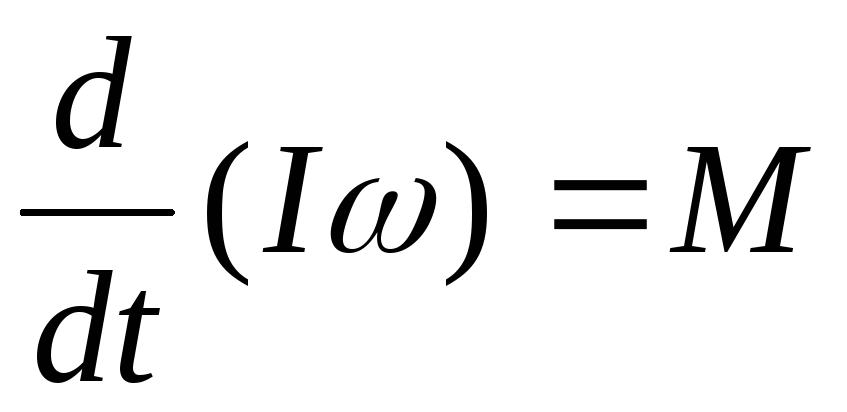 (4.9)
(4.9)
где М – момент внешних сил относительно оси вращения.
Это
– основное
уравнение динамики вращательного
движения вокруг неподвижной оси. Оно напоминает уравнение Ньютона для
движения материальной точки. Роль массы
играет момент инерции I,
роль скорости – угловая скорость ,
роль силы – момент силы М, роль импульса – момент импульса L.
Важным частным случаем является вращение
неизменяемой системы материальных
точек или твердого тела вокруг неподвижной
оси. В этом случае момент инерции I при вращении
остается постоянным, и уравнение (4.9)
переходит в 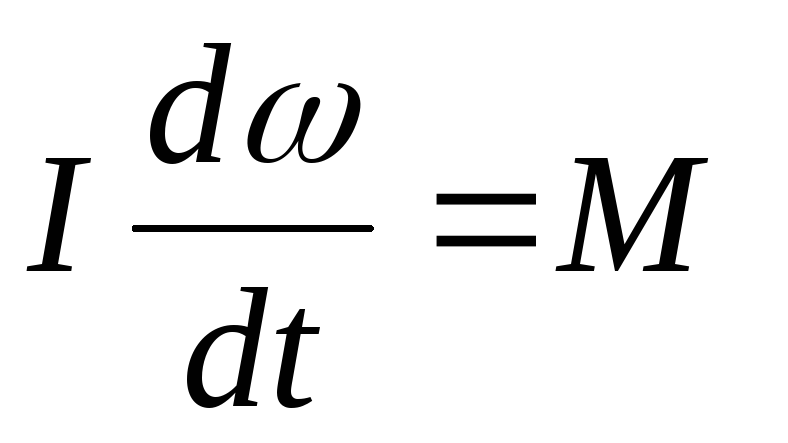 или
или
I = M, (4.10)
где = d/dt – угловое ускорение.
Кинетическая энергия вращающегося твердого тела представляется в виде
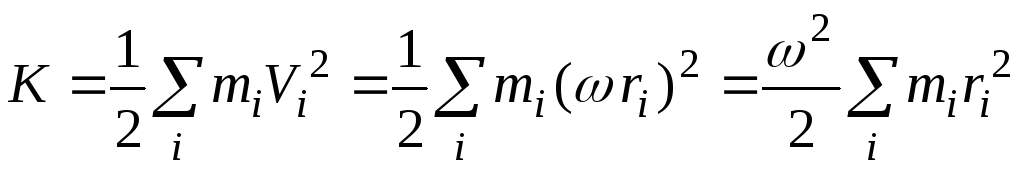 ,
,
или
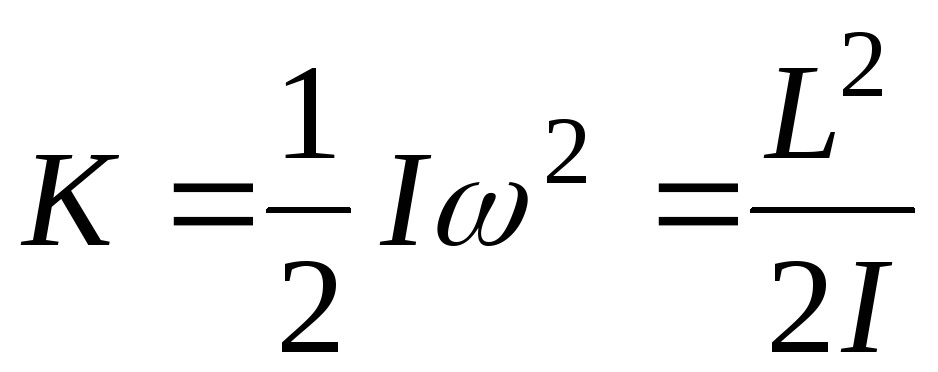 . (4.11)
. (4.11)
Эти выражения напоминают соответствующие выражения для кинетической энергии материальной точки. Они получаются из последних формальной заменой mI, V, pL.
Момент силы относительно оси — Лекции и примеры решения задач технической механики
Момент силы относительно оси, например Oz (рисунок 1.18), равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси (F’) относительно точки пересечения оси с плоскостью, т.е.
Mz(F) = MO(F’) = F’∙ h’. (1.9)
Момент считается положительным, если мы смотрим навстречу оси и видим проекцию силы, стремящуюся повернуть плоскость чертежа в направлении против хода часовой стрелки.
Момент силы относительно оси равен нулю, если линия действия силы пересекает ось, т.е. h=0 (например Mz(P)), или сила параллельна оси, т.е. ее проекция на плоскость равна нулю, например, Mz(Q).
Наш короткий видеоурок про момент силы с примерами:
Момент силы относительно оси – скалярная величина.
Рисунок 1.18
Моменты силы относительно координатных осей можно получить, расписав векторное произведение
Величины, стоящие в скобках, представляют собой моменты силы F относительно соответствующих осей.
>> Пара сил