11.Векторный момент силы относительно центра. Выражение векторного момента силы в виде векторного произведения. Аналитическое выражение момента силы относительно центра.
Векторный момент силы относительно центра – векторное произведение радиус-вектора точи приложения силы относительно центра на вектор силы.
Теорема Вариньона: Если система сил, приложенных к абсолютно твердому телу имеет равнодействующую, то момент равнодействующей относительно произвольного центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).
Алгебраическим
моментом силы F
относительно некоторого центра называется
взятое со знаком + или — произведение
модуля силы F
на плечо (кротчайшее расстояние от точки
до линии действия силы). Момент положителен,
если сила стремиться вращать плоскость
действия против часовой стрелки и
наоборот. (M=F*h)
Но при этом h
можно выразить через радиус-вектор r
(h=r*sin
α), тогда M
= F*r*sin
α = (F
x
r).
Получаем, что векторный момент силы
относительно точки – векторная величина.
12. Момент силы относительно оси. Аналитическое выражение момента силы относительно оси.
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Момент относительно оси положителен, если сила стремится вращать плоскость перпендикулярную оси против часовой стрелки, если смотреть навстречу оси.
Момент силы относительно оси равен 0 в двух случаях:
Если линия действия и ось лежат в одной плоскости, то момент силы относительно оси равен 0.
13. Связь между моментом силы относительно оси и векторным моментом силы относительно точки.
Mz(F)=Mo(F)*cosα Момент силы, относительно оси равен прекции вектора момента сил, относительно точки оси на эту ось.
9. Сложение параллельных сил.
Равнодействующая
двух параллельных сил, направленных в
одну сторону равна алгебраической сумме
модулей составляющих сил. Линия действия
равнодействующей делит отрезок,
заключённый между точками приложения
сил внутренним образом на части, обратно
пропорциональные модулям этих сил.
9. Пара сил. Векторный момент пары сил. Алгебраический момент пары сил.
Пара сил – совокупность двух противоположно направленных равных по модулю параллельных сил, действующих по несовпадающим линиям действия.
Плоскость, в которой действует пара сил, называется плоскостью действия пары.
Момент пары сил не зависит от выбора центра привидения, а определяется лишь модулями сил и расстоянием между л.д. – плечом пары.
Векторный
момент пары сил – вектор, равный векторному произведению
радиус-вектора ρ, соединяющий точки
приложения сил на вектор силы и
направленный перпендикулярно плоскости
действия пары сил таким образом, чтобы,
смотря ему навстречу, пара сил стремилась
поворачивать плоскость действия против
часовой стрелки.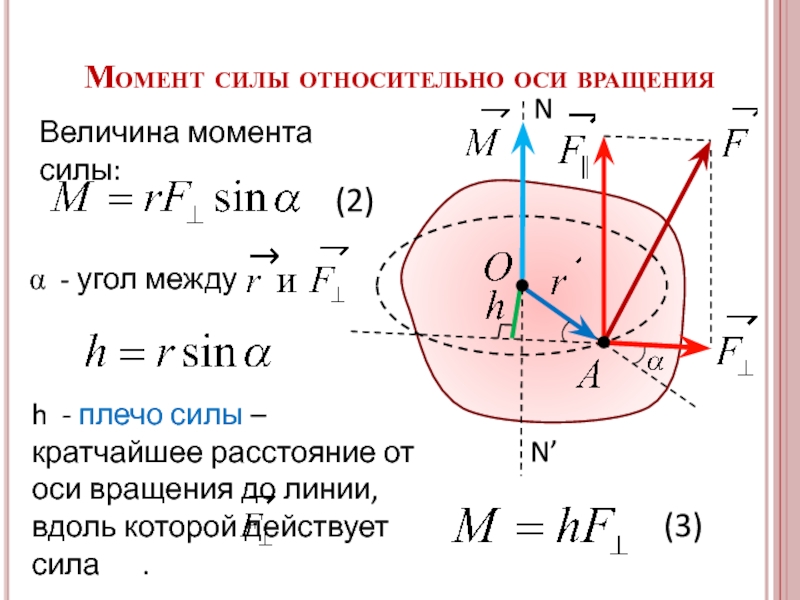
Алгебраический момент пары сил равен произведению модуля одной из сил, составляющих пару, на плечо пары и имеет знак в соответствии с правилом знаков для момента силы.
Техническая механика — Тема1.3. Пара сил и момент силы
§1. Момент силы относительно центра (или точки)
Опыт показывает, что под действием силы твердое тело может наряду с поступательным перемещением совершать вращение вокруг того или иного центра. Вращательный эффект силы характеризуется ее моментом.
Рассмотрим силу , приложенную в точке А твердого тела (рис. 1). Допустим, что сила стремится повернуть тело вокруг центра О. Перпендикуляр h, опущенный из центра O на линию действия силы
, называется плечом силы относительно центра О. Так как точку приложения силы можно произвольно перемещать вдоль линии действия, то, очевидно, вращательный эффект силы будет зависеть:
1) от модуля силы F и длины плеча h;
2) от положения плоскости поворота ОАВ, проходящей через центр О и силу F;
3) от направления поворота к этой плоскости.
Рис.1. Сила, приложенная к телу
Ограничимся пока рассмотрением систем сил, лежащих в одной плоскости. В этом случае плоскость поворота для всех сил является общей и в дополнительном задании не нуждается.
Тогда для количественного измерения вращательного эффекта можно ввести следующее понятие о моменте силы: моментом силы относительно центра О называется величина, равная взятому с соответствующим знаком произведению модуля силы на длину плеча.
Момент силы относительно центра О будем обозначать M.
Следовательно, М= ±Fh. Единицы измерения в системе СИ : Н·м,
Правило знаков для момента силы: момент пары сил будем считать положительным, если пара стремиться повернуть тело по направлению хода часовой стрелки, и отрицательным, если пара сил стремится вращать тело против хода часовой стрелки.
Отметим следующие свойства момента силы:
1) Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия.
2) Момент силы относительно центра О равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр О (плечо равно нулю).
3) Момент силы численно выражается удвоенной площадью треугольника ОАВ (рис. 1)
M= ± 2пл.ΔOAB
§2.Теорема Вариньона о моменте равнодействующей
Докажем следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.
Рис.2. Сходящаяся система сил
Рассмотрим систему сил , сходящихся в точке А (рис. 2). Возьмем произвольный центр О и проведем через него ось Ох, перпендикулярную к прямой ОА; положительное направление оси Ох выбираем так, чтобы знак проекции любой из сил на эту ось совпадал со знаком ее момента относительно центра О.
Для доказательства теоремы найдем соответствующие выражения моментов М(), М(), … .
По формуле М() = +2пл.ΔОАВ1. Но, как видно из рисунка, где F1x — проекция силы на ось Ох; следовательно М() = ОА · F1x
Аналогично вычисляются моменты всех других сил.
Обозначим равнодействующую сил , через , где . Тогда, по теореме о проекции суммы сил на ось, получим . Умножая обе части этого равенства на ОА, найдем:
или .
§3. Пара сил. Момент пары
Парой сил (или просто парой) называются две силы, равные по величине, параллельные и направленные в противоположные стороны (рис. 3). Очевидно, и
Рис. 3. Пара сил
Несмотря на то, что сумма сил равна нулю, эти силы не уравновешиваются. Под действием этих сил, пары сил, тело начнёт вращаться. И вращательный эффект будет определяться моментом пары:
.
Расстояние a между линиями действия сил называется плечом пары.
Если пара вращает тело против часовой стрелки, момент её считается отрицательным (как на рис. 3), если по часовой стрелке – положительным.
Для того, чтобы момент пары указывал и плоскость, в которой происходит вращение, его представляют вектором.
Вектор момента пары направляется перпендикулярно плоскости, в которой расположена пара, в такую сторону, что если посмотреть оттуда, увидим вращение тела против часовой стрелки (рис. 4).
Нетрудно доказать, что вектор момента пары – есть вектор этого векторного произведения (рис. 4). И заметим, что он равен вектору момента силы относительно точки А, точки приложения второй силы:
.
Рис.4. Вектор момента пары сил
Видео-урок «Пара сил и ее свойства»
youtube.com/embed/wEN0Sukn_n4″ allowfullscreen=»»/>§4. Свойства пар сил
1) Проекция пары на любую ось равна нулю. Это следует из определения пары сил.
2) Найдём сумму моментов сил оставляющих пару, относительно какой-либо точки О (рис.5).
Рис.5. Пара сил
Покажем радиусы-векторы точек А1 и А2 и вектор , соединяющий эти точки. Тогда момент пары сил относительно точки О
.
Но
. Поэтому .
Но .
Значит .
Момент пары сил относительно любой точки равен моменту этой пары.
Отсюда следует, что, во-первых, где бы не находилась точка О и, во-вторых, где бы не располагалась эта пара в теле и как бы она не была повёрнута в своей плоскости, действие её на тело будет одинаково. Так как момент сил, составляющих пару, в этих случаях один и тот же, равный моменту этой пары
.
3) Пару можно перемещать в пределах тела по плоскости действия и переносить в любую другую параллельную плоскость.
4) Так как действие на тело сил, составляющих пару, определяется лишь её моментом, произведением одной из сил на плечо, то у пары можно изменять силы и плечо, но так, чтобы момент пары остался прежним. Например, при силах F1=F2=5 H и плече а = 4 см момент пары m = 20 H∙см. Можно силы сделать равными 2 Н, а плечо а = 10 см. При этом момент останется прежним 20 Н∙см и действие пары на тело не изменится.
Все эти свойства можно объединить и, как следствие, сделать вывод, что пары с одинаковым вектором момента и неважно где расположенные на теле, оказывают на него равное действие. То есть такие пары эквивалентны.
Исходя из этого, на расчётных схемах пару изображают в виде дуги со стрелкой, указывающей направление вращения, и рядом пишут величину момента m (рис. 6). Или, если это пространственная конструкция, показывают только вектор момента этой пары.
И вектор момента пары можно прикладывать к любой точке тела. Значит вектор момента пары
– свободный вектор. Такое упрощенное изображение оправдано тем, что пара сил характеризуется моментом, а не ее положением в плоскости. Но если необходимо определять не внешние силы, а внутренние в разных сечениях элемента, как это делается в сопротивлении материалов, то важен знак и место приложения пары сил.
Рис.6. Эквивалентные пары сил
И ещё одно дополнительное замечание. Так как момент пары равен вектору момента одной из сил её относительно точки приложения второй силы, то момент пары сил относительно какой-либо оси z – есть проекция вектора момента пары
на эту ось: , где – угол между вектором и осью z.
Видео-уроки «Эквивалентность пар»
youtube.com/embed/eijMAsCf68w» allowfullscreen=»»/>§5. Сложение пар
Пусть даны две пары с моментами m1 и m2, расположенные в пересекающихся плоскостях (рис. 7).
Сделаем у пар плечи одинаковыми, равными а = АВ. Тогда модули сил, образующих первую пару, должны быть равны: , а образующих вторую пару:
.
Эти пары показаны на рис. 7, где . И расположены они в своих плоскостях так, что плечи пар совпадают с прямой АВ на линии пересечения плоскостей.
Рис.7. Пары сил с моментами m1 и m2
Сложив силы, приложенные к точкам А и В, построением параллелограммов, получим их равнодействующие .
Так как , то эти силы и будут образовывать пару, момент которой
, где – радиус-вектор точки В, совпадающий с АВ.
Так как
, то момент полученной пары .
Следовательно, в результате сложения пар, расположенных в пересекающихся плоскостях, получится пара сил. Момент её будет равен векторной сумме моментов слагаемых пар.
При сложении нескольких пар, действующих в произвольных плоскостях, получим пару с моментом .
Конечно, эта результирующая пара будет располагаться в плоскости перпендикулярной вектору .
Равенство нулю результирующей пары будет означать, что пары, действующие на тело, уравновешиваются. Следовательно, условие равновесия пар =0.
Это является необходимым и достаточным условием равновесия систем пар.
Если пары расположены в одной плоскости, векторы моментов их будут параллельны.
И момент результирующей пары можно определить как алгебраическую сумму моментов пар.
Рис.8. Моменты пар сил, расположенные в одной плоскости
Например, пары, показанные на рис.8, расположены в одной плоскости и моменты их:
m1=2 Hсм , m2=5 Hсм, m3=3 Hсм. Пары уравновешиваются, потому что алгебраическая сумма их моментов равна нулю:
Вопросы для самопроверки:
— Что называется моментом силы относительно центра на плоскости?
— Какая система сил называется парой?
— Можно ли заменить действие пары сил на тело одной силой?
— Что такое момент пары?
— Какая плоскость называется плоскостью действия пары?
— Какие пары называются эквивалентными?
— Что называется плечом пары?
— Запишите векторную и скалярную зависимости между элементами пары.
— Почему пара сил не имеет равнодействующей?
— Имеет ли пара сил равнодействующую?
— Каким образом можно уравновесить действие на тело пары сил?
— Что такое момент пары сил?
— Изменятся ли моменты пар сил, если положения сил, показанные на рис.
а, изменить на положения, показанные на рис. б?
— Какие пары называются эквивалентными?
— Эквивалентны ли пары сил, изображенные на рисунке?
— Каким образом производится сложение пар сил?
— Сформулируйте условие равновесия пар сил.
— Чем характеризуется действие пары сил на твердое тело?
— Как направлен вектор момента пары сил?
— Как определяются моменты пар сил, лежащих в одной плоскости?
— Какие преобразования пары сил не изменяют ее действия на твердое тело?
— Сформулируйте теоремы об эквивалентности пар.
— Что называется результирующей парой?
— Запишите формулу для определения результирующей системы пар.
— Назовите условия равновесия плоской системы пар.
— Приведите векторную запись условия равновесия произвольной системы пар.
— Будет ли изменяться момент силы относительно точки, если, не меняя направления, переносить силу вдоль линии ее действия?
— На тело действуют две силы F1 = 40 Н и F2 = 50 Н, как показано на рисунке (а = 0,5 м, b = 0,8 м, ).
Какая из сил создает больший момент относительно точки О?
— Что такое главный вектор и главный момент плоской системы сил?
— Как аналитически найти главный вектор и главный момент данной плоской системы сил?
— В чем сходство и в чем различие между главным вектором плоской системы сил и ее равнодействующей?
— Сформулируйте теорему Вариньона.
— Приведите векторную запись теоремы Вариньона.
— Чему равен главный вектор системы сил?
— Чему равен главный момент системы сил при приведении ее к точке?
— Тело движется равномерно и прямолинейно (равновесие). Чему равны главный вектор и главный момент системы?
ньютоновской механики — равен ли момент силы работе, совершаемой силой, и равен потенциальной энергии гравитации? (M = W = g.p.e.)
спросил
Изменено 2 года, 11 месяцев назад
Просмотрено 2к раз
Смешной вопрос, но.
..
Если эти уравнения верны:
Момент силы = сила * расстояние по перпендикуляру от оси вращения до силы (M=Fd)
А
Работа силы = сила * расстояние, пройденное силой в направлении действия силы ( W = Fd)
Значит ли это…
Момент силы = работа, совершенная силой
(Я знаю, что расстояния здесь неодинаковы, одно, когда речь идет о поворотах, а другое для работы)
Но оба имеют одинаковые единицы измерения, Нм (Ньютон * метр)
И
Сила и расстояние в обоих уравнениях косвенно пропорциональны, либо прямо пропорциональны их умноженному значению..:
Если расстояние постоянно, а сила увеличивается, момент силы увеличивается..
Если сила постоянна, а расстояние уменьшается, работа, совершаемая работами, уменьшается..
Кроме того, Ньютон * метр равен Джоулю.. в случае работы.. (Nm = J)
Означает ли это..
Момент силы = работа силы ?
НО ЭТО НЕ ОСТАНАВЛИВАЕТСЯ.
Если вес = масса * ускорение свободного падения = сила (W = mg = F)
А
гравитационная потенциальная энергия = вес * высота = масса * г * высота = сила * высота = МОМЕНТ СИЛЫ = РАБОТА, СОВЕРШАЕМАЯ СИЛОЙ.
Делая вывод, что…
Момент силы = работа, совершаемая силой = потенциальная энергия гравитации (M = Вт = g.p.e.)
— Я нахожу это смешным, но меня очень беспокоит тот факт, что это не обсуждалось и не было ответа раньше (насколько я видел)
- ньютоновская механика
- динамика вращения
- работа
- потенциальная энергия
- крутящий момент
Прежде всего, я предлагаю вам взглянуть на то, как использовать MathJax для правильного форматирования вопроса, поскольку его немного сложно читать.
Теперь к физике. На самом деле момент силы определяется как
$$\vec{M}=\vec{r}\times \vec{F}$$
где $\vec{r}$ — расстояние от некоторой точки до точки приложения силы. Работа определяется как
$$W=\int \vec{F}\cdot d\vec{r}$$
где $d\vec{r}$ определяет траекторию в пространстве.
Несмотря на то, что они имеют одинаковые единицы измерения ($\mbox{сила} \times \mbox{расстояние}$), они не представляют одни и те же физические величины. Вы должны заметить, что крутящий момент определяется относительно одной точки, что видно на следующем изображении (извините за размеры).
С другой стороны, для работы необходимо определить путь, путь, по которому действует сила $\vec{F}$. Поскольку это интеграл, его можно интерпретировать как площадь под кривой:
Еще одно очень важное отличие состоит в том, что работа — это всегда скалярная величина, т. е. число, тогда как крутящий момент — это вектор. Единственная «эквивалентность», которую вы можете найти в своих рассуждениях, — это между работой и энергией, которые на самом деле представляют собой одну и ту же физическую величину, как указано в первом законе термодинамики. Надеюсь, это решит ваш вопрос.
$\endgroup$ $\begingroup$Значит ли это… Момент силы = работа силы
№
В случае углового движения (движения, вызванного крутящим моментом, или, как вы говорите, моментом) сила заменяется крутящим моментом, а линейное перемещение заменяется угловым перемещением.
Или
$$W=\int \overrightarrow F.d\overrightarrow x$$
Заменяется на
$$W=\int \overrightarrow τ.d\overrightarrowθ$$
Где $θ$ — угловое смещение в радианах в результате приложения крутящего момента.
Крутящий момент и сила связаны соотношением
$$\overrightarrow τ=\overrightarrow r x \overrightarrow F=rFsinθ$$
Где в данном случае $θ$ — угол между векторами силы $F$ и перемещения $r$ , а последний член уравнения представляет собой величину крутящего момента.
НО ЭТО НЕ ОСТАНАВЛИВАЕТСЯ.
Если вес = масса * ускорение свободного падения = сила (Вт = мг = F)
и
гравитационная потенциальная энергия = вес * высота = масса * г * высота = сила * высота = МОМЕНТ СИЛЫ = РАБОТА СИЛЫ. (g.p.e. = mgh = Fh = Fd = M = W )
Делая вывод, что…
Момент силы = работа силы = потенциальная энергия гравитации (M = W = g.p.e.)
Неверный вывод.
Крутящий момент (момент) представляет собой векторное произведение векторов силы и смещения, третье уравнение выше.
Надеюсь, это поможет.
$\endgroup$Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и парольОпубликовать как гость
Электронная почтаТребуется, но никогда не отображается
Опубликовать как гость
Электронная почтаТребуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.
| Вопрос Как сила связана с импульсом? Автор вопроса: Мелисса Томас Ответить Импульс измеряет «содержимое движения» объекта и основан на произведении массы объекта и скорости. Импульс удваивается, например, когда удваивается скорость. Точно так же, если два объекта движутся с одинаковой скоростью, один из них с удвоенной массой другого также имеет удвоенный импульс. Сила, с другой стороны, — это толчок или тяга, которые применяются к объекту для ИЗМЕНЕНИЯ его импульса. Второй закон движения Ньютона определяет силу как произведение массы на УСКОРЕНИЕ (против скорости). Поскольку ускорение — это изменение скорости, деленное на время, вы можете связать эти две концепции следующим отношением: сила = масса x (скорость/время) = (масса x скорость)/время = импульс/время Умножение обеих частей этого уравнения на время: сила x время = импульс Чтобы ответить на ваш первоначальный вопрос, разница между силой и импульсом есть время. Ответить Интересно, что это, наряду с третьим законом Ньютона, дает нам закон сохранения импульса. Третий закон Ньютона гласит, что для силы, действующей со стороны объекта 1 на объект 2, объект 2 действует на объект 1 с силой, равной по величине и противоположной по направлению силе, действующей на объект 1. Или, короче, F[1->2] = -F[2->1]. Аналогичный аргумент в пользу сохранения энергии можно привести, используя тот факт, что энергия является интегралом силы по положению. Ответить Ф = м * об/т Умножьте обе стороны на время, чтобы получить F т = м v Поскольку mv — это импульс, мы можем видеть, что импульс, сообщаемый объекту силой, равен произведению силы на время приложения силы. Таким образом, если к изначально неподвижному объекту приложить вправо силу в 15 ньютонов в течение 3 секунд, он будет иметь импульс вправо 45 кг м/с.  |
Зная величину силы и время, в течение которого сила прикладывается к объекту,
сообщить вам результирующее изменение его импульса. 
Теперь полное изменение импульса для любого взаимодействия равно интегралу от F[1->2] по времени плюс интеграл от F[2->1] по времени, что равно интегралу от F[1->2] за вычетом интеграл от F[1->2], равный нулю — всегда!