Момент силы | 7 класс
Содержание
Момент силы зависит от длины плеча. Для многих подобная фраза — просто сухой набор фактов. На самом деле, если разобраться, за терминами «длина плеча», «момент силы» прячутся удобные и вполне понятные физические концепции. На данном уроке мы приподнимем над всем этим завесу тайны, а также откроем для себя условие равновесия и правило моментов. Нюансы а-ля в чем там измеряется момент силы и формула момента силы прилагаются!
Момент силы: вновь Архимед и его рычаг
Поговаривают, что древнейшим открытием и в какой-то степени самым первым научным достижением человека можно смело называть рычаг. Удивительно, но наши предки на уровне интуиции понимали, что увесистый камень намного проще поднять или передвинуть с помощью самой обычной палки. При этом удивляет больше не наличие палки во всей этой истории, а осознание первобытным человеком принципа простых механизмов. Ведь палки первые разумные жители планеты специально искали подлиннее. Они понимали: чем длиннее, тем будет проще совершить работу.
Они понимали: чем длиннее, тем будет проще совершить работу.
«Катить проще, чем тянуть» — еще одно древнейшее «научное» открытие примитивного человека наряду с рычагом.
Принцип рычага передавался из уст в уста, от одного племени к другому, от одного поколения к следующему. Мы не знали, почему это работает. У нас не было формул, не было определений. Был лишь рычаг в самых его разных формах проявления и четкое знание — возьмись подальше от точки опоры, если тяжело.
И лишь в третьем веке до нашей эры Архимед впервые произвел необходимые математические расчеты. Он наконец описал теорию рычага, которой мы пользуемся и по сей день. Он первым связал друг с другом понятия груза, плеча и силы. Как гласит легенда, осознав масштабы своего открытия, воскликнул: «Дайте мне точку опоры, и я переверну Землю!»
Благодаря опытам Архимеда, его фундаментальному пониманию закона равновесия рычага, впоследствии возникла крайне важная физическая величина — момент силы.
Закон равновесия: опыт с грузами
Определить момент силы можно разными способами. Мы воспользуемся самым простым. Нам достаточно вспомнить условие равновесия рычага и провести несложный опыт с подвешенными грузами.
Во-первых, возьмем небольшую деревянную балку. К ее верхнему концу прикрепим болтом мерную линейку таким образом, чтобы крепление располагалось в центре тяжести линейки (рисунок 1). Далее к линейке прикрепим по сантиметровым делениям два крючка, за которые будем подвешивать грузики разной массы. Начнем с отметок $10 \space см$ и $20 \space см$ — по пять влево и вправо от центра тяжести в $15 \space см$.
Рисунок 1. Простая система из линейки, балки, крепления и крючковВозьмем грузик массой $20 \space г$ и подвесим его за крючок (рисунок 2). Очевидно, что рычаг в результате не окажется в положении равновесия.
Рисунок 2. Справа от точки опоры рычага подвешиваем первый грузик массой $20 \space г$Теперь с другой стороны от центра тяжести подвесим грузик массой $40 \space г$ (рисунок 3). Очевидно, что рычаг снова не окажется в положении равновесия: с левой стороны на плечо рычага действует бóльшая сила $mg$.
Очевидно, что рычаг снова не окажется в положении равновесия: с левой стороны на плечо рычага действует бóльшая сила $mg$.
Приводим рычаг в равновесие
Интуитивно мы понимаем, что дабы соблюсти условие равновесия данной системы, один из грузиков нужно куда-то сместить. Мы так же интуитивно понимаем, что если смещать грузик массой $40 \space г$, его нужно подвесить за крючок, располагающийся ближе к точке опоры. Смещать грузик массой $20 \space г$ нужно в другую сторону — подальше от точки опоры.
Вопрос на миллион: если, скажем, мы хотим перевесить двадцатиграммовый грузик, на сколько делений должно увеличиться плечо груза?
Используем стандартный метод проб и ошибок. Перевешивая крючок с грузиком по разным отметкам на линейке, мы обнаружим, что рычаг придет в положение равновесия, если двадцатиграммовый грузик подвесить на расстоянии десяти сантиметров от точки опоры — на отметке $25 \space см$ (рисунок 4). Обратите внимание на то, как пропорциональны получаемые величины: грузики массой $40 \space г$ и $20 \space г$ уравновешивают друг друга на плечах длиной $5 \space см$ и $10 \space см$ соответственно.
Обратите внимание на то, как пропорциональны получаемые величины: грузики массой $40 \space г$ и $20 \space г$ уравновешивают друг друга на плечах длиной $5 \space см$ и $10 \space см$ соответственно.
Условие равновесия
Именно таким образом Архимедом было сформулировано условие равновесия рычага. Можно долго перевешивать грузики, пользоваться различными массами, рычагами короткими, рычагами длинными, но одна вещь всегда будет объединять все элементы и переменные:
Рычаг находится в положении равновесия при условии, что отношение масс, подвешенных грузов, будет обратно пропорционально отношению расстояний от точки опоры до центров тяжести грузов:
$\frac{m_1}{m_2}=\frac{l_2}{l_1}$.
Если от масс перейти к силам, формулу можно улучшить до следующего вида:
$\frac{m_1g}{m_2g} = \frac{l_2}{l_1}$.
Лучше, но все равно не то. Где гарантии, что на наш абстрактный грузик будет действовать только сила тяжести? Ведь на грузик можно и надавить. Так что улучшим пропорцию еще раз и придем к окончательному математическому выражению под условие равновесия:
Так что улучшим пропорцию еще раз и придем к окончательному математическому выражению под условие равновесия:
$\frac{F_1}{F_2} = \frac{l_2}{l_1}$,
где $F_1$ и $F_2$ — силы, действующие на рычаг, $l_1$ и $l_2$ — плечи сил.
Таким образом:
Рычаг находится в положении равновесия, когда отношение сил, действующих на рычаг, обратно пропорционально отношению плеч этих сил.
А теперь заметим, что согласно основному свойству пропорции из формулы выше получается следующее равенство:
$F_1\cdot l_1 = F_2\cdot l_2$.
Ранее мы с подобным не сталкивались — с произведением силы на плечо силы. Именно это произведение и называется в физике момент силы.
Определение момента силы
Момент силы — физическая величина, характеризующая действие силы. Равняется произведению модуля силы на ее плечо.
Формула момента силы соответственно следующая:
$M = F \cdot l$,
где $F$ — модуль силы, $l$ — длина плеча.
Обратите внимание на то, как выглядит формула момента силы: в физике момент силы обозначается заглавной латинской литерой $M$ и измеряется в $Н \cdot м$ — в ньютонах на метр. Характеризует момент силы, как мы указали в определении, действие силы.
Так-так, в чем измеряется момент силы?Еще раз, формула момента силы включает в себя произведение модуля силы на длину плеча. Сила $F$ измеряется в ньютонах. Длина плеча, как и любая другая длина, согласно СИ измеряется в метрах. Ну и в чем же тогда измеряется момент силы? В ньютонах на метр ($H\cdot м$), разумеется.
И как понять, что характеризует момент силы?Возьмем гаечный ключ. Ухватимся рукой за его конец и приложим некоторое усилие, чтобы провернуть гайку. После перехватим гаечный ключ примерно до середины ручки и также попробуем приложить некоторое усилие. Во втором случае провернуть гайку будет сложнее, чем если бы мы держались за конец ручки инструмента.
Причина? Образуются разные величины момента силы! Помните, как мы говорили о механическом выигрыше на прошлом уроке? При нем образуется бóльший момент силы.
Иными словами, момент силы — это и есть в своем роде величина усилия. Чем больше момент, тем быстрее двигается предмет, тем проще он проворачивается, тем легче выполняется действие. Формула момента силы наглядно это демонстрирует.
Как рассчитать момент силы
Момент силы всегда рассчитывается как произведение модуля силы на плечо силы:
$M = F \cdot l$.
Иногда определять приходится результирующий момент — когда на тело действует несколько разнонаправленных сил. Однако подобные «превратности» нам встретятся в программе лишь через пару лет.
Момент силы трапеции
Для примера возьмем нечто отвлеченное от привычных нам двуплечих рычагов — ясно, что внутри подобной механической системы плечо силы чаще всего будет совпадать с плечом рычага, так что сложности как таковой с расчетом плеча силы не возникнет.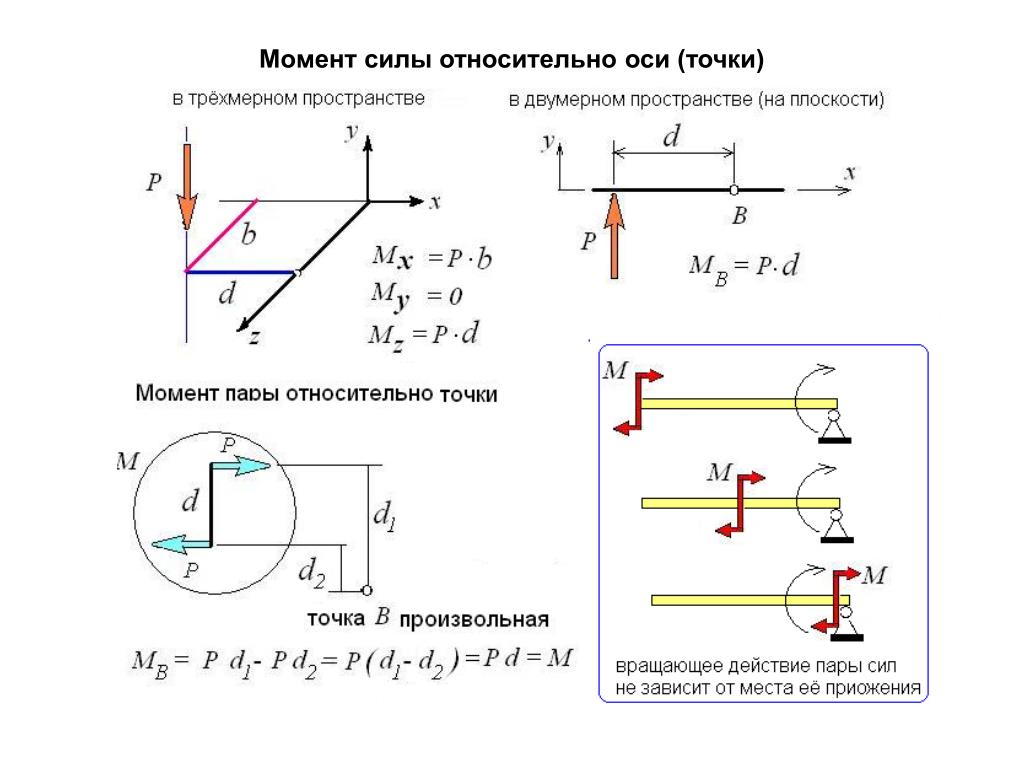 Представим вместо этого, что мы раскручиваем прикрепленную к поверхности фигуру в форме трапеции. Ого!..
Представим вместо этого, что мы раскручиваем прикрепленную к поверхности фигуру в форме трапеции. Ого!..
Итак, наша вращающаяся трапеция. Силу мы прикладываем к концу фигуры — направление силы указано на изображении (рисунок 6). Согласитесь, увидеть плечо силы для подобной схемы движения уже не так просто, особенно когда глаз привык к рычагам.
Рисунок 6. Приложение силы к трапецииНе паникуем и вспоминаем, что плечо силы есть перпендикуляр к линии действия силы, опущенный из точки опоры или, вернее сказать, из оси вращения (рисунок 7).
Рисунок 7. Плечо силы трапецииПлечо силы будет равно длине отрезка $OA$. Ось вращения трапеции находится в точке $О$. Все гениальное просто, согласны?
Знак момента силы
Еще один немаловажный момент при расчете момента силы — знак величины. Момент может быть отрицательным или положительным. Это зависит от того, в каком направлении действует сила, приложенная к телу. Если она вращает тело по часовой стрелке, то момент силы считается положительным. Если наоборот — против часовой стрелки, то момент считается отрицательным.
Если наоборот — против часовой стрелки, то момент считается отрицательным.
Может ли момент быть нулевым? Конечно, почему нет. Логично предположить, что в случае, если плечо силы равно нулю, то сила не создает никакого момента. Например, если вы надавите на ось вращения, сдвинуть при таком приложении силы что-либо невозможно.
Задача на моменты
Образавр предлагает решить задачу самостоятельно!
На земле лежит палка массой $20 \space кг$ и длиной $4 \space м$. Палку приподнимают за конец, прикладывая усилие в $120 \space Н$. Какие моменты при этом создают силы, действующие на доску? Моменты силы тяжести в поднятом положении палки и в вертикальном положении к земле равны.
Дано:
$m = 20 \space кг$
$d = 4 \space м$
$F = 120 \space Н$
$M — ?$
Рисунок 9. Схема рычага к задачеРешение задачи на моменты
Показать решение и ответ
Скрыть
На палку действуют: сила реакции опоры $\vec{N}$, сила тяжести $m\vec{g}$ и внешняя сила, которую мы прикладываем к концу, $\vec{F}$. Ось вращения при этом располагается в точке $B$: мысленно представим, что палка совершает вращательное движение, а так как точка $B$ будет находиться в центре полученной окружности, она и будет считаться осью вращения.
Ось вращения при этом располагается в точке $B$: мысленно представим, что палка совершает вращательное движение, а так как точка $B$ будет находиться в центре полученной окружности, она и будет считаться осью вращения.
Плечо силы реакции опоры $\vec{N}$ равно нулю: точка приложения силы и ось вращения совпадают. Следовательно $M_N$ силы реакции опоры мы можем определить сразу. Он равен нулю:
$M_N = 0$.
Далее опускаем перпендикуляр из оси вращения $B$ к внешней силе $\vec{F}$. Получаем, что плечо внешней силы $\vec{F}$ равно длине палки $d$:
$l_F = d$.
По формуле $M = F \cdot l$, зная, что по условию задачи длина палки составляет $4 \space м$, а модуль внешней силы равен $120 \space Н$, рассчитаем момент внешней силы $M_F$. Вращение происходит по часовой стрелке, следовательно, момент будет положительным по знаку.
Считаем:
$M_F = 120 \cdot 4 = 480 \space H \cdot м$.
Нюанс и финальный расчет
Если допустить, что момент силы тяжести $M_{mg}$ в поднятом положении палки равен моменту в вертикальном положении к земле, то плечо силы тяжести $l_{mg}$ равно половине длины палки:
$l_{mg} = \frac{1}{2} \cdot d =2 \space м$.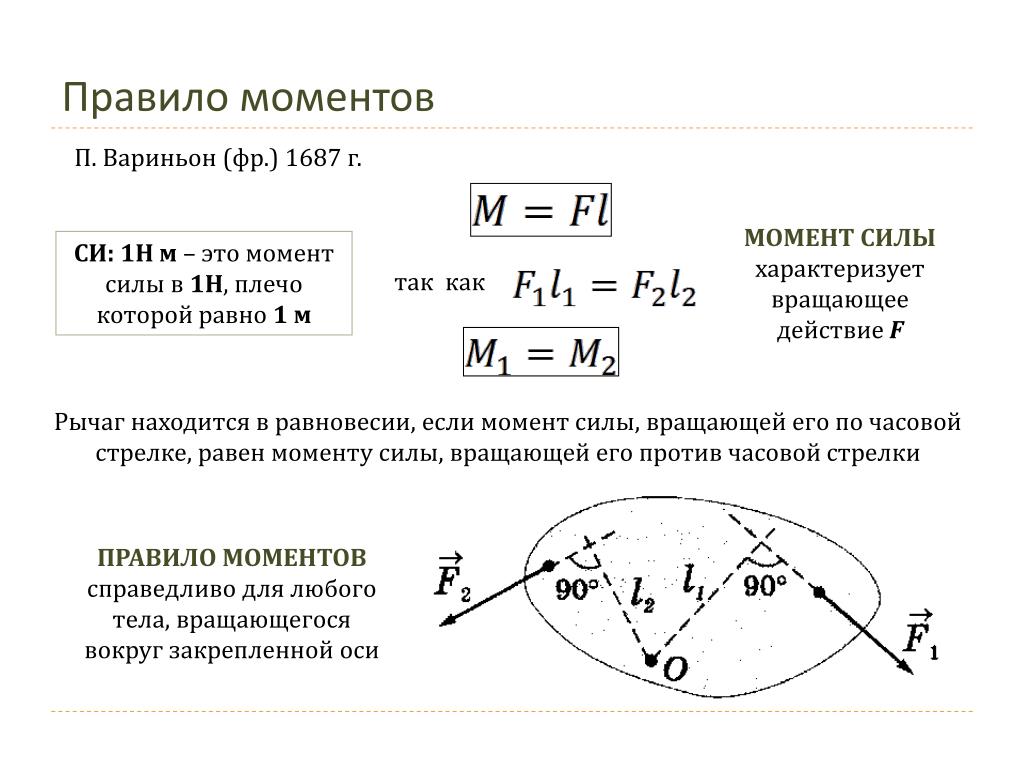
Примечание. Подобное допущение необходимо исключительно для простоты расчетов. Если бы пришлось определять плечо силы тяжести «честно», в задаче также должны фигурировать как минимум высота подъема палки и угол подъема. Для вычисления плеча в треугольнике понадобились бы теорема косинусов и признаки подобия треугольников. Такие дела… Поэтому считаем «нечестно». Нахождением сложных плеч вы будете заниматься в курсе статики для 10 класса.
Теперь рассчитаем момент силы тяжести $M_{mg}$ по формуле моментов, учитывая, что движение происходит против часовой стрелки. Момент отрицательный:
$M_{mg}=-\frac{1}{2}\cdot mg\cdot l_{mg}=-0.5 \cdot 20 \cdot 9.8 \cdot 2 =-196~Н \cdot м$.
Ответ: $M_N = 0$, $M_F = 480 \space Н\cdot м$, $M_{mg} = -196 \cdot Н \cdot м$.
Правило моментов
Остается последнее — разобраться, зачем нужно отрицательное значение момента силы.
Ранее мы говорили о том, что условие равновесия рычага — обратная пропорциональность отношений сил к плечам этих сил. Однако условие равновесия можно задать и через смежное понятие момента силы. В некоторых случаях даже удобнее для вычислений.
Однако условие равновесия можно задать и через смежное понятие момента силы. В некоторых случаях даже удобнее для вычислений.
Вернемся к нашей вращающейся трапеции. Представим, что вы стоите и прикладываете к одному концу трапеции силу $\vec{F}_1$. Ваш друг берется за другой конец трапеции и тянет фигурку в противоположную сторону c силой $\vec{F}_2$. Вы в одну сторону, он в другую. При этом трапеция вращаться никуда не хочет. Она упрямо находится в положении равновесия. Но, казалось бы, моменты сил создаются. Где движение?
Правило моментов — формула
Дело в том, что один момент силы, условно говоря, «гасит» другой. Математически вычитается. Как только создаваемый вами момент силы превысит тот, что создается вашим другом, фигурка начнет движение по часовой стрелке, к вам. Если друг поднажмет, то трапеция пойдет против часовой стрелки, от вас.
Таким образом, мы можем складывать все моменты, действующие на тело, чтобы понимать, движется ли тело, и если да, то в какую сторону.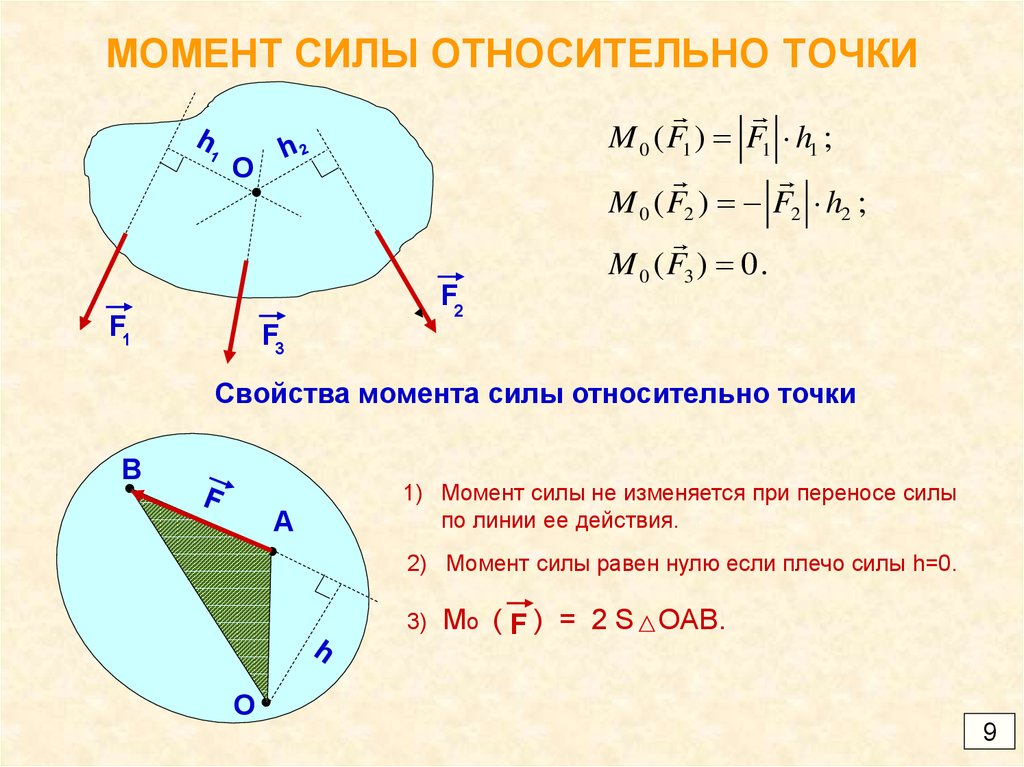 Знак числа — удобный математический инструмент, позволяющий работать с направлениями. Если сумма всех моментов положительна, вращательное движение идет по часовой стрелке. Если отрицательна — против часовой.
Знак числа — удобный математический инструмент, позволяющий работать с направлениями. Если сумма всех моментов положительна, вращательное движение идет по часовой стрелке. Если отрицательна — против часовой.
А если сумма моментов равна нулю?
Логично, что тогда тело находится в положении равновесия. Оно не двигается. Вот как мы можем получить условие равновесия (неважно — рычага или другого тела), выраженное через момент силы.
Подобное равенство называется правило моментов.
Тело находится в состоянии покоя, если алгебраическая сумма всех моментов сил, приложенных к телу, равняется нулю:
$\sum_i M_i= M_1+M_2+…+M_i =0$.
{"questions":[{"content":"Момент силы рассчитывается по формуле[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["$M = \\frac{F}{l}$","$M = Fl$","$M = \\frac{F_1l_1}{F_2l_2}$","$M = Al$"],"answer":[1]}},"hints":[]}]}Момент силы относительно оси его свойства.
 Момент силы относительно оси
Момент силы относительно осиКогда решают задачи на перемещение объектов, то в ряде случаев пренебрегают их пространственными размерами, вводя понятие материальной точки. Для другого типа задач, в которых рассматриваются покоящиеся или вращающиеся тела, важно знать их параметры и точки приложения внешних сил. В этом случае речь идет о моменте сил относительно оси вращения. Рассмотрим этот вопрос в статье.
Понятие о моменте силы
Перед тем как приводить относительно оси вращения неподвижной, необходимо пояснить, о каком явлении пойдет речь. Ниже дан рисунок, на котором изображен гаечный ключ длиной d, к концу его приложена сила F. Нетрудно представить, что результатом ее воздействия будет вращение ключа против часовой стрелки и откручивание гайки.
Согласно определению, момент силы относительно оси вращения представляет собой произведение плеча (d в данном случае) на силу (F), то есть можно записать следующее выражение: M = d*F. Сразу же следует оговориться, что приведенная формула записана в скалярном виде, то есть она позволяет рассчитать абсолютное значение момента M.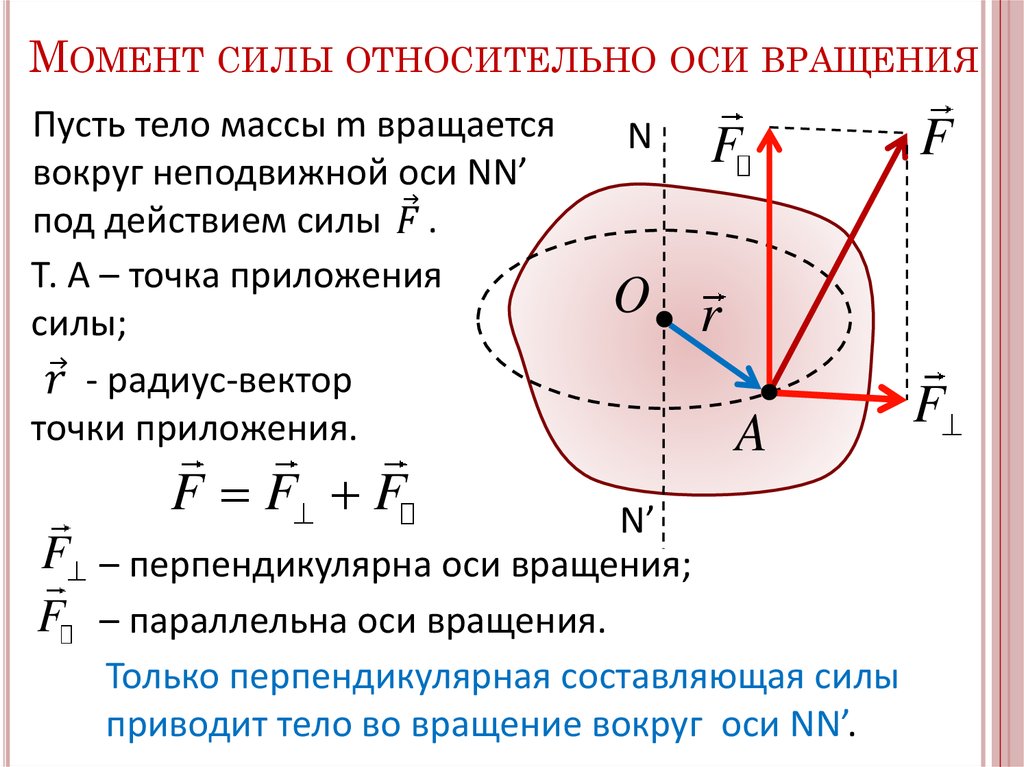 Как видно из формулы, единицей измерения рассматриваемой величины являются ньютоны на метр (Н*м).
Как видно из формулы, единицей измерения рассматриваемой величины являются ньютоны на метр (Н*м).
— векторная величина
Как выше было оговорено, момент M в действительности представляет собой вектор. Для пояснения этого утверждения рассмотрим другой рисунок.
Здесь мы видим рычаг длиной L, который закреплен на оси (показано стрелкой). К его концу приложена сила F под углом Φ. Нетрудно себе представить, что эта сила будет вызывать подъем рычага. Формула для момента в векторной форме в этом случае запишется так: M¯ = L¯*F¯, здесь черта над символом означает, что рассматриваемая величина — это вектор. Следует пояснить, что L¯ направлен от к точке приложения силы F¯.
Приведенное выражение является векторным произведением. Его результирующий вектор (M¯) будет направлен перпендикулярно плоскости, образованной L¯ и F¯. Для определения направления момента M¯ существуют несколько правил (правой руки, буравчика). Чтобы не заучивать их и не путаться в порядке умножения векторов L¯ и F¯ (от него зависит направление M¯), следует запомнить одну простую вещь: момент силы будет направлен таким образом, что если смотреть с конца его вектора, то воздействующая сила F¯ будет вращать рычаг против часовой стрелки. Это направление момента условно принято за положительное. Если же система совершает вращение по часовой стрелки, значит, результирующий момент сил имеет отрицательное значение.
Это направление момента условно принято за положительное. Если же система совершает вращение по часовой стрелки, значит, результирующий момент сил имеет отрицательное значение.
Таким образом, в рассматриваемом случае с рычагом L величина M¯ направлена вверх (от рисунка к читателю).
В скалярной форме формула для момента запишется в виде: M = L*F*sin(180-Φ) или M = L*F*sin(Φ) (sin(180-Φ) = sin(Φ)). Согласно определению синуса, можно записать равенство: M = d*F, где d = L*sin(Φ) (см. рисунок и соответствующий прямоугольный треугольник). Последняя формула является аналогичной той, которая была приведена в предыдущем пункте.
Проведенные выше вычисления демонстрируют, как работать с векторными и скалярными величинами моментов сил, чтобы не допустить ошибок.
Физический смысл величины M¯
Поскольку два рассмотренных в предыдущих пунктах случая связаны с вращательным движением, то можно догадаться, какой смысл несет момент силы. Если сила, действующая на материальную точку, является мерой увеличения скорости линейного перемещения последней, то момент силы — это мера ее вращательной способности применительно к рассматриваемой системе.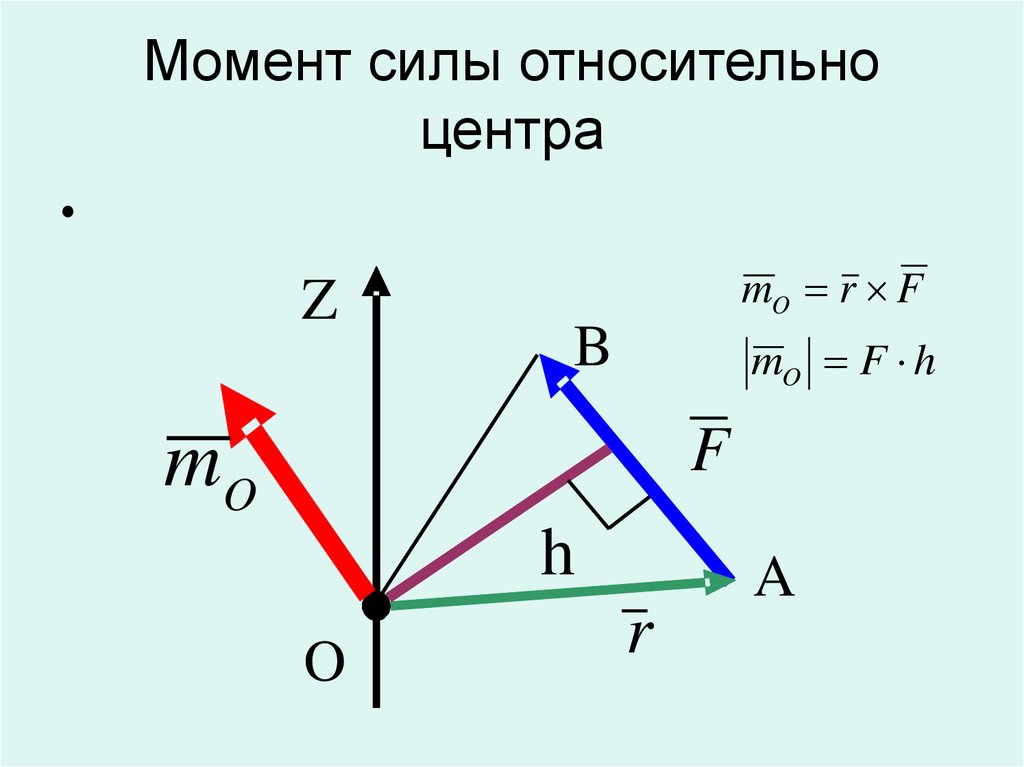
Приведем наглядный пример. Любой человек открывает дверь, взявшись за ее ручку. Также это можно сделать, если толкнуть дверь в зоне ручки. Почему никто не открывает ее, толкая в области петель? Очень просто: чем ближе к петлям приложена сила, тем труднее открыть дверь, и наоборот. Вывод предыдущего предложения следует из формулы для момента (M = d*F), откуда видно, что при M = const величины d и F находятся в обратной зависимости.
Момент силы — аддитивная величина
Во всех рассмотренных выше случаях имела место лишь одна действующая сила. При решении же реальных задач дело обстоит гораздо сложнее. Обычно на системы, которые вращаются или находятся в равновесии, действуют несколько сил кручения, каждая из которых создает свой момент. В этом случае решение задач сводится к нахождению суммарного момента сил относительно оси вращения.
Суммарный момент находится путем обычной суммы отдельных моментов для каждой силы, однако, следует не забывать использовать правильный знак для каждого из них.
Пример решения задачи
Для закрепления полученных знаний предлагается решить следующую задачу: необходимо вычислить суммарный момент силы для системы, изображенной на рисунке ниже.
Мы видим, что на рычаг длиной 7 м действуют три силы (F1, F2, F3), причем они имеют разные точки приложения относительно оси вращения. Поскольку направление сил перпендикулярно рычагу, то нет необходимости применять векторное выражение для момента кручения. Можно рассчитать суммарный момент M, используя скалярную формулу и не забывая о постановке нужного знака. Поскольку силы F1 и F3 стремятся повернуть рычаг против часовой стрелки, а F2 — по часовой стрелке, то момент вращения для первых будет положительным, а для второй — отрицательным. Имеем: M = F1*7-F2*5+F3*3 = 140-50+75 = 165 Н*м. То есть суммарный момент является положительным и направлен вверх (на читателя).
Моментом силы относительно оси вращения называется физическая величина, равная произведению силы на ее плечо.
Момент силы определяют по формуле:
М — FI , где F — сила, I — плечо силы.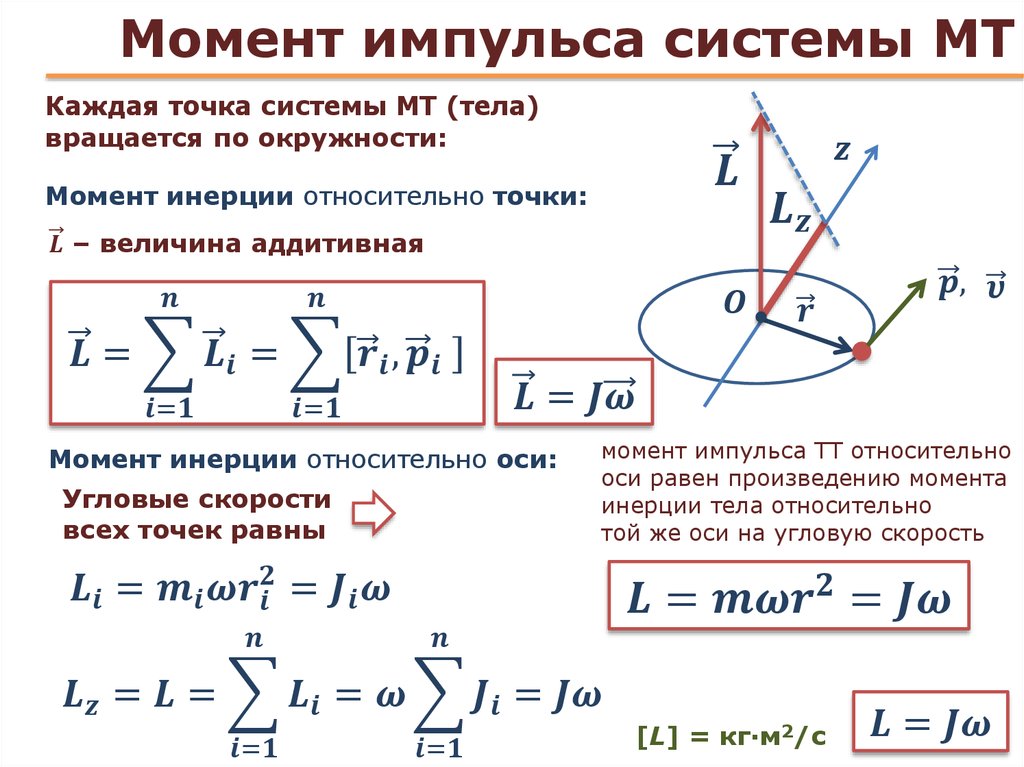
Плечом силы называется кратчайшее расстояние от линии действия силы до оси вращения тела.
На рис. 1.33, а изображено твердое тело, способное вращаться вокруг оси. Ось вращения этого тела перпендикулярна плоскости рисунка и проходит через точку, обозначенную буквой О. Плечом силы F здесь является расстояние 1Хот оси вращения до линии действия силы. Находят его следующим образом. Сначала проводят линию действия силы. Затем из точки О, через которую проходит ось вращения тела, опускают на линию действия силы перпендикуляр. Длина этого перпендикуляра является плечом данной силы.
Момент силы характеризует вращающее действие силы. Это действие зависит как от силы, так и от плеча. Чем больше плечо, тем меньшую силу надо приложить, чтобы получить желаемый результат, т. е. один и тот же момент силы (см. (1.33)). Именно поэтому открыть дверь, толкая ее возле петель, гораздо труднее, чем берясь за ручку, а гайку отвернуть гораздо проще длинным, чем коротким гаечным ключом.
За единицу момента силы в СИ принимается момент силы в 1 Н, плечо которой равно 1м — ньютон-метр (Н м).
Правило моментов
Твердое тело, способное вращаться вокруг неподвижной оси, находится в равновесии, если момент силы М, вращающей его по часовой стрелке, равен моменту силы М2, вращающей его против часовой стрелки:
М1 = -М2 или F 1 ll = — F 2 l 2 .
Правило моментов является следствием одной из теорем механики, сформулированной французским ученым П. Вариньоном в 1687 г.
Если на тело действуют две равные и противоположно направленные силы, не лежащие на одной прямой, то такое тело не находится в равновесии, поскольку результирующий момент этих сил относительно любой оси не равен нулю, т. к. обе силы имеют моменты, направленные в одну сторону. Две такие силы, одновременно действующие на тело, называют парой сил. Если тело закреплено на оси, то под действием пары сил оно будет вращаться. Если пара сил приложена ксвободному телу, то оно будет вращаться вокруг оси, проходящей через центр тяжести тела, рис.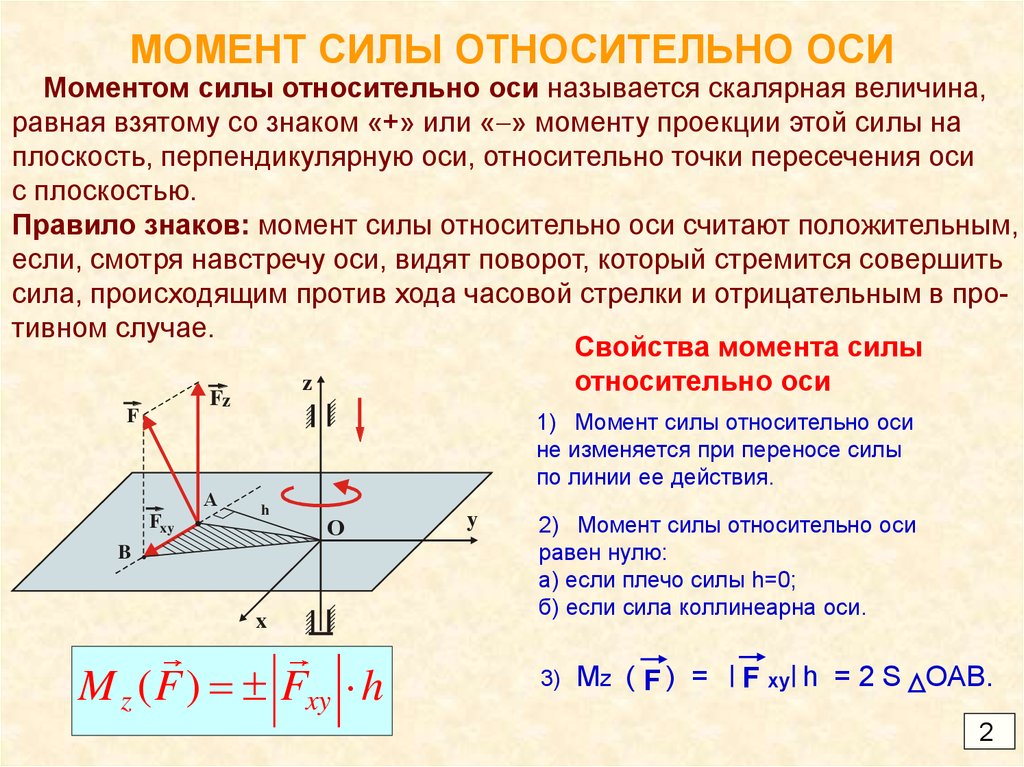
Момент пары сил одинаков относительно любой оси, перпендикулярной к плоскости пары. Суммарный момент М пары всегда равен произведению одной из сил F на расстояние I между силами, которое называется плечом пары,независимо от того, на какие отрезки и /2 разделяет положение оси плечо пары:
M = Fll + Fl2=F(l1 + l2) = Fl.
Момент нескольких сил, равнодействующая которых равна нулю, будет одинаковым относительно всех осей, параллельных друг другу, поэтому действие всех этих сил на тело можно заменить действием одной пары сил с тем же моментом.
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент ) — векторная физическая величина , равная векторному произведению радиус-вектора , проведённого от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело .
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Энциклопедичный YouTube
1 / 5
7 кл — 39. Момент силы. Правило моментов
Момент силы тяжести.Гантеля и рука
Сила и масса
Момент силы. Рычаги в природе, технике, быту | Физика 7 класс #44 | Инфоурок
Зависимость углового ускорения от момента сил 1
Субтитры
Общие сведения
Специальные случаи
Формула момента рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
| M → | = | M → 1 | | F → | {\displaystyle \left|{\vec {M}}\right|=\left|{\vec {M}}_{1}\right|\left|{\vec {F}}\right|} , где: | M → 1 | {\displaystyle \left|{\vec {M}}_{1}\right|} — момент рычага, | F → | {\displaystyle \left|{\vec {F}}\right|} — величина действующей силы.
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину. Если сила перпендикулярна вектору r → {\displaystyle {\vec {r}}} , момент рычага будет равен расстоянию до центра и момент силы будет максимален:
| T → | = | r → | | F → | {\displaystyle \left|{\vec {T}}\right|=\left|{\vec {r}}\right|\left|{\vec {F}}\right|}
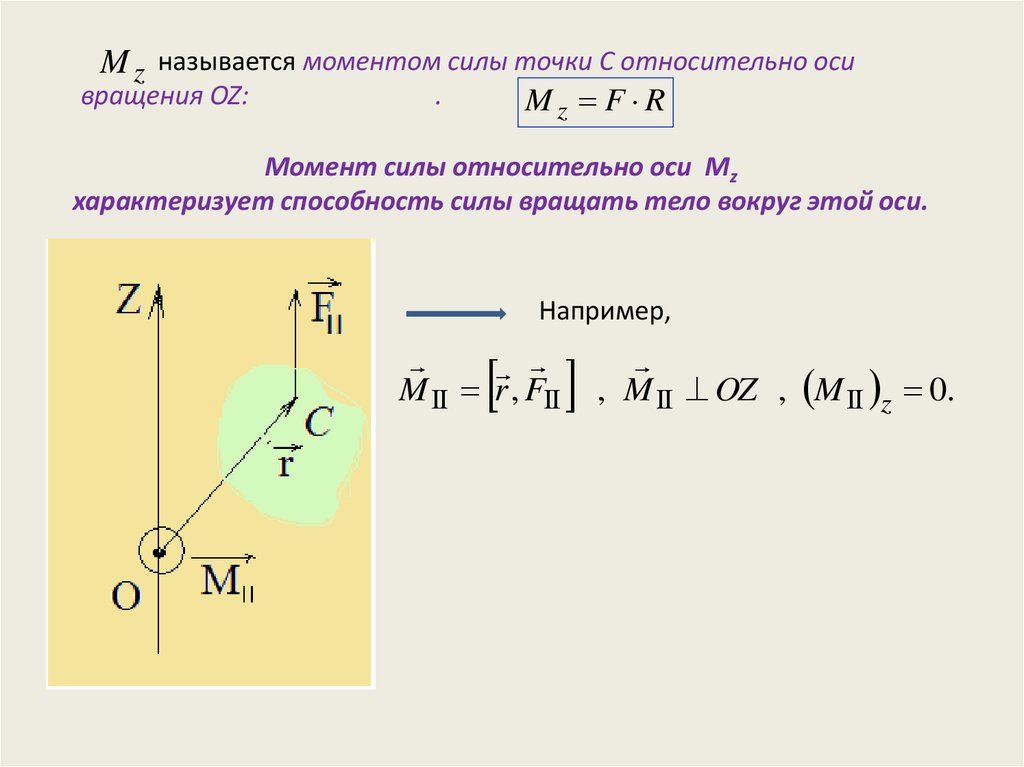
Сила под углом
Если сила
F
→
{\displaystyle {\vec {F}}}
направлена под углом
θ
{\displaystyle \theta }
к рычагу r, то
M
=
r
F
sin
θ
{\displaystyle M=rF\sin \theta }
.
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для двумерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении ΣM=0.
Момент силы как функция от времени
M → = d L → d t {\displaystyle {\vec {M}}={\frac {d{\vec {L}}}{dt}}} ,
где L → {\displaystyle {\vec {L}}} — момент импульса.
Возьмём твердое тело. Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.
Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.
L o → = I c ω → + [ M (r o → − r c →) , v c → ] {\displaystyle {\vec {L_{o}}}=I_{c}\,{\vec {\omega }}+}
Будем рассматривать вращающиеся движения в системе координат Кёнига , так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.
Продифференцируем это выражение по времени. И если I {\displaystyle I} — постоянная величина во времени, то
M → = I d ω → d t = I α → {\displaystyle {\vec {M}}=I{\frac {d{\vec {\omega }}}{dt}}=I{\vec {\alpha }}} ,
где α → {\displaystyle {\vec {\alpha }}} — угловое ускорение , измеряемое в радианах в секунду за секунду (рад/с 2). Пример: вращается однородный диск.
Если тензор инерции меняется со временем, то движение относительно центра масс описывается с помощью динамического уравнения Эйлера:
M c → = I c d ω → d t + [ w → , I c w → ] {\displaystyle {\vec {M_{c}}}=I_{c}{\frac {d{\vec {\omega }}}{dt}}+[{\vec {w}},I_{c}{\vec {w}}]} .
В физике рассмотрение задач с вращающимися телами или системами, которые находятся в равновесии, осуществляется с использованием концепции «момент силы». В этой статье будет рассмотрена формула момента силы, а также ее использование для решения указанного типа задач.
в физике
Как было отмечено во введении, в данной статье пойдет речь о системах, которые могут вращаться либо вокруг оси, либо вокруг точки. Рассмотрим пример такой модели, изображенной на рисунке ниже.
Мы видим, что рычаг серого цвета закреплен на оси вращения. На конце рычага имеется черный кубик некоторой массы, на который действует сила (красная стрелка). Интуитивно понятно, что результатом воздействия этой силы будет вращение рычага вокруг оси против часовой стрелки.
Моментом силы называется величина в физике, которая равна векторному произведению радиуса, соединяющего ось вращения и точку приложения силы (зеленый вектор на рисунке), и самой внешней силе. То есть силы относительно оси записывается следующим образом:
Результатом этого произведения будет вектор M¯. Направление его определяют, исходя из знания векторов-множителей, то есть r¯ и F¯. Согласно определению векторного произведения, M¯ должен быть перпендикулярен плоскости, образованной векторами r¯ и F¯, и направлен в соответствии с правилом правой руки (если четыре пальца правой руки расположить вдоль первого умножаемого вектора в направлении к концу второго, то отставленный вверх большой палец укажет, куда направлен искомый вектор). На рисунке можно видеть, куда направлен вектор M¯ (синяя стрелка).
На рисунке можно видеть, куда направлен вектор M¯ (синяя стрелка).
Скалярная форма записи M¯
На рисунке в предыдущем пункте сила (красная стрелка) действует на рычаг под углом 90 o . В общем же случае она может быть приложена под совершенно любым углом. Рассмотрим изображение ниже.
Здесь мы видим, что на рычаг L сила F уже действует под некоторым углом Φ. Для этой системы формула момента силы относительно точки (показана стрелкой) в скалярном виде примет форму:
M = L * F * sin(Φ)
Из выражения следует, что момент силы M будет тем больше, чем ближе направление действия силы F к углу 90 o по отношению к L. Наоборот, если F действует вдоль L, то sin(0) = 0, и сила не создает никакого момента (M = 0).
При рассмотрении момента силы в скалярной форме часто пользуются понятием «рычага силы». Эта величина представляет собой расстояние между осью (точкой вращения) и вектором F. Применяя это определение к рисунку выше, можно сказать, что d = L * sin(Φ) — это рычаг силы (равенство следует из определения тригонометрической функции «синус»). Через рычаг силы формулу для момента M можно переписать так:
Через рычаг силы формулу для момента M можно переписать так:
Физический смысл величины M
Рассматриваемая физическая величина определяет способность внешней силы F оказывать вращательное воздействие на систему. Чтобы привести тело во вращательное движение, ему необходимо сообщить некоторый момент M.
Ярким примером этого процесса является открывание или закрывание двери в комнату. Взявшись за ручку, человек прикладывает усилие и поворачивает дверь на петлях. Каждый сможет это сделать. Если же попытаться открыть дверь, воздействуя на нее вблизи петель, то потребуется приложить большие усилия, чтобы сдвинуть ее с места.
Другим примером является откручивание гайки ключом. Чем короче будет этот ключ, тем труднее выполнить поставленную задачу.
Указанные особенности демонстрирует формула момента силы через плечо, которая была приведена в предыдущем пункте. Если M считать постоянной величиной, то чем меньше d, тем большую F следует приложить для создания заданного момента силы.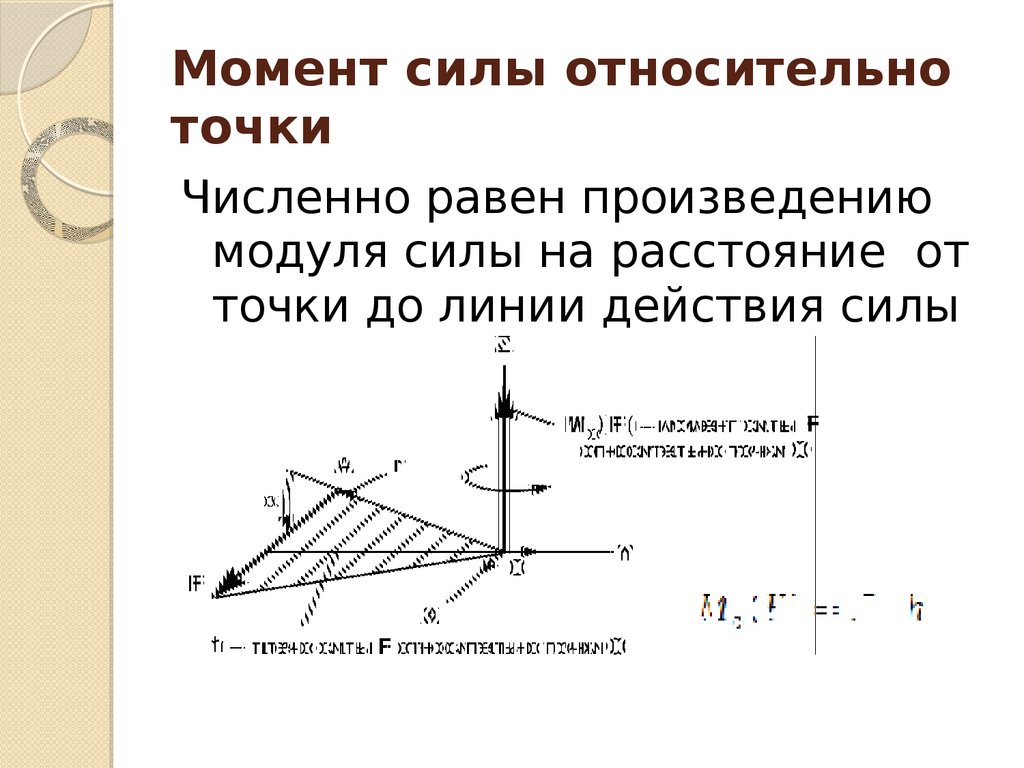
Несколько действующих сил в системе
Выше были рассмотрены случаи, когда на систему, способную к вращению, действует всего одна сила F, но как быть, когда таких сил несколько? Действительно, эта ситуация является более частой, поскольку на систему могут действовать силы различной природы (гравитационная, электрическая, трение, механическая и другие). Во всех этих случаях результирующий момент силы M¯ может быть получен с помощью векторной суммы всех моментов M i ¯, то есть:
M¯ = ∑ i (M i ¯), где i — номер силы F i
Из свойства аддитивности моментов следует важный вывод, который получил название теоремы Вариньона, названной так по фамилии математика конца XVII — начала XVIII века — француза Пьера Вариньона. Она гласит: «Сумма моментов всех сил, оказывающих воздействие на рассматриваемую систему, может быть представлена в виде момента одной силы, которая равна сумме всех остальных и приложена к некоторой точке». Математически теорему можно записать так:
∑ i (M i ¯) = M¯ = d * ∑ i (F i ¯)
Эта важная теорема часто используется на практике для решения задач на вращение и равновесие тел.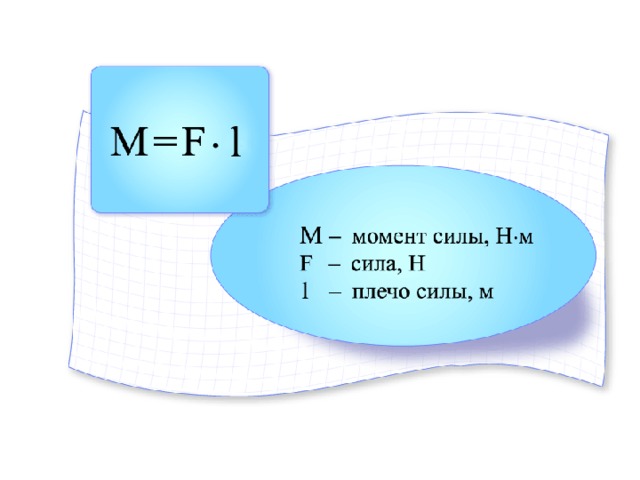
Совершает ли работу момент силы?
Анализируя приведенные формулы в скалярном или векторном виде, можно прийти к выводу, что величина M — это некоторая работа. Действительно, ее размерность равна Н*м, что в СИ соответствует джоулю (Дж). На самом деле момент силы — это не работа, а лишь величина, которая способна ее совершить. Чтобы это произошло, необходимо наличие кругового движения в системе и продолжительного во времени действия M. Поэтому формула работы момента силы записывается в следующем виде:
В этом выражении θ — это угол, на который было произведено вращение моментом силы M. В итоге единицу работы можно записать как Н*м*рад или же Дж*рад. Например, значение 60 Дж*рад говорит о том, что при повороте на 1 радиан (приблизительно 1/3 окружности) создающая момент M сила F совершила работу в 60 джоулей. Эту формулу часто используют при решении задач в системах, где действуют силы трения, что будет показано ниже.
Момент силы и момент импульса
Как было показано, воздействие на систему момента M приводит к появлению в ней вращательного движения. Последнее характеризуется величиной, которая получила название «момент импульса». Его можно вычислить, применяя формулу:
Последнее характеризуется величиной, которая получила название «момент импульса». Его можно вычислить, применяя формулу:
Здесь I — это момент инерции (величина, которая играет такую же роль при вращении, что и масса при линейном движении тела), ω — угловая скорость, она связана с линейной скоростью формулой ω = v/r.
Оба момента (импульса и силы) связаны друг с другом следующим выражением:
M = I * α, где α = dω / dt — угловое ускорение.
Приведем еще одну формулу, которая важна для решения задач на работу моментов сил. С помощью этой формулы можно вычислить кинетическую энергию вращающегося тела. Она выглядит так:
Равновесие нескольких тел
Первая задача связана с равновесием системы, в которой действуют несколько сил. На рисунке ниже приведена система, на которую действуют три силы. Необходимо рассчитать, какой массы предмет необходимо подвесить к этому рычагу и в какой точке это следует сделать, чтобы данная система находилась в равновесии.
Из условия задачи можно понять, что для ее решения следует воспользоваться теоремой Вариньона.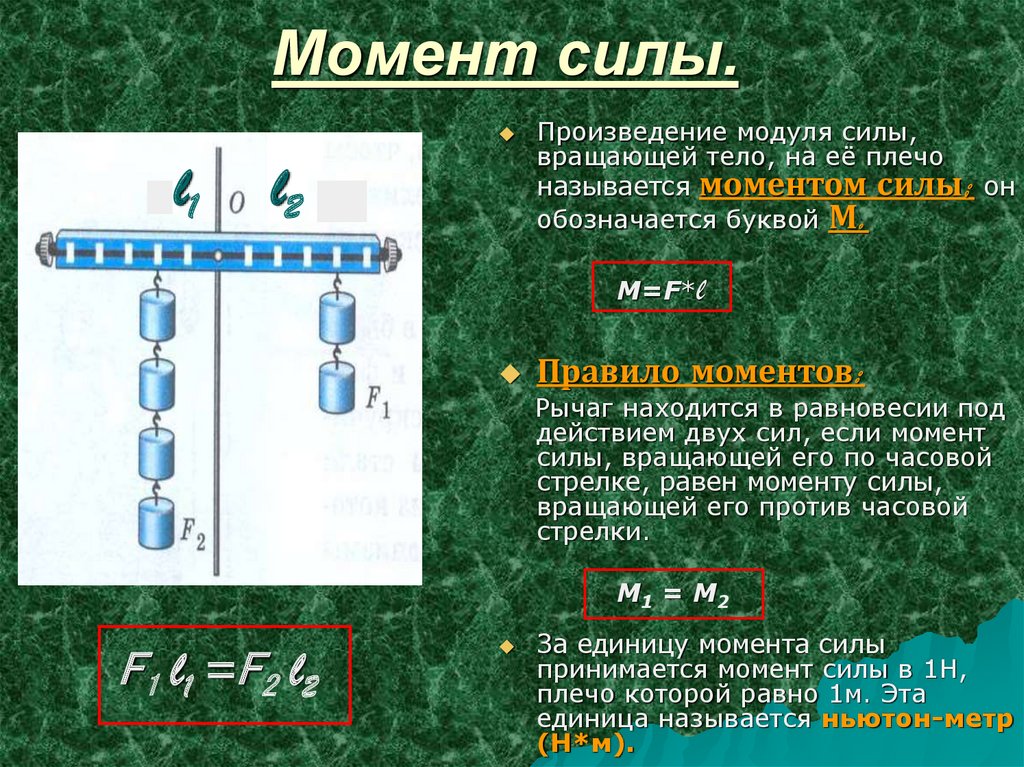 На первую часть задачи можно ответить сразу, поскольку вес предмета, которые следует подвесить к рычагу, будет равен:
На первую часть задачи можно ответить сразу, поскольку вес предмета, которые следует подвесить к рычагу, будет равен:
P = F 1 — F 2 + F 3 = 20 — 10 + 25 = 35 Н
Знаки здесь выбраны с учетом того, что сила, вращающая рычаг против часовой стрелки, создает отрицательный момент.
Положение точки d, куда следует подвесить этот вес, вычисляется по формуле:
M 1 — M 2 + M 3 = d * P = 7 * 20 — 5 * 10 + 3 * 25 = d * 35 => d = 165/35 = 4,714 м
Отметим, что с помощью формулы момента силы тяжести мы вычислили эквивалентную величину M той, которую создают три силы. Чтобы система находилась в равновесии, необходимо подвесить тело весом 35 Н в точке 4,714 м от оси с другой стороны рычага.
Задача с движущимся диском

Эту задачу легче всего решить, если воспользоваться законом сохранения энергии. Мы располагаем начальной кинетической энергией диска. Когда он начнет катиться, то вся эта энергия расходуется на нагрев поверхности за счет действия силы трения. Приравнивая обе величины, получим выражение:
I * ω 2 /2 = μ * N/r * r * θ
Первая часть формулы — это кинетическая энергия диска. Вторая часть — это работа момента силы трения F = μ * N/r, приложенной к краю диска (M=F * r).
Учитывая, что N = m * g и I = 1/2m * r 2 , вычисляем θ:
θ = m * r 2 * ω 2 /(4 * μ * m * g) = r 2 * ω 2 /(4 * μ *g) = 0,3 2 * 1 2 /(4 * 0,001 * 9,81) = 2,29358 рад
Поскольку 2pi радиан соответствуют длине 2pi * r, тогда получаем, что искомое расстояние, которое пройдет диск, равно:
s = θ * r = 2,29358 * 0,3 = 0,688 м или около 69 см
Отметим, что на данный результат масса диска никак не влияет.
Моментом
силы относительно
произвольного центра в плоскости
действия силы, называется произведение
модуля силы на плечо.
Плечо — кратчайшее расстояние от центра О до линии действия силы, но не до точки приложения силы, т.к. сила-скользящий вектор.
Знак момента:
По часовой-минус, против часовой-плюс;
Момент силы можно выразить как вектор. Это перпендикуляр к плоскости по правилу Буравчика.
Если в плоскости расположены несколько сил или система сил, то алгебраическая сумма их моментов даст нам главный момент системы сил.
Рассмотрим момент силы относительно оси, вычислим момент силы относительно оси Z;
Спроецируем F на XY;
F xy =Fcosα = ab
m 0 (F xy)=m z (F), то есть m z =F xy * h = Fcosα * h
Момент силы относительно оси равен моменту ее проекции на плоскость перпендикулярную оси, взятому на пересечении осей и плоскости
Если сила параллельна оси или пересекает ее, то m z (F)=0
Выражение момента силы в виде векторного выражения
Проведем
r а
в точку A.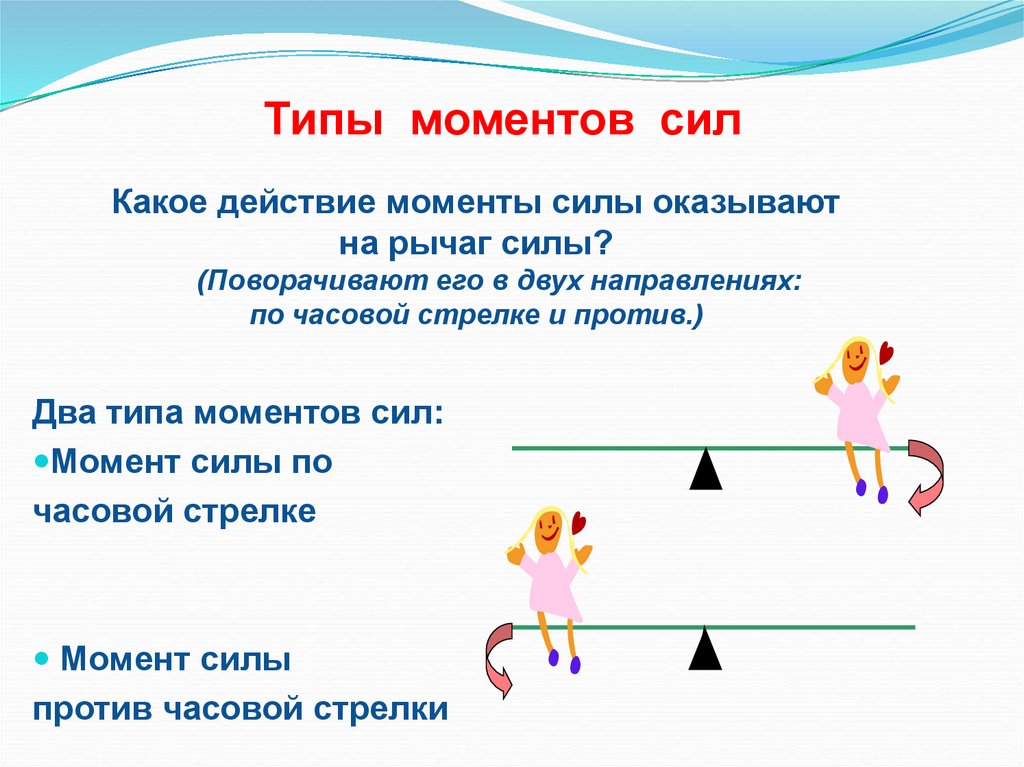 Рассмотрим OA
x
F.
Рассмотрим OA
x
F.
Это третий вектор m o , перпендикулярный плоскости. Модуль векторного произведения можно вычислить с помощью удвоенной площади заштрихованного треугольника.
Аналитическое выражение силы относительно координатных осей.
Предположим, что с точкой О связаны оси Y и Z, X с единичными векторами i, j, k Учитывая, что:
r x =X * Fx ; r y =Y * F y ; r z =Z * F y получим: m o (F)=x =
Раскроем определитель и получим:
m x =YF z — ZF y
m y =ZF x — XF z
m z =XF y — YF x
Эти формулы дают возможность вычислить проекцию вектор-момента на оси, а потом и сам вектор-момент.
Теорема Вариньона о моменте равнодействующей
Если система сил имеет равнодействующую, то её момент относительно любого центра равен алгебраической сумме моментов всех сил относительно этой точки
Если приложить Q= -R , то система (Q,F 1 … F n) будет равен уравновешиваться.
Сумма
моментов относительно любого центра
будет равен нулю.
Аналитическое условие равновесия плоской системы сил
Это плоская система сил, линии действия которых расположены в одной плоскости
Цель расчета задач данного типа — определение реакций внешних связей. Для этого используются основные уравнения в плоской системе сил.
Могут использоваться 2 или 3 уравнения моментов.
Пример
Составим уравнение суммы всех сил на ось X и Y.
I.4.1 МОМЕНТ СИЛЫ И МОМЕНТ ИНЕРЦИИ
Основная задача динамики вращательного движения — определение угловых координат точек вращающегося тела в любой момент времени по известным начальным угловым координатам, угловым скоростям и по заданным моментам внешних сил, действующих на тело.
Твёрдое тело – тело, все части которого неизменно сохраняют своё расположение; конфигурация частей твёрдого тела не изменяется даже при действии внешних сил. В частности, неизменными остаются расстояния между его частями.
Это идеальное представление об абсолютно твёрдом теле (см. определение в § I.1.1). В реальности же все существующие в природе твёрдые тела деформируются под действием сил, однако, деформации многих твёрдых тел очень малы относительно прикладываемых к ним сил и поэтому мы можем смело пользоваться упрощённой моделью абсолютно твёрдого тела.
определение в § I.1.1). В реальности же все существующие в природе твёрдые тела деформируются под действием сил, однако, деформации многих твёрдых тел очень малы относительно прикладываемых к ним сил и поэтому мы можем смело пользоваться упрощённой моделью абсолютно твёрдого тела.
Абсолютно твёрдое тело, имеющее закреплённую ось вращения, без воздействия моментов внешних сил не изменяет угловой скорости вращательного движения. При этом в инерциальной системе отсчёта тело либо покоится ( ), либо вращается с постоянной угловой скоростью, одинаковой для всех точек тела и .
Вращение тела вокруг оси под действием одной силы может быть остановлено действием второй силы (рис.33). Если две силы и по отдельности вызывают вращение тела в противоположных направлениях, то при их одновременном действии тело находится в равновесии, если выполняется условие: ;
где и — радиус-вектор (плечо силы – кратчайшее расстояние от оси вращения до линии действия силы).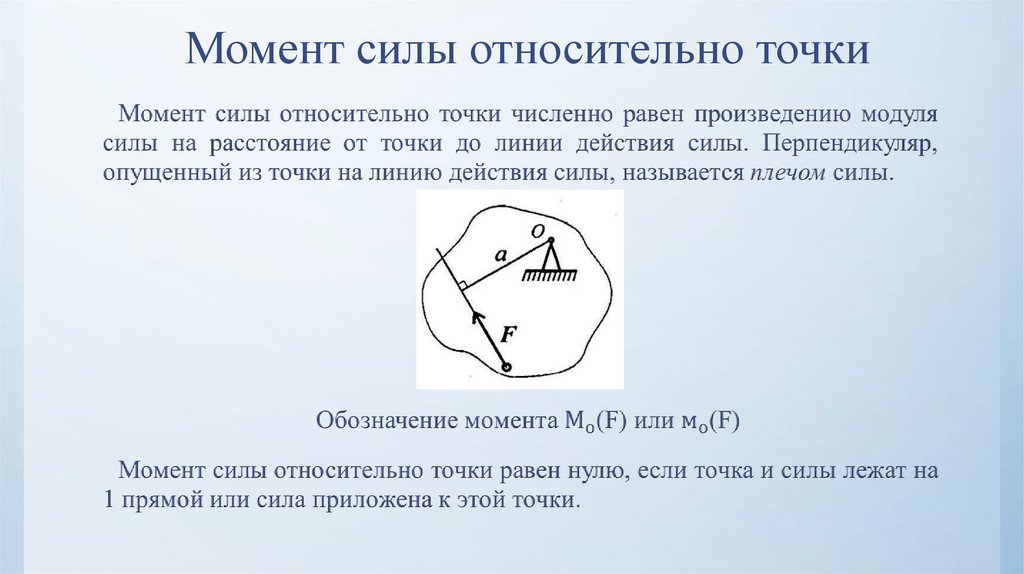 Из рисунка 35следует, что а .
Из рисунка 35следует, что а .
Моментом силы относительно неподвижной точки называется физическая величина, определяемая векторным произведением радиус-вектора , проведённого из точки в точку приложения силы (на рис. 33, это точки и ), на силу :
(I.96)
|
Момент силы является псевдовектором, его направление совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора к силе .
Модуль момента силы:
(I.97)
За единицу вращающего момента в СИ принимается момент силы в 1Н, линия действия которой находится на расстоянии 1 м от оси вращения. Эту единицу называют ньютон – метром (Н·м).
Суммарный момент нескольких сил, действующих на тело, равен алгебраической сумме моментов всех сил относительно данной оси:
. (I.98)
(I.98)
Если моментам сил, вызывающим вращение тела вокруг оси по часовой стрелке, приписать положительный знак, а моментам сил, вызывающим вращение против часовой стрелки, — отрицательный знак, то условие равновесия тела, имеющего ось вращения, можно сформулировать в виде правила моментов.
Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
.
Общее условие равновесия тел: тело находится в равновесии, если равны нулю геометрическая сумма векторов всех приложенных к нему сил и алгебраическая сумма моментов этих сил относительно оси вращения.
Моментом инерции материальной точки относительно данной оси называется физическая величина , равная произведению массы точки на квадрат её расстояния от оси:
.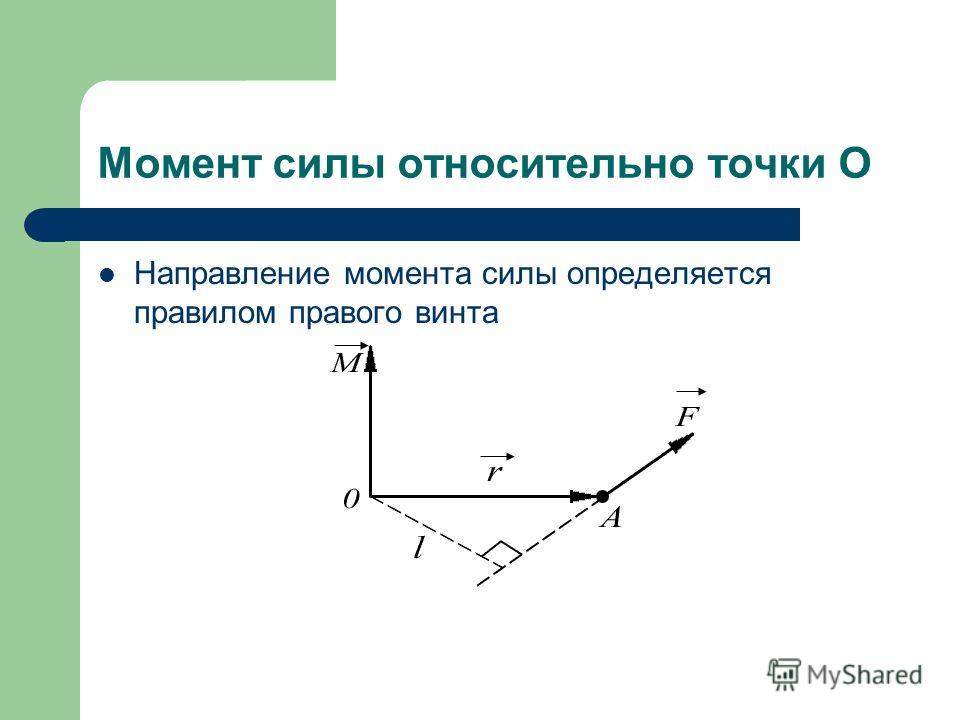 (I.99)
(I.99)
Рассматривая твёрдое тело как систему неизменно соединённых между собой материальных точек с массами , расположенных на расстояниях от оси вращения (рис.34). Каждая из этих точек имеет свой момент инерции ; сумму моментов инерции всех точек, составляющих данное тело, будем называть — моментом инерции тела относительно оси вращения: ; или
. (I.100)
Исходя из формулы (I.100), можно дать следующее определение момента инерции тела.
Моментом инерции тела (механической системы) относительно неподвижной оси называется физическая величина , равная сумме произведений масс всех материальных точек тела (системы) на квадраты их расстояний до оси.
В случае непрерывного распределения масс эта сумма сводится к интегралу вида:
, (I.101)
где — масса малого элемента объёма тела.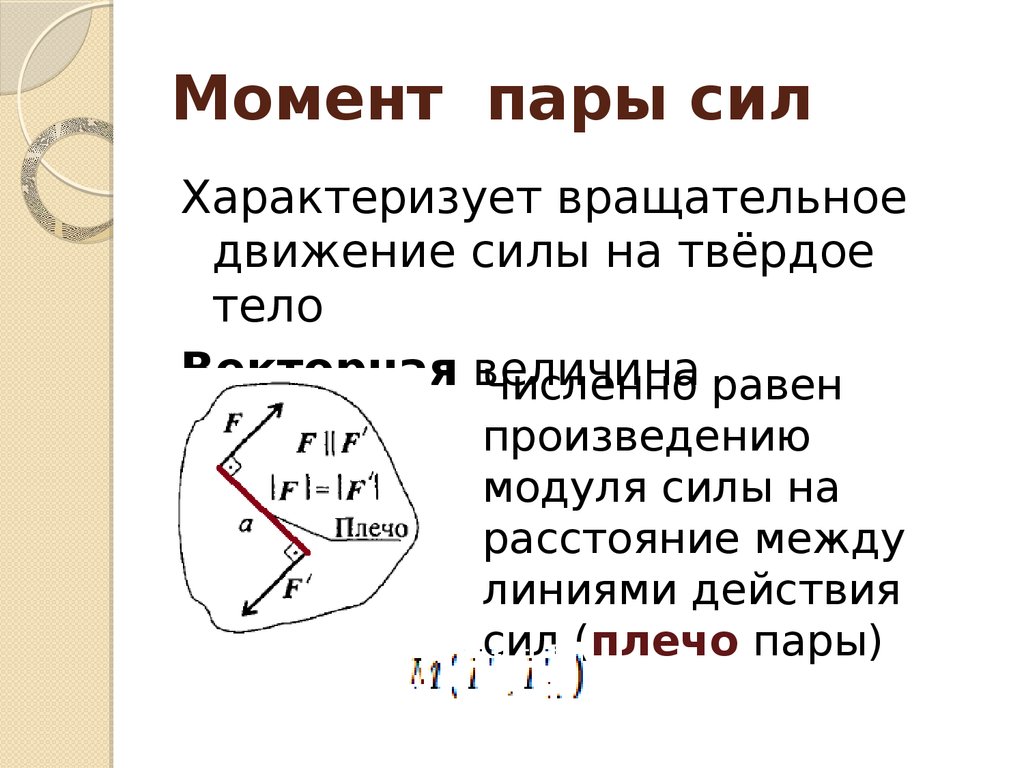 Пределы интегрирования определяются формой и размерами тела.
Пределы интегрирования определяются формой и размерами тела.
Из формул (I.100) и (I.101) следует, что момент инерции тела зависит от:
§ его массы;
§ распределения массы относительно данной оси.
Момент инерции является мерой инертности тела при вращательном движении. Он играет такую же роль, что и масса при описании поступательного движения тела. Но если масса данного тела считается величиной постоянной, то момент инерции данного тела зависит от положения оси вращения. Кроме того, на момент инерции влияют форма и размеры тела.
Согласно теореме Гюйгенса – Штейнера (теореме о переносе осей инерции): момент инерции тела (рис. 35) относительно произвольной оси равен сумме момента инерции этого тела относительно оси, проходящей через центр инерции тела (центр масс) параллельно рассматриваемой оси, и произведения массы тела на квадрат расстояния между осями:
.
Из теоремы Гюйгенса – Штейнера, следует, что:
q параллельное смещение оси вращения, проходящей через центр масс, приводит к увеличению момента инерции данного тела;
q момент инерции тела минимален, если ось вращения проходит через центр масс: ;
q оси, проходящие через точку и через центр масс (точку ), должны быть параллельны.
Формула (I.101), позволяет рассчитать моменты инерции тел простейшей формы относительно некоторых осей.
1. Момент инерции однородного прямого тонкого цилиндрического стержня длины и массы относительно оси проходящей через его середину и перпендикулярной к его длине:
. (I.102)
2. Момент инерции однородного сплошного цилиндра (или диска) радиуса и массы относительно оси симметрии перпендикулярной к его плоскости и проходящей через его центр:
. (I.103)
3. Момент инерции цилиндра радиуса , массы и высоты относительно оси, перпендикулярной к его высоте и проходящей через её середину:
. (I.104)
4. Момент инерции шара (тонкостенной сферы) радиуса и массы относительно его диаметра (или оси проходящей через центр сферы):
. (I.105)
5. Момент инерции стержня длины и массы , относительно оси проходящей через один из его концов и перпендикулярной к его длине:
. (I.106)
(I.106)
6. Момент инерции полого тонкостенного цилиндра радиуса и массы , относительно оси цилиндра:
. (I.107)
7. Момент инерции цилиндра с отверстием (колесо, муфта):
, (I.108)
где и — радиусы цилиндра и отверстия в нём.
Дата добавления: 2016-09-06; просмотров: 4533; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Момент силы. Движение. Теплота
Момент силы
Попробуйте рукой привести во вращение тяжелое маховое колесо. Тяните за спицу. Вам будет тяжело, если вы ухватитесь рукой слишком близко к оси. Переместите руку к ободу, и дело пойдет легче.
Что же изменилось? Ведь сила в обоих случаях одна и та же. Изменилась точка приложения силы.
Во всем предыдущем изложении вопрос о месте приложения силы не возникал, так как в рассмотренных задачах форма и размер тела роли не играли. По сути дела мы мысленно заменяли тело точкой.
Пример с вращением колеса показывает, что вопрос о точке приложения силы далеко не праздный, когда речь идет о вращении или повороте тела.
Для того чтобы понять роль точки приложения силы, вычислим работу, которую надо проделать, чтобы повернуть тело на некоторый угол. При этом расчете, конечно, предполагается, что все частички твердого тела жестко сцеплены между собой (мы оставляем пока без внимания способность тела гнуться, сжиматься – вообще менять свою форму). Поэтому сила, приложенная к одной точке тела, сообщает кинетическую энергию всем его частям.
При вычислении этой работы роль точки приложения сил отчетливо видна.
На рис. 49 показано закрепленное на оси тело. При повороте тела на маленький угол ? точка приложения силы переместилась по дуге – прошла путь s.
Проектируя силу на направление движения, т.е. на касательную к окружности, по которой движется точка приложения, напишем знакомое выражение работы A:
A = Fпрод·s
Но дуга s может быть представлена как
s = r?,
где r – расстояние от оси вращения до точки приложения силы. Итак,
Итак,
A = Fпрод·r?.
Поворачивая тело на один и тот же угол разными способами, мы можем затратить различную работу в зависимости от того, где приложена сила.
Если угол задан, то работа определяется произведением Fпрод·r. Такое произведение называют моментом силы:
M = Fпрод·r
Формуле момента силы можно придать другой вид. Пусть O – ось вращения и B – точка приложения силы (рис. 50). Буквой d обозначена длина перпендикуляра, опущенного из O на направление силы. Два треугольника, построенные на рисунке, подобны. Поэтому
Величина d называется плечом силы. Новая формула M = Fd читается так: момент силы равен произведению силы на ее плечо.
Если точку приложения силы перемещать вдоль направления силы, то плечо d, а вместе с ним и момент силы не будут меняться. Значит, безразлично, где именно на линии силы лежит точка приложения.
При помощи нового понятия формула для работы запишется короче:
A = M?,
т.е. работа равняется произведению момента силы на угол поворота.
Пусть на тело действуют две силы с моментами M1 и M2. При повороте тела на угол ? будет совершена работа M1? + M2? = (M1 + M2)?. Эта краткая запись показывает, что две силы с моментами M1 и M2 вращают тело так, как это делала бы одна сила с моментом M, равным сумме M1 + M2. Моменты сил могут как помогать, так и мешать друг другу. Если моменты M1 и M2 стремятся повернуть тело в одну и ту же сторону, то мы должны считать их величинами, имеющими одинаковый алгебраический знак. Напротив, моменты сил, поворачивающие тело в разные стороны, имеют разные знаки.
Как мы знаем, работа всех сил, действующих на тело, идет на изменение кинетической энергии.
Вращение тела замедлилось или ускорилось – значит, изменилась его кинетическая энергия. Это может произойти лишь в том случае, если суммарный момент сил не равен нулю.
А если суммарный момент равен нулю? Ответ ясен – кинетическая энергия не изменяется, следовательно, тело или вращается равномерно по инерции, или покоится.
Итак, равновесие способного вращаться тела требует уравновешивания действующих на него моментов сил. Если действуют две силы, равновесие требует равенства
M1 + M2 = 0.
Пока нас интересовали такие задачи, в которых тело можно было рассматривать как точку, условия равновесия были проще: чтобы тело покоилось или двигалось равномерно, говорил закон Ньютона для таких задач, надо, чтобы результирующая сила равнялась нулю; силы, действующие вверх, должны уравновеситься силами, направленными вниз; сила вправо должна компенсироваться силой влево.
Этот закон действителен и для нашего случая. Если маховое колесо находится в покое, то действующие на него силы уравновешиваются реакцией оси, на которую насажено колесо.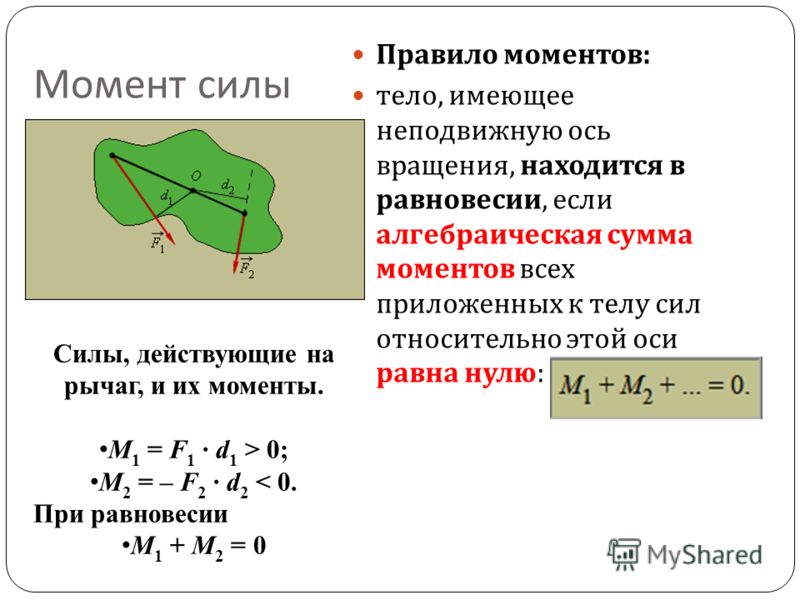
Но этих необходимых условий становится недостаточно. Кроме уравновешивания сил требуется еще уравновешивание моментов сил. Уравновешивание моментов является вторым необходимым условием покоя или равномерного вращения твердого тела.
Моменты сил, если их много, без труда разбиваются на две группы: одни стремятся вращать тело вправо, другие – влево. Эти-то моменты и должны компенсироваться.
НА НАС ВЛИЯЮТ ПРИРОДНЫЕ СИЛЫ
НА НАС ВЛИЯЮТ ПРИРОДНЫЕ СИЛЫ Приняв, что все это истинно, мы приходим к рассмотрению некоторых сил и влияний, которые воздействуют на этот чудесный сложный автоматический механизм с органами невообразимо чувствительными и изящными, когда его несет вращающийся
IV Можно ли укрыться от силы тяжести?
IV Можно ли укрыться от силы тяжести? Мы слишком привыкли к тому, что все вещи, все физические тела прикованы своим весом к земле; нам трудно поэтому даже мысленно отрешиться от силы тяжести и представить себе картину того, что было бы, если бы мы обладали способностью
Заслон от силы тяжести
Заслон от силы тяжести
Остроумный английский писатель Герберт Уэльс подробно развил эту мысль в научно-фантастическом романе „Первые люди на Луне»[4]. Ученый герой романа, изобретатель Кевор, открыл способ изготовления именно такого вещества, непроницаемого для
Ученый герой романа, изобретатель Кевор, открыл способ изготовления именно такого вещества, непроницаемого для
К главе II 1. Силы тяготения
К главе II 1. Силы тяготения Приведенные в начале главы II примеры действия силы тяготения могут быть проверены несложными расчетами, основанными, на законе Ньютона и элементах механики. Напомним сначала, что в механике за единицу измерения силы принята сила, которая,
IV. Откуда же берутся эти силы?
IV. Откуда же берутся эти силы? Наш разговор мы начали с того, что фундаментальные силы похожи на игры, однако в нашей игре не хватает одного компонента, без которого ничего не получится: это мяч. Задумайтесь об этом. Без мяча теннис — не более чем конвульсивное размахивание
16. Без юридической силы
16. Без юридической силы
Хотя меня в некоторой степени утешала новообретенная независимость духа, семейный катаклизм на самом деле сломил меня. Во тьме поражения я чувствовала, что опозорена и что от меня все отреклись, что я неуклюже пытаюсь вновь найти свою личность, как
Без юридической силы
Хотя меня в некоторой степени утешала новообретенная независимость духа, семейный катаклизм на самом деле сломил меня. Во тьме поражения я чувствовала, что опозорена и что от меня все отреклись, что я неуклюже пытаюсь вновь найти свою личность, как
Четыре силы
Четыре силы Словно мало было хлопот с новыми частицами, в те же 1930 — е годы были открыты еще и новые поля. К уже известному тяготению и электромагнетизму добавились силы ядерного взаимодействия, удерживающие протоны и нейтроны в ядре, и силы слабого взаимодействия,
83 Еще раз про силы сцепления
83 Еще раз про силы сцепления Для опыта нам потребуются: два кусочка стекла или два маленьких зеркальца. Мы помним, как иголка плавала на воде в одном из наших опытов. Помогали ей плавать силы поверхностного натяжения. Но вот вопрос: можно ли почувствовать силу
Движение под действием силы тяжести
Движение под действием силы тяжести
Будем скатывать небольшую тележку с двух очень гладких наклонных плоскостей. Одну доску возьмем значительно короче другой и положим их на одну и ту же опору. Тогда одна наклонная плоскость будет крутой, а другая – пологой. Верхушки
Одну доску возьмем значительно короче другой и положим их на одну и ту же опору. Тогда одна наклонная плоскость будет крутой, а другая – пологой. Верхушки
Вращательный момент
Вращательный момент Сейчас мы познакомимся еще с одним механическим понятием, которое позволяет сформулировать новый для нас важный закон движения.Это понятие называется вращательным моментом, или моментом импульса, или моментом количества движения. Уже названия
Вращательный момент как вектор
Вращательный момент как вектор До сих пор речь шла о величине вращательного момента. Но вращательный момент обладает свойствами векторной величины.Рассмотрим вращение точки по отношению к какому-либо «центру». На рис. 62 изображены два близких положения точки.
Поверхностные силы
Поверхностные силы
Можно ли выйти сухим из воды? Конечно, для этого нужно смазаться несмачивающимся водой веществом. Натрите палец парафином и опустите в воду. Когда вы его вынете, окажется, что воды на пальце нет, если не считать двух-трех капелек. Небольшое движение – и
Натрите палец парафином и опустите в воду. Когда вы его вынете, окажется, что воды на пальце нет, если не считать двух-трех капелек. Небольшое движение – и
Силы трения
Силы трения Мы не в первый раз говорим о трении. И правда, как можно было, рассказывая о движении, обойтись без упоминания о трении? Почти любое движение окружающих нас тел сопровождается трением. Останавливается автомобиль, у которого водитель выключил мотор,
Силы сопротивления при больших скоростях
Силы сопротивления при больших скоростях Но вернемся к законам «мокрого» трения. Как мы выяснили, при малых скоростях сопротивление зависит от вязкости жидкости, скорости движения и линейных размеров тела. Рассмотрим теперь законы трения при больших скоростях. Но
IV. Откуда же берутся эти силы?
IV. Откуда же берутся эти силы?
Наш разговор мы начали с того, что фундаментальные силы похожи на игры, однако в нашей игре не хватает одного компонента, без которого ничего не получится: это мяч. Задумайтесь об этом. Без мяча теннис – не более чем конвульсивное размахивание
Откуда же берутся эти силы?
Наш разговор мы начали с того, что фундаментальные силы похожи на игры, однако в нашей игре не хватает одного компонента, без которого ничего не получится: это мяч. Задумайтесь об этом. Без мяча теннис – не более чем конвульсивное размахивание
Обозначение момента. Статика
На данном уроке, тема которого: «Момент силы», мы поговорим о силе, с которой нужно подействовать на тело, чтобы изменить его скорость, а также о точке приложения этой силы. Рассмотрим примеры поворота разных тел, например качели: в какую точку нужно подействовать силой, чтобы качели начали движение или остались в равновесии.
Представьте, что вы футболист и перед вами футбольный мяч. Чтобы он полетел, его нужно ударить. Всё просто: чем сильнее ударите, тем быстрее и дальше полетит, и бить будете, скорее всего, в центр мяча (см. рис. 1).
А чтобы мяч в полете вращался и летел по искривленной траектории, вы ударите не в центр мяча, а сбоку, что и делают футболисты, чтобы обмануть соперника (см.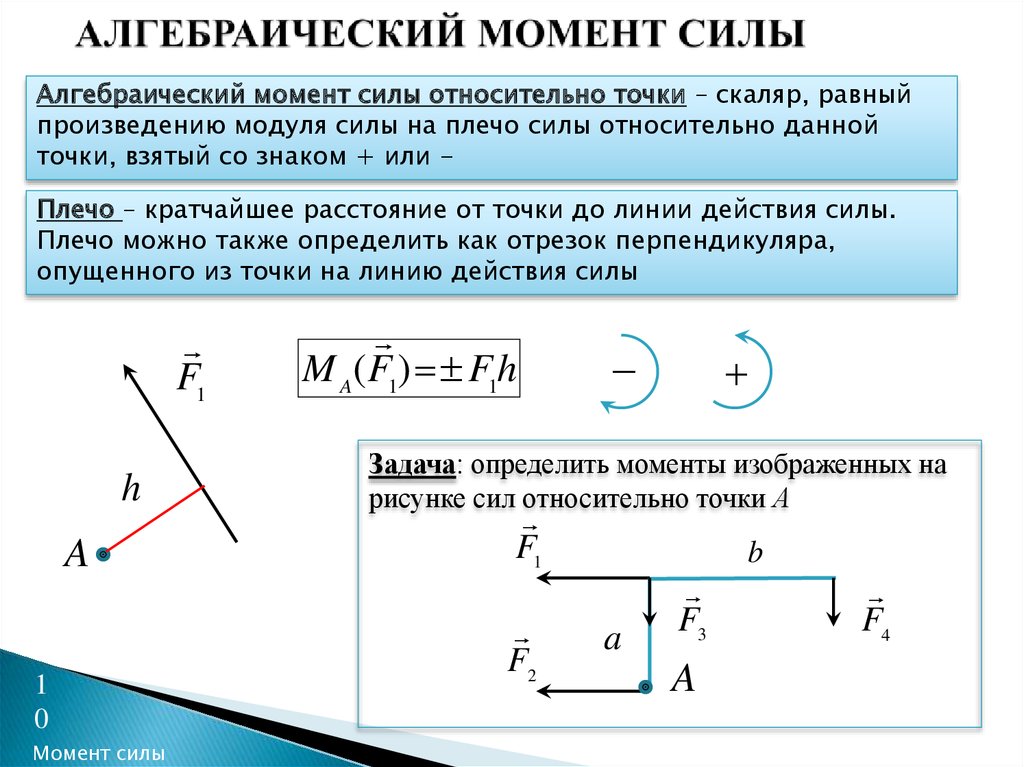 рис. 2).
рис. 2).
Рис. 2. Кривая траектория полета мяча
Здесь уже важно, в какую точку бить.
Еще один простой вопрос: в каком месте нужно взять палку, чтобы она при подъеме не перевернулась? Если палка равномерная по толщине и плотности, то возьмем мы её посередине. А если она с одного края массивнее? Тогда мы возьмем её ближе к массивному краю, иначе он перевесит (см. рис. 3).
Рис. 3. Точка подъема
Представьте: папа сел на качели-балансир (см. рис. 4).
Рис. 4. Качели-балансир
Чтобы его перевесить, вы сядете на качели поближе к противоположному концу.
Во всех приведённых примерах нам важно было не просто подействовать на тело с некоторой силой, но и важно, в каком месте, на какую именно точку тела действовать. Эту точку мы выбирали наугад, пользуясь жизненным опытом. А если на палке будет три разных груза? А если поднимать ее вдвоем? А если речь идёт о подъемном кране или вантовом мосте (см. рис. 5)?
Рис. 5. Примеры из жизни
Для решения таких задач интуиции и опыта недостаточно. Без четкой теории их решить уже нельзя. О решении таких задач сегодня и пойдёт речь.
Без четкой теории их решить уже нельзя. О решении таких задач сегодня и пойдёт речь.
Обычно в задачах у нас есть тело, к которому приложены силы, и мы их решаем, как всегда до этого, не задумываясь над точкой приложения силы. Достаточно знать, что сила приложена просто к телу. Такие задачи встречаются часто, мы умеем их решать, но бывает, что недостаточно приложить силу просто к телу, — становится важно, в какую точку.
Пример задачи, в которой размеры тела не важны
Например, на столе лежит маленький железный шарик, на который действует сила тяжести 1 Н. Какую силу нужно приложить, чтобы его поднять? Шарик притягивается Землей, мы будем действовать на него вверх, прикладывая некоторую силу.
Силы, действующие на шарик, направлены в противоположные стороны, и, чтобы поднять шарик, нужно подействовать на него с силой, большей по модулю, чем сила тяжести (см. рис. 6).
Рис. 6. Силы, действующие на шарик
Сила тяжести равна , значит, на шарик нужно подействовать вверх с силой:
Мы не задумывались, как именно мы берем шарик, мы его просто берем и поднимаем. Когда мы показываем, как мы поднимали шарик, мы вполне можем нарисовать точку и показать: мы воздействовали на шарик (см. рис. 7).
Когда мы показываем, как мы поднимали шарик, мы вполне можем нарисовать точку и показать: мы воздействовали на шарик (см. рис. 7).
Рис. 7. Действие на шарик
Когда мы можем так поступить с телом, показать его на рисунке при объяснении в виде точки и не обращать внимания на его размеры и форму, мы считаем его материальной точкой. Это модель. Реально же шарик имеет форму и размеры, но мы на них в этой задаче не обращали внимания. Если тот же шарик нужно заставить вращаться, то просто сказать, что мы воздействуем на шарик, уже нельзя. Здесь важно, что мы толкали шарик с краю, а не в центр, заставляя его вращаться. В этой задаче тот же шарик уже нельзя считать точкой.
Мы уже знаем примеры задач, в которых нужно учитывать точку приложения силы: задача с футбольным мячом, с неоднородной палкой, с качелями.
Точка приложения силы важна также в случае с рычагом. Пользуясь лопатой, мы действуем на конец черенка. Тогда достаточно приложить небольшую силу (см. рис. 8).
Рис. 8. Действие малой силы на черенок лопаты
Что общего между рассмотренными примерами, где нам важно учитывать размеры тела? И мяч, и палка, и качели, и лопата — во всех этих случаях речь шла о вращении этих тел вокруг некоторой оси. Мяч вращался вокруг своей оси, качели поворачивались вокруг крепления, палка — вокруг места, в котором мы ее держали, лопата — вокруг точки опоры (см. рис. 9).
Рис. 9. Примеры вращающихся тел
Рассмотрим поворот тел вокруг неподвижной оси и увидим, что заставляет тело поворачиваться. Будем рассматривать вращение в одной плоскости, тогда можно считать, что тело поворачивается вокруг одной точки О (см. рис. 10).
Рис. 10. Точка вращения
Если мы захотим уравновесить качели, у которых балка будет стеклянной и тонкой, то она может просто сломаться, а если балка из мягкого металла и тоже тонкая — то согнуться (см. рис. 11).
Такие случаи мы рассматривать не будем; будем рассматривать поворот прочных жестких тел.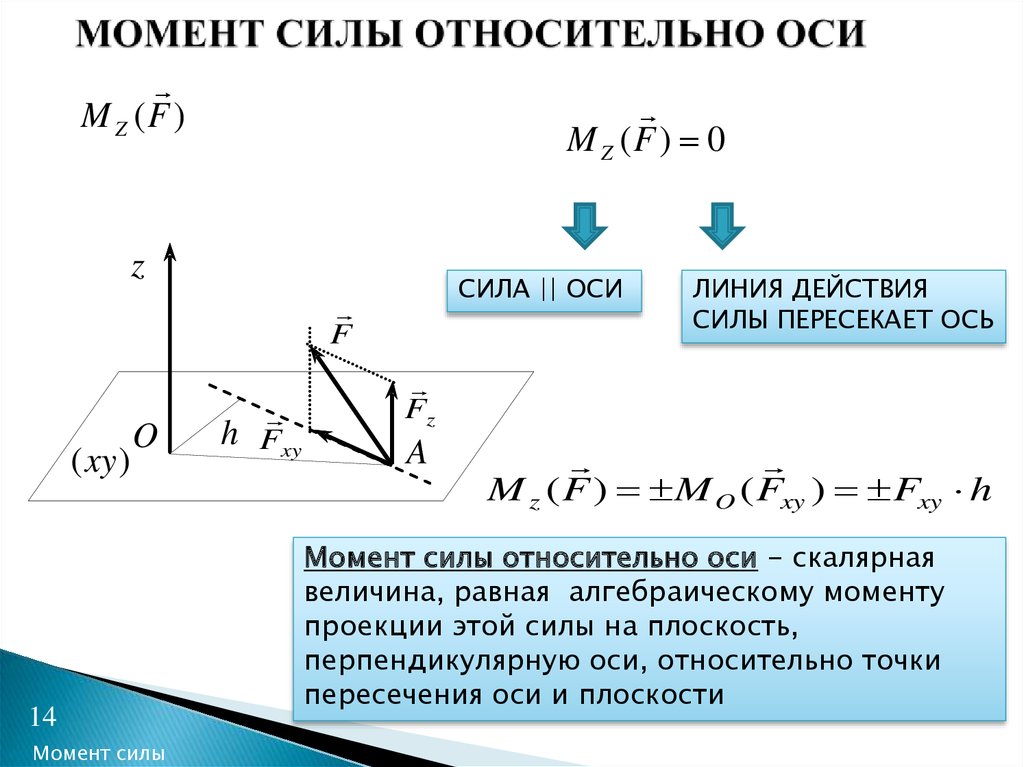
Неправильно будет сказать, что вращательное движение определяется только силой. Ведь на качелях одна и та же сила может вызвать их вращение, а может и не вызвать, смотря где мы сядем. Дело не только в силе, но и в расположении точки, на которую воздействуем. Все знают, насколько трудно поднять и удержать груз на вытянутой руке. Чтобы определять точку приложения силы, вводится понятие плеча силы (по аналогии с плечом руки, которой поднимают груз).
Плечо силы — это минимальное расстояние от заданной точки до прямой, вдоль которой действует сила.
Из геометрии вы наверняка уже знаете, что это перпендикуляр, опущенный из точки О на прямую, вдоль которой действует сила (см. рис. 12).
Рис. 12. Графическое изображение плеча силы
Почему плечо силы — минимальное расстояние от точки О до прямой, вдоль которой действует сила
Может показаться странным, что плечо силы измеряется от точки О не до точки приложения силы, а до прямой, вдоль которой эта сила действует.
Проделаем такой опыт: привяжем к рычагу нить. Подействуем на рычаг с некоторой силой в точке, где привязана нить (см. рис. 13).
Рис. 13. Нить привязана к рычагу
Если создастся момент силы, достаточный для поворота рычага, он повернется. Нить покажет прямую, вдоль которой направлена сила (см. рис. 14).
Попробуем потащить рычаг с той же силой, но теперь взявшись за нить. В воздействии на рычаг ничего не изменится, хотя точка приложения силы поменяется. Но сила будет действовать вдоль той же прямой, ее расстояние до оси вращения, то есть плечо силы, останется тем же. Попробуем подействовать на рычаг под углом (см. рис. 15).
Рис. 15. Действие на рычаг под углом
Теперь сила приложена к той же точке, но действует вдоль другой прямой. Ее расстояние до оси вращения стало малό, момент силы уменьшился, и рычаг может уже не повернуться.
На тело оказывается воздействие, направленное на вращение, на поворот тела. Это воздействие зависит от силы и от её плеча. Величина, характеризующая вращательное воздействие силы на тело, называется момент силы , иногда его называют еще вращающим или крутящим моментом.
Величина, характеризующая вращательное воздействие силы на тело, называется момент силы , иногда его называют еще вращающим или крутящим моментом.
Значение слова «момент»
Нам привычно употреблять слово «момент» в значении очень короткого промежутка времени, как синоним слова «мгновение» или «миг». Тогда не совсем понятно, какое отношение имеет момент к силе. Обратимся к происхождению слова «момент».
Слово происходит от латинского momentum, что означает «движущая сила, толчок». Латинский глагол movēre означает «двигать» (как и английское слово move, а movement означает «движение»). Теперь нам ясно, что вращающий момент — это то, что заставляет тело вращаться.
Момент силы — это произведение силы на ее плечо.
Единица измерения — ньютон, умноженный на метр: .
Если увеличивать плечо силы, можно уменьшить силу и момент силы останется прежним. Мы очень часто используем это в повседневной жизни: когда открываем дверь, когда пользуемся плоскогубцами или гаечным ключом.
Остался последний пункт нашей модели — надо разобраться, что делать, если на тело действует несколько сил. Мы можем вычислить момент каждой силы. Понятно, что если силы будут вращать тело в одном направлении, то их действие сложится (см. рис. 16).
Рис. 16. Действие сил складывается
Если в разных направлениях — моменты сил будут уравновешивать друг друга и логично, что их нужно будет вычесть. Поэтому моменты сил, которые вращают тело в разных направлениях, будем записывать с разными знаками. Например, запишем, если сила предположительно вращает тело вокруг оси по часовой стрелке, и — если против (см. рис. 17).
Рис. 17. Определение знаков
Тогда мы можем записать одну важную вещь: чтобы тело пребывало в равновесии, сумма моментов действующих на него сил должна быть равна нулю .
Формула для рычага
Мы уже знаем принцип действия рычага: на рычаг действуют две силы, и во сколько раз больше плечо рычага, во столько раз меньше сила:
Рассмотрим моменты сил, которые действуют на рычаг.
Выберем положительное направление вращения рычага, например против часовой стрелки (см. рис. 18).
Рис. 18. Выбор направления вращения
Тогда момент силы будет со знаком плюс, а момент силы — со знаком минус. Чтобы рычаг был в равновесии, сумма моментов сил должна быть равна нулю. Запишем:
Математически это равенство и соотношение, записанное выше для рычага, — одно и то же, и то, что мы получили экспериментально, подтвердилось.
Например, определим, будет ли пребывать в равновесии рычаг, изображенный на рисунке. На него действуют три силы (см. рис. 19). , и . Плечи сил равны , и .
Рис. 19. Рисунок к условию задачи 1
Чтобы рычаг пребывал в равновесии, сумма моментов сил, которые на него действуют, должен быть равен нулю.
На рычаг по условию действуют три силы: , и . Их плечи соответственно равны , и .
Направление вращения рычага по часовой стрелке будем считать положительным.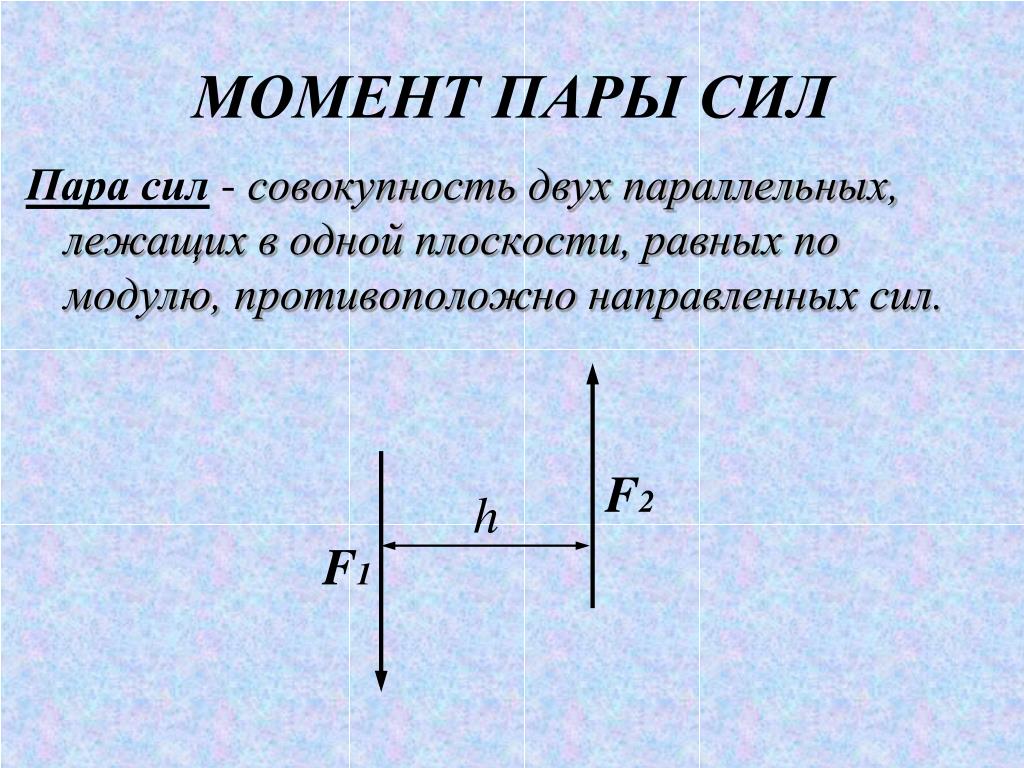 В этом направлении рычаг вращает сила , ее момент равен:
В этом направлении рычаг вращает сила , ее момент равен:
Силы и вращают рычаг против часовой стрелки, их моменты запишем со знаком минус:
Осталось вычислить сумму моментов сил:
Суммарный момент не равен нулю, значит, тело не будет пребывать в равновесии. Суммарный момент положительный, значит, рычаг будет поворачиваться по часовой стрелке (в нашей задаче это положительное направление).
Мы решили задачу и получили результат: суммарный момент сил, действующих на рычаг, равен . Рычаг начнет поворачиваться. И при его повороте, если силы не изменят направление, будут изменяться плечи сил. Они будут уменьшаться, пока не станут равны нулю, когда рычаг повернется вертикально (см. рис. 20).
Рис. 20. Плечи сил равны нулю
А при дальнейшем повороте силы станут направлены так, чтобы вращать его в противоположном направлении. Поэтому, решив задачу, мы определили, в какую сторону начнет вращаться рычаг, не говоря о том, что будет происходить потом.
Теперь вы научились определять не только силу, с которой нужно действовать на тело, чтобы изменить его скорость, но и точку приложения этой силы, чтобы оно не поворачивалось (или поворачивалось, как нам нужно).
Как толкать шкаф, чтобы он не перевернулся?
Мы знаем, что, когда мы толкаем шкаф с силой в верхней его части, он переворачивается, а чтобы этого не произошло, мы толкаем его ниже. Теперь мы можем объяснить это явление. Ось его вращения находится на том его ребре, на котором он стоит, при этом плечи всех сил, кроме силы , либо малы, либо равняются нулю, поэтому под действием силы шкаф падает (см. рис. 21).
Рис. 21. Действие на верхнюю часть шкафа
Прикладывая силу ниже, мы уменьшаем ее плечо , а значит, и момент этой силы, и опрокидывания не происходит (см. рис. 22).
Рис. 22. Сила приложена ниже
Шкаф как тело, размеры которого мы учитываем, подчиняется тому же закону, что и гаечный ключ, дверная ручка, мосты на опорах и т. п.
На этом наш урок окончен. Спасибо за внимание!
Список литературы
- Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. — 2-е издание передел. — X.: Веста: Издательство «Ранок», 2005.
 — 464 с.
— 464 с. - Перышкин А.В. Физика. 7 кл.: учеб. для общеобразоват. учреждений — 10-е изд., доп. — М.: Дрофа, 2006. — 192 с.: ил.
- Abitura.com ().
- Solverbook.com ().
Домашнее задание
Почти две тысячи лет просуществовало правило рычага, открытое Архимедом еще в третьем веке до нашей эры, пока в семнадцатом веке с легкой руки французского ученого Вариньона не получило более общую форму.
Правило момента сил
Было введено понятие момента сил. Момент силы — это физическая величина, равная произведению силы на ее плечо:
где M — момент силы,
F — сила,
l — плечо силы.
Из правила равновесия рычага напрямую вытекает правило моментов сил:
F1 / F2 = l2 / l1 или, по свойству пропорции F1 * l1= F2 * l2, то есть M1 = M2
В словесном выражении правило моментов сил звучит следующим образом: рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.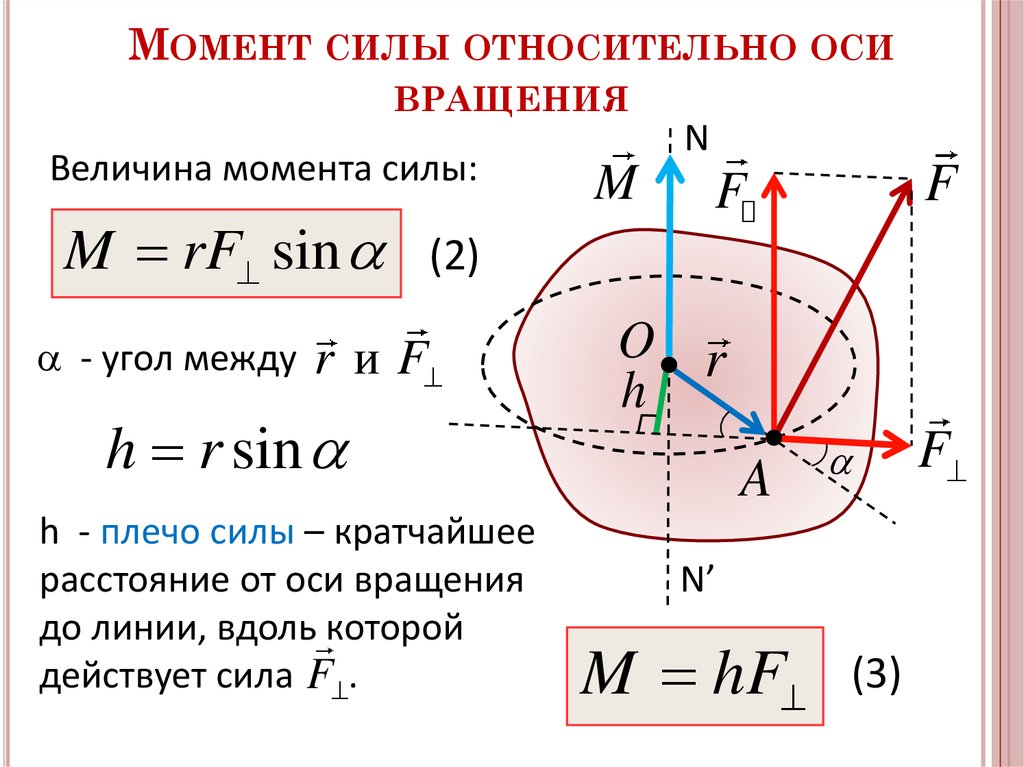 Правило моментов сил справедливо для любого тела, закрепленного вокруг неподвижной оси. На практике момент силы находят следующим образом: по направлению действия силы проводят линию действия силы. Потом из точки, в которой находится ось вращения, проводят перпендикуляр до линии действия силы. Длина этого перпендикуляра будет равняться плечу силы. Умножив значение модуля силы на ее плечо, получаем значение момента силы относительно оси вращения. То есть, мы видим, что момент силы характеризует вращающее действие силы. Действие силы зависит и от самой силы и от ее плеча.
Правило моментов сил справедливо для любого тела, закрепленного вокруг неподвижной оси. На практике момент силы находят следующим образом: по направлению действия силы проводят линию действия силы. Потом из точки, в которой находится ось вращения, проводят перпендикуляр до линии действия силы. Длина этого перпендикуляра будет равняться плечу силы. Умножив значение модуля силы на ее плечо, получаем значение момента силы относительно оси вращения. То есть, мы видим, что момент силы характеризует вращающее действие силы. Действие силы зависит и от самой силы и от ее плеча.
Применение правила моментов сил в различных ситуациях
Отсюда вытекает применение правила моментов сил в различных ситуациях. Например, если мы открываем дверь, то толкать ее мы будем в районе ручки, то есть, подальше от петель. Можно проделать элементарный опыт и убедиться, что толкать дверь тем легче, чем дальше мы прилагаем силу от оси вращения. Практический эксперимент в данном случае прямо подтверждается формулой.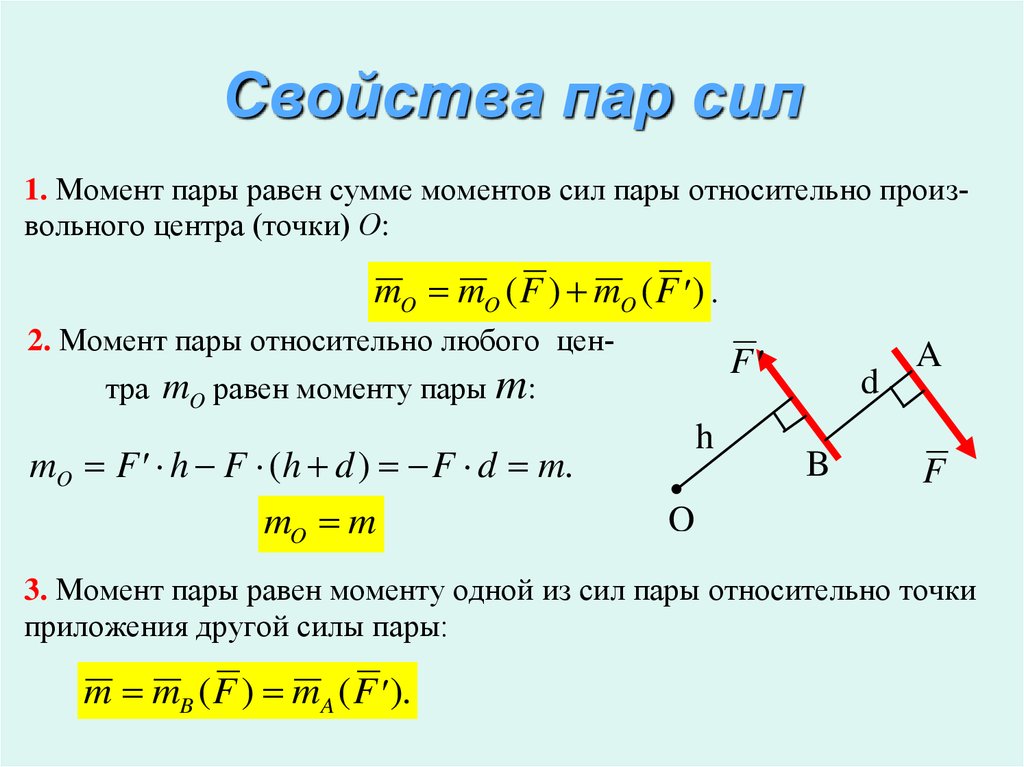 Так как, дабы моменты сил при разных плечах были равны, надо, чтобы большему плечу соответствовала меньшая сила и наоборот, меньшему плечу соответствовала большая. Чем ближе к оси вращения мы прилагаем силу, тем она должна быть больше. Чем дальше от оси мы воздействуем рычагом, вращая тело, тем меньшую силу нам необходимо будет приложить. Числовые значения легко находятся из формулы для правила моментов.
Так как, дабы моменты сил при разных плечах были равны, надо, чтобы большему плечу соответствовала меньшая сила и наоборот, меньшему плечу соответствовала большая. Чем ближе к оси вращения мы прилагаем силу, тем она должна быть больше. Чем дальше от оси мы воздействуем рычагом, вращая тело, тем меньшую силу нам необходимо будет приложить. Числовые значения легко находятся из формулы для правила моментов.
Именно исходя из правила моментов сил мы берем лом или длинную палку, если нам надо приподнять что-то тяжелое, и, подсунув под груз один конец, тянем лом возле другого конца. По этой же причине шурупы мы вворачиваем отверткой с длинной ручкой, а гайки закручиваем длинным гаечным ключом.
Моментом силы относительно произвольного центра в плоскости действия силы, называется произведение модуля силы на плечо.
Плечо — кратчайшее расстояние от центра О до линии действия силы, но не до точки приложения силы, т.к. сила-скользящий вектор.
Знак момента:
По часовой-минус, против часовой-плюс;
Момент
силы можно выразить как вектор.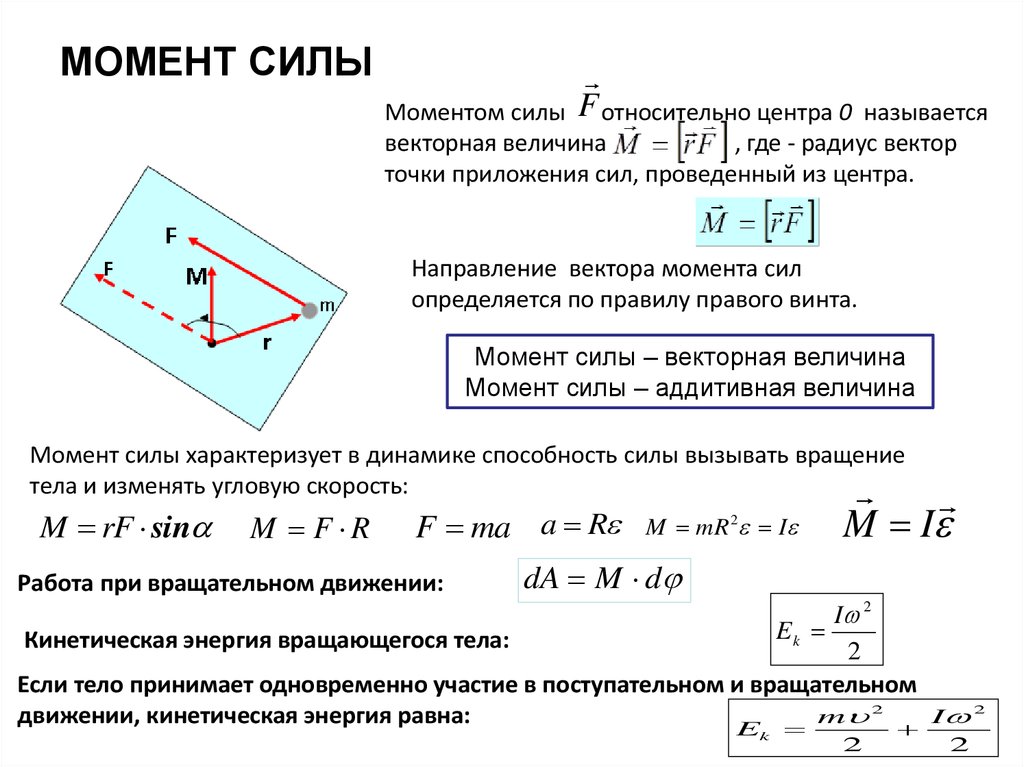 Это
перпендикуляр к плоскости по правилу
Буравчика.
Это
перпендикуляр к плоскости по правилу
Буравчика.
Если в плоскости расположены несколько сил или система сил, то алгебраическая сумма их моментов даст нам главный момент системы сил.
Рассмотрим момент силы относительно оси, вычислим момент силы относительно оси Z;
Спроецируем F на XY;
F xy =Fcosα = ab
m 0 (F xy)=m z (F), то есть m z =F xy * h = Fcosα * h
Момент силы относительно оси равен моменту ее проекции на плоскость перпендикулярную оси, взятому на пересечении осей и плоскости
Если сила параллельна оси или пересекает ее, то m z (F)=0
Выражение момента силы в виде векторного выражения
Проведем r а в точку A. Рассмотрим OA x F.
Это третий вектор m o , перпендикулярный плоскости. Модуль векторного произведения можно вычислить с помощью удвоенной площади заштрихованного треугольника.
Аналитическое
выражение силы относительно координатных
осей.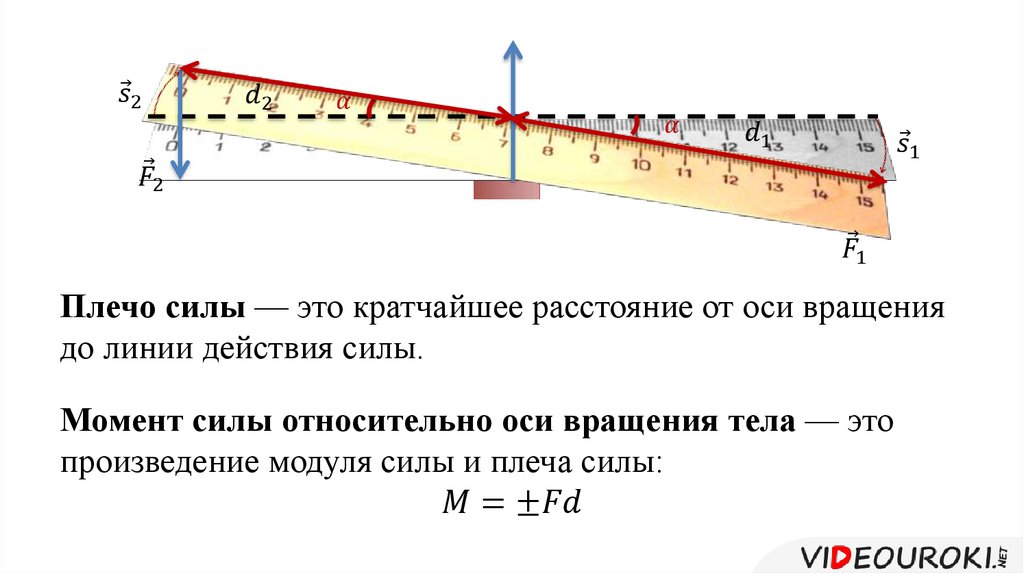
Предположим, что с точкой О связаны оси Y и Z, X с единичными векторами i, j, k Учитывая, что:
r x =X * Fx ; r y =Y * F y ; r z =Z * F y получим: m o (F)=x =
Раскроем определитель и получим:
m x =YF z — ZF y
m y =ZF x — XF z
m z =XF y — YF x
Эти формулы дают возможность вычислить проекцию вектор-момента на оси, а потом и сам вектор-момент.
Теорема Вариньона о моменте равнодействующей
Если система сил имеет равнодействующую, то её момент относительно любого центра равен алгебраической сумме моментов всех сил относительно этой точки
Если приложить Q= -R , то система (Q,F 1 … F n) будет равен уравновешиваться.
Сумма моментов относительно любого центра будет равен нулю.
Аналитическое условие равновесия плоской системы сил
Это плоская система сил, линии действия которых расположены в одной плоскости
Цель
расчета задач данного типа — определение
реакций внешних связей. Для этого
используются основные уравнения в
плоской системе сил.
Для этого
используются основные уравнения в
плоской системе сил.
Могут использоваться 2 или 3 уравнения моментов.
Пример
Составим уравнение суммы всех сил на ось X и Y:
Сумма моментов всех сил относительно точки А:
Параллельные силы
Уравнение относительно точки А:
Уравнение относительно точки В:
Сумма проекций сил на ось У.
Момент силы относительно оси или просто момент силы называется проекция силы на прямую, которая перпендикулярна радиусу и проведена в точке приложения силы умноженная на расстояние от этой точки до оси. Либо произведение силы на плечо ее приложения. Плечо в данном случае это расстояние от оси до точки приложения силы. Момент силы характеризует вращательное действие силы на тело. Ось в данном случае это место крепления тела, относительно которого оно может совершать вращение. Если тело не закреплено, то осью вращения можно считать центр масс.
Формула 1 — Момент силы.
F — Сила действующая на тело.
r — Плечо силы.
Рисунок 1 — Момент силы.
Как видно из рисунка, плечо силы это расстояние от оси до точки приложения силы. Но это в случае если угол между ними равен 90 градусов. Если это не так, то необходимо вдоль действия силы провести линию и из оси опустить на нее перпендикуляр. Длинна этого перпендикуляра и будет равна плечу силы. А перемещение точки приложения силы вдоль направления силы не меняет ее момента.
Принято считать положительным такой момент силы, который вызывает поворот тела по часовой стрелки относительно точки наблюдения. А отрицательным соответственно вызывающий вращение против нее. Измеряется момент силы в Ньютонах на метр. Один Ньютонометр это сила в 1 Ньютон действующая на плечо в 1 метр.
Если сила, действующая на тело, проходит вдоль лини идущей через ось вращения тела, или центр масс, если тело не имеет оси вращения. То момент силы в этом случае будет равен нулю. Так как эта сила не будет вызывать вращения тела, а попросту будет перемещать его поступательно вдоль лини приложения.
Рисунок 2 — Момент силы равен нулю.
В случае если на тело действует несколько сил, то момент силы будет определять их равнодействующая. К примеру, на тело могут действовать две силы равные по модулю и направленные противоположно. При этом суммарный момент силы будет равен нулю. Так как эти силы будут компенсировать друг друга. Если по простому, то представьте себе детскую карусель. Если один мальчик ее толкает по часовой стрелке, а другой с той же силой против, то карусель останется неподвижной.
Определение
Векторное произведение радиус – вектора (), который проведен из точки О (рис.1) в точку к которой приложена сила на сам вектор называют моментом силы ()по отношению к точке O:
На рис.1 точка О и вектор силы ()и радиус – вектор
находятся в плоскости рисунка. В таком случае вектор момента силы
() перпендикулярен плоскости рисунка и имеет направление от нас. Вектор момента силы является аксиальным. Направление вектора момента силы
выбирается таким образом, что вращение вокруг точки О в направлении силы и вектор
создают правовинтовую систему. Направление момента сил и углового ускорения совпадают.
Направление момента сил и углового ускорения совпадают.
Величина вектора равна:
где – угол между направлениями радиус – вектора и вектора силы, – плечо силы относительно точки О.
Момент силы относительно оси
Моментом силы по отношению к оси является физическая величина, равная проекции вектора момента силы относительно точки избранной оси на данную ось. При этом выбор точки значения не имеет.
Главный момент сил
Главным моментом совокупности сил относительно точки О называется вектор (момент силы), который равен сумме моментов всех сил, действующих в системе по отношению к той же точке:
При этом точку О называют центром приведения системы сил.
Если имеются два главных моменты ( и )для одной системы сил для разных двух центров приведение сил (О и О’), то они связаны выражением:
где — радиус-вектор, который проведен из точки О к точке О’, – главный вектор системы сил.
В общем случае результат действия на твердое тело произвольной системы сил такое же, как действие на тело главного момента
системы сил и главного вектора системы сил, который приложен в центре приведения (точка О).
Основной закон динамики вращательного движения
где – момент импульса тела находящегося во вращении.
Для твердого тела этот закон можно представить как:
где I – момент инерции тела, – угловое ускорение.
Единицы измерения момента силы
Основной единицей измерения момента силы в системе СИ является: [M]=Н м
В СГС: [M]=дин см
Примеры решения задач
Пример
Задание. На рис.1 показано тело, которое имеет ось вращения OO». Момент силы, приложенный к телу относительно заданной оси, будет равен нулю? Ось и вектор силы расположены в плоскости рисунка.
Решение. За основу решения задачи примем формулу, определяющую момент силы:
В векторном произведении (видно из рисунка) . Угол между вектором силы и радиус – вектором также будет отличен от нуля (или ), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.
Ответ.
Пример
Задание.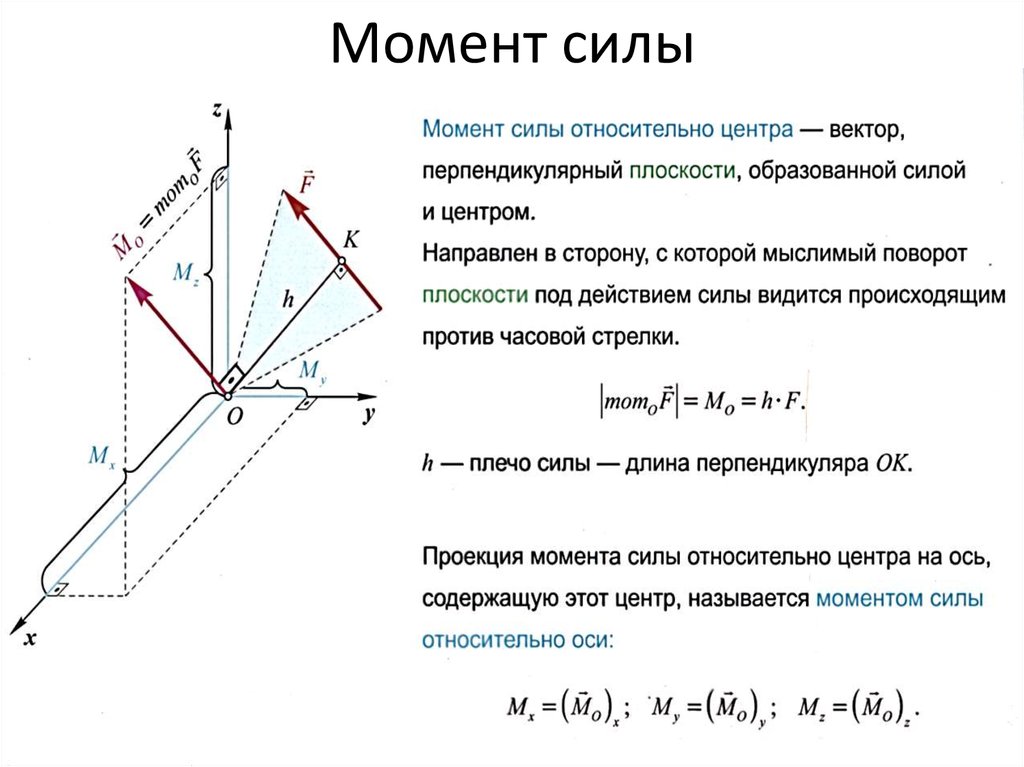 Угловая скорость вращающегося твердого тела изменяется в соответствии с графиком, который представлен на рис.2.
В какой из указанных на графике точек момент сил, приложенных к телу равен нулю?
Угловая скорость вращающегося твердого тела изменяется в соответствии с графиком, который представлен на рис.2.
В какой из указанных на графике точек момент сил, приложенных к телу равен нулю?
Момент силы 7 класс онлайн-подготовка на Ростелеком Лицей
Введение
Представьте, что вы футболист и перед вами футбольный мяч. Чтобы он полетел, его нужно ударить. Всё просто: чем сильнее ударите, тем быстрее и дальше полетит, и бить будете, скорее всего, в центр мяча (см. рис. 1).
Рис. 1. Прямая траектория полета мяча
А чтобы мяч в полете вращался и летел по искривленной траектории, вы ударите не в центр мяча, а сбоку, что и делают футболисты, чтобы обмануть соперника (см. рис. 2).
Рис. 2. Кривая траектория полета мяча
Здесь уже важно, в какую точку бить.
Еще один простой вопрос: в каком месте нужно взять палку, чтобы она при подъеме не перевернулась? Если палка равномерная по толщине и плотности, то возьмем мы её посередине. А если она с одного края массивнее? Тогда мы возьмем её ближе к массивному краю, иначе он перевесит (см. рис. 3).
А если она с одного края массивнее? Тогда мы возьмем её ближе к массивному краю, иначе он перевесит (см. рис. 3).
Рис. 3. Точка подъема
Представьте: папа сел на качели-балансир (см. рис. 4).
Рис. 4. Качели-балансир
Чтобы его перевесить, вы сядете на качели поближе к противоположному концу.
Во всех приведённых примерах нам важно было не просто подействовать на тело с некоторой силой, но и важно, в каком месте, на какую именно точку тела действовать. Эту точку мы выбирали наугад, пользуясь жизненным опытом. А если на палке будет три разных груза? А если поднимать ее вдвоем? А если речь идёт о подъемном кране или вантовом мосте (см. рис. 5)?
Рис. 5. Примеры из жизни
Для решения таких задач интуиции и опыта недостаточно. Без четкой теории их решить уже нельзя. О решении таких задач сегодня и пойдёт речь.
Тело и материальная точка
Обычно в задачах у нас есть тело, к которому приложены силы, и мы их решаем, как всегда до этого, не задумываясь над точкой приложения силы. Достаточно знать, что сила приложена просто к телу. Такие задачи встречаются часто, мы умеем их решать, но бывает, что недостаточно приложить силу просто к телу, – становится важно, в какую точку.
Достаточно знать, что сила приложена просто к телу. Такие задачи встречаются часто, мы умеем их решать, но бывает, что недостаточно приложить силу просто к телу, – становится важно, в какую точку.
Пример задачи, в которой размеры тела не важны
Например, на столе лежит маленький железный шарик, на который действует сила тяжести 1 Н. Какую силу нужно приложить, чтобы его поднять? Шарик притягивается Землей, мы будем действовать на него вверх, прикладывая некоторую силу.
Силы, действующие на шарик, направлены в противоположные стороны, и, чтобы поднять шарик, нужно подействовать на него с силой, большей по модулю, чем сила тяжести (см. рис. 6).
Рис. 6. Силы, действующие на шарик
Сила тяжести равна , значит, на шарик нужно подействовать вверх с силой:
Мы не задумывались, как именно мы берем шарик, мы его просто берем и поднимаем. Когда мы показываем, как мы поднимали шарик, мы вполне можем нарисовать точку и показать: мы воздействовали на шарик (см. рис. 7).
рис. 7).
Рис. 7. Действие на шарик
Когда мы можем так поступить с телом, показать его на рисунке при объяснении в виде точки и не обращать внимания на его размеры и форму, мы считаем его материальной точкой. Это модель. Реально же шарик имеет форму и размеры, но мы на них в этой задаче не обращали внимания. Если тот же шарик нужно заставить вращаться, то просто сказать, что мы воздействуем на шарик, уже нельзя. Здесь важно, что мы толкали шарик с краю, а не в центр, заставляя его вращаться. В этой задаче тот же шарик уже нельзя считать точкой.
Мы уже знаем примеры задач, в которых нужно учитывать точку приложения силы: задача с футбольным мячом, с неоднородной палкой, с качелями.
Точка приложения силы важна также в случае с рычагом. Пользуясь лопатой, мы действуем на конец черенка. Тогда достаточно приложить небольшую силу (см. рис. 8).
Рис. 8. Действие малой силы на черенок лопаты
Что общего между рассмотренными примерами, где нам важно учитывать размеры тела? И мяч, и палка, и качели, и лопата – во всех этих случаях речь шла о вращении этих тел вокруг некоторой оси. Мяч вращался вокруг своей оси, качели поворачивались вокруг крепления, палка – вокруг места, в котором мы ее держали, лопата – вокруг точки опоры (см. рис. 9).
Мяч вращался вокруг своей оси, качели поворачивались вокруг крепления, палка – вокруг места, в котором мы ее держали, лопата – вокруг точки опоры (см. рис. 9).
Рис. 9. Примеры вращающихся тел
Рассмотрим поворот тел вокруг неподвижной оси и увидим, что заставляет тело поворачиваться. Будем рассматривать вращение в одной плоскости, тогда можно считать, что тело поворачивается вокруг одной точки О (см. рис. 10).
Рис. 10. Точка вращения
Если мы захотим уравновесить качели, у которых балка будет стеклянной и тонкой, то она может просто сломаться, а если балка из мягкого металла и тоже тонкая – то согнуться (см. рис. 11).
Рис. 11. Стеклянная балка (слева) и балка из мягкого металла (справа)
Такие случаи мы рассматривать не будем; будем рассматривать поворот прочных жестких тел.
Плечо силы
Неправильно будет сказать, что вращательное движение определяется только силой. Ведь на качелях одна и та же сила может вызвать их вращение, а может и не вызвать, смотря где мы сядем. Дело не только в силе, но и в расположении точки, на которую воздействуем. Все знают, насколько трудно поднять и удержать груз на вытянутой руке. Чтобы определять точку приложения силы, вводится понятие плеча силы (по аналогии с плечом руки, которой поднимают груз).
Дело не только в силе, но и в расположении точки, на которую воздействуем. Все знают, насколько трудно поднять и удержать груз на вытянутой руке. Чтобы определять точку приложения силы, вводится понятие плеча силы (по аналогии с плечом руки, которой поднимают груз).
Плечо силы – это минимальное расстояние от заданной точки до прямой, вдоль которой действует сила.
Из геометрии вы наверняка уже знаете, что это перпендикуляр, опущенный из точки О на прямую, вдоль которой действует сила (см. рис. 12).
Рис. 12. Графическое изображение плеча силы
Почему плечо силы – минимальное расстояние от точки О до прямой, вдоль которой действует сила
Может показаться странным, что плечо силы измеряется от точки О не до точки приложения силы, а до прямой, вдоль которой эта сила действует.
Проделаем такой опыт: привяжем к рычагу нить. Подействуем на рычаг с некоторой силой в точке, где привязана нить (см. рис. 13).
13).
Рис. 13. Нить привязана к рычагу
Если создастся момент силы, достаточный для поворота рычага, он повернется. Нить покажет прямую, вдоль которой направлена сила (см. рис. 14).
Рис. 14. Направление силы
Попробуем потащить рычаг с той же силой, но теперь взявшись за нить. В воздействии на рычаг ничего не изменится, хотя точка приложения силы поменяется. Но сила будет действовать вдоль той же прямой, ее расстояние до оси вращения, то есть плечо силы, останется тем же. Попробуем подействовать на рычаг под углом (см. рис. 15).
Рис. 15. Действие на рычаг под углом
Теперь сила приложена к той же точке, но действует вдоль другой прямой. Ее расстояние до оси вращения стало малό, момент силы уменьшился, и рычаг может уже не повернуться.
Момент силы
На тело оказывается воздействие, направленное на вращение, на поворот тела. Это воздействие зависит от силы и от её плеча. Величина, характеризующая вращательное воздействие силы на тело, называется момент силы, иногда его называют еще вращающим или крутящим моментом.
Значение слова «момент»
Нам привычно употреблять слово «момент» в значении очень короткого промежутка времени, как синоним слова «мгновение» или «миг». Тогда не совсем понятно, какое отношение имеет момент к силе. Обратимся к происхождению слова «момент».
Слово происходит от латинского momentum, что означает «движущая сила, толчок». Латинский глагол movēre означает «двигать» (как и английское слово move, а movement означает «движение»). Теперь нам ясно, что вращающий момент – это то, что заставляет тело вращаться.
Момент силы – это произведение силы на ее плечо.
Единица измерения – ньютон, умноженный на метр: .
Если увеличивать плечо силы, можно уменьшить силу и момент силы останется прежним. Мы очень часто используем это в повседневной жизни: когда открываем дверь, когда пользуемся плоскогубцами или гаечным ключом.
Остался последний пункт нашей модели – надо разобраться, что делать, если на тело действует несколько сил.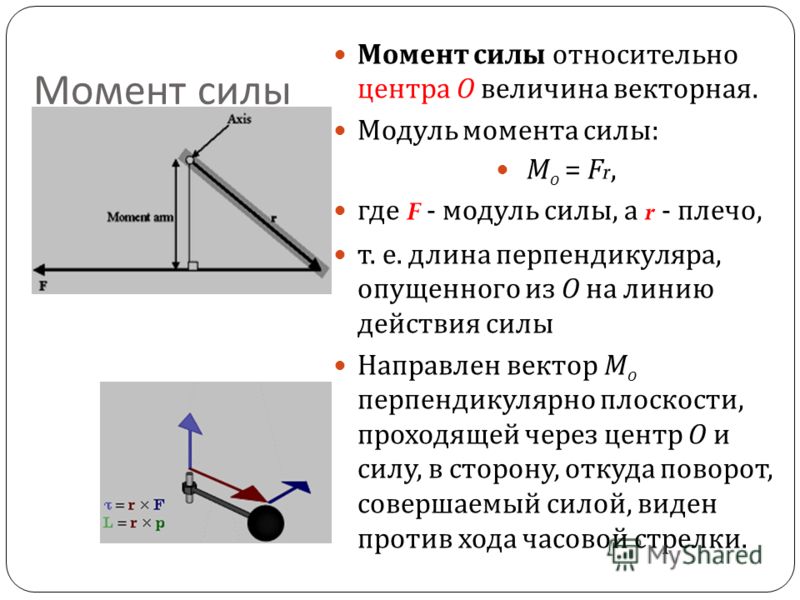 Мы можем вычислить момент каждой силы. Понятно, что если силы будут вращать тело в одном направлении, то их действие сложится (см. рис. 16).
Мы можем вычислить момент каждой силы. Понятно, что если силы будут вращать тело в одном направлении, то их действие сложится (см. рис. 16).
Рис. 16. Действие сил складывается
Если в разных направлениях – моменты сил будут уравновешивать друг друга и логично, что их нужно будет вычесть. Поэтому моменты сил, которые вращают тело в разных направлениях, будем записывать с разными знаками. Например, запишем, если сила предположительно вращает тело вокруг оси по часовой стрелке, и – если против (см. рис. 17).
Рис. 17. Определение знаков
Тогда мы можем записать одну важную вещь: чтобы тело пребывало в равновесии, сумма моментов действующих на него сил должна быть равна нулю.
Формула для рычага
Мы уже знаем принцип действия рычага: на рычаг действуют две силы, и во сколько раз больше плечо рычага, во столько раз меньше сила:
Рассмотрим моменты сил, которые действуют на рычаг.
Выберем положительное направление вращения рычага, например против часовой стрелки (см.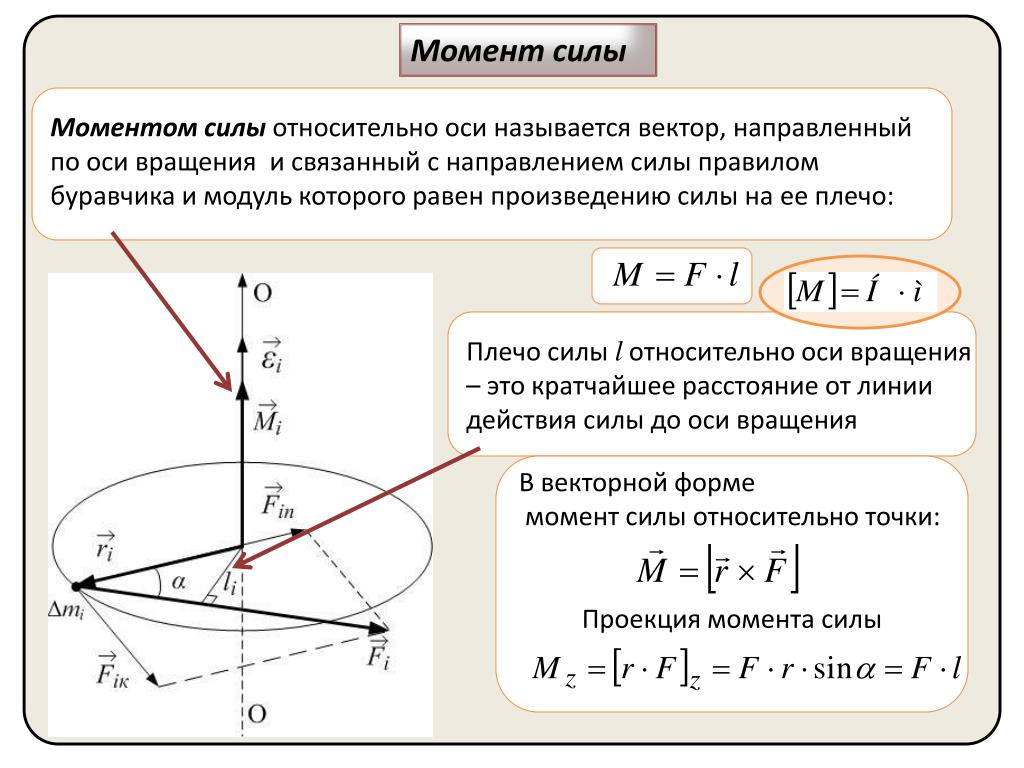 рис. 18).
рис. 18).
Рис. 18. Выбор направления вращения
Тогда момент силы будет со знаком плюс, а момент силы – со знаком минус. Чтобы рычаг был в равновесии, сумма моментов сил должна быть равна нулю. Запишем:
Математически это равенство и соотношение, записанное выше для рычага, – одно и то же, и то, что мы получили экспериментально, подтвердилось.
Задача
Например, определим, будет ли пребывать в равновесии рычаг, изображенный на рисунке. На него действуют три силы (см. рис. 19). , и . Плечи сил равны , и .
Рис. 19. Рисунок к условию задачи 1
Чтобы рычаг пребывал в равновесии, сумма моментов сил, которые на него действуют, должен быть равен нулю.
На рычаг по условию действуют три силы: , и . Их плечи соответственно равны , и .
Направление вращения рычага по часовой стрелке будем считать положительным.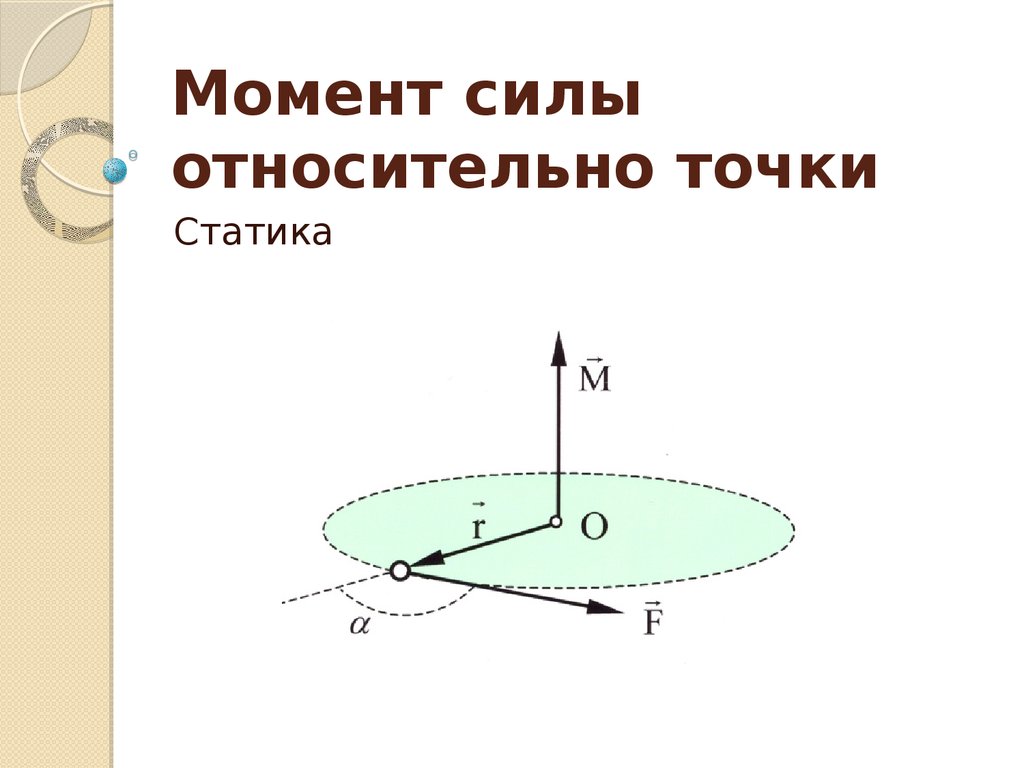 В этом направлении рычаг вращает сила , ее момент равен:
В этом направлении рычаг вращает сила , ее момент равен:
Силы и вращают рычаг против часовой стрелки, их моменты запишем со знаком минус:
Осталось вычислить сумму моментов сил:
Суммарный момент не равен нулю, значит, тело не будет пребывать в равновесии. Суммарный момент положительный, значит, рычаг будет поворачиваться по часовой стрелке (в нашей задаче это положительное направление).
Что произойдет с рычагом дальше?
Мы решили задачу и получили результат: суммарный момент сил, действующих на рычаг, равен . Рычаг начнет поворачиваться. И при его повороте, если силы не изменят направление, будут изменяться плечи сил. Они будут уменьшаться, пока не станут равны нулю, когда рычаг повернется вертикально (см. рис. 20).
Рис. 20. Плечи сил равны нулю
А при дальнейшем повороте силы станут направлены так, чтобы вращать его в противоположном направлении. Поэтому, решив задачу, мы определили, в какую сторону начнет вращаться рычаг, не говоря о том, что будет происходить потом.
Выводы
Теперь вы научились определять не только силу, с которой нужно действовать на тело, чтобы изменить его скорость, но и точку приложения этой силы, чтобы оно не поворачивалось (или поворачивалось, как нам нужно).
Как толкать шкаф, чтобы он не перевернулся?
Мы знаем, что, когда мы толкаем шкаф с силой в верхней его части, он переворачивается, а чтобы этого не произошло, мы толкаем его ниже. Теперь мы можем объяснить это явление. Ось его вращения находится на том его ребре, на котором он стоит, при этом плечи всех сил, кроме силы , либо малы, либо равняются нулю, поэтому под действием силы шкаф падает (см. рис. 21).
Рис. 21. Действие на верхнюю часть шкафа
Прикладывая силу ниже, мы уменьшаем ее плечо , а значит, и момент этой силы, и опрокидывания не происходит (см. рис. 22).
Рис. 22. Сила приложена ниже
Шкаф как тело, размеры которого мы учитываем, подчиняется тому же закону, что и гаечный ключ, дверная ручка, мосты на опорах и т. п.
п.
На этом наш урок окончен. Спасибо за внимание!
Список литературы
- Соколович Ю. А., Богданова Г. С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Перышкин А. В. Физика. 7 кл.: учеб. для общеобразоват. учреждений — 10-е изд., доп. – М.: Дрофа, 2006. – 192 с.: ил.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «abitura.com» (Источник)
- Интернет-портал «solverbook.com» (Источник)
Домашнее задание
- Дайте определение плеча силы, момента сил.
- Чему равна размерность момента сил?
- Подвешенный однородный стержень с двумя грузами на концах находится в равновесии. Как нужно изменить плечо , чтобы стержень остался в равновесии, если массу первого груза увеличили в 2 раза?
Момент силы: определение, принцип, типы, применение
Камаль Двиведи
11 мая 2022 г.
Привет, друзья, сегодня я собираюсь обсудить «момент силы », в котором вы будете знать обо всех аспектах, связанных с моментом силы, таких как их классификация, принцип, геометрическое представление, применение, и т.д.
Итак, не теряя времени, приступим.
Что такое момент силы?
Стремление сил состоит не только в перемещении тела, но и во вращении тела.
Эта вращательная тенденция силы называется моментом или моментом силы.
Математически его можно определить как «Произведение силы и перпендикулярного расстояния от точки до линии действия силы называется моментом силы относительно этой точки».
Его можно обозначить через M.
Итак,
Формула момента силы может быть записана как,
M = F × d
0003
d = Перпендикулярное расстояние
Единицей момента силы в системе СИ является ньютон-метр (Н-м), а в СГС ее можно записать как ньютон-сантиметр (Н-см).
Направление момента
В зависимости от направления момента он делится на два типа.
- Момент по часовой стрелке
- Момент против часовой стрелки
См. на рисунке направление моментов, которые подробно описаны ниже.
Момент по часовой стрелке
Если сила, действующая на тело, имеет тенденцию вращать тело по часовой стрелке, то создаваемый момент называется моментом по часовой стрелке.
Момент против часовой стрелки
Если сила, действующая на тело, стремится повернуть тело против часовой стрелки, то создаваемый таким образом момент называется моментом против часовой стрелки.
Классификация момента силы
Существуют следующие классификации моментов:
- Крутящий момент
- Изгибающий момент
- Крутящий момент в деталях.
Крутящий момент
Этот момент стремится повернуть тело вокруг точки опоры. В этом случае тело может свободно вращаться вокруг точки опоры.
Изгибающий момент
Этот момент стремится согнуть тело вокруг одного из закрепленных концов.

Крутящий момент
Этот момент закручивает вал вокруг одного из его неподвижных концов.
Геометрическое представление момента силы
Момент силы относительно точки равен удвоенной площади треугольника, образованного таким образом, если принять точку за вершину треугольника и линию за основание треугольника.
Рассмотрим силу F, действующую на тело и представленную вектором AB.
Пусть O будет точкой, относительно которой должен быть рассчитан момент силы.
Тогда,
Момент силы относительно O, M =Fx OC
Момент силы относительно O, M = AB x OC
(Отчетливо видно на рисунке F = AB)
Теперь умножьте и разделите на 2
Тогда
M = 2 x 1/2 AB x OC
Как мы знаем,
Площадь треугольника = 1/2 × основание × высота
Итак,
M = 2 x Площадь △OAB
Принцип момента силы
Если тело находится в равновесии под действием ряда сил, действующих одновременно на тело, то алгебраическая сумма моментов всех сил относительно точки, в их плоскости, равен нулю».
 сил, приложенных к точке, равен сумме моментов сил, действующих против часовой стрелки, приложенных к той же точке».
сил, приложенных к точке, равен сумме моментов сил, действующих против часовой стрелки, приложенных к той же точке».Это означает, что алгебраическая сумма всех моментов должна быть равна нулю.
ΣM = 0
Рассмотрим четыре копланарные силы F1, F2, F3 и F4, действующие на тело, когда оно находится в равновесии.
Пусть О — точка, вокруг которой может вращаться тело. Пусть d1, d2, d3 и d4 — расстояние по перпендикуляру от точки O до линии действия сил F1, F2, F3 и F4 соответственно.
Тогда
Момент силы F1 = F1 x d1 (против часовой стрелки)
Момент силы F2 = F2 x d2 (против часовой стрелки)
Момент силы F3 = F3 x d3 (по часовой стрелке)
Момент силы F4= F4 x d4 (по часовой стрелке)
Результирующий момент = M
Σ x d1 + F2 x d2 — F3 x d3 — F4 x d4
Согласно принципу момента силы алгебраическая сумма всех моментов должна быть равна нулю.
Итак,
ΣM = 0
F1 x d1 + F2 x d2 — F3 x d3 — F4 x d4 =0
F1 x d1 + F2 x d2 = F3 x d3 + F4 x d4
Сумма моментов против часовой стрелки = Сумма моментов по часовой стрелке
Это подтверждает принцип силовых моментов.

Применение моментов силы
Моменты силы имеют множество инженерных применений, таких как рычаги, обычные стальные верфи, рычажные предохранительные клапаны и т. д.
Связанные статьи:
Теорема Вариньона
. Закон параллелограмма сил
. Теории неудач
. Изгиб
Итак, здесь я обсуждал, что такое момент силы? Классификация момента, принцип действия момента силы, а также приложение момента силы.
Надеюсь, вам понравится эта тема.
Спасибо.
ньютоновская механика — Равен ли момент силы работе силы и потенциальной энергии гравитации? (M = W = g.p.e.)
Вопрос
Изменено 2 года, 3 месяца назад
Просмотрено 1к раз
$\begingroup$
Смешной вопрос, но.
 ..
Если эти уравнения верны:
..
Если эти уравнения верны:Момент силы = сила * расстояние по перпендикуляру от оси вращения до силы (M=Fd)
А
Работа силы = сила * расстояние, пройденное силой в направлении действия силы ( W = Fd)
Значит ли это…
Момент силы = работа, совершаемая силой
(я знаю, что расстояния здесь неодинаковы, одно для поворотов, а другое для работы)
Но оба имеют одинаковые единицы, Нм (Ньютон * метр)
И
Сила и расстояние в обоих уравнениях косвенно пропорциональны, причем либо прямо пропорциональны их умноженному значению..:
Если расстояние постоянно и сила увеличивается, момент силы увеличивается..
Если сила постоянная и расстояние уменьшаются, работа, совершаемая работами, уменьшается..
Дополнительно Ньютон * метр Джоули..в случае работы.. (Нм = Дж)
Означает ли это…
Момент силы = работа, совершаемая силой?
НО ЭТО НЕ ОСТАНАВЛИВАЕТСЯ.
Если вес = масса * ускорение свободного падения = сила (W = mg = F)
А
гравитационная потенциальная энергия = вес * высота = масса * г * высота = сила * высота = МОМЕНТ СИЛЫ = РАБОТА, СОВЕРШАЕМАЯ СИЛОЙ.
 (g.p.e. = mgh = Fh = Fd = M = W )
(g.p.e. = mgh = Fh = Fd = M = W )Заключение, что…
Момент силы = работа силы = потенциальная энергия гравитации (M = W = g.p.e.)
— Я нахожу это смешным, но меня очень беспокоит тот факт, что это не обсуждалось и не было ответа раньше (насколько я видел)
- ньютоновское -механика
- вращательная динамика
- работа
- потенциальная энергия
- крутящий момент
$\endgroup$
1
$\begingroup$
Прежде всего, я предлагаю вам взглянуть на то, как использовать MathJax для правильного форматирования вопроса, так как его немного сложно читать.
Теперь к физике. На самом деле момент силы определяется как $$\vec{M}=\vec{r}\times \vec{F}$$ где $\vec{r}$ — расстояние от некоторой точки до точки приложения силы. Работа определяется как $$W=\int \vec{F}\cdot d\vec{r}$$ где $d\vec{r}$ определяет траекторию в пространстве.
 Несмотря на то, что они имеют одинаковые единицы измерения ($\mbox{сила} \times \mbox{расстояние}$), они не представляют одни и те же физические величины. Вы должны заметить, что крутящий момент определяется относительно одной точки, что видно на следующем изображении (извините за размеры).
Несмотря на то, что они имеют одинаковые единицы измерения ($\mbox{сила} \times \mbox{расстояние}$), они не представляют одни и те же физические величины. Вы должны заметить, что крутящий момент определяется относительно одной точки, что видно на следующем изображении (извините за размеры).С другой стороны, для работы необходимо определить путь, путь, по которому действует сила $\vec{F}$. Поскольку это интеграл, его можно интерпретировать как площадь под кривой:
Еще одно очень важное отличие состоит в том, что работа — это всегда скалярная величина, т. е. число, тогда как крутящий момент — это вектор. Единственная «эквивалентность», которую вы можете найти в своих рассуждениях, — это между работой и энергией, которые на самом деле представляют собой одну и ту же физическую величину, как указано в первом законе термодинамики. Надеюсь, это решит ваш вопрос.
$\endgroup$
$\begingroup$
Значит ли это.
 ..
..Момент силы = работа силы
№
В случае углового движения (движения, вызванного крутящим моментом, или, как вы говорите, моментом) сила заменяется крутящим моментом, а линейное перемещение заменяется угловым перемещением. Или
$$W=\int \overrightarrow F.d\overrightarrow x$$
Заменяется на
$$W=\int \overrightarrow τ.d\overrightarrowθ$$
Где $θ$ — угловое смещение в радианах в результате приложения крутящего момента.
Крутящий момент и сила связаны соотношением
$$\overrightarrow τ=\overrightarrow r x \overrightarrow F=rFsinθ$$
Где в данном случае $θ$ — угол между векторами силы $F$ и перемещения $r$ , а последний член уравнения представляет собой величину крутящего момента.
НО ЭТО НЕ ОСТАНАВЛИВАЕТСЯ.
Если вес = масса * ускорение свободного падения = сила (Вт = мг = F)
и
гравитационная потенциальная энергия = вес * высота = масса * г * высота = сила * высота = МОМЕНТ СИЛЫ = РАБОТА СИЛЫ.
 (g.p.e. = mgh =
Fh = Fd = M = W )
(g.p.e. = mgh =
Fh = Fd = M = W )Делаем вывод…
Момент силы = работа силы = потенциальная энергия гравитации (M = W = g.p.e.)
Неверный вывод.
Крутящий момент (момент) представляет собой векторное произведение векторов силы и смещения, третье уравнение выше. Поскольку угол между силой тяжести и смещением $h$ равен нулю, крутящий момент или момент не задействованы, и, следовательно, крутящий момент или момент силы не совершают никакой работы, когда сила тяжести действует на падающий объект.
Надеюсь, это поможет.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Определение, Первая и Вторая, Сила, Уравнение
Почему дверные ручки всегда находятся с противоположной стороны дверных петель? Если вы попытаетесь толкнуть дверь рядом с петлей, а затем с противоположного конца, вы заметите большую разницу. Находясь рядом с петлей, трудно закрыть дверь; на дверной ручке, это довольно легко. Причина этого в том, что чем дальше от шарнира, тем сильнее эффект поворота.
Что вызывает эффект поворота?
Если объект неподвижен или находится в статическом равновесии, все силы, действующие на этот объект, уравновешивают друг друга. Но если они уравновешивают друг друга и общей силы нет, означает ли это, что объект находится в статическом равновесии?
Взгляните на следующую схему:
Рис. 1 – Две силы, действующие на объект в разных точках
В первом примере обе силы имеют одинаковую величину и действуют в одной и той же точке, но в противоположном направлении, что заставляет бар оставаться неподвижным.

Во втором примере, поскольку силы не действуют в одной и той же точке, они создают эффект вращения, известный как крутящий момент . В этом случае стержень начнет вращаться против часовой стрелки и, следовательно, не будет находиться в статическом равновесии.
Моменты
Величина поворотного эффекта, создаваемого силой, называется моментом силы . Это происходит, когда силы заставляют объект вращаться вокруг некоторого шарнира .
Момент силы рассчитывается следующим образом:
Моменты измеряются в ньютон-метрах, записывается Нм. Сила в ньютонах, расстояние в метрах.
То, что мы исследовали до сих пор, объясняет, почему дверные ручки расположены по другую сторону дверных петель, которые действуют как стержень. Максимальное расстояние между силой, которую мы прикладываем к дверной ручке, и шарниром, приводит к большему моменту. Это облегчает открытие или закрытие двери. Тот же принцип применим к гаечным ключам с длинными рукоятками для увеличения величины момента, что облегчает затяжку болтов.

Груз массой 100 кг подвешен на расстоянии 30 м от оси, на которую опирается стальной стержень. Предполагая, что вес стержня пренебрежимо мал, каков крутящий момент относительно оси вращения?
Рис. 2. Масса 100 кг создает момент
Во-первых, нам нужно определить силу, создаваемую массой. Это его вес или его масса, умноженная на константу гравитационного ускорения. Это дает нам:
Теперь у нас есть сила, приложенная к стержню, в то время как перпендикулярное расстояние от силы до оси вращения было указано выше. Все, что нам тогда нужно сделать, это использовать момент силового уравнения следующим образом:
Пары
Уникальный случай моментов — это когда две параллельные силы, равные по величине, но противоположные по направлению, а также разделенные расстоянием d, заставляют объект вращаться. Это известно как пара .
Пара не имеет равнодействующей силы; он производит только поворотный эффект.

Например, ваши руки производят пару на руле автомобиля, чтобы повернуть руль.
Рис. 3 — Поворот руля на примере пары
Момент пары рассчитывается по следующему уравнению:
Давайте рассчитаем пару, создаваемую силами, действующими на этот стальной стержень длиной 1 м.
Рис. 4. Две силы, действующие на стальной стержень и создающие пару
Все, что нам нужно сделать, это применить уравнение, используя приведенные выше значения: против часовой стрелки.
Представьте себе двух детей, играющих на качелях, причем мальчик сидит слева, а девочка справа.
Вес мальчика слева создает момент, направленный против часовой стрелки, а вес девочки справа создает момент, который поворачивает качели по часовой стрелке.
Что означали бы два момента, созданные детьми, если бы качели были сбалансированы? Чтобы объект находился в равновесии — чтобы качели были сбалансированы — ни в одной точке не должно быть общего эффекта поворота.
 Таким образом, моменты по часовой стрелке и против часовой стрелки должны уравновешивать друг друга.
Таким образом, моменты по часовой стрелке и против часовой стрелки должны уравновешивать друг друга.Это суммируется принцип моментов . Объект находится в статическом равновесии, когда:
Качели на следующей диаграмме сбалансированы. Рассчитайте W, вес блока слева от оси, используя принцип моментов.
Рис. 5 – Различные силы, действующие на качели
Для расчета W применяем уравнение, складывая значения из диаграммы: вращательный эффект, производимый силой.
- Чтобы рассчитать момент, мы умножаем силу и перпендикулярное расстояние между силой и осью вращения.
- Пара – это эффект вращения, создаваемый двумя равными силами, действующими в противоположных направлениях.
- В соответствии с принципом моментов для объекта, находящегося в статическом равновесии, сумма моментов по часовой стрелке равна сумме моментов против часовой стрелки в любой заданной точке.
Преобразователь случайных чисел | Преобразователь момента силы Преобразователь длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (в расчете на массу)Конвертер удельной энергии, теплоты сгорания (в объеме) Конвертер температуры Конвертер интервала Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияТеплопровод Конвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяженияМодерация проницаемости, проницаемости, паропроницаемости Преобразователь скорости пропускания паровПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеПреобразователь оптической силы (диоптрий) в увеличение (X)Электрический заряд КонвертерКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаОбъемный заряд De Преобразователь электрического токаПреобразователь линейной плотности токаПреобразователь поверхностной плотности токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электропроводностиПреобразователь емкостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь калибров проводов в СШАПреобразование уровней в дБм, дБВ, Ватт и других единицахПреобразователь силы магнитного поля КонвертерПлотность магнитного потокаМощность поглощенной дозы излучения, Мощность общей дозы ионизирующего излучения КонвертерРадиоактивность. Откуда: ньютон-метркилоньютон-метрмиллиньютон-метрмикроньютон метртонна-сила (короткий) метртон-сила (длинный) метртон-сила (метрическая) метр-килограмм-сила метрграмм-сила сантиметрфунт-сила фут-фунт фут-фунт дюйм Кому: 03 новый метркилоньютон-метрмиллиньютон-метрмикроньютон метртон-сила (короткий) метртон-сила (длинный) метртон-сила (метрическая) метркилограмм-сила метрграмм-сила сантиметрфунт-сила фут-фунт-фунт-фунт-дюйм Наука приготовления эспрессо: давлениеИтак, вы любите кофе? Узнайте, какое давление необходимо для приготовления действительно хорошего эспрессо! Двутавровые балки в строительстве Обзор Терминология Использование на английском языке Примеры момента силы Заключение Обзор крутящий момент. Две силы, которые рука прикладывает к отвертке, а отвертка прикладывает к головке винта, создают крутящий момент В этой статье мы подробно обсуждаем разницу между моментом силы и крутящим моментом, но следует отметить, что в большинстве случаев и крутящий момент, и момент силы в английском языке относятся к одному и тому же понятию и используются взаимозаменяемо. В употреблении этих слов есть очень незначительные нюансы, и это часто вызывает путаницу. Терминология Использование на английском языкеКак мы уже упоминали выше, и момент силы, и крутящий момент используются для описания одного и того же явления, но иногда используются в разных контекстах. В этом разделе мы рассмотрим контексты, в которых «момент силы» используется чаще, чем «крутящий момент». Крутящий момент часто определяют как явление, вызывающее изменение углового момента. С другой стороны, момент силы не должен вызывать это изменение. Это означает, что крутящий момент является частным случаем момента силы. Мы также можем сказать, что крутящий момент — это момент силы, но момент силы не обязательно является крутящим моментом. Ниже мы рассмотрим некоторые примеры этого. Однако мы должны еще раз повторить, что эта разница между моментом силы и крутящим моментом различается в некоторых контекстах, но в других ситуациях крутящий момент и момент силы используются взаимозаменяемо. Две руки воздействуют на вороток, создавая две силы, и это создает крутящий момент Чтобы понять, что такое момент силы, нам нужно понять, что такое момент в физике вообще. Момент указывает величину, с которой данная сила действует на объект с заданного расстояния. Эта величина зависит как от величины действительной силы, действующей на предмет, так и от расстояния от точки приложения силы до некоторой точки предмета. Как мы видели в определении выше, для момента силы эта точка находится на оси вращения. Момент силы пропорционален силе и радиусу. Это означает, что если к объекту приложена данная сила на данном расстоянии от оси вращения, то величина этой силы увеличивается на радиус, и действие силы на объект больше фактической величины сама сила. Этот принцип используется при создании механического преимущества с помощью систем рычагов, шестерен и шкивов. Когда мы рассматриваем момент силы в этом контексте, мы часто рассматриваем, например, приложение силы к плечу рычага. Изгибающий момент. В этой конструкции нет вращения и, следовательно, нет крутящего момента, а присутствует только момент силы Крутящий момент и момент силы также иногда различают по-другому. Крутящий момент иногда относится к моменту «пары». Здесь пара — это две силы одинаковой величины, действующие в противоположных направлениях и заставляющие объект вращаться. Сумма этих векторов равна нулю. Таким образом, момент силы является более общим термином, а крутящий момент — частным случаем. В некоторых контекстах крутящий момент используется, когда объект движется или вращается, тогда как момент силы используется, когда движение не происходит, например, в таких системах, как опорные балки и другие конструктивные элементы. В этих системах края балки или конструкции могут быть закреплены или вращаться. В последнем случае говорят, что балки свободно оперты. Когда на балку действует сила, например, в направлении, перпендикулярном ее поверхности, создается момент силы. Примеры момента силыЗдесь момент силы равен весу, который каждый ребенок прикладывает к качелям, умноженному на расстояние до точки опоры. Девочка находится ближе к точке опоры, но прикладывает больше усилий, чем мальчик, и это помогает удерживать качели почти в равновесии. Момент силы в сочетании с изгибающим моментом, который мы обсуждали выше, является одним из примеров момента силы в реальной жизни. Момент силы — полезная концепция в строительстве и проектировании конструкций, поскольку знание момента силы, действующей на элемент конструкции, позволяет нам определить величину нагрузки, которую должна выдерживать система. Двутавровые балки широко применялись при строительстве моста Ройял Александра через реку Оттава в 1900 г. растяжение других частей. Например, представьте себе балку, на которую действует сила, направленная вниз и приложенная к середине этой балки. Из-за этой силы луч принимает форму «смайлика». Его верхняя часть сжимается, особенно посередине, где прикладывается сила. Нижняя часть, особенно вокруг центра, растягивается. Если момент слишком велик для материала, чтобы выдержать, то балка ломается. Максимальное напряжение приходится на самый верхний и самый нижний слои, поэтому при проектировании конструкций обычно армируют эти области. Хорошим примером является I -луч . Его поперечное сечение имеет форму прописной буквы « I » с верхней и нижней засечками. Иногда это больше похоже на заглавную букву «H». Это очень эффективная конструкция, так как участки, испытывающие наибольшую нагрузку, усилены, но использование материала минимально. Часто двутавровые балки делают из стали, но можно использовать и другие материалы для изготовления прочных балок, выдерживающих большие нагрузки. На YouTube можно найти примеры экспериментов по проверке прочности двутавровых балок из менее прочных, чем сталь, материалов, таких как фанера и пенопласт. Двутавровые балки часто выбирают, когда на конструкцию воздействует изгибающий момент. Они также полезны при работе с напряжением сдвига , которое представляет собой напряжение, действующее параллельно поверхности конструкции. Крутящий момент двигателя создает скручивающую нагрузку на фюзеляж этого турбовинтового самолета Заключение В этой статье мы рассмотрели разницу между крутящим моментом и моментом силы в англоязычной терминологии и рассмотрели некоторые примеры момента силы. Здесь мы в основном рассматривали помехи, создаваемые моментом силы, но есть много ситуаций, когда момент силы полезен. В статье о крутящем моменте подробно рассматриваются эти примеры. Различие в терминологии, которое мы обсуждали, в основном относится к машиностроению США и Великобритании, но в физике США и Великобритании термины крутящий момент и момент силы обычно используются взаимозаменяемо. Список литературы Эта статья была написана Kateryna Yuri . Вы можете быть заинтересованы в других преобразователях в группе механиков:Угловой преобразователь Англосная скорость и конвертер с частотой вращения Преобразователь Преобразователь плотности Преобразователь энергии и работы Преобразователь силы Преобразователь длины и расстояния массовый преобразователь Момент преобразователя инерции Конвертер мощности Давление, напряжение, конвертер модуля Янга Специфический объемный преобразователь Преобразование крутящего момента и общие измерения приготовления. Преобразователь линейной скорости и скорости Компактный калькулятор Полный калькулятор Определения единиц измерения У вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и через несколько минут вы получите ответ от опытных технических переводчиков. |
Q6 Укажите единицу момента силы в системе СИ.
 ..
..Перейти к
- Объективные вопросы
- Вопросы с короткими/длинными ответами
- Числа
- Иметь значение
- Физические величины и измерения
- Сила и давление
- Энергия
- Световая энергия
- Теплопередача
- Звук
- Электричество
Главная > Селина Солюшнс Класс 8 Физика > Глава 3 — Сила и давление > Упражнение: Вопросы с короткими/длинными ответами > Вопрос 6
Вопрос 6 Вопросы с короткими/длинными ответами
Q6) Укажите единицу измерения момента силы в системе СИ.
Ответ:
Решение:
СИ единицей момента силы является ньютон-метр (Н·м).
Стенограмма видео
«Привет, студенты, добро пожаловать в Лидо вопрос обучения и ответ видео сейчас, прежде чем двигаться дальше с си единица момента силы понять, что мы подразумеваем под моментом сила правильно, чтобы понять, что у меня есть очень красивая картинка этого колеса сюда поэтому, когда мы прикладываем силу к этому колесу, колесо не может двигаться с этой стороны вы можете сказать мне, почему да потому что он повернут здесь или есть повернуть здесь или мешает колесу двигаться предстоящий но вместо того, где что будет эта сила вместо этого делай то, что будет с колесом v начнет вращаться поэтому колесо начинает вращаться вдоль ось вращения вы все видите ось вращение на этой картинке да это ось вращения, поэтому с что давайте быстро определим, что мы делаем имею в виду момент силы так, как мы видели, когда сила применены колесо поворачивается или начинает вращаться такой поворотный эффект силы на тело называется моментом силы, так что это было просто право теперь он представлен символом тау или крутящий момент это также называется крутящим моментом теперь давайте придем есть математический формула момента силы тоже который дает сила, которая является силой, которую мы применяем здесь на перпендикулярном расстоянии от вращаться так что это перпендикулярное расстояние от стержня поэтому сила в перпендикулярном расстоянии от стержня даст вам момент силы в единица си, как мы знаем из математическая формула сила си единицей силы является ньютон давайте напишем, что вниз символ n и на перпендикулярном расстоянии от развернуться так для расстояния единица s i — метр, поэтому давайте просто запишем это поэтому единица si для тау или крутящего момента становится ньютон-метр или нм, так что это единица СИ для момент силы, надеюсь, это было понятно, если у вас есть дополнительные вопросы пожалуйста, оставьте свои комментарии ниже, спасибо ты
Связанные вопросы
Q1) Дайте определение силы. Укажите его единицу СИ.
Укажите его единицу СИ.
Q2) Назовите два действия силы, приложенной к телу.
В3) Чем отличается действие силы, когда она приложена к (а) твердому телу (б) нетвердому телу?
Q4) Укажите действие силы F на следующей диаграмме.
Q5) Дайте определение термину «момент силы».
Q7) Укажите два фактора, которые влияют на момент силы.
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Объективные вопросы
Короткие/длинные вопросы. Вопросы
Вопросы
Числовые
Главы
Маттер
Физические величины и измерения
Сила и давление
Энергия
Энергия LIGH Электричество
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
Формула момента — GeeksforGeeks
Момент — это сила, которая определяется как движение, направленное на вращение тела вокруг определенного положения. Давайте разберемся в этом моменте на примерах. Если кто-то хочет закрыть окно, он просто отталкивает ручку пальцем, и окно плавно закрывается. Теперь попробуйте снова закрыть окно, но на этот раз поднесите палец слишком близко к петле и посмотрите, не слишком ли тяжело. Силы используются для того, чтобы заставить любое тело или объект вращаться. Следовательно, поворотное действие силы известно как момент силы. Есть еще много примеров моментов в нашей повседневной жизни, и это
- Осмотр достопримечательностей в парке
- Открытие консервной банки
- Использование рычага для подъема большого груза
- Молоток используется для удаления гвоздей и т.
 д.
д.
Момент силы
Момент силы – это движение который заставляет тело или объект вращаться и также известен как крутящий момент. Он также определяется как произведение силы и перпендикулярного расстояния. Момент имеет как величину, так и направление.
Формула момента
Рассчитывается по формуле
M = F × d
Где M — момент силы,
F — приложенная сила
d — расстояние от фиксированного положения.
Эта формула применима как для уравновешенных, так и для неуравновешенных сил. Единицей измерения момента в системе СИ является ньютон-метр (Нм). Его размеры составляют [ML 2 T -2 ], а его направление задается правилом большого пальца правой руки.
Принцип момента
Он утверждает, что если система находится в равновесии, то сумма ее моментов по часовой стрелке будет равна сумме ее моментов против часовой стрелки.
Момент по часовой стрелке = момент против часовой стрелки.
F 1 × d 1 = F 2 × d 2.
- Момент по часовой стрелке. Сила заставляет объект или тело вращаться по часовой стрелке. Это воспринимается как положительное.
- Момент против часовой стрелки — Сила заставляет объект или тело поворачиваться против часовой стрелки. Он воспринимается как отрицательный.
Термин Равновесие определяется как «это происходит, когда все силы, действующие на тело, уравновешены».
Применение принципа моментов
- Мы можем найти массу объекта.
- В простых машинах.
- Помогает понять, как расположены и организованы физические величины.
Пара
Пара определяется как пара двух сил, которые равны по величине, но их направления противоположны друг другу, а движения линий не совпадают.
Формула пары:
τ = F × d.
S.I единица пары = ньютон-метр (Нм) и размеры [ML 2 T 2 ].
Здесь силы равны и противоположны, поэтому мы получаем, что сила равна нулю, а линейное ускорение отсутствует.
Несколько применений пары
- Открытие и закрытие крышки бутылки.
- С помощью ключа откройте шкафчик.
- Поворот отвертки.
- Штурвал, установленный водителем автобуса.
Импульс
Называется свойством движения объекта. Импульс определяется как произведение массы и скорости объекта. Обозначается символом «р».
Формула импульса,
p = m × v
Где p = импульс тела или объекта
m = масса объекта
v = скорость объекта.
Единица количества движения в системе СИ – кг м/с.
Вот несколько задач на данный момент.
Примеры задач
Вопрос 1. Мальчик сидит на одной стороне качелей в 3 м от точки. Найдите момент, если вес мальчика 20 Н.
Мальчик сидит на одной стороне качелей в 3 м от точки. Найдите момент, если вес мальчика 20 Н.
Решение:
Учитывая, что вес мальчика создавал момент, направленный против часовой стрелки.
Момент = Сила × расстояние0003
М = 20 × 3
М = 60 Нм.
Вопрос 2: Момент силы 20 Н относительно неподвижной точки равен 2 Нм. Вычислите расстояние от точки до линии действия силы.
Решение :
Дано, Сила = 20 Н и Момент = 2 Нм.
Используя формулу момента M = F × d
2 = 20 × d
d = 2/20
d = 0,1 м.
Вопрос 3: Найдите силу, приложенную к двери, вызывающую момент 10 Нм, если расстояние от оси петли до точки на двери, где была приложена сила, составляет 2 м.
Решение:
Дано, момент (М) = 10 Нм
Расстояние (d) = 2 м.
Как известно, M = F × d
10 = F × 2
F = 10/2
F = 5N.
Вопрос 4: Балансовые весы имеют длину плеч 100см и 80см. Какой вес, помещенный на сковороду с более длинным плечом, уравновесит предмет весом 200 г, находящийся на других кастрюлях?
Решение:
По принципу моментов
Момент по часовой стрелке = Момент против часовой стрелки
Вт × 100 = 200 × 80
Вт = (200 × 80)/100
Вт = 160 г.
Вопрос 5: Два человека сидят на качелях противоположными сторонами, один человек весит 100 Н и находится на расстоянии 2 м от оси вращения, а вес другого человека составляет 200 Н. найти, где человек сидит, чтобы сбалансировать качели.
Решение:
Согласно принципу моментов,
Момент по часовой стрелке = Момент против часовой стрелки
100 × 2 = 200 × d
d = (100 × 2)/200
d = 1 м.


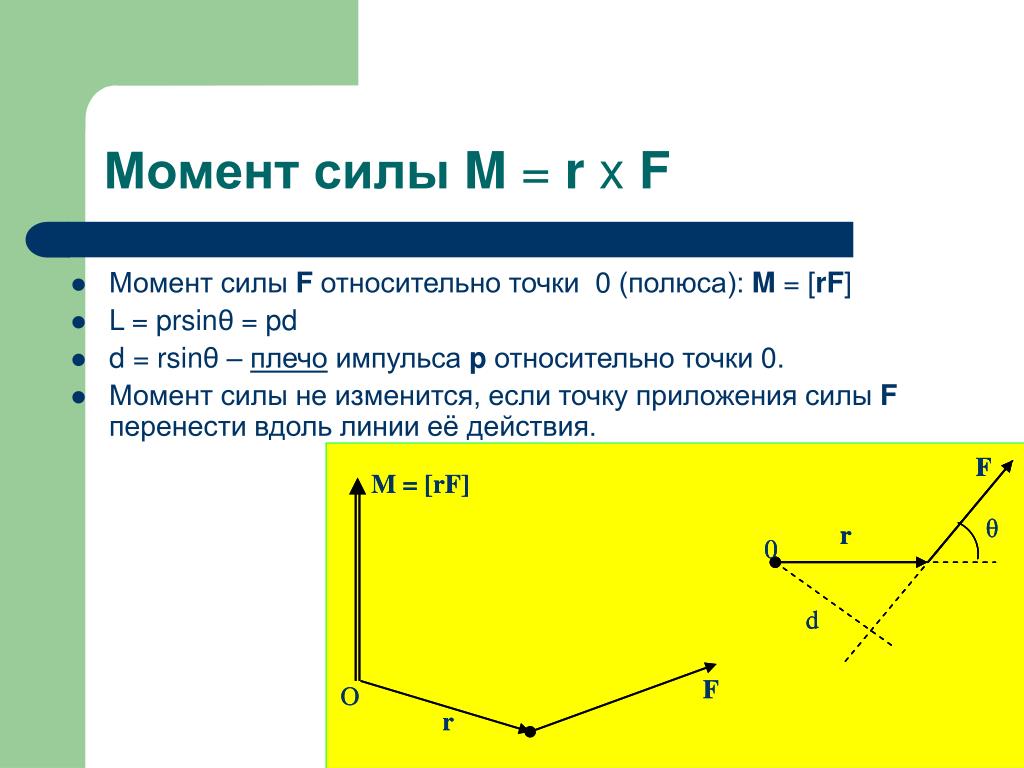 — 464 с.
— 464 с.