ИНЕРЦИЯ И МОМЕНТ ИНЕРЦИИ: базовые сведения » РобоВики
В этой статье
- История понятия «инерция»
- Инерция, кинетическая энергия, работа
- Момент инерции
- Вопросы
До эпохи Возрождения, в Средние века, в западной философии общепринятой была аристотелевская теория движения. Ученик Платона, древнегреческий философ Аристотель (384 – 322 гг. до н. э.) утверждал, что в отсутствии внешней силы все объекты остановятся, и что движущиеся объекты продолжают двигаться только до тех пор, пока есть побуждающая к движению сила.
Бюст Аристотеля. Римская копия греческого бронзового оригиналаЭто утверждение закономерно вытекало из реальных наблюдений. При этом Аристотель объяснял движение снарядов, выпущенных из орудия, невидимым действием окружающей среды, которая каким-то образом продолжает двигать снаряд. При этом философ пришел к выводу, что такое движение в пустоте невозможно.
Принцип движения по инерции, который возник у Аристотеля для «движений в пустоте», гласил, что объект имеет тенденцию сопротивляться изменению движения.
Эта теория движения неоднократно оспаривалась. Например, в 6 веке византийский филолог Иоанн Александрийский (Иоанн Грамматик) раскритиковал тезисы Аристотеля, что среда поддерживает движения тела и что тело остановится в пустоте. В 11 веке персидский исламский врач, астроном, философ и писатель Ибн Сина [Авиценна] (980 – 1037 гг.) сделал вывод, что снаряд при отсутствии действия внешних сил, то есть в пустоте, не остановится.
Окончательно от аристотелевской теории отказались в ходе ряда открытий, предшествовавших научной революции XVII века.
Портрет Кеплера в 1610 годуТермин «инерция», от латинского слова «безделье» или «лень» (лат. inertia), был впервые использован немецким математиком и астрономом Иоганном Кеплером (1571 – 1630 гг.) в его книге «Epitome Astronomiae Copernicanae», которая была опубликована в трех частях в 1617–1621 гг. Но Кеплер определял инерцию только как сопротивление движению, основываясь на старом предположении, что покой – это естественной состояние вещей, которое не нужно объяснять и к которому стремятся тела.
Но Кеплер определял инерцию только как сопротивление движению, основываясь на старом предположении, что покой – это естественной состояние вещей, которое не нужно объяснять и к которому стремятся тела.
Покой и движение объединил единым принципом современник Кеплера Галилео Галилей (1564 — 1642) — итальянский физик, механик, астроном, философ и математик. Он первый, кто направил зрительную трубу в небо, превратив её в телескоп. В 1609 году он создал свой первый телескоп с трёхкратным увеличением. Галилео Галилей писал, что «если устранить все внешние препятствия, то тяжелое тело на сферической поверхности, концентрической Земле, будет поддерживать себя в том состоянии, в котором оно находилось; если его поместить в движение к западу (например), то оно будет поддерживать себя в этом движении».
Чтобы оспорить идею Аристотеля о естественности состояния покоя, Галилей проводил один из таких мысленных экспериментов.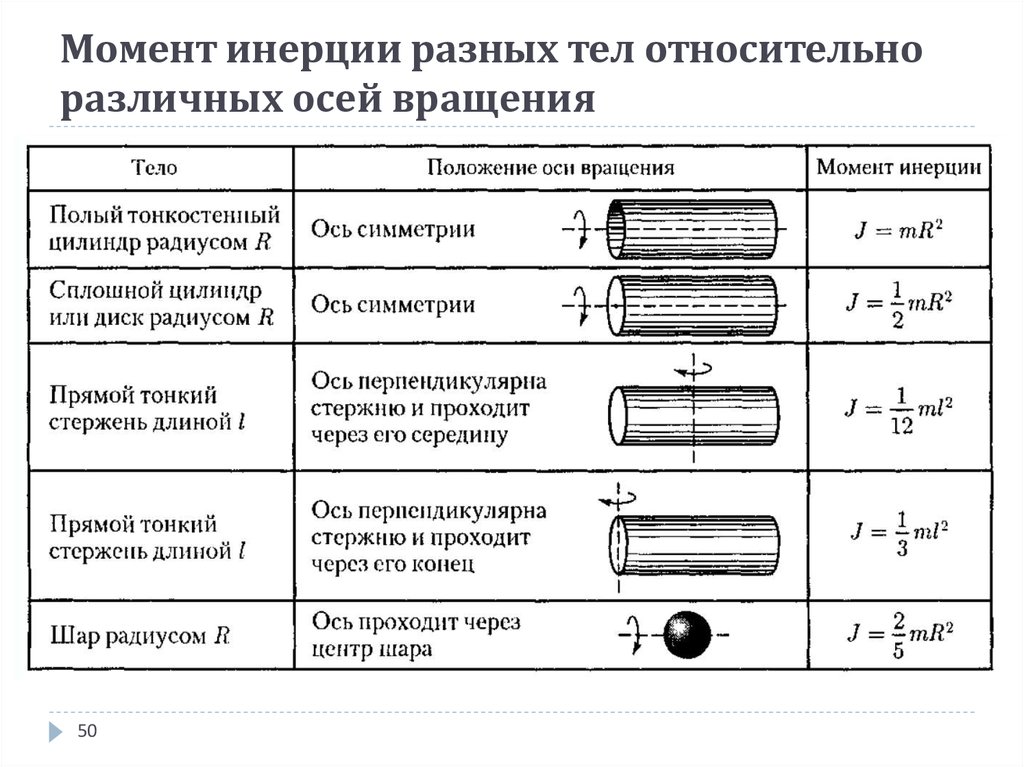 Если исключить силу трения, то шар, катящийся по склону оврага (холма), взлетит до той же высоты на противоположной стороне. Если второй склон постепенно наклонять, шар будет катиться все дальше и дальше и в горизонтальном положении склона будет катиться бесконечно долго.
Если исключить силу трения, то шар, катящийся по склону оврага (холма), взлетит до той же высоты на противоположной стороне. Если второй склон постепенно наклонять, шар будет катиться все дальше и дальше и в горизонтальном положении склона будет катиться бесконечно долго.
Галилей сделал вывод, что «Тело, движущееся по ровной поверхности, будет продолжать движение в том же направлении с постоянной скоростью, если движение не будет нарушено».
Готфрид Кнеллер. Портрет Исаака Ньютона. 1689Позднее, мысли Галилея будут уточнены и систематизированы Исааком Ньютоном. Исаак Ньютон (1642 – 1727) — английский физик, математик, механик и астроном, основатель классической физики. В своем труде «Математические начала натуральной философии» (Philosophiae Naturalis Principia Mathematica), впервые опубликованном в 1687 году, он изложил закон всемирного тяготения и три закона динамики.
Явление инерции, изначально сформулированное Галилеем, вошло в первый закон Ньютона.
Оговоримся, что согласно определению, законы Ньютона справедливы только для систем отсчета (система отсчета – это тело отсчета со связанной с ним системой координат, относительно которого можно вычислять положение тел, и система измерения времени, т.е. некоторые часы), которые принято называть инерциальными. Инерциальная система отсчета – это такая система, в которой ускорение тел зависит только от приложенных сил, а не свойством самой системы отсчета (наблюдателя) перемещаться с ускорением.
Посмотрим на второй закон Ньютона.
Чаще его записывают в виде:
так как в инерциальной системе отсчета сила является причиной ускорения тела.
Как видно из второй формулы, для тела неизменной массы ускорение тела (скорость изменения его скорости) прямо пропорционально силе, приложенной к телу (чем сильнее толкаем, тем быстрее тело разгоняется) и обратно пропорционально его массе (чем тяжелее тело, тем сложнее его разгонять).
Представим, что тело движется в вакууме и на него не действуют никакие силы (F=0). Значит и скорость его меняться не будет (a=0).
Инерция (лат. inertia — покой, постоянство, неизменность) – природное явление сохранения равномерного прямолинейного движения или состояния покоя любого тела, пока на него не действуют внешние силы или если действие сил скомпенсировано.
Инертность – свойство конкретного тела оставаться в покое или равномерно прямолинейно двигаться. От инертности зависит ускорение тела при приложении к нему внешних сил. Мерой количественного измерения инертности тела в прямолинейном движении является его масса. Больше масса – больше инертность тела, т.е. тем сложнее придать ему ускорение (разогнать или остановить).
Тормозной путь грузовика и легковушкиИз-за большей чем у легковушки массы у грузовика инертность выше. Соответственно, и тормозной путь у него будет больше – нужно приложить большую силу, чтоб его остановить (хотя, можно поставить очень мощные тормоза). Говорить, что у грузовика больше инерция – некорректно.
Говорить, что у грузовика больше инерция – некорректно.
Мерой инертности тела в прямолинейном движении выступает его масса. Больше масса – больше инертность тела.
Инерция, кинетическая энергия, работа
Приведем другой пример. Представь тяжелоатлета… Даже двух, которые решили поставить мировой рекорд и сдвинуть самолет. Им придется приложить немало сил, чтобы вначале разогнать самолет от нуля до некоторой скорости, а потом поддерживать эту скорость, преодолевая силу трения, направленную назад. Конечно, проще сдвинуть с места (преодолеть инерцию покоя) и разогнать до большой скорости тело меньшей массы, например, футбольный мяч. Инертность самолета во много раз больше инертности футбольного мяча.
Силачи тянут Ил-76А к какому трюку прибегает фокусник, чтобы в случае со скатертью все предметы остались на столе? Правильно, нужно выдернуть скатерть за наименьшее время. Чем меньше время, тем меньше энергии перейдет с силой трения на предметы и они просто не успеют разогнаться.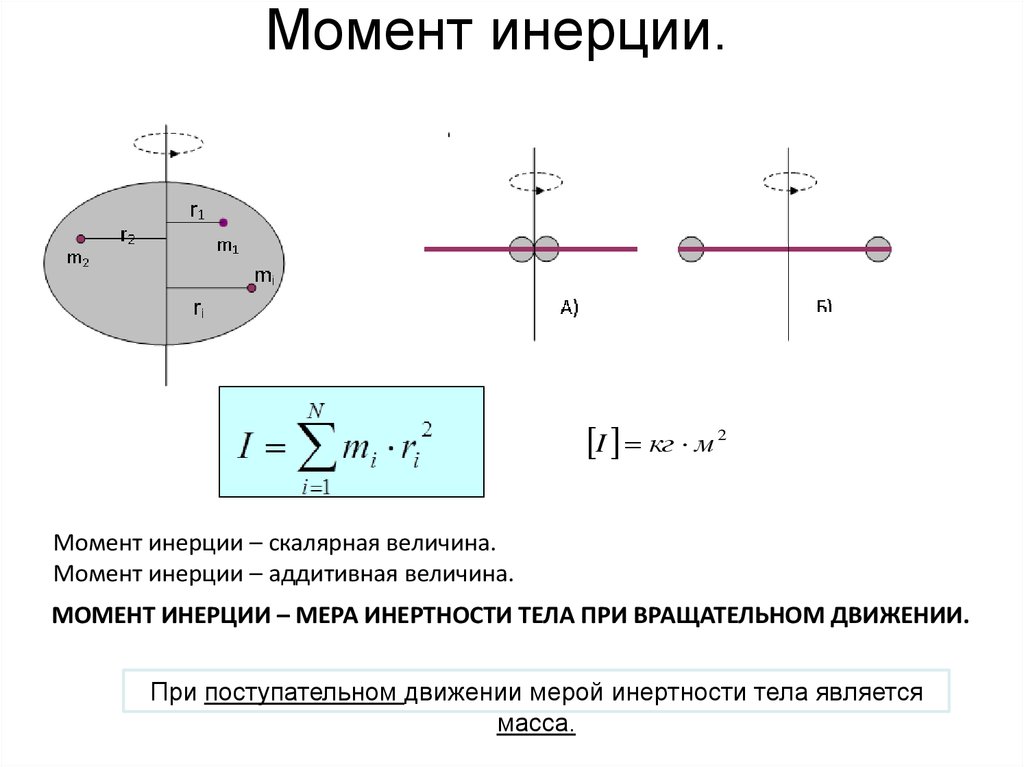
Энергия движущегося тела называется кинетической энергией и измеряется в Джоулях. Если тело неподвижно, кинетическая энергия равна нулю.
Чтобы разогнать тело массой m до нужной скорости V из состояния покоя (например, самолет), нужно выполнить работу, равную кинетической энергии разогнанного тела (без учета разных потерь):
Работа по изменению кинетической энергии тела совершается за счет приложения к нему некоторой силы – силы тяжести, силы трения, силы воздействия на него другого тела (тяжелоатлета-силача, дующего ветра, реактивной тяги ракетного двигателя и пр.).
Пусть силач разогнал до 0.1 м/с (10 сантиметров в секунду) легковую машину массой 1200 кг и самолет Ил-76 массой 88 500 кг в космосе (не будем учитывать силу трения). Тогда для преодоления инерции этих тел ему пришлось сжечь мышечной энергии на 6 Дж и 442,5 Дж соответсвенно. Т.е. на преодоление инерции покоя у самолета у спортсмена уйдет в 74 раза больше энергии, чем на автомобиль.
Чтобы остановить тело массой m, движущееся со скоростью V, нужно совершить обратную работу, равную отрицательному значению кинетической энергии этого тела:
Т.е. чем больше скорость тела и его масса, тем больше энергии на преодоление инерции движения надо затратить.
Если выключить мотор, машина под действием силы трения ее движущихся частей друг о друга, силы трения о воздух корпуса и силы трения колес об асфальт остановится сама. Но остановить машину можно и быстрее, увеличив силу трения с помощью тормозных дисков, т.е. выжав педаль тормоза.
При равной скорости масса грузовика намного больше, а значит больше его кинетическая энергия. Двигаясь накатом грузовик остановится дальше, чем легковой автомобиль – его инертность выше. Кстати, можно ли остановить грузовик быстрее легкового автомобиля и при каких условиях?
Момент инерцииИнерция проявляется не только для прямолинейного движения, но и при вращении тел. В двигателе есть специальное устройство – маховик (на рисунке справа маховик покрашен темно-серым цветом и имеет зубчики). Инерция его вращения помогает работать двигателю нормально. Энергия расширяющихся газов при воспламенении топлива толкает поршень вниз, а затем ему нужно идти вверх, выталкивая продукты сгорания. Без маховика поршень не смог бы провернуть коленвал без рывков. Двигатель без маховика заглохнет.
Инерция его вращения помогает работать двигателю нормально. Энергия расширяющихся газов при воспламенении топлива толкает поршень вниз, а затем ему нужно идти вверх, выталкивая продукты сгорания. Без маховика поршень не смог бы провернуть коленвал без рывков. Двигатель без маховика заглохнет.
Ну а со спинерами и волчками знакомы многие.
Вот только в приведенных примерах форма тела не меняется. А изменится ли инертность тела при изменении его формы?
Вращение на фигурном катанииМногие могут вспомнить фигурное катание. Масса тела фигуриста за выступление не меняется. Но его скорость вращения мгновенно увеличивается, стоит прижать руки и ноги, и вытянуться в струнку. Т.е. при уменьшении радиуса тела скорость вращения увеличивается. Т.е. инертность тела должна уменьшиться? Давайте разбираться.
Вернемся к формулам. Скорость вращающегося тела описывается как произведение угловой скорости (омега) на радиус:
Скорость вращающегося телаПри этом кинетическая энергия вращающегося тела примет вид:
Синим цветом выделено произведение массы тела на радиус в квадрате.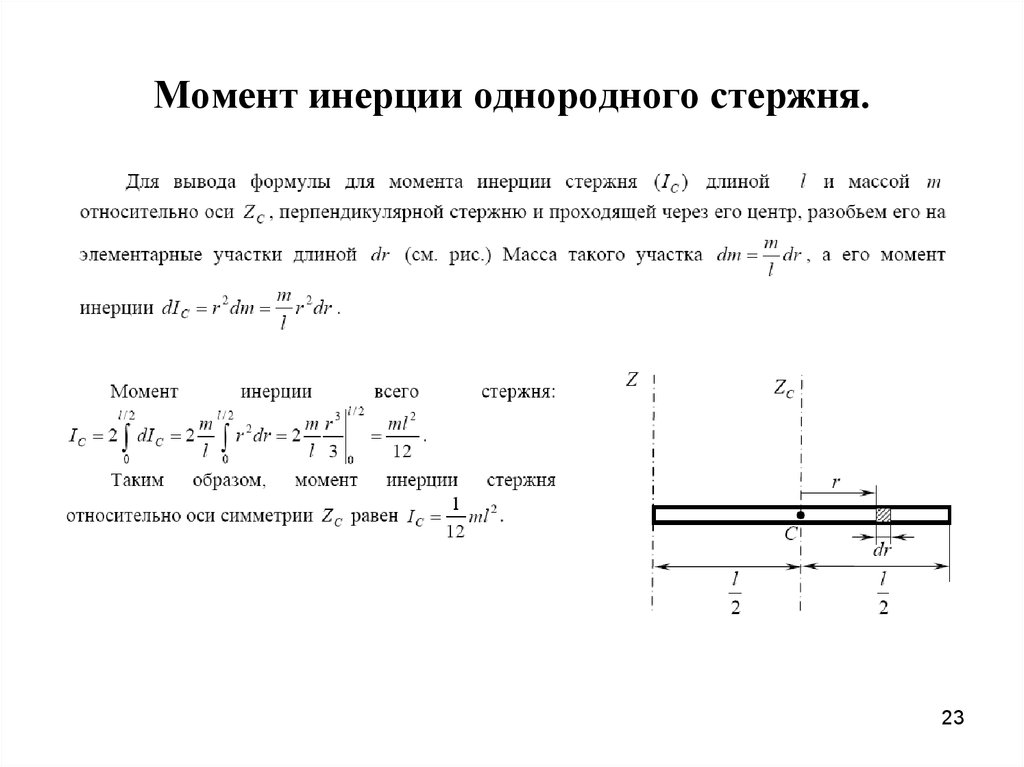 Эта величина называется моментом инерции вращающегося тела и обозначается латинской буквой I (и).
Эта величина называется моментом инерции вращающегося тела и обозначается латинской буквой I (и).
Мерой инертности вращающего тела выступает момент инерции, который зависит от массы тела и расстояния этой массы от центра вращения.
Представим, что девочка не только вращает груз над собой, но и идет. Тогда полная кинетическая энергия девочки с грузом примет вид:
Первая часть описывает кинетическую энергию двигающейся прямолинейно с некоторой скоростью девочки с грузом, а вторая – кинетическую энергию вращающегося груза. Полная кинетическая энергия — это сумма энергии прямолинейно движущегося тела и энергии вращающегося тела. Точно так же кинетическая энергия будет рассчитываться для движущегося по столу раскрученного волчка или съезжающего с наклонной плоскости цилиндра.
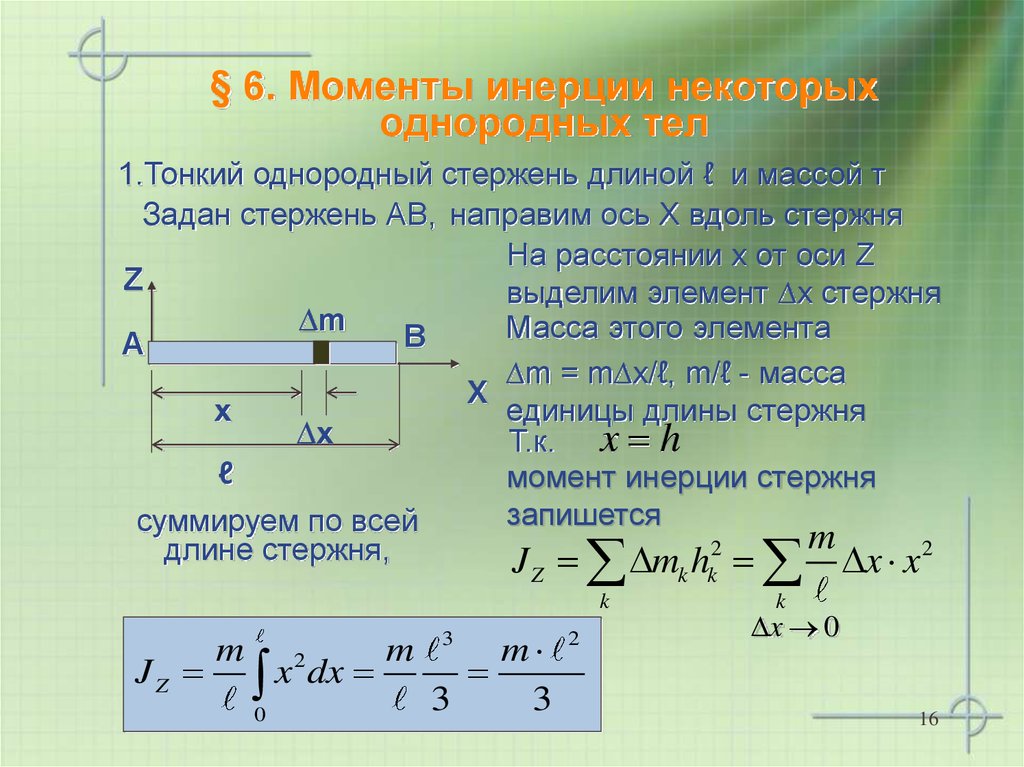
Так как вращающееся тело может иметь форму, отличную от точки или маленького шарика, то и формула момента инерции для более точных расчетов может принимать разный вид.
Некоторые формулы для расчета момента инерции для тел разной формыПример.
Цилиндры одинаковой массы (m1 = m2), но разного радиуса (r1 < r2), скатываются с горки высотой h. Какой цилиндр скатится быстрее? Какое из тел обладает меньшей инертностью?
Цилиндры одинаковой массы, но разного радиуса, скатываются с горки высотой hВ верхней точке кинетическая энергия обоих цилиндров будет равна нулю, так как скорость равна нулю. Потенциальная энергия будет одинаковой и максимальной.
Потенциальная и кинетическая энергия 1 и 2 цилиндра верхней точкеПри скатывании цилиндров по закону сохранения энергии потенциальная энергия переходит в кинетическую и в самой нижней точке будет равна нулю, так как высота равна нулю. А кинетическая энергия в нижней точке будет складываться из поступательной кинетической энергии и кинетической энергии вращающегося тела и у обоих тел также будет одинаковой, так как их потенциальные энергии были равны.
Кинетическая энергия первого и второго цилиндра в нижней точкеНо так как радиус первого тела меньше второго, то и момент инерции первого тела меньше второго и будет справедливо:
Тогда для кинетической энергии поступательного движения будет справедливо отношение:
Следовательно, скорость первого цилиндра должна быть выше скорости второго, и он скатится быстрее. Так как мерой инертности вращающегося тела является момент инерции, то первое тело с меньшим радиусом и меньшим моментом инерции будет обладать меньшей инертностью, чем второе. Разогнаться под действием каких-либо сил (силы тяжести) такому телу проще.
Так как мерой инертности вращающегося тела является момент инерции, то первое тело с меньшим радиусом и меньшим моментом инерции будет обладать меньшей инертностью, чем второе. Разогнаться под действием каких-либо сил (силы тяжести) такому телу проще.
Вопросы
1. Посмотри на картинку с формулами для расчета момента инерции для тел разной формы. Как ты думаешь, какая формула лучше подходит для расчёта момента инерции маховика автомобиля. Варианты ответа: a, b, c, d, e, f, g, h, или i
Маховик автомобиля2. Два волчка одинаковой массы раскрутили до одинаковой угловой скорости, но диаметр первого волчка меньше диаметра второго. Какой из них упадет раньше?
3. На рисунке показаны три варианта конструкции. Какой вариант машинки имеет наименьшую инертность, а какой максимальную? Почему?
Видео:
- Инерция. GetAClass
- Момент инерции. GetAClass
- Момент инерции вращающихся тел. Эксперимент. Зависимость момента инерции от распределения массы
- Момент инерции вращающихся тел.
 Эксперимент. Скатывание цилиндров с наклонной плоскости одинаковой массы и размера
Эксперимент. Скатывание цилиндров с наклонной плоскости одинаковой массы и размера - Момент инерции вращающихся тел. Фигурное катание. Юлия Липницкая, вращение
- Момент инерции. Работа двигателя с маховиком и без него
Статьи:
- Первый закон Ньютона и инерциальные системы отсчёта
- Второй закон Ньютона
- Равнодействующая
- Третий закон Ньютона
- Неинерциальные системы отсчёта
Определение моментов инерции модели. Один на один с врагом [Русская школа рукопашного боя]
Определение моментов инерции модели
Момент инерции тела есть мера инертности тела при вращательном движении.
Моментом инерции модели (системы тел) относительно некоторой оси называется физическая величина, равная сумме произведений масс mi отдельных звеньев (тел) на квадрат их расстояний ri от рассматриваемой оси:
Это означает, что в деформирующейся биомеханической системе тел, когда ее звенья отдаляются от оси вращения, момент инерции системы увеличивается.
Основными факторами, влияющими на момент инерции, являются масса и длина тела. На рис. 38 показана зависимость момента инерции (в условных единицах) от позы тела и положения оси вращения. Как видно, изменением позы можно очень сильно влиять на момент инерции. Например, группировка при выполнении сальто (в) уменьшает момент инерции по сравнению с прямым положением тела (г) в три раза.
Момент инерции тела I0 относительно оси вращения, проходящей через ЦМ, называется центральным.
При его определении можно воспользоваться данными таблицы 4. Расстояния ri относительно оси вращения О—О определяются просто.
Для звеньев тела, расположенных выше оси:
ri = yi – yцм;
для остальных звеньев, расположенных ниже оси:
ri = yцм – yi.
Центральный момент инерции модели:
Таблица 4
Рис. 36
Рис. 37
I0 = ?miri2 = (m1r12 + m2r22 +…+ mnrn2) = (5,5.
В других случаях предварительно следует вычертить рабочую модель в масштабе и произвести предварительные расчеты.
Момент инерции относительно любой оси, параллельной центральной, можно рассчитать по формуле:
Ic = Io + mil2,
где Ic – искомый момент инерции;
Io – центральный момент инерции;
mi – масса звена;
l – расстояние между осями.
Рис. 38
Инерционное сопротивление увеличивается с отдалением частей тела от оси вращения пропорционально квадрату расстояния. Поскольку материальные точки в теле расположены на разных расстояниях от оси вращения, для ряда задач оказалось удобным ввести понятие «радиуса инерции».
Радиус инерции Rин – это сравнительная мера инертности данного тела относительно его разных осей. Из выражения для момента инерции относительно данной оси I = MRин2 следует:
где М – масса тела.
Найдя опытным путем момент инерции Io, можно рассчитать радиус инерции Rин, величина которого характеризует распределение материальных точек в теле относительно данной оси. Но точное количественное определение этой величины в конкретных случаях нередко затруднено.
Инерционно-массовые характеристики, такие, как масса тела, положение центра масс, величина момента инерции, оказывают существенное влияние на параметры устойчивости, а также на инерционное сопротивление тела вращательному движению.
В частности, чем больше инерционное сопротивление тела, тем меньше угловая скорость его вращения. Например, при вращении тела вокруг вертикальной оси (рис. 38а) с угловой скоростью ?1 увеличение инерционного сопротивления (I2>I1) разведением рук в стороны (рис. 38б) приводит к уменьшению угловой скорости (?
Данный текст является ознакомительным фрагментом.
1.2. Определение работы тренера
1.2. Определение работы тренера Проводя тренерские семинары, я часто задаю участникам вопрос: «В чём заключается работа тренера, что для вас в ней главное?»Действительно, ведь из массы наваливающихся на тренера обязанностей какие-то должны быть более важными, и в конечном
Определение силы ветра
ОПРЕДЕЛЕНИЕ ПЕДАГОГИЧЕСКИХ ПОКАЗАТЕЛЕЙ
ОПРЕДЕЛЕНИЕ ПЕДАГОГИЧЕСКИХ ПОКАЗАТЕЛЕЙ
1. Контроль физической подготовленностиПедагогический контроль в спортивной деятельности дзюдоистов детско-юношеского возраста приоритетно направлен на изучение показателей их физической подготовленности по
Контроль физической подготовленностиПедагогический контроль в спортивной деятельности дзюдоистов детско-юношеского возраста приоритетно направлен на изучение показателей их физической подготовленности по
ОПРЕДЕЛЕНИЕ СОЦИАЛЬНО-ПСИХОЛОГИЧЕСКИХ ПОКАЗАТЕЛЕЙ
ОПРЕДЕЛЕНИЕ СОЦИАЛЬНО-ПСИХОЛОГИЧЕСКИХ ПОКАЗАТЕЛЕЙ Наиболее сложный раздел контроля определяет психические состояния, личностно-характерологогические особенности, микроклимат в коллективе дзюдоистов и другие показатели. Получаемые результаты будут более надежными,
ОПРЕДЕЛЕНИЕ МЕДИКО-БИОЛОГИЧЕСКИХ ПОКАЗАТЕЛЕЙ
ОПРЕДЕЛЕНИЕ МЕДИКО-БИОЛОГИЧЕСКИХ ПОКАЗАТЕЛЕЙ Определение медико-биологических показателей проводится систематически, т. к. выявляет физическое развитие и здоровье занимающихся. У дзюдоистов обычно применяют тестовые методики двух видов.а) Тесты, проводимые в покое,
Определение своих ограничителей
Определение своих ограничителей
В главе 5 вы определили свои сильные и слабые стороны с использованием профиля врожденных способностей.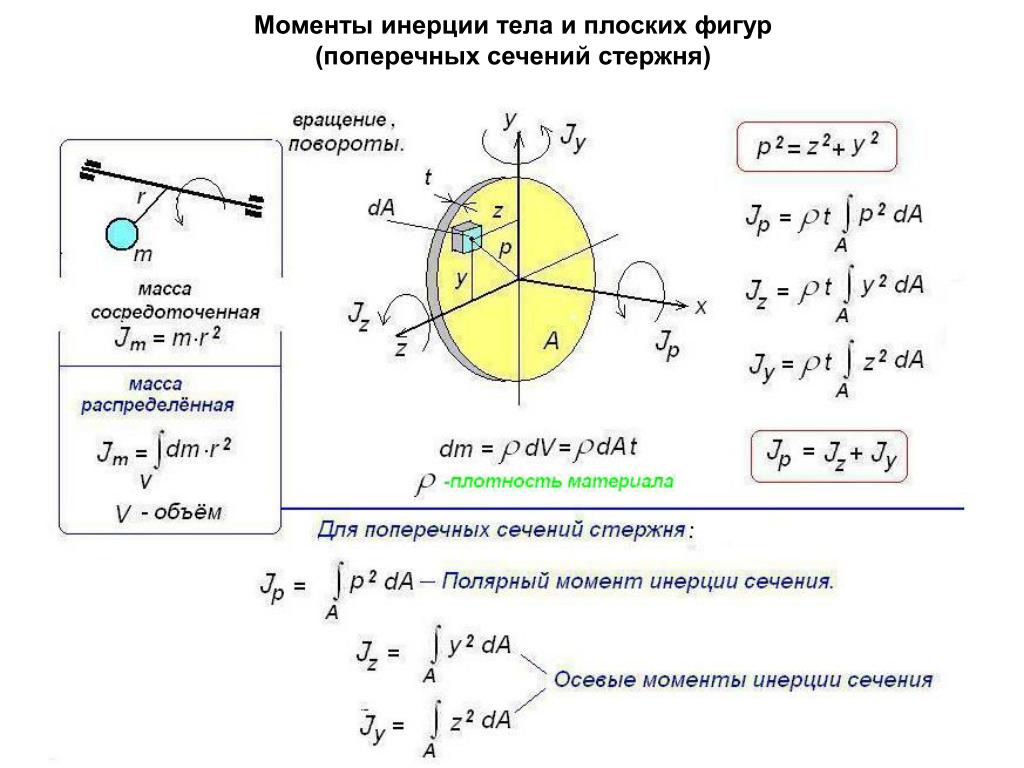 Там же была приведена характеристика ряда факторов, связанных с успехом в многоборье. Вы оценили свои способности в области плавания,
Там же была приведена характеристика ряда факторов, связанных с успехом в многоборье. Вы оценили свои способности в области плавания,
Глава 5. Разъяснение 16 моментов, касающихся важного в тайцзицюань
Глава 5. Разъяснение 16 моментов, касающихся важного в тайцзицюань Подвижность — в пояснице;находчивость — в макушке;пронизанность духом — в спине;текучесть движения — в ци;движение — в ногах;толчок ногой — в стопе;соединение — в ладони;стопа — в пальцах;собирание — в
Массово-инерционные характеристики модели
Массово-инерционные характеристики модели В биомеханике совокупность показателей, характеризующих распределение масс в теле человека, принято называть геометрией масс. Для биомеханических расчетов нужны точные сведения об этих показателях.Таблица 3 К
Определение положения центра масс модели
Определение положения центра масс модели
При исследовании движений человека, как правило, возникает необходимость учитывать не только величину массы, но и ее распределение в теле.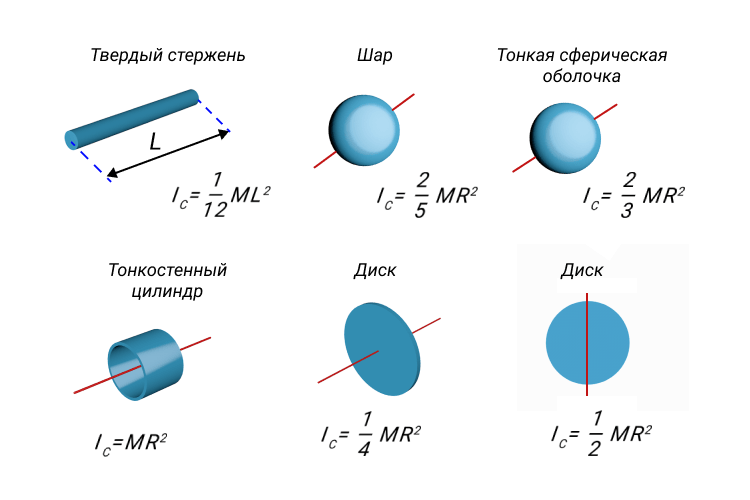
3. ИСПОЛЬЗОВАНИЕ ВЫГОДНЫХ МОМЕНТОВ ДЛЯ НАПАДЕНИЯ
3. ИСПОЛЬЗОВАНИЕ ВЫГОДНЫХ МОМЕНТОВ ДЛЯ НАПАДЕНИЯ Можно утверждать, что нет такого мгновения в схватке, когда для самбиста не было бы выгодных для нападения положений, передвижений или действий противника. Но во время борьбы действует так много различных факторов, что
4.3. Процесс развития интеллектуальных способностей подростка-спортсмена: взаимообусловленность актуальной модели интеллекта и модели деятельности
Состояние вращения и момент инерции Венеры
- Артикул
- Опубликовано:
- Жан-Люк Марго Orcid: orcid.org/0000-0001-9798-1797 1,2 ,
- Дональд Б. Кэмпбелл 3 ,
- Jon D. Giorgini 4 ,
- Joseph S. Jao 4 ,
- Joseph S. Jao 4 ,
- .
- Лоуренс Г. Снедекер 4 ,
- Фрэнк Д. Гиго 5 и
- …
- Эмбер Бонсолл 5
1064 доступа
10 цитирований
743 Альтметрический
Сведения о показателях
Предметы
- Динамика атмосферы
- Геодинамика
- Внутренние планеты
Abstract
Фундаментальные свойства планеты Венера, такие как распределение ее внутренней массы и вариации продолжительности дня, остались неизвестными.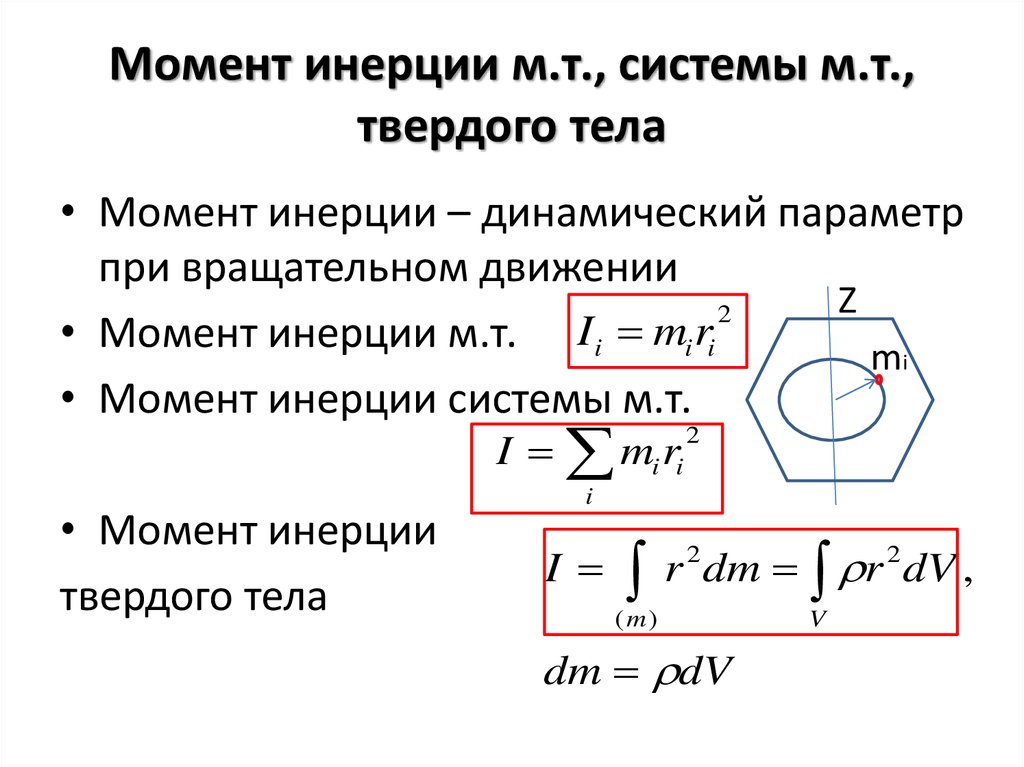 Мы использовали наземные наблюдения радиолокационных спеклов, связанных с вращением Венеры, полученные в 2006–2020 годах, для измерения ориентации ее оси вращения, скорости прецессии вращения, момента инерции и вариаций длины дня. Венера наклонена на 2,6392 ± 0,0008 градуса (1 σ ) по отношению к плоскости своей орбиты. Ось вращения прецессирует со скоростью 44,58 ± 3,3 угл.сек в год (1 σ ), что дает нормированный момент инерции 0,337 ± 0,024 и дает грубую оценку размера ядра. Средний звездный день на Венере в интервале 2006–2020 гг. составляет 243,0226 ± 0,0013 земных суток (1 σ ). Период вращения твердой планеты изменяется на 61 ppm (~20 мин) с возможным суточным или полусуточным воздействием. Изменения длины дня означают, что изменения углового момента атмосферы не менее ~ 4% передаются твердой планете.
Мы использовали наземные наблюдения радиолокационных спеклов, связанных с вращением Венеры, полученные в 2006–2020 годах, для измерения ориентации ее оси вращения, скорости прецессии вращения, момента инерции и вариаций длины дня. Венера наклонена на 2,6392 ± 0,0008 градуса (1 σ ) по отношению к плоскости своей орбиты. Ось вращения прецессирует со скоростью 44,58 ± 3,3 угл.сек в год (1 σ ), что дает нормированный момент инерции 0,337 ± 0,024 и дает грубую оценку размера ядра. Средний звездный день на Венере в интервале 2006–2020 гг. составляет 243,0226 ± 0,0013 земных суток (1 σ ). Период вращения твердой планеты изменяется на 61 ppm (~20 мин) с возможным суточным или полусуточным воздействием. Изменения длины дня означают, что изменения углового момента атмосферы не менее ~ 4% передаются твердой планете.
Это предварительный просмотр содержимого подписки, доступ через ваше учреждение
Соответствующие статьи
Статьи открытого доступа, цитирующие эту статью.
Недра землеподобных планет и спутников Солнечной системы
- Дорис Брейер
- , Тилман Спон
- … Николя Рамбо
Геофизические исследования Открытый доступ 14 декабря 2021 г.
Варианты доступа
Подписаться на журнал
Получите полный доступ к журналу на 1 год
118,99 €
всего 9,92 € за выпуск
Подписка
Расчет налогов будет завершен во время оформления заказа.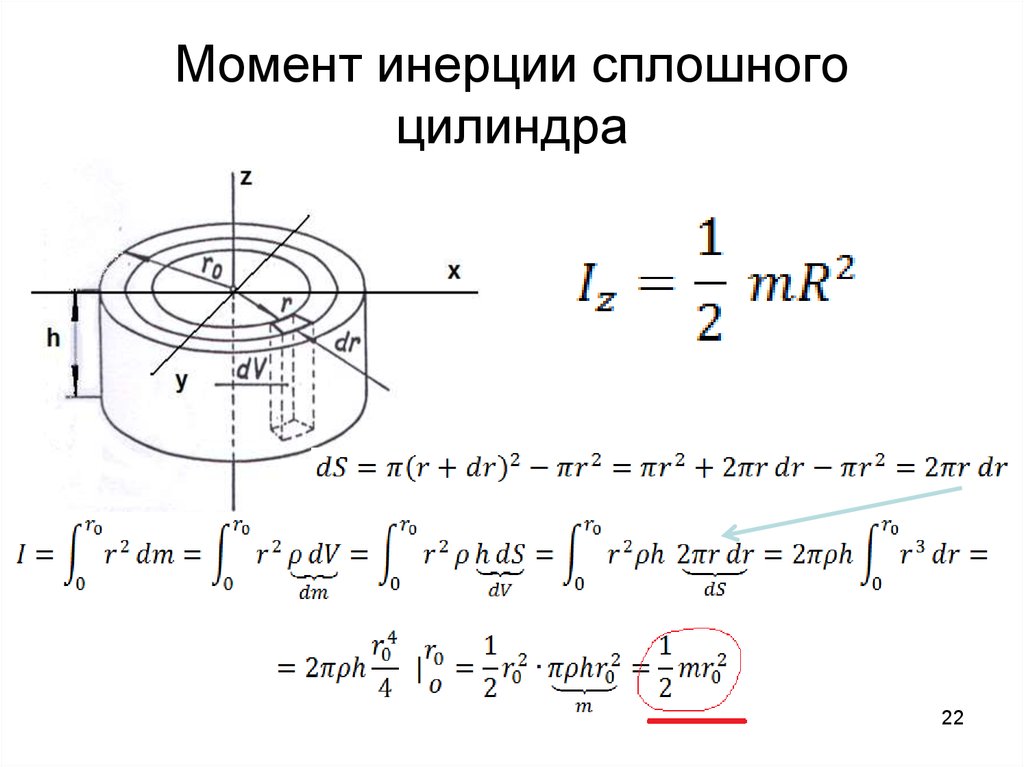
Купить статью
Получите ограниченный по времени или полный доступ к статье на ReadCube.
32,00 $
Купить
Все цены указаны без учета стоимости.
Рис. 1: Пространственно-временная корреляция радарных спеклов Венеры. Рис. 2: Ориентация оси вращения Венеры. Рис. 3: Измерения мгновенного периода вращения Венеры.Доступность данных
Наборы данных, созданные и/или проанализированные в ходе текущего исследования, можно получить у соответствующего автора по обоснованному запросу.
Доступность кода
Программное обеспечение, используемое для получения и обработки временных рядов радиолокационных эхо-сигналов, можно получить по запросу, связавшись с соответствующим автором.
Ссылки
Смрекар, С. Э., Давайль, А. и Сотин, К.
 Внутренняя структура и динамика Венеры. Космические науки. Откр. 214 , 88 (2018).
Внутренняя структура и динамика Венеры. Космические науки. Откр. 214 , 88 (2018).Артикул ОБЪЯВЛЕНИЯ Google ученый
Дюмулен К., Тоби Г., Верховен О., Розенблатт П. и Рамбо Н. Приливные ограничения внутренней части Венеры. Ж. Геофиз. Рез. Планеты 122 , 1338–1352 (2017).
Артикул ОБЪЯВЛЕНИЯ Google ученый
О’Рурк, Дж. Г., Гиллманн, К. и Тэкли, П. Перспективы древнего динамо и современного остаточного магнетизма земной коры на Венере. Планета Земля. науч. лат. 502 , 46–56 (2018).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Davies, M.E. et al. Период вращения, направление Северного полюса и опорная геодезическая сеть Венеры. Ж. Геофиз. Рез. Планеты 97 , 13141–13151 (1992).

Артикул ОБЪЯВЛЕНИЯ Google ученый
Мюллер, Н. Т., Хелберт, Дж., Эрард, С., Пиччони, Г. и Дроссарт, П. Период вращения Венеры, оцененный по изображениям Venus Express VIRTIS и альтиметрии Магеллана. Икар 217 , 474–483 (2012).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Campbell, B. A. et al. Средняя скорость вращения Венеры по данным наземных радиолокационных наблюдений за 29 лет. Икар 332 , 19–23 (2019).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Йодер, К.Ф. в Венера II: геология, геофизика, атмосфера и среда солнечного ветра (под редакцией Bougher, SW и др.) 1087–1124 (Univ. of Arizona Press, 1997).
Санчес-Лавега А., Лебоннуа С., Имамура Т., Рид П. и Луз Д.
 Динамика атмосферы Венеры. Космические науки. Ред. 212 , 1541–1616 (2017).
Динамика атмосферы Венеры. Космические науки. Ред. 212 , 1541–1616 (2017).Артикул ОБЪЯВЛЕНИЯ Google ученый
Horinouchi, T. et al. Как волны и турбулентность поддерживают сверхвращение атмосферы Венеры. Наука 368 , 405–409 (2020).
Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый
Дорожная карта для исследования Венеры (Группа по оценке исследования Венеры, 2019 г.).
Каула, В. М. Введение в планетарную физику: планеты земной группы (Wiley, 1968).
Уильямс, Дж. Г. Вклад в скорость наклона Земли, прецессию и нутацию. Астрон. J. 108 , 711–724 (1994).
Артикул ОБЪЯВЛЕНИЯ Google ученый
«>Стэндиш, Э. М. и Уильямс, Дж. Г. в Пояснительном приложении к астрономическому альманаху , 3-е изд. (ред. Урбан, С. Э. и Зайдельманн, П. К.), гл. 8 (Университетские научные книги, 2013 г.).
Коноплив А.С., Банердт В.Б. и Шегрен В.Л. Гравитация Венеры: 180-й градус и модель порядка. Икар 139 , 3–18 (1999).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Cottereau, L. & Souchay, J. Вращение твердой Венеры: полная модель прецессии-нутации. Астрон. Астрофиз. 507 , 1635–1648 (2009).

Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google ученый
Saunders, R. S. et al. Краткое содержание миссии Магеллана. Ж. Геофиз. Рез. Планеты 97 , 13067–13090 (1992).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Шапиро И.И., Кэмпбелл Д.Б. и де Кампли В.М. Нерезонансное вращение Венеры. Астрофиз. Дж. Летт. 230 , Л123–Л126 (1979).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Зоар, С., Гольдштейн, Р. М. и Рамси, Х. К. Новое радиолокационное определение вектора вращения Венеры. Астрон. J. 85 , 1103–1111 (1980).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Шапиро И.И., Чендлер Дж.Ф., Кэмпбелл Д.Б., Хайн А.А. и Стейси Н.
 Дж.С. Вектор вращения Венеры. Астрон. J. 100 , 1363–1368 (1990).
Дж.С. Вектор вращения Венеры. Астрон. J. 100 , 1363–1368 (1990).Артикул ОБЪЯВЛЕНИЯ Google ученый
Слэйд, М. А., Зохар, С. и Юргенс, Р. Ф. Венера: улучшенный вектор вращения по данным радиолокационных наблюдений Голдстоуна. Астрон. J. 100 , 1369–1374 (1990).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Голдрайх П. и Пил С. Спин-орбитальная связь в солнечной системе. Астрон. J. 71 , 425–437 (1966).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Гольдрайх П. и Пил С. Спин-орбитальная связь в солнечной системе. II. Резонансное вращение Венеры. Астрон. J. 72 , 662–668 (1967).
Артикул ОБЪЯВЛЕНИЯ Google ученый
«>Ингерсолл А. П. и Добровольскис А. Р. Вращение Венеры и атмосферные приливы. Природа 275 , 37–38 (1978).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Добровольскис А. Р. и Ингерсолл А. П. Атмосферные приливы и вращение Венеры. I. Теория приливов и баланс моментов. Икар 41 , 1–17 (1980).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Коррейя, А.К.М. и Ласкар, Дж. Четыре последних состояния вращения Венеры. Природа 411 , 767–770 (2001).
Артикул ОБЪЯВЛЕНИЯ Google ученый
«>Хайд Р., Берч Н. Т., Моррисон Л. В., Ши Д. Дж. и Уайт А. А. Колебания атмосферного углового момента и изменения продолжительности дня. Природа 286 , 114–117 (1980).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Лебоннуа, С. и др. Суперротация атмосферы Венеры проанализирована с помощью модели полной общей циркуляции. Ж. Геофиз. Рез. Планеты 115 , E06006 (2010).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Коттеро, Л., Рамбо, Н., Лебоннуа, С. и Суше, Дж. Различные вклады в скорость вращения Венеры и LOD.
 Астрон. Астрофиз. 531 , А45 (2011).
Астрон. Астрофиз. 531 , А45 (2011).Артикул ОБЪЯВЛЕНИЯ Google ученый
Приход, H. F. et al. Десятилетние вариации в модели общей циркуляции Венеры. Икар 212 , 42–65 (2011).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Марго Ж.-Л. Система сбора данных для планетарных радаров. Дж. Астрон. Инструм. 10 , 2150001 (2021).
Артикул Google ученый
Марго, Дж.-Л., Пил, С.Дж., Юргенс, Р.Ф., Слэйд, М.А. и Холин, И.В. Большая долготная либрация Меркурия обнаруживает расплавленное ядро. Наука 316 , 710–714 (2007).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Марго Ж.-Л. Момент инерции Меркурия по данным о вращении и гравитации.
 Ж. Геофиз. Рез. Планеты 117 , E00L09 (2012).
Ж. Геофиз. Рез. Планеты 117 , E00L09 (2012).Артикул Google ученый
Старк, А. и др. Первые орбитальные наблюдения MESSENGER за либрациями Меркурия. Геофиз. Рез. лат. 42 , 7881–7889 (2015).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Bendat, J.S. & Piersol, A.G. Случайные данные: процедуры анализа и измерения 2-е изд. (Wiley, 1986).
Коррейя, А.К.М., Ласкар, Дж. и Нерон де Сурги, О. Долговременная эволюция вращения Венеры: I. теория. Икар 163 , 1–23 (2003).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Коррейя А.К.М. и Ласкар Дж. Долговременная эволюция вращения Венеры: II. численное моделирование. Икар 163 , 24–45 (2003).

Артикул ОБЪЯВЛЕНИЯ Google ученый
Гросс, Р. в Трактат по геофизике 1-е изд. (изд. Шуберт, Г.) 239–294 (Elsevier, 2007).
Гольдрайх П. и Пил С. Дж. Резонансное вращение Венеры? Природа 209 , 1117–1118 (1966).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Наварро Т., Шуберт Г. и Лебоннуа С. Генерация атмосферных горных волн на Венере и ее влияние на скорость вращения твердой планеты. Нац. Geosci. 11 , 487–491 (2018).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Fukuhara, T. et al. Большая стационарная гравитационная волна в атмосфере Венеры. Нац. Geosci. 10 , 85–88 (2017).
Артикул ОБЪЯВЛЕНИЯ Google ученый
«>Митчелл, Дж. Л. Связь конвективной атмосферной циркуляции с вращением поверхности: свидетельство активной метановой погоды в наблюдаемом дрейфе скорости вращения Титана. Астрофиз. J. 692 , 168–173 (2009).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Грин, ЧП Методы радиолокационных астрономических измерений Технический отчет № 282 (Лаборатория Линкольна Массачусетского технологического института, 1962 г.).
Green, PE in Radar Astronomy (ред. Evans, JV & Hagfors, T.) Ch. Радарные измерения (McGraw-Hill, 1968).

Холин И. В. Пространственно-временная когерентность сигнала, диффузно рассеянного произвольно движущейся поверхностью, для случая монохроматического освещения. Радиофиз. Квант. Электр. 31 , 371–374 (1988).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Холин И.В. Точность измерения параметров вращения тела при монохроматическом освещении и двухэлементном приеме. Радиофиз. Квант. Электр. 35 , 284–287 (1992).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Марго, Дж. Л., Хаук, С. А., Мазарико, Э., Падован, С. и Пил, С. Дж. в Меркурий: вид после MESSENGER (под редакцией Соломона, С.К. и др.) 85–113 (Cambridge Univ. Press, 2018).
Duan, X., Moghaddam, M., Wenkert, D., Jordan, R.L. & Smrekar, S.E. X-диапазонная модель диэлектрической проницаемости атмосферы Венеры.
 Радионауч. 45 , 1–19 (2010).
Радионауч. 45 , 1–19 (2010).Артикул Google ученый
Дзиевонски А. М. и Андерсон Д. Л. Предварительная эталонная модель Земли. физ. Планета Земля. Интер. 25 , 297–356 (1981).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Press, WH, Teukolsky, SA, Vetterling, WT & Flannery, B.P. Численные рецепты в C , 2-е изд. (Cambridge Univ. Press, 1992).
Уильямс П.К.Г., Клавель М., Ньютон Э. и Рыжков Д. pwkit: Astronomical Utilities in Python ascl:1704.001 (2017).
Фолкнер, В. М., Йодер, К. Ф., Юань, Д. Н., Стэндиш, Э. М. и Престон, Р. А. Внутренняя структура и сезонное массовое перераспределение Марса по радиоотслеживанию Mars Pathfinder. Наука 278 , 1749–1751 (1997).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Голд, Т. и Сотер, С. Атмосферные приливы и резонансное вращение Венеры. Икар 11 , 356–366 (1969).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Биллс, Б. Г. Изменения скорости вращения Венеры из-за модуляции эксцентриситета орбиты солнечных приливных моментов. Ж. Геофиз. Рез. 110 , E11007 (2005).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Kouyama, T. et al. Топографическая и локальная временная зависимость больших стационарных гравитационных волн, наблюдаемых в верхней части облаков Венеры. Геофиз. Рез. лат. 44 , 12098–12105 (2017).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Скачать ссылки
Благодарности
Эта статья посвящена памяти Рэймонда Ф. Юргенса, который сыграл важную роль в сборе данных для этой работы. Мы благодарим М. А. Слейда, Дж. Т. Лацио, Т. Минтера, К. О’Нила и Ф. Дж. Локмана за помощь в планировании наблюдений. Мы благодарим Б. А. Арчинала, П. М. Дэвиса, С. Лебоннуа, Дж. Л. Митчелла и К. Ф. Уилсона за полезные комментарии и А. Лама за помощь с рис. 1. Обсерватория Грин-Бэнк является объектом Национального научного фонда, управляемым по соглашению о сотрудничестве с ассоциированными университетами. , Inc. Часть этой работы была поддержана Лабораторией реактивного движения, управляемой Калифорнийским технологическим институтом по контракту с НАСА. Мы благодарны за программное обеспечение NASA Navigation and Ancillary Information Facility и ядра данных, которые значительно облегчили это исследование. Ж.-Л.М. частично финансировался за счет гранта НАСА №. NNG05GG18G, NNX09AQ69G, NNX12AG34G и 80NSSC19K0870.
Мы благодарим Б. А. Арчинала, П. М. Дэвиса, С. Лебоннуа, Дж. Л. Митчелла и К. Ф. Уилсона за полезные комментарии и А. Лама за помощь с рис. 1. Обсерватория Грин-Бэнк является объектом Национального научного фонда, управляемым по соглашению о сотрудничестве с ассоциированными университетами. , Inc. Часть этой работы была поддержана Лабораторией реактивного движения, управляемой Калифорнийским технологическим институтом по контракту с НАСА. Мы благодарны за программное обеспечение NASA Navigation and Ancillary Information Facility и ядра данных, которые значительно облегчили это исследование. Ж.-Л.М. частично финансировался за счет гранта НАСА №. NNG05GG18G, NNX09AQ69G, NNX12AG34G и 80NSSC19K0870.
Информация об авторе
Авторы и организации
Департамент наук о Земле, планетах и космосе, Калифорнийский университет в Лос-Анджелесе, Лос-Анджелес, Калифорния, США
Жан-Люк Марго
Департамент физики и астрономии Калифорнийского университета в Лос-Анджелесе, Лос-Анджелес , Калифорния, США
Жан-Люк Марго
Кафедра астрономии, Корнельский университет, Итака, штат Нью-Йорк, США
Дональд Б.
 Кэмпбелл
КэмпбеллЛаборатория реактивного движения, Пасадена, Калифорния, США
Джон Д. Джорджини, Джозеф С. Джао и Лоуренс Г. Снедекер
Национальная радиоастрономическая лаборатория, Грин-Бэнк, Западная Вирджиния, США
Фрэнк Д. Гиго и Эмбер Бонсолл
Авторы
- Жан-Люк Марго
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Дональд Б. Кэмпбелл
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Jon D. Giorgini
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Joseph S. Jao
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Лоуренс Г.
 Снедекер
СнедекерПосмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Frank D. Ghigo
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Amber Bonsall
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Contributions
J.-L.M. провел расследование и написал программное обеспечение и рукопись. D.B.C. внес свой вклад в методику. J.D.G., J.S.J., L.G.S., F.D.G. и А.Б. способствовал сбору данных. Все авторы просмотрели и отредактировали рукопись.
Автор, ответственный за переписку
Жан-Люк Марго.
Заявление об этике
Конкурирующие интересы
Авторы не заявляют об отсутствии конкурирующих интересов.
Дополнительная информация
Информация о рецензировании Nature Astronomy благодарит Alexandre Correia, Attilio Rivoldini и других анонимных рецензентов за их вклад в рецензирование этой работы.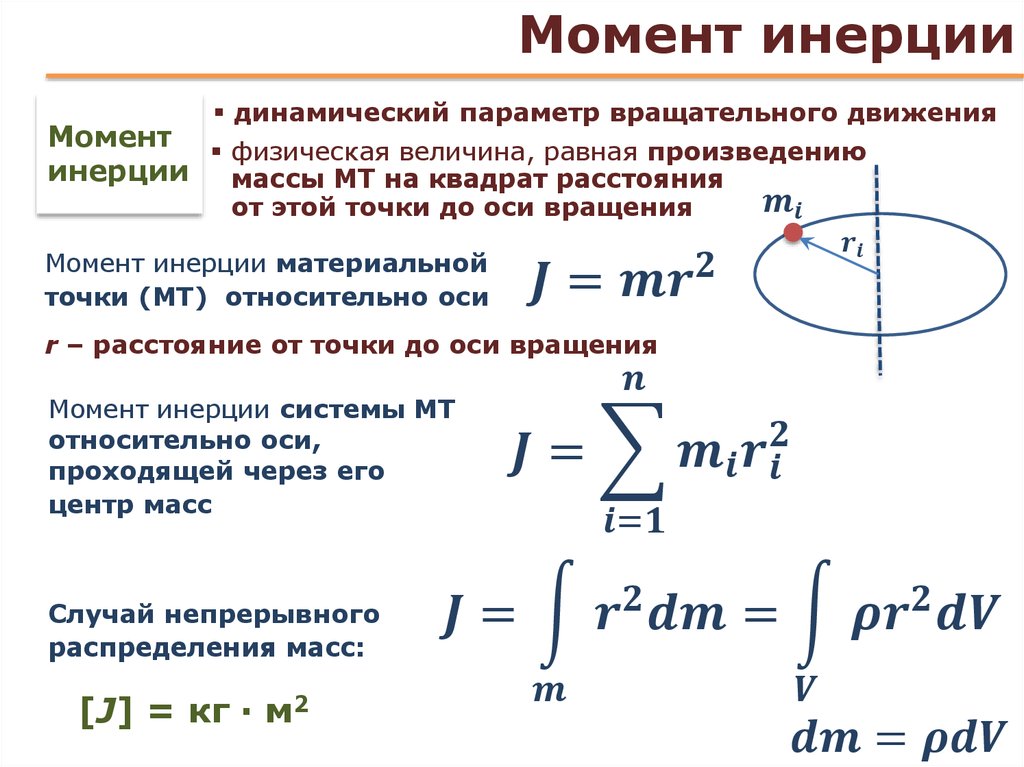
Примечание издателя Springer Nature сохраняет нейтралитет в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Расширенные данные
Расширенные данные Рис. 1 Проиллюстрированы случайные изменения мощности эхо-сигнала радара.
Representative variations in radar echo power ( s p e c k l e s ) from observations of Venus with the Goldstone Solar System Radar and Green Bank Telescope at 8560 МГц, 26 ноября 2016 г. Эхо-сигнал GBT был сдвинут по времени на 20 с, чтобы проиллюстрировать высокую степень корреляции между полученными формами сигналов, когда траектория спекла совмещена с базовой линией антенны.
Расширенные данные Рис. 2 Проиллюстрирована траектория гофрирования волнового фронта, охватывающего антенны Голдстоуна и Грин-Бэнк.
Радиолокационные эхосигналы от Венеры охватывают поверхность Земли во время наблюдений 08 сентября 2020 года. На диаграммах показана траектория спеклов за час до (слева), во время (в центре) и через час после (справа) эпохи максимальной корреляции. Эхосигналы от двух приемных станций (красные треугольники) демонстрируют сильную корреляцию, когда антенны соответствующим образом выровнены по траектории спеклов (зеленые точки показаны с временным интервалом в 1 ~ с).
На диаграммах показана траектория спеклов за час до (слева), во время (в центре) и через час после (справа) эпохи максимальной корреляции. Эхосигналы от двух приемных станций (красные треугольники) демонстрируют сильную корреляцию, когда антенны соответствующим образом выровнены по траектории спеклов (зеленые точки показаны с временным интервалом в 1 ~ с).
Расширенные данные Рис. 3 Проиллюстрированы ограничения на ориентацию оси вращения Венеры, полученные с помощью наблюдений радиолокационных спеклов Голдстоуна-GBT.
Каждая цветная линия представляет собой измерение эпохи максимума корреляции, описывающего узкий эллипс ошибки на небесной сфере. Ориентация каждой линии связана с эклиптической долготой проецируемой базовой линии во время наблюдений (дополнительная таблица 2). Наилучшая ориентация оси вращения показана ромбом на пересечении цветных линий. Все измерения прецессированы до эпохи J2000.0. Черная пунктирная линия представляет собой след ориентации оси вращения на небесной сфере в результате прецессии спина между 1950 и 2050.
Расширенные данные Рис. 4 Проиллюстрировано распределение нормированных моментов инерции из бутстрап-анализа.
Оценки нормализованного момента инерции Венеры, полученные с помощью радиолокационных спекл-трекингов, предполагают остаточную погрешность в 7% с данными, полученными на сегодняшний день.
Дополнительная информация
Дополнительная информация
Дополнительные таблицы 1–6 и рис. 1–7.
Права и разрешения
Перепечатка и разрешения
Об этой статье
Эту статью цитирует
Недра землеподобных планет и спутников Солнечной системы
- Дорис Брейер
- Тилман Спон
- Николя Рамбо
Геофизические исследования (2022)
Тензор момента инерции
Тензор момента инерцииСледующая: Вращательная кинетическая энергия Вверх: Вращение жесткого корпуса Предыдущий: Фундаментальные уравнения Рассмотрим твердое тело, вращающееся с фиксированной угловой скоростью около ось, проходящая через начало координат — см.
 рисунок 28.
Пусть – вектор положения th-го элемента массы, масса которого
является .
Мы ожидаем, что этот вектор положения равен прецесс вокруг оси вращения
(что параллельно )
с угловой скоростью . Следовательно, из уравнения (A.1309) следует
что
рисунок 28.
Пусть – вектор положения th-го элемента массы, масса которого
является .
Мы ожидаем, что этот вектор положения равен прецесс вокруг оси вращения
(что параллельно )
с угловой скоростью . Следовательно, из уравнения (A.1309) следует
что | (457) |
Таким образом, приведенное выше уравнение определяет скорость, , каждого элемента массы при вращении тела с фиксированной угловой скоростью около ось, проходящая через начало координат.
Полный момент количества движения тела (о начале координат) записывается
| (458) |
где использовалось уравнение (457) и некоторый стандартный вектор личности (см.
 раздел A.10). Приведенную выше формулу можно записать в виде матричного уравнения
формы
раздел A.10). Приведенную выше формулу можно записать в виде матричного уравнения
формы | (459) |
куда
| (460) | |||
| (461) | |||
| (462) | |||
| (463) | |||
| (464) | |||
| (465) |
Здесь называется момент инерции относительно -оси, момент инерции относительно оси, произведение инерции , произведение инерция, и т.
 д. . Матрица значений
известный как момент тензора инерции . Обратите внимание, что каждый компонент
тензора момента инерции можно представить как сумму по отдельным
элементы массы или как интеграл по бесконечно малым элементам массы.
В интегралах , где – массовая плотность, а
объемный элемент.
Уравнение (459) можно записать более кратко как
д. . Матрица значений
известный как момент тензора инерции . Обратите внимание, что каждый компонент
тензора момента инерции можно представить как сумму по отдельным
элементы массы или как интеграл по бесконечно малым элементам массы.
В интегралах , где – массовая плотность, а
объемный элемент.
Уравнение (459) можно записать более кратко как | (466) |
Здесь понятно, что и оба вектора-столбца , и матрица значений. Обратите внимание, что это настоящая симметричная матрица : т.е. , а также .
В целом, вектор углового момента, , полученный из уравнения (466), указывает в направлении, отличном от вектора угловой скорости, . Другими словами, обычно не параллельны .
Наконец, хотя приведенные выше результаты были получены в предположении
фиксированной угловой скорости, они остаются в силе в каждый момент времени, если угловая скорость изменяется.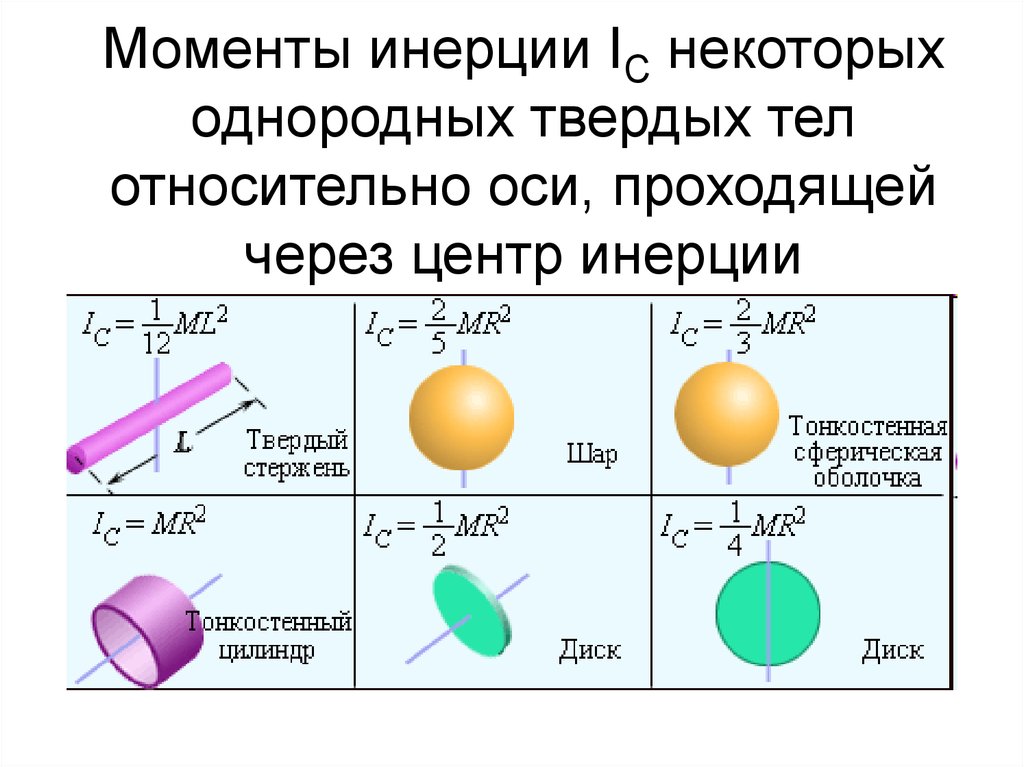


 Эксперимент. Скатывание цилиндров с наклонной плоскости одинаковой массы и размера
Эксперимент. Скатывание цилиндров с наклонной плоскости одинаковой массы и размера Внутренняя структура и динамика Венеры. Космические науки. Откр. 214 , 88 (2018).
Внутренняя структура и динамика Венеры. Космические науки. Откр. 214 , 88 (2018).
 Динамика атмосферы Венеры. Космические науки. Ред. 212 , 1541–1616 (2017).
Динамика атмосферы Венеры. Космические науки. Ред. 212 , 1541–1616 (2017).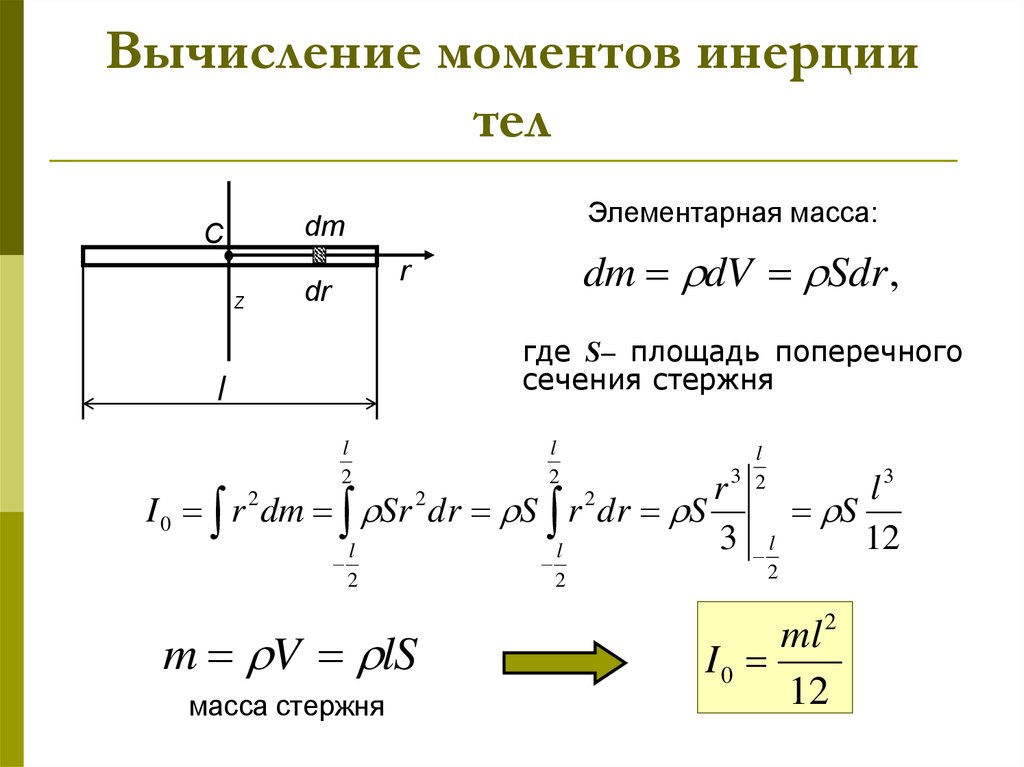
 Дж.С. Вектор вращения Венеры. Астрон. J. 100 , 1363–1368 (1990).
Дж.С. Вектор вращения Венеры. Астрон. J. 100 , 1363–1368 (1990). Астрон. Астрофиз. 531 , А45 (2011).
Астрон. Астрофиз. 531 , А45 (2011). Ж. Геофиз. Рез. Планеты 117 , E00L09 (2012).
Ж. Геофиз. Рез. Планеты 117 , E00L09 (2012).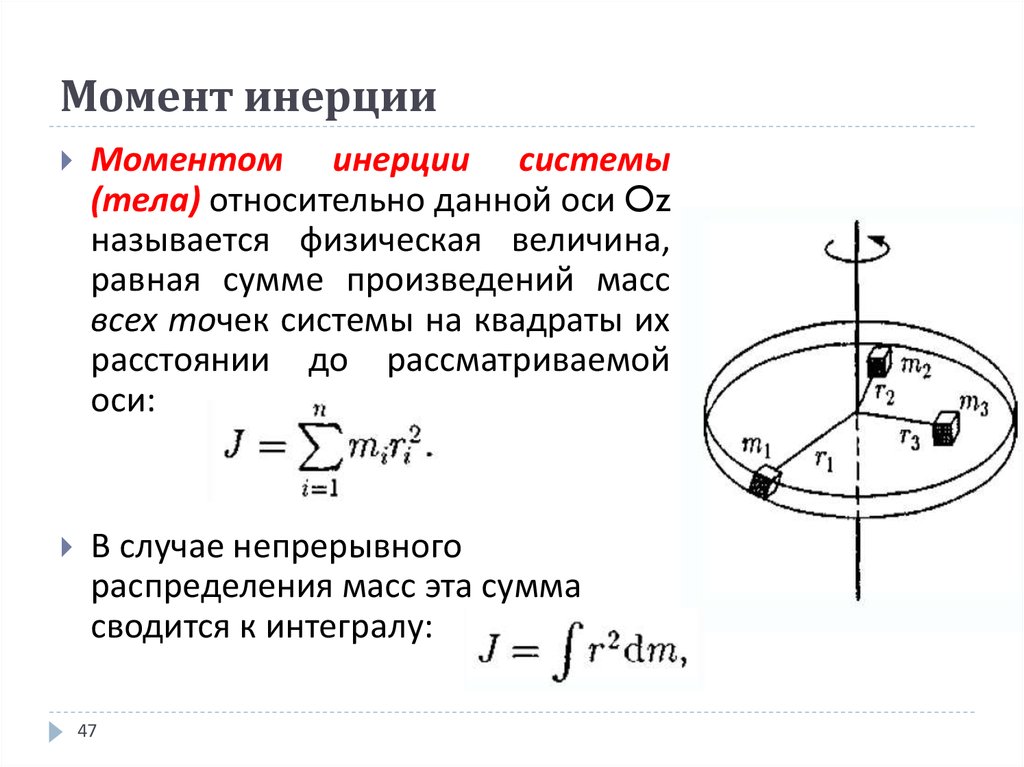

 Радионауч. 45 , 1–19 (2010).
Радионауч. 45 , 1–19 (2010). Кэмпбелл
Кэмпбелл Снедекер
Снедекер