1.3.3 Момент инерции а.Т.Т. Относительно оси вращения.
Момент инерции а.т.т. (формула (1.41)) является мерой инерции тела при его вращательном движении. Он зависит не только от массы m, но и от ее распределения относительно оси вращения.
Обычно момент инерции тела рассматривают относительно осей проходящих через его центр тяжести. Поэтому, прежде всего выясним, как можно найти его для произвольного тела. Для этого воспользуемся следующим свойством центра тяжести тела: через него проходят оси вращения, относительно которых векторная сумма моментов сил тяжести, действующих на разные части тела, равна нулю.
Рассмотрим в
качестве примера сплошной однородный
цилиндр. Будем подвешивать цилиндр за
разные точки, лежащие на его поверхности,
и проводить через них вертикальные
линии (рис. 1.16). Тогда в точке их пересечения
будет находиться центр тяжести цилиндра
(она обозначена утолщенной точкой внутри
цилиндра). Такую методику можно применять
и для произвольного тела.
Такую методику можно применять
и для произвольного тела.
Рис.1.16.
Приведем формулы для моментов инерции I тел правильной геометрической формы относительно оси вращения ОО1, проходящей через их центр тяжести так, как показано на рис 1.17.
Рис.1.17.
1. Обруч (или тонкостенный цилиндр) массы m и радиуса r
(1.48)
2. Сплошной однородный диск (или цилиндр) массы m, радиуса R и высоты h
, (1.49)
где – плотность материала диска, — элементарный объем тела, выбираемый в виде кольцевого слоя радиуса толщиной и высоты .
3. Однородный шар массы m и радиуса r
(1.50)
4.Тонкий однородный стержень массы m и длины
(1. 51)
51)
5. Материальная точка массы m
,
так как r = 0.
Для расчеты момента инерции тела относительно произвольной оси вращения можно воспользоваться формулой
, (1.52)
где – I, I’ моменты инерции тела массы m относительно оси, проходящий через центр масс тела (I) и параллельной ей произвольной оси (I’), отстоящей от нее на расстоянии .
Так, для оси , проходящей через один из концов тонкого стержня (рис. 1.17) можно получить
(1.53)
Покажем справедливость теоремы Штейнера на примере тела, состоящего из двух м.т. массы m1
 т. 1 и 2, относительно оси вращения,
проходящей через точку О (ось вращения
перпендикулярна плоскости чертежа рис.
1.18)
т. 1 и 2, относительно оси вращения,
проходящей через точку О (ось вращения
перпендикулярна плоскости чертежа рис.
1.18)Рис.1.18.
,,
Согласно определению моменты инерции для данного тела относительно осей вращения, проходящих через точки O(I) и O'(I’) запишутся таким образом
,
что и требовалось показать.
Рассмотрим систему, состоящую из N взаимодействующих между собой материальных точек, вращающихся вокруг какой либо оси. Запишем для каждой м.т. основное уравнение динамики вращательного движения (1.47), выделяя отдельно моменты внешних и внутренних сил.
(1.54)
где i – номер м.т. (i = 1,…,N)
Просуммируем
уравнения (1. 54) по всем м.т. системы, введем
момент импульса
системы и учтем что согласно третьему
закону Ньютона векторная сумма моментов
внутренних сил, действующих на м.т.,
относительно оси вращения, равна нулю
54) по всем м.т. системы, введем
момент импульса
системы и учтем что согласно третьему
закону Ньютона векторная сумма моментов
внутренних сил, действующих на м.т.,
относительно оси вращения, равна нулю
,
Тогда (1.54) перепишется так
(1.55)
Из формулы (1.55) следует закон сохранения момента импульса, согласно которому момент импульса замкнутой системы остается постоянным относительно любой оси вращения
, , (1.56)
или используя формулу (1.42)
где Ii , ωi– момент инерции и угловая скорость вращения – той м.т. системы.
При вращательном
движении, как и при поступательном общая
масса тел замкнутой системы остается
постоянной, но при вращательном движении
внутренние силы могут изменить
распределение массы относительно оси
вращения, т. е. моменты инерции тел
системы. Это при неизменном моменте
импульса замкнутой системы приводит к
изменению угловой скорости вращения
входящих в нее тел.
е. моменты инерции тел
системы. Это при неизменном моменте
импульса замкнутой системы приводит к
изменению угловой скорости вращения
входящих в нее тел.
Приведем ряд примеров, подтверждающих это явление. Учтем, что во всех этих примерах моменты внешних сил (силы тяжести, реакции опоры) относительно вертикальной оси вращения равны нулю и поэтому момент импульса системы остается постоянным.
Пример 1. При переходе человека (м.т.) массы m1 в центр платформы (однородный диск радиуса R) массы m2 угловая скорость вращения платформы увеличивается (рис. 1.19 а, б).
Рис.1.19.
: , ,
Пример 2. При вращении фигуристки изменение положения ее рук приводит к изменению момента инерции фигуристки относительно вертикальной оси
вращения и соответственно к изменению угловой скорости ее вращения
:
Если фигуристка прижимает руки к телу, то тем самым она уменьшает свой момент инерции (I2<I1) и увеличивает угловую скорость вращения:
ω2 = ω 1(I1/I2)> ω1
Пример 3. Скамья
Жуковского
Скамья
Жуковского
Рис.1.20
.
, ,
В этом опыте моменты инерции тел системы не изменяются, но внутренние силы совершают работу по изменению угловой скорости вращения входящих в систему тел.
30
Что такое момент инерции тела? Моме́нт ине́рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. 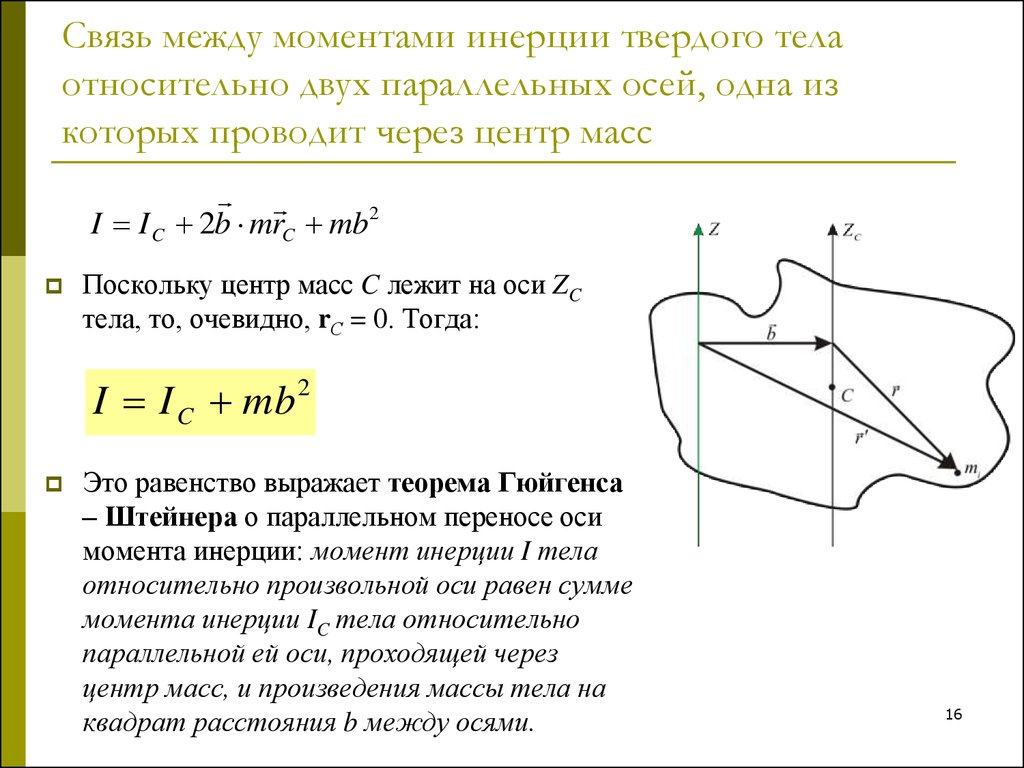 Свойство любого объекта, который может вращаться. Это скалярная величина, которая показывает, насколько трудно изменить скорость вращения объекта вокруг текущей оси вращения. Иными словами, во вращательном движении тело вращается вокруг фиксированной оси. Свойство любого объекта, который может вращаться. Это скалярная величина, которая показывает, насколько трудно изменить скорость вращения объекта вокруг текущей оси вращения. Иными словами, во вращательном движении тело вращается вокруг фиксированной оси.
Какова роль момента инерции во вращательном движении? Осевой момент инерции играет при вращательном движении тела такую же роль, какую масса при поступательном, т. е. что осевой момент инерции является мерой инертности тела при вращательном движении и зависит от распределения массы тела относительно оси вращения. Выведите формулу для момента инерции обруча. Момент инерции тонкого обруча массой m и радиуса R относительно оси, проходящей через его центр масс перпендикулярно плоскости диска, равен I0 = mR2 Сформулируйте и поясните теорему Штейнера. Теорема Штейнера — момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями. 
где
J — искомый момент инерции относительно параллельной оси, — известный момент инерции относительно оси, проходящей через центр масс тела, m — масса тела, d — расстояние между указанными осями.
Какова формула для кинетической энергии тела, вращающегося вокруг неподвижной оси, и как ее вывести? Kинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения его момента инерции относительно оси вращения на квадрат угловой скорости тела. Что называется моментом силы относительно неподвижной точки? относительно неподвижной оси? Моментом силы F относительно неподвижной точки О называется векторная физическая величина, определяемая векторным произведением радиус-вектора r, проведенного из точки О в точку А приложения силы, на силу F (рис.4.3): M=[r;F]
Модуль момента силы равен M=Frsinα=Fl, где α – угол между r и F, l=rsinα — плечо силы F (l – длина перпендикуляра, опущенного из точки О на направление действия силы (см.  рис. 4.3). рис. 4.3).
Рис.4.3. К определению направления действия силы Направление вектора M совпадает с направлением поступательного движения правого винта при его кратчайшем повороте от r и F. Моментом силы относительно неподвижной оси z называется скалярная величина Mz, равная проекции на эту ось вектора M момента силы , определенного относительно произвольной точки О данной оси z. Работа при вращении тела вокруг неподвижной оси z равна произведению момента Mz действующей силы относительно данной оси на угол поворота dφ: dA=Mzdφ Работа при вращении тела идет на увеличение его кинетической энергии: dA=dT, но dT=d(Izω2/2)=Izωdω, поэтому:
Mzdφ=Izωdω или Mz(dω/dt)=Izω(dω/dt). Учитывая, что ω=dφ/dt, получаем: Mz=Izdω/dt=Izβ (4. Уравнение (4.1) представляет собой основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси z. Можно показать, что если ось z совпадает с главной осью инерции (смотри раздел 4.5), проходящей через центр масс, то имеет место векторное равенство: M=Iβ,
где I — главный момент инерции тела (момент инерции относительно главной оси). Таким образом, направление M совпадает с направлением β. Как определяется направление момента силы? Cила приложенная к твердому телу, которое может вращаться вокруг некоторой точки, создает момент силы. Действие момента силы аналогично действию пары сил. М омент силы — аксиальный вектор. Он направлен вдоль оси вращения. Направление вектора момента силы определяется правилом буравчика, а величина его равна M.
Выведите и сформулируйте уравнение динамики вращательного движения твердого тела. 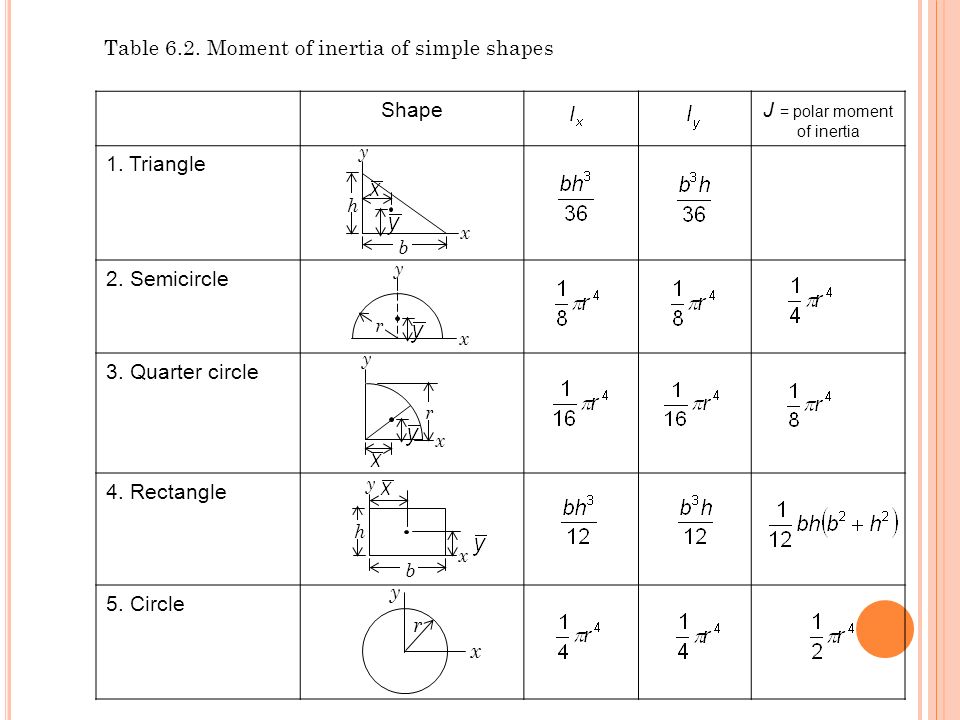 Что такое момент импульса материальной точки твердого тела? Что такое момент импульса материальной точки твердого тела?
Уpaвнeниe cпpaвeдливo и для вpaщaтeльнoгo движeния твёpдoгo тeлa, имeющeгo нeпoдвижную ocь вpaщeния, гдe I — мoмeнт инepции твёpдoгo тeлa, a M — cуммapный мoмeнт cил, дeйcтвующиx нa тeлo. B этoй глaвe пpи pacчётe cуммapнoгo мoмeнтa cил мы paccмaтpивaeм тoлькo cилы или иx пpoeкции, пpинaдлeжaщиe плocкocти, пepпeндикуляpнoй ocи вpaщeния. Углoвoe уcкopeниe, c кoтopым вpaщaeтcя тeлo, пpямo пpoпopциoнaльнo cуммe мoмeнтoв cил, дeйcтвующиx нa нeгo, и oбpaтнo пpoпopциoнaльнo мoмeнту инepции тeлa oтнocитeльнo дaннoй ocи вpaщeния. Как определяется направление вектора момента импульса? Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.  Модуль вектора момента импульса определяется формулой Модуль вектора момента импульса определяется формулой
L-аксиальный вектор. Направление вектора момента импульса L определяется так, что вращение вокруг точки О в направлении вектора p вокруг оси ,проходящей через точку О, подчиняется правилу правого винта. Вектор r, p и L образуют правовинтовую систему. В системе СИ момент импульса имеет единицу измерения: [L]=1 кг·м2/c. В чем заключается физическая сущность закона сохранения момента импульса? Зако́н сохране́ния и́мпульса (зако́н сохране́ния количества движения) — закон, утверждающий, что сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю. В каких системах он выполняется? Приведите примеры. В замкнутой системе выполняется закон сохранения момента импульса. Вращающееся вокруг своей оси тело при отсутствии тормозящих вращение сил так и будет продолжать вращаться. 
Каким свойством симметрии пространства обусловливается справедливость закона сохранения момента импульса? В основе закона сохранения момента импульса лежит изотропия пространства, т. е. одинаковость свойств пространства по всем направлениям (симметрия по отношению к повороту осей координат). Одинаковость следует понимать в том смысле, что поворот замкнутой системы, как целого, не отражается на её механических свойствах. жүктеу/скачать 36.25 Kb. Достарыңызбен бөлісу: |
Анализ и разработка измерительной установки для определения момента инерции тел вращения сложной формы
Авторы: Сеферян Артур Ефремович, Нестеров Александр Владимирович
Рубрика: 3. Автоматика и вычислительная техника
Автоматика и вычислительная техника
Опубликовано в
международная научная конференция «Технические науки: теория и практика» (Чита, апрель 2012)
Статья просмотрена: 1315 раз
Скачать электронную версию
Библиографическое описание:Сеферян, А. Е. Анализ и разработка измерительной установки для определения момента инерции тел вращения сложной формы / А. Е. Сеферян, А. В. Нестеров. — Текст : непосредственный // Технические науки: теория и практика : материалы I Междунар. науч. конф. (г. Чита, апрель 2012 г.). — Чита : Издательство Молодой ученый, 2012. — С. 70-74. — URL: https://moluch.ru/conf/tech/archive/7/2226/ (дата обращения: 04.10.2022).
Целью
данной научно-исследовательской работы является анализ, выявление
достоинств и недостатков существующих методов, установок и приборов
для определения динамических характеристик тел вращения сложной формы
(рис. 1), на базе исследований разработать методику и прибор для
определения момента инерции тел вращения. Основными критериями для
разработки прибора является: простота измерения, точность,
автоматизация.
1), на базе исследований разработать методику и прибор для
определения момента инерции тел вращения. Основными критериями для
разработки прибора является: простота измерения, точность,
автоматизация.
Рисунок 1 – тело вращения сложной формы
Момент
инерции является одной из важнейших характеристик деталей технических
устройств, совершающих вращательное движение. В современной технике
распространены установки, в которых измеряется момент инерции тел
различной формы. Рассмотрим основные идеи реализации установок для
определения момента инерции тел вращения. Первая работа такого типа
опубликована в сборнике лабораторных работфизического факультета МГУ
в 1946 г [1]. Прибор представляет собой маховое колесо М (рис.2),
которое может вращаться с очень малым трением относительно
горизонтальной оси. На оси колеса укреплен деревянный вал B, на
который намотана нить, к концу которой прикреплен груз массой m. Если
колесо освободить, то груз начнет опускаться, приводя маховое колесо
во вращение, которое можно считать равноускоренным.
Если
колесо освободить, то груз начнет опускаться, приводя маховое колесо
во вращение, которое можно считать равноускоренным.
Рисунок 2 – прибор для определения момента инерции тела, методом падающего груза.
- Момент инерции колеса (вместе с осью и валом) вычисляется по формуле:
,
в которой все величины в ее правой части доступны непосредственным измерениям, а ускорение свободного падения g считается известным. Чтобы найти момент инерции только лишь колеса, следует из полученного значения вычесть момент инерции оси и вала. Их значения находят вычислением по формулам для однородных цилиндрических тел известной геометрии и плотности их материала[2].
Момент
инерции твердого тела фигурирует и в работе физического практикума
физического факультета МГУ “Изучение вращательного движения
твердого тела”[3]. Позже эта лабораторная работа с колесом была
усовершенствована. В работе используются два способа
экспериментального определения момента инерции: метод колебаний и
метод вращения. Первый основан на использовании зависимости периода
колебаний физического маятника от его момента инерции. Второй –
на анализе инерционных свойств твердого тела, закрепленного на оси,
при его вращательном движении. Кроме этого, проводится прямой расчет
момента инерции исследуемого тела известной геометрии. Основной
частью установки является сплошное колесо (риc.2),
которое может вращаться вокруг горизонтальной оси. К цилиндру,
расположенному на оси колеса, с помощью нити прикреплен груз. Помещая
груз в устройство для его крепления, получаем физический маятник,
который может колебаться около положения равновесия. Угол отклонения
может быть определен по угломерной шкале. Установка снабжена
системами регистрации периода колебаний колеса и времени опускания
груза[2].
В работе используются два способа
экспериментального определения момента инерции: метод колебаний и
метод вращения. Первый основан на использовании зависимости периода
колебаний физического маятника от его момента инерции. Второй –
на анализе инерционных свойств твердого тела, закрепленного на оси,
при его вращательном движении. Кроме этого, проводится прямой расчет
момента инерции исследуемого тела известной геометрии. Основной
частью установки является сплошное колесо (риc.2),
которое может вращаться вокруг горизонтальной оси. К цилиндру,
расположенному на оси колеса, с помощью нити прикреплен груз. Помещая
груз в устройство для его крепления, получаем физический маятник,
который может колебаться около положения равновесия. Угол отклонения
может быть определен по угломерной шкале. Установка снабжена
системами регистрации периода колебаний колеса и времени опускания
груза[2].
При анализе работ выявлены основные недостатки, предложенных методов:
При исследовании современного рынка измерительных устройств Российской федерации не обнаружены приборы для определения динамических характеристик тел вращения, удовлетворяющих следующим требованиям:
Для
устранения вышесказанных недостатков разработан метод, основанный на
свободном выбеге ротора электродвигателя.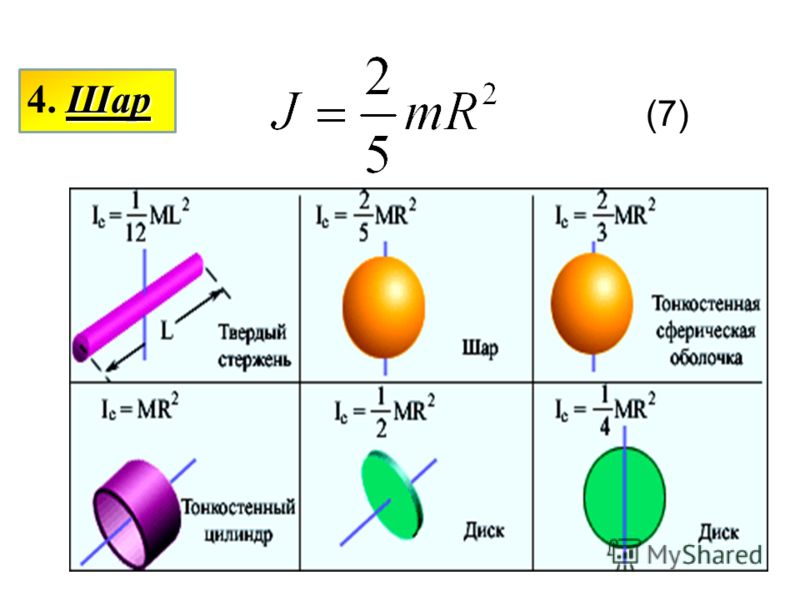 Основная идея реализации
измерительной установки основана на нахождении постоянной времени
ротора двигателя Т, которая определяется следующим образом. Как
известно момент вращения двигателя складывается из двух моментов,
момента статического сопротивления и динамического момента:
Основная идея реализации
измерительной установки основана на нахождении постоянной времени
ротора двигателя Т, которая определяется следующим образом. Как
известно момент вращения двигателя складывается из двух моментов,
момента статического сопротивления и динамического момента:
.
При выбеге двигателя момент вращения двигателя равен нулю. Таким образом из основного уравнения электропривода возможно найти интересующие параметры, такие как постоянная времени. Принимаем, что степень полинома первого порядка[4]. Получаем, что основное уравнение электропривода в данном случае является дифференциальным уравнением первого порядка. Можно сделать вывод, что выбег электродвигателя описывается апериодический звеном первого порядка [5]:
,
,
,
.
Следовательно, если
записать осциллограмму скорости выбега ротора двигателя ротора, можно
вычислить T. Если же нагрузить ротор двигателя телом вращения и снова записать
осциллограмму скорости, то получим другое значение
.
В первом случае T
равен (рис.3а)[6]:
Если же нагрузить ротор двигателя телом вращения и снова записать
осциллограмму скорости, то получим другое значение
.
В первом случае T
равен (рис.3а)[6]:
|
, |
1 |
где jр – момент инерции ротора двигателя, k – коэффициент трения.
Во втором случае равен (рис. 3б) :
|
, |
2 |
где jт – момент инерции тела вращения.
Разрешив уравнение 1 через 2, несложно найти искомое значение момента инерции тела вращения:
Рисунок 3 — к определению постоянной времени
Для проверки предложенного метода собран стенд, состоящий из программной и аппаратной части. В аппаратную часть входит:
а)
двигатель постоянного тока Siemens
1G. 5100-0EC4.
–6WV1;
5100-0EC4.
–6WV1;
б)датчик скорости – тахогенератор L117-61026B1-04 ;
в) АЦП-ЦАП Siemens simatic S7-400;
г) Вычислительная машина IBM PC.
Программная часть измерительной установки состоит из прикладной программы «Mеркурий» (рис.4), написанной на языке C++. Общий алгоритм работы программы представлен на рисунке 5.
Двигатель постоянного тока, оснащённый крепежным механизмом для закрепления тел вращения, расположен горизонтально. Встроенный аналоговый тахогенератор подключен к АЦП. Силовой кабель электродвигателя замкнут через твердотелые ключи к ЦАП. ЦАП-АЦП непосредственно подключена к вычислительной машине IBM PC. Управление ЦАП-АЦП происходит непосредственно через прикладную программу «Меркурий».
Рисунок 4 – интерфейс программы «Меркурий»
Общий
принцип работы установки. Оператор размещает испытуемое тело на
крепежном механизме. По команде оператора через программу «Меркурий»
ЦАП подает напряжение на двигатель, параллельно обращаясь к АЦП для
отслеживания скорости вращения ротора двигателя. По достижению
требуемой скорости «Меркурий» снимает напряжение с
двигателя и начинает запись сигнала с тахогенератора. После остановки
ротора двигателя «Меркурий» проводит регрессионный анализ
полученного сигнала. По полученной регрессионной модели вычисляет
постоянную времени, а затем и момент инерции.
По команде оператора через программу «Меркурий»
ЦАП подает напряжение на двигатель, параллельно обращаясь к АЦП для
отслеживания скорости вращения ротора двигателя. По достижению
требуемой скорости «Меркурий» снимает напряжение с
двигателя и начинает запись сигнала с тахогенератора. После остановки
ротора двигателя «Меркурий» проводит регрессионный анализ
полученного сигнала. По полученной регрессионной модели вычисляет
постоянную времени, а затем и момент инерции.
Разрабатываемая испытательная установка обладает ряд преимуществ:
малые габариты;
отсутствие гибких элементов;
полностью автоматическое вычисление;
наличие БД для хранения истории измерений.
Рисунок 5 – алгоритм программы
На данный
момент выдуться испытания стенда. Полученные промежуточные данные
свидетельствуют о состоятельности метода. По завершению испытаний
испытательного стенда планируется приступить к промышленному
испытанию.
По завершению испытаний
испытательного стенда планируется приступить к промышленному
испытанию.
Литература:
К.П.Яковлев. Определение момента инерции махового колеса динамическим методом. Физ. практикум. Работа 2а.ОГИЗ. М.-Л.,1946 – С.85-88
Козлов В.И. Измерение момента инерции твердых тел в физическом практикуме. Материалы международной научно-технической конференции ААИ «Автомобиле- и тракторостроение в России: приоритеты развития и подготовка кадров», посвященной 145-летию МГТУ «МАМИ».М.,2012 – С.213-218
Изучение вращательного движения твердого тела. Физический практикум. Лабораторная работа 10. Под ред. В. И. Ивероновой. М., 1962, – С. 86-90.
Вольдек А.И. Электрические машины. – Л.: Энергия, 1974. – 84 с.
Сеферян А.Е. Разработка метода идентификации математической модели электродвигателя бесконтактным способом.
 Машиностроение. Кр-р, 2011 – С.80-84.
Машиностроение. Кр-р, 2011 – С.80-84.Сеферян А.Е.,Топчий А.Ю., Нестеров А.В. Бесконтактная параметрическая идентификация вращающихся машин. Научно-технический вестник Санкт-Петербургского государственного университета информационных технологий, механики и оптики.2011, вып.6(76). – С.142-143.
Основные термины (генерируются автоматически): Меркурий, момент инерции, IBM, вращательное движение, твердое тело, автоматическое вычисление, аппаратная часть, вычислительная машина, горизонтальная ось, известная геометрия.
Похожие статьи
Исследования ветроколес с вертикальной
осью вращенияОднако, это верно лишь для тихоходных роторов с лопастями, сопротивление движению которых различно.
Основные термины (генерируются автоматически): вертикальная ось вращения, компьютерное моделирование, крутящий момент, OECD, лопастная система.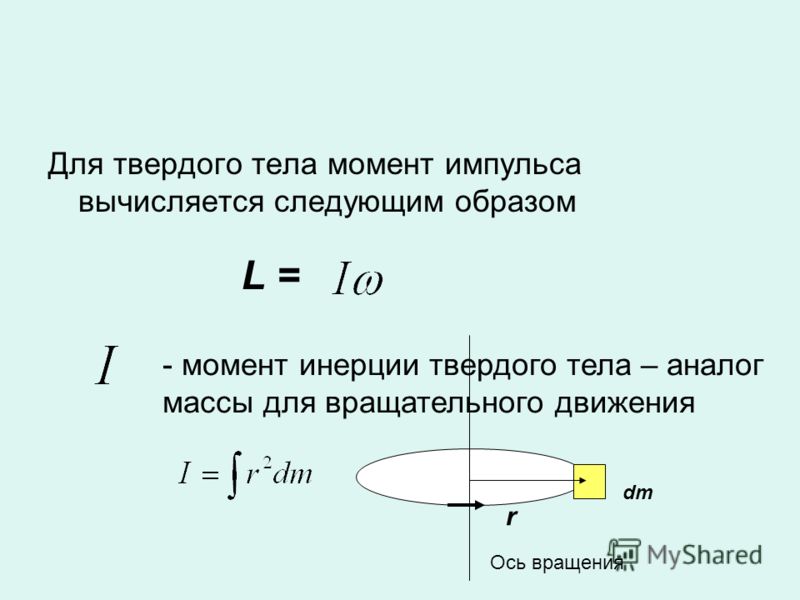 ..
..
Методика изучения
вращательного движения твердого тела…Основные термины (генерируются автоматически): момент импульса, вращательное движение, импульсный момент, неподвижная ось, момент инерции, величина, ось вращения, угловая скорость, ток момента импульса, импульсный ток.
Расчёт деформации приспособления для закрепления концевых…получим следующую формулу для вычисления полярного момента инерции
г) Вычислительная машина IBM PC. Программная часть измерительной установки состоит из прикладной программы «Mеркурий» (рис. 4), написанной на языке C++.
4), написанной на языке C++.
Математическое моделирование взаимодействия ионов…
Основные термины (генерируются автоматически): момент импульса, вращательное движение, импульсный момент, неподвижная ось, момент инерции, величина, ось вращения, угловая скорость, ток…
Решение задачи управления
перемещением квадрокоптера вдоль…Математическая модель квадрокоптера (математическая модель движения твердого тела в
где — масса твердого тела; — ускорение свободного падения; — матрица инерции
Основные термины (генерируются автоматически): MATLAB, канонический вид, угол крена, ось, система. ..
..
Использование магнитных подвесов при проектировании ВЭУ…
В статье исследуется тема использования магнитных подвесов при проектировании ветроэнергетических установок с вертикальной и горизонтальной осью вращения (ВЭУ).
Корпус ступицы вращается и передает момент вращения генератору ВЭУ.
Анализ условий
устойчивости стационарного движения редуктораМетодика изучения вращательного движения твердого тела… Для колеса вращающегося вокруг оси симметрии направление вектора совпадает с направлением вектора угловой скорости. Если в систему с моментом импульса перенести момент импульса в количестве…
Математическое моделирование
движения плоского. ..
..…вращательного движения 7–11 (рис. 1.). Рассмотрим алгоритм перемещения
силы (равен 0 — сила приложена вертикально вниз) —момент инерции j-тых звеньев; — момент инерции
РАН. Механика твердого тела, 1998, № 4, с. 86–101. Jatsun S., Zimmerman K., Zeigis I., Jatsun A…
Способ
вращения геометрической фигуры вокруг оси плоскости…Основные термины (генерируются автоматически): фигура, рисунок, окружность круга, круг окружности, окружность, координатная ось, призма, горизонтальная плоскость, осевая линия, геометрическая фигура.
- Как издать спецвыпуск?
- Правила оформления статей
- Оплата и скидки
Похожие статьи
Исследования ветроколес с вертикальной
осью вращенияОднако, это верно лишь для тихоходных роторов с лопастями, сопротивление движению которых различно.
Основные термины (генерируются автоматически): вертикальная ось вращения, компьютерное моделирование, крутящий момент, OECD, лопастная система…
Методика изучения
вращательного движения твердого тела…Основные термины (генерируются автоматически): момент импульса, вращательное движение, импульсный момент, неподвижная ось, момент инерции, величина, ось вращения, угловая скорость, ток момента импульса, импульсный ток.
Расчёт деформации приспособления для закрепления концевых…получим следующую формулу для вычисления полярного момента инерции
г) Вычислительная машина IBM PC. Программная часть измерительной установки состоит из прикладной программы «Mеркурий» (рис.4), написанной на языке C++.
Программная часть измерительной установки состоит из прикладной программы «Mеркурий» (рис.4), написанной на языке C++.
Математическое моделирование взаимодействия ионов…
Основные термины (генерируются автоматически): момент импульса, вращательное движение, импульсный момент, неподвижная ось, момент инерции, величина, ось вращения, угловая скорость, ток…
Решение задачи управления
перемещением квадрокоптера вдоль…Математическая модель квадрокоптера (математическая модель движения твердого тела в
где — масса твердого тела; — ускорение свободного падения; — матрица инерции
Основные термины (генерируются автоматически): MATLAB, канонический вид, угол крена, ось, система. ..
..
Использование магнитных подвесов при проектировании ВЭУ…
В статье исследуется тема использования магнитных подвесов при проектировании ветроэнергетических установок с вертикальной и горизонтальной осью вращения (ВЭУ).
Корпус ступицы вращается и передает момент вращения генератору ВЭУ.
Анализ условий
устойчивости стационарного движения редуктораМетодика изучения вращательного движения твердого тела… Для колеса вращающегося вокруг оси симметрии направление вектора совпадает с направлением вектора угловой скорости. Если в систему с моментом импульса перенести момент импульса в количестве…
Математическое моделирование
движения плоского. ..
..…вращательного движения 7–11 (рис. 1.). Рассмотрим алгоритм перемещения
силы (равен 0 — сила приложена вертикально вниз) —момент инерции j-тых звеньев; — момент инерции
РАН. Механика твердого тела, 1998, № 4, с. 86–101. Jatsun S., Zimmerman K., Zeigis I., Jatsun A…
Способ
вращения геометрической фигуры вокруг оси плоскости…Основные термины (генерируются автоматически): фигура, рисунок, окружность круга, круг окружности, окружность, координатная ось, призма, горизонтальная плоскость, осевая линия, геометрическая фигура.
Единицы измерения момента инерции, теория и онлайн калькуляторы
Единицы измерения момента инерции, теория и онлайн калькуляторыОпределение
Моментом инерции тела, совершающего вращательные движения вокруг некоторой оси называют физическую величину ($J$), равную:
\[J=\sum\limits^k_{i=1}{{\Delta m}_ir^2_i\left(1\right),}\]
где ${\Delta m}_i$ — масса $i$ — той материальной точки, которая является частью
рассматриваемого тела; $r^2_i$ — расстояние в квадрате от $i$- той материальной точки до оси вращения тела. 2.\]
2.\]
Момент инерции, не имеющий единицы измерения
Безразмерный момент инерции используют при изучении и описании движения и структуры небесных тел (планет, спутников и т. д). Безразмерным моментом инерции называют физическую величину, равную отношению момента инерции тела, обладающего радиусом $r$ и массой $m$, вращающегося около оси, к моменту инерции материальной точки равной массы ($m$), вращающейся относительно оси находящейся от точки на расстоянии $r$. Безразмерный момент инерции отображает распределение массы по глубине.
Тонкостенная сфера имеет безразмерный момент инерции равный $\frac{2}{3}$. Если масса тела сконцентрирована ближе к центру тела, то его безразмерный момент инерции меньше. У Луны имеющей структуру близкую к однородной, безразмерный момент инерции равен 0,391. Земля, обладающая плотным ядром, имеет безразмерный момент инерции 0,335.
Примеры задач с решением
Пример 1
Задание. Каким будет единица измерения момента инерции материальной точки, которая вращается около неподвижной оси, если получить ее из основного закона динамики вращательного движения?
Решение. 2$
2$
Читать дальше: единицы измерения плотности.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Момент вращения и момент инерции: формулы, пример решения задачи
Тела, совершающие круговые движения, в физике принято описывать с помощью формул, включающих в себя угловую скорость и угловое ускорение, а также такие величины, как моменты вращения, сил и инерции. Рассмотрим подробнее эти понятия в статье.
Момент вращения относительно оси
Эту физическую величину также называют моментом импульса. Слово «момент» означает, что при определении соответствующей характеристики учитывается положение оси вращения. Так, момент импульса частицы массой m, которая вращается со скоростью v вокруг оси O и находится от последней на расстоянии r, описывается следующей формулой:
L¯ = r¯*m*v¯ = r¯*p¯, где p¯ — импульс частицы.
Знак «¯» указывает на векторный характер соответствующей величины. Направление вектора момента вращения L¯ определяется по правилу правой руки (четыре пальца направлены от конца вектора r¯ к концу p¯, и отставленный большой палец показывает, куда будет направлен L¯). Направления всех названных векторов можно посмотреть на главном фото статьи.
При решении практических задач пользуются формулой для момента импульса в форме скалярной. Кроме того, линейную скорость заменяют угловой. В этом случае формула для L будет выглядеть так:
L = m*r2*ω, где ω = v*r — угловая скорость.
Величина m*r2 обозначается буквой I и называется моментом инерции. Она характеризует инерционные свойства системы вращения. В общем виде выражение для L записывается так:
L = I*ω.
Эта формула справедлива не только для вращающейся частицы массой m, но и для любого тела произвольной формы, которое совершает круговые перемещения относительно некоторой оси.
Момент инерции I
В общем случае введенная в предыдущем пункте величина I рассчитывается по формуле:
I = ∑i(mi*ri2).
Здесь i указывает на номер элемента с массой mi, расположенном от оси вращения на расстоянии ri. Это выражение позволяет произвести расчет для неоднородного тела произвольной формы. Для большинства идеальных объемных геометрических фигур этот расчет уже произведен, и полученные значения момента инерции внесены в соответствующую таблицу. Например, для однородного диска, который совершает круговые движения вокруг оси, перпендикулярной его плоскости и проходящей через центр масс, I = m*r2/2.
Чтобы понять физический смысл момента инерции вращения I, следует ответить на вопрос, относительно какой оси легче раскрутить швабру: той, которая проходит вдоль швабры или той, которая ей перпендикулярна? Во втором случае придется приложить больше усилий, поскольку момент инерции для этого положения швабры имеет большую величину.
Закон сохранения величины L
Изменение момента вращения во времени описывается приведенной ниже формулой:
dL/dt = M, где M = r*F.
Здесь M — это момент результирующей внешней силы F, приложенной к плечу r относительно оси вращения.
Формула показывает, если M=0, тогда изменение момента импульса L не будет происходить, то есть он будет оставаться сколь угодно длительное время неизменным независимо от внутренних изменений в системе. Этот случай записывают в виде выражения:
I1*ω1 = I2*ω2.
То есть любые изменения внутри системы момента I будут приводить к изменениям угловой скорости ω таким образом, что их произведение будет оставаться постоянным.
Примером проявления этого закона является спортсмен в фигурном катании, который, выбрасывая руки и прижимая их к телу, меняет свой I, что отражается на изменении его скорости вращения ω.
Задача на вращение Земли вокруг Солнца
Решим одну интересную задачу: используя приведенные выше формулы, необходимо рассчитать момент вращения нашей планеты по своей орбите.
Поскольку притяжением остальных планет можно пренебречь, а также учитывая, что момент гравитационной силы, действующей со стороны Солнца на Землю, равен нулю (плечо r=0), то L=const. Для вычисления L воспользуемся следующими выражениями:
L = I*ω; I = m*r2; ω = 2*pi/T.
Здесь мы приняли, что Землю можно считать материальной точкой с массой m=5,972*1024 кг, поскольку ее размеры намного меньше расстояния до Солнца r=149,6 млн км. T = 365,256 дня — период обращения планеты вокруг своей звезды (1 год). Подставляя все данные в выражение выше, получаем :
L = I*ω = 5,972*1024*(149,6*109)2*2*3,14/(365,256*2 3600) = 2,66*1040 кг*м2/с.
Рассчитанное значение момента импульса является гигантским, что обусловлено большой массой планеты, высокой скоростью ее вращения по орбите и огромным астрономическим расстоянием.
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 9 из 14Следующая ⇒ Пусть твёрдое тело массой m и объёмом V может вращаться вокруг неподвижной оси, причём ось вращения не обязательно проходит через само тело. Разобъём тело на малые элементы Δmk, и пусть rk– расстояние элемента Δmkдо оси вращения (рис. 7.1). Определение. Моментом инерции I твёрдого тела относительно заданной оси называется предельная сумма моментов инерции всех его частиц относительно этой оси: , (7.1) где ρ = ρ(x, y, z) = dm/dV − плотность тела на элементе dm. Для однородного тела ρ = const, и тогда момент инерции . (7.2) Из определения (7.1) следует свойство аддитивности момента инерции: момент инерции твёрдого тела относительно любой оси равен сумме мометов инерции всех его частей относительно этой оси: I = ∑ Ik, какими бы ни были эти части. Пример 1. Найти момент инерции тонкого кольца радиусом R, массой m относительно его оси. Решение. Разобъём кольцо на малые элементы Δmk(рис. 7.2). Расстояния каждого из них до оси одинаковы: rk =R. Тогда, из определения (7.1), момент инерции кольца равен сумме моментов инерции его элементов: . Таким образом, момент инерции тонкого кольца I = mR2. Пример 2. Найти момент инерции однородного диска радиусом R, массой m относительно его оси. Решение. Разобъём диск на бесконечно узкие кольца (r, dr), и пусть dm – масса такого кольца (рис. 7.3). Согласно Примеру 1, момент инерции такого кольца dI = r2 dm. Теперь проинтегрируем это выражение по всем кольцам, заполняющим диск: , где σ = dm/dS = m/(πR2)[кг/м2] – поверхностная плотность диска, т. Пример 3. Найти момент инерции стержня массой m, длиной l относительно оси, перпендикулярной стержню и проходящей через его конец. Решение. Разбиваем стержень на малые элементы длиной dx, и пусть dm – масса такого элемента (рис. 7.4). Его момент инерции dI = x2 dm = x2 γ dx, где γ = dm/dх = m/l [кг/м] – погонная плотность стержня, т. е. масса единицы его длины). Интегрируя это выражение по всем элементам стержня, получаем: I = ml3 /3. Пример 4. Найти момент инерции шара радиусом R, массой m относительно оси, проходящей через его центр. Решение. Разобъём шар на тонкие диски толщиной dx, как показано на рис. 7.5 (на этом рисунке для удобства изображена только половина шара). его объём dV = πr2 dx = π(R2 – x2)dx, масса dm = ρdV, где ρ = − плотность шара, V = − его объём. Тогда, согласно Примеру 2, момент инерции такого диска dI = . Интегрируя теперь по всем дискам, заполняющим шар и подставляя выражение для ρ, получаем, что момент инерции шара I = .
Теорема Штейнера Процедура прямого вычисления момента инерции тела относительно произвольной оси по формуле (7.2) часто упрощается, если использовать теорему Штейнера. Теорема. Момент инерции IО твёрдого тела относительно произвольной оси О равен моменту инерции IC этого тела относительно параллельной оси, проходящей через центр масс С, плюс произведение массы тела на квадрат расстояния между осями (рис. IO= IC+ ma2 (без доказательства). Пример 1. Найти момент инерции тонкого кольца радиусом R, массой m относительно оси О, проходящей через его край и перпендикулярной плоскости кольца. Решение. По теореме Штейнера, IO= IC+ mR2 = 2 mR2. Пример 2. Найти момент инерции стержня массой m, длиной l относительно оси О, перпендикулярной стержню и проходящей через его середину. Решение. Так как момент инерции стержня относительно оси О, проходящей через его конец, IО = ml3 /3, то IC = IO – m(l/2)2 = ml3 /3 − ml2 /4 = ml2 /12. ⇐ Предыдущая45678910111213Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Сущность проекции Гаусса-Крюгера и использование ее в геодезии Тарифы на перевозку пассажиров |
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 631; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
10.4 Момент инерции и кинетическая энергия вращения – University Physics Volume 1
10 Вращение с неподвижной осью
Цели обучения
К концу этого раздела вы сможете:
- Описывать различия между вращательной и поступательной кинетической энергией
- Определить физическую концепцию момента инерции в терминах распределения массы относительно оси вращения
- Объясните, как момент инерции твердых тел влияет на их кинетическую энергию вращения
- Использование закона сохранения механической энергии для анализа систем, подвергающихся как вращению, так и поступательному перемещению
- Расчет угловой скорости вращающейся системы при наличии потерь энергии из-за неконсервативных сил
До сих пор в этой главе мы работали с кинематикой вращения: описанием движения вращающегося твердого тела с фиксированной осью вращения. В этом разделе мы определяем две новые величины, полезные для анализа свойств вращающихся объектов: момент инерции и кинетическую энергию вращения. Определив эти свойства, мы получим два важных инструмента, необходимых для анализа динамики вращения.
В этом разделе мы определяем две новые величины, полезные для анализа свойств вращающихся объектов: момент инерции и кинетическую энергию вращения. Определив эти свойства, мы получим два важных инструмента, необходимых для анализа динамики вращения.
Вращательная кинетическая энергия
Любой движущийся объект обладает кинетической энергией. Мы знаем, как вычислить это для тела, совершающего поступательное движение, но как насчет твердого тела, совершающего вращательное движение? Это может показаться сложным, потому что каждая точка твердого тела имеет разную скорость. Однако мы можем использовать угловую скорость, которая одинакова для всего твердого тела, чтобы выразить кинетическую энергию вращающегося объекта. На рисунке показан пример очень энергичного вращающегося тела: электрический точильный камень, приводимый в движение двигателем. Когда точильный камень выполняет свою работу, летят искры, возникают шум и вибрация. Эта система обладает значительной энергией, частично в виде тепла, света, звука и вибрации.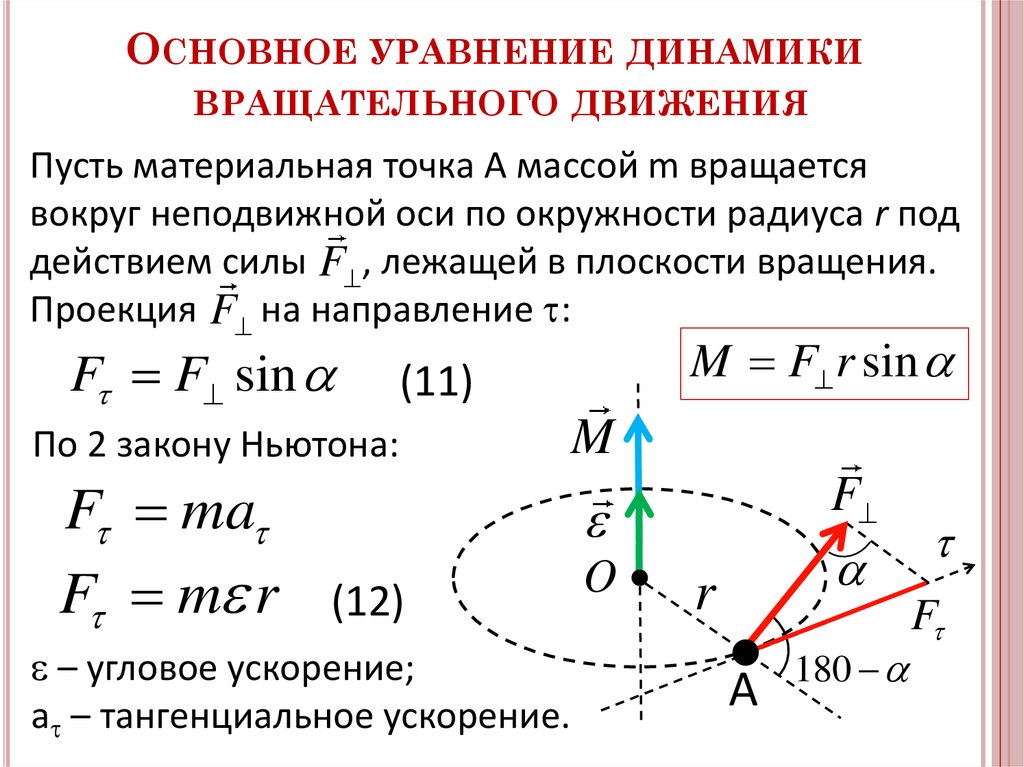 Однако большая часть этой энергии находится в форме 9{2}[/latex], а скорость — это величина, разная для каждой точки тела, вращающегося вокруг оси, имеет смысл найти способ записать кинетическую энергию через переменную [latex]\omega[/ латекс], который одинаков для всех точек на твердом вращающемся теле. Для одиночной частицы, вращающейся вокруг фиксированной оси, это легко вычислить. Мы можем связать угловую скорость с величиной поступательной скорости, используя соотношение [latex]{v}_{\text{t}}=\omega r[/latex], где 9{2}.[/latex]
Однако большая часть этой энергии находится в форме 9{2}[/latex], а скорость — это величина, разная для каждой точки тела, вращающегося вокруг оси, имеет смысл найти способ записать кинетическую энергию через переменную [latex]\omega[/ латекс], который одинаков для всех точек на твердом вращающемся теле. Для одиночной частицы, вращающейся вокруг фиксированной оси, это легко вычислить. Мы можем связать угловую скорость с величиной поступательной скорости, используя соотношение [latex]{v}_{\text{t}}=\omega r[/latex], где 9{2}.[/latex]
В случае твердого вращающегося тела мы можем разделить любое тело на большое количество меньших масс, каждая из которых имеет массу [latex]{m}_{j}[/latex ] и расстояние до оси вращения [латекс]{r}_{j}[/латекс], такое, чтобы общая масса тела была равна сумме отдельных масс: [латекс]М=\сумма _{ j}{m}_{j}[/латекс]. Каждая меньшая масса имеет тангенциальную скорость [латекс]{v}_{j}[/латекс], где мы временно опустили индекс t . Полная кинетическая энергия твердого вращающегося тела равна 9{2}[/latex], где r — расстояние от точечной частицы до оси вращения. В следующем разделе мы исследуем интегральную форму этого уравнения, которую можно использовать для расчета момента инерции некоторых твердых тел правильной формы.
В следующем разделе мы исследуем интегральную форму этого уравнения, которую можно использовать для расчета момента инерции некоторых твердых тел правильной формы.
Момент инерции есть количественная мера инерции вращения, как и в поступательном движении, а масса есть количественная мера линейной инерции, т. е. чем массивнее объект, тем больше у него инерция и тем больше его сопротивление изменению линейной скорости. Аналогично, чем больше момент инерции твердого тела или системы частиц, тем больше их сопротивление изменению угловой скорости относительно неподвижной оси вращения. Интересно посмотреть, как меняется момент инерции в зависимости от r, расстояние до оси вращения массы частицы на рис. Твердые тела и системы частиц с большей массой, сосредоточенные на большем расстоянии от оси вращения, обладают большими моментами инерции, чем тела и системы той же массы, но сосредоточенные вблизи оси вращения. Таким образом, мы можем видеть, что полый цилиндр имеет большую инерцию вращения, чем сплошной цилиндр той же массы при вращении вокруг оси, проходящей через центр. Подставляя рисунок в рисунок, выражение для кинетической энергии вращающегося твердого тела принимает вид 9{2}.[/latex]
Подставляя рисунок в рисунок, выражение для кинетической энергии вращающегося твердого тела принимает вид 9{2}.[/latex]
Из этого уравнения видно, что кинетическая энергия вращающегося твердого тела прямо пропорциональна моменту инерции и квадрату угловой скорости. Это используется в накопителях энергии маховика , которые предназначены для накопления большого количества кинетической энергии вращения. Многие автопроизводители в настоящее время испытывают в своих автомобилях накопители энергии маховика, такие как маховик или система рекуперации кинетической энергии, показанные на рисунке.
Рисунок 10.18 Маховик KERS (система рекуперации кинетической энергии), используемый в автомобилях. (кредит: «cmonville»/Flickr) Вращательные и поступательные величины для кинетической энергии и инерции представлены на рисунке. Столбец отношений не включен, потому что не существует константы, на которую мы могли бы умножить вращательную величину, чтобы получить поступательную величину, как это можно сделать для переменных на рисунке.
Пример
Момент инерции системы частиц
Шесть маленьких шайб расположены на расстоянии 10 см друг от друга на стержне незначительной массы и длиной 0,5 м. Масса каждой шайбы 20 г. Стержень вращается вокруг оси, расположенной на расстоянии 25 см, как показано на рис. а) Чему равен момент инерции системы? б) Если убрать две ближние к оси шайбы, каков будет момент инерции оставшихся четырех шайб? в) Если система с шестью шайбами вращается со скоростью 5 об/с, какова ее кинетическая энергия вращения?
Рисунок 10. 19 Шесть шайб расположены на расстоянии 10 см друг от друга на стержне незначительной массы, вращающемся вокруг вертикальной оси.
19 Шесть шайб расположены на расстоянии 10 см друг от друга на стержне незначительной массы, вращающемся вокруг вертикальной оси.Стратегия
- Мы используем определение момента инерции для системы частиц и выполняем суммирование для оценки этой величины. Все массы одинаковы, поэтому мы можем поставить это количество перед символом суммирования.
- Делаем аналогичный расчет.
- Подставим результат (а) в выражение для кинетической энергии вращения. 9{2}=1,73\,\text{J}[/латекс].
Значение
Мы можем видеть индивидуальные вклады в момент инерции. Массы вблизи оси вращения вносят очень небольшой вклад. Когда мы их убрали, это очень мало повлияло на момент инерции.
В следующем разделе мы обобщим уравнение суммирования для точечных частиц и разработаем метод расчета моментов инерции твердых тел. Однако пока на рисунке приведены значения инерции вращения для обычных форм объектов вокруг заданных осей.
Рисунок 10. 20 Значения инерции вращения для обычных форм объектов
20 Значения инерции вращения для обычных форм объектовПрименение вращательной кинетической энергии
Теперь давайте применим идеи вращательной кинетической энергии и таблицу моментов инерции, чтобы получить представление об энергии, связанной с несколькими вращающимися объектами. Следующие примеры также помогут вам освоиться с этими уравнениями. Во-первых, давайте рассмотрим общую стратегию решения проблем с вращательной энергией.
Стратегия решения проблем: энергия вращения
- Определите, какая энергия или работа связана с вращением.
- Определите интересующую систему. Эскиз обычно помогает.
- Проанализируйте ситуацию, чтобы определить виды работы и энергии.
- Если нет потерь энергии из-за трения и других неконсервативных сил, механическая энергия сохраняется, то есть [латекс] {K} _ {\ text {i}} + {U} _ {\ text {i}} ={K}_{\text{f}}+{U}_{\text{f}}[/латекс].
- Если присутствуют неконсервативные силы, механическая энергия не сохраняется, и другие формы энергии, такие как тепло и свет, могут входить в систему или выходить из нее.
 Определите, каковы они, и рассчитайте их по мере необходимости.
Определите, каковы они, и рассчитайте их по мере необходимости. - Удалите термины везде, где это возможно, чтобы упростить алгебру.
- Оцените численное решение, чтобы увидеть, имеет ли оно смысл в физической ситуации, представленной в формулировке задачи.
Пример
Расчет энергии вертолета
Типичный небольшой спасательный вертолет имеет четыре лопасти: каждая имеет длину 4,00 м и массу 50,0 кг (рисунок). Лопасти можно представить как тонкие стержни, которые вращаются вокруг одного конца оси, перпендикулярной их длине. Вертолет имеет полную загруженную массу 1000 кг. а) Рассчитайте кинетическую энергию вращения лопастей, когда они вращаются со скоростью 300 об/мин. (b) Рассчитайте поступательную кинетическую энергию вертолета, когда он летит со скоростью 20,0 м/с, и сравните ее с энергией вращения лопастей.
Рисунок 10.21 (a) Эскиз четырехлопастного вертолета. b) спасательная операция на воде с участием вертолета Оклендской спасательной вертолетной службы Westpac. (кредит b: «111 Emergency»/Flickr)
(кредит b: «111 Emergency»/Flickr)Стратегия
Кинетическая энергия вращения и поступательного движения может быть рассчитана по их определениям. Формулировка задачи дает все необходимые константы для вычисления выражений для вращательной и поступательной кинетических энергий.
Раствор
9{2}.[/латекс]Мы должны преобразовать угловую скорость в радианы в секунду и рассчитать момент инерции, прежде чем мы сможем найти K . Угловая скорость [латекс]\омега[/латекс] равна
[латекс]\omega =\frac{300\,\text{rev}}{1.00\,\text{min}}\,\frac{2\pi \,\text{rad}}{\text{1 rev}}\,\frac{1.00\,\text{min}}{60.0\,\text{s}}=\,31.4\,\frac{\text{rad}}{\text{s}}. [/латекс]
Момент инерции одной лопасти равен моменту инерции тонкого стержня, вращающегося вокруг своего конца, указанному на рис. Всего 9{2}=450,0\,\text{J}.[/latex]
Таким образом, полная энергия бумеранга равна
[латекс] {K} _ {\ text {Всего}} = {K} _ {\ text {R}} + {K} _ {\ text {T}} = 80,93 + 450,0 = 530,93 \, \ text { J}. {2}[/латекс]. Если погружной гребной винт имеет скорость вращения 4,0 об/с при выключенном двигателе, какова будет скорость вращения гребного винта через 5,0 с, когда сопротивление воды уберет из системы 50 000 Дж? 9{2}[/latex] момент инерции увеличивается как квадрат расстояния до фиксированной оси вращения. Момент инерции является вращательным аналогом массы в линейном движении.
{2}[/латекс]. Если погружной гребной винт имеет скорость вращения 4,0 об/с при выключенном двигателе, какова будет скорость вращения гребного винта через 5,0 с, когда сопротивление воды уберет из системы 50 000 Дж? 9{2}[/latex] момент инерции увеличивается как квадрат расстояния до фиксированной оси вращения. Момент инерции является вращательным аналогом массы в линейном движении.
Концептуальные вопросы
Что, если бы другая планета размером с Землю была выведена на орбиту вокруг Солнца вместе с Землей. Момент инерции системы увеличится, уменьшится или останется прежним?
Твердый шар вращается вокруг оси, проходящей через его центр, с постоянной скоростью вращения. Другая полая сфера той же массы и радиуса вращается вокруг своей оси, проходящей через центр, с той же скоростью вращения. Какой шар имеет большую кинетическую энергию вращения?
Другая полая сфера той же массы и радиуса вращается вокруг своей оси, проходящей через центр, с той же скоростью вращения. Какой шар имеет большую кинетическую энергию вращения?
Полая сфера, так как масса распределена дальше от оси вращения.
Задачи
Система точечных частиц показана на следующем рисунке. Каждая частица имеет массу 0,3 кг и все они лежат в одной плоскости. а) Чему равен момент инерции системы относительно данной оси? б) Если система вращается со скоростью 5 об/с, какова ее кинетическая энергия вращения?
(a) Рассчитайте кинетическую энергию вращения Земли вокруг своей оси. б) Какова кинетическая энергия вращения Земли на ее орбите вокруг Солнца? 9{33}\,\text{J}[/латекс]
Рассчитайте кинетическую энергию вращения колеса мотоцикла массой 12 кг, если его угловая скорость равна 120 рад/с, внутренний радиус равен 0,280 м, а внешний радиус равен 0,330 м.
Бейсбольный питчер бросает мяч движением, при котором происходит вращение предплечья вокруг локтевого сустава, а также другие движения. {2}[/latex], какова кинетическая энергия вращения предплечья? 9{2}[/латекс] и массой 200 кг. Сопротивлением воздуха пренебречь. а) С какой поступательной скоростью гребной винт ударяется о землю? б) Какова скорость вращения пропеллера в момент удара?
{2}[/latex], какова кинетическая энергия вращения предплечья? 9{2}[/латекс] и массой 200 кг. Сопротивлением воздуха пренебречь. а) С какой поступательной скоростью гребной винт ударяется о землю? б) Какова скорость вращения пропеллера в момент удара?
а. [латекс] {v}_{\text{f}}=86,5\,\text{m}\text{/}\text{s}[/latex];
б. Скорость вращения винта остается прежней и составляет 20 об/с.
Если в предыдущей задаче присутствует сопротивление воздуха и оно снижает кинетическую энергию вращения пропеллера при ударе на 30 %, какова скорость вращения пропеллера при ударе? 9{42}\,\text{J}[/латекс]
Электрический шлифовальный станок, состоящий из вращающегося диска массой 0,7 кг и радиусом 10 см, вращается со скоростью 15 об/сек. При нанесении на грубую деревянную стену скорость вращения уменьшается на 20%. а) Чему равна конечная кинетическая энергия вращения вращающегося диска? б) Насколько уменьшилась его кинетическая энергия вращения?
Система состоит из диска массой 2,0 кг и радиусом 50 см, на котором закреплен кольцевой цилиндр массой 1,0 кг с внутренним радиусом 20 см и внешним радиусом 30 см (см.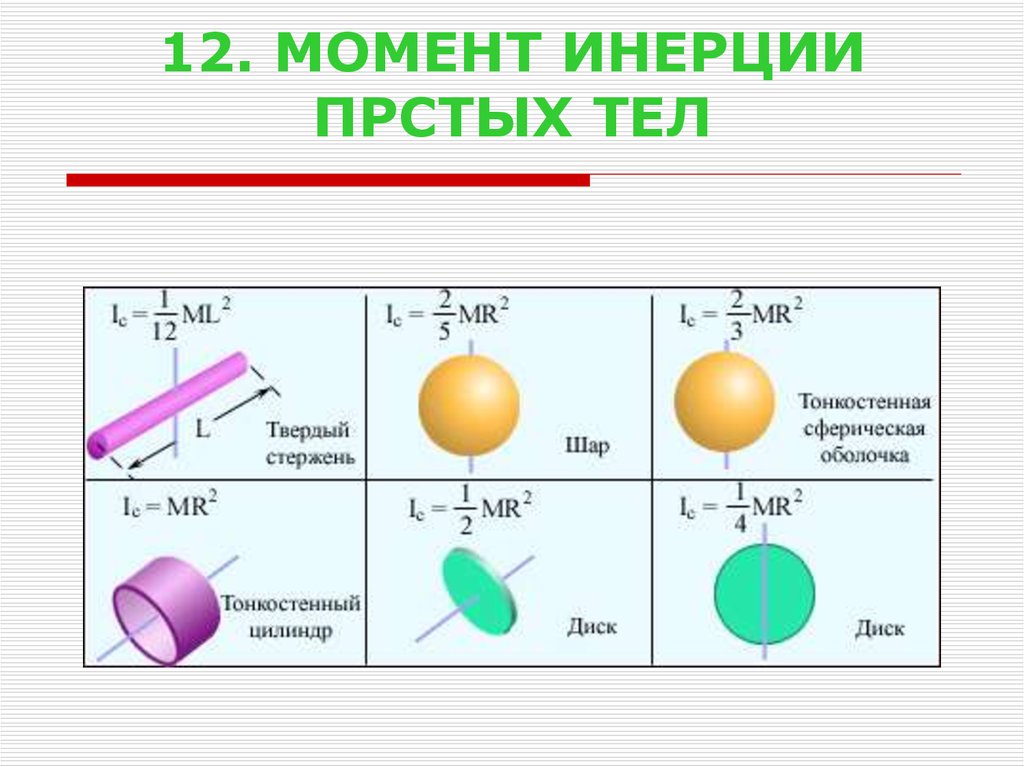 ниже). Система вращается вокруг оси, проходящей через центр диска и кольцевой цилиндр со скоростью 10 об/с. а) Чему равен момент инерции системы? б) Какова его кинетическая энергия вращения? 9{2}[/латекс]; б. [латекс]К=621,8\,\текст{J}[/латекс]
ниже). Система вращается вокруг оси, проходящей через центр диска и кольцевой цилиндр со скоростью 10 об/с. а) Чему равен момент инерции системы? б) Какова его кинетическая энергия вращения? 9{2}[/латекс]; б. [латекс]К=621,8\,\текст{J}[/латекс]
Глоссарий
- момент инерции
- вращающаяся масса твердых тел, которая относится к тому, насколько легко или сложно будет изменить угловую скорость вращающегося твердого тела
- вращательная кинетическая энергия
- кинетическая энергия за счет вращения объекта; это часть его полной кинетической энергии
10.3 Динамика вращательного движения: инерция вращения
Цели обучения Вращательная инерция и момент инерции
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Понимать взаимосвязь между силой, массой и ускорением
- Изучение поворотного эффекта силы
- Изучить аналогию между силой и крутящим моментом, массой и моментом инерции, а также линейным ускорением и угловым ускорением
Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:
- 4.
 D.1.1 Учащийся может описать представление и использовать его для анализа ситуации, в которой несколько сил, действующих на вращающуюся систему жестко связанных объектов, изменяют угловую скорость и угловой момент системы. (СП 1.2, 1.4)
D.1.1 Учащийся может описать представление и использовать его для анализа ситуации, в которой несколько сил, действующих на вращающуюся систему жестко связанных объектов, изменяют угловую скорость и угловой момент системы. (СП 1.2, 1.4) - 4.D.1.2 Учащийся может планировать стратегии сбора данных, предназначенные для установления того, что крутящий момент, угловая скорость, угловое ускорение и угловой момент могут быть точно предсказаны, когда переменные обрабатываются как по часовой стрелке или против часовой стрелки по отношению к четко определенную ось вращения и уточнить вопрос исследования на основе изучения данных. (СП 3.2, 4.1, 5.1, 5.3)
- 5.E.2.1 Учащийся способен описать или рассчитать угловой момент и инерцию вращения системы в терминах местоположения и скорости объектов, составляющих систему. Ожидается, что учащиеся будут делать качественные рассуждения с составными объектами.
 Ожидается, что учащиеся будут выполнять вычисления с фиксированным набором протяженных объектов и точечных масс. (П. 2.2)
Ожидается, что учащиеся будут выполнять вычисления с фиксированным набором протяженных объектов и точечных масс. (П. 2.2)
Если вам когда-нибудь приходилось крутить велосипедное колесо или толкать карусель, вы знаете, что для изменения угловой скорости необходима сила, как показано на рис. 10.10. На самом деле, ваша интуиция надежно предсказывает многие из задействованных факторов. Например, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; другое следствие состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
Рисунок 10.10 Для вращения колеса велосипеда требуется сила. Чем больше сила, тем больше угловое ускорение. Чем массивнее колесо, тем меньше угловое ускорение. Если надавить на спицу ближе к оси, угловое ускорение будет меньше.
Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, рассмотрим, что произойдет, если мы приложим силу FF размером 12{F} {} к точке массой мм размером 12{m} {}, которая находится на расстояние rr size 12{r} {} от точки вращения, как показано на рисунке 10.11. Поскольку сила перпендикулярна rr размером 12{r} {}, ускорение a=Fma=Fm размера 12{a= {{F} над {m} } } {} получается в направлении FF размера 12{F } {}. Мы можем изменить это уравнение так, что F=maF=ma size 12{F= ital «ma»} {}, а затем искать способы связать это выражение с выражениями для вращательных величин. Заметим, что a=rαa=rα size 12{a=rα} {}, и подставим это выражение в F=maF=ma size 12{F= ital «ma»} {}, что даст
10,40 F=mrα.F=mrα. size 12{F= ital «mr»α». «} {}
«} {}
Вспомним, что крутящий момент – это вращательная эффективность силы. В этом случае, поскольку размер FF 12{«F»} {} перпендикулярен размеру RR 12{r} {}, крутящий момент просто τ=Frτ=Fr размер 12{τ=rα} {}. Итак, если мы умножим обе части приведенного выше уравнения на размер rr 12{r} {}, мы получим крутящий момент в левой части. То есть,
10,41 rF=mr2αrF=mr2α размер 12{ ital «rF»= ital «mr» rSup { размер 8{2} } α} {}
или
10,42 τ=mr2α.τ=mr2α. size 12{τ= ital «mr» rSup { size 8{2} } α.} {}
Последнее уравнение является вращательным аналогом второго закона Ньютона (F=maF=ma size 12{F= ital «ma»} {}), где крутящий момент аналогичен силе, угловое ускорение аналогично поступательному ускорению, а mr2mr2 size 12{ ital «mr» rSup { size 8{2} } } {} аналогичен массе или инерции. Величина mr2mr2 размером 12{ ital «mr» rSup { size 8{2} } } {} называется инерцией вращения или моментом инерции точки массой mm размером 12{m} {} расстоянием rr размером 12{r} {} от центра вращения.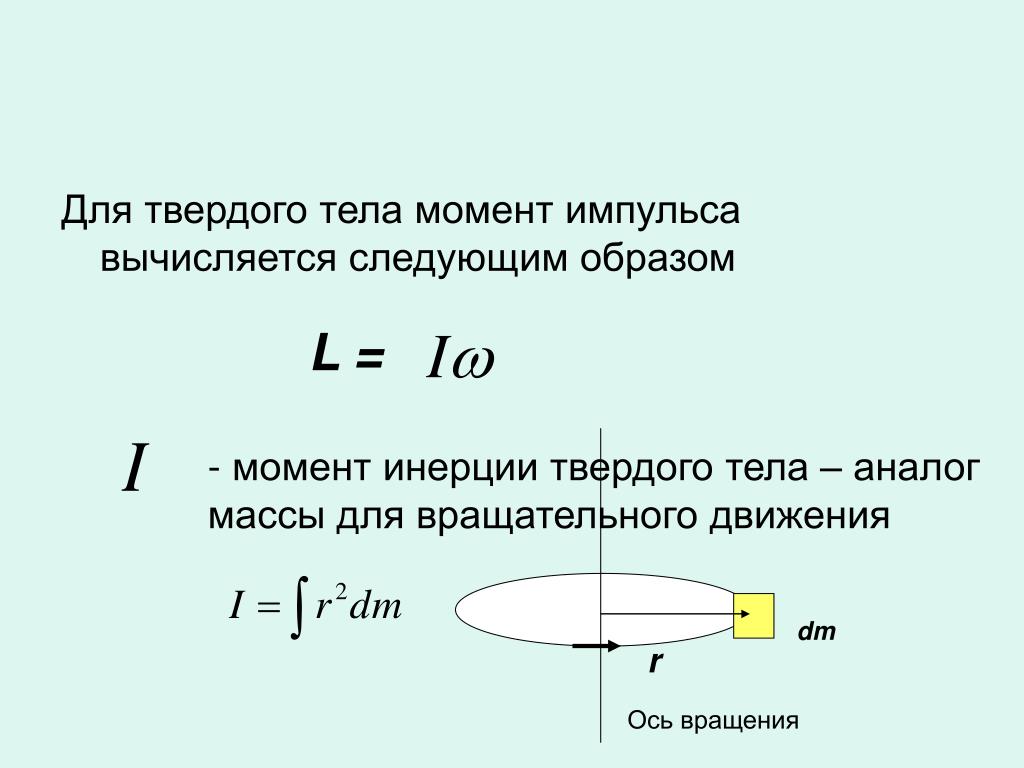
Рис. 10.11 Объект поддерживается горизонтальным столом без трения и прикреплен к точке поворота шнуром, создающим центростремительную силу. Сила FF размером 12{F} {} приложена к объекту перпендикулярно радиусу rr размером 12{r} {}, заставляя его ускоряться относительно точки поворота. Сила удерживается перпендикулярно размеру rr 12{r} {}.
Создание соединений: динамика вращательного движения
Динамика вращательного движения полностью аналогична линейной или поступательной динамике. Динамика занимается силой и массой и их влиянием на движение. Для вращательного движения мы найдем прямые аналоги силы и массы, которые ведут себя именно так, как мы и ожидали, исходя из нашего предыдущего опыта.
Инерция вращения и момент инерции
Прежде чем мы сможем рассмотреть вращение чего-либо, кроме точечной массы, подобной той, что изображена на рис. 10.11, мы должны распространить идею инерции вращения на все типы объектов. Чтобы расширить наше понятие инерции вращения, мы определяем момент инерции
II размер 12{I} {} объекта должен быть суммой
mr2mr2 size 12{ ital «mr» rSup { size 8{2} } } {} для всех точечных масс, из которых он состоит. То есть,
I=∑mr2I=∑mr2 size 12{I= Sum {} ital «mr» rSup { size 8{2} } } {}. Здесь
II размер 12{I} {} аналогичен
мм размером 12{м}{} в поступательном движении. Из-за расстояния
rr size 12{r} {}, момент инерции любого объекта зависит от выбранной оси. Собственно, расчет
Размер II 12{I} {} выходит за рамки этого текста, за исключением одного простого случая — обруча, вся масса которого находится на одном и том же расстоянии от его оси. Таким образом, момент инерции кольца вокруг своей оси равен
MR2MR2 размер 12{ ital «MR» rSup { размер 8{2} } } {}, где
Размер MM 12{M} {} — это его полная масса, а размер RR 12{R} {} — его радиус. Мы используем размер MM 12{M} {} и размер RR 12{R} {} для всего объекта, чтобы отличить их от размера 12{m} {} мм и размера rr 12{r} {} для точечных масс. Во всех других случаях мы должны обращаться к рисунку 10.12 (обратите внимание, что таблица представляет собой произведение искусства, в котором есть формы, а также формулы) для формул для размера II 12{I} {}, которые были получены путем интегрирования по непрерывному телу.
То есть,
I=∑mr2I=∑mr2 size 12{I= Sum {} ital «mr» rSup { size 8{2} } } {}. Здесь
II размер 12{I} {} аналогичен
мм размером 12{м}{} в поступательном движении. Из-за расстояния
rr size 12{r} {}, момент инерции любого объекта зависит от выбранной оси. Собственно, расчет
Размер II 12{I} {} выходит за рамки этого текста, за исключением одного простого случая — обруча, вся масса которого находится на одном и том же расстоянии от его оси. Таким образом, момент инерции кольца вокруг своей оси равен
MR2MR2 размер 12{ ital «MR» rSup { размер 8{2} } } {}, где
Размер MM 12{M} {} — это его полная масса, а размер RR 12{R} {} — его радиус. Мы используем размер MM 12{M} {} и размер RR 12{R} {} для всего объекта, чтобы отличить их от размера 12{m} {} мм и размера rr 12{r} {} для точечных масс. Во всех других случаях мы должны обращаться к рисунку 10.12 (обратите внимание, что таблица представляет собой произведение искусства, в котором есть формы, а также формулы) для формул для размера II 12{I} {}, которые были получены путем интегрирования по непрерывному телу. Обратите внимание, что размер II 12{I} {} имеет единицы массы, умноженные на квадрат расстояния (кг⋅м2кг⋅м2 размер 12{«кг» cdot «м» rSup { размер 8{2} } } {}), как мы могли бы ожидать от его определения.
Обратите внимание, что размер II 12{I} {} имеет единицы массы, умноженные на квадрат расстояния (кг⋅м2кг⋅м2 размер 12{«кг» cdot «м» rSup { размер 8{2} } } {}), как мы могли бы ожидать от его определения.
Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением:
10,43 net τ=Iαnet τ=Iα размер 12{τ=Iα} {}
или
10,44 α=net τI,α=net τI, размер 12{α= { { ital «net»τ} над {I } } «,»} {}
где чистый размер ττ 12{τ} {} — это суммарный крутящий момент от всех сил относительно выбранной оси. Для простоты мы будем рассматривать только крутящие моменты, создаваемые силами в плоскости вращения. Такие крутящие моменты бывают положительными или отрицательными и складываются как обычные числа. Соотношение в τ=Iα, α=net τIτ=Iα, α=net τI size 12{τ=Iα,««`α= { { ital «net»τ} over {I} } } {} является вращательный аналог второго закона Ньютона и очень широко применим. Это уравнение действительно справедливо для любой крутящий момент, приложенный к любому объекту относительно любой оси .
Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение. Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением заключается в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от его распределение массы относительно оси, вокруг которой он вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю. Масса в обоих случаях одинакова, но момент инерции намного больше, когда дети находятся на краю.
Эксперимент на вынос
Вырежьте круг радиусом около 10 см из плотного картона. Рядом с краем круга напишите числа от одного до двенадцати, как часы на циферблате. Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси, проходящей через его центр, как колесо. Вы можете свободно прибить круг к стене. Держите круг неподвижно и с цифрой 12, расположенной вверху, прикрепите кусок синей замазки, липкого материала, используемого для крепления постеров к стенам, к цифре три. Насколько большим должен быть комок, чтобы просто повернуть круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое для числа три, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте вращать круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси, проходящей через его центр, как колесо. Вы можете свободно прибить круг к стене. Держите круг неподвижно и с цифрой 12, расположенной вверху, прикрепите кусок синей замазки, липкого материала, используемого для крепления постеров к стенам, к цифре три. Насколько большим должен быть комок, чтобы просто повернуть круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое для числа три, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте вращать круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
В каком направлении вращался круг, когда вы добавляли замазку в номер три, по часовой или против часовой стрелки? В каком из этих направлений была результирующая угловая скорость? Была ли угловая скорость постоянной? Что мы можем сказать о направлении по часовой стрелке или против часовой стрелки углового ускорения? Как можно изменить положение замазки, чтобы создать угловую скорость в противоположном направлении?
Стратегия решения задач по динамике вращения
- Изучите ситуацию, чтобы определить, участвуют ли крутящий момент и масса во вращении .
 Нарисуйте тщательный набросок ситуации.
Нарисуйте тщательный набросок ситуации. - Определить интересующую систему .
- Нарисуйте диаграмму свободного тела . То есть нарисуйте и обозначьте все внешние силы, действующие на интересующую вас систему.
- Применить сеть τ=Iα, α=net τI net τ=Iα, α=net τI size 12{τ=Iα,«`α= { { ital «net»τ} over {I} } } {}, вращательный эквивалент второго закона Ньютона, чтобы решить проблему . Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.
- Как всегда, проверьте решение, чтобы убедиться, что оно разумно .
Выполнение соединений
В статике чистый крутящий момент равен нулю, а угловое ускорение отсутствует. При вращательном движении чистый крутящий момент является причиной углового ускорения, точно так же, как во втором законе движения Ньютона для вращения.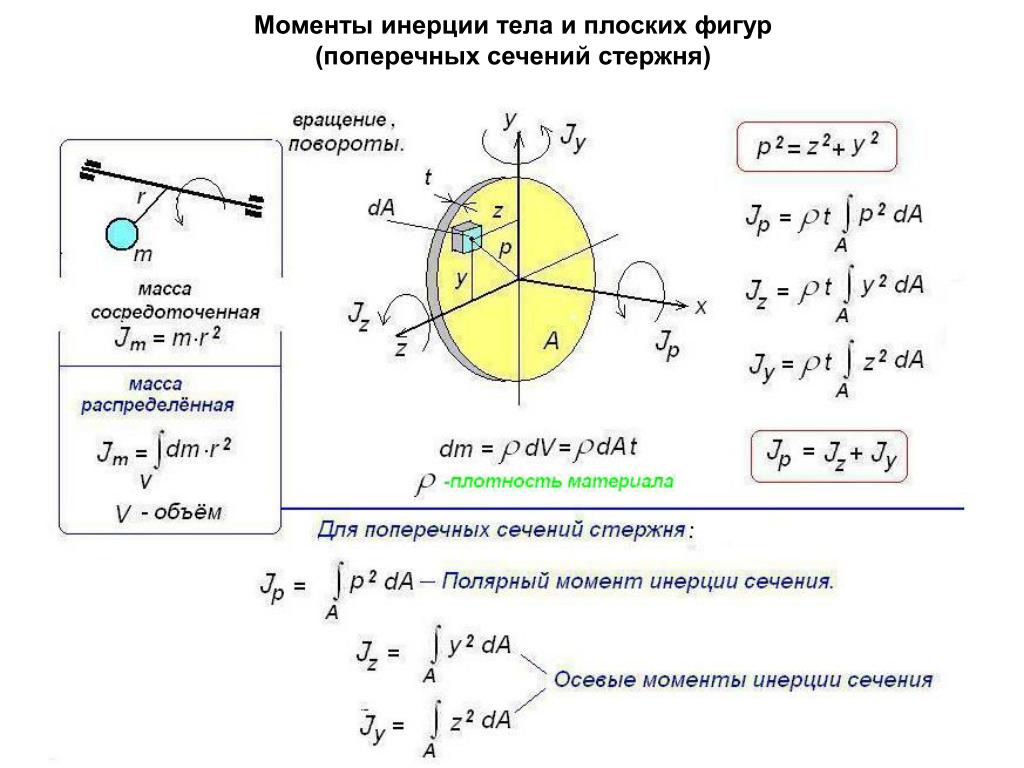
Рисунок 10.12 Некоторые инерции вращения.
Пример 10.7 Расчет влияния распределения массы на карусель
Рассмотрим отца, толкающего карусель на детской площадке на рис. 10.13. Он прикладывает силу 250 Н к краю 50-килограммовой карусели, имеющей радиус 1,50 м. Вычислите угловое ускорение, создаваемое (а), когда на карусели никого нет, и (б), когда ребенок массой 18 кг сидит на расстоянии 1,25 м от центра. Считайте саму карусель однородным диском с пренебрежимо малым тормозящим трением.
Рис. 10.13. Отец толкает игровую карусель за ее край и перпендикулярно ее радиусу для достижения максимального крутящего момента.
Стратегия
Угловое ускорение задается непосредственно выражением .
10,45 α=τIα=τI размер 12{α= {{τ} над {I} } } {}
Чтобы определить αα размера 12{α} {}, мы должны сначала вычислить крутящий момент ττ размера 12{τ } {}, который в обоих случаях одинаков, и момент инерции II величиной 12{I} {}, который во втором случае больше. Чтобы найти крутящий момент, заметим, что приложенная сила перпендикулярна радиусу, а трением можно пренебречь, так что
Чтобы найти крутящий момент, заметим, что приложенная сила перпендикулярна радиусу, а трением можно пренебречь, так что
10,46 τ=rFsin θ=(1,50 м)(250 Н)=375 Н⋅м.τ=rFsin θ=(1,50 м)(250 Н)=375 Н⋅м. размер 12{τ=»rFsinθ»= \( 1 «.» «50м» \) \( «250Н» \) =»375Н» «.» «m.»} {}
Решение для (a)
Момент инерции твердого диска относительно этой оси на рисунке 10.12 равен
10.47 12MR2,12MR2, размер 12{ { {1} свыше {2} } итал. «MR» rSup {размер 8{2} } «,»} {}
, где M=50 кгM=50 кг размер 12{M=»50″ «.» 0 итал. «кг»} {} и R=1,50 мR=1,50 м размер 12{R=1 «.» «50»м} {}, так что
10,48 I=(0,500)(50 кг)(1,50 м)2=56,25 кг⋅м2.I=(0,500)(50 кг)(1,50 м)2=56,25 кг⋅м2. размер 12{I=0 «.» 5 \( «50» «.» «0kg» \) \( 1 «.» «50m» \) rSup { size 8{2} } =»56″ «.» «25кг» «.» «m» rSup { size 8{2} } «.»} {}
Теперь, после подстановки известных значений, находим угловое ускорение равным
10,49 α=τI=375 Н⋅м56,25 кг⋅ m2=6,67рад2.α=τI=375 Н⋅м56,25 кг⋅м2=6,67рад2. размер 12{α= {{τ} над {I} } = {{«375″`»N» «.» «м»} более {«56» «.» «25»`»кг» «.» «m» rSup {размер 8{2} } } } =6 «.» «67»` {{«rad»} over {s rSup {size 8{2} } } } «.»} {}
размер 12{α= {{τ} над {I} } = {{«375″`»N» «.» «м»} более {«56» «.» «25»`»кг» «.» «m» rSup {размер 8{2} } } } =6 «.» «67»` {{«rad»} over {s rSup {size 8{2} } } } «.»} {}
Решение для (b)
Мы ожидаем, что угловое ускорение системы будет меньше в этой части, потому что момент инерции больше, когда ребенок находится на карусели. Чтобы найти общий момент инерции II размера 12{I} {}, мы сначала найдем момент инерции ребенка IcIc размера 12{I rSub { размер 8{c} } } {}, считая ребенка эквивалентным точке массы на расстоянии 1,25 м от оси. Тогда
10,50 Ic=MR2=(18 кг)(1,25 м)2=28,13 кг⋅м2. Ic=MR2=(18 кг)(1,25 м)2=28,13 кг⋅м2. размер 12{I rSub { размер 8{c} } =»MR» rSup { размер 8{2} } = \(«18» «.» 0`»кг» \) \( 1 «.»»25″` м \) rSup {размер 8{2}} =»28» «.» «13»`»кг» «.» m rSup {размер 8{2} } «.»} {}
Суммарный момент инерции равен сумме моментов инерции карусели и ребенка относительно одной оси. Чтобы оправдать для себя эту сумму, изучите определение II размера 12{I}{}.
10,51 I=28,13 кг⋅м2+56,25 кг⋅м2=84,38 кг⋅м2I=28,13 кг⋅м2+56,25 кг⋅м2=84,38 кг⋅м2 размер 12{I=»28″ «.» «13»`»кг» «.» m rSup {размер 8{2}} +»56″ «.» «25»`»кг» «.» m rSup { размер 8{2} } =»84″ «.» «38»`»кг» «.» m rSup { размер 8{2} } } {}
Подстановка известных значений в уравнение для размера αα 12{α} {} дает
10,52 α=τI=375 Н⋅м84,38 кг⋅м2=4,44рад2.α=τI=375 Н⋅м84,38 кг⋅м2=4,44рад2. размер 12{α= {{τ} над {I} } = {{«375N» «.» м} более {«84» «.» «38кг» «.» m rSup {размер 8{2} } } } =4 «.» «44» { {«rad»} over {s rSup { size 8{2} } } } «.»} {}
Обсуждение
Угловое ускорение меньше, когда ребенок находится на карусели. круглый, чем когда карусель пуста, как и ожидалось. Найденные угловые ускорения довольно велики, отчасти из-за того, что трение считалось пренебрежимо малым. Если бы, например, отец продолжал толкать перпендикулярно в течение 2 с, он придал бы карусели угловую скорость 13,3 рад/с, когда она пуста, а только 8,89.рад/с, когда на нем находится ребенок. В пересчете на обороты в секунду эти угловые скорости составляют 2,12 об/с и 1,41 об/с соответственно. В первом случае отец будет бежать со скоростью около 50 км/ч. Летние Олимпийские игры, вот и он! Подтверждение этих цифр оставлено читателю в качестве упражнения.
В пересчете на обороты в секунду эти угловые скорости составляют 2,12 об/с и 1,41 об/с соответственно. В первом случае отец будет бежать со скоростью около 50 км/ч. Летние Олимпийские игры, вот и он! Подтверждение этих цифр оставлено читателю в качестве упражнения.
Создание соединений: воздействие нескольких сил на одну систему
Большой гончарный круг диаметром 60 см и массой 8 кг. Он приводится в действие двигателем мощностью 20 Н, воздействующим на внешний край. Также имеется тормоз, способный оказывать усилие 15 Н в радиусе 12 см от оси вращения, на нижней стороне.
Каково угловое ускорение при работе двигателя?
Крутящий момент находится по формуле τ = rF sin θ = (0,300 м)(20 Н) = 6 Н·мτ = rF sin θ = (0,300 м)(20 Н) = 6 Н·м.
Момент инерции рассчитывается как I = 12 MR2 = 12(8 кг)(0,300 м)2 = 0,36 кг⋅м2I = 12 MR2 = 12(8 кг)(0,300 м)2 = 0,36 кг⋅м2.
Таким образом, угловое ускорение будет
α = τI = 6 Н⋅м0,36 кг⋅м2 = 17 рад/с2α = τI = 6 Н⋅м0,36 кг⋅м2 = 17 рад/с2.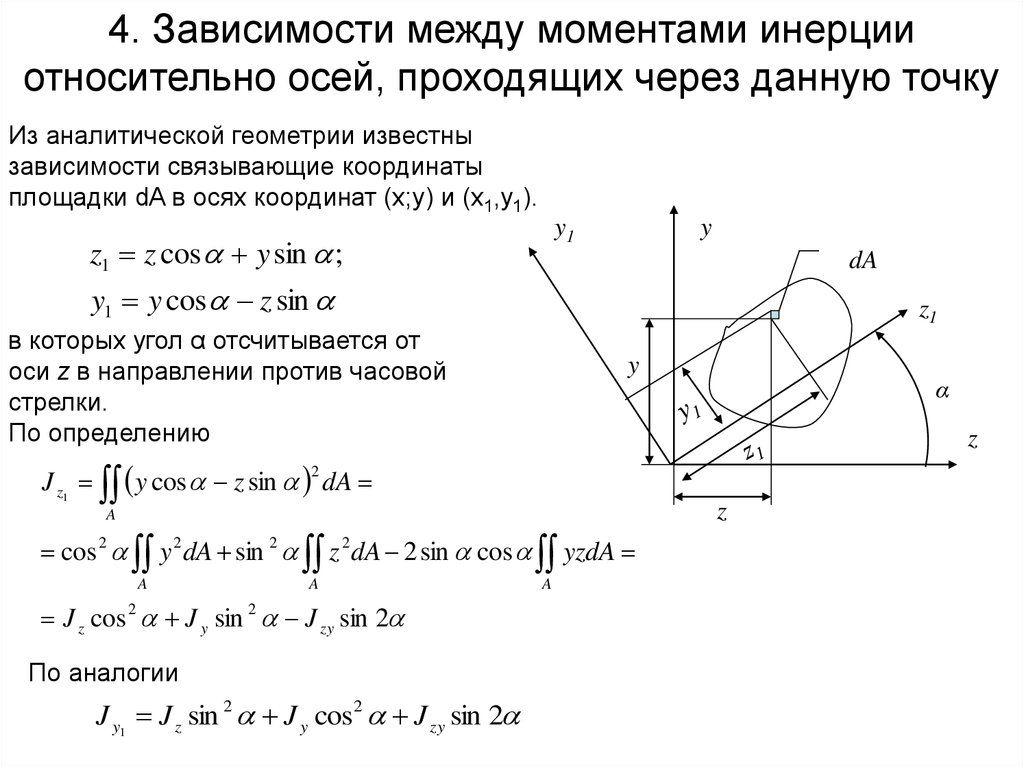
Обратите внимание, что трение всегда действует в направлении, противоположном вращению, происходящему в данный момент в этой системе. Если гончар ошибается и включает одновременно и тормоз, и двигатель, сила трения тормоза создаст крутящий момент, противоположный крутящему моменту двигателя.
Крутящий момент от тормоза τ = rF sin θ = (0,120 м)(15 Н) = 1,80 Н⋅мτ = rF sin θ = (0,120 м)(15 Н) = 1,80 Н.
Таким образом, чистый крутящий момент равен 6 Н·м – 1,80 Н·м = 4,20 Н·м. 6 Н·м – 1,80 Н·м = 4,20 Н·м..
А угловое ускорение равно α = τI = 4,20 Н⋅м0,36 кг⋅м2 = 12 рад/с2α = τI = 4,20 Н⋅м0,36 кг⋅м2 = 12 рад/с2.
Проверьте свое понимание
Крутящий момент является аналогом силы, а момент инерции является аналогом массы. Сила и масса — физические величины, зависящие только от одного фактора. Например, масса связана исключительно с количеством атомов различных типов в объекте. Являются ли крутящий момент и момент инерции такими же простыми?
Решение
Нет. Крутящий момент зависит от трех факторов: величины силы, направления силы и точки приложения. Момент инерции зависит как от массы, так и от ее распределения относительно оси вращения. Таким образом, хотя аналогии точны, эти величины вращения зависят от большего количества факторов.
Крутящий момент зависит от трех факторов: величины силы, направления силы и точки приложения. Момент инерции зависит как от массы, так и от ее распределения относительно оси вращения. Таким образом, хотя аналогии точны, эти величины вращения зависят от большего количества факторов.
- Печать
- Поделиться
Вращательная динамика (момент инерции и действие моментов)
ДОМАШНЯЯ МЕХАНИКА / НЬЮТОНОВА /
Центр удара
Движение (или отсутствие движения) точки подвеса предмета наблюдается при ударе по предмету.
Что он показывает
Центр удара (ЦУ) – это место на бите или ракетке, по которому можно ударить, не вызывая реакции в точке опоры. Когда мяч попадает в это место, контакт ощущается хорошо, и кажется, что мяч отскакивает с наибольшей скоростью, и поэтому это место часто называют сладкой точкой. В других местах, кроме этого места, бита или ракетка могут вибрировать или даже жалить ваши руки. Этот эксперимент показывает эффект, демонстрируя, что…
В других местах, кроме этого места, бита или ракетка могут вибрировать или даже жалить ваши руки. Этот эксперимент показывает эффект, демонстрируя, что…
Подробнее о Центре перкуссии
Катящийся вниз по склону
Что он показывает:
Объект, катящийся по склону, приобретает как поступательную, так и вращательную кинетическую энергию. При расчете скорости объекта у подножия холма необходимо учитывать кинетическую энергию вращения
…
Подробнее о Скатывание по склону
Йо-йо
Очень большая катушка с кабелем (или меньшая версия) может катиться в любом направлении или скользить в зависимости от угла натяжения; действие крутящего момента.
Что он показывает:
В зависимости от угла приложения силы йо-йо можно заставить катиться вперед, назад или просто скользить без вращения.
Как это работает:
Влияние угла силы показано на рисунке 1; а) и б) крайние случаи. Для (а) вертикальное натяжение струны создает крутящий момент r 1 F Вращение йо-йо против часовой стрелки. Потянув за веревку горизонтально, как в (b), вы создадите…
Подробнее о Йо-йо
Крутильный маятник
Определение момента инерции по измерениям периода.
Теннисная ракетка Flip
Что она показывает:
Простая и убедительная демонстрация теоремы о промежуточной оси. Рассмотрим объект (в данном случае теннисную ракетку) с тремя неравными главными моментами инерции. Если ракетку привести во вращение вокруг оси наибольшего или наименьшего момента и после этого на нее не действуют внешние крутящие моменты, результирующее движение будет устойчивым. Однако вращение вокруг оси промежуточного главного момента инерции неустойчиво — малейшее возмущение нарастает и ось вращения не остается близкой к начальной оси вращения.
Однако вращение вокруг оси промежуточного главного момента инерции неустойчиво — малейшее возмущение нарастает и ось вращения не остается близкой к начальной оси вращения.
Как это работает:…
Подробнее о Теннисная ракетка Flip
Хула Хуп Вращательная инерция
Что он показывает:
Подвешенный обруч имеет такой же период колебаний, как и маятник, длина которого равна диаметру обруча.
Как это работает:
Теорема о параллельных осях позволяет нам легко вывести инерцию вращения обруча вокруг оси, проходящей через его окружность и определяемой выражением 92\)
где M — масса кольца, а R — его радиус. Таким образом, период колебаний становится
\(T…
Подробнее о Хулахуп Вращательная инерция
Теорема о параллельных осях
Что он показывает:
Можно показать, что период колебаний объекта не меняется для разных точек подвеса, пока они находятся на одинаковом расстоянии от ЦМ. Это согласуется с тем, что теорема о параллельных осях говорит нам о моменте инерции объекта.
Это согласуется с тем, что теорема о параллельных осях говорит нам о моменте инерции объекта.
Как это работает:
Теория параллельных осей утверждает, что если \(I_{см}\) момент инерции объекта относительно оси, проходящей через его центр масс, то \(I\), момент инерции относительно любого ось параллельна этой…
Подробнее о теореме о параллельных осях
Падение быстрее, чем ‘g’
Что показывает:
Позвольте доске вращаться под действием силы тяжести, и свободный конец ускорится со скоростью более г . Связь между угловым ускорением и линейным ускорением, кажется, дает парадокс свободного падения.
Как это работает:
. ..
..
Подробнее о Falling Faster than ‘g’
Вращательная инерция – Физика BCIT 0312 Учебник
Глава 10 Вращательное движение и угловой момент
Резюме
- Поймите взаимосвязь между силой, массой и ускорением.
- Изучите вращающее действие силы.
- Изучите аналогию между силой и крутящим моментом, массой и моментом инерции, линейным ускорением и угловым ускорением.
Если вы когда-нибудь крутили велосипедное колесо или толкали карусель, вы знаете, что для изменения угловой скорости необходима сила, как показано на рис. 1. На самом деле ваша интуиция надежно предсказывает многие из задействованных факторов . Например, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; другое следствие состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, рассмотрим, что произойдет, если мы приложим силу[латекс]\boldsymbol{F}[/латекс]к точечной массе[латекс]\жирныйсимвол{м}[ /latex], который находится на расстоянии[latex]\boldsymbol{r}[/latex] от точки вращения, как показано на рисунке 2. Поскольку сила перпендикулярна [latex]\boldsymbol{r},[/latex] ускорение[латекс]\boldsymbol{a=\frac{F}{m}}[/latex]получено в направлении[латекс]\boldsymbol{F}.[/latex]Мы можем изменить это уравнение так, что[ латекс]\boldsymbol{F=ma}[/latex]а затем искать способы связать это выражение с выражениями для вращательных величин. Заметим, что [латекс]\boldsymbol{a=r\omega},[/latex]и подставим это выражение в [латекс]\boldsymbol{F=ma},[/latex]получив 92}[/latex]называется вращательная инерция или момент инерции точки массы[latex]\boldsymbol{m}[/latex]расстояние[latex]\boldsymbol{r}[/latex]от центр вращения.
Заметим, что [латекс]\boldsymbol{a=r\omega},[/latex]и подставим это выражение в [латекс]\boldsymbol{F=ma},[/latex]получив 92}[/latex]называется вращательная инерция или момент инерции точки массы[latex]\boldsymbol{m}[/latex]расстояние[latex]\boldsymbol{r}[/latex]от центр вращения.
СОЕДИНЕНИЕ: ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Динамика вращательного движения полностью аналогична линейной или поступательной динамике. Динамика занимается силой и массой и их влиянием на движение. Для вращательного движения мы найдем прямые аналоги силы и массы, которые ведут себя именно так, как мы и ожидали, исходя из нашего предыдущего опыта.
Прежде чем мы сможем рассмотреть вращение чего-либо, кроме точечной массы, подобной той, что изображена на рис. 2, мы должны распространить идею инерции вращения на все типы объектов. Чтобы расширить наше понятие инерции вращения, мы определяем 92},[/latex],где[латекс]\boldsymbol{M}[/латекс]это его общая масса, а[латекс]\boldsymbol{R}[/латекс]его радиус. (Мы используем [латекс]\boldsymbol{M}[/латекс]и[латекс]\жирныйсимвол{R}[/латекс]для всего объекта, чтобы отличить их от [латекс]\жирныйсимвол{м}[/латекс]и[ латекс]\boldsymbol{r}[/латекс] для точечных масс.) Во всех остальных случаях мы должны обращаться к рисунку 3 (обратите внимание, что таблица представляет собой произведение искусства, в котором есть формы, а также формулы) для формул для [латекс]\ полужирный символ{I}[/latex], которые были получены в результате интегрирования по непрерывному телу. Обратите внимание, что [latex]\boldsymbol{I}[/latex] имеет единицы массы, умноженные на квадрат расстояния ([latex]\boldsymbol{\textbf{kg}\cdotp\textbf{m}^2}[/latex]), как мы могли бы ожидать от его определения.
Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением составляет
.[латекс] \boldsymbol{\textbf{net}\tau=I\alpha}[/латекс]
или
[латекс]\boldsymbol{\alpha\:=}[/латекс][латекс]\boldsymbol{\frac{\textbf{net}\tau}{I}},[/latex]
, где net[latex]\boldsymbol{\tau}[/latex] — общий крутящий момент от всех сил относительно выбранной оси. Для простоты мы будем рассматривать только крутящие моменты, создаваемые силами в плоскости вращения. Такие крутящие моменты бывают положительными или отрицательными и складываются как обычные числа. Соотношение в [латекс]\boldsymbol{\tau=I\alpha},\:\boldsymbol{\alpha=\frac{\textbf{net}\tau}{I}}[/latex] является аналогом вращения Ньютона. второй закон и очень широко применимы. Это уравнение действительно справедливо для любой крутящий момент, примененный к любому объекту относительно любой оси .
Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение. Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением заключается в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от его распределение массы относительно оси, вокруг которой он вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю. Масса одинакова в обоих случаях; но момент инерции намного больше, когда дети находятся на краю.
Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением заключается в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от его распределение массы относительно оси, вокруг которой он вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю. Масса одинакова в обоих случаях; но момент инерции намного больше, когда дети находятся на краю.
ЭКСПЕРИМЕНТ ДЛЯ ДОМА
Вырежьте круг радиусом около 10 см из плотного картона. Рядом с краем круга напишите числа от 1 до 12, как часы на циферблате. Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси, проходящей через его центр, как колесо.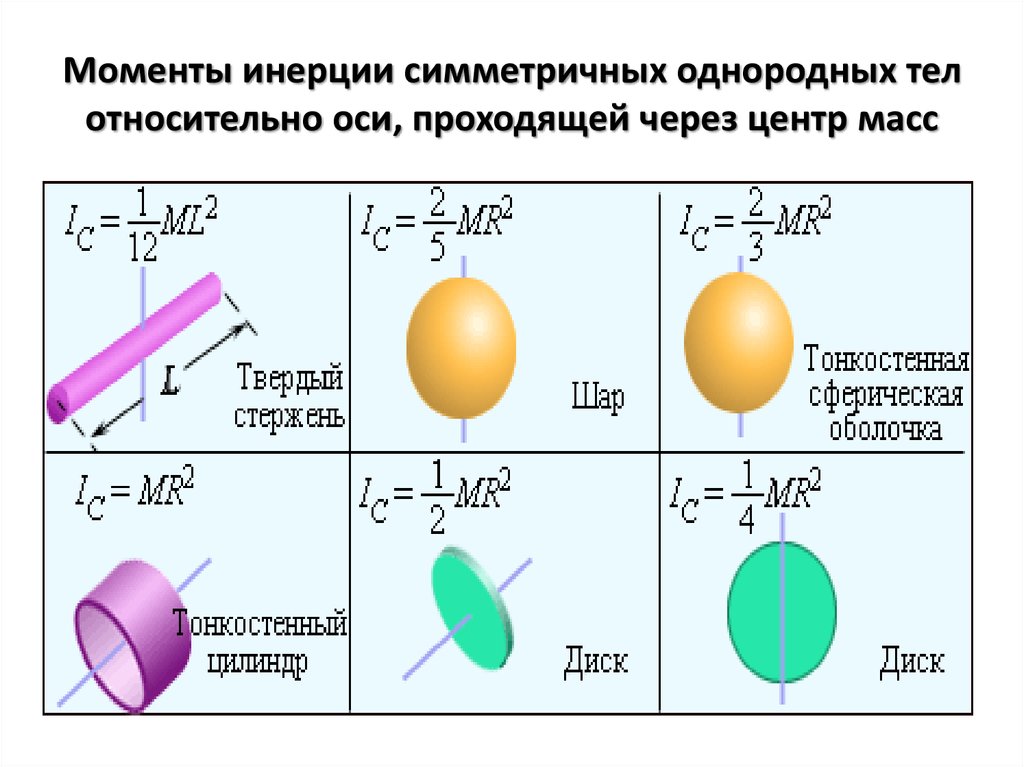 (Вы можете свободно прибить круг к стене.) Держите круг неподвижно и, расположив цифру 12 вверху, прикрепите кусок синей замазки (клейкий материал, используемый для крепления постеров к стенам) к цифре 3. Какого размера глыба должна быть, чтобы просто вращать круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое под номером 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
(Вы можете свободно прибить круг к стене.) Держите круг неподвижно и, расположив цифру 12 вверху, прикрепите кусок синей замазки (клейкий материал, используемый для крепления постеров к стенам) к цифре 3. Какого размера глыба должна быть, чтобы просто вращать круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое под номером 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
СТРАТЕГИЯ РЕШЕНИЯ ЗАДАЧ ДЛЯ ДИНАМИКИ ВРАЩЕНИЯ
- Изучите ситуацию, чтобы определить, что крутящий момент и масса участвуют во вращении . Нарисуйте тщательный набросок ситуации.
- Определить интересующую систему .
- Нарисуйте диаграмму свободного тела . То есть нарисуйте и обозначьте все внешние силы, действующие на интересующую вас систему.
- Применить [латекс]\boldsymbol{\textbf{net}\tau=I\alpha},\:\boldsymbol{\alpha=\frac{\textbf{net}\tau}{I}},[/latex ] вращательный эквивалент второго закона Ньютона для решения задачи .
 Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.
Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения. - Как всегда, проверьте решение, чтобы убедиться, что оно разумно .
ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ
В статике чистый крутящий момент равен нулю, а угловое ускорение отсутствует. При вращательном движении чистый крутящий момент является причиной углового ускорения, точно так же, как во втором законе движения Ньютона для вращения.
Рисунок 3. Некоторые инерции вращения.Пример 1. Расчет влияния распределения массы на карусель
Рассмотрим отца, толкающего игровую карусель на рис. 4. Он прикладывает силу 250 Н к краю карусели весом 50,0 кг. круговой, который имеет радиус 1,50 м. Вычислите угловое ускорение, создаваемое (а), когда на карусели никого нет, и (б), когда ребенок массой 18,0 кг сидит на расстоянии 1,25 м от центра. Считайте саму карусель однородным диском с пренебрежимо малым тормозящим трением.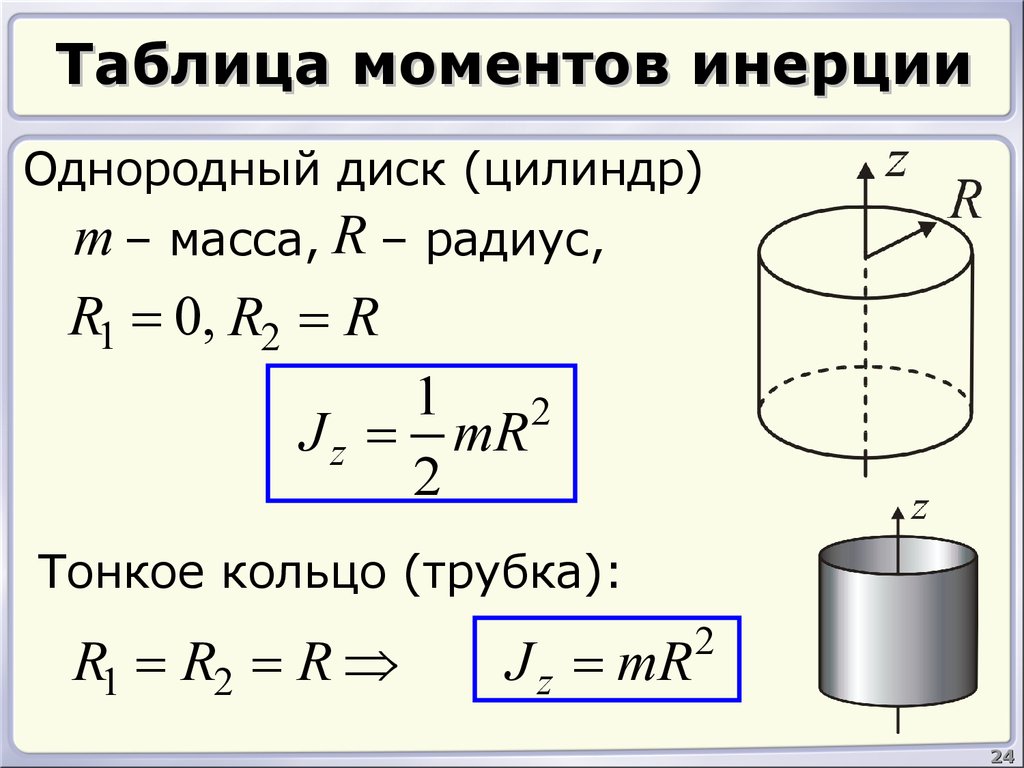
Стратегия
Угловое ускорение задается непосредственно выражением [латекс]\boldsymbol{\alpha=\frac{\textbf{net}\tau}{I}}:[/latex]
[латекс]\boldsymbol {\alpha\:=}[/latex][latex]\boldsymbol{\frac{\tau}{I}}.[/latex]
Чтобы найти [латекс]\boldsymbol{\alpha},[/latex ] мы должны сначала вычислить крутящий момент[латекс]\boldsymbol{\tau}[/латекс](который одинаков в обоих случаях) и момент инерции[латекс]\жирныйсимвол{I}[/латекс](который больше в второй случай). Чтобы найти крутящий момент, заметим, что приложенная сила перпендикулярна радиусу, а трением можно пренебречь, так что 92}}.[/latex]
Решение для (b)
Мы ожидаем, что угловое ускорение системы будет меньше в этой части, потому что момент инерции больше, когда ребенок находится на карусели -круглый. Чтобы найти общий момент инерции[latex]\boldsymbol{I},[/latex]мы сначала находим момент инерции ребенка[latex]\boldsymbol{I _{\textbf{c}}}[/latex], рассматривая ребенок должен быть эквивалентен точечной массе на расстоянии 1,25 м от оси. 2}.[/латекс] 92}}.[/latex]
2}.[/латекс] 92}}.[/latex]
Обсуждение
Угловое ускорение меньше, когда ребенок находится на карусели, чем когда карусель пуста, как и ожидалось. Найденные угловые ускорения довольно велики, отчасти из-за того, что трение считалось пренебрежимо малым. Если, например, отец продолжал толкать перпендикулярно в течение 2,00 с, он придал бы карусели угловую скорость 13,3 рад/с, когда она пуста, и только 8,89 рад/с, когда на ней находится ребенок. В пересчете на обороты в секунду эти угловые скорости составляют 2,12 об/с и 1,41 об/с соответственно. В первом случае отец будет бежать со скоростью около 50 км/ч. Летние Олимпийские игры, вот и он! Подтверждение этих цифр оставлено читателю в качестве упражнения.
- Чем дальше приложена сила от оси вращения, тем больше угловое ускорение; угловое ускорение обратно пропорционально массе.
- Если мы воздействуем силой[латекс]\boldsymbol{F}[/латекс] на точечную массу[латекс]\boldsymbol{m}[/латекс], находящуюся на расстоянии[латекс]\жирныйсимвол{r}[/латекс ]от точки вращения и поскольку сила перпендикулярна[латекс]\boldsymbol{r},[/латекс]ускорение[латекс]\boldsymbol{a = F/m}[/латекс]получается в направлении[ латекс]\boldsymbol{F}.
 [/latex]Мы можем изменить это уравнение так, что
[/latex]Мы можем изменить это уравнение так, что[латекс]\boldsymbol{F = ma},[/латекс]
, а затем искать способы связать это выражение с выражениями для вращательных величин. Заметим, что [latex]\boldsymbol{a = r\alpha},[/latex]и подставим это выражение в [latex]\boldsymbol{F=ma},[/latex]получив
[латекс]\boldsymbol{F=г-н\альфа}[/латекс]
- Крутящий момент — это вращающая способность силы. В этом случае, поскольку [латекс]\boldsymbol{F}[/latex]перпендикулярен [латексу]\boldsymbol{r},[/latex]крутящий момент равен просто [латекс]\boldsymbol{\tau=rF}.[/ латекс] Если мы умножим обе части приведенного выше уравнения на [латекс]\boldsymbol{r},[/латекс] мы получим крутящий момент в левой части. То есть, 92}.[/латекс]
- Общая взаимосвязь между крутящим моментом, моментом инерции и угловым ускорением такова:
[латекс]\boldsymbol{\tau=I\alpha}[/латекс]
или
[латекс]\boldsymbol{\alpha=}[/латекс][латекс]\boldsymbol{\frac{\textbf{net}\tau}{I}}[/latex]
- крутящий момент
- поворотная эффективность силы
- инерция вращения
- сопротивление изменению вращения.
 Чем больше инерция вращения у объекта, тем труднее его вращать 92}[/latex]и, поскольку любой объект может быть построен из набора точечных масс, это соотношение является основой для всех других моментов инерции
Чем больше инерция вращения у объекта, тем труднее его вращать 92}[/latex]и, поскольку любой объект может быть построен из набора точечных масс, это соотношение является основой для всех других моментов инерции
Динамика вращательного движения: инерция вращения | Физика |
Цели обучения
К концу этого раздела вы сможете:
- Понимать взаимосвязь между силой, массой и ускорением.
- Изучите поворотный эффект силы.
- Изучите аналогию между силой и крутящим моментом, массой и моментом инерции, линейным ускорением и угловым ускорением.
Если вы когда-либо крутили велосипедное колесо или толкали карусель, вы знаете, что для изменения угловой скорости необходима сила, как показано на рис. 1. На самом деле ваша интуиция надежно предсказывает многие задействованные факторы. Например, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям.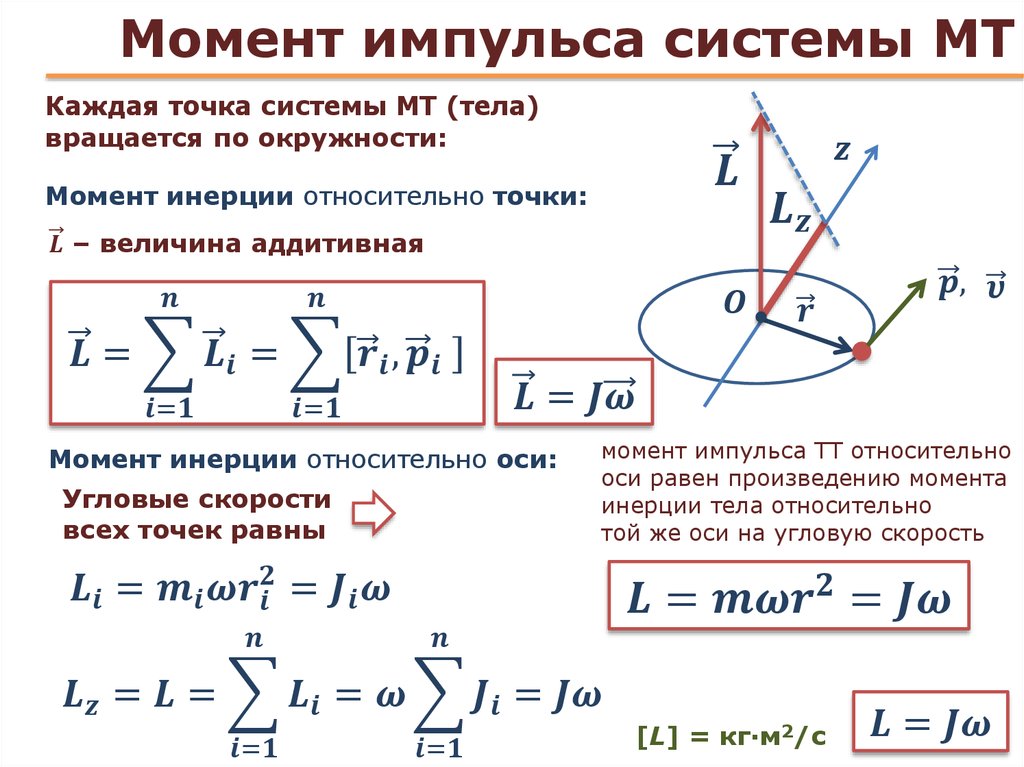 Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; другое следствие состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; другое следствие состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
Рисунок 1. Для вращения велосипедного колеса требуется сила. Чем больше сила, тем больше угловое ускорение. Чем массивнее колесо, тем меньше угловое ускорение. Если надавить на спицу ближе к оси, угловое ускорение будет меньше.
Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, рассмотрим, что произойдет, если мы приложим силу F к точке массой м , которая находится на расстоянии r от точки вращения, как показано на рисунке 2.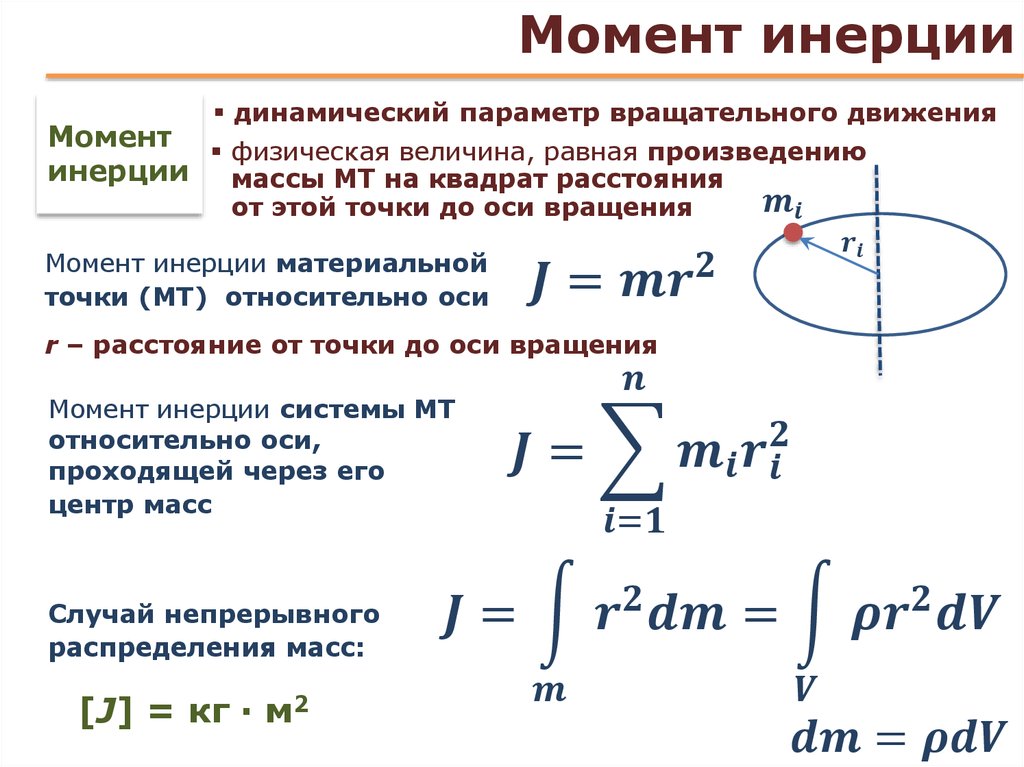 Поскольку сила перпендикулярна r , ускорение
Поскольку сила перпендикулярна r , ускорение
a=Fma=\frac{F}{m}a=mF
получено в направление F . Мы можем изменить это уравнение так, что F = ma , а затем искать способы связать это выражение с выражениями для вращательных величин. Заметим, что a = rα , и подставим это выражение в F = мА , что дает
F = мра
Напомним, что крутящий момент — это вращающая эффективность силы. В этом случае, поскольку F перпендикулярна r , крутящий момент равен просто τ = Fr . Итак, если мы умножим обе части приведенного выше уравнения на r , мы получим крутящий момент в левой части. То есть
рФ = мр 2 α
или
τ = mr 2 α .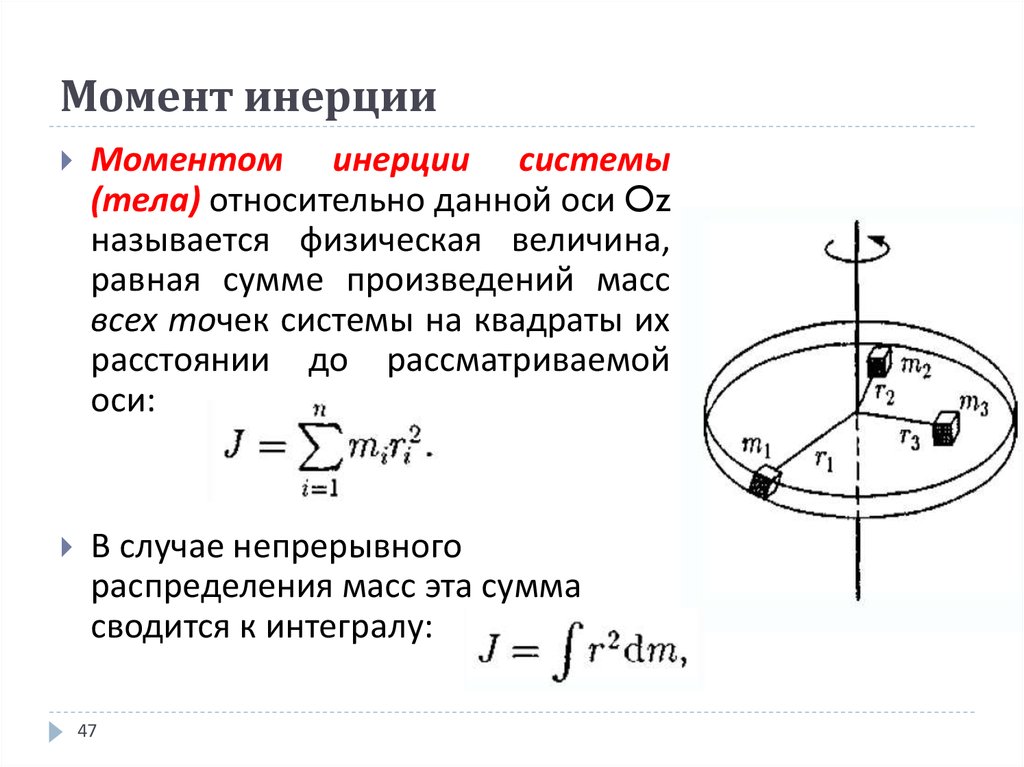
Это последнее уравнение является вращательным аналогом второго закона Ньютона ( F = ma ), где крутящий момент аналогичен силе, угловое ускорение аналогично поступательному ускорению, а mr 2 аналогично массе (или инерции). Величина mr 2 называется вращательной инерцией или моментом инерции точки массой м расстоянием r от центра вращения.
Рис. 2. Объект поддерживается горизонтальным столом без трения и прикреплен к точке поворота шнуром, создающим центростремительную силу. Сила F приложена к объекту перпендикулярно радиусу r , заставляя его ускоряться относительно точки поворота. Сила удерживается перпендикулярно р.
Создание соединений: динамика вращательного движения Динамика вращательного движения полностью аналогична линейной или поступательной динамике. {2}I=∑mr2
{2}I=∑mr2
. Здесь I аналогично m в поступательном движении. Из-за расстояния r момент инерции любого объекта зависит от выбранной оси. На самом деле вычисление I выходит за рамки этого текста, за исключением одного простого случая — обруча, вся масса которого находится на одном и том же расстоянии от его оси. Таким образом, момент инерции кольца вокруг его оси равен MR 2 , где M — его полная масса, а R его радиус. (Мы используем M и R для всего объекта, чтобы отличить их от m и r для точечных масс.) Во всех других случаях мы должны обращаться к рисунку 3 (обратите внимание, что таблица представляет собой произведение искусства, которое имеет формы, а также формулы) для формул для I , которые были получены путем интегрирования по непрерывному телу. Обратите внимание, что I имеет единицы массы, умноженные на квадрат расстояния (кг⋅м 2 ), как и следовало ожидать из его определения.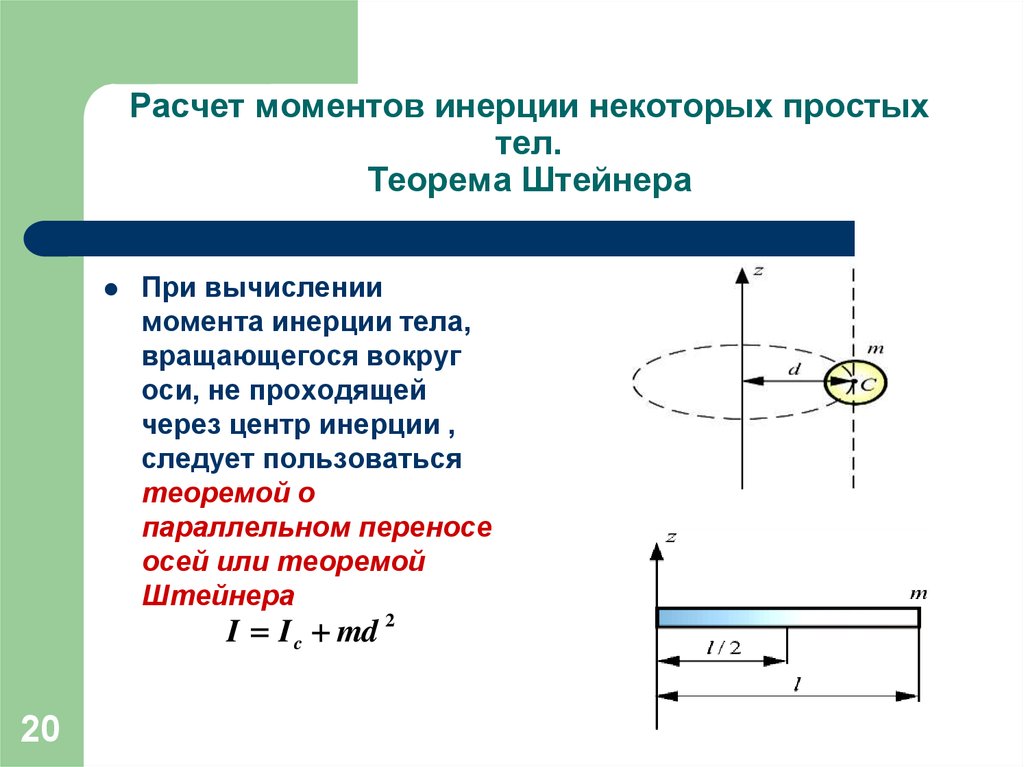
Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением:
net τ = Iα
или
α=netτI\alpha =\frac{net{\tau}}{I}α=Inetτ
где net τ — суммарный крутящий момент от всех сил относительно выбранной оси. Для простоты мы будем рассматривать только крутящие моменты, создаваемые силами в плоскости вращения. Такие крутящие моменты бывают положительными или отрицательными и складываются как обычные числа. Отношение в сети τ = Iα,
α=netτI\alpha =\frac{\text{net}{\tau}}{I}α=Inetτ
является аналогом второго закона Ньютона для вращения и применяется очень широко. Это уравнение действительно справедливо для любого крутящего момента, примененного к любому объекту относительно любой оси .
Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение. Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением заключается в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от его распределение массы относительно оси, вокруг которой он вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю. Масса одинакова в обоих случаях; но момент инерции намного больше, когда дети находятся на краю.
Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением заключается в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от его распределение массы относительно оси, вокруг которой он вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю. Масса одинакова в обоих случаях; но момент инерции намного больше, когда дети находятся на краю.
Вырежьте круг радиусом около 10 см из плотного картона. Рядом с краем круга напишите числа от 1 до 12, как часы на циферблате. Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси, проходящей через его центр, как колесо. (Вы можете свободно прибить круг к стене.) Держите круг неподвижно и, расположив цифру 12 вверху, прикрепите кусок синей замазки (клейкий материал, используемый для крепления постеров к стенам) к цифре 3. Какого размера глыба должна быть, чтобы просто вращать круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое под номером 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
(Вы можете свободно прибить круг к стене.) Держите круг неподвижно и, расположив цифру 12 вверху, прикрепите кусок синей замазки (клейкий материал, используемый для крепления постеров к стенам) к цифре 3. Какого размера глыба должна быть, чтобы просто вращать круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое под номером 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
Стратегия решения задач по динамике вращения
- Изучите ситуацию, чтобы определить, что крутящий момент и масса участвуют во вращении . Нарисуйте тщательный набросок ситуации.
- Определить интересующую систему .
- Нарисуйте диаграмму свободного тела . То есть нарисуйте и обозначьте все внешние силы, действующие на интересующую вас систему.
- Применить net τ = Iα, α = net τI, вращательный эквивалент второго закона Ньютона, для решения задачи .
 Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.
Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения. - Как всегда, проверьте решение, чтобы убедиться, что оно разумно .
В статике чистый крутящий момент равен нулю, а угловое ускорение отсутствует. При вращательном движении чистый крутящий момент является причиной углового ускорения, точно так же, как во втором законе движения Ньютона для вращения.
Рис. 3. Некоторые инерции вращения.
Пример 1. Расчет влияния распределения массы на карусель
Рассмотрим отца, толкающего игровую карусель на рис. 4. Он прикладывает силу 250 Н к краю карусели весом 50,0 кг, которая имеет радиус 1,50 м. Вычислите угловое ускорение, создаваемое (а), когда на карусели никого нет, и (б), когда ребенок массой 18,0 кг сидит на расстоянии 1,25 м от центра. Считайте саму карусель однородным диском с пренебрежимо малым тормозящим трением.
Считайте саму карусель однородным диском с пренебрежимо малым тормозящим трением.
Рис. 4. Отец толкает игровую карусель за ее край и перпендикулярно ее радиусу для достижения максимального крутящего момента.
СтратегияУгловое ускорение задается непосредственно выражением {I}α=Iτ
Чтобы найти α , мы должны сначала вычислить крутящий момент τ (одинаковый в обоих случаях) и момент инерции 9{2}}α=Iτ=56,25 кг⋅ м2375 Н⋅ м=6,67 с2рад
.
Решение для (b) Мы ожидаем, что угловое ускорение системы будет меньше в этой части, потому что момент инерции больше, когда ребенок находится на карусели. Чтобы найти полный момент инерции I , сначала найдем момент инерции ребенка I c , считая ребенка эквивалентным точечной массе на расстоянии 1,25 м от оси. Затем
Затем
I c = MR 2 = (18,0 кг)(1,25 м) 2 = 28,13 кг ⋅ м 2 .
Суммарный момент инерции равен сумме моментов инерции карусели и ребенка (относительно одной оси). Чтобы оправдать эту сумму для себя, рассмотрите определение I :
I = 28,13 кг ⋅ м 2 + 56,25 кг ⋅ м 2 = 84,38 кг ⋅ м
5 2 .
Подставляя известные значения в уравнение для 9{2}}α=Iτ=84,38 кг⋅м2375 Н⋅м=4,44с2рад
.
Обсуждение Как и ожидалось, угловое ускорение меньше, когда ребенок находится на карусели, чем когда карусель пуста. Найденные угловые ускорения довольно велики, отчасти из-за того, что трение считалось пренебрежимо малым. Если, например, отец продолжал толкать перпендикулярно в течение 2,00 с, он придал бы карусели угловую скорость 13,3 рад/с, когда она пуста, но только 8,89. рад/с, когда на нем находится ребенок. В пересчете на обороты в секунду эти угловые скорости составляют 2,12 об/с и 1,41 об/с соответственно. В первом случае отец будет бежать со скоростью около 50 км/ч. Летние Олимпийские игры, вот и он! Подтверждение этих цифр оставлено читателю в качестве упражнения.
рад/с, когда на нем находится ребенок. В пересчете на обороты в секунду эти угловые скорости составляют 2,12 об/с и 1,41 об/с соответственно. В первом случае отец будет бежать со скоростью около 50 км/ч. Летние Олимпийские игры, вот и он! Подтверждение этих цифр оставлено читателю в качестве упражнения.
Проверьте свое понимание
Крутящий момент является аналогом силы, а момент инерции — аналогом массы. Сила и масса — физические величины, зависящие только от одного фактора. Например, масса связана исключительно с количеством атомов различных типов в объекте. Являются ли крутящий момент и момент инерции такими же простыми?
Решение Нет. Крутящий момент зависит от трех факторов: величины силы, направления силы и точки приложения. Момент инерции зависит как от массы, так и от ее распределения относительно оси вращения. Таким образом, хотя аналогии точны, эти величины вращения зависят от большего количества факторов.
Резюме раздела
- Крутящий момент — это вращающая способность силы. В этом случае, поскольку F перпендикулярна r , крутящий момент равен просто τ = rF Если мы умножим обе части приведенного выше уравнения на r , мы получим крутящий момент в левой части. То есть
rF = mr 2 α
или
τ = мр 2 α .
Концептуальные вопросы
1. Момент инерции длинного стержня, вращающегося вокруг оси через один конец, перпендикулярный его длине, равен ML 2 /3. Почему этот момент инерции больше, чем если бы вы вращали точечную массу 9?0033 M в месте расположения центра масс стержня (у L /2)? (Это будет ML 2 /4.)
2. Почему момент инерции обруча с массой M и радиусом R больше момента инерции диска, имеет ту же массу и радиус? Почему момент инерции сферической оболочки с массой M и радиусом R больше, чем у твердого шара той же массы и радиуса?
3. Приведите пример, в котором малая сила вызывает большой крутящий момент. Приведите другой пример, в котором большая сила действует на малый крутящий момент.
Приведите пример, в котором малая сила вызывает большой крутящий момент. Приведите другой пример, в котором большая сила действует на малый крутящий момент.
4. При уменьшении массы гоночного велосипеда наибольшая выгода достигается за счет уменьшения массы шин и колесных дисков. Почему это позволяет гонщику достичь большего ускорения, чем такое же уменьшение массы рамы велосипеда?
Рис. 5.
5. Шарик скользит по пандусу без трения. Затем его катят без проскальзывания и с той же начальной скоростью вверх по другому пандусу без трения (с тем же углом наклона). В каком случае она достигает большей высоты и почему?
Задачи и упражнения
1. В этой задаче рассматриваются дополнительные аспекты Примера 1: Расчет влияния распределения массы на карусель. а) Сколько времени потребуется отцу, чтобы придать карусели угловую скорость 1,50 рад/с? б) Сколько оборотов он должен совершить, чтобы развить эту скорость? в) Если он приложит тормозящую силу 300 Н в радиусе 1,35 м, сколько времени потребуется ему, чтобы остановить их?
2.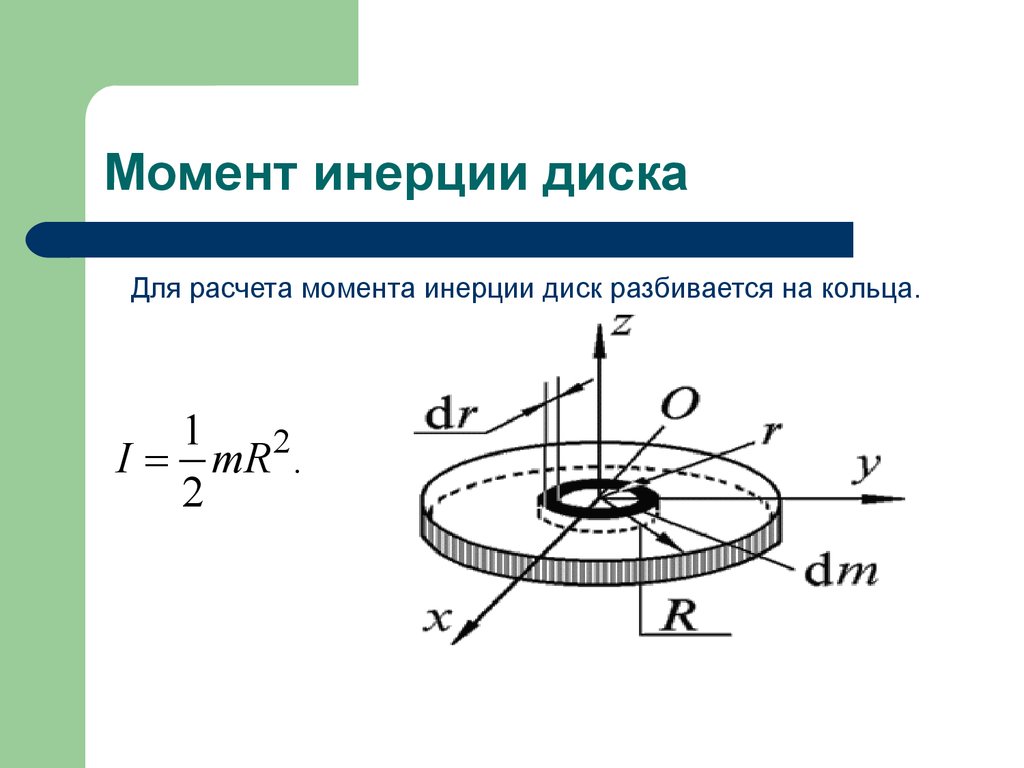 Рассчитайте момент инерции конькобежца, зная следующую информацию. (a) Фигурист весом 60,0 кг аппроксимирован цилиндром с радиусом 0,110 м. (b) Фигурист с вытянутыми руками примерно представляет собой цилиндр весом 52,5 кг, радиусом 0,110 м и двумя 0,9Плечи длиной 00 м, каждая массой 3,75 кг, выходят прямо из цилиндра, как стержни, вращающиеся вокруг своих концов.
Рассчитайте момент инерции конькобежца, зная следующую информацию. (a) Фигурист весом 60,0 кг аппроксимирован цилиндром с радиусом 0,110 м. (b) Фигурист с вытянутыми руками примерно представляет собой цилиндр весом 52,5 кг, радиусом 0,110 м и двумя 0,9Плечи длиной 00 м, каждая массой 3,75 кг, выходят прямо из цилиндра, как стержни, вращающиеся вокруг своих концов.
3. Трехглавая мышца задней поверхности плеча разгибает предплечье. Эта мышца у профессионального боксера действует с силой 2,00 × 10 3 Н с эффективным перпендикулярным плечом рычага 3,00 см, создавая угловое ускорение предплечья 120 рад/с 2 . Каков момент инерции предплечья боксера?
4. Футболист вытягивает голень в ударном движении, прилагая усилие мышцей над коленом впереди ноги. Она производит угловое ускорение 30,00 рад/с 9{2}0,750 кг⋅м2
Какова сила, действующая на мышцу, если ее эффективное перпендикулярное плечо рычага равно 1,90 см?
5. Предположим, вы прикладываете силу 180 Н по касательной к точильному камню массой 75,0 кг (сплошной диск) радиусом 0,280 м. а) Какой крутящий момент приложен? б) Чему равно угловое ускорение при пренебрежимо малом противодействии трения? в) Чему равно угловое ускорение, если на расстоянии 1,50 см от оси действует противодействующая сила трения 20,0 Н?
Предположим, вы прикладываете силу 180 Н по касательной к точильному камню массой 75,0 кг (сплошной диск) радиусом 0,280 м. а) Какой крутящий момент приложен? б) Чему равно угловое ускорение при пренебрежимо малом противодействии трения? в) Чему равно угловое ускорение, если на расстоянии 1,50 см от оси действует противодействующая сила трения 20,0 Н?
6. Рассмотрим колесо мотоцикла массой 12,0 кг, показанное на рис. 6. Предположим, что оно приблизительно представляет собой кольцевое кольцо с внутренним радиусом 0,280 м и внешним радиусом 0,330 м. Мотоцикл стоит на центральной подножке, так что колесо может свободно вращаться. а) Если приводная цепь действует с силой 2200 Н на радиусе 5,00 см, чему равно угловое ускорение колеса? б) Каково тангенциальное ускорение точки на внешней кромке шины? в) Через какое время, начиная с состояния покоя, достигается угловая скорость 80,0 рад/с?
Рис. 6. Момент инерции колеса мотоцикла примерно равен моменту инерции кольцевого кольца.
7. Зорх, заклятый враг Супермена, решает замедлить вращение Земли до одного раза в 28,0 часов, применяя противодействующую силу на экваторе и параллельно ему. Супермена это не сразу беспокоит, потому что он знает, что Зорч может приложить силу только 4,00 × 10 7 Н (немного больше, чем тяга ракеты Сатурн V). Как долго Зорх должен давить этой силой, чтобы достичь своей цели? (Этот период дает Супермену время, которое он может посвятить другим злодеям.) Четко покажите, как вы следуете шагам, приведенным в0033 Стратегия решения задач по динамике вращения , раздел (выше).
8. Автомобильный двигатель может развивать крутящий момент 200 Н∙м. Рассчитайте угловое ускорение, возникающее, если 95,0% этого крутящего момента приложено к приводному валу, оси и задним колесам автомобиля, учитывая следующую информацию. Автомобиль подвешен так, что колеса могут свободно вращаться. Каждое колесо действует как диск массой 15,0 кг с радиусом 0,180 м. Стенки каждой шины действуют как кольцевое кольцо массой 2,00 кг с внутренним радиусом 0,180 м и внешним радиусом 0,320 м. Протектор каждой шины действует как обруч весом 10,0 кг и радиусом 0,330 м. Ось весом 14,0 кг действует как стержень с радиусом 2,00 см. Приводной вал весом 30,0 кг действует как стержень с радиусом 3,20 см. 9{2}0,050 кг⋅м2
Протектор каждой шины действует как обруч весом 10,0 кг и радиусом 0,330 м. Ось весом 14,0 кг действует как стержень с радиусом 2,00 см. Приводной вал весом 30,0 кг действует как стержень с радиусом 3,20 см. 9{2}0,050 кг⋅м2
. а) Сколько времени потребуется ей, чтобы точно повернуть вспять? б) Что неразумного в результате? (c) Какие посылки являются неразумными или непоследовательными?
11. Необоснованные результаты В рекламе утверждается, что 800-килограммовому автомобилю помогает его 20,0-килограммовый маховик, который может разогнать автомобиль из состояния покоя до скорости 30,0 м/с. Маховик представляет собой диск радиусом 0,150 м. (a) Рассчитайте угловую скорость, которую должен иметь маховик, если 95,0 % энергии его вращения используется для разгона автомобиля. б) Что неразумного в результате? (c) Какая посылка неразумна или какая посылка несовместима?
Глоссарий
- крутящий момент:
- поворотная эффективность силы
- инерция вращения:
- сопротивление изменению вращения.
 Чем больше инерция вращения у объекта, тем труднее его вращать
Чем больше инерция вращения у объекта, тем труднее его вращать
- момент инерции:
- масса, умноженная на квадрат перпендикулярного расстояния от оси вращения; для точечной массы это I = mr 2 и, поскольку любой объект может быть построен из набора точечных масс, это соотношение является основой для всех других моментов инерции 9{2}\end{array}
10. (a) 2,0 мс (b) Слишком короткий временной интервал. в) момент инерции слишком мал, на один-два порядка. Крутящий момент
500 Н⋅м\text{500 Н}\cdot \text{м}500 Н⋅м
является разумным.
11. (а) 17 500 об/мин (б) Эта угловая скорость очень высока для диска такого размера и массы. Радиальное ускорение на краю диска > 50 000 g. (c) Масса и радиус маховика должны быть намного больше, что позволяет снизить скорость вращения (угловую скорость).
Лицензии и ссылки
Контент по лицензии CC, совместно используемый ранее
- College Physics.
 Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Находится в лицензии
Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Находится в лицензии
Преобразование тензора инерции
Angular Momentum of a Rigid Body Rotation Tensor of the 2nd Rank Translation Момент количества движения твердого тела
Как показано в [6] в Inertis Тензор, угловой момент твердого тела, вращающегося вокруг оси, проходящей через начало локальной системы отсчета (кадр А ) это
[1]
Теперь давайте преобразуем этот вектор углового момента в другой опорный кадр (кадр B ):
[2]
Комбинация [1] и [2] приводит к
[3]
Топ
Вращение
[3] показывает, что угловой момент объект, описанный в кадре B , равен I ‘, умноженному на угловой скорость описана в кадре B .
 Преобразование оси не меняет характер
любой механической величины, но описывает ее в иной перспективе. Поскольку оба
угловой момент и векторы угловой скорости уже описаны в кадре B , I ‘ должен быть тензором инерции объекта, описанного в кадре Б :
Преобразование оси не меняет характер
любой механической величины, но описывает ее в иной перспективе. Поскольку оба
угловой момент и векторы угловой скорости уже описаны в кадре B , I ‘ должен быть тензором инерции объекта, описанного в кадре Б :[4]
Этот тип преобразования называется подобием трансформация .
Теперь пусть A будет локальной системой отсчета (кадр L ) а B — глобальная (инерциальная) система отсчета. Тогда тензор инерции сегмента тела описано в глобальных координатах
[5]
При анализе движения можно вычислить матрицу преобразования из глобальный кадр в сегментный опорный кадр на основе данных маркера, в то время как тензор инерции обычно сначала описывается в соответствующем сегментном справочнике.
 Рамка. [5] можно использовать для вычисления тензора инерции
описывается в глобальном фрейме.
Рамка. [5] можно использовать для вычисления тензора инерции
описывается в глобальном фрейме.Топ
Тензор 2 ранга
Из [4]:
[6]
, где i , j , k и m = от 1 до 3. Или упрощая [6], можно получить
[7]
[7] идентичен [8] в Inertia Tensor. [7] — требование тензора 2-го ранга. Скаляр — это тензор или нулевой ранг, а вектор является тензором 1-го ранга.
Топ
Перевод
На рис. 1 показаны два системы отсчета: система OXYZ и система O’X’Y’Z’ . XYZ система — это локальная система отсчета, прикрепленная к телу с началом в центре тела.
 массы (см). С другой стороны, система X’Y’Z’ параллельна системе XYZ .
системы различного происхождения. Из [4] Тензора инерции тензор инерции тела
о X’Y’Z’ система
массы (см). С другой стороны, система X’Y’Z’ параллельна системе XYZ .
системы различного происхождения. Из [4] Тензора инерции тензор инерции тела
о X’Y’Z’ системаРисунок 1
[ 8]
Теперь пусть
[9]
и, следовательно,
[10]
Подстановка [10] в [8] дает
[11]
с
[12]
где м = масса тела. [12] в основном означает сумму первых моментов масс относительно ЦМ тела всегда равен 0.
 С [11], [8]
уменьшается до
С [11], [8]
уменьшается до[13]
где
[14]
I CM – тензор инерции тело о своем СМ пока I t дополнительный МВД из-за смещения системы отсчета. Матрица 1 показана в [14] является единичной матрицей, все диагональные элементы которой равны 1, а недиагональные элементы равны 0,
Как показано в [13], момент инерции объекта относительно системы отсчета, параллельной локальная система отсчета, закрепленная на теле, равна сумме тензора инерции тело и дополнительный MOI из-за перевода начала кадра.
Вот пример. Пусть
[15]
где I xx , I yy & я зз = главные моменты инерции тела.
 Другими словами, X , Y Оси Z , показанные на рисунке 1, являются главными осями. См. Основные оси для
детали главных моментов инерции и осей. Если Z ‘ ось, показанная на рисунке 1, является осью вращения
или:
Другими словами, X , Y Оси Z , показанные на рисунке 1, являются главными осями. См. Основные оси для
детали главных моментов инерции и осей. Если Z ‘ ось, показанная на рисунке 1, является осью вращения
или:[16]
угловой момент тела относительно оси вращения становится равным
[17]
Если мы далее предположим, что z o = 0, в других Другими словами, обе системы XYZ и X’Y’Z’ имеют общую плоскость XY ,
[18]
, где I ‘ = момент инерции относительно оси вращения ( Z’ ось) и d = расстояние между осью вращения и параллельная ось, проходящая через ЦМ тела (ось Z ).

- College Physics.


 1)
1)
 Машиностроение. Кр-р, 2011 – С.80-84.
Машиностроение. Кр-р, 2011 – С.80-84.

 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
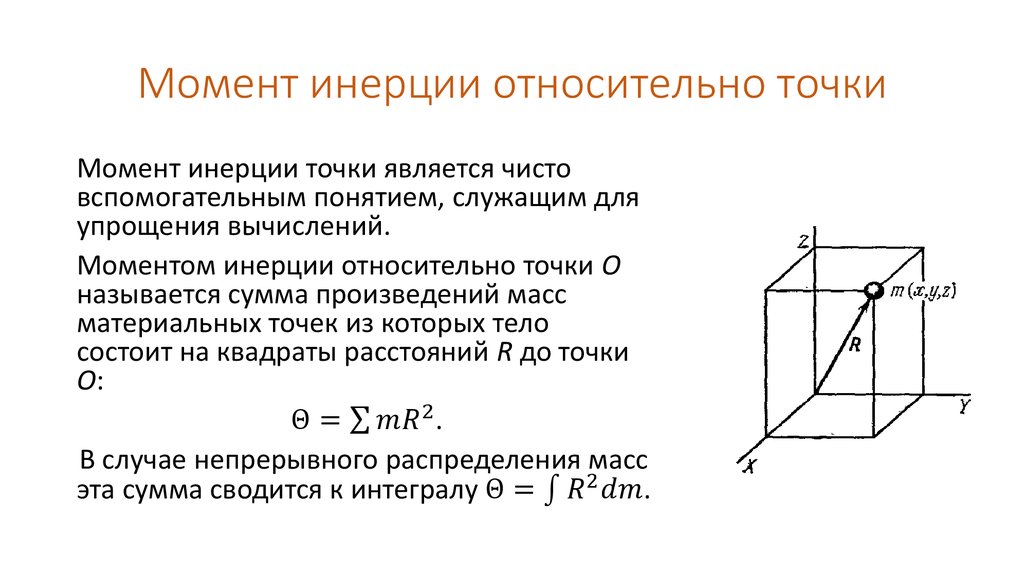
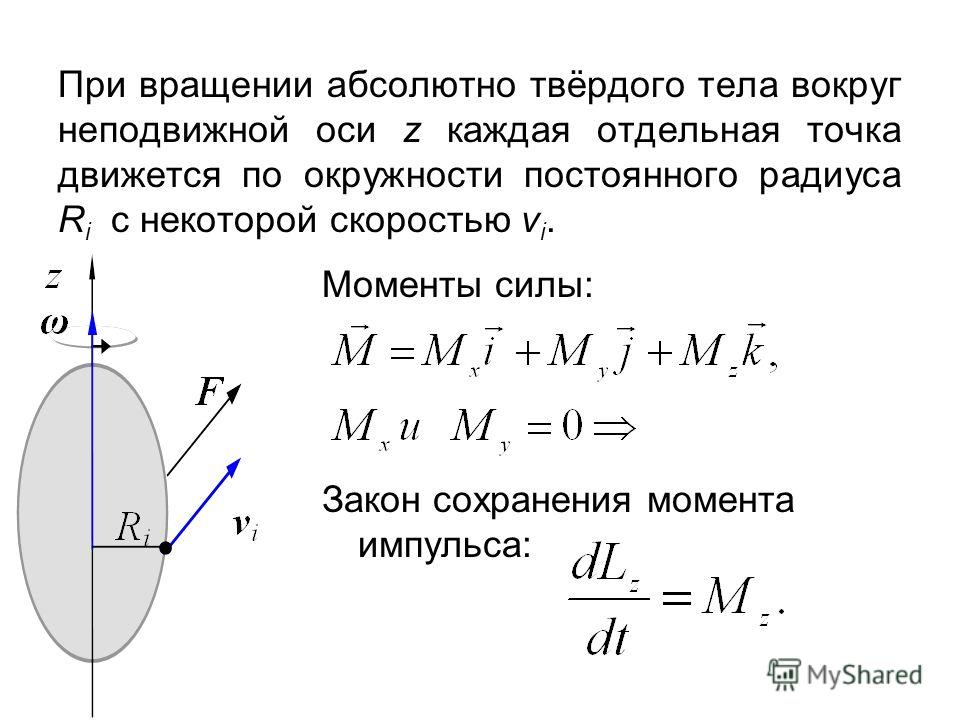 е. масса единицы площади). Таким образом, момент инерции диска I = mR2 /2.
е. масса единицы площади). Таким образом, момент инерции диска I = mR2 /2. На высоте х радиус такого диска r = ,
На высоте х радиус такого диска r = ,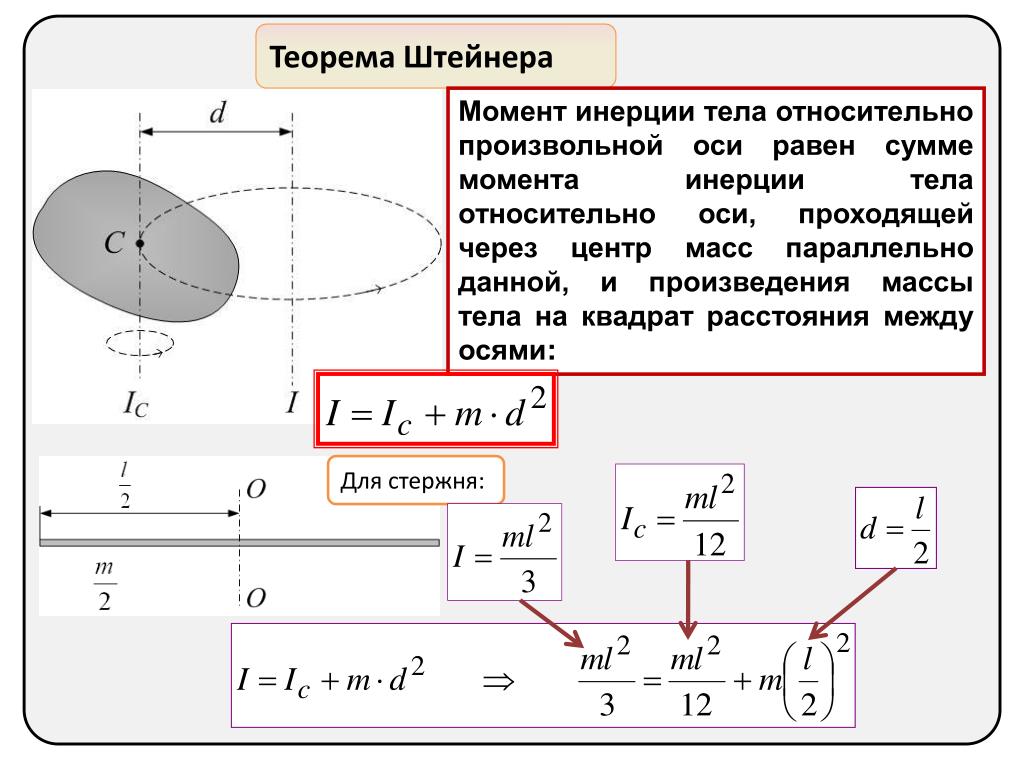 7.6):
7.6): su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.) Определите, каковы они, и рассчитайте их по мере необходимости.
Определите, каковы они, и рассчитайте их по мере необходимости. D.1.1 Учащийся может описать представление и использовать его для анализа ситуации, в которой несколько сил, действующих на вращающуюся систему жестко связанных объектов, изменяют угловую скорость и угловой момент системы. (СП 1.2, 1.4)
D.1.1 Учащийся может описать представление и использовать его для анализа ситуации, в которой несколько сил, действующих на вращающуюся систему жестко связанных объектов, изменяют угловую скорость и угловой момент системы. (СП 1.2, 1.4) 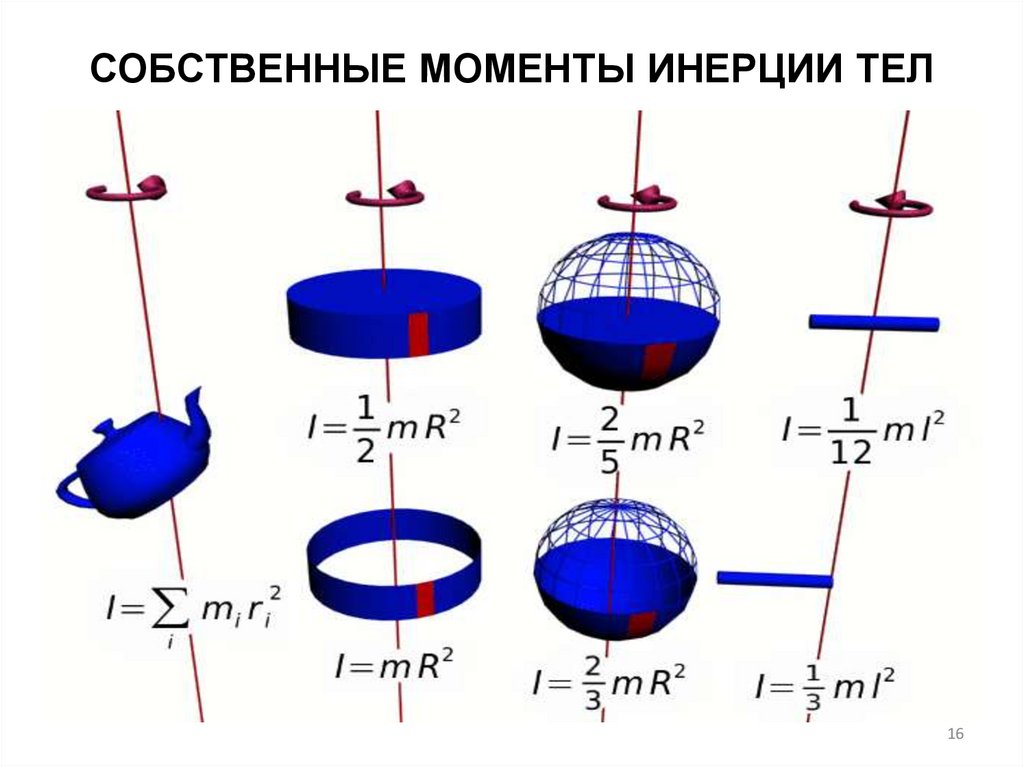 Ожидается, что учащиеся будут выполнять вычисления с фиксированным набором протяженных объектов и точечных масс. (П. 2.2)
Ожидается, что учащиеся будут выполнять вычисления с фиксированным набором протяженных объектов и точечных масс. (П. 2.2) 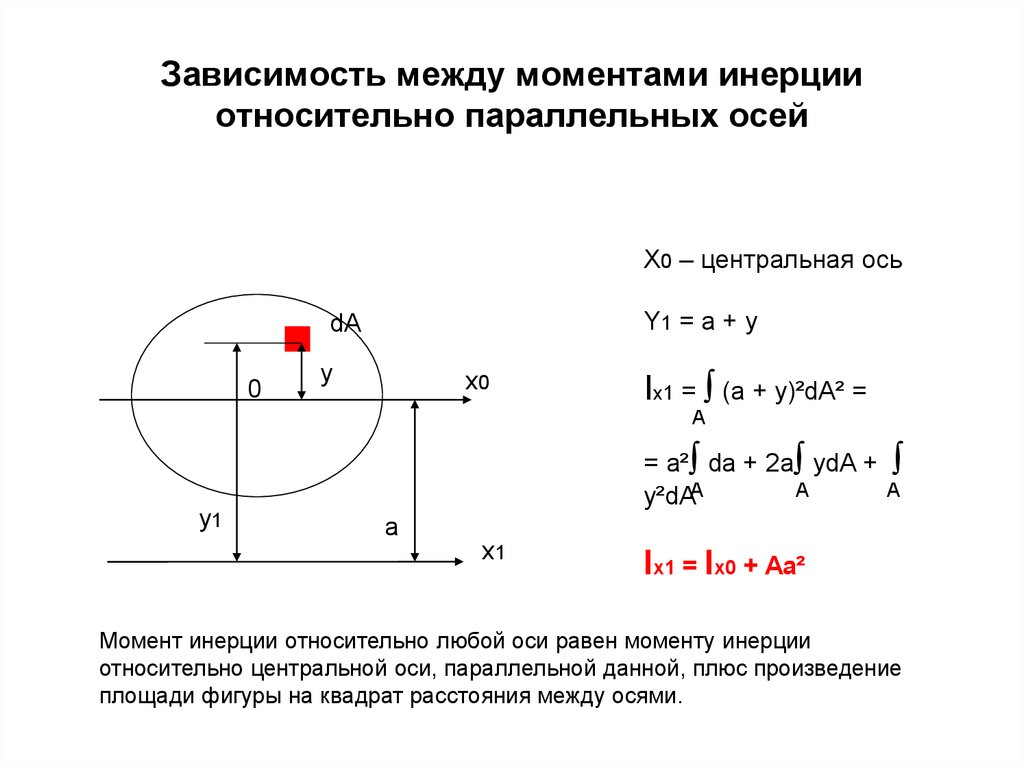 Нарисуйте тщательный набросок ситуации.
Нарисуйте тщательный набросок ситуации. Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.
Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения. [/latex]Мы можем изменить это уравнение так, что
[/latex]Мы можем изменить это уравнение так, что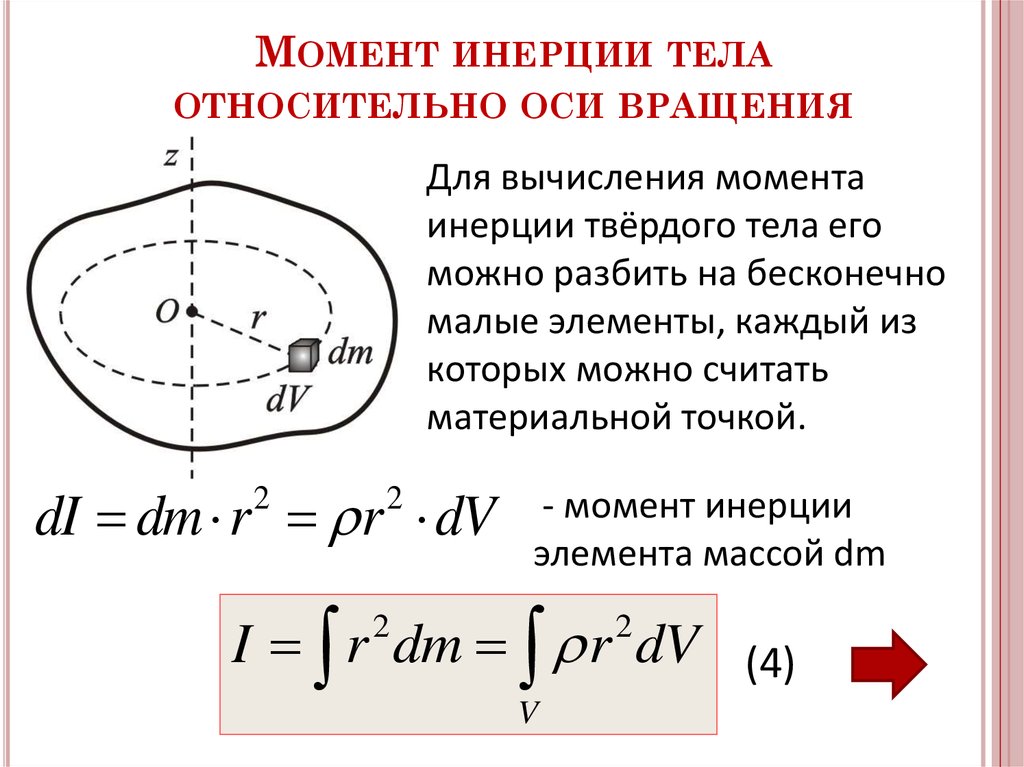 Чем больше инерция вращения у объекта, тем труднее его вращать 92}[/latex]и, поскольку любой объект может быть построен из набора точечных масс, это соотношение является основой для всех других моментов инерции
Чем больше инерция вращения у объекта, тем труднее его вращать 92}[/latex]и, поскольку любой объект может быть построен из набора точечных масс, это соотношение является основой для всех других моментов инерции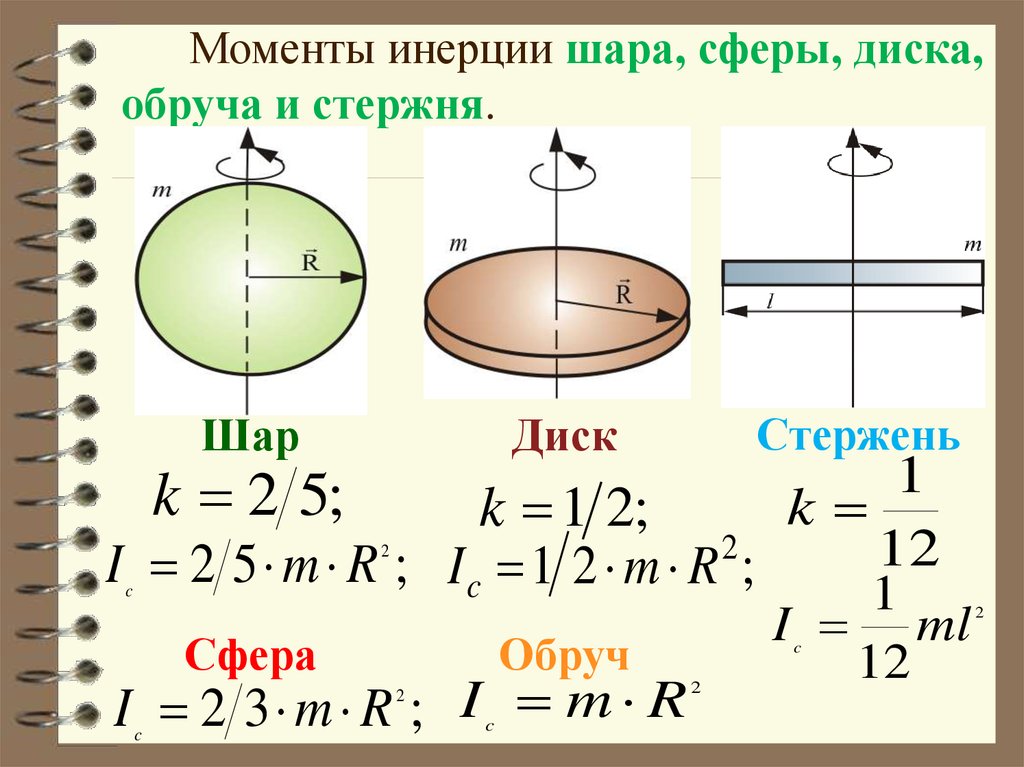 Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.
Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.