Момент инерции массы прямоугольной пластины относительно оси x через центр тяжести, параллельный длине Калькулятор
✖Масса – это количество вещества в теле независимо от его объема или действующих на него сил.ⓘ масса [M] | Ассарий (Библейская Roman)Масс-атомная единицаАттограммаЭвердюпуа драмБекан (Библейский иврит)КаратсантиграммДалтонДекаграммДециграммDenarius (Библейская Roman)Didrachma (Библейский греческий)Драхма (Библейский греческий)Масса электрона (Rest)ExagramFemtogramГаммаGerah (Библейский иврит)ГигаграммГигатонназернаграммГектограммЦентнер (Великобритания)Центнер (США)Масса ЮпитераКилограммКилограмм-сила в квадрате в секунду на метркилофунтКилотонна (метрическая)ЛЕПТОН (Библейская Roman)Масса ДейтронаМасса ЗемлиМасса нейтонаМасса протонаМасса СолнцамегаграммМегатоннамикрограммМиллиграммMina (Библейский греческий)Mina (Библейский иврит)масса мюонананограммунцияПеннивейтPetagramпикограммамасса ПланкафунтФунт (Troy или фармацевтическое)ПаундалФунт-сила в квадрате в секунду на футQuadrans (Библейская Roman)Четверть (Великобритания)Четверть (США)Квинтал (метрическая система)Скрупл (аптекарь)Шекель (библейский иврит)тихоходСолнечная массаСтоун (Великобритания)Камень (США)Талант (Библейский греческий)Талант (Библейский иврит)ТераграммаТетрадрахма (Библейский греческий)Тон (анализ) (Великобритания)Тон (анализ) (США)Тон (длинный)Тон (метрической размерности)Тон (короткометражный)Тонна | +10% -10% | |
✖Ширина прямоугольного сечения – наименьшая длина. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
ⓘ Ширина прямоугольного сечения [B]|
✖Массовый момент инерции относительно оси x твердого тела — это величина, которая определяет крутящий момент, необходимый для желаемого углового ускорения вокруг оси вращения. |
Грамм квадратный сантиметрГрамм квадратный миллиметрКилограмм квадратный сантиметрКилограмм квадратный метрКилограмм квадратный миллиметрКилограмм-сила, метр в квадрате, секундаУнция квадратный дюймУнция-сила, дюйм в квадрате, секундаФунт квадратный футфунт квадратный дюймФунт-сила-фут-квадрат-секундаФунт-сила, дюйм в квадрате, секундаСлаг Квадратный фут |
⎘ копия |
ⓘ Момент инерции массы прямоугольной пластины относительно оси x через центр тяжести, параллельный длине [Ixx]
👎
Формула
сбросить
👍
Момент инерции массы прямоугольной пластины относительно оси x через центр тяжести, параллельный длине Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.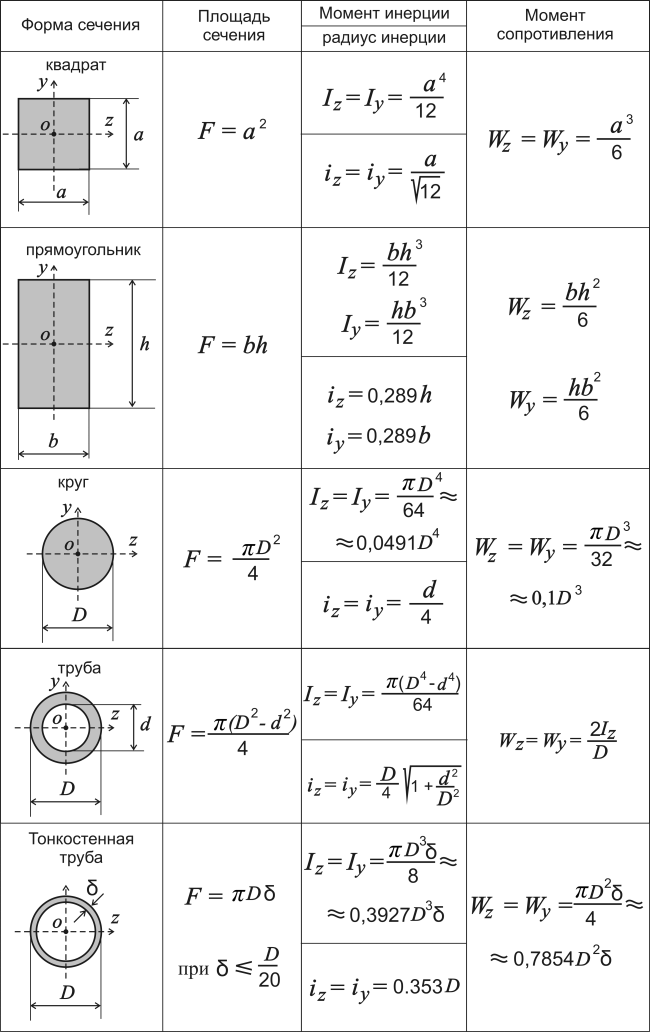
2)/12
Что такое момент инерции массы?
Момент инерции тела измеряет способность тела противостоять изменениям скорости вращения вокруг определенной оси. Чем больше массовый момент инерции, тем меньше угловое ускорение вокруг этой оси для данного крутящего момента. Он в основном характеризует ускорение, которому подвергается объект или твердое тело при приложении крутящего момента.
Share
Copied!
Фейнмановские лекции по физике: Т.2 Пространство. Время. Движение
Фейнмановские лекции по физике: Т.2 Пространство. Время. Движение
ОглавлениеГлава 15. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ§ 1. Принцип относительности § 2. Преобразование Лоренца § 3. Опыт Майкельсона-Морли § 4. Преобразование времени § 5. Лоренцево сокращение § 6. Одновременность § 7. Четырехвекторы § 8. Релятивистская динамика § 9. Связь массы и энергии Глава 16. РЕЛЯТИВИСТСКАЯ ЭНЕРГИЯ И РЕЛЯТИВИСТСКИЙ ИМПУЛЬС § 1. Относительность и «философы» § 2. Парадокс близнецов § 3. Преобразование скоростей § 4. Релятивистская масса § 5. Релятивистская энергия § 1. Геометрия пространства-времени § 2. Пространственно-временные интервалы § 3. Прошедшее, настоящее, будущее § 4. Еще о четырехвекторах § 5. Алгебра четырехвекторов Глава 18. ДВУМЕРНЫЕ ВРАЩЕНИЯ § 1. Центр масс § 2. Вращение твердого тела § 3. Момент количества движения § 4. Закон сохранения момента количества движения Глава 19.  ЦЕНТР МАСС; МОМЕНТ ИНЕРЦИИ§ 1. Свойства центра масс § 2. Положение центра масс § 3. Вычисление момента инерции § 4. Кинетическая энергия вращения Глава 20. ВРАЩЕНИЕ В ПРОСТРАНСТВЕ § 1. Моменты сил в трехмерном пространстве § 3. Гироскоп § 4. Момент количества движения твердого тела Глава 21. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР § 1. Линейные дифференциальные уравнения § 2. Гармонический осциллятор § 3. Гармоническое движение и движение по окружности § 4. Начальные условия § 5. Колебания под действием внешней силы Глава 22. АЛГЕБРА § 1. Сложение и умножение § 2. Обратные операции § 3. Шаг в сторону и обобщение § 4. Приближенное вычисление иррациональных чисел § 5. Комплексные числа § 6. Мнимые экспоненты Глава 23. РЕЗОНАНС § 1. Комплексные числа и гармоническое движение § 2. Вынужденные колебания с торможением § 3. Электрический резонанс Главa 24.  ПЕРЕХОДНЫЕ РЕШЕНИЯ§ 1. Энергия осциллятора § 2. Затухающие колебания § 3. Переходные колебания в электрических цепях Глава 25. ЛИНЕЙНЫЕ СИСТЕМЫ И ОБЗОР § 1. Линейные дифференциальные уравнения § 2. Суперпозиция решений § 3. Колебания в линейных системах § 4. Аналогии в физике § 5. Последовательные и параллельные сопротивления |
Они совсем не похожи ни на один известный курс. Это может показаться странным: основные принципы классической физики, да и не только классической, но в квантовой, давно установлены, курс общей физики читается во всем мире в тысячах учебных заведений уже много лет и ему пора превратиться в стандартную последовательность известных фактов и теорий, подобно, например, элементарной геометрии в школе. Однако даже математики считают, что их науке надо учить по-другому. А уж о физике и говорить нечего: она столь интенсивно развивается, что даже лучшие педагоги все время сталкиваются с большими трудностями, когда им надо рассказывать студентам о современной пауке. Они жалуются, что им приходится ломать то, что принято называть старыми или привычными представлениями. Но откуда берутся привычные представления? Обычно они попадают в молодые головы в школе от таких же педагогов, которые потом будут говорить о недоступности идей современной науки. Поэтому прежде чем подойти к сути дела, приходится тратить много времени на то, чтобы убедить слушателей в ложности того, что было ранее внушено им как очевидная и непреложная истина.
Момент инерции прямоугольника
Что такое Момент инерции прямоугольника? Как рассчитать момент инерции прямоугольного сечения? Эта статья отвечает на все ваши вопросы и предоставляет читателям всю необходимую информацию.
(1) Ось, проходящая через центроидВ конкретном случае, когда ось проходит через центроид, момент инерции прямоугольника задается следующим образом:
Зарегистрируйтесь, чтобы получить бесплатный пробный тест и Учебный материал
+91
Подтвердить OTP-код (обязательно)
Я согласен с условиями и политикой конфиденциальности.
I = bh 3 / 12
Ширина прямоугольника (размер, параллельный оси) обозначена как b, а высота обозначена как h (размер, перпендикулярный оси).
(2) Ось, проходящая через основаниеМомент инерции прямоугольника выражается следующим образом, когда ось проходит через основание:
I = bh 3 / 3
Это легко определяется с помощью применения теоремы о параллельных осях, поскольку центр тяжести прямоугольника расположен на расстоянии, равном h/2 от основания.
Теорема о параллельной осиТеорема о параллельной оси может быть использована для вычисления момента инерции площади любой формы, присутствующей на любой параллельной оси. Если мы узнаем момент инерции нецентроидальной оси по отношению к центроидальной оси, параллельной первой, мы можем найти его здесь. Обычно уравнение записывается как;
I = I x + Ad 2
I x = момент инерции произвольной оси оси х.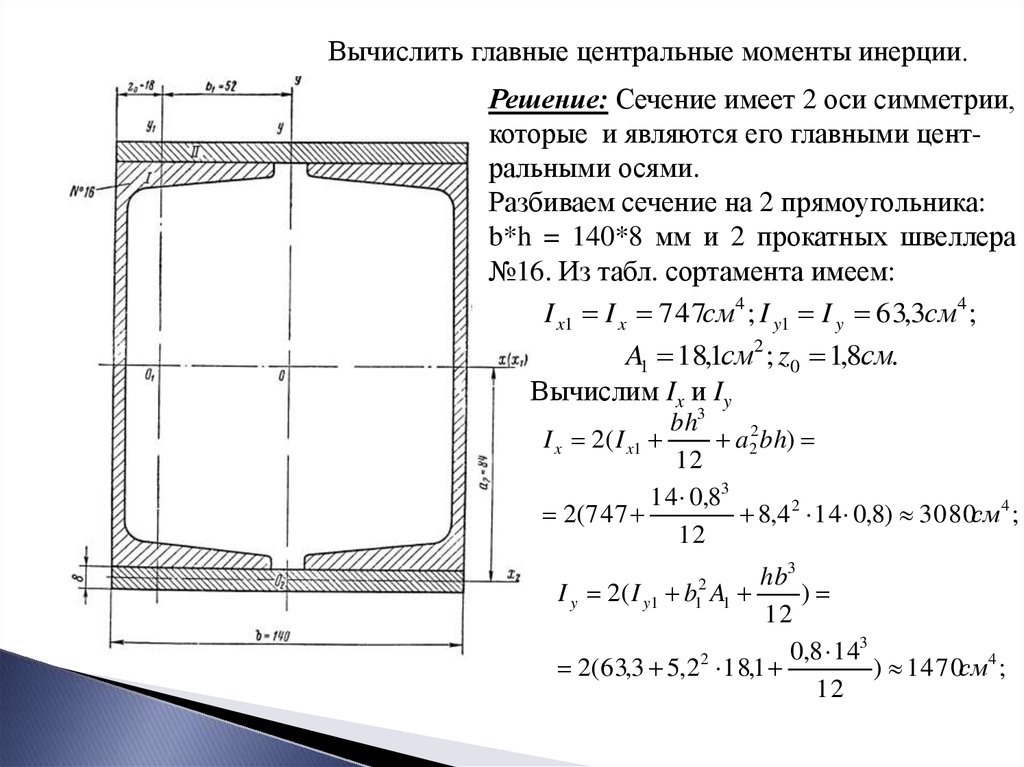
Чередуя размеры b и h из первого приведенного выше уравнения, мы можем определить момент инерции прямоугольника, взяв центральную ось перпендикулярно его основанию. В результате получим следующее уравнение:
I y = hb 3 / 12
Начнем с одного прямоугольного сечения ABCD, как показано на рисунке ниже. Тогда мы предположим, что одна из линий будет проходить через основание прямоугольного сечения. Мы будем использовать эту линию как линию CD. Теперь вычислим момент инерции площади для прямоугольного сечения с центром на этой линии CD.
B называется шириной прямоугольного сечения ABCD
D называется глубиной прямоугольного сечения ABCD
I CD называется моментом инерции прямоугольного сечения относительно линии CD
Следующим шагом является вычисление или выражение момента инерции прямоугольной пластины относительно линии CD.
В этом случае мы будем использовать одну прямоугольную элементарную полосу толщиной dY, которая находится на расстоянии Y от линии CD.
dA = dY.B – площадь прямоугольной элементарной полосы.
Момент инерции относительно линии CD = dA.Y 2 = B Y 2 dY
После определения момента инерции прямоугольного сечения относительно линии CD перейдем к определению момента инерции всей площади прямоугольного сечения с центром на линии CD. Затем мы проинтегрируем приведенное выше уравнение от предела 0 до предела D.
Момент инерции всего прямоугольного сечения относительно линии CD обычно задается как;
I CD = O ∫ D B Y 2 dY
I CD = B O ∫ D Y 2 dY
I CD = B [y 3 / 3] O D
I CD = BD 3 /3
Таким образом, момент инерции прямоугольной секции около линии CD
I CD = BD 3 /3
9000 3 .
Вы хотите быть IITian? Что ж, вот хорошие новости. Infinity Learn ежегодно выпускает 20 % сотрудников IIT. Присоединяйтесь к нашему специально подобранному курсу JEE , чтобы воплотить свою мечту в IIT на предстоящем экзамене JEE 2023.
Часто задаваемые вопросыКак рассчитать момент инерции?
Моменты инерции можно рассчитать путем сложения или интегрирования суммы всех «частей массы», составляющих объект, умноженной на квадрат расстояния каждой «части массы» от оси.
Чему равен момент инерции прямоугольника?
В случае, когда ось проходит через центр тяжести, момент инерции прямоугольника определяется как I = bh4 / 12.
Приложение Infinity Learn
Экзамены в нашем приложении для подготовки к экзаменам – Infinity Learn.
Связанный контент
| Основные вопросы JEE 2023 с решениями |
| JEE Main 2024 Syllabus |
| Best Books for JEE Main 2024 |
| JEE Advanced 2024: Exam date, Syllabus, Eligibility Criteria |
| JEE Main 2024: Exam dates, Syllabus, Eligibility Criteria |
| JEE 2024: дата экзамена, программа, критерии приемлемости0187 |
| JEE Advanced Crash Course – JEE Advanced Crash Course 2023 |
| NEET Cut off 2023 – квалификационные баллы и итоговый балл Момент инерции площади относительно оси — понятие, фигурирующее в формулировках нескольких физических явлений. Математическое определение момента инерции площади (двумерной области) относительно оси, (10.1) где – момент инерции площадки относительно оси в плоскости площадки, а – расстояние по перпендикуляру от оси м до дифференциальной площадки, как показано на рис. 10.1. Ось называется осью вращения . Дифференциальный элемент в этом определении бесконечно мал (приближается к нулю) в любых направлениях на плоскости. Значение зависит от расположения и направления оси, а также от формы области. Эта величина имеет размерность длины в степени четыре (например, ). Рис. 10.1 Члены, участвующие в расчете момента инерции площади относительно оси м . Момент инерции также называют вторым моментом площади . Центроид области , называется первым моментом области . Когда момент инерции рассчитывается относительно двух ортогональных осей в плоскости площади, он называется прямоугольным моментом инерции . Если 90 236 х 90 237 и 90 236 y 90 237 являются двумя перпендикулярными осями (рис. 10.2), моменты инерции площади вокруг осей 90 236 х 90 237 и 90 236 y 90 237 обозначаются как и и определяются как, (10.2) где и — квадраты расстояний от дифференциальной площади (бесконечно малой во всех направлениях) до x и y осей соответственно (т. е. координаты дифференциальной области). Интеграция в уравнениях. 10.2 обычно можно вычислить с помощью двойных интегралов в декартовой системе координат, например, .(10.3) где — дифференциальный элемент площади (в декартовой системе координат), как показано на рис. В качестве альтернативы можно пропустить двойное интегрирование, используя дифференциальные полосы, т. е. прямоугольные элементы, дифференциальные только в одном направлении, и записать интегралы как интегралы с одной переменной. С этой целью рассмотрим . Если , будучи полосой вдоль x , как показано на рис. 10.3a, то интегрирование можно записать как (10.4а) , который является интегралом с одной переменной. Как показано на рис. 10.3b, ширина полосы может быть фиксированной длиной или функцией интегральной переменной y , т.е. Обратите внимание, что поскольку полоса является дифференциальной (бесконечно малой) в направлении х , расстояние от оси х до этого элемента четко определено (т. е. приближается к нулю). Рис. 10.3 Выбор дифференциальной полосы для расчета (а) и (б). Используя тот же подход, мы можем выбрать полосу вдоль оси y , как показано на рис. (10.4б) Обратите внимание, что в этом случае высота полосы является функцией x как , и является дифференциальной в направлении x . Примечание: в качестве общего подхода дифференциальные планки выбираются параллельными оси вращения. Если полосы не параллельны оси вращения, формулировка другая. Более подробная информация будет предоставлена позже. ПРИМЕР 10.1.1Определите момент инерции прямоугольного участка относительно осей, пересекающих его центр тяжести и параллельных его краям, как показано на рисунке. РЕШЕНИЕДля расчета рассмотрите дифференциальную полосу, параллельную оси x и имеющую площадь, как показано ниже. Используя уравнение 10.4а, поэтому мы можем написать
Обратите внимание, что пределы интеграла определяются на основе положения области в выбранной системе координат. Для расчета рассмотрите дифференциальную полосу, параллельную оси y , с площадью, как показано ниже. Таким образом, уравнение. 10.4b приводит нас к
Момент инерции зависит от оси, относительно которой он рассчитывается. Обратите внимание, что ось вращения может находиться за пределами области. В целях демонстрации момент инерции прямоугольного участка относительно оси, проходящей вдоль его основания, вычисляется в следующем примере. ПРИМЕР 10.1.2Определите момент инерции прямоугольного участка относительно осей x вдоль его основания, как показано на рисунке. Сравните результат с результатом примера 10.1.1. РЕШЕНИЕВыберите показанную дифференциальную полосу и рассчитайте уравнение. 10.4а.
Как вы можете заметить, момент инерции прямоугольной области относительно оси вдоль ее основания такой же, как если бы ось сместилась, чтобы пересечь центр тяжести области. В следующих примерах показано использование дифференциальных полос для расчета моментов инерции треугольной и круглой областей. ПРИМЕР 10.1.3Определите момент инерции изображенного треугольного участка относительно осей x и y , как показано. РЕШЕНИЕДля расчета рассмотрите дифференциальную полосу, параллельную оси x , и площадь которой является (линейной) функцией y , как показано ниже. Используя уравнение прямой, мы можем написать и, следовательно,
Следовательно, мы можем вычислить уравнение. 10.4b as,
Для расчета рассмотрите дифференциальную полосу, параллельную оси y , и с площадью такой, которая является (линейной) функцией x , как показано ниже. Таким образом, и уравнение. 10.4b становится
ПРИМЕР 10.1.4Определить момент инерции круглой площадки относительно y оси, пересекающие центр (центроид) области, как показано. РЕШЕНИЕ Рассмотрим вертикальный дифференциальный элемент площадью, как показано на рисунке. Следовательно,
Попробуйте вычислить площадь круга. Вы должны рассмотреть дифференциальную полосу, как показано ниже. Вы заметите это для круглой области. Физическое применение момента инерции площади: жесткость на изгиб Деформация балки при изгибе напрямую связана с ее изгибной жесткостью. В дополнение к другим факторам, таким как материал и длина балки, жесткость на изгиб напрямую зависит от момента инерции поперечного сечения (сечений) балки, перпендикулярного продольной оси балки. В качестве примера рассмотрим изгиб деревянной балки, нагруженной одной силой, как показано на рис. 10.4. В первом случае балка размещается на опорах горизонтально, а во втором — вертикально. При одинаковой нагрузке заметно, что изгибаемая балка в случае 1 деформируется меньше, чем в случае 2. Жесткость на изгиб напрямую связана с моментом инерции поперечного сечения балки, как показано на рис. 10.5. Для этого поперечного сечения момент инерции его сечения (перпендикулярного оси балки) приходится на ось, пересекающую центр тяжести сечения; см. рис. 10.5. Представление и доказательство уравнений, касающихся жесткости на изгиб, выходит за рамки этого курса. Рис. 10.5 Участки, вращающиеся и участвующие в изгибе балок, обозначены как случай 1 и 2. Каждая ось, x , пересекает центроид и параллелен основанию области.Момент инерции сечения балки для каждого случая следующий. Случай 1:
Случай 2:
Следовательно, можно сказать, что балка в случае 2 в 100 раз жестче на изгиб, чем балка в случае 1; качественно, согнуть деревянную балку, расположенную как в случае 2, намного сложнее, чем согнуть балку, расположенную как в случае 1.  |
Момент инерции площади является геометрическим свойством площади. Его значение отражает, насколько сильно объект (т.е. жесткость) сопротивляется изгибу или скручиванию вокруг некоторой оси.
Слово момент используется потому, что такие термины, как значение расстояния до оси, умноженное на площадь, аналогичны определению момента силы, выражающему расстояние до оси, умноженное на силу.
10.2.
10.3б, и пусть . Следовательно, можно записать как
Из уравнения окружности можно получить две функции as и (показаны на рисунке ниже). Поскольку полоса заключена между этими двумя функциями, высота полосы равна (обратите внимание, что она должна быть положительной, поскольку это высота элемента).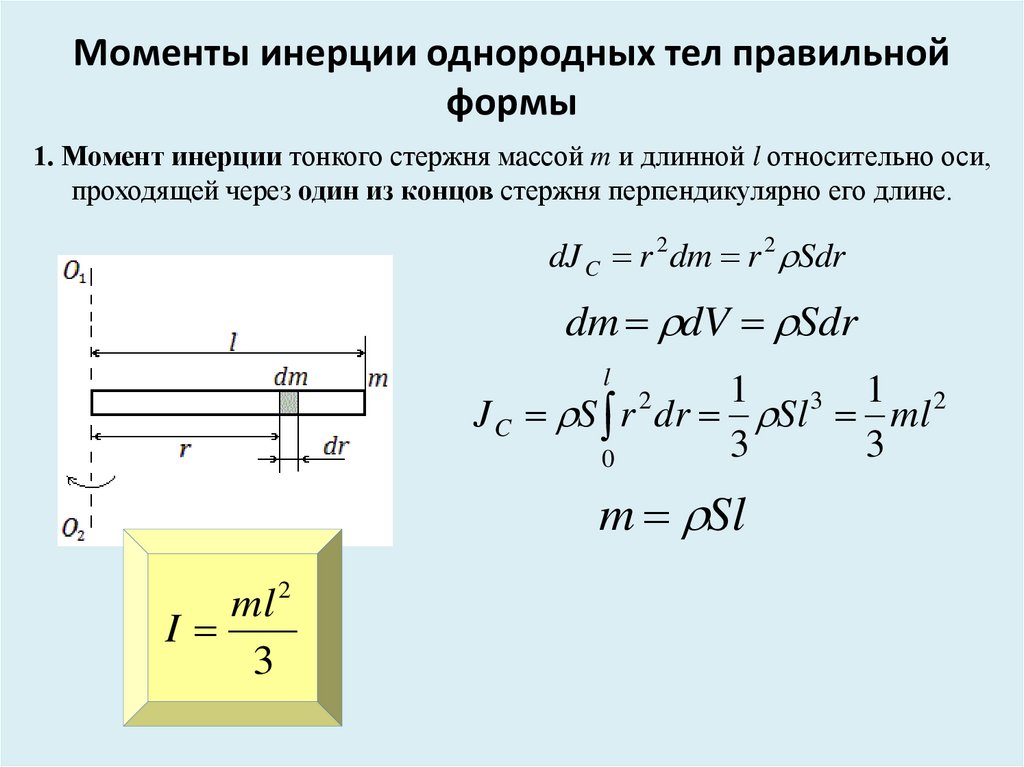
Если измерять деформацию по прогибу балки на половине ее длины, то можно наблюдать, что и . Такое структурное поведение объясняется жесткостью балки на изгиб.