Помогите решить / разобраться (Ф)

Все-таки возьму на себя смелость прояснить ситуацию, если мои действия некорректны — данное сообщение можно удалить, а меня подвергнуть нужной мере репрессий. По определению момент инерции точечного тела относительно оси есть следующая величина: , где — масса частицы, а — квадрат расстояния от частицы до оси. Для системы из точек данное определение записывается в целом также, только надо просуммировать эту величину по всем точкам: , где обозначения те же, индекс указывает на принадлежность к той или иной частице. Отсюда легко понять как определить момент инерции для объемного тела, если известная его плотность: необходимо разбить сие тело на маленькие кубики размер которых достаточно мал для того, чтобы можно было считать плотность в них постоянной, тогда момент инерции будет суммой величины по всем таким кубикам, устремляя мелкость кубиков к нулю мы разумеется получим интеграл следующего вида: , где интеграл берется по всему объему тела . Величина несет смысл массы элементарного кубика, так как — произведение сторон такого кубика, что дает его объем, а — плотность, а плотность помноженная на объем, как известно, дает массу. Если тело представляет из себя поверхность (для простоты будем считать, что она плоская как в вашем примере) — происходит все тоже самое, только надо брать интеграл по поверхности, и вместо объемной плотность использовать поверхностную плотность, которая несет в себе смысл веса элемента поверхности нашего тела. То есть в вашей задаче предлагается вычислить интеграл: Все пляски дальше только вокруг способа вычисления этой штуки, поскольку мы умеем хорошо брать интегралы по одномерным штуковинам, то нам очень хотелось бы придумать такое разбиение нашего тела, чтобы интегрировать было бы как можно проще, например, если бы тело было бы кругом, а ось проходила бы через его центр, — мы могли бы попытаться разбить круг на колечки площадь каждого колечка толщины вычислялась бы так: — это просто увидеть, если понимать, что такое малое колечко мало чем отличается от прямоугольника (его можно разрезать и выпрямить например), так что его площадь есть произведение длин его сторон: — шаг вглубину, а — шаг в сторону, то есть длина окружности. Далее надо вычислить момент инерции каждого колечка относительно оси (что весьма просто, попробуйте сделать это по определению), а потом просуммировать получившийся ответ по все таким колечкам, то есть проинтегрировать получившуюся формулу по радиусам. В случае вашей задачи удобнее разбить пластинку на полоски параллельные оси, вычислить для каждой полоски момент инерции и так же собрать ответ воедино. Поэтому Ваш преподаватель и говорил разбить тело на цилиндры, чтобы вычислить момент инерции каждого цилиндра по отдельности, а потом просуммировать получившийся ответ. Чтобы правильно решить задачу надо понять чему равна площадь каждой маленькой полоски, и верно взять все интегралы.

1. Момент инерции твердого тела относительно плоскости, относительно оси, относительно полюса.

Лекция №12

План

1)Момент инерции твердого тела относительно плоскости, относительно оси, относительно полюса.

2)Момент инерции относительно декартовых координат.

3)Моменты инерции относительно параллельных осей. Момент инерции однородного тонкого стержня относительно оси. Момент инерции однородной круглой пластины. Момент инерции однородного круглого цилиндра.

4)Количество движения точки и системы. Элементарный и полный импульс силы.

5) Теорема об изменении количества движения механической системы. Момент количества движения материальной точки и системы.

6) Теорема об изменении момента количества движения материальной точки. Теорема об изменении кинетического момента механической системы.

Движение тел существенным образом зависит от характера распределения масс. Положение центра масс не характеризует распределения массы. Поэтому при изучении динамики механических систем точек и при изучении динамики твердого тела, вводится еще одна характеристика –момент инерции системы материальных точек и момент инерции твердого тела.

Моментом инерции системы материальных точек массой m_k относительно точки О, состоящий из

N точек, называется сумма произведений масс этих точек на квадраты их расстояний а_k до точки О.

L

k=1,2,3…N

М

h_k

dm_k

омент инерции относительно

точки называется полярным

моментом инерции

Момент инерции твердого тела относительно точки О будет определяться:

где dm-масса элементарной части тела ,принимаемой в пределе за точку.

а- расстояние частиц тела до точки О.

Интегрирование ведется по всему объему.

Моментом инерции J_kсистемы материальных точек относительно оси L называется сумма произведений масс этих точек на квадраты их расстояний h_k до оси L.

k=1,2,3…N

В случае твердого тела сумму следует заменить интегралом

dm=ρdV, ρ — плотность тела, V-объем тела.

Моменты инерции одинаковых по форме тел, изготовленных из различных материалов ,отличаются друг от друга характеристикой, не зависящей от массы тела является радиус инерции.

Радиус инерции относительно осиL определяется равенством :

Тогда момент инерции относительно оси можно определить по формуле

J_L =Mi²

2. Момент инерции относительно декартовых координат.

Выразим момент инерции системы материальных точек относительно оси J_L для декартовых осей координат. Расстояние k-ой частицы до оси Х определяется из геометрии.

Подставим в формулу J_L = m_kh получим моменты инерции относительно осей координат:

Расстояние k-ой частицы до центра О определяется

Момент инерции относительно этого центра

Для сплошных твердых тел

Центробежные моменты инерции

В механике в качестве характеристик, учитывающих несимметричность в распределении масс, вводят еще так называемые центробежные моменты инерции. Если через любую точку О провести координатные оси OXYZ ,то по отношению к этим осям центробежными моментами инерции называют величины I,I,I

I

I

I

где m–массы точек ,

x-координаты точек .

Очевидно, что I и т.д.

Для твердых тел формулы примут вид:

В отличии от осевых моменты инерции могут быть как положительными, так и отрицательными.

Момент инерции относительно параллельных осей .

Существует простая связь между моментом инерции тела относительно параллельных осей .Одна из которых проходит через центр масс.

Теорема

Момент инерции тела Iz, относительно некоторой оси Z1 равен сумме момента инерции Izc тела относительно оси Zc проходящий через центр масс параллельно данной и произведения массы тела на квадрат расстояний между осями:

М-масса тела

d- расстояние между двумя параллельными осями

3. Момент инерции однородного тонкого стержня относительно оси. Момент инерции однородной круглой пластины.

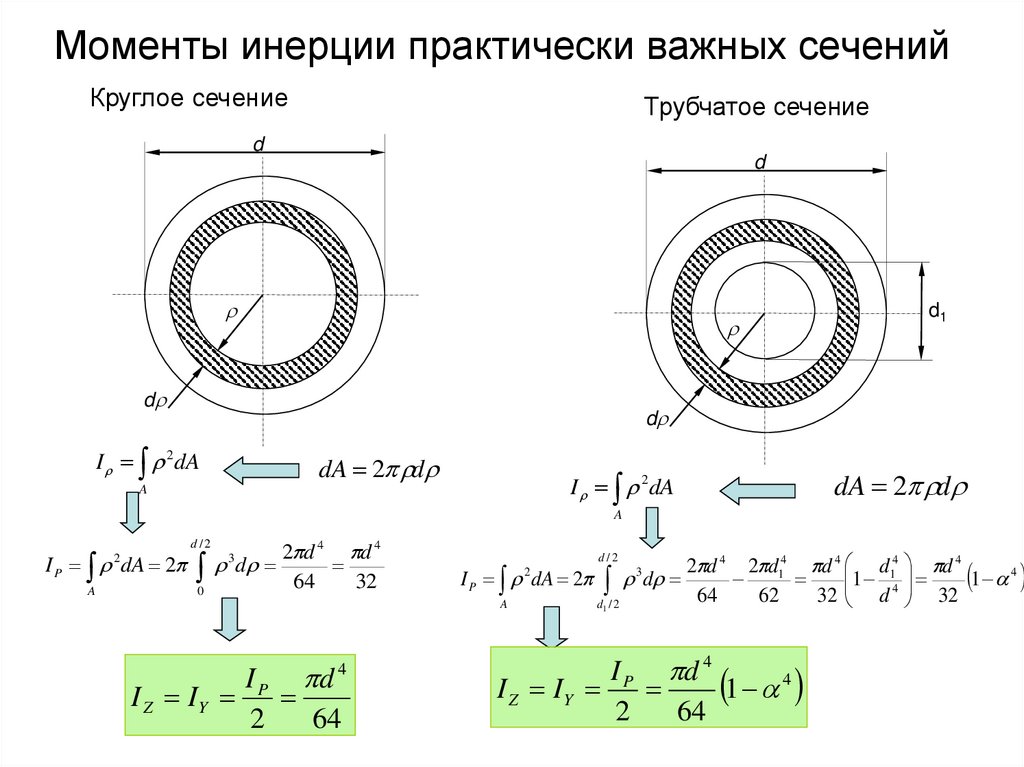Момент инерции однородного круглого цилиндра.

а) однородный стержень длиной L и массой М. Вычислим момент инерции относительно C_Z ,проходящей через центр масс стержня и перпендикулярной к нему.

Z1

Z

Размерность момента инерции [кг∙м] так, что единственная величина, которую мы вычисляем ,это множитель

Момент инерции относительно оси z’ ,проходящей перпендикулярно стержню через его конец, параллельно Z_C , определяется по теореме Гюйгенса-Штейнера.

б)Момент инерции однородной круглой пластинки.

Имеем тонкий однородный диск радиусом R ,массой М. Вычисляем момент инерции относительно точки О.

Z

O

R

X

Y

в) Момент инерции однородного круглого цилиндра.

Радиус цилиндра R, массой М высотой Н.

2}} \справа)$. Найдите значение $x$.

Ответ

Проверено

251.7k+ views

Подсказка: мы воспользуемся теоремой о параллельных осях, чтобы найти момент инерции пластины относительно оси, которая перпендикулярна и проходит через вершины пластины, поскольку мы знаем момент инерции пластины относительно оси, перпендикулярной плоскости и проходящей через центр пластины.

Полный пошаговый ответ:
Пусть момент M.I пластины относительно оси, перпендикулярной плоскости и проходящей через центр, равен ${I_c}$, а M.I пластины относительно оси, перпендикулярной плоскости плоскости и проходящей через одну из вершин прямоугольной пластины есть ${I_v}$. 92}$но она изменится, когда мы изменим распределение массы вокруг оси вращения.

Примечание. Теорема о параллельных осях также действительна в случае трехмерных объектов, таких как конус, полусфера. Теорема о перпендикулярной оси всегда действительна только для 2D-форм.