формула. Момент инерции тела :: SYL.ru
Чтобы изменить скорость перемещения тела в пространстве, необходимо приложить некоторое усилие. Этот факт относится ко всем видам механического движения и связан с наличием инерционных свойств у объектов, имеющих массу. В данной статье рассматривается вращение тел и дается понятие об их моменте инерции.
Что такое вращение с точки зрения физики?
Ответ на этот вопрос может дать каждый человек, поскольку этот физический процесс ничем не отличается от его понятия в обиходе. Процесс вращения представляет собой перемещение объекта, обладающего конечной массой, по круговой траектории вокруг некоторой воображаемой оси. Можно привести следующие примеры вращения:
- Движение колеса автомобиля или велосипеда.
- Вращение лопастей вертолета или вентилятора.
- Движение нашей планеты вокруг оси и вокруг Солнца.
Какие физические величины характеризуют процесс вращения?
Перемещение по окружности описывается набором величин в физике, основные из которых перечислены ниже:
- r — расстояние до оси материальной точки массой m.

- ω и α — угловая скорость и ускорение, соответственно. Первая величина показывает, на сколько радиан (градусов) поворачивается тело вокруг оси за одну секунду, вторая величина описывает скорость изменения во времени первой.
- L — момент импульса, который подобен аналогичной характеристике при линейном движении.
- I — момент инерции тела. Эта величина рассматривается ниже в статье подробно.
- M — момент силы. Он характеризует степень изменения величины L, если приложена внешняя сила.
Перечисленные величины связаны друг с другом следующими формулами вращательного движения:
L = I*ω
M = I*α
Первая формула описывает круговое движение тела в отсутствие действия внешних моментов сил. В приведенном виде она отражает закон сохранения момента импульса L. Второе выражение описывает случай ускорения или замедления вращения тела в результате действия момента силы M. Оба выражения часто используются при решении задач динамики по круговой траектории.
Как видно из этих формул, момент инерции относительно оси (I) в них используется в качестве некоторого коэффициента. Рассмотрим подробнее эту величину.
Откуда появляется величина I?
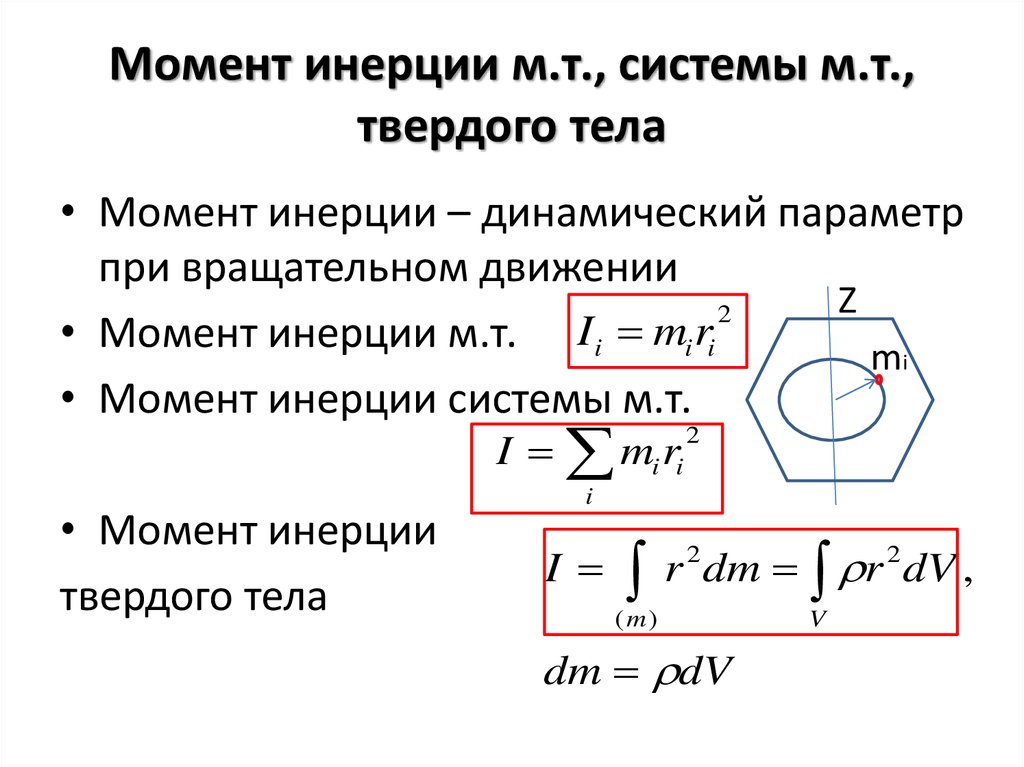
В этом пункте рассмотрим самый простой пример вращения: круговое перемещение материальной точки массой m, дистанция которой от оси вращения составляет r. Эта ситуация приведена на рисунке.
Согласно определению, момент импульса L записывается, как произведение плеча r на линейный импульс p точки:
L = r*p = r*m*v, поскольку p = m*v
Учитывая, что линейная и угловая скорость связаны друг с другом через расстояние r, это равенство можно переписать так:
v = ω*r => L = m*r2*ω
Произведение массы материальной точки на квадрат расстояния до оси вращения принято называть моментом инерции. Формула выше перепишется в таком случае следующим образом:
I = m*r2 => L = I*ω
То есть мы получили выражение, которое было приведено в предыдущем пункте, и ввели в использование величину I.
Общая формула для величины I тела
Выражение для момента инерции массой m материальной точки является базовым, то есть оно позволяет рассчитать эту величину для любого тела, имеющего произвольную форму и неоднородное распределение массы в нем. Для этого необходимо разбить рассматриваемый объект на маленькие элементы массой mi (целое число i — номер элемента), затем, умножить каждый из них на квадрат расстояния ri2 до оси, вокруг которой рассматривают вращение, и сложить полученные результаты. Описанную методику нахождения величины I можно записать математически так:
I = ∑i(mi*ri2)
Если тело разбито таким образом, что i->∞, тогда приведенная сумма заменяется интегралом по массе тела m:
I = ∫m(ri2*dm)
Этот интеграл эквивалентен другому интегралу по объему тела V, поскольку dV=ρ*dm:
I = ρ*∫V(ri2*dV)
Все три формулы используются для вычисления момента инерции тела. При этом в случае дискретного распределения масс в системе предпочтительнее пользоваться 1-м выражением. При непрерывном распределении массы применяют 3-е выражение.
При этом в случае дискретного распределения масс в системе предпочтительнее пользоваться 1-м выражением. При непрерывном распределении массы применяют 3-е выражение.
Свойства величины I и ее физический смысл
Описанная процедура получения общего выражения для I позволяет сделать некоторые выводы о свойствах этой физической величины:
- она является аддитивной, то есть полный момент инерции системы можно представить, как сумму моментов отдельных ее частей;
- она зависит от распределения массы внутри системы, а также от расстояния до оси вращения, чем больше последнее, тем больше I;
- она не зависит от действующих на систему моментов сил M и от скорости вращения ω.
Физический смысл I заключается в том, насколько сильно система препятствует любому изменению скорости ее вращения, то есть момент инерции характеризует степень «плавности» возникающих ускорений. Например, колесо велосипеда можно легко раскрутить до больших угловых скоростей и также легко его остановить, но чтобы изменить вращение маховика на коленвале автомобиля, понадобится приложить значительное усилие и некоторое время. В первом случае имеет место система с маленьким моментом инерции, во втором — с большим.
В первом случае имеет место система с маленьким моментом инерции, во втором — с большим.
Значение I некоторых тел для оси вращения, проходящей через центр масс
Если применить интегрирование по объему для любых тел с произвольным распределением массы, то можно получить для них величину I. В случае однородных объектов, которые имеют идеальную геометрическую форму, эта задача уже решена. Ниже приводятся формулы момента инерции для стержня, диска и шара массой m, в которых составляющее их вещество распределено равномерно:
- Стержень. Ось вращения проходит перпендикулярно ему. I = m*L2/12, где L — длина стержня.
- Диск произвольной толщины. Момент инерции с осью вращения, проходящей перпендикулярно его плоскости через центр масс, вычисляется так: I = m*R2/2, где R — радиус диска.
- Шар. В виду высокой симметрии этой фигуры, для любого положения оси, проходящей через ее центр, I = 2/5*m*R2, здесь R — шара радиус.
Далее приведем два примера решения задач на применение общей формулы для расчета I и на использование свойства аддитивности этой величины.
Задача на расчет значения I для системы с дискретным распределением массы
Представим себе стержень длиною 0,5 метра, который сделан из твердого и легкого материала. Этот стержень закреплен на оси таким образом, что она проходит перпендикулярно ему точно посередине. На этот стержень подвешены 3-и груза следующим образом: с одной стороны оси имеются два груза массами 2 кг и 3 кг, находящиеся на расстояниях 10 см и 20 см от его конца, соответственно; с другой стороны подвешен один груз массой 1,5 кг к концу стержня. Для этой системы необходимо рассчитать момент инерции I и определить, с какой скоростью ω стержень будет вращаться, если к одному из его концов приложить силу 50 Н в течение 10 секунд.
Поскольку массой стержня можно пренебречь, тогда необходимо рассчитать момент I для каждого груза и сложить полученные результаты, чтобы получить полный момент системы. Согласно условию задачи от оси груз массой 2 кг находится на расстоянии 0,15 м (0,25-0,1), груз 3 кг — 0,05 м (0,25-0,20), груз 1,5 кг — 0,25 м.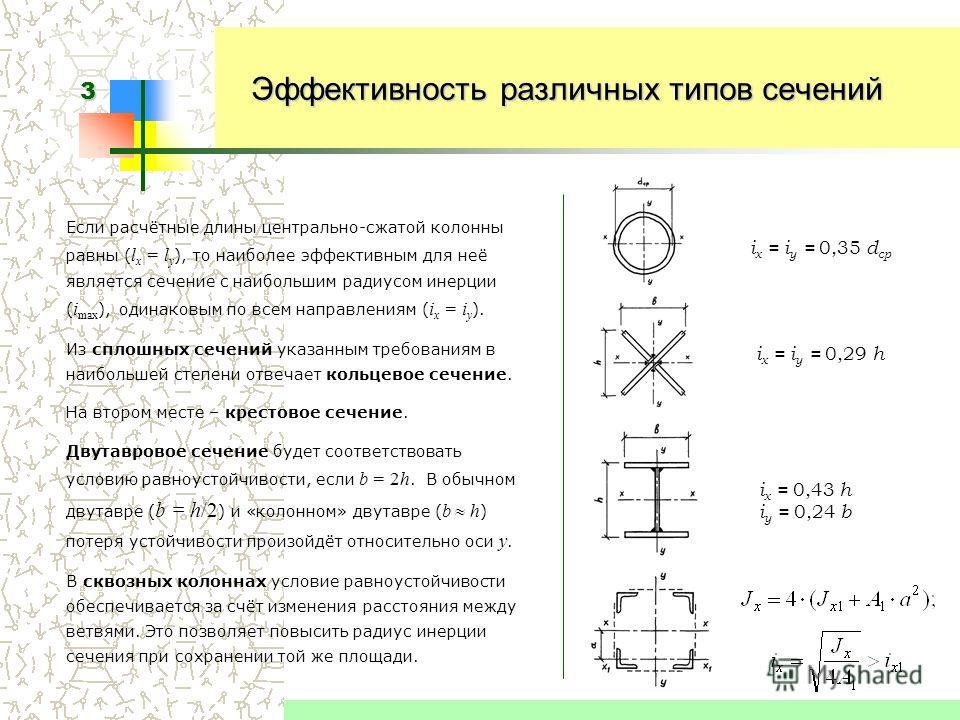 Воспользовавшись формулой для момента I материальной точки, получаем:
Воспользовавшись формулой для момента I материальной точки, получаем:
I = I1+I2+I3 = m1*r12 + m2*r22 + m3*r32 = 2*(0,15)2+3*(0,05)2+1,5*(0,25)2 = 0,14 625 кг*м2.
Обратим внимание, что при выполнении вычислений все единицы измерения были переведены в систему СИ.
Чтобы определить угловую скорость вращения стержня после действия силы, следует применить формулу с моментом силы, которая была приведена во втором пункте статьи:
M = I*α
Поскольку α = Δω/Δt и M = r*F, где r — длина плеча, получаем:
r*F = I*Δω/Δt => Δω = r*F*Δt/I
Учитывая, что r = 0,25 м, подставляем числа в формулу, получаем:
Δω = r*F*Δt/I = 0,25*50*10/0,14625 = 854,7 рад/с
Полученная величина является достаточно большой. Чтобы получить привычную частоту вращения, следует поделить Δω на 2*pi радиан:
Чтобы получить привычную частоту вращения, следует поделить Δω на 2*pi радиан:
f = Δω/(2*pi) = 854,7/(2*3,1416) = 136 с-1
Таким образом, приложенная сила F к концу стержня с грузами за 10 секунд раскрутит его до частоты 136 оборотов в секунду.
Расчет значения I для стержня, когда ось проходит через его конец
Пусть имеется однородный стержень массой m и длиной L. Необходимо определить момент инерции, если ось вращения расположена на конце стержня перпендикулярно ему.
Воспользуемся общим выражением для I:
I = ρ*∫V(ri2*dV)
Разбивая рассматриваемый объект на элементарные объемы, заметим, что dV может быть записано, как dr*S, где S — площадь сечения стержня, а dr — толщина элемента разбиения. Подставляя это выражение в формулу, имеем:
I = ρ*S*∫L(r2*dr)
Этот интеграл вычислить достаточно просто, получаем:
I = ρ*S* (r3/3)∣0L => I = ρ*S*L3/3
Поскольку объем стержня равен S*L, а масса — ρ*S*L, то получаем конечную формулу:
Любопытно отметить, что момент инерции для того же стержня, когда ось проходит через его центр масс, в 4 раза меньше полученной величины (m*L2/3/(m*L2/12)=4).
Вывод формулы момента инерции кольца : Чулан (Ф)
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
| Nikolay_90 |
| ||
17/12/07 |
| ||
| |||
| photon |
| |||||||||
23/12/05 |
| |||||||||
| ||||||||||
| Eiktyrnir |
| ||
30/11/07 |
| ||
| |||
| peregoudov |
| ||
10/03/07 |
| ||
| |||
| Eiktyrnir |
| ||
30/11/07 |
| ||
| |||
| Zai |
| |||
11/04/07 Москва |
| |||
| ||||
| Eiktyrnir |
| ||
30/11/07 |
| ||
| |||
| peregoudov |
| ||
10/03/07 |
| ||
| |||
| Zai |
| |||
11/04/07 |
| |||
| ||||
| Eiktyrnir |
| ||
30/11/07 |
| ||
| |||
| peregoudov |
| ||
10/03/07 |
| ||
| |||
| Eiktyrnir |
| ||
30/11/07 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Список формул момента инерции для различных форм
Механика
Формулы момента инерции
В этом посте вы узнаете список формул момента инерции для различных форм с примерами.
Содержание:
- Моменты инерции определение
- Формула момента инерции
- Уравнение
- Блок
- гораздо больше
Продолжение чтения…
Что является моментом inertia?
Момент инерции ( I ) определяется как сумма произведений массы каждой частицы тела на квадрат ее перпендикулярного расстояния от оси. Это также известно как вращательная инерция. Момент инерции отражает распределение массы тела или системы вращающихся частиц относительно оси вращения. Момент инерции зависит только от геометрии тела и положения оси вращения, но не зависит от сил, участвующих в движении.
Момент инерции отражает распределение массы тела или системы вращающихся частиц относительно оси вращения. Момент инерции зависит только от геометрии тела и положения оси вращения, но не зависит от сил, участвующих в движении.
Момент инерции играет роль, аналогичную роли инерционной массы в случае прямолинейного и равномерного движения. Это скалярное значение продольного углового момента твердого тела.
Это скалярное значение продольного углового момента твердого тела.
I = mr²
Для твердого тела, движущегося вокруг неподвижной оси, законы движения имеют ту же форму, что и законы прямолинейного движения, с моментом инерции вместо массы, угловым вместо линейной скорости, угловым моментом вместо линейного импульс и т. д. Следовательно, кинетическая энергия тела, вращающегося вокруг неподвижной оси с угловой скоростью ω, равна ½ω², что соответствует ½mv² для кинетической энергии тела массы m, переведенной со скоростью v. См. также правило Рауса; теорема о параллельных осях.
Уравнение момента инерции
Рассмотрим массу m, прикрепленную к концу безмассового стержня. Предположим, что подшипник в точке вращения O не имеет трения. Пусть система находится в горизонтальной плоскости. Сила F действует на массу перпендикулярно стержню и, следовательно, будет ускорять массу в соответствии с: до углового
ускорения α по уравнению.
угловое ускорение = rα
Поскольку вращательный эффект создается крутящим моментом τ, поэтому было бы лучше записать уравнение вращения в терминах крутящего момента.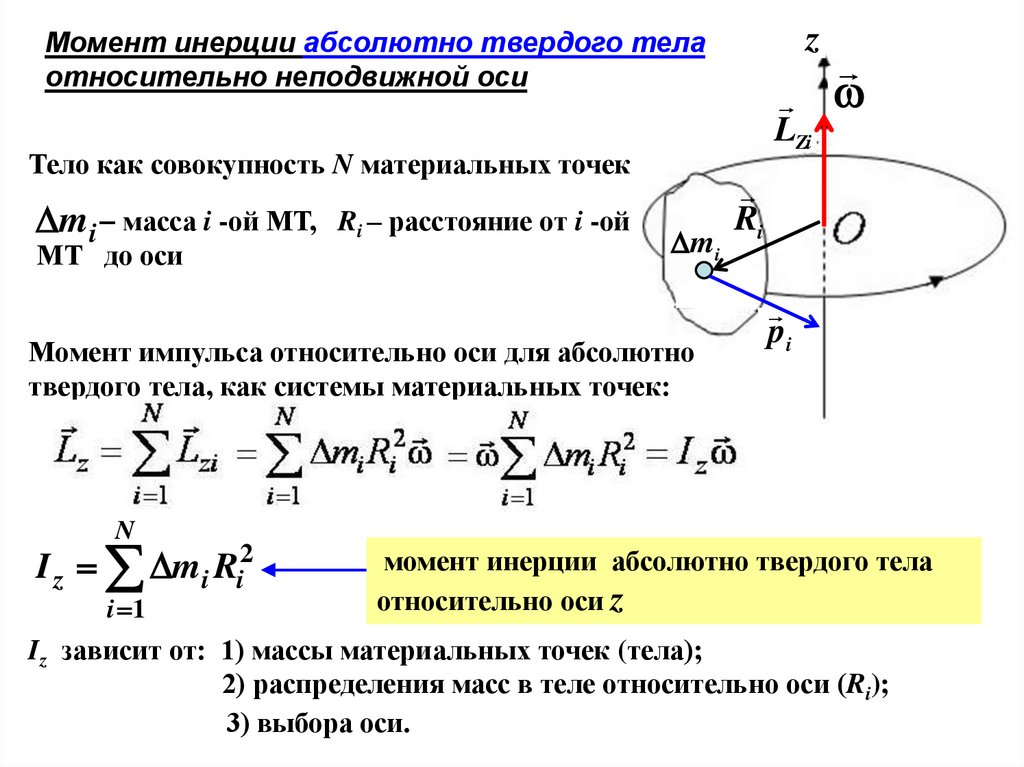 Это можно сделать, умножив обе части вышеприведенного уравнения на r. Таким образом,
Это можно сделать, умножив обе части вышеприведенного уравнения на r. Таким образом,
rF = τ = крутящий момент = mr²α
Какой вращательный аналог второго закона Ньютона?
Здесь F заменено на τ, a на α и m на mr². Величина mr² известна как момент инерции и обозначается I.
Значение момента инерции
Момент инерции играет ту же роль в угловом движении, что и масса в прямолинейном движении. Можно заметить, что момент инерции зависит не только от массы m, но и от r².
Момент инерции Формулы
Вот список формул момента инерции различных форм:
момент инерции оболочки цилиндраМомент инерции диска Момент инерции твердого цилиндрамомент инерции полого цилиндра момент инерции длинного тонкого стержня
момент инерции прямоугольника
:
- Типы движения
- Ускорение
- Равномерное и неравномерное движение
- Крутящий момент
Похожие статьи
Проверьте также
0106 Закрыть
Момент инерции — веб-формулы
· Момент инерции
· Волна 2
· Кинетическая и потенциальная энергия
· Работа 2
· Сила и трение
· Первый закон Ньютона (закон инерции)
· Второй закон Ньютона (закон равнодействующей силы)
· Третий закон Ньютона (закон действия и противодействия)
· Закон Гука
· Скорость/скорость
· Движение и скорость
· Скорость и ускорение
· Ускорение
· Угловое ускорение
· Угловая частота/угловая скорость
Текущее местоположение > Физические формулы > Механика > Момент инерции
Не забудьте попробовать наше бесплатное приложение — Agile-журнал , который поможет вам отслеживать время, потраченное на различные проекты и задачи, 🙂
Попробуй сейчас
Момент инерции определяется как:
Где мы имеем:
м: масса
R: радиус (от оси O до объекта)
Ниже приведен список моментов инерции для некоторых распространенных однородных объектов, где M означает массу, а красная линия — ось, вокруг которой вращаются объекты.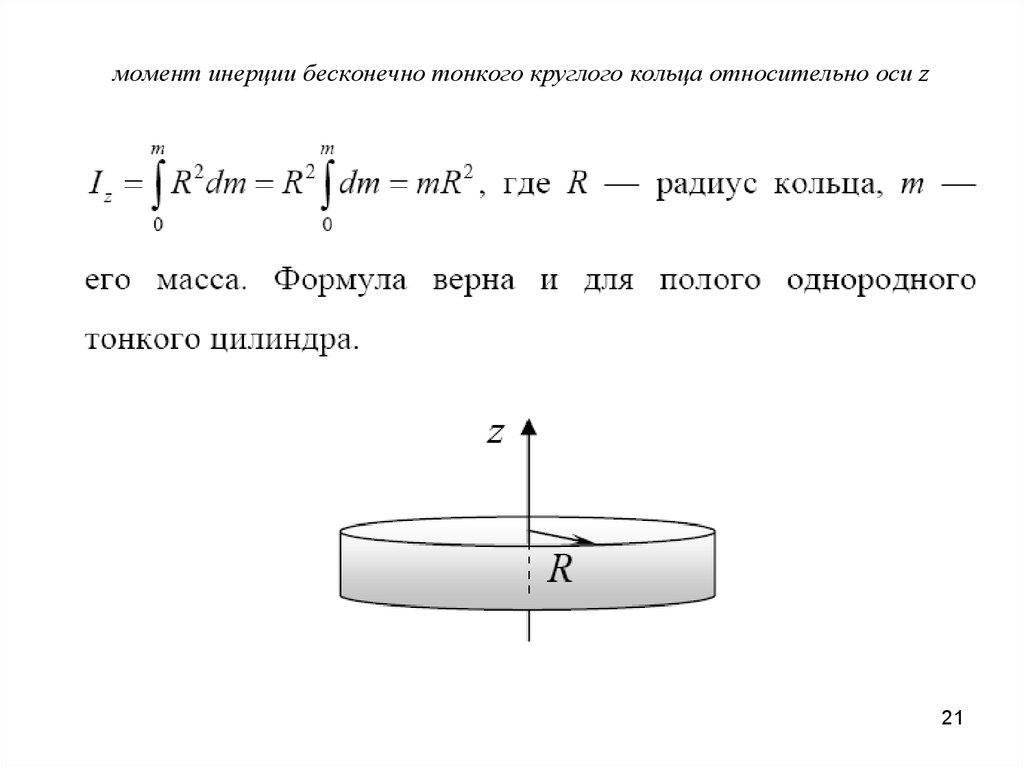



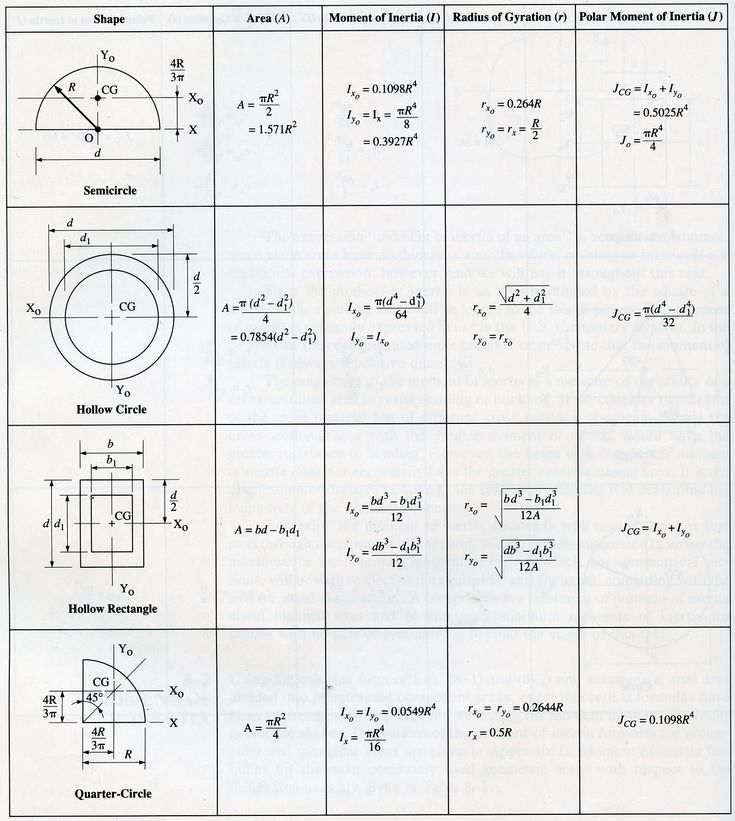 через диаметр, а также ч-з центр.)
через диаметр, а также ч-з центр.) После внесения исправлений сообщите одному из модераторов, чтобы тема была возвращена
После внесения исправлений сообщите одному из модераторов, чтобы тема была возвращена через диаметр, а также ч-з центр.)
через диаметр, а также ч-з центр.) 12.2007, 23:35
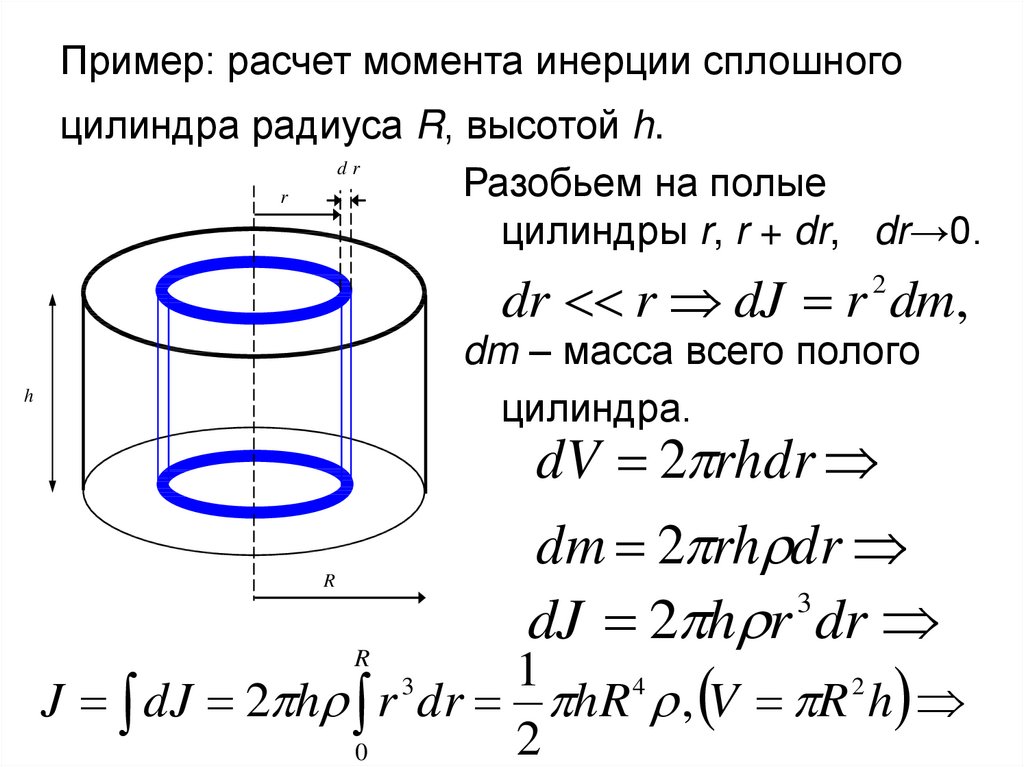
12.2007, 23:35  Воспользовавшись аддитивностью массы и момента инерции, можно записать
Воспользовавшись аддитивностью массы и момента инерции, можно записать 


 12.2007, 19:29
12.2007, 19:29  12.2007, 16:22
12.2007, 16:22