Возможно, вам больше понравится обновленная версии калькулятора моментов инерции и моментов сопротивления
Партнерская программа
Мы согласны отдать Вам 30% своего дохода за рекламу нашего сайта на Вашей площадке ПодробнееПомощь: сопромат, строймеханика, прикладная механика Telegram bluewhite22WhatsAppInstagram
Помогите решить / разобраться (Ф)
Сообщения без ответов | Активные темы | Избранное
| Spice |
| ||
05/04/10 |
| ||
| |||
| |
| ||
01/12/06 |
| ||
| |||
| Spice |
| ||
05/04/10 |
| ||
| |||
| Андрей123 |
| ||
01/12/06 |
| ||
| |||
| Spice |
| ||
05/04/10 |
| ||
| |||
| sumus17 |
| ||
11/09/10 |
| ||
| |||
| sumus17 |
| ||
11/09/10 |
| ||
| |||
| Spice |
| ||
05/04/10 |
| ||
| |||
| sumus17 |
| ||
11/09/10 |
| ||
| |||
| Spice |
| ||
05/04/10 |
| ||
| |||
| sumus17 |
| ||
11/09/10 |
| ||
| |||
| Spice |
| ||
05/04/10 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Момент Инерции Треугольника
Момент инерции треугольника может быть выражен различными способами. Обычно можно рассмотреть три момента. Они есть;
Обычно можно рассмотреть три момента. Они есть;
- Ось, проходящая через центр тяжести.
- Ось, проходящая через базу.
- Ось перпендикулярна его основанию.
Ниже мы рассмотрим каждое выражение.
1. Ось, проходящая через центр тяжести
Момент инерции треугольника, ось которого проходит через центр тяжести и параллельна его основанию, выражается как;
| I = bh 3 / 36 |
Здесь b = ширина основания и h = высота
2. Ось, проходящая через основание
Если взять ось, проходящую через основание, момент инерции треугольника определяется как;
| I = bh 3 / 12 |
Далее мы можем использовать теорему о параллельных осях, чтобы доказать выражение, в котором центр тяжести треугольника расположен или находится на расстоянии, равном h/3 от основания.
3. Ось, перпендикулярная его основанию
Когда мы хотим определить момент инерции треугольника, когда его ось перпендикулярна его основанию, мы должны сначала учесть, что ось y’-y’ используется для деления всего треугольника на два прямоугольных треугольника соответственно A и B. Однако , эти треугольники будут иметь общее основание, равное h, и высоты b 1 и b 2 . Момент инерции для обоих будет:
I у’ = чб 1 3 / 12 + ступица 2 3 / 12
Если мы рассмотрим b 2 = b – b 1 , где параллельная ось y-y, проходящая через центр тяжести, находится на расстоянии ⅔ ( b / 2 – b 1 ) от y’-y’, то мы можем легко найти или рассчитать момент инерции. Для этого мы можем использовать теорему о параллельных осях. В любом случае, после алгебраических подстановок получим выражение в виде:
| I у’ = (чб/36) (б 2 – б 1 б + б 1 2 ) |
Возьмем случай, когда нам нужно определить момент инерции относительно центроида y. Рассмотрим момент инерции y относительно оси x.
Рассмотрим момент инерции y относительно оси x.
Мы будем использовать теорему о параллельных осях и в этом случае возьмем центр тяжести в качестве точки отсчета.
Здесь,
I AA’ = I BB’ + Ad 2
я BB’ = IAA’ – Ad 2
= (1/12) шв 3 – 1/2 шв (1/3) в 2
= чч 3 / 36
Далее найдем момент инерции при прохождении оси через его основание.
Будем рассматривать дифференциальную полосу, параллельную оси x для da. Это дается как;
дл x = у 2 дА
дА = l dy
Если мы возьмем подобные треугольники, мы получим
(л/б) = (ч – у)/ч
л = b (ч – у )/ ч
dA = b [(h – y) / h]dy
Теперь проинтегрируем dl x от y = 0 до y = h.
I x = ∫ y 2 дА
I x = O ∫ h y 2 b (h – y)/h dy
I x = ч/ч O ∫ h (hy 2 – y 3 ) dy
I х = (б/ч)[ч (у 3 / 3)- (у 4 / 4) ] 0 ч
Следовательно, I х = чч 3 / 12
Теорема о параллельных осях
⇒ Проверить момент инерции другого объекта:
- Момент инерции эллипса
- Момент инерции конуса
- Момент инерции квадрата
- Момент инерции полуокружности
- Момент инерции сплошного конуса
Что такое момент инерции треугольника? Расчет, пример
В этой статье мы изучим момент инерции треугольника, а также примеры, расчеты и т. д. Давайте исследуем!
д. Давайте исследуем!
Что такое момент инерции треугольника? Определение
Попробуем разобраться в моменте инерции основ треугольника. Некоторые основы момента инерции треугольника изложены ниже.
- Момент инерции треугольника можно рассматривать и формулировать в трех основных аспектах. Во-первых, это прохождение оси через центр тяжести. Второй – прохождение линии через базу. Третьей является ось, перпендикулярная основанию.
- Момент инерции любой формы, в том числе треугольника относительно нецентроидальной и произвольной оси можно определить, если уже известен момент инерции центроидальной оси, параллельной первой. В этом случае мы используем теорему о параллельных осях.
Теорема о параллельных осях обычно используется для определения момента инерции составных сечений.
Как выразить момент инерции треугольника?
Выражение Момента инерции треугольника может быть задано различными способами в зависимости от положения оси. Момент инерции треугольника различен для разных положений оси. Есть квадратная мера иногда 3 момента, о которых можно подумать. Они есть;
Момент инерции треугольника различен для разных положений оси. Есть квадратная мера иногда 3 момента, о которых можно подумать. Они есть;
- Ось проходит через центр масс.
- Ось, проходящая через дно.
- Ось перпендикулярна его основанию.
Мы рассмотрим каждое выражение ниже, а позже мы вычислим и узнаем, как вычислить момент инерции треугольника.
Ось, проходящая через центр масс
Момент инерции треугольника, ось которого параллельна его основанию и проходит через центр масс, выражается как; я = чч 3 /36; Здесь
- b = ширина основания и
- ч = высота
Ось, проходящая через дно
Момент инерции треугольника определяется как; если мы имеем тенденцию брать ось, проходящую через дно: I = bh 3 / 12
Мы можем дополнительно использовать теорему о параллельной оси, чтобы доказать выражение везде, где центр масс треугольника находится или находится на расстоянии способный h/3 от дна.
Ось, перпендикулярная его основанию
Давайте попробуем увидеть момент инерции треугольника, когда его ось перпендикулярна его основанию, мы должны сначала учесть, что ось y’-y’ используется для разделения всего треугольника на два прямоугольных треугольника. , A и B. С другой стороны, эти треугольники могут иметь стандартное основание, способное принимать h, и высоты b1 и b2. Для каждого момент инерции может быть: Iy’ = hb1 3 / 12 + hb2 3 / 12
Если мы склонны думать о b 2 = b – b 1 везде, где параллельная ось y-y, проходящая через центр масс, находится на расстоянии ⅔ ( b/2 – b 1 ) от y’-y’, тогда мы можем просто реализовать или вычислить момент инерции.
В какой момент ось треугольника инерции перпендикулярна основаниюМы можем использовать теорему о параллельной оси, чтобы попытаться сделать. Таким образом, в любом случае после чисто математических подстановок мы имеем тенденцию получать выражение в виде:0024 2 )
Как рассчитать момент инерции треугольника?
Мы возьмем случай везде, где мы должны увидеть момент инерции относительно центра масс y. Будем учитывать момент инерции y относительно оси координат.
Будем учитывать момент инерции y относительно оси координат.
Мы можем использовать теорему о параллельных осях и что в этом случае мы возьмем центр масс в качестве точки отсчета. Здесь I AA’ = I BB’ + Ad 2
- I BB’ = I AA’ – Ad 2
- I BB’ = (1/12) шв 3 – 1/2 шв (1/3) в 2
- I BB’ = bh 3 / 36
Далее мы собираемся реализовать момент инерции, когда ось проходит через его основание.
- дл x = у 2 да
- дА = l dy
Если у нас есть склонность брать подобные треугольники, которые у нас будут,
- (л/б) = (ч – у)/ч
- л = b (ч – у)/ч
- dA = b [(h – y) / h]dy
Теперь мы собираемся интегрировать dl x от y = нуля до y = h.
- I x = ∫ y2 dy
- I x = 0 ∫ ч г 2 б (ч – у)/ ч
- I x = ч/ч 0 ∫ h (hy 2 – y 3 )
- I х = (б/ч)[ч (у 3 / 3)- (у 4 / 4) ] 0 ч
Следовательно, Ix = bh 3 / 12.
Момент инерции треугольника Решенная задача или расчет
Вопрос № 1 Расчет момента инерции равностороннего треугольника
Задача при образовании равностороннего треугольника 3 стержня массой m и длиной l соединены вместе. Определить момент инерции системы относительно оси, проходящей через ее центр масс и перпендикулярной плоскости треугольника.
Какой момент треугольника инерции решил задачу номер одинРешение: Момент инерции стержня BC определяется формулой: I 1 = m l 2 / 12
Из теоремы о параллельности осей момент инерции
- I 2 = I 1 + mr 2 = m l 2 / 12 + m ( 1/ 2 √ 904 = 1/ 2 √904 2 2 2 2 / 6
Так как треугольник состоит из трех стержней, то момент инерции всех трех стержней равен:
- Я = 3И 2
- I = 3 (м л 2 /6)
- I = м л 2 /2
Вопрос №2 Вычисление произведения инерции прямоугольного треугольника относительно двух случаев
Задача : Определить произведение инерции прямоугольного треугольника 1) относительно осей x и y 2) относительно центроидальных осей параллельно осям х и у.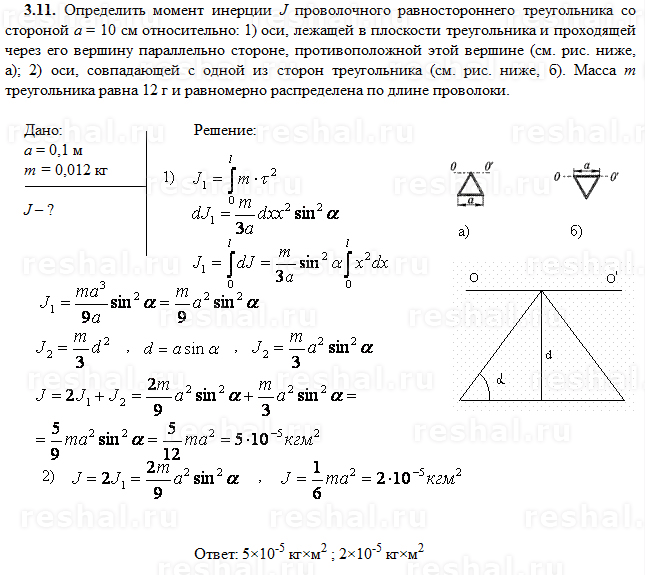
Случай-1
Случай-1: какой момент треугольника инерции решил задачу номер дваСлучай-2
Случай-2: какой момент треугольника инерции решил вторую задачуРешение: Случай-1: Нахождение произведения инерции путем прямого интегрирования с теоремой о параллельных осях на вертикальных дифференциальных полосах площадей.
Y= h(1- x/b) d A= ydx = h (1- x/b) dx
X’ el = x y’ el = ½ y= ½ h= (1- x/b)
Теперь, интегрируя d I x от x = 0 до x = b
I xy = ∫ d I xy = ∫ X’ EL Y ‘ EL D A = B 0 ∫ x (1/2) H 2 (1-x/B) 2 DX
= H 2 B
= H 2 B
I xy = 1/24 b 2 h 2
Случай 2.


 Насколько я понимаю эта задача сводится к нахождению момента инерции всех треугольников, составляющих это тело.
Насколько я понимаю эта задача сводится к нахождению момента инерции всех треугольников, составляющих это тело. 04.2010, 14:51
04.2010, 14:51  04.2010, 11:26
04.2010, 11:26  С нахождением параметрических уравнений для каждого из отрезков, ограничивающих фигуру тоже тоже.
С нахождением параметрических уравнений для каждого из отрезков, ограничивающих фигуру тоже тоже. Для моих целей так будет даже проще
Для моих целей так будет даже проще
 Подынтегральное выражение записывается следующим образом:
Подынтегральное выражение записывается следующим образом: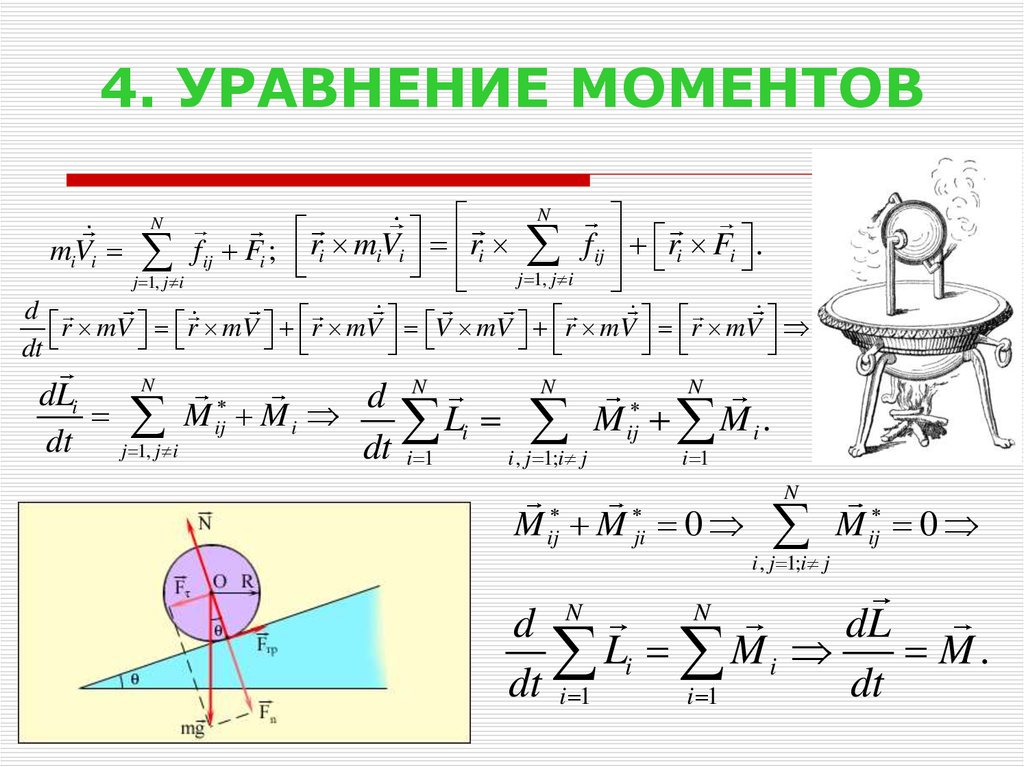
 Видимо где-то ошибка, но не пойму где. Поэтому хотел бы увидеть как другие люди решили бы данный пример.
Видимо где-то ошибка, но не пойму где. Поэтому хотел бы увидеть как другие люди решили бы данный пример. Там исходные интегралы по площади другие будут (как например здесь
Там исходные интегралы по площади другие будут (как например здесь
 Поэтому остается вопрос, о том почему производная берется то с плюсом, то минусом. Судя по рисунку Вы с минусом взяли для первого и третьего участка. Это связано с возрастанием или убыванием функции или как-то со знаками самого аргумента , можете объяснить правило?
Поэтому остается вопрос, о том почему производная берется то с плюсом, то минусом. Судя по рисунку Вы с минусом взяли для первого и третьего участка. Это связано с возрастанием или убыванием функции или как-то со знаками самого аргумента , можете объяснить правило? Как видно для 1-ой и 3-ей системы производная от Y дает -1. От сюда и знак минус)
Как видно для 1-ой и 3-ей системы производная от Y дает -1. От сюда и знак минус) Это уравнение вида:
Это уравнение вида: 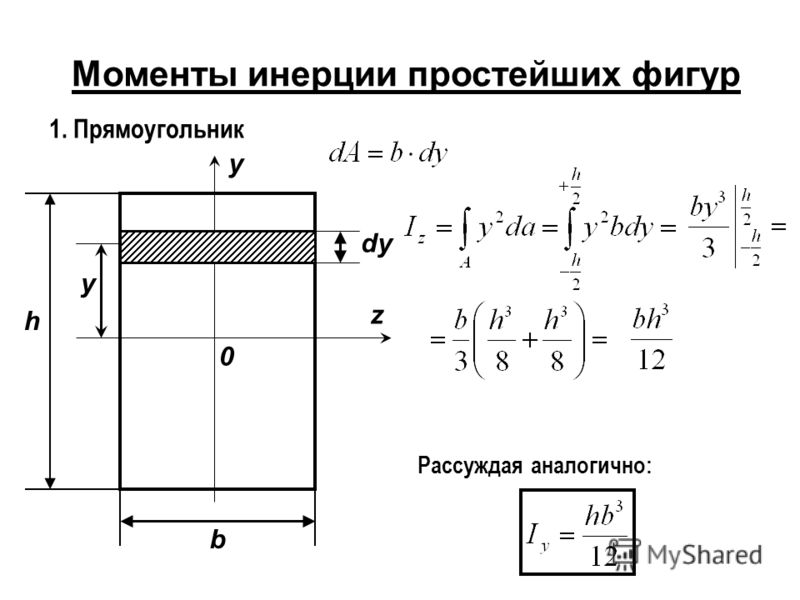 Если разберешься в них, все станет ясно.
Если разберешься в них, все станет ясно.