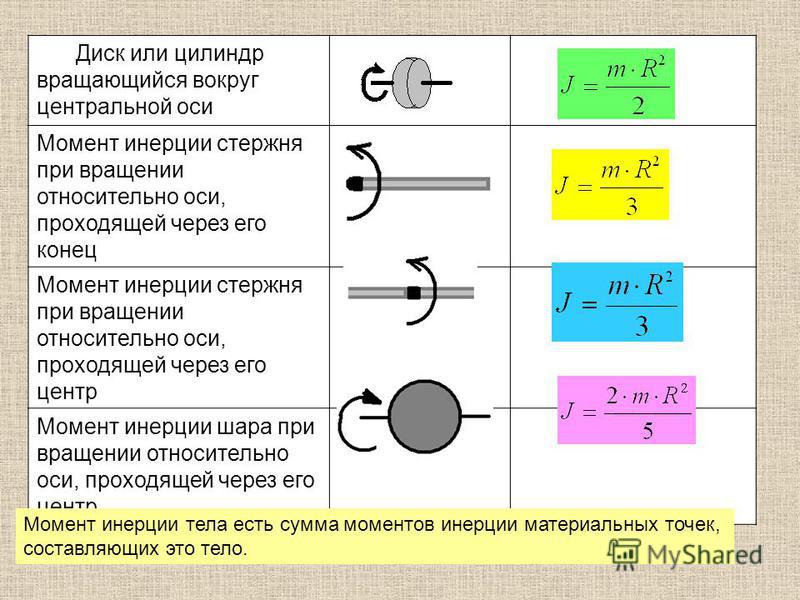
Расчёт моментов инерции некоторых тел
Момент инерции тела относительно оси и относительно точки. Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки до оси. Чтобы найти момент инерции тела (с непрерывным распределением вещества) относительно оси, надо мысленно разбить его на такие малые элементы, чтобы каждый из них можно было считать материальной точкой бесконечно малой массыdm = dV. Тогда момент инерции тела относительно оси равен интегралу по объёму тела:
(1)
Рис. 1
где r– расстояние элементаdmдо оси.
Вычисление момента инерции тела относительно оси часто упрощается, если предварительно вычислить его момент инерции относительно точки .Он вычисляется по формуле, аналогичной (1):
где r– расстояние элементаdmдо выбранной точки (относительно которой
вычисляется). Пусть эта точка является началом системы
координатX, Y, Z(рис. 1). Квадраты
расстояний элементаdmдо координатных осейX, Y, Z и до начала координат равны
соответственноy2+z2, z2+x2, x2+y2, x2+y2+z2
Пусть эта точка является началом системы
координатX, Y, Z(рис. 1). Квадраты
расстояний элементаdmдо координатных осейX, Y, Z и до начала координат равны
соответственноy2+z2, z2+x2, x2+y2, x2+y2+z2
Рис. 2
Из этих соотношений следует, что
(3)
Таким образом, сумма моментов инерции тела относительно
трёх любых взаимно перпендикулярных
осей , проходящих через одну точку,
равна удвоенному моменту инерции тела
относительно этой точки.
Момент инерции тонкого кольца.
Рис. 3
(4)
Момент инерции тонкого диска.Пусть тонкий однородный диск массыmс концентрическим отверстием (рис. 3) имеет внутренний и внешний радиусыR1иR2. Мысленно разобьём диск на тонкие кольца радиусаr, толщиныdr. Момент инерции такого кольца относительно осиY(рис. 3, она перпендикулярна рисунку и не показана), в соответствии с (4):
(5)
Момент инерции диска:
(6)
В частности, полагая в (6) R1 = 0, R2 = R,получим формулу для вычисления момента инерции тонкого сплошного однородного диска относительно его оси:
(7)
Момент инерции
диска относительно его оси симметрии
не зависит от толщины диска. Поэтому
по формулам (6) и (7) можно вычислять
моменты инерции соответствующих
цилиндров относительно их осей симметрии.
Поэтому
по формулам (6) и (7) можно вычислять
моменты инерции соответствующих
цилиндров относительно их осей симметрии.
Момент инерции тонкого диска относительно его центра также вычисляется по формуле (6), = Jy,а моменты инерции относительно осейXиZравны между собой,Jx = Jz. Поэтому, в соответствии с (3): 2Jx +Jy = 2Jy, Jx = Jy/2,или
(8)
Рис. 4
Момент инерции цилиндра.
 Найдём его момент инерции относительно
осиZ, проведенной
через центр масс перпендикулярно оси
цилиндра (рис. 4). Для этого мысленно
разобьём его на диски бесконечно малой
толщиныdy. Один из
таких дисков, массойdm = mdy/h,
расположенный на расстоянииyот начала координат, показан на рис. 4.
Его момент инерции относительно оси
Найдём его момент инерции относительно
осиZ, проведенной
через центр масс перпендикулярно оси
цилиндра (рис. 4). Для этого мысленно
разобьём его на диски бесконечно малой
толщиныdy. Один из
таких дисков, массойdm = mdy/h,
расположенный на расстоянииyот начала координат, показан на рис. 4.
Его момент инерции относительно оси(9)
Момент инерции всего цилиндра
(10)
Момент инерции цилиндра относительно оси Z(оси вращения маятника) найдём по теореме Гюйгенса – Штейнера
где d– расстояние от центра масс цилиндра до осиZ. В работе 16 этот момент инерции обозначен какJц
(11)
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Нанесение
экспериментальных точек и проведение
по ним графика «на глаз», а также
определение по графику абсцисс и ординат
точек, не отличаются высокой точностью.
Рис. 5
(1)
имела минимум. Здесь xi и yi значения величин х и у в i-том измерении, n количество измерений. Величина S будет минимальной, если её частные производные по параметрам а и b будут равны нулю:
(2)
Отсюда наилучшие значения параметров «а» и «b» равны:
(3)
где средние
значения
,.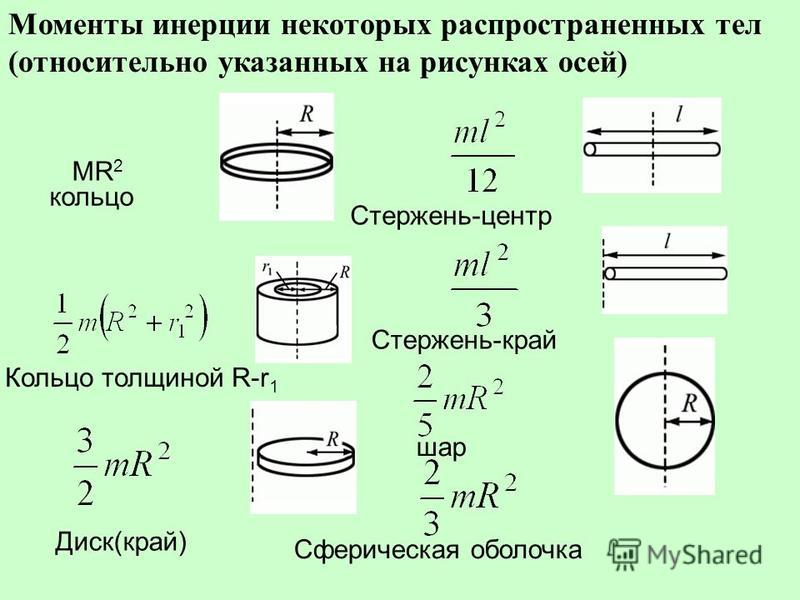
Введем обозначения
и (4)
Абсолютные случайные погрешности асл и bсл определяются по формулам:
и (5)
где tp,n-2 коэффициент Стьюдента для доверительной вероятности P и (n-2) измерений. При P = 0,95 и n 12-15 коэффициент tp,n-2 = 2,25
16
Момент — инерция — диск
Cтраница 2
Таким образом, момент инерции диска относительно диаметра в два раза меньше, чем относительно оси, перпендикулярной к плоскости диска и проходящей через ее центр.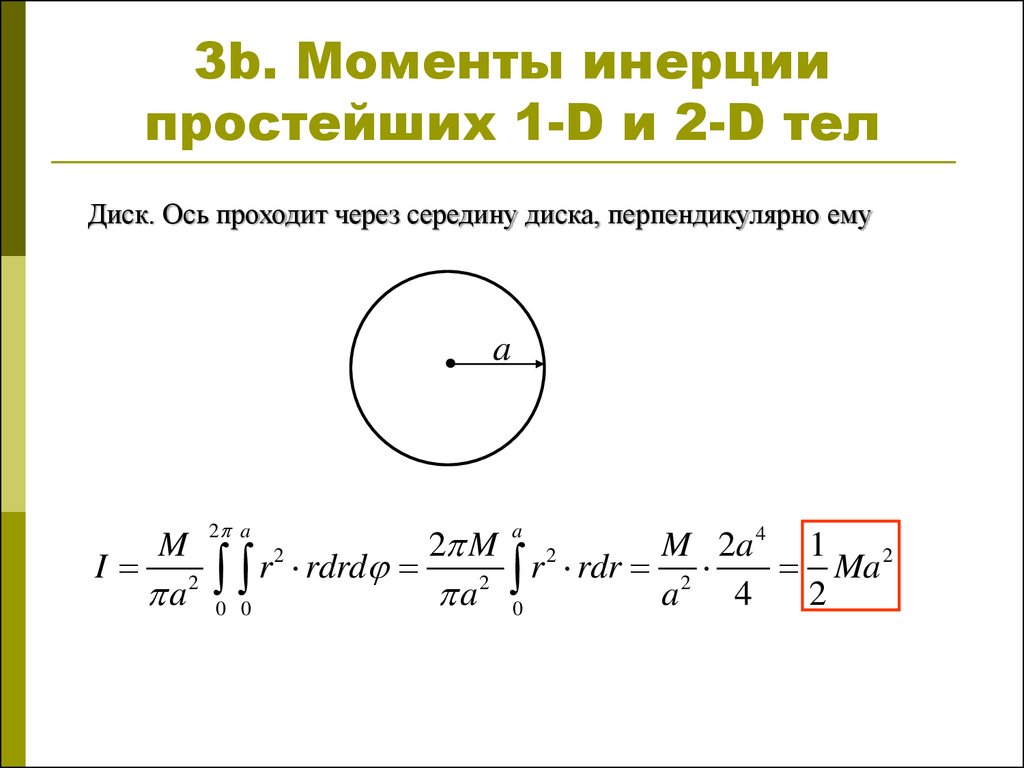 [16]
[16]
Считая, что момент инерции диска относительно оси вращения равен I, определить закон изменения его угловой скорости. [17]
Таким образом, момент инерции диска относительно указанной оси
J — радиус и момент инерции диска относительно оси вращения. Наибольшее распространение получили вискозиметры 1 — й группы. Большая часть этих приборов служит для относит, измерений; они градуируются по эталонным жидкостям ( гли-церинововодные растворы, растворы тростникового сахара, минеральные масла и их смеси и др.), вязкость к-рых определена абс. [19]
J — радиус и момент инерции диска относительно оси вращения. [20]
Выведите формулу для подсчета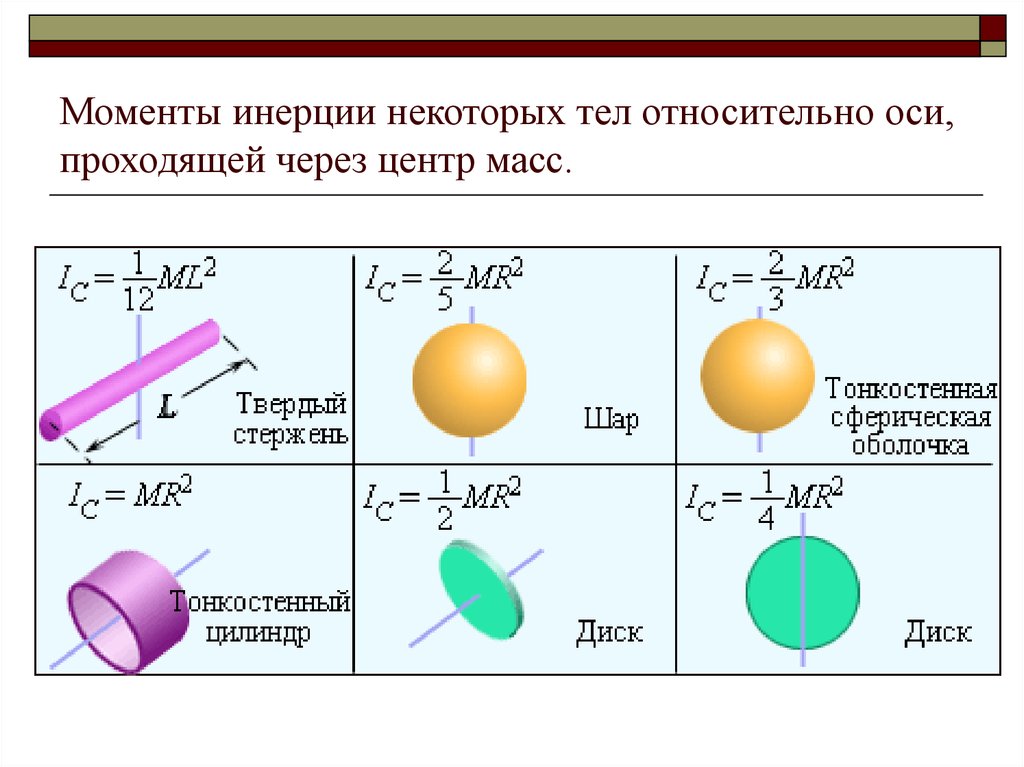 Как найти момент инерции диска относительно оси, проходящей через центр масс, но не перпендикулярной плоскости диска.
[21]
Как найти момент инерции диска относительно оси, проходящей через центр масс, но не перпендикулярной плоскости диска.
[21]
Момент инерции нагрузки равен моменту инерции диска диаметром 457 и толщиной 34 3 мм, а упругость соответствует упругости стального вала диаметром 76 2 и длиной 660 мм. [22]
По данным задачи 34.24 вычислить момент инерции диска относительно оси г, лежащей в вертикальной плоскости xz и образующей с осью z угол ср. [23]
К — полярный и экваториальный моменты инерции диска; х0, их — постоянные коэффициенты линейной и нелинейной части в выражениях для внешнего трения; Е — модуль упругости; / — экваториальный момент инерции площади сечения вала; I — длина вала; оа — угловая скорость ротора. [24]
Мы видим, что изменение момента инерции диска относительно его диаметра есть тоже конечная величина, пропорциональная пятой степени диаметра диска. [25]
[25]
По данным условия задачи 34.25 вычислить момент инерции диска относительно оси z, лежащей в вертикальной плоскости xz и образующей с осью z угол ср. [26]
В цельнокованых роторах это увеличе — альный моменты инерции диска; знак ние менее значительно. [27]
Энергия, поглощаемая гасителем, зависит от момента инерции дисков и момента тре-кпя между элементами гасителя. При малом моменте трения гаситель не будет поглощать достаточного количества энергии, а при моменте трения, превышающем инерционный момент дисков, энергия вообще не поглощается, так как диски ие перемещаются относительно втулки 7, закрепленной на переднем конце вала. При расчете гасителя сухого трения необходимо выбрать оптимальное соотношение между инерционным моментом дисков 4 и моментом трения. [28]
А и С — поперечный и осе вой моменты инерции диска, р, q, r — проекции мгновенной угло вой скорости диска на оси О г ], где ось Ох. [29]
[29]
Если моменты инерции зубчатых колес малы по сравнению с моментами инерции дисков и ими при расчете можно пренебречь, то новая динамически эквивалентная система представляет вал с двумя дисками ( фиг. [30]
Страницы: 1 2 3 4
[Решено] Найти момент инерции диска массой 1 кг и радиусом
- 6 кг м 2
- 3 кг м 2
- 8 кг м 4 90 м 90 3 90 90
Вариант 1: 6 кг·м 2
Бесплатно
Электрические заряды и закон Кулона (базовый)
82,1 тыс. пользователей
10 вопросов
10 баллов
10 минут
КОНЦЕПЦИЯ:
Момент инерции (I): Зависит от суммы масс каждой частицы и их расстояния от оси вращения
I = Σ MR 2
- тело зависит от
- Масса тела
- Размер и форма объекта
- Распределение массы вокруг оси вращения
- Положение и ориентация оси вращения относительно корпуса.
 Момент инерции также известен как вращательная инерция. 92}\)
Момент инерции также известен как вращательная инерция. 92}\) - Parallel axis theorem: The moment of inertia of a body about an axis parallel to the body passing through its center is equal to the sum of moment of инерция тела относительно оси, проходящей через центр и произведение массы тела умножить на квадрат расстояние между двумя осями .
I = I com + M x 2 , где I — полный момент инерции тела, I com — момент инерции относительно центра масс, M — масса, x — расстояние по перпендикуляру от оси, проходящей из центра масс.
Где I момент инерция тела, М 92}\) ⇒ 6 кг м 2
I = 6 кг м 2
Значит, вариант 1 правильный.
Поделиться в WhatsApp
Последние обновления NDA
Последнее обновление: 21 декабря 2022 г.
UPSC NDA (I) Срок подачи заявок продлен до 12 января 2023 г. до 18:00. Союзная комиссия по государственной службе (UPSC) выпустила Уведомление NDA I 2023 о 395 вакансиях. Процесс отбора на экзамен включает в себя письменный экзамен и собеседование SSB. Кандидаты, прошедшие успешный отбор в соответствии с UPSC NDA, получат заработную плату в диапазоне от рупий до от 15 600 до рупий. 39, 100. Ожидается, что будет выпущено новое уведомление для UPSC NDA.
Предлагаемые экзамены
Что такое момент инерции диска?
[smartslider3 slider=»2″]
Введение Слово инерция происходит от латинского слова iners, что означает праздный или медленный. Инерция, количественная характеристика физических систем, является одним из основных выражений массы.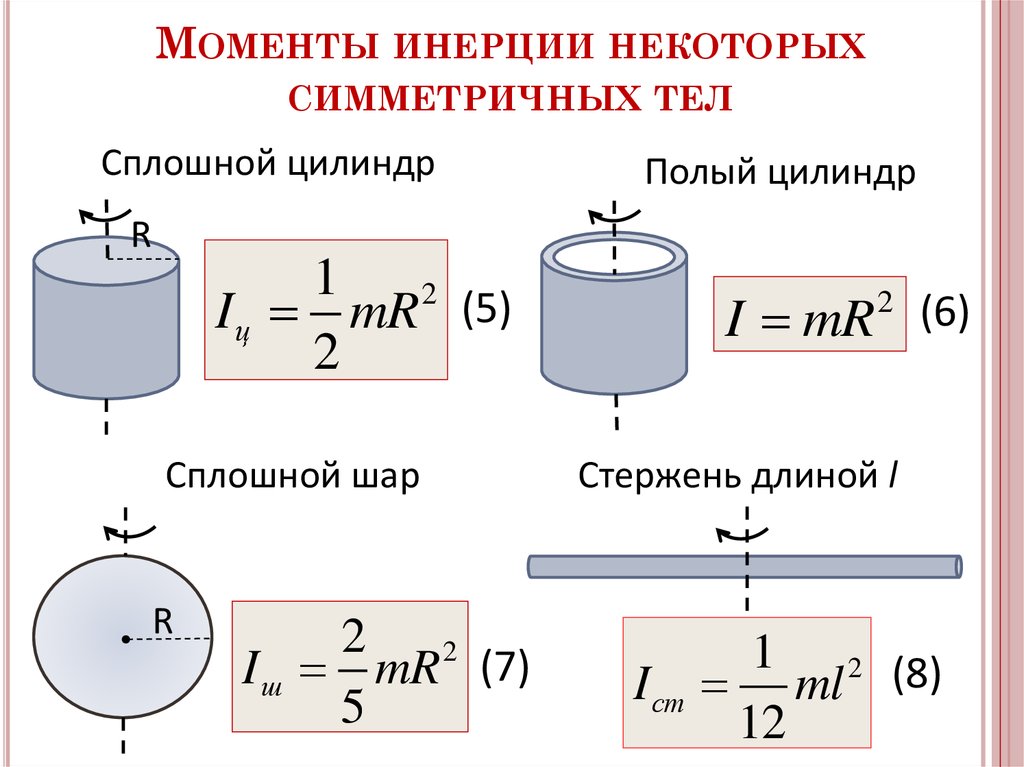 В своей «Philosophy Naturalis Principia Mathematica» Исаак Ньютон определяет инерцию как свой первый закон, который гласит: «Врожденная сила материи, или vis insita, есть сопротивляющаяся сила, с помощью которой каждый, насколько она покоится внутри него, стремится сохранить свою текущее состояние, независимо от того, движется ли оно равномерно или находится в состоянии покоя по прямой линии. Теперь давайте разберемся с понятием момента инерции диска.
В своей «Philosophy Naturalis Principia Mathematica» Исаак Ньютон определяет инерцию как свой первый закон, который гласит: «Врожденная сила материи, или vis insita, есть сопротивляющаяся сила, с помощью которой каждый, насколько она покоится внутри него, стремится сохранить свою текущее состояние, независимо от того, движется ли оно равномерно или находится в состоянии покоя по прямой линии. Теперь давайте разберемся с понятием момента инерции диска.
Зарегистрируйтесь, чтобы получить бесплатный пробный тест и учебные материалы
+91
Подтвердите OTP-код (обязательно)
Я согласен с условиями и политикой конфиденциальности.
Термин «момент инерции» относится к инерции системы. Момент инерции, также известный как момент инерции массы, представляет собой статистику, определяющую инерцию объекта как крутящий момент, необходимый для желаемого углового ускорения на вращающейся оси. Это сравнимо с тем, как масса определяет силу, необходимую для желаемого ускорения. Это зависит от выбранной оси и распределения массы тела с большими моментами, которым требуется больший крутящий момент, чтобы повлиять на скорость вращения.
Это зависит от выбранной оси и распределения массы тела с большими моментами, которым требуется больший крутящий момент, чтобы повлиять на скорость вращения.
Ниже приведены основные факторы, влияющие на момент инерции:
- На момент инерции влияет плотность вещества.
- Размер материала
Второй момент площади — другое его название. Он изображает точечную дисперсию вдоль случайной оси. Двумерная плоскость является его атрибутом.
Момент инерции массыМомент инерции массы, также известный как инерция вращения, представляет собой объем, который количественно определяет сопротивление объекта при изменении его углового момента. На момент инерции массы влияют следующие факторы:
- Ускорение под углом
- Кинестетическое накопление энергии — это разновидность кинестетического накопления энергии.

- Когда на тело действует скручивающая сила, момент инерции масс обратно пропорционален угловому ускорению.
- Внешний вид материала
Вращательный аналог массы — это момент инерции, который также обозначается буквой «i». Он измеряет степень, в которой сопротивление объекта отражает ускорение вращения вокруг заданной оси.
Размерность моментов инерции масс измеряется в ML2 (масса-длина3). Важно не перепутать второй момент площади с моментом, который используется в расчетах луча. Массовый момент инерции, также известный как вращательная инерция или угловая масса, является термином, используемым для описания вращательной инерции.
Часто задаваемые вопросыЧто такое коэффициенты момента инерции?
Момент инерции определяется массой тела, а также его формой или геометрией, которая определяется расстоянием от оси вращения.
Что такое момент инерции и как он работает?
Если величина инерции или сопротивления заряду в колесе с осью в центре довольно мала, это пример момента инерции.


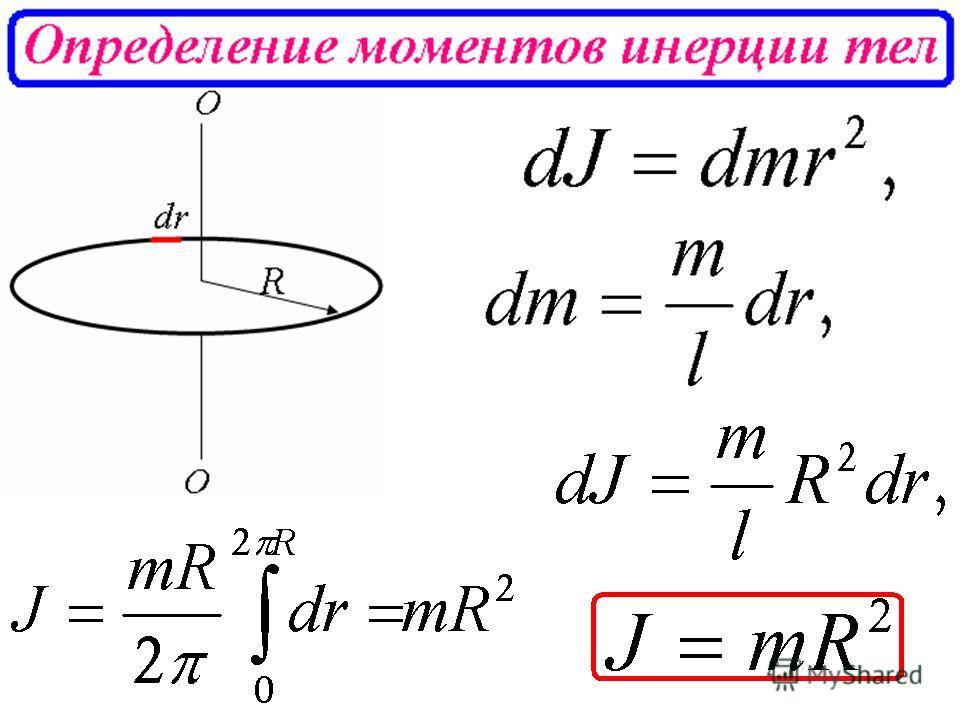 Момент инерции также известен как вращательная инерция. 92}\)
Момент инерции также известен как вращательная инерция. 92}\)