9. Момент инерции твердого тела
Из формулы (7.24) видно, что угловое ускорение, сообщаемое телу вращающим моментом, зависит от момента инерции тела; чем больше момент инерции, тем меньше угловое ускорение. Следовательно, момент инерции характеризует инерционные свойства тела при вращательном движении, как и масса при поступательном движении. В отличие от массы тела момент инерции зависит от радиуса окружности, описываемой точкой приложения силы, а, следовательно, от выбора оси вращения.
Из формулы следует, что единицей измерения момента инерции является кг.мІ.
Из определения момента инерции
(7.25)
видно, что момент инерции есть величина аддитивная. Это означает, что момент инерции тела равен сумме моментов инерции его частей:
(7.26)
Момент
инерции существует безотносительно к
вращению. Каждое тело независимо от
того, вращается оно или покоится, обладает
определенным моментом инерции относительно
любой оси.
Для неоднородных тел и тел неправильной формы момент инерции определяют экспериментально, а для однородных тел геометрически правильной формы – посредством интегрирования.
Как было ранее указано, в силу формулы (7.3) элементарная масса равна произведению плотности тела в данной точке на соответствующий элементарный объем: .
Следовательно, момент инерции можно представить в виде: .
Если плотность тела постоянна, её можно вынести за знак суммы задача нахождения моментов инерции сводится к интегрированию:
(7.27)
Интегралы в (7.27) берутся по всему объему тела. Величины и r в этих интегралах являются функциями точки.
В качестве примера вычислим момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рис. 7.10).
Рис. 7.10.
Разобьем
диск на кольцевые слои толщиной
.
Все точки одного слоя будут находиться
на одинаковом расстоянии от оси, равном
.
Объем такого слоя равен
,
где – толщина диска. Поскольку диск однороден,
плотность его во всех точках одинакова,
(7.27) можем вынести за знак интеграла:
,
где
–
радиус диска.
Так как масса диска , то получим
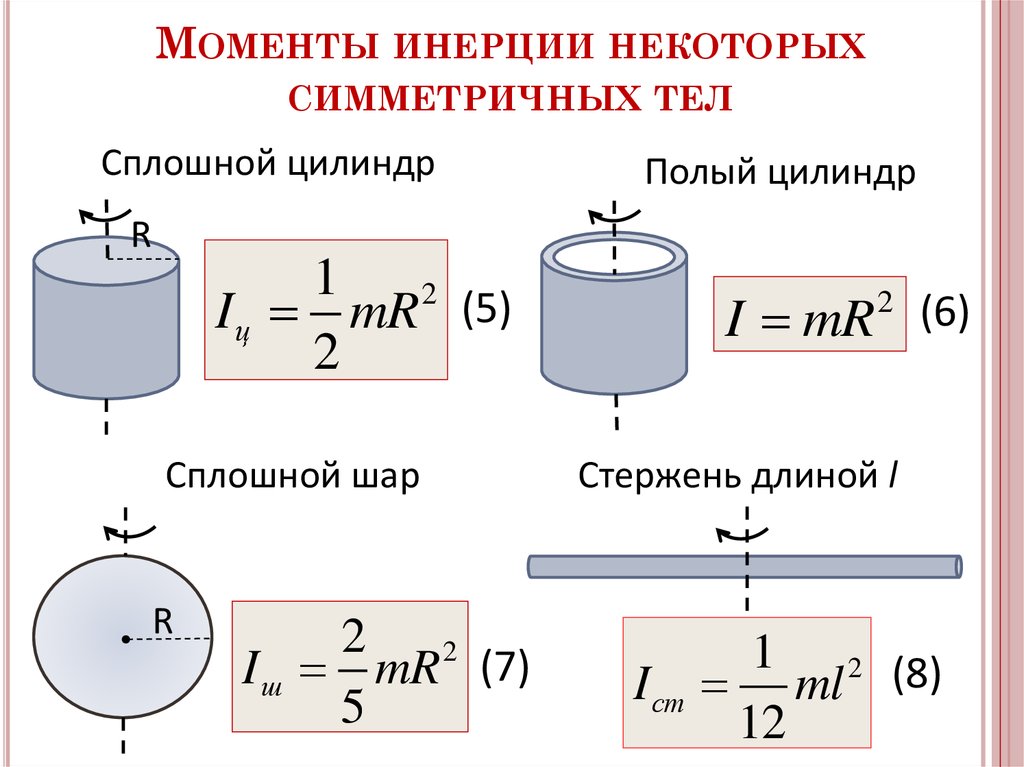
Для однородных и симметричных тел обычно основной осью вращения является ось симметрии. В этом случае момент инерции, как мы видели, легко вычисляется.
Для некоторых тел правильной формы значение моментов инерции относительно осей, проходящих через центр их симметрии приведены в таблице 2.
Таблица 2
Форма тела | Расположение оси | Величина момента инерции |
Обруч | ||
Цилиндр | ||
Шар | ||
Примечание: m – масса тела, R0 – его радиус | ||
Рассмотрим
произвольное тело и две параллельные
друг другу оси, одна из которых (ось С)
проходит через центр масс тела, а другая
(ось О) отстоит от первой на расстояние а (рис.
Рис. 7.11
Момент инерции относительно оси О определяется выражением
Разобьем это выражение на три суммы:
Первая сумма представляет собой момент инерции относительно оси, проходящей через центр масс. Сумма дает массу тела . Наконец, , где – координата центра масс, которая при сделанном выборе начала координат равна нулю. Таким образом, мы приходим к соотношению:
(7.29)
Это соотношение выражает теорему Штейнера, которая гласит, что момент инерции
В
соответствии с теоремой Штейнера момент
инерции диска относительно оси ОґОґ,
отстоящей на расстоянии от
оси, проходящей через центр масс, равен
найденному нами моменту инерции (7.
28) относительно
оси, проходящей через центр диска, плюс : .
Определение момента инерции твердого тела методом крутильных колебаний
Лабораторная работа 7
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА
МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Цель работы: определить момента инерции твердого тела методом крутильных колебаний.
Оборудование: лабораторная установка — крутильный маятник.
1. ОБЩИЕ СВЕДЕНИЯ
Вращательным движением твердого тела называется такое движение, при котором все точки тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения
В твёрдом теле все точки жестко связаны между собой и могут вращаться вокруг неподвижной оси под действием момента внешней силы. При этом вектор момента силы М и вектор углового ускорения ε всегда направлены в одну сторону и справедлив основной закон динамики вращательного движения
M = I ε
где I — момент инерции твердого тела относительно неподвижной
оси вращения, кг· м2.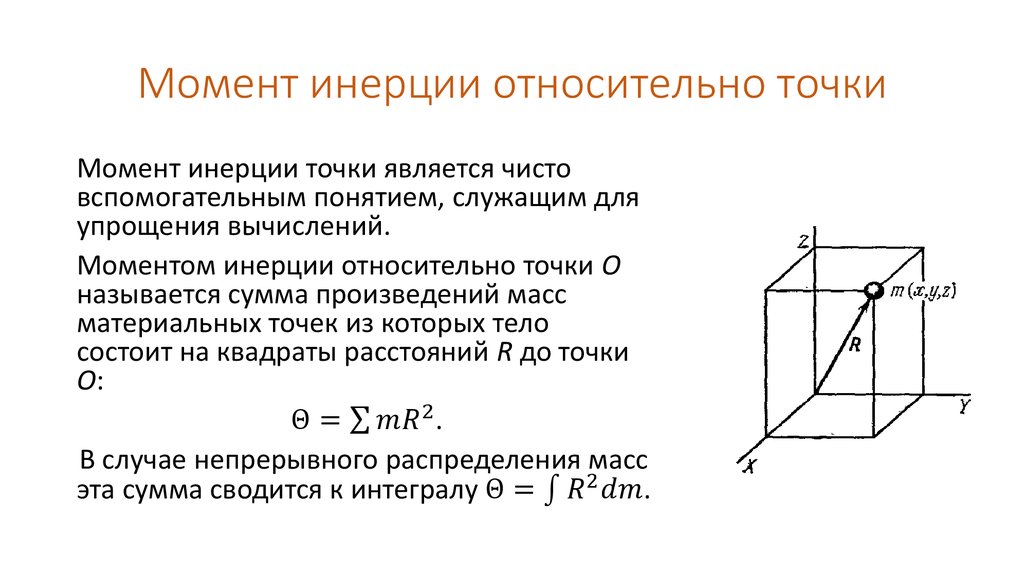
Момент инерции I характеризует инертные свойства твердого тела при вращательном движении и зависит от распределения массы тела относительно оси вращения.
Рассмотрим твёрдое тело и выделим в нём материальную точку массой mi. Её удаление от оси вращения обозначим через r
vi = ωiri, где ωi — угловая скорость вращения, рад/с.
Момент импульса относительно оси вращения равен
Li = miViri = miriωi.
Величина равная Ii = miri2 называется
моментом инерции материальной точки.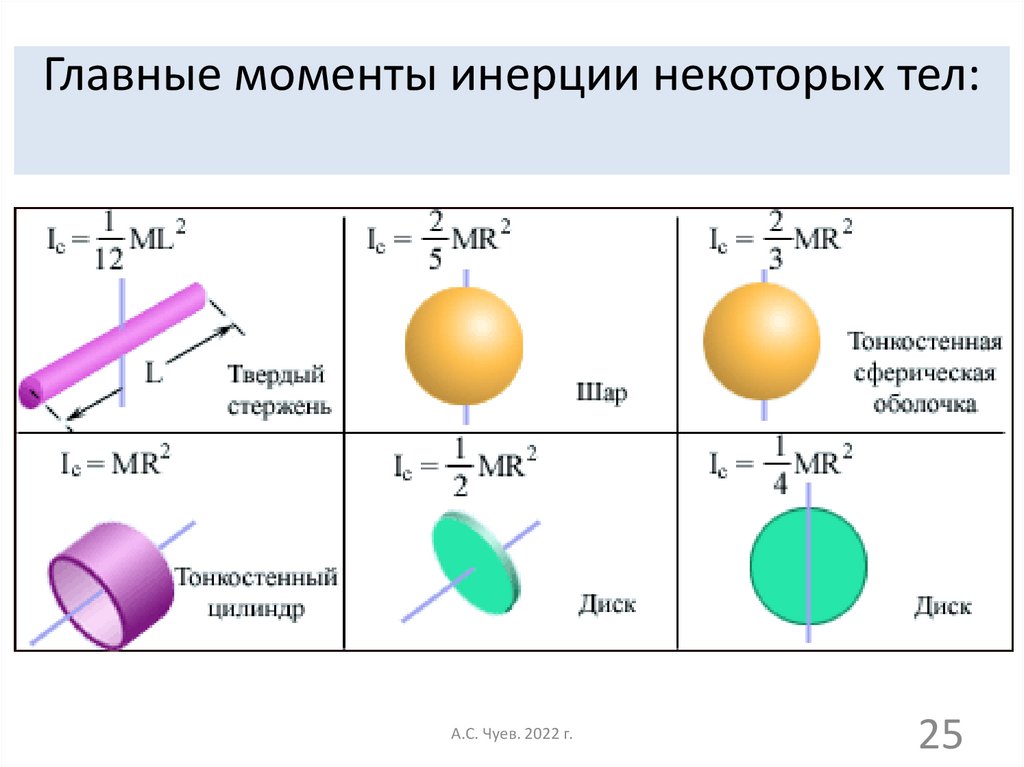
Для твёрдого тела моменты импульсов складываются по всем материальным точкам, образующим это тело. Тогда суммарный момент импульса равен
или
L = Iω.
Здесь
и есть момент инерции твердого тела относительно оси вращения.
Суммирование производится по всем материальным точкам, входящих в твердое тело.
Практически вычисление такой суммы сводится к вычислению соответствующего интеграла, что для однородных тел симметричной формы труда не составляет, то есть
где ρ — плотность, кг/м3, V — объем, занимаемый телом, м3.
Интегрирование производится по всему объёму тела.
Для любого твёрдого тела можно указать три взаимно
перпендикулярные оси, проходящие через его центр инерции. Эти оси называются
главными осями тела. А момент инерции относительно любой оси вращения
выражается через моменты инерции тела относительно этих главных осей.
Главные оси просто определить для однородных симметричных тел (шара, куба, параллелепипеда и т.д.). Главные оси инерции таких тел всегда совпадают с осями симметрии тела.
Например, главные оси однородного прямоугольного параллелепипеда проходят через его геометрический центр перпендикулярно граням (рис. 2).
Для тел сложной формы главные оси и моменты инерции определяют экспериментально.
Если известны главные оси твердого тела, то с ними связывают прямоугольную систему координат О, X, У, Z. Начало координат находится в центре инерции твердого тела.
Возьмём произвольную ось вращения, проходящую через центр инерции, ось ОС (рис. 3).
Момент инерции тела относительно оси ОС выражается через моменты инерции главных осей, то есть
где Ix, Iy, Iz — моменты инерции тела относительно осей ОХ, OY, OZ; α, β, γ —
углы между осью вращения и осями прямоугольной системы координат.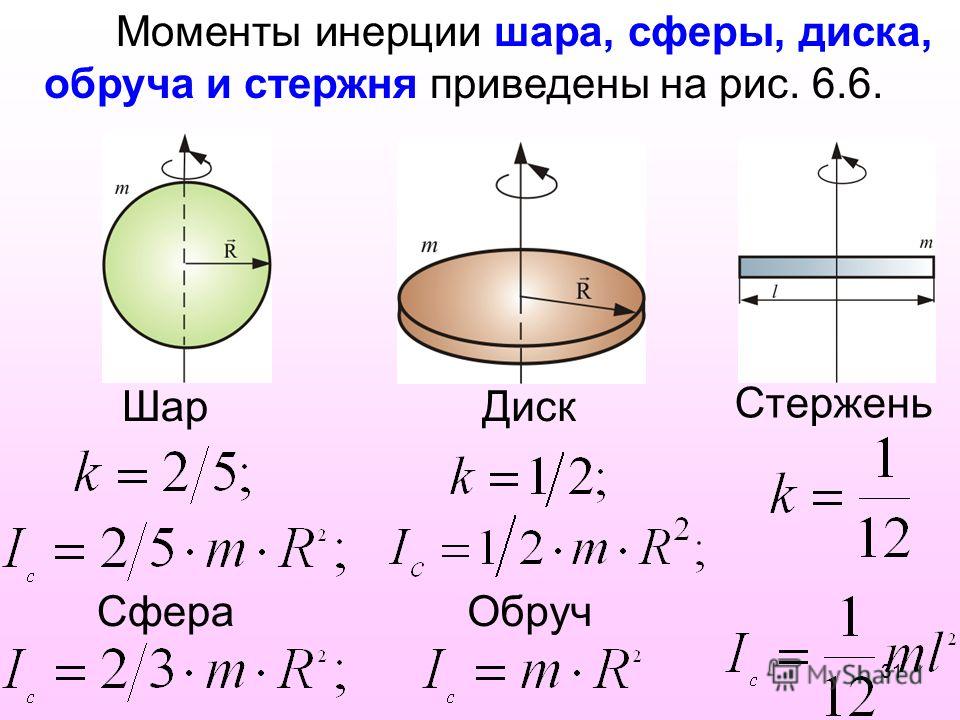
Моменты инерции Ix, Iy, Iz определяются экспериментально. Момент инерции тела относительно произвольной оси вращения находится простым суммированием по формуле (1).
Момент инерции тела зависит от выбора оси вращения. Однако это не значит, что для всякой новой оси момент инерции следует вычислять заново.
Если известен момент инерции тела относительно оси, проходящей через центр инерции, то момент инерции тела относительно любой оси, параллельной первой и смещенной на расстояние d, находится по теореме Штейнера (рис. 4):
где I0 — момент инерции относительно оси вращения, проходящей через центр инерции, кг · м3; m — масса тела, кг; d — расстояние между осями, м.
Используемый в лабораторной работе крутильный маятник позволяет определить момент инерции тел любой формы.
Такой маятник представляет собою рамку, подношенную на
тонкой упругой струне.
При повороте рамки из положения равновесия на некоторый
угол Θ, со стороны нити на нее действует упругий момент равный
Mупр = —D Θ, где Θ — угол поворота рамки, рад; D — коэффициент, характеризующий момент упругих сил, Н · м.
При достаточно тонкой и длинной струне зависимость М(Θ) выполняется и для больших углов поворота, а затухания при крутильных колебаниях можно считать малыми.
Пренебрегай затуханиями, движение рамки записывают уравнением для свободных незатухающих колебаний
или
(2)
где — угловое ускорение, рад · с2, вторая производная по времени от угла попорота; ω0 — циклическая частота колебаний, рад/с. Циклическая частота колебаний выражается как
Период таких колебаний равен
(3)
Решение дифференциального уравнения (2) имеет вид
где Θ0 — угловая амплитуда колебаний, рад; α — начальная фаза
колебаний, рад.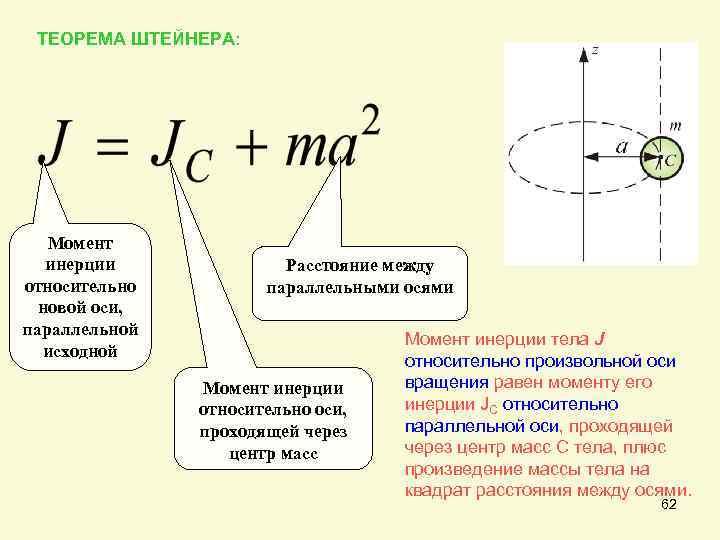
Если известен момент инерции I, то найти период колебаний рамки не составляет труда, а следовательно, и найти постоянную D. И наоборот, зная постоянную D, используя формулу (3) можно рассчитать момент инерции тела.
В данной лабораторной работе постоянная D не определяется. Для нахождения момента инерции рамки используется тело с известным моментом инерции. В качестве такого тела взят куб с достаточно идеальными поверхностями и гранями. Его момент инерции относительно оси, походящей через центр, вычисляется по формуле
(4)
где m — масса куба, кг, а — сторона куба, м.
Такой куб жестко закрепляется в рамке крутильного маятника. Если вывести нагруженную рамку из положения равновесия, то она будет совершать крутильные колебания, а её период колебаний равен
[Решено] От какого из следующих свойств зависит момент инерции тела
От какого из следующих свойств зависит момент инерции тела?
1.
Угловая скорость
2. Положение оси вращения
3. Распределение массы
- 1 и 2
- 1 и 3
- 2 и 3
- 1, 2 и 3
Вариант 3 и 3
Вариант 3 и 3 : 2 и 3
Бесплатно
Главный констебль CRPF Министерский 22 февраля 2023 г. (смена 1) Тест на основе памяти
1,3 миллиона пользователей
100 вопросов
100 баллов
90 минут
ПОНЯТИЕ :
- Момент инерции: Величина, выражающая тенденцию тела сопротивляться угловому ускорению, называется моментом инерции.
- Для точечной массы. Момент инерции – это просто произведение массы на квадрат перпендикулярного расстояния до оси вращения.
I = m × r2
где I – момент инерции, m – масса точки, r – расстояние по перпендикуляру от оси вращения.
9{2}\)
где I — момент инерции, m — масса точки, r — расстояние по перпендикуляру от оси вращения.
ОБЪЯСНЕНИЕ :
- Если масса расположена близко к оси, то момент инерции будет мал, потому что расстояние частиц массы от оси вращения будет мало.
- Если масса расположена на большом расстоянии от оси, момент инерции будет большим, потому что расстояние частиц массы от оси вращения будет большим.
- Итак, момент Инерции зависит от положения оси вращения, а также от распределения масс.
- Момент инерции — это физическое свойство распределения массы конфигурации и оси вращения.
- Но угловая скорость не играет роли для нахождения момента инерции. (см. также формулу)
- Итак, зависит от 2. Положения оси вращения 3. Распределения массы, но не зависит от 1. Угловой скорости .
- Следовательно, правильный ответ – вариант 3 (т.е. 2 и 3)
Поделиться в WhatsApp
Последние обновления Airforce Group X
Последнее обновление: 11 ноября 2022 г.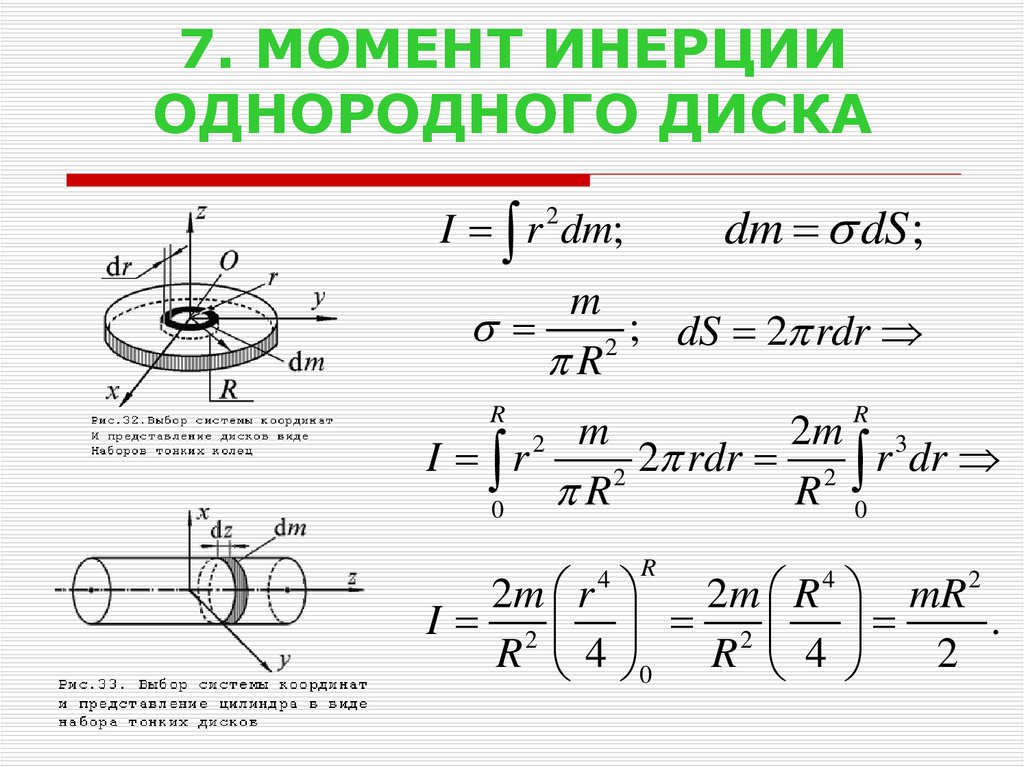
Выдача пропускной карты Airforce Group X Phase 2. 7 ноября 2022 года ВВС Индии (IAF) выпустили официальное уведомление о группе X IAF (01/2023). Отбор кандидатов будет зависеть от трех этапов: фаза 1 (письменный онлайн-тест), фаза 2 ( DV, тест на физическую подготовку, тест на адаптацию I и II) и этап 3 (медицинское обследование). Письменный экзамен проводился с 18 по 24 января 2023 года. Кандидаты, прошедшие все этапы процесса отбора, будут отобраны на должности группы X ВВС и получат зарплату в размере рупий. 30 000. Это одна из самых востребованных вакансий. Кандидаты могут проверить соответствие требованиям Airforce Group X здесь.
Импульс и момент инерции: понимание «желчи» | Машиностроение и инженерия
07.02.2020 15:50:21 Вероника Холлоуэй
гимнастки Университета Иллинойса. Фото Иллинойского университета. Когда я был ребенком, мой отец был школьным тренером по гимнастике. Его любовь к спорту привела к тому, что меня записали в лагерь в районе парка, чтобы познакомить меня с ним, и именно тогда я узнал, что очень боюсь высоты.
Возможно, мое непосредственное отвращение к тому, что я не стою на земле, разрушило мой гимнастический потенциал (прости, папа!), но это только добавило мне признательности тем, кто хорош в этом! Олимпийские игры в Токио не за горами, давайте поговорим об абсолютной КОЗЕ — Симоне Байлз.
Симона Байлз, родилась 14 марта 1997 года, рост 4 фута 8 дюймов. Уроженка Колумбуса, штат Огайо, за последние полвека стала нарицательной как самая титулованная гимнастка США всех времен, завоевавшая 30 олимпийских медалей и медалей чемпионатов мира. Только в цифрах Симона считается легендарной спортсменкой, но она также оставляет свой след в гимнастике, выполняя невероятно сложные упражнения. Я говорю о The Biles, наиболее известном из которых можно было увидеть на чемпионате мира 2013 года. На видео ниже умение можно посмотреть на 0:28.
«Жечь» — это прием, выполняемый во время упражнения на полу.
Это делается во время акробатического прохода и требует, чтобы гимнастка сделала два сальто в исходном положении (без подведения и сгибания коленей) с поворотом на 180 градусов в конце второго сальто. Из-за поворота на 180 градусов приземление становится еще сложнее. Симона создала этот прием, и очень немногие другие гимнастки в мире могут успешно его выполнять из-за механики этого движения! Чтобы понять, почему это так, мы должны исследовать два основных понятия: момент инерции и сохранение импульса.
Момент инерции в основном является вращательным эквивалентом массы. Под этим я подразумеваю, что точно так же, как масса определяет, какая сила требуется для ускорения объекта на определенную величину, момент инерции определяет, какой крутящий момент требуется для достижения определенного углового ускорения. Момент инерции полностью зависит от того, насколько далеко масса находится от оси вращения объекта. Чем дальше масса, тем выше момент инерции, а чем выше момент инерции, тем больший крутящий момент требуется для ускорения.
На видео ниже показан обычный урок физики, используемый для демонстрации этой концепции.
Импульс — это вектор, состоящий из массы, умноженной на скорость, и основная идея заключается в том, что в замкнутой системе общее изменение этого значения всегда равно нулю. Существует два основных типа импульса — линейный и вращательный, причем вращательный импульс представляет собой момент инерции объекта, умноженный на его угловую скорость. В системе, к которой не приложены внешние силы, сумма линейного и вращательного количества движения имеет постоянное значение до тех пор, пока не будет приложена сила для ее изменения.
Объединив эти понятия, вы сможете понять сложность с точки зрения физики «желчи». Помните, что движение представляет собой два переворота в положении раскладывания, и с точки зрения нашей новой механики это означает две вещи: из-за момента инерции мы знаем, что в положении раскладывания гораздо труднее достичь требуемого углового ускорения, чем в подвернутом положении и из-за сохранения импульса мы знаем, что все, что делает Симона после отрыва от земли, связано с начальным импульсом, с которым она взлетает.
Таким образом, ей нужно не только создать достаточный импульс, чтобы выдержать поступательное движение из исходного положения по воздуху туда, где она приземлится, но и создать достаточный импульс для одновременного переворота и скручивания.
Если я недостаточно ценил ее талант спортсмена-подражателя, то я ценю его как инженера-механика! Как Симоне удалось это сделать? Начнем с того, что ее невероятная сила и идеальное время позволяют ей создавать сумасшедший импульс от разбега до акробатического паса. Еще один очень важный фактор — ее рост. Момент инерции зависит от расстояния массы от оси вращения, а Симона короткая. Итак, поскольку ее масса не так далеко от оси вращения, как у других гимнасток, у нее есть физическое преимущество, когда дело доходит до выполнения этого навыка.
Помимо необходимой силы и низкого момента инерции, Симона также должна обладать невероятным пространственным восприятием. Во всех гимнастических навыках это в значительной степени зависит от времени, от небольших изменений момента инерции для создания углового ускорения и от контроля перенаправления импульса.
